基于MATLAB的AHP(层次分析法)的

2017年第8期(总第457期)金融理论与实践李韫繁（开封大学，河南开封475004）摘要：在我国当前金融业不断发展的社会背景下，对于农产品生产、加工企业而言，其面临的最大困难就是融资。

而农产品物流金融的开展，不仅能够破解企业融资难的困境，而且可以有效化解企业的金融风险。

在对相关学者关于农产品金融研究的理论进行综述的基础上，结合企业农产品物流金融模式中的产品价值属性，构建了一种农产品物流金融风险评估模型，以此引入AHP 层次分析法，对企业农产品物流金融风险进行定性分析、定量评估，以期找到农产品物流金融模式运作过程中存在的主要风险因子，帮助农产品企业化解金融风险。

关键词：AHP ；农产品；物流金融；风险评估文章编号：1003-4625（2017）08-0105-04中图分类号：F832.44文献标识码：A 基于层次分析法（AHP ）的农产品物流金融风险评估在电子商务及互联网金融不断发展的时代背景下，我国农产品金融模式应运而生。

作为物流业中的一大分支，其在推动我国农村金融和物流业快速发展中起着重要作用。

当前，我国农村物流金融业的发展依然受国家政策和金融机构、农业产业化经营模式等因素影响，所以，在农产品物流金融交易和实施中存在诸多风险。

故寻找破解农产品金融物流风险的应时之策，不能仅从农产品企业角度入手，而是要从农产品企业和银行及物流企业三方复杂的责、权、利方面着手，通过风险源识别、风险因素分析、评估，最终采用合理的对策控制和处理风险。

一、农产品物流金融风险研究的理论基础（一）农产品金融概念界定农产品物流金融相对物流金融而言是一种新型的概念，其主要是指在农产品物流业运作流程，通过对各种新型金融产品进行开发与应用，以此对农产品物流领域的有关资金货币活动进行有效调节的一种金融模式。

这一货币资金活动主要包括农产品在整个物流交易、经营中产生的存贷款、投资、抵押、租赁、保险、有价证券交易、贴现、信托以及农产品企业在金融机构中间业务办理中所产生的一切事宜等。

function [w,CR]=mycom(A,m,RI)[x,lumda]=eig(A);r=abs(sum(lumda));n=find(r==max(r));max_lumda_A=lumda(n,n);max_x_A=x(:,n);w=A/sum(A);CR=(max_lumda_A-m)/(m-1)/RI;end本matlab程序用于层次分析法中计算判断矩阵给出的权值已经进行一致性检验。

其中A为判断矩阵，不同的标度和评定A将不同。

m为A的维数RI为判断矩阵的平均随机一致性指标：根据m的不同值不同。

当CR<0.1时符合一致性检验，判断矩阵构造合理。

下面是层次分析法的简介，以及判断矩阵构造方法。

一.层次分析法的含义层次分析法（The analytic hierarchy process）简称AHP，在20世纪70年代中期由美国运筹学家托马斯·塞蒂（T.L.Saaty）正式提出。

它是一种定性和定量相结合的、系统化、层次化的分析方法。

由于它在处理复杂的决策问题上的实用性和有效性，很快在世界范围得到重视。

它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。

二.层次分析法的基本思路与人对一个复杂的决策问题的思维、判断过程大体上是一样的。

（1）层次分析法的原理层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构，然后得用求解判断矩阵特征向量的办法，求得每一层次的各元素对上一层次某元素的优先权重，最后再加权和的方法递阶归并各备择方案对总目标的最终权重，此最终权重最大者即为最优方案。

这里所谓“优先权重”是一种相对的量度，它表明各备择方案在某一特点的评价准则或子目标，标下优越程度的相对量度，以及各子目标对上一层目标而言重要程度的相对量度。

层次分析法比较适合于具有分层交错评价指标的目标系统，而且目标值又难于定量描述的决策问题。

层次分析法(AHP)在虚拟企业合作伙伴选择中的应用
郭瑞军;王晚香;朱国宝
【期刊名称】《机械制造》
【年(卷),期】2003(041)008
【摘要】介绍虚拟企业的基本概念和层次分析法的基本原理,给出如何利用 AHP 对组建虚拟企业的候选伙伴进行优选的方法.并用 Matlab做出软件模型,结合某供应商的选择过程,给出应用实例.
【总页数】3页(P53-55)
【作者】郭瑞军;王晚香;朱国宝
【作者单位】武汉理工大学,430063;武汉理工大学,430063;武汉理工大学,430063【正文语种】中文
【中图分类】F270.7
【相关文献】
1.粗糙集理论在虚拟企业合作伙伴选择中的应用 [J], 章帆;马卫
2.层次分析法(AHP)在虚拟企业合作伙伴选择中的应用 [J], 郭瑞军;王晚香;朱国宝
3.含AHP约束锥DEA模型在虚拟企业合作伙伴选择中的应用 [J], 郑政平;周燕飞
4.基于三角模糊数比较大小原理的模糊层次分析法在供应商合作伙伴选择中的应用[J], 刘礼金;范如国
5.虚拟企业合作伙伴选择方法在煤炭行业中的应用 [J], 黄敏;邵良杉
因版权原因，仅展示原文概要，查看原文内容请购买。

使用Matlab程序实现层次分析法（AHP）的简捷算法作者：于晶来源：《科技风》2016年第16期摘要：层次分析法简便易懂，可操作性和实用性强，但是构造判断矩阵往往不容易，计算判断矩阵的特征值特别繁琐且易出错，得到的一致性检验不易调整，这些都给使用层次分析法带来困难，以往使用办公软件电子表格（Excel）的方法计算单层次排序和总层次排序，这种方法使得计算和一致性检验变得容易，文本使用Matlab程序使得计算变得更容易，也使得层次分析法在多个领域得到推广和应用。

关键词：层次分析法；Excel；matlab1 层次分析法（AHP法）的原理和解决思路层次分析法是对定性问题进行定量分析的一种简便、灵活而又实用的多准则决策方法。

它的原理是模拟人的决策过程，具有思路清晰、方法简便、适用面广、系统性强等特点。

是解决多目标、多准则、多层次复杂问题决策或者大型工程风险分析的有力工具。

层次分析法解决问题的思路就是用下一次因素的相对排序求得上一次因素的相对排序。

按照因素之间的相互影响和隶属关系将各层次因素聚类组合，形成一个递进有序的层次结构模型。

2 层次分析法的应用难点2.1合适的判断矩阵构造不易模型确定后，按照模型层次结构和模型的各因素的相对重要性，综合专家群体咨询意见，采用标度法[ 1 ]，从数字1/9一9中选取恰当值，构造各层的判断矩阵，并使之尽量符合一致性检验，这一步成为问题的关键。

但实际上系统越复杂，判定矩阵的阶数就会越高，计算就会越困难。

2.2计算量大，步骤繁琐层次分析法首先要求的就是判断矩阵的最大特征值？姿max，及其正规化的特征向量w，向量w的分量wi是相应因素的单层次权值，这部分计算理论上基于线性代数知识，不用计算机也可以将其计算出来。

但实际上，当矩阵的阶数高于4阶时，人工计算就变得相当困难且易出错，如使用计算机计算，就容易得多，常用的方法有Basic语言，电子表格Excel等方法。

但计算量都有待改进。

基于MATLAB的AHP实现层次分析法（Analytic Hierarchy Process，AHP）是一种用于多准则决策问题的定量分析方法，它被广泛应用于各个领域，例如工程、管理、经济等。

基于MATLAB的AHP实现可以帮助决策者更好地进行权重分配和决策。

在MATLAB中，可以通过以下步骤实现AHP：1.构建层次结构：首先，需要明确决策问题的层次结构，包括目标、准则和方案。

目标是决策的最终目标，准则是评估和比较方案的标准，方案是待选的决策方案。

2.构建判断矩阵：决策者需要对层次结构中的准则和方案进行两两比较，得到一个判断矩阵。

判断矩阵的元素代表了准则或方案之间的重要程度比较，通常使用1-9的尺度进行比较。

3.计算权重向量：根据判断矩阵，可以计算出准则和方案的权重向量。

计算准则的权重时，需要对判断矩阵进行特征向量分解，得到最大特征值和对应的特征向量，再进行归一化处理。

计算方案的权重时，需要使用准则的权重向量和方案与准则之间的判断矩阵进行加权求和。

4. 一致性检验：在计算权重向量之前，需要进行一致性检验，以确保判断矩阵的一致性。

一致性检验使用一致性指标CR（Consistency Ratio），计算公式为CR = CI/RI，其中CI为一致性指标，RI为随机一致性指标。

如果CR小于0.1，则认为判断矩阵是一致的。

5.决策结果：根据准则和方案的权重向量，可以得到决策结果。

可以通过计算方案的加权得分，或者进行灵敏度分析，评估方案对权重变化的敏感程度。

MATLAB提供了一些函数和工具箱，可以帮助实现AHP。

例如，可以使用eig函数进行特征向量分解，使用sum函数进行加权求和，使用eigs 函数计算随机一致性指标等。

在实际应用中，基于MATLAB的AHP实现可以帮助决策者更好地进行权重分配和决策。

通过对准则和方案进行比较和评估，可以得到准确的权重向量，并且可以进行灵敏度分析，帮助决策者了解方案对权重变化的敏感程度。

基于AHP的动态模糊评价法在科技人力资源竞争力评价中的应用摘要文章分析了科技人力资源竞争力评价方法选择的特殊要求，在对当前现有的评价方法进行述评的基础上，提出了基于ahp （层次分析法）的动态模糊评价法。

关键词科技人力资源竞争力评价动态模糊评价法0 引言科技人力资源指的是实际从事或有潜力从事系统性科学和技术知识的产生、促进、传播和应用活动的人力资源。

我国的科技人力资源包括科技活动人员、专业技术人员、研究与试验（r&d）人员等三类。

①科技人力资源竞争力是指科技人力资源自身拥有的综合竞争力，包括规模、结构、科技投入、科技产出、科技创新和科技环境支撑等。

②科技人力资源综合竞争力与区域科技创新、经济发展和综合实力密切相关，其综合竞争力强弱直接关系着一个地区的整体经济发展和社会进步。

所以如何正确评价科技人力资源的竞争力，直接关系到能否将科技人力资源优化配置以及充分利用，从而促进经济的发展和社会的进步。

1 科技人力资源竞争力评价方法的选择要求科技人力资源竞争力评价方法虽然有很多，但对其的选择并不是主观随意的。

在选择评价方法过程中，应遵循一定的原则，包括一般原则与特殊原则（特定评价对象对评价方法的特殊要求）。

评价方法选择的一般原则包括：科学性原则、③系统性原则、可比性原则、④可行性原则等。

由于科技人力资源自身的复杂性与发展性，科技人力资源竞争力的评价方法的选择除了要考虑以上一般原则外，还有其自身的特殊要求。

1.1 综合性由于科技人力资源竞争力涉及到规模、结构、科技投入、科技产出、科技创新、科技环境支撑等多种因素，因此在对其进行评价时，一方面要全面、系统地而不能孤立地单从某一个方面对科技人力资源竞争力进行评价；另一方面要尽量地多考虑与之相关联的一切因素，做到综合分析，统筹兼顾。

只有这样，才能完整、准确地去评价一个国家或地区的科技人力资源竞争力的强弱。

1.2 模糊性在对科技人力资源竞争力进行定性分析过程中，会遇到具有很强不明确性的概念，比如科技环境支撑的好与坏、创新能力的高与低等。

基于层次分析法（AHP）的绩效指标权重选择摘要：文章运用层次分析法对平衡计分卡四个维度中的8个考核指标的权重进行筛选排序，通过排序依次列出所要考核的指标对企业的重要影响程度。

从而为企业绩效评价奠定了基础。

关键词：层次分析法（ahp）指标权重排序中图分类号：f234 文献标识码：a文章编号：1004-4914（2012）11-127-02一、层次分析法在融合方案指标中的应用在平衡记分卡融合方案对绩效指标进行考核评价过程中，笔者充分结合昆仑工程公司特点，从平衡记分卡中的财务指标和非财务指标中选取了8个重要的考核指标，通过层次分析法（ahp）对8个指标的权重进行排序，把8个指标评分相加最后形成综合得分，最终得出企业绩效评价结论。

要想实现精确科学的得分，首先要对这8个指标在融合方案中所占比重进行选用排序，如图1。

二、层次分析法（ahp）的指标比重选择1.层次分析法。

层次分析法（ahp）是美国运筹学家沙旦于20世纪70年代提出的，是一种定性与定量相结合的多目标决策分析方法{1}。

提出一个总目标，然后将问题按层次分解，对同一层次的诸因素通过两两比较的方法确定出相对于上一层目标的权系数。

这样层层分析下去，直到最后一层，即可以给出所有因素（或方案）。

2.将系统分为几个等级层次。

第一层为总目标，中间层可以根据问题性质划分为目标层、部门层、约束层等，最低一层一般为方案层。

通过计算各层元素对系统目标的合成权重，进行总排序，以确定各最低层元素在总目标中的重要程度。

特别是将决策者的经验判断给予量化，在目标（因素）结构复杂而且缺乏必要数据的情况下更为实用，近几年来此法在我国实际应用中发展较快。

{2}3.运用层次分析法分析问题。

运用层次分析法分析社会的、经济的以及科学领域的问题。

首先要把问题条理化、层次化，构造出一个层次分析结构的模型，通过数学运算可计算出最低层方案对最高总目标相对优劣的排序权值，从而对备选方案进行排序。

{3}在前述财务指标、顾客需求、学习与成长、优化企业内部流程的基础上，要使融合理念应用方案取得更大的成功，必须对资源进行优化，确定四个指标及分项指标的权重比例。

层次分析法判断矩阵层次分析法判断矩阵程序先确定判断矩阵；然后用以下程序就好了：%层次分析法的matlab程序%%%%diertimoxingyiclc,cleardisp(输入判断矩阵);% 在屏幕显示这句话A=input(A=);% 从屏幕接收判断矩阵[n,n]=size(A);% 计算A的维度，这里是方阵，这么写不太好x=ones(n,100);% x为n行100列全1的矩阵y=ones(n,100);% y同xm=zeros(1,100);% m为1行100列全0的向量m(1)=max(x(:,1));% x第一列中最大的值赋给m的第一个分量y(:,1)=x(:,1);% x的第一列赋予y 的第一列x(:,2)=A*y(:,1);% x的第二列为矩阵A*y(:,1)m(2)=max(x(:,2));% x 第二列中最大的值赋给m的第二个分量y(:,2)=x(:,2)/m(2);% x的第二列除以m(2)后赋给y的第二列p=0.0001;i=2;k=abs(m(2)-m(1));% 初始化p，i，k为m(2)-m(1)的绝对值while k>p% 当k>p是执行循环体i=i+1;% i 自加1x(:,i)=A*y(:,i-1);% x的第i列等于A*y的第i-1列m(i)=max(x(:,i));% m的第i个分量等于x第i列中最大的值y(:,i)=x(:,i)/m(i);% y的第i列等于x的第i列除以m的第i个分量k=abs(m(i)-m(i-1));% k等于m(i)-m(i-1)的绝对值enda=sum(y(:,i));% y的第i列的和赋予aw=y(:,i)/a;% y的第i 列除以at=m(i);% m的第i个分量赋给tdisp(权向量:);disp(w);% 显示权向量wdisp(最大特征值:);disp(t);% 显示最大特征值t %以下是一致性检验CI=(t-n)/(n-1);% t-维度再除以维度-1的值赋给CIRI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];% 计算的标准CR=CI/RI(n);% 计算一致性if CR摘要在定性问题的决策中，ＡＨＰ是一种优秀的方法，其基础是对评价对象的两两比较，并用比较结果构造判断矩阵，而这些都依赖于决策者选用的偏好关系。

第八章 层次分析法层次分析法（Analytic Hierarchy Process ，简称AHP ）是对一些较为复杂、较为模糊的问题作出决策的简易方法，它特别适用于那些难于完全定量分析的问题。

它是美国运筹学家T. L. Saaty 教授于70年代初期提出的一种简便、灵活而又实用的多准则决策方法。

§1 层次分析法的基本原理与步骤人们在进行社会的、经济的以及科学管理领域问题的系统分析中，面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。

层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。

运用层次分析法建模，大体上可按下面四个步骤进行：（i ）建立递阶层次结构模型；（ii ）构造出各层次中的所有判断矩阵；（iii ）层次单排序及一致性检验；（iv ）层次总排序及一致性检验。

下面分别说明这四个步骤的实现过程。

1.1 递阶层次结构的建立与特点应用AHP 分析决策问题时，首先要把问题条理化、层次化，构造出一个有层次的结构模型。

在这个模型下，复杂问题被分解为元素的组成部分。

这些元素又按其属性及关系形成若干层次。

上一层次的元素作为准则对下一层次有关元素起支配作用。

这些层次可以分为三类：（i ）最高层：这一层次中只有一个元素，一般它是分析问题的预定目标或理想结果，因此也称为目标层。

（ii ）中间层：这一层次中包含了为实现目标所涉及的中间环节，它可以由若干个层次组成，包括所需考虑的准则、子准则，因此也称为准则层。

（iii ）最底层：这一层次包括了为实现目标可供选择的各种措施、决策方案等，因此也称为措施层或方案层。

递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关，一般地层次数不受限制。

每一层次中各元素所支配的元素一般不要超过9个。

这是因为支配的元素过多会给两两比较判断带来困难。

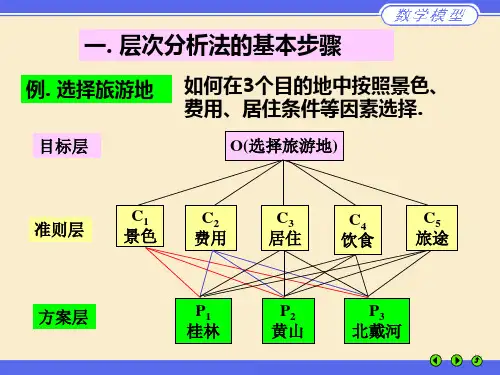
下面结合一个实例来说明递阶层次结构的建立。

例1 假期旅游有1P 、2P 、3P 3个旅游胜地供你选择，试确定一个最佳地点。

基于AHP的模糊综合评价方法研究及应用一、本文概述本文旨在探讨和研究基于层次分析法（AHP）的模糊综合评价方法，并探讨其在实际问题中的应用。

层次分析法是一种定性与定量相结合的决策方法，它通过构建层次结构模型，将复杂问题分解为若干层次和因素，利用数学方法确定各因素的权重，从而为决策者提供科学、合理的决策依据。

模糊综合评价方法则是一种处理模糊信息、进行多属性决策的有效手段，它通过对评价对象的各个属性进行模糊量化，实现对评价对象的综合评价。

将AHP与模糊综合评价方法相结合，可以充分发挥两者的优势，提高评价的准确性和有效性。

本文首先介绍了层次分析法和模糊综合评价方法的基本原理和步骤，然后详细阐述了基于AHP的模糊综合评价方法的构建过程，包括层次结构模型的建立、判断矩阵的构造、权重的计算以及模糊综合评价模型的构建等。

接着，本文通过具体案例，展示了该方法在实际问题中的应用过程和应用效果，验证了其可行性和实用性。

本文总结了研究成果，指出了研究中存在的不足和未来的研究方向，为相关研究提供了参考和借鉴。

二、基于AHP的模糊综合评价方法理论基础在复杂系统的评价过程中，往往需要综合考虑多个因素，每个因素又可能包含多个子因素，这就形成了一个多层次的评价结构。

在这种背景下，层次分析法（Analytic Hierarchy Process，AHP）和模糊综合评价方法（Fuzzy Comprehensive Evaluation，FCE）的结合就显得尤为重要。

这种方法结合了AHP的层次化结构和FCE的模糊处理特性，使得评价过程更加科学、合理。

层次分析法（AHP）是由美国运筹学家T.L.Saaty在20世纪70年代提出的一种定性与定量相结合的多准则决策方法。

它将复杂问题分解为各个组成因素，并将这些因素按支配关系分组形成递阶层次结构。

通过两两比较的方式确定层次中诸因素的相对重要性，然后综合人的判断以决定诸因素相对重要性的总的顺序。

基于AHP分析法的大学生就业能力评价体系层次研究
郑元凯
【期刊名称】《高校辅导员学刊》
【年(卷),期】2013(005)006
【摘要】本研究综合国内外学者关于就业能力的相关论述,构建一个综合的就业能力评价体系,并通过层次分析法,对影响大学生就业能力的各类指标权重进行测算与分析,结果显示,大学生创新能力、团队协作能力与自学能力在就业能力评价体系中所占权重较高.
【总页数】4页(P78-81)
【作者】郑元凯
【作者单位】福建师范大学经济学院,福州350108
【正文语种】中文
【中图分类】G641
【相关文献】
1.基于层次分析法构建独立学院大学生就业能力评价体系 [J], 王天予;赵怡欣;芮媛媛
2.基于AHP层次分析法的图书馆知识型馆员能力评价体系研究 [J], 史朝霞;余程淑
3.基于层次分析法的大学生就业能力评价体系研究 [J], 龙映宏; 陈明锐
4.基于层次分析法的大学生就业能力评价体系研究 [J], 龙映宏; 陈明锐
5.艺术经纪人职业能力评价体系的构建——基于AHP层次分析法 [J], 岑雪怡;张纯
因版权原因，仅展示原文概要，查看原文内容请购买。

模糊综合评价方法及其应用研究模糊综合评价方法是一种基于模糊数学和模糊逻辑理论的评价方法，它在多个领域都有广泛的应用。

特别是在需要综合考虑多个因素和条件的复杂系统中，模糊综合评价方法能够有效地处理不确定性、不完全性和主观性，为决策提供科学依据。

本文将介绍模糊综合评价方法的基本原理、应用范围和优点，并通过具体应用实例探讨其在不同领域的效果和优势。

模糊综合评价方法的基本原理是利用模糊数学和模糊逻辑理论，将不确定的、复杂的评价对象转化为可量化的数学模型。

该方法通过引入模糊矩阵、模糊运算等概念，将多个因素和条件的评价结果进行集成，得到一个综合的评价结果。

模糊综合评价方法具有处理不确定性、不完全性和主观性的能力，同时能够考虑多种因素和条件，为决策提供更为全面的支持。

在进行模糊综合评价之前，首先需要对评价对象进行关键词识别。

关键词识别是指从输入的文本中提取出与评价对象相关的关键词，并根据这些关键词确定文章的主题和类型。

关键词识别的方法包括基于规则的方法和基于机器学习的方法。

基于规则的方法是根据预先定义的规则和算法，从输入文本中提取出相关关键词；基于机器学习的方法则是利用机器学习算法，对输入文本进行训练和学习，自动识别出相关关键词。

在完成关键词识别后，接下来进行模糊综合评价。

模糊综合评价以识别出的关键词为基础，结合相关规则和算法，对文章进行综合评价。

具体步骤如下：建立评价指标体系：根据评价对象的特点和评价目标，建立相应的评价指标体系。

评价指标体系应包括多个层次和多个指标，用以全面反映评价对象的各个方面。

确定评价因素权重：针对每个评价指标，确定其对应的权重。

权重的确定可以采用层次分析法、熵值法等权重确定方法，也可以根据实际经验和专家意见进行赋值。

建立模糊关系矩阵：根据评价指标体系和权重，建立相应的模糊关系矩阵。

模糊关系矩阵中的元素表示不同指标之间的模糊关系，通常采用三角函数或其他函数进行计算。

进行模糊运算：将模糊关系矩阵与权重向量进行模糊运算，得到综合评价结果。