(完整版)职高数学第十章概率与统计初步习题及答案

2020年中职升学数学考试单元测试题（100分）第十单元概率与初步统计（2）一 、选择题：本大题共8小题，每小题5分，共40分。

在每小题给1、书架第一层有不同年级的语文书8本，第二层有不同年级的英语书12本，从中任取一本书来阅读，有（ ）种取法。

A 、96B 、20C 、21D 、192、某商店有4种衣服，3种裤子，要从中买一套衣服，有（ ）种买法。

A 、7B 、3C 、12D 、43、某篮球运动员投篮10次，命中6次，这是（ ）A 、必然事件B 、不可能事件C 、随机事件D 、确定性事件4、下列属于必然事件的是（ ）A 、种子发芽了；B 、一副扑克牌中，抽出一张是方块；C 、没有水、空气，种子发芽了；D 、太阳从东方升起。

5、小如抛骰子，抛两次骰子出现数字之和为2的概率为（ ）A 、361；B 、121；C 、181；D 、61。

6、某袋子中有8个黄球，9个白球，13个红球。

若从中任抽取一个球，抽中黄球的概率是（ ）A 、3017；B 、3013；C 、103；D 、154。

7、小明和小王同时练习投篮，小明投中的概率是0.5，小王投中的概率是0.6，若两人同时投篮都投进的概率是（ ）A 、0.3B 、0.5C 、0.6D 、1.18、小李四科平均成绩是80分，语文78分，数学82分，英语比政治多2分，问小李英语分数是（ ）A 、78B 、79C 、80D 、81二、填空题：本大题共4小题，每小题5分，共20分.请把正确答案填在题中横线上，答错不得分.9、由数字1,2,3,4,5,6可以组成个没有重复数字的两位数；10、从10人的小队中选出正负队长各一名，有种选法；11、从一副54张的扑克牌中抽1张，抽中方块的概率是；12、在1000张奖券中，有5张一等奖，20张二等奖，100张三等奖，某人从中任意摸出一张，那么他中二等奖及以上的概率是。

三、解答题：本大题共3小题，共40分. 解答应写出推理、演算步骤，只写结果不得分。

K中等职业学校对口升学专项练习测试卷(二十七)第10章概率与统计(B 卷)(本卷满分120分，考试时间为60分钟)选择题(共30小题，每小题4分，满分120分。

在每小题给出的四个选项中，选出一个符合题目要求的选项)1.学校要在全校2000名学生中，选取200名学生进行视力检查，较好的抽样方法是 () A. 简单随机抽样 B. 系统抽样 C. 分层抽样 D.以上均可以2.已知5件产品中有2件次品，其余为合格品。

现从这5件产品中任取1件，取到次品的概率为()A B. C.3.已知一组数据：4,6,5,8,7,6,则该组数据的方差为A B C.4.掷一枚骰子，则出现奇数点的概率为B. 5.某校高一、高二、高三的学生人数之比为3:3:4,若用分层抽样的方法从中抽取容量为100的 样本，则应从高三学生中抽取的人数为 ( ) A.20 B.30C.40D.506.设某厂产品的次品率为0.03,估计该厂8000件产品中次品的件数为 ( ) A.3 B.160 C.240 D.247.某校有40个班级，每班60人，从中选派100人参加某项活动，这个问题中样本容量是()A.40B.60C.2400D.1008.为美化教室环境，现从红、黄、白、紫4种颜色的菊花中任选2种放在教室里，则红色和紫色同时被选中的概率为 ( )A B. C. 口·105 ·9.为了解1200名学生对学校某项教学实验的意见，打算从中抽取一个容量为60的样本，考虑采用系统抽样的方法，则抽样距k 为 A.40 B.30 C.2010.掷一枚均匀的硬币3次，出现正面向上的次数恰好为两次的概率为C. ( )D.12( )口11.一个口袋中装有2个白球和3个黑球，这5个球除颜色外完全相同，从中摸出2个小球，则这2 个球颜色相同的概率为 ( )A日 C. 口12.从甲、乙等5名学生中随机选出2人，则甲或乙被选中的概率为 ( )A B. C. 口13.某班有学生60人，将这60名学生随机编号为1～60号，用系统抽样的方法从中抽出4名学 生，已知3号、33号、48号学生在样本中，则样本中另一名学生的编号为 ( ) A.28 B.18 C.23 D.1314.从1,2,3,4这四个数中一次随机抽取2个数，则取出的数中一个是奇数一个是偶数的概率为( )C.15.某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为300,200,400,300件，为检验产品 的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产 品中抽取的件数为 ( ) A.10 B.15 C.20 D.2516.某校调查高三200名学生寒假中每天在家学习所用的时间情况，绘制了如图所示的频率分布 直方图，则每天在家学习超过8小时的人数是 ( )·106 ·频 率组距0.150 0.1250.1000.0750.025时间(小时)2 4 6 810 12专 业 姓 名 准考证号密． : 封． : 一 线． 不． ……．．得． …．得分 阅卷人A.40B.35C.30D.20口 口 口学 校C.( )( )口A AB AB.17.将一颗骰子连续掷2次，则向上的点数之和为8的概率为A18.3名男选手和2名女选手组成乒乓球混双组合，则不同的组合方式有 ( )口( )A.5 种B.6 种C.4 种D.2 种19.有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相 同，则这两位同学参加同一个兴趣小组的概率为 (.)A B.c.3口20.为了解全校2400名学生的身高情况，从中抽取60名学生进行测量，下列说法正确的是()A.总体是2400B. 个体是每一个学生C. 样本是60名学生D.样本容量是6021.一个容量为n 的样本，分成若干组，已知某组的频数和频率分别为100和0.125,则n=( ) A.1200 B.800 C.1600 D.125022.从1,2,3,4,5这五个数中一次随机抽取2个数，则取出的这2个数之和是偶数的概率为( )A B.C. 口23.在某项体育比赛中，七位裁判为一位选手打出的分数为90,89,90,95,93,94,93,去掉一个最高分和一个最低分后，所剩数据的平均值和方差分别为 ( )A.92,2B.93,2.8C.93,2D.92,2.824.甲、乙两个人进行“剪刀、石头、布”的游戏，两个人都随机出拳，则一次游戏中两人平局的概 率为 ( )日 25.已知甲、乙两位选手进行射击比赛，命中的环数分别为：甲8,9,9,9,10,乙6,10,10,10,9.它 们的标准差分别为sm,sz,则下列各项正确的是 A.sm>sz B.sm=sz C.sm<s 乙 D.不能确定 26.甲、乙、丙三位同学站成一排照相，则甲、丙相邻的概率为B.27.容量为20的样本数据，分组后的频率如下表，则样本数据落在区间[20,40]的频率为()分组[10,20] (20,30) [30,40] (40,50) (50,60) [60,70] 频数 1 3 4 6 4 2 A.0.35 B.0.2 C.0.7 D.0.4 28.某学校的高一、高二、高三共有学生1350人，其中高一500人，高三比高二少50人，为了解该校学生健康状况，现采用分层抽样方法进行抽查，在抽取的样本中有高一学生120人，则该样本中的高二学生人数为 ( ) A.80 B.96 C.108 D.11029.若样本数据x ₁,x ₂,…,x ₁o 的方差为8,则2x ₁-1,2x ₂-1,…,2x ₁o —1 的方差为 ( ) A.31 B.32 C.15 D.1630.高三(1)班20名学生在某次数学考试成绩(单位：分)的频率分布直方图如图所示，则图·107 · ·108 ·频率组 距7a6a3a2a成绩(分)0 5060708090100中a=( ) A.0.005 B.0.05 C.0.001 D.0.01( )()AA口口C.C.C.及。

第十章 概率
一、选择题
1. 掷一枚骰子，出现点数为1的概率是（ ） A. 3
1 B.
41 C. 51 D.6
1 2. 某班有男生20人，女生25人，从中任选一人担任信息委员，共有多少种不同的选法（ ） A. 15 B. 25 C.45 D.50
3. 有一项活动，要在2名老师和5名学生中选人参加，若需要老师和学生各一人参加，有（ ）种选法。

A. 6 B.8 C.10 D.12
4. 把一枚硬币任意地抛掷一次，出现正面向上的概率是（ ）
A. 41
B.21
C. 8
1
D. 1 5. 为检查期末考试试卷分数的统计的工作质量，将考生考号尾数是5的全部抽取出来复查，这种抽样方法是（ ） A. 简单随机抽样 B. 系统抽样 C.分层抽样 D. 间断抽样
6. 某地区为了掌握7岁儿童身高状况，随机抽取200名儿童
测试身高，则样本容量为（ ） A. 50 B. 100 C.150 D.200 二、判断题
1. 两个袋子中分别装有10个红色球和6个白色球，从中取出一个红色球和一个白色球，共有16种取法。

（）
2. 在一定条件下，必然发生的事件叫必然事件。

（）
3. 不可能事件的概率为1. （）
4. 已知一组数据5,4,3,2,1.则它的平均值等于2. （）
5. 在100张奖券中，有20张中奖券，从中任取一张，中奖的概率为20%。

（）
6. 某种商品共有50个，其中有2个次品，现从中随机抽取一个，抽到次品的概率为50
1。

（） 答案： 一、选择题 1-6 DCCBBD 二、判断题 1-5 ×√××√×。

第十章 概率与统计初步测试本试卷共十题，每题10分，满分100分。

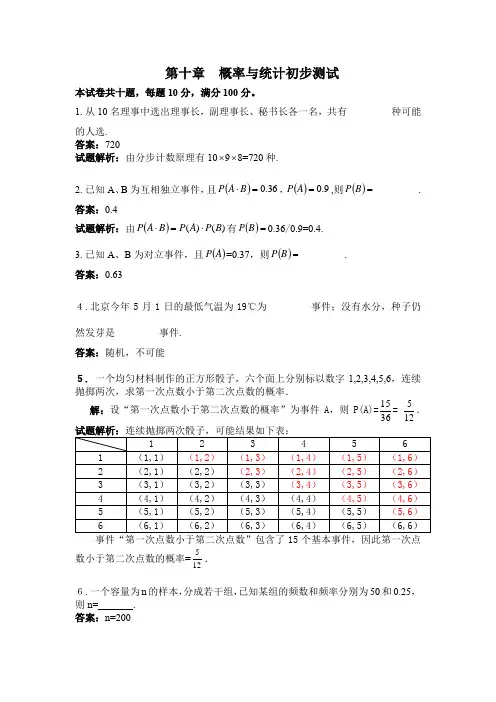
1.从10名理事中选出理事长，副理事长、秘书长各一名，共有________种可能的人选.答案：720试题解析：由分步计数原理有10⨯9⨯8=720种.2.已知A 、B 为互相独立事件，且()36.0=⋅B A P ，()9.0=A P ,则()=B P ________. 答案：0.4试题解析：由())()(B P A P B A P ⋅=⋅有()=B P 0.36/0.9=0.4.3.已知A 、B 为对立事件，且()A P =0.37，则()=B P ________.答案：0.63４.北京今年5月1日的最低气温为19℃为________事件；没有水分，种子仍然发芽是________事件.答案：随机，不可能５. 一个均匀材料制作的正方形骰子，六个面上分别标以数字1,2,3,4,5,6，连续抛掷两次，求第一次点数小于第二次点数的概率．解：设“第一次点数小于第二次点数的概率”为事件A ，则P(A)=3615= 125．数小于第二次点数的概率=125．６.一个容量为n 的样本，分成若干组，已知某组的频数和频率分别为50和0.25，则n=_______.答案：n=200７.如果x ，y 表示0，1，2，···，10中任意两个不等的数，P(x ，y)在第一象限的个数是（ ）.A 、72B 、90C 、110D 、121答案：B８.甲、乙、丙三人射击的命中率都是0.5，它们各自打靶一次，那么他们都没有中靶的概率是（ ）.A 、 0.5B 、0.25C 、 0.3D 、 0.125答案：D９.两个盒子内各有3个同样的小球，每个盒子中的小球上分别标有1，2，3三个数字。

从两个盒子中分别任意取出一个球，则取出的两个球上所标数字的和为3的概率是（ ）.A 、91B 、92C 、31D 、32 答案：B10.下面属于分层抽样的特点的是（ ）.A 、从总体中逐个抽样B 、将总体分成几层，分层进行抽取C 、将总体分成几个部分，按事先确定的规则在各部分抽取D 、将总体随意分成几个部分，然后再进行随机选取答案：B。

概率与统计初步例1、某商场有4个大门，若从一个门进去，购买商品后再从另一个门出去，不同的走法共有多少 种？ 解：4×3=12例2.指出下列事件是必然事件，不可能事件，还是随机事件？①某乒乓球运动员在某运动会上获得冠军。

②掷一颗骰子出现8点。

③如果0=−b a ，则b a =。

④某人买某一期的体育彩票中奖。

解：①④为随机事件，②是不可能事件，③是必然事件。

例3.某活动小组有20名同学，其中男生15人，女生5人，现从中任选3人组成代表队参加比赛， A 表示“至少有1名女生代表”，求)(A P 。

解：)(A P =15×14×13/20×19×18=273/584例4.在50件产品中，有5件次品，现从中任取2件。

以下四对事件哪些是互斥事件？哪些是对立 事件？哪些不是互斥事件？①恰有1件次品和恰有2件次品 互斥事件②至少有1件次品和至少有1件正品 不是互斥事件③最多有1件次品和至少有1件正品 不是互斥事件④至少有1件次品和全是正品 对立事件例5.从1,2,3,4,5,6六个数字中任取两个数，计算它们都是偶数的概率。

解：P(A)=3×2/6×5=1/5例6.抛掷两颗骰子，求：①总点数出现5点的概率；②出现两个相同点数的概率。

解：容易看出基本事件的总数是6×6=36(个),所以基本事件总数n=36. (1)记“点数之和出现5点”的事件为A,事件A 包含的基本事件共6个：(1,4)、(2,3)、(3,2)、 (4,1)、,所以P(A)=.4/36=1/9(2)记“出现两个相同的点”的事件为B,则事件B 包含的基本事件有6个：（1，1）、（2，2）、（3，3）、(4,4)、（5，5）、（6，6）.所以P(B)=6/36=1/6例7.甲、乙两人各进行一次射击，如果两人击中目标的概率都是0.6，计算：①两人都未击中目标的概率；②两人都击中目标的概率；③其中恰有1人击中目标的概率；④至少有1人击中目标的概率。

第十章 概率与统计初步测试本试卷共十题,每题10分,满分100分。

1。

从10名理事中选出理事长，副理事长、秘书长各一名，共有________种可能的人选． 答案：72０试题解析:由分步计数原理有10⨯9⨯8=7２0种。

2。

已知Ａ、B 为互相独立事件,且()36.0=⋅B A P ,()9.0=A P ，则()=B P ________。

答案:0.4试题解析:由())()(B P A P B A P ⋅=⋅有()=B P ０.3６/０.9=0。

4. 3．已知A 、B 为对立事件,且()A P =０．37,则()=B P ________. 答案：0.634.北京今年5月1日的最低气温为19℃为________事件;没有水分，种子仍然发芽是________事件. 答案:随机，不可能５. 一个均匀材料制作的正方形骰子，六个面上分别标以数字１,2，3，4,5，6，连续抛掷两次,求第一次点数小于第二次点数的概率.解:设“第一次点数小于第二次点数的概率”为事件Ａ，则P （A)=3615＝ 125． 试题解析:连续抛掷两次骰子，可能结果如下表：事件“第一次点数小于第二次点数”包含了15个基本事件，因此第一次点数小于第二次点数的概率=125．６。

一个容量为n 的样本,分成若干组,已知某组的频数和频率分别为50和0.２5,则n ＝_＿__＿_＿. 答案:n ＝２007．如果ｘ，y 表示0，1,2，···,10中任意两个不等的数，P(x,ｙ）在第一象限的个数是( ）.A 、72B 、９0 Ｃ、110 D 、１21 答案:B8.甲、乙、丙三人射击的命中率都是0.5,它们各自打靶一次,那么他们都没有中靶的概率是( ).A 、 0.5 Ｂ、0。

25 C 、 ０。

3 Ｄ、 0。

1２5 答案:D９。

两个盒子内各有3个同样的小球，每个盒子中的小球上分别标有１,２,3三个数字。

从两个盒子中分别任意取出一个球,则取出的两个球上所标数字的和为３的概率是（ ).A 、91 Ｂ、92 C 、31 D 、32答案：Ｂ10.下面属于分层抽样的特点的是( )。

中职数学第十章《概率与统计初步》单元检测（满分100分，时间：90分钟）一.选择题（3分*10=30分）1、下列语句中，表示随机事件的是（ ）A 、掷三颗骰子出现点数之和为19B 、从54张扑克牌中任意抽取5张C 、型号完全相同的红、白球各3个，从中任取一个是红球D 、异性电荷互相吸引2、下列语句中，不表示复合事件的是（ ）A 、掷三颗骰子出现点数之和为8B 、掷三颗骰子出现点数之和为奇数C 、掷三颗骰子出现点数之和为3D 、掷三颗骰子出现点数之和大于133、同时抛掷两枚质地均匀的硬币，则出现两个正面的的概率是( ) A. 21 B. 41 C. 31 D. 814、用数字0，1，2，3可组成n 个3位奇数，则n ＝（ ）A 、64B 、24C 、27D 、365、同时抛掷两枚质地均匀的硬币，则出现不同的两面的的概率是( ) A. 21 B. 41 C. 31 D. 816、掷一颗骰子，观察点数，这一试验的基本事件数为（ ）A 、 1B 、3C 、6D 、127、在100张奖券中有2张中奖，从中任抽一张，则中奖的概率是（ ）A 、1100B 、150C 、125D 、15 8、任选一个两位数，它既是奇数，又是偶数的概率是（ ）A 、797B 、2190C 、5190D 、0 9、在一个不透明的盒子中装有8个白球，若干个黄球，它们除颜色不同外， 其余均相同.若从中随机摸出一个球，它是白球的概率为2/3，则黄球的 个数为（ ）A.2B.4C.12D.1610.同时掷两枚均匀骰子，出现数字和大于10的概率是：（ ） A. 61 B.121 C. 181 D. 24111．在10000张奖券中，有1张一等奖，5张二等奖，2000张三等奖，某人从中任意摸出一张，那么他中三等奖的概率是（ ）A ．110B ．201C ．51D ．100016 12.在一个不透明的袋子中，有10个蓝球，6个红球，4个绿球，某人从中任意取出一个球，那么取中红球的概率是（ ）. A.21 B.103 C.51 D.61 二.填空题（4分*8=32分）1、某小组有三名女生，两名男生，现从这个小组任意选一名组长，则其中一名女生小李当选为组长的概率为_______2、任选一个两位数，它是偶数的概率是________．3、已知x 1,x 2,x 3的平均数是a ，则5x 1+7、5x 2+7、5x 3+7的平均数是______4、将5封信投入3个邮筒，不同的投法有__________5、投掷两枚骰子，出现点数之和为3的概率为________6、在“石头、剪子、布”的游戏中，两人做同样手势的概率是________．7、某中职学校共有20名男足球运动员，从中选出3人调查学习成绩情况，调查应采用的抽样方法是_____8.某小组5名同学一次测验的平均成绩是82分，已知其中4名同学的成绩分别是82分，78分，90分，75分，则另一名同学的成绩是分．9. 某班有男生30人，女生20人，如果选男、女各1人作为学生代表参加学校伙食管理委员会，共有种方法。

（完整版）职高数学第十章概率与统计初步习题及答案.doc第 10 章概率与统计初步习题练习 10.1.11、一个三层书架里，依次放置语文书12 本，数学书14 本，英语书 11 本，从中取出 1 本，共有多少种不同的取法？2、高一电子班有男生28 人，女生19 人，从中派1 人参加学校卫生检查，有多少种选法？3、某超市有4 个出口，小明约好和朋友在出口处见面，请问他们见面的地方有多少种选择？答案：1、 372、 473、4练习 10.1.21、一个三层书架里，依次放置语文书12 本，数学书14 本，英语书 11 本，从中取出语文，数学和英语各 1 本，共有多少种不同的取法？2、将 5 封信投入 3 个邮筒，不同的投法有多少种？3、某小组有8 名男生， 6 名女生，从中任选男生和女生各一人去参加座谈会，有多少种不同的选法？答案：1、12× 14× 11=1848（种）2、3×3× 3× 3× 3=3 5 （种）3、8× 6=48（种）练习 10.2.11、掷一颗骰子，观察点数，这一试验的基本事件数为--------------- （）A、 1 B 、 3 C 、 6D 、 122、下列语句中，表示随机事件的是-------------------------- （）A、掷三颗骰子出现点数之和为19 B 、从54 张扑克牌中任意抽取 5 张C、型号完全相同的红、白球各3 个，从中任取一个是红球D 、异性电荷互相吸引3、下列语句中，不表示复合事件的是-------------------------- （）A、掷三颗骰子出现点数之和为8 B 、掷三颗骰子出现点数之和为奇数C、掷三颗骰子出现点数之和为 3 D 、掷三颗骰子出现点数之和大于13答案：1、 C2、B3、 C练习 10.2.21、某学校要了解学生对自己专业的满意程度，进行了5 次“问卷”，结果如表2-1 所示：表 2-1被调查500 502 504 496 505人数 n满意人404 476 478 472 464数 m满意频m率n（1）计算表中的各个频率；（2）学校学生对自己所学专业满意的概率P(A)约是多少？2、某数控班要了解学生对五门任课教师的满意程度，进行了“问卷”，结果如表 2-2 所示：表 2-2被调查 5052544950 人数 n满意人 3747464748数 m满意频率m n（ 1）计算表中的各个频率；（ 2）学生对任课教师的满意的概率P(A)约是多少？答案：1、（ 1） 0.808， 0.948， 0.948，0.952，0.919 （2） 0.952、（ 1） 0.74， 0.904， 0.852，0.959,0.96 (2)0.9练习 10.2.31、在掷一颗骰子的试验中，下列 A 和 B 是互斥事件的是 ---------------------（）A 、 A=｛ 1,5 ｝ ,B= ｛ 3， 5， 6｝B 、A=｛ 2,3 ｝ ,B= ｛ 1，3， 5｝C 、 A=｛ 2，3， 4,5 ｝,B= ｛ 1，2｝ D、A=｛ 2， 4， 6｝ ,B= ｛ 1， 3｝2、在100 张奖券中有2 张中奖，从中任抽一张，则中奖的概率是------------（）A 、1 B、1C、1D、1100502553、任选一个两位数，它既是奇数，又是偶数的概率是--------------------- （）A 、7B、 21C、 51D、 0979090答案：1、 D2、 B3、 D练习 10.3.11、某地区为了掌握 70 岁老人身体三高状况，随机抽取 150 名老人测试体验，请指出其中的总体、个体、样本与样本容量．2、要测定一批炮弹的射程，随机抽取 30 颗炮弹通过发射进行测试 . 指出其中的总体、个体、样本与样本容量． 3、在某班级中，随机选取 15 名同学去参加学校的学生代表大会，指出其总体、个体、样本与样本容量．答案：1、该地区所有抽取的 150 名70 岁老人的身体三高情况是总体，每一个70 岁老人的身体三高情况是样本，样本容量是70 岁老人的身体情况是个体，被150． 2、一批炮弹是总体，每个炮弹是个体，被抽取的3、某班级中所有学生是总体，每一名学生是个体，30 颗炮弹是样本，样本容量是 30.被选取的 15 名学生是样本，样本容量是15.练习 10.3.21、某中职学校共有20 名男足球运动员，从中选出3人调查学习成绩情况，调查应采用的抽样方法是 ---------------- （）A、随机抽样法B、分层抽样法C、系统抽样法D、无法确定2、请用抽签法从某班40 人中抽出8 人参加学校的教学质量调查会议，写出抽取的过程。

第十章 概率与统计初步第1节 计数原理一、分类计数原理（加法原理）完成一件事，有n 类方式。

第一类方式有1k 种方法，第2类方式有2k ，...第n 类方式有n k 种方法，那么完成这件事的方法共有n k k k N +⋅⋅⋅++=21（种）二、分步计数原理（乘法原理）完成一件事，有n 个步骤，完成第1步有1k 种方法，完成第2步方式有2k ，...完成第n 步方式有n k 种方法，那么完成这件事的方法共有n k k k N •⋅⋅⋅••=21（种）第2节 随机事件三、事件随机事件:可能发生，可能不发生（表示：A,B,C ） 必然事件：一定发生（表示：Ω） 不可能事件：一定不发生（表示：Φ）举例说明生活中哪些是随机事件，哪些是必然事件，哪些是不可能事件。

事件的描述：加大括号 A=｛抛掷一枚硬币，出现正面向上｝任意抛掷一颗骰子，观察掷出的点数。

事件A=｛点数是1｝，B={点数是2}.C={点数不超过2}之间存在着什么联系呢？基本事件：不能再分的最简单事件 复合事件：基本事件组成的事件 二、概率回忆频率的概念，频数：出现的次数总数频数频率=举例：抛掷一枚硬币25次，出现13次正面向上，则正面向上的频率为2513；大量重复地抛一枚硬币，发现事件A 发生的频率稳定在21，事件A 发生的概率为21概率：在大量重复试验中，事件发生的频率的稳定值记为()A P 。

频率与概率的区别：1、频率是试验中的近似值，概率是理论上的准确值；2、概率是频率在大量试验中的稳定值。

三、事件的概率的性质1.对于任意事件A ，有()10≤≤A P2.必然事件的概率为1，()1=ΩP ;3.不可能事件的概率为0，();0=ΦP第3节 古典概型一、古典概型 满足（1）有限性：基本事件有有限个；（2）等可能性：每个基本事件发生的可能性相等。

的试验称为古典概型。

举例：1.在圆内随机找一点，如果找出的每个点都是等可能的，这是古典概型吗？ 分析：满足等可能性不满足有限性2.在射击训练中，结果有“命中10环”，“命中9环”，“命中8环”，“命中7环”，“命中6环”，“命中5环”，“不中环”，你认为这是古典概型吗？ 分析：满足有限性不满足等可能性。