信阳市羊山中学 八年级期末试题

2022—2023学年河南省信阳市八年级下学期期末数学试卷一、单选题1. 下列二次根式中，是最简二次根式的是（）A．B．C．D．2. 下列计算中正确的是（）A．B．C．D．3. 下列四组条件中，不能判定四边形ABCD是平行四边形的是（）．A．AB＝DC，AD＝BC B．C．，AB＝DC D．，AD＝BC4. 某校七年级有名同学参加百米竞赛，预赛成绩各不相同，要取得前名才能参加决赛，小明已经知道了自己的成绩，他想知道自己能否进入决赛，还需要知道这名同学成绩的（）A．中位数B．众数C．平均数D．最大和最小值5. 人体生命活动所需能量主要由食物中的糖类提供．如图是小南早餐后一段时间内血糖浓度变化曲线图．下列描述正确的是（）A．从9时至10时血糖呈下降状态B．10时血糖最高D．这段时间有3个时刻血糖浓度达到C．从11时至12时血糖呈上升状态6. 将一次函数y＝﹣3 x的图象沿y轴向下平移4个单位长度后，所得图象的函数表达式为（）A．y＝﹣3（x﹣B．y＝﹣3x+4C．y＝﹣3（x+4）D．y＝﹣3x﹣44）7. 已知关于x的一次函数的图象上两点，，若时，，则m的取值范围是（）A．B．C．D．8. 数形结合是解决数学问题常用的的思想方法.如图，一次函数与一次函数的图象交于点，根据图象可知，关于x的不等式的解集是（）A．B．C．D．9. 如图，矩形中，连接，分别以B、D为圆心，大于的长为半径画弧，两弧交于P、Q两点，作直线，分别与、交于点M、N，连接、．若，．则四边形的周长为（）A．24B．20C．16D．1210. 如图1，在菱形中，，动点从点出发，沿折线方向匀速运动，运动到点停止．设点的运动路程为，的面积为，与的函数图象如图2所示，则的长为（）A．B．C．D．二、填空题11. 函数中，自变量的取值范围是 _____ ．12. 如图，四边形 ABCD的对角线相交于点 O，若 AB//CD，请添加一个条件_____________ (写一个即可 )，使四边形 ABCD是平行四边形．13. 新冠疫情期间，小李同学连续两周居家健康检测，如图是小李记录的体温情况折线统计图，记第一周体温的方差为，第二周体温的方差为，试判断两者之间的大小关系 ______ ．（用“”“”“”填空）14. 如图，在中，平分，于点，交BC于点F，点是的中点，若，，则的长为 ______ ．15. 如图，矩形ABCD中，AB=1，BC=2，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处．当△CEB′为直角三角形时，BE的长为___________ ．三、解答题16. 计算：17. 如图，点A、F、C、D在一条直线上，AB∥DE且AB＝DE，AF＝DC，求证：四边形BCEF是平行四边形．18. 某校七、八年级各有1000名学生，为加强安全教育，开展了“防溺水”安全知识检测．现从七、八年级学生中各随机抽取了m名学生进行测试，将测试成绩按以下六组进行整理（得分用表示）：：，：，：，：，：，：．并绘制七年级测试成绩频数分布直方图和八年级测试成绩扇形统计图，部分信息如下：已知八年级测试成绩组的全部数据为，，，．根据以上信息，回答下列问题：(1) ______，______．(2)请直接写出七年级测试成绩的中位数落在哪一组．(3)若测试成绩不低于85分，则认定该学生对“防溺水”安全知识了解程度高，请估计该校七、八两个年级对“防溺水”安全知识了解程度高的学生一共有多少人，并说明理由．19. 超速行驶是引发交通事故的主要原因．上周末，小威等三位同学在幸福大道段，尝试用自己所学的知识检测车速，观测点设在到公路l的距离为的P处．这时，一辆红旗轿车由西向东匀速驶来，测得此车从A处行驶到B处所用的时间为，并测得，，(1)求AP的长？(2)试判断此车是否超过了/ 的限制速度？（）20. 如图1，可以用秤砣到秤纽的水平距离，来得出秤钩上所挂物体的质量．称重时，若秤杆上秤砣到秤纽的水平距离为x（厘米），秤钩所挂物重为y （斤），则y是x的一次函数．表中为若干次称重时记录的一些数据．(1)在如表x，y的数据中，发现有一对数据记录错误在图2中，通过描点的方法，观察判断哪一对是错误的．(2)根据（1）的发现，问当杆秤上秤砣到秤纽的水平距离为10厘米时，秤钩所挂物重是多少21. “4 G改变生活，5 G改变社会”，不一样的5 G手机给人们带来了全新的体验，某营业厅现有A，B两种型号的5 G手机出售，售出1部A型、1部B型手机共获利600元，售出3部A型、2部B型手机共获利1400元．(1)求A，B两种型号的手机每部利润各是多少元；(2)某营业厅再次购进A，B两种型号手机共20部，其中B型手机的数量不超过A型手机数量的，请设计一个购买方案，使营业厅销售完这20部手机能获得最大利润，并求出最大利润．22. 如图，直角坐标系xOy中，一次函数y x+5的图象l1分别与x，y轴交于A，B两点，正比例函数的图象l2与l1交于点C（m，4）．（1）求m的值及l2的解析式；；（2）求△AOC的面积S△AOC（3）一次函数y= kx+1的图象与线段AC有交点，直接写出k的值．23. 已知，在△ABC中，∠BAC=90°，∠ABC=45°，点D为直线BC上一动点（点D不与点B，C重合）．以AD为边做正方形ADEF，连接CF（1）如图1，当点D在线段BC上时．求证CF+CD=BC；（2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出CF，BC，CD三条线段之间的关系；（3）如图3，当点D在线段BC的反向延长线上时，且点A，F分别在直线BC 的两侧，其他条件不变；①请直接写出CF，BC，CD三条线段之间的关系；②若正方形ADEF的边长为，对角线AE，DF相交于点O，连接OC．求OC的长度．。

2023--2024学年度上期期末调研考试试卷八年级语文注意事项：1．本试卷共6页，四个大题，满分120分，时间120分钟。

2．本试卷上不要答题，请按答题卡上注意事项的要求，直接把答案填写在答题卡上。

答在试卷上的答案无效。

一、积累与运用（共28分）1．观看了央视创意节目《满庭芳·国色》后，八年级某班准备开展一场“寻色”之旅，下面是小语同学为此次“寻色”之旅拟写的开场白，请帮助他加以完善。

（共4分）色彩的①____（迭叠）代，代表文化的更替。

每种色彩都是古人观察万物后用时间镌刻出的智慧结晶。

春晚创意节目《满庭芳·国色》彰显传统文化底色，演②____（译绎）东方色彩美学。

一袭水袖舞出桃红之柔美，一把纸扇展现出凝脂之灵秀，一舞翎子宛如群青之灵动，一曲长剑挥洒沉香之苍劲．。

其如诗如画的中国色彩，给观众带来震撼的视觉体验。

让我们一起开启一场“寻色”之旅，了解中国传统色彩背后蕴藏．的东方美学吧！（1）语段中两个加点字的读音小语拿不准，请帮他作出选择。

（）（2分）A．jìn cáng B．jìng zàng C．jìng cáng D．jìn zàng（2）语段中两个横线处应分别选用哪个字？请工整书写在横线上。

（2分）2．古诗文默写。

（8分）中国的古诗文是浩渺璀璨的文化星空，令人神往。

在那里，我们可以领略崔颢笔下“①___________，芳草萋萋鹦鹉洲。

”的自然之景（《黄鹤楼》）；欣赏王维在塞外所见“②___________，③___________。

”的壮美风光（《使至塞上》）；饱览陶弘景“④___________，⑤___________。

”两句中对山高水净风景的描摹（《答谢中书书》）；还可以感受陶渊明《饮酒》中传达“山气日夕佳，⑥___________。

”的恬淡心境；聆听刘桢《赠从弟（其二）》中表达“⑦___________？松柏有本性。

2022—2023学年度下学期八年级期末教学质量检测
数学试题
注意事项：
1．本试卷共8页，三大题，23小题，满分120分，考试时间100分钟。

2．使用答题卡的学校，请按答题卡上注意事项的要求直接把答案写在答题卡上。

答在试卷上的答案无效。

3．未使用答题卡的学校，请在试卷上做答。

1．下列二次根式中，最简二次根式是（ ）
A
B
C D 2．下列计算正确的是（ ）
A 2=±
B =
C =
D ．3=
3．下列各组线段a 、b 、c 中不能组成直角三角形的是（ ） A ．7a =，24b =，25c =
B ．40a =，50b =，60c =
C ．54a =
，1b =，34
c = D ．a =4b =，5c = 4．如图，在ABC △中，40A ∠=︒，AB AC =，点D 在AC 边上，以CB ，CD 为边作平行四边形BCDE ，则E ∠的度数为（ ）
A ．40°
B ．50°
C ．60°
D ．70°
5．“强国达人”张老师每天登录“学习强国”App 进行学习，在获得积分的同时，还可获得“点点通”附加奖励，他最近一周“点点通”每日收入明细如下表，则这组数据的众数和中位数分别是（ ）
星期 一 二 三 四 五 六 日 6．对于一次函数34y x =-+，下列结论错误的是（ ） A ．函数的图象与x 轴的交点坐标是()0,4 B ．函数值随自变量的增大而减小 C ．函数的图象不经过第三象限。

八年级下学期数学期末考试试卷一、选择题（共10题；共20分）1.下列式子中，属于最简二次根式的是（）A. B. C. D.2.在直角坐标系中，点P(-2，3)到原点的距离是( )A. B. C. D. 23.“倡导全民阅读”、“推动国民素质和社会文明程度显著提高”已成为新时期的重要工作.教育主管部门对某学校青年教师2019年度阅读情况进行了问卷调查，并将收集的数据统计如表，根据表中的信息判断，下列结论错误．．的是( )A. 该学校中青年教师2019年度看书数量的中位数为4本B. 该学校中青年教师2019年平均每人阅读8本书C. 该学校中参与调查的青年教师人数为40人D. 该学校中青年教师2019年度看书数量的众数为4本4.有100名学生参加两次科技知识测试，条形图显示两次测试的分数分布情况如图所示：根据条形图提供的信息，下列说法中，正确的是( )A. 两次测试，最低分在第二次测试中B. 第一次测试和第二次测试的平均分相同C. 第一次分数的中位数在20～39分数段D. 第二次分数的中位数在60～79分数段5.小明的作业本上做了以下四题：① ② ③ ④其中做错的题是（）A. ①B. ②C. ③D. ④6.已知四边形ABCD中，AC与BD交于点O，如果只给出条件“AB∥CD”，那么还不能判定四边形ABCD为平行四边形，给出以下四种说法：①如果再加上条件“BC＝AD”，那么四边形ABCD一定是平行四边形；②如果再加上条件“∠BAD＝∠BCD”，那么四边形ABCD一定是平行四边形；③如果再加上条件“OA＝OC”，那么四边形ABCD一定是平行四边形；④如果再加上条件“∠DBA＝∠CAB”，那么四边形ABCD一定是平行四边形.其中正确的说法是（）A. ①②B. ①③④C. ②③D. ②③④7.已知a、b、c是三角形的三边长，如果满足=0，则三角形的形状是（）A. 底与边不相等的等腰三角形B. 等边三角形C. 钝角三角形D. 直角三角形8.如图所示，梯子AB靠在墙上，梯子的底端A到墙根O的距离为2m，梯子的顶端B到地面距离为7m，现将梯子的底端A向外移到A'，使梯子的底端A'到墙根O距离为3m，同时梯子顶端B下降至B'，那么BB' ( )A. 等于1mB. 小于1mC. 大于1mD. 以上都不对9.八个边长为1的正方形如图摆放在平面直角坐标系中，经过P点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（）A. B. C. D.10.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示.则下列结论：①A，B两城相距300千米；②乙车比甲车晚出发1小时，却早到1.5小时；③乙车出发后2.5小时追上甲车；④当甲、乙两车相距40千米时，t＝或t＝，其中正确的结论有（）A. 1个B. 2个C. 3个D. 4个二、填空题（共5题；共5分）11.在函数y= 中，自变量x的取值范围是________．12.某校规定学生的学期学业成绩由三部分组成：平时占20%，期中占30%，期末占50%，小颖的平时、期中、期末成绩分别为85分、90分、92分，则她本学期的学业成绩为________分.13.如图，点O是矩形ABCD的对角线AC的中点，OM∥AB交AD于点M，若OM=2，BC=6，则OB的长为________.14.如图，一次函数y=﹣x+1与y=2x+m的图象相交于点P(n，2)，则关于x的不等式﹣x+1 ≥ 2x+m的解集为________.15.如图，正方形ABCD的边长是18，点E是AB边上的一个动点，点F是CD边上一点，，连接EF，把正方形ABCD沿EF折叠，使点A，D分别落在点，处，当点落在直线BC上时，线段AE 的长为________.三、解答题（共8题；共73分）16.计算.（1）；（2）.17.某校举办了一次知识竞赛，满分10分，学生得分均为整数，成绩达到6分以上（包括6分）为合格，达到9分以上（包括9分）为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如图所示.（1）补充完成下面的成绩统计分析表:（2）小明同学说:“这次竞赛我得了7分，在我们小组中排名属中游偏上!”观察上表可知，小明是________组的学生；（填“甲”或“乙”）（3）甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组，请你给出两条支持乙组同学观点的理由.18.先阅读下面的解题过程，然后再解答.形如的化简，我们只要找到两个数a，b，使，，即，，那么便有：.例如化简：.解：首先把化为，这里，，由于，，所以，所以.根据上述方法化简：.19.如图在平静的湖面上，有一支红莲BA，高出水面的部分AC为1米，一阵风吹来，红莲被吹到一边，花朵齐及水面(即AB=DB)，已知红莲移动的水平距离CD为3米，则湖水深CB为多少？20.如图，▱ABCD中，G是CD的中点，E是边长AD上的动点，EG的延长线与BC的延长线相交于点F，连接CE，DF.（1）求证：四边形CEDF是平行四边形.（2）填空：若AB＝3cm，BC＝5cm，∠B＝60°，则①当AE＝________时，四边形CEDF是矩形；②当AE ＝________时，四边形CEDF是菱形.21.如图是某型号新能源纯电动汽车充满电后，蓄电池剩余电量（千瓦时）关于已行驶路程（千米）的函数图象.（1）根据图象，直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程，当时，求1千瓦时的电量汽车能行驶的路程；（2）当时求关于的函数表达式，并计算当汽车已行驶180千米时，蓄电池的剩余电量.22.如图，直线y=kx+b经过点A（-5，0），B（-1，4）（1）求直线AB的表达式；（2）求直线CE：y=-2x-4与直线AB及y轴围成图形的面积；（3）根据图象，直接写出关于x的不等式kx+b＞-2x-4的解集.23.如图1，我们把对角线互相垂直的四边形叫做垂美四边形.（1）概念理解：我们已经学习了平行四边形、菱形、矩形、正方形，在这四种图形中是垂美四边形的是________.（2）性质探究：如图2，已知四边形ABCD是垂美四边形，试探究其两组对边AB，CD与BC，AD之间的数量关系，并写出证明过程.（3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，CE交AB于点M，已知AC=4，AB=5，求GE的长.答案解析部分一、选择题1.【解析】【分析】判断一个二次根式是否为最简二次根式主要方法是根据最简二次根式的定义进行，或直观地观察被开方数的每一个因数（或因式）的指数都小于根指数2，且被开方数中不含有分母，被开方数是多项式时要先因式分解后再观察．【解答】A、=3，故A错误；B、是最简二次根式，故B正确；C、=2，不是最简二次根式，故C错误；D、=，不是最简二次根式，故D错误；故选：B．【点评】本题考查了最简二次根式的定义．在判断最简二次根式的过程中要注意：（1）被开方数不含分母；（2）被开方数不含能开得尽方的因数或因式．2.【解析】【解答】解：过P作PE⊥x轴，连接OP，∵P（-2，3），∴PE=3，OE=2，∴在Rt△OPE中，根据勾股定理得：OP2=PE2+OE2，∴OP= ，则点P在原点的距离为.故答案为：B.【分析】在平面直角坐标系中找出P点，过P作PE垂直于x轴，连接OP，由P的坐标得出PE及OE的长，在直角三角形OPE中，由PE及OE的长，利用勾股定理求出OP的长，即为P到原点的距离.3.【解析】【解答】解：A、中间两个数都是4，所以中位数为4，故该学校中青年教师2016年度看书数量的中位数为4本是正确的，不符合题意；B、平均数为：140×（15×8+11×6+8×5+4×10+3×4+2×7）=7.3，原来的说法错误，符合题意；C、8+6+5+10+4+7=40（人）故该学校中参与调查的青年教师人数为40人是正确的，不符合题意.D、4出现的次数最多，是10次，众数为4本是正确的，不符合题意.故答案为：B.【分析】根据统计表可得出每个月课外阅读书籍的数量，即可求得平均数；出现次数最多的数据是众数；将这些数据按大小顺序排列，中间两个数的平均数为中位数；依此即可求解.4.【解析】【解答】解：根据统计图各部分表示的意义，发现：A、两次测试，最低分在第一次测试中，错误；B、根据此条形统计图，显然第二次测试的分数明显高于第一次的分数，错误；C、共有100名学生，所以中位数应是第50和51的平均数，显然第一次测试的中位数落在20～39段内，正确；D、第二次测试的中位数应落在40～59段内，错误.故答案为：C.【分析】观测分析已知的统计图，小长方形的宽指分数段，小长方形的高指各分数段的频数，小长方形的高越高，频数越大，再根据加权平均数的计算公式、中位数的定义即可判断求解.5.【解析】【解答】，所以①符合题意；，所以②符合题意；因为，则，所以③符合题意；与不是同类二次根式，不能合并，所以④不符合题意.故答案为：D.【分析】根据二次根式的性质可判断①，根据二次根式的乘法运算可判断②，根据二次根式的性质和乘法可判断③，根据同类二次根式的定义可判断6.【解析】【解答】解：其中正确的说法是②、③.因为再加上条件“∠BAD=∠BCD”，即可求得另一组对角相等，那么四边形ABCD一定是平行四边形；如果再加上条件“AO=OC”，即可证明△AOB≌△COD，从而得出AB=DC，那么四边形ABCD一定是平行四边形.故正确的说法②、③.故答案为：C.【分析】①一组对边平行、另一组对边相等不能判断四边形是平行四边形，它还可能是等腰梯形；②根据内错角相等两直线平行可得BC∥AD，根据两组对边分别平行的四边形是平行四边形可得四边形ABCD是平行四边形；③结合已知可证△ABO≌△CDO，于是可得AB=DC，根据一组对边平行且相等的四边形是平行四边形可得四边形ABCD是平行四边形；④不能判定四边形ABCD是平行四边形.7.【解析】【解答】解：∵（a﹣6）2≥0，≥0，|c﹣10|≥0，∴a﹣6=0，b﹣8=0，c﹣10=0，解得：a=6，b=8，c=10，∵62+82=36+64=100=102，∴是直角三角形．故选D．【分析】首先根据绝对值，平方数与算术平方根的非负性，求出a，b，c的值，在根据勾股定理的逆定理判断其形状是直角三角形．8.【解析】【解答】解：由题意得：，在中，，，在中，，，，，即小于，故答案为：B.【分析】先在中，利用勾股定理求出AB的长，从而可得的长，再在中，利用勾股定理求出的长，然后根据线段的和差可得的长，最后根据实数的大小比较即可得.9.【解析】【解答】解：直线l和八个正方形的最上面交点为P，过P作PB⊥OB于B，过P作PC⊥OC于C，直线L交y轴于点A，∵正方形的边长为1，∴PB=4，OB=3,∴点P（4,3）∵经过P点的一条直线l将这八个正方形分成面积相等的两部分，∴三角形ABP面积是8÷2+1=5，∴BP•AB=5，∴AB=2.5，∴OA=3-2.5=0.5，∴点A（0,0.5）由此可知直线l经过（0，0.5），（4，3）设直线方程为y=kx+b，则，解得.∴直线l解析式为.故答案为：A.【分析】直线l和八个正方形的最上面交点为P，过P作PB⊥OB于B，过P作PC⊥OC于C，直线L交y 轴于点A，易知OB＝3，PB=4，即可得出点A的坐标，利用三角形的面积公式和已知条件求出点A的坐标，根据待定系数法即可得到该直线l的解析式．10.【解析】【解答】解：由图象可知A、B两城市之间的距离为300km，故①正确；甲行驶的时间为5小时，而乙是在甲出发1小时后出发的，且用时3小时，即比甲早到1小时，故②错误；设甲车离开A城的距离y与t的关系式为y甲＝kt，把（5，300）代入可求得k＝60，∴y甲＝60t，把y＝150代入y甲＝60t，可得：t＝2.5，设乙车离开A城的距离y与t的关系式为y乙＝mt+n，把（1，0）和（2.5，150）代入可得，解得，∴y乙＝100t﹣100，令y甲＝y乙可得：60t＝100t﹣100，解得t＝2.5，即甲、乙两直线的交点横坐标为t＝2.5，此时乙出发时间为1.5小时，即乙车出发1.5小时后追上甲车，故③错误；令|y甲﹣y乙|＝40，可得|60t﹣100t+100|＝40，即|100﹣40t|＝40，当100﹣40t＝40时，可解得t＝，当100﹣40t＝﹣40时，可解得t＝，又当t＝时，y甲＝40，此时乙还没出发，当t＝时，乙到达B城，y甲＝260；综上可知当t的值为或或或t＝时，两车相距40千米，故④不正确；故答案为：A.【分析】由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式，可求得两函数图象的交点，进而判断，再令两函数解析式的差为40，可求得t，可得出答案.二、填空题11.【解析】【解答】解：由题意得，x+2≠0，解得x≠﹣2．故答案为：x≠﹣2．【分析】根据分式有意义，分母不等于0列式计算即可得解．12.【解析】【解答】解:85×20%+90×30%+92×50%=90，故答案为：90.【分析】根据加权平均数的计算公式即可求解.13.【解析】【解答】解：∵四边形ABCD是矩形，∴∠ABC=90°，AD=BC=6，∵O是矩形ABCD的对角线AC的中点，OM∥AB，∴OM是△ADC的中位线，∵OM=2，∴DC=4，∴AC= =2 ，又∵O是矩形ABCD的对角线AC的中点∴BO= AC= ，故答案为：【分析】已知OM是△ADC的中位线，再结合已知条件则DC的长可求出，所以利用勾股定理可求出AC的长，由直角三角形斜边上中线的性质则BO的长即可求出.14.【解析】【解答】解：∵一次函数y= -x+1和y=-2x+m相交于点P（n，2），∴-n+1=2，解得：n= -1，观察图象知：关于x的不等式﹣x+1 ≥ 2x+m的解集为x≤-1，故答案为：x≤-1.【分析】首先将已知点的坐标代入直线y= -x+1求得n的值，由于求关于x的不等式﹣x+1 ≥ 2x+m的解集，就是求直线y= -x+1都在直线y=-2x+m的上方部分相应的自变量的取值范围，然后观察函数图象得到在点P 的左边，直线y= -x+1都在直线y=-2x+m的上方，据此求解.15.【解析】【解答】解：分两种情况：①当D′落在线段BC上时，连接ED、ED′、DD′，如图1所示：由折叠可得，D，D'关于EF对称，即EF垂直平分DD'，∴DE＝D′E，∵正方形ABCD的边长是18，∴AB＝BC＝CD＝AD＝18，∵CF＝8，∴DF＝D′F＝CD−CF＝10，∴CD′＝＝6，∴BD'＝BC−CD'＝12，设AE＝x，则BE＝18−x，在Rt△AED和Rt△BED'中，由勾股定理得：DE2＝AD2＋AE2＝182＋x2，D'E2＝BE2＋BD'2＝（18−x）2＋122，∴182＋x2＝（18−x）2＋122，解得：x＝4，即AE＝4；②当D′落在线段BC延长线上时，连接ED、ED′、DD′，如图2所示：由折叠可得，D，D'关于EF对称，即EF垂直平分DD'，∴DE＝D′E，∵正方形ABCD的边长是18，∴AB＝BC＝CD＝AD＝18，∵CF＝8，∴DF＝D′F＝CD−CF＝10，CD'＝＝6，∴BD'＝BC＋CD'＝24，设AE＝x，则BE＝18−x，在Rt△AED和Rt△BED'中，由勾股定理得：DE2＝AD2＋AE2＝182＋x2，D'E2＝BE2＋BD'2＝（18−x）2＋242，∴182＋x2＝（18−x）2＋242，解得：x＝16，即AE＝16；综上所述，线段AE的长为4或16；故答案为：4或16.【分析】分两种情况：①D′落在线段BC上，②D′落在线段BC延长线上，分别连接ED、ED′、DD′，利用折叠的性质以及勾股定理，即可得到线段AE的长.三、解答题16.【解析】【分析】（1）先根据二次根式的乘除法法则计算二次根式的乘法和除法，再根据二次根式的性质进行化简，然后合并同类二次根式即可；（2）先根据二次根式的性质将各个二次根式化为最简二次根式，再合并括号内的同类二次根式，接着利用二次根式的乘法法则计算二次根式的乘法，最后合并同类二次根式得出答案.17.【解析】【解答】解：（2）观察上表可知，小明是甲组的学生；故答案为：甲；【分析】（1）将甲组成绩按照从小到大的顺序排列，找出第5、6个成绩，求出平均数即为甲组的中位数；找出乙组成绩，求出乙组的平均分，填表即可；（2）观察表格，成绩为7分处于中游略偏上，应为甲组的学生；（3）乙组的平均分高于甲组，中位数高于甲组，方差小于甲组，所以乙组成绩好于甲组.18.【解析】【分析】应先找到哪两个数的和为13，积为42.再判断是选择加法，还是减法，进而根据完全平方公式分解因式，最后根据二次根式的性质即可算出答案.19.【解析】【分析】在Rt△BCD中，运用勾股定理求解即可.20.【解析】【解答】解：（2）①如图四边形CEDF是矩形时，在Rt△CDF中，CD＝AB＝3，∠DCF＝60°，∠CFD＝90°，∴CF＝CD＝.∵ED＝CF＝，∴AE＝AD﹣DE＝②如图四边形CEDF是菱形时，易知△CDF，△CDE都是等边三角形，∴DE＝CD＝AB＝3，∴AE＝AD﹣ED＝5﹣3＝2.故答案为：，2.【分析】（1）只要证明△FCG≌△EDG，可得FG=EG，结合CG=GD即可证明；（2）①如图四边形CEDF是矩形时，在Rt△CDF中，CD=AB=3，∠DCF=60°，∠CFD=90°，易知CF= CD= ，由ED=CF= ，即可推出AE=AD-DE= ②如图四边形CEDF是菱形时，易知△CDF，△CDE都是等边三角形，推出DE=CD=AB=3，可得AE=AD-ED=5-3=2.21.【解析】【分析】（1）由图象可知，蓄电池剩余电量为35千瓦时时汽车已行驶了150千米，据此即可求出1千瓦时的电量汽车能行驶的路程；（2）运用待定系数法求出y关于x的函数表达式，再把x=180代入即可求出当汽车已行驶180千米时，蓄电池的剩余电量.22.【解析】【分析】（1）利用待定系数法求一次函数解析式即可；（2）联立两直线解析式，解方程组可得到两直线交点C的坐标，即可求直线CE：y=-2x-4与直线AB及y轴围成图形的面积；（3）根据图形，找出点C右边的部分的x的取值范围即可.23.【解析】【解答】解：（1）菱形，正方形；故答案为：菱形，正方形；【分析】（1）根据垂美四边形的性质即可判断；（2）连接AC,BD,设交点为E,由垂美四边形的性质得AC⊥BD,故得∠AED=∠AEB=∠BEC=∠CED=90°，由勾股定理可得结果；（3）连接CG，BE，根据条件可得△GAB≌△CAE，可得∠ABG=∠AEC，根据条件证明四边形CGEB是垂美四边形，由勾股定理，得CB2=9，CG2=32，BE2=50，GE2=CG2+BE2-CB2=73，即可得到GE= .。

第 1 页 共 23 页
2019-2020学年河南省信阳市八年级下学期期末考试数学试卷
一．选择题（共10小题，每小题3分，满分30分）
1．计算√8√2
=（ ） A ．4 B ．2 C ．2√2 D ．√2
2．下列各式属于最简二次根式的是（ ）
A ．√8
B ．√x 2+1
C ．√y 2
D ．√12 3．计算（√3）2的结果是（ ）
A ．3
B ．﹣3
C ．9
D ．﹣9
4．下列说法中，错误的是（ ）
A ．对角线互相垂直的四边形是菱形
B ．对角线互相平分的四边形是平行四边形
C ．菱形的对角线互相垂直
D ．平行四边形的对角线互相平分
5．如图，在△ABC 中，∠C ＝60°，AD 是BC 边上的高，点E 为AD 的中点，连接BE 并
延长交AC 于点F ．若∠AFB ＝90°，EF ＝2，则BF 长为（ ）
A ．4
B ．6
C ．8
D ．10
6．由于台风的影响，一棵树在离地面6m 处折断，树顶落在离树干底部8m 处，则这棵树在
折断前（不包括树根）长度是（ ）
A ．8m
B ．10m
C ．16m
D ．18m
7．顺次连结菱形四边中点所得的四边形一定是（ ）
A ．平行四边形 B
．矩形
C ．菱形
D ．正方形。

河南省信阳市八年级下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）(2017·徐州模拟) 下列说法中正确的是（）A . 有两个角为直角的四边形是矩形B . 矩形的对角线互相垂直C . 平行四边形的对角线互相平分D . 对角线互相垂直的四边形是菱形2. （2分）如图，将△ABC沿DE，EF翻折，顶点A，B均落在点O处，且EA与EB重合于线段EO，若∠DOF=142°，则∠C的度数为（）A . 38°B . 39°C . 42°D . 48°3. （2分） (2019八下·南县期中) 下列判断错误的是（）A . 四个角相等的四边形是矩形B . 对角线垂直的四边形是菱形C . 对角线相等的平行四边形是矩形D . 对角线垂直的平行四边形是菱形4. （2分）(2017·临沂模拟) 如图，已知△ABC中，AB=AC=2，∠B=30°，P是BC边上一个动点，过点P作PD⊥BC，交△ABC的AB边于点D．若设PD为x，△BPD的面积为y，则y与x之间的函数关系的图象大致是（）A .B .C .D .5. （2分） (2020八上·邛崃期末) 在平面直角坐标系中，点P与点M关于y轴对称，点N与点M关于x轴对称，若点P的坐标为(－2,3)，则点N的坐标为（）A . (－3,2)B . (2,3)C . (2,－3)D . (－2,－3)6. （2分） (2016八上·孝南期中) 如图是一个五角星图案，则∠A+∠B+∠C+∠D+∠E的度数是（）A . 180°B . 150°C . 135°D . 120°7. （2分） (2016九上·浦东期中) 在△ABC中，点D，E分别在边AB，AC上，AD：BD=1：2，那么下列条件中能够判断DE∥BC的是（）A .B .C .D .8. （2分） (2019八上·南岗期末) 若，，则的值为（）A .B .C .D .9. （2分） (2016七下·随县期末) 实数a、b在数轴上的位置如图所示，且|a|＞|b|，则化简的结果为（）A . 2a+bB . ﹣2a+bC . bD . 2a﹣b10. （2分） (2017七下·门头沟期末) 在下列命题中，为真命题的是（）A . 相等的角是对顶角B . 平行于同一条直线的两条直线互相平行C . 同旁内角互补D . 垂直于同一条直线的两条直线互相垂直11. （2分）(2016·慈溪模拟) 在平面直角坐标系中，二次函数y=﹣x2+6x﹣9的图象顶点为A，与y轴交于点B．若在该二次函数图形上取一点C，在x轴上取一点D，使得四边形ABCD为平行四边形，则D点的坐标为（）A . （﹣9，0）B . （﹣6，0）C . （6，0）D . （9，0）12. （2分）(2018·阳信模拟) 已知a，b，c为常数，点P(a，c)在第二象限，则关于x的方程ax2＋bx＋c ＝0的根的情况是（）A . 有两个相等的实数根B . 有两个不相等的实数根C . 没有实数根D . 无法判断二、填空题 (共4题；共4分)13. （1分） (2016八上·台安期中) 如果一个正多边形的每个内角为150°，则这个正多边形的边数是________．14. （1分） (2016八上·杭州期末) 有一块直角三角形绿地，量得两直角边长分别为3m，4m，现在要将绿地扩充成等腰三角形，且扩充时只能延长两条直角边中的一条，则扩充后等腰三角形绿地的面积为________m2 ．15. （1分） (2016九上·松原期末) 已知关于x的方程 +6x+k=0的两个根分别是、，且，则k的值为________．16. （1分） (2019八上·确山期中) 如图，在三角形纸片中，，沿过点的直线折叠这个三角形，使点落在边上的点处，折痕为，则的周长等于________ .三、解答题 (共4题；共55分)17. （20分）用合适的方法解下列方程：（1） x2=x（2） x2﹣2x﹣3=0（3）（x﹣2）2﹣5=0（4） x（x﹣2）+x﹣2=0．18. （10分） (2016七下·柯桥期中) 如图：在正方形网格中有一个△ABC，按要求进行下列作图（只借助于网格，需写出结论）：（1）过点A画出BC的平行线；（2）画出先将△ABC向右平移5格，再向上平移3格后的△DEF；19. （15分）(2018·高安模拟) 如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC于点D，过点E做直线l∥BC．（1）判断直线l与⊙O的位置关系，并说明理由；（2）若∠ABC的平分线BF交AD于点F，求证：BE=EF；（3）在（2）的条件下，若DE=4，DF=3，求AF的长．20. （10分） (2019九上·顺德月考) 如图，在□ABCD中，AB＝ BC，点E是BC的中点，且EF//AB，AE、BF交于点O，连接EF，OC．（1）求证：四边形ABEF是菱形；（2）若BC＝8，∠ABC＝60°，求△OEC的面积．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共4题；共55分)17-1、17-2、17-3、17-4、18-1、18-2、19-1、19-2、19-3、20-1、20-2、。

河南省信阳市2020版八年级上学期期末数学试卷（II）卷姓名:________ 班级:________ 成绩:________一、选择题 (共8题；共16分)1. （2分） 2的算术平方根是（）A .B .C . 4D . 42. （2分）面积为10m2的正方形地毯，它的边长介于（）A . 2m与3m之间B . 3m与4m之间C . 4m与5m之间D . 5m与6m之间3. （2分）下列各组数中互为相反数的是（）A . 5和B . -|-5|和-(-5)C . -5和D . -5和4. （2分）计算(－4x)3÷(－2x)2的结果是（）A . －16xB . 16xC . 2xD . －2x5. （2分）小雷为表示出自己七年级几次数学测试成绩的变化情况，他应该采用的统计图是（）A . 折线统计图B . 条形统计图C . 扇形统计图D . 以上均可以6. （2分）如图，把矩形纸片ABCD纸沿对角线折叠，设重叠部分为AEBD，那么，下列说法错误的是（）A . △EBD是等腰三角形，EB=EDB . 折叠后∠ABE和∠CBD一定相等C . 折叠后得到的图形是轴对称图形D . △EBA和△EDC一定是全等三角形7. （2分）(2017·平南模拟) 如图，在矩形ABCD中，AB=3，BC=2，点E为AD中点，点F为BC边上任一点，过点F分别作EB，EC的垂线，垂足分别为点G，H，则FG+FH为（）A .B .C .D .8. （2分）如图，正六边形螺帽的边长是2cm，这个扳手的开口a的值应是（）A . 2cmB . 5cmC . 4cmD . cm二、填空题 (共6题；共6分)9. （1分） (2016八上·长泰期中) 计算：（﹣0.125）2016×82016=________．10. （1分）(2017·青浦模拟) 在实数范围内分解因式：x2﹣3=________．11. （1分） (2017八上·南安期末) 写出命题“内错角相等”的逆命题________．12. （1分）(2018·十堰) 如图，Rt△ABC中，∠BAC=90°，AB=3，AC=6 ，点D，E分别是边BC，AC上的动点，则DA+DE的最小值为________．13. （1分）如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于E，F两点，再分别以E、F为圆心，大于EF的长为半径画弧，两弧交于点P，作射线AP，交CD于点M．若∠ACD=120°，则∠MAB的度数为________ ．14. （1分）(2018·广安) 如图，∠AOE=∠BOE=15°，EF∥OB，EC⊥OB于C，若EC=1，则OF=________．三、解答题 (共8题；共63分)15. （10分） (2017八上·德惠期末) 计算下面各题（1）计算：（x2y﹣ xy2﹣xy）÷ xy．（2）若10m=3，10n=2，求102m+n的值．16. （5分）计算：(2x－5)2－(2x+5)217. （5分）在五边形ABCDE中，∠A＝∠B＝∠C＝∠D＝120°，AB＝4，BC＝4，CD＝8，求五边形的周长和面积．18. （5分）如图所示，在△ABC中，∠BAC=90°，AD⊥BC于D，∠ACB的平分线交AD于E，交AB于F，FG⊥BC 于G，请猜测AE与FG之间有怎样的数量关系，并说明理由．19. （5分） (2016九上·芦溪期中) 如图，在边长为10的正方形ABCD中，△PAQ是正三角形，求PB的长．20. （13分） (2016七下·玉州期末) 某校为了增强学生的安全意识，组织全校学生參加安全知识竞赛，赛后组委会随机抽查部分学生的成绩进行统计（由高到低分四个等级）．根据调査的数据绘制成如下的条形统计图和扇形统计图．根据以上不完整的统计图提供的信息，解答下列问题：（1）组委会共抽査了________名学生的安全知识竞赛成绩，扇形统计图中B级所占的百分比 b=________扇形统计图中．C级所对应的圆心角的度数是________度．（2）补全条形统计图：（3）若该校共有800名学生，请估算该校安全知识竞赛成绩获得A级的人数．21. （5分）超速行驶容易引发交通事故．如图，某观测点设在到公路l的距离为100米的点P处，一辆汽车由西向东匀速驶来，测得此车从A处行驶到B处所用的时间为3秒，并测得∠APO=60°，∠BPO=45°，是判断此车是否超过了每小时80千米的限制速度？（参考数据：=1.41，=1.73）22. （15分）(2019·新宾模拟) 如图，四边形中，，将绕点顺时针旋转一定角度后，点的对应点恰好与点重合，得到 .（1）请求出旋转角的度数；（2）请判断与的位置关系，并说明理由；（3）若，，试求出四边形的对角线的长.参考答案一、选择题 (共8题；共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、填空题 (共6题；共6分)9-1、10-1、11-1、12-1、13-1、14-1、三、解答题 (共8题；共63分)15-1、15-2、16-1、17-1、18-1、19-1、20-1、20-2、20-3、21-1、22-1、22-2、22-3、第11 页共11 页。

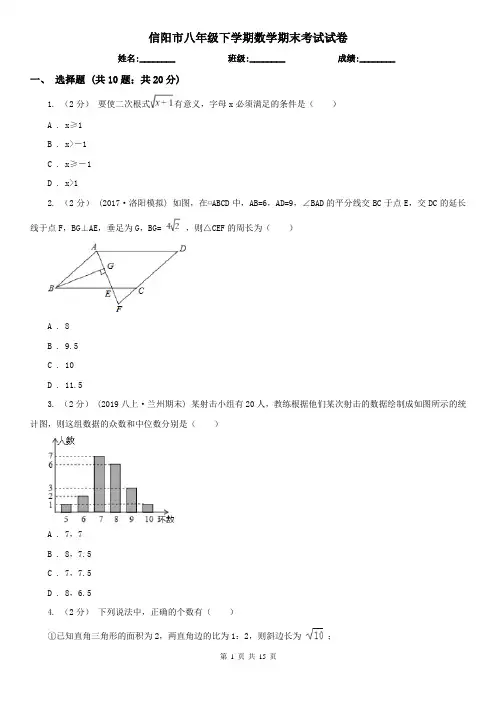
信阳市八年级下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分）要使二次根式有意义，字母x必须满足的条件是（）A . x≥1B . x>－1C . x≥－1D . x>12. （2分）(2017·洛阳模拟) 如图，在▱ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG= ，则△CEF的周长为（）A . 8B . 9.5C . 10D . 11.53. （2分） (2019八上·兰州期末) 某射击小组有20人，教练根据他们某次射击的数据绘制成如图所示的统计图，则这组数据的众数和中位数分别是（）A . 7，7B . 8，7.5C . 7，7.5D . 8，6.54. （2分）下列说法中，正确的个数有（）①已知直角三角形的面积为2，两直角边的比为1：2，则斜边长为；②直角三角形的最大边长为，最短边长为1，则另一边长为；③在△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC为直角三角形；④等腰三角形面积为12，底边上的高为4，则腰长为5．A . 1个B . 2个C . 3个D . 4个5. （2分）若x﹣y= ，xy=，则代数式（x﹣1）（y+1）的值等于（）A .B .C .D . 26. （2分） (2019七下·营口月考) 下列计算正确的是（）A .B .C .D .7. （2分） (2018八上·河口期中) 下列各曲线表示的y与x的关系中，y不是x的函数的是（）A .B .C .D .8. （2分） (2017八下·长春期末) 如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，∠BED=150°，则∠A的大小为（）A . 150°B . 130°C . 120°D . 100°9. （2分） (2017九下·盐都开学考) 如图，边长分别为2和4的两个全等三角形，开始它们在左边重叠，大△ABC固定不动，然后把小△A′B′C′自左向右平移，直至移到点B′到C重合时停止，设小三角形移动的距离为x，两个三角形的重合部分的面积为y，则y关于x的函数图象是（）A .B .C .D .10. （2分）如图，直线y= 与y轴交于点A，与直线y=﹣交于点B，以AB为边向右作菱形ABCD，点C恰与原点O重合，抛物线y=（x﹣h）2+k的顶点在直线y=﹣上移动．若抛物线与菱形的边AB、BC都有公共点，则h的取值范围是（）A . ﹣2B . ﹣2≤h≤1C . ﹣1D . ﹣1二、填空题 (共6题；共8分)11. （1分）(2017·丰县模拟) 计算： =________．12. （2分） (2017七下·朝阳期中) 命题“两直线平行，内错角相等”的题设是________，结论是________．13. （1分）中国跳水队的奥运选拔赛中，甲、乙、丙、丁四名运动员的平均成绩与标准差S如下表，因为中国跳水队的整体水平高，所以要从中选一名参赛，应选择________ .14. （1分） (2017九上·顺德月考) 已知菱形的边长是10cm，较短的对角线长为12cm，则较长的对角线为________。

信阳市八年级下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分） (2019七上·如皋期末) 据江苏省统计局统计：2018年三季度南通市GDP总量为亿元，位于江苏省第4名，将这个数据用科学记数法表示为A . 亿元B . 亿元C . 亿元D . 亿元2. （2分）(2020·北京模拟) 如图，在数轴上，点B在点A的右侧．已知点A对应的数为，点B对应的数为m ．若在之间有一点C ，点C到原点的距离为2，且，则m的值为（）A . 4B . 3C . 2D . 13. （2分）下列二次根式中属于最简二次根式的是（）A .B .C .D .4. （2分） (2017八下·德州期末) 函数y=2x﹣5的图象经过（）A . 第一、三、四象限B . 第一、二、四象限C . 第二、三、四象限D . 第一、二、三象限5. （2分） (2017九上·河东开学考) 如图，矩形ABCD中，对角线AC，BD交于点O．若∠AOB=60°，BD=8，则AB的长为（）A . 4B .C . 3D . 56. （2分） (2017八下·德州期末) 如图，正方形ABCD中，AE垂直于BE，且AE=3，BE=4，则阴影部分的面积是（）A . 16B . 18C . 19D . 217. （2分） (2017八下·德州期末) 某市一周的日最高气温如图所示，则该市这周的日最高气温的众数是（）A . 25B . 26C . 27D . 288. （2分） (2017八下·德州期末) 已知P1（﹣3，y1），P2（2，y2）是一次函数y=﹣x﹣1的图象上的两个点，则y1 ， y2的大小关系是（）A . y1=y2B . y1＜y2C . y1＞y2D . 不能确定9. （2分） (2017八下·德州期末) 2022年将在北京﹣张家口举办冬季奥运会，很多学校开设了相关的课程．如表记录了某校4名同学短道速滑选拔赛成绩的平均数与方差s2：队员1队员2队员3队员4平均数（秒）51505150方差s2（秒2） 3.5 3.514.515.5根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（）A . 队员1B . 队员2C . 队员3D . 队员410. （2分）(2017·河北模拟) 如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F，若BF=12，AB=10，则AE的长为（）A . 13B . 14C . 15D . 1611. （2分） (2017八下·德州期末) 如图，菱形ABCD的一边中点M到对角线交点O的距离为5cm，则菱形ABCD的周长为（）A . 5cmB . 10cmC . 20cmD . 40cm12. （2分） (2017八下·盐湖期末) 一次函数y1=kx+b与y2=x+a的图象如图，则下列结论①k＜0；②a＞0；③当x＜3时，y1＜y2中，正确的个数是（）A . 0B . 1C . 2D . 3二、填空题 (共5题；共5分)13. （1分）已知数据x1 ， x2 ， x3的方差为5，则资料2x1－1，2x2－1，2x3－1的方差为________ ．14. （1分） (2016九上·思茅期中) 函数中，自变量x的取值范围是________．15. （1分） (2017八下·德州期末) 计算 =________．16. （1分） (2017八下·德州期末) 矩形纸片ABCD的边长AB=8，AD=4，将矩形纸片沿EF折叠，使点A与点C重合，折叠后在某一面着色（如图），则着色部分的面积为________．17. （1分） (2017八下·德州期末) 如图，直线y=kx+b（k≠0）与x轴交于点（﹣4，0），则关于x的方程kx+b=0的解为x=________．三、解答题 (共7题；共65分)18. （10分） (2019七下·嘉兴期中)（1）计算：；（2）化简： .19. （5分） (2017八下·德州期末) 一艘轮船以16海里/时的速度离开港口（如图），向北偏东40°方向航行，另一艘轮船在同时以12海里/时的速度向北偏西一定的角度的航向行驶，已知它们离港口一个半小时后相距30海里（即BA=30），问另一艘轮船的航行的方向是北偏西多少度？20. （5分） (2017八下·德州期末) 已知：如图，点E，F分别为▱ABCD的边BC，AD上的点，且∠1=∠2．求证：AE=CF．21. （10分） (2017八下·德州期末) 阅读对人成长的影响是巨大的，一本好书往往能改变人的一生，每年的4月23日被联合国教科文组织确定为“世界读书日”．某校本学年开展了读书活动，在这次活动中，八年级（1）班40名学生读书册数的情况如表：读书册数45678人数（人）6410128根据表中的数据，求：（1）该班学生读书册数的平均数；（2）该班学生读书册数的中位数．22. （10分） (2017八下·德州期末) 世界上大部分国家都使用摄氏温度（℃），但美国、英国等国家的天气预报使用华氏温度（℉）．两种计量之间有如表对应：摄氏温度x（℃）…0510152025…华氏温度y（℉）…324150596877…已知华氏温度y（℉）是摄氏温度x（℃）的一次函数．（1）求该一次函数的表达式；（2）当华氏温度﹣4℉时，求其所对应的摄氏温度．23. （10分） (2017八下·德州期末) 如图，矩形ABCD的对角线AC、BD交于点O，且DE∥AC，CE∥BD．（1）求证：四边形OCED是菱形；（2）若∠BAC=30°，AC=4，求菱形OCED的面积．24. （15分） (2017八下·德州期末) 已知：甲乙两车分别从相距300千米的A、B两地同时出发相向而行，其中甲到达B地后立即返回，如图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．（1）求甲车离出发地的距离y甲（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；（2）它们出发小时时，离各自出发地的距离相等，求乙车离出发地的距离y乙（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；（3）在（2）的条件下，求它们在行驶的过程中相遇的时间．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共5题；共5分)13-1、14-1、15-1、16-1、17-1、三、解答题 (共7题；共65分)18-1、18-2、19-1、20-1、21-1、21-2、22-1、22-2、23-1、23-2、24-1、24-2、24-3、。

2023-2024学年度下期期末调研考试试卷八年级数学注意事项：1.本试卷分试卷和答题卡两部分。

试卷共6页，三大题，满分120分，考试时间100分钟。

2.试题卷上不要答题。

请用0.5毫米黑色签字水笔直接把答案写在答题卡上，答在试卷上的答案无效。

3.答题前，考生务必将本人姓名、准考证号填写在答题卡第一面的指定位置上。

一、选择题：本题共10小题，每小题3分，共30分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.若代数式x−5有意义，则x的取值范围是 ( )A. x≥0B. x<5C. x≤5D. x≥52.在▱ABCD 中,∠A:∠B:∠C:∠D的比值可能是 ( )A.1:2:3:4B.3:4:4:3C.3:4:3:4D.1:2:2:13.第七届全国人民代表大会常务委员会第十七次会议审议通过的《中华人民共和国残疾人保障法》第14条规定：“每年五月第三个星期日，为全国助残日.”在第33个“全国助残日”到来之际，某校举行了捐款活动，并调查了某班30名同学的捐款情况如下表：捐款5元10元15元20元25元30元人数1196211则该班同学捐款的平均数为 ( )A.11元B.13元C.15元D.20元4.在下列各组数据中，不能作为直角三角形的三边长的是 ( )A.3,4,6B.7,24,25C.6,8,10D.9,12,155.如图描述了林老师某日傍晚的一段生活过程：他晚饭后，从家里散步到超市，在超市停留了一会儿，马上又去书店，看了一会儿书，然后快步走回家.在平面直角坐标系中，x轴表示时间，y轴表示林老师离家的距离，根据图象提供的信息，下列说法错误的是( ) A.林老师家距超市1.5千米B.林老师在书店停留了30分C.林老师从家里到超市的平均速度与从超市到书店的平均速度相等D.林老师从书店到家的平均速度是10 千米/时6.下列有关一次函数y=-3x+2 的说法中，错误的是 ( )A.y的值随着x值的增大而减小B.函数图象与y轴的交点坐标为(0，2)C.当x>0时,y>2D.函数图象经过第一、二、四象限7.某幼儿园对全体小朋友爱吃哪种粽子做调查，以决定最终买哪种口味的粽子，下面的调查数据最值得关注的是 ( )A.方差B.平均数C.中位数D.众数8.菱形OABC 在平面直角坐标系中的位置如图所示，若OA=2,∠AOC=45°,则B的坐标是 ( )A.(2+2,2)B.(2−2,2)C.(−2+2,2)D.(−2−2,2)9.若kb<0,b−k>0,则函数y=kx+b与y=bx+k在同一坐标系中的大致图象是( )10.如图,在四边形ABCD 中, ∠ABC=90°,AD‖BC,AE‖DC交BC 于点E,AE 平分∠BAC,AO=CO,AD=DC=2,下面结论：①AC=2AB;②AB=3;③S ADC=2S ABE;④BO⊥AE.其中正确的个数有（）A.1个B.2个C.3个D.4个二、填空题。

2020-2021学年河南省信阳市八年级数学第二学期期末质量检测试题注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（每题4分，共48分）1．一元二次方程x2﹣8x+20=0的根的情况是（）A．没有实数根B．有两个相等的实数根C．只有一个实数根D．有两个不相等的实数根2．如图，将△ABC绕点B逆时针旋转α，得到△EBD，若点A恰好在ED的延长线上，则∠CAD的度数为（）A．90°﹣αB．αC．180°﹣αD．2α3．已知一个多边形的内角和为1080°，则这个多边形是（）A．九边形B．八边形C．七边形D．六边形4．等腰三角形的底角是70°，则顶角为（）A．40B．70C．55D．455．某学校要种植一块面积为100 m2的长方形草坪，要求两边长均不小于5 m，则草坪的一边长为y（单位：m）随另一边长x（单位：m）的变化而变化的图象可能是（）A．B．C．D．6．七巧板是我国祖先的一项卓越创造．下列四幅图中有三幅是小明用如图所示的七巧板拼成的，则不是小明拼成的那副图是（）A．B． C．D．7．如图，菱形ABCD的一边AB的中点E到对角线交点O的距离为4cm，则此菱形的周长为()A．8 cm B．16 cm C．162cm D．32 cm8．关于正比例函数y＝﹣3x，下列结论正确的是（）A．图象不经过原点B．y随x的增大而增大C．图象经过第二、四象限D．当x＝时，y＝19．如图，将一根长为24cm的筷子，置于底面直径为5cm，高为12cm的圆柱水杯中，设筷子露在杯子外面的长度为hcm，则h的取值范围是（）A ．12cm ≤h ≤19cmB ．12cm ≤h ≤13cmC ．11cm ≤h ≤12cmD ．5cm ≤h ≤12cm 10．下列三角形纸片，能沿直线剪一刀得到直角梯形的是（ ）A ．B ．C ．D ．11．如图所示，在ABC 中，AB 的垂直平分线DE 交AC 于点D ，交AB 于点E ，如果5,4AC BC ==，则BCD ∠的周长是（ ）A ．6B ．7C ．8D ．912．如图，在平面直角坐标系中，线段AB 的端点坐标为A （-2,4），B （4,2），直线y=kx-2与线段AB 有交点，则K 的值不可能是（ ）A ．-5B ．-2C ．3D ．5二、填空题（每题4分，共24分）13．如图，AD ∥EF ∥GH ∥PQ ∥BC ，AE ＝EG ＝GP ＝PB ，AD ＝2，BC ＝10，则EF ＋PQ 长为__________．14． 若A （x 1，y 1）和B （x 2，y 2）在反比例函数2y x=的图象上，且0＜x 1＜x 2，则y 1与y 2的大小关系是y 1 y 2；15．根据指令[,](0,0180)S S αα≥<<，机器人在平面上能完成下列动作：先原地逆时针旋转角度α，再朝其面对的方向沿直线行走距离S ，现机器人在平面直角坐标系的坐标原点，且面对x 轴正方向．请你给机器人下一个指令__________，使其移动到点()3,3-．16．若关于x 的不等式2x ﹣3a +2≥0的最小整数解为5，则实数a 的值为_____ 17．（1）()25=____________；（2）126÷=____________． 18．如图，矩形ABCD 的对角线AC 与BD 相交于点O ，，．若，，则四边形OCED的面积为___.三、解答题（共78分）19．（8分）如图，AD 是等腰△ABC 底边BC 上的高，点O 是AC 中点，延长DO 到E ，使AE ∥BC ，连接AE ． （1）求证：四边形ADCE 是矩形；（2）①若AB ＝17，BC ＝16，则四边形ADCE 的面积＝ ． ②若AB ＝10，则BC ＝ 时，四边形ADCE 是正方形．20．（8分）某学校计划在总费用2300元的限额内，租用汽车送234名学生和6名教师集体参加校外实践活动，为确保安全，每辆汽车上至少要有1名教师．现有甲、乙两种大客车，它们的载客量和租金如下表所示．（1）根据题干所提供的信息，确定共需租用多少辆汽车？ （2）请你给学校选择一种最节省费用的租车方案． 21．（8分）如图，函数23y x =-+与12y x m =-+的图象交于(),2P n -．（1）求出m ，n 的值． （2）直接写出不等式1232x m x -+>-+的解集； （3）求出ABP ∆的面积22．（10分）抗震救灾中，某县粮食局为了保证库存粮食的安全，决定将甲、乙两个仓库的粮食，全部转移到具有较强抗震功能的A 、B 两仓库．已知甲库有粮食100吨，乙库有粮食80吨，而A 库的容量为70吨，B 库的容量为110吨．从甲、乙两库到A 、B 两库的路程和运费如下表：（表中“元/吨•千米”表示每吨粮食运送1千米所需人民币）路程（千米）运费（元/吨•千米）甲库乙库 甲库 乙库 A 库 20 15 12 12 B 库2520108（1）若甲库运往A 库粮食x 吨，请写出将粮食运往A 、B 两库的总运费y （元）与x （吨）的函数关系式； （2）当甲、乙两库各运往A 、B 两库多少吨粮食时，总运费最省，最省的总运费是多少？ 23．（10分）（1）计算：124216831252÷（2）已知：3﹣1，求代数式x 2+2x ﹣2的值．24．（10分）已知：如图，平行四边形ABCD 中，AC ，BD 交于点O ，AE ⊥BD 于点E ，CF ⊥BD 于点F ．求证：OE ＝OF ．25．（12分）阅读下列材料：数学课上，老师出示了这样一个问题：如图，菱形ABCD 和四边形ABCE ，60BAD ∠=︒，连接BD ，BE ，BD BE =. 求证：ADC AEC ∠=∠；某学习小组的同学经过思考，交流了自己的想法：小明：“通过观察分析，发现ABE ∠与EBC ∠存在某种数量关系”； 小强：“通过观察分析，发现图中有等腰三角形”；小伟：“利用等腰三角形的性质就可以推导出ADC AEC ∠=∠”. ……老师：“将原题中的条件‘BD BE =’与结论‘ADC AEC ∠=∠’互换，即若ADC AEC ∠=∠，则BD BE =，其它条件不变，即可得到一个新命题”. …… 请回答：（1）在图中找出与线段BE 相关的等腰三角形（找出一个即可），并说明理由； （2）求证：ADC AEC ∠=∠；（3）若ADC AEC ∠=∠，则BD BE =是否成立？若成立，请证明；若不成立，请说明理由. 26．甲、乙两组数据(单位：)mm 如下表： 甲 11 9 6 9 14 7 7 7 10 10 乙34581288131316（1）根据以上数据填写下表；平均数众数中位数方差（2）根据以上数据可以判断哪一组数据比较稳定．参考答案一、选择题（每题4分，共48分）1、A【解析】【分析】先计算出△，然后根据判别式的意义求解．【详解】∵△=（-8）2-4×20×1=-16＜0，∴方程没有实数根．故选A．【点睛】本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．2、C【解析】分析：根据旋转的性质和四边形的内角和是360°，可以求得∠CAD的度数，本题得以解决．详解：由题意可得，∠CBD＝α，∠ACB＝∠EDB，∵∠EDB＋∠ADB＝180°，∴∠ADB＋∠ACB＝180°，∵∠ADB＋∠DBC＋∠BCA＋∠CAD＝360°，∠CBD＝α，∴∠CAD＝180°−α，故选C．点睛：本题考查旋转的性质，解答本题的关键是明确题意，利用数形结合的思想解答．3、B【解析】【分析】n边形的内角和是（n﹣2）•180°，如果已知多边形的边数，就可以得到一个关于边数的方程，解方程就可以求出多边形的边数．【详解】根据n边形的内角和公式，得（n﹣2）•180=1080，解得n=8，∴这个多边形的边数是8，故选B．【点睛】本题考查了多边形的内角与外角，熟记内角和公式和外角和定理并列出方程是解题的关键．根据多边形的内角和定理，求边数的问题就可以转化为解方程的问题来解决．4、A【解析】【分析】根据等腰三角形的性质可得另一底角的度数，再根据三角形内角和定理即可求得顶角的度数．【详解】解：∵等腰三角形的底角是70°，∴其顶角=180°-70°-70°=40°，故选：A．【点睛】此题主要考查等腰三角形的性质及三角形内角和定理，熟练掌握等腰三角形的性质是解题的关键．5、C【解析】【分析】【详解】由草坪面积为100m2，可知x、y存在关系y=，然后根据两边长均不小于5m，可得x≥5、y≥5，则x≤20，故选：C．6、C观察可得，选项C中的图形与原图中的④、⑦图形不符，故选C.7、D【解析】【分析】根据菱形的性质可知AO=OC，继而根据中位线定理求得BC长，再根据菱形的四条边相等即可求得答案. 【详解】∵四边形ABCD是菱形，∴AB=BC=CD=AD，AO=OC，∵AE=BE，∴BC=2EO=2×4cm=8cm，即AB=BC=CD=AD=8cm，即菱形ABCD的周长为32cm，故选D．【点睛】本题考查了菱形的性质，三角形中位线定理，熟练掌握相关性质与定理是解题的关键.8、C【解析】【分析】根据正比例函数的性质直接解答即可．【详解】解：A、显然当x=0时，y=0，故图象经过原点，错误；B、k＜0，应y随x的增大而减小，错误；C、k＜0，图解经过二、四象限，正确；D、把x=代入，得：y=-1，错误．故选C．【点睛】本题考查了正比例函数的性质，解题的关键是了解正比例函数的比例系数的符号与正比例函数的关系. 9、C【解析】先根据题意画出图形，再根据勾股定理解答即可．【详解】当筷子与杯底垂直时h最大，h最大=24-12=12cm．当筷子与杯底及杯高构成直角三角形时h最小，如图所示：此时，AB= 2222+=+=13cm，125AC BC故h=24-13=11cm．故h的取值范围是11cm≤h≤12cm．故选C．【点睛】此题将勾股定理与实际问题相结合，考查了同学们的观察力和由具体到抽象的推理能力，有一定难度．10、C【解析】【分析】本题就是应用直角梯形的这个性质作答的，直角梯形：有一个角是直角的梯形叫直角梯形.由梯形的定义得到直角梯形必有两个直角.【详解】直角梯形应该有两个角为直角，C中图形已经有一直角，再沿一直角边剪另一直角边的平行线即可.如图：故选：C．【点睛】此题是考查了直角梯形的性质与三角形的内角和定理的应用，掌握直角梯形的性质是解本题的关键.11、D【分析】根据线段垂直平分线的性质得出AD＝BD，推出CD＋BD＝5，即可求出答案．【详解】解：∵DE是AB的垂直平分线，∴AD＝DB，∵AC＝5，∴AD＋CD＝5，∴CD＋BD＝5，∵BC＝4，∴△BCD的周长为：CD＋BD＋BC＝5＋4＝9，故选D．【点睛】本题考查了线段垂直平分线的性质，注意：线段垂直平分线上的点到线段两个端点的距离相等．12、B【解析】【分析】当直线y=kx-2与线段AB的交点为A点时，把A（-2，4）代入y=kx-2，求出k=-3，根据一次函数的有关性质得到当k≤-3时直线y=kx-2与线段AB有交点；当直线y=kx-2与线段AB的交点为B点时，把B（4，2）代入y=kx-2，求出k=1，根据一次函数的有关性质得到当k≥1时直线y=kx-2与线段AB有交点，从而能得到正确选项．【详解】把A（-2，4）代入y=kx-2得，4=-2k-2，解得k=-3，∴当直线y=kx-2与线段AB有交点，且过第二、四象限时，k满足的条件为k≤-3；把B（4，2）代入y=kx-2得，4k-2=2，解得k=1，∴当直线y=kx-2与线段AB有交点，且过第一、三象限时，k满足的条件为k≥1．即k≤-3或k≥1．所以直线y=kx-2与线段AB有交点，则k的值不可能是-2．故选B．【点睛】本题考查了一次函数y=kx+b（k≠0）的性质：当k＞0时，图象必过第一、三象限，k越大直线越靠近y轴；当k＜0时，图象必过第二、四象限，k越小直线越靠近y轴．二、填空题（每题4分，共24分）13、1【解析】【分析】由AD ∥EF ∥GH ∥PQ ∥BC ，AE ＝EG ＝GP ＝PB ，可得GH 是梯形ABCD 的中位线，EF 是梯形AGHD 的中位线，PQ 是梯形GBCH 的中位线，然后根据梯形中位线的性质求解即可求得答案．【详解】∵AD ∥EF ∥GH ∥PQ ∥BC ，AE ＝EG ＝GP ＝PB∴GH 是梯形ABCD 的中位线，EF 是梯形AGHD 的中位线，PQ 是梯形GBCH 的中位线∵AD ＝2，BC ＝10 ∴()162GH AD BC =+= ∴()()114,822EF AD GH PQ GH BC =+==+= ∴12EF PQ +=故答案为：1．【点睛】本题考查了梯形中位线的问题，掌握梯形中位线的性质是解题的关键．14、>；【解析】 试题解析：∵反比例函数2y x=中，系数20>， ∴反比例函数在每个象限内，y 随x 的增大而减小， ∴当120x x <<时，12.y y >故答案为.>15、 ，135°]． 【解析】【分析】解决本题要根据旋转的性质，构造直角三角形来解决．【详解】解：如图所示，设此点为C ，属于第二象限的点，过C 作CD ⊥x 轴于点D ，那么OD ＝DC ＝3，∴∠COD＝45°，OC＝OD÷cos45°＝32则∠AOC＝180°−45°＝135°，那么指令为：[32135°]故答案为：[32135°]【点睛】本题考查求新定义下的点的旋转坐标；应理解运动指令的含义，构造直角三角形求解．16、103＜a≤1【解析】【分析】先将a看作常数解不等式，根据最小整数解为5，得1＜322a-≤5，解出即可．【详解】解不等式2x-3a+2≥0得x≥322a-，∵不等式的最小整数解为5，∴1＜322a-≤5，∴103＜a≤1，故答案为103＜a≤1．【点睛】本题考查了一元一次不等式的整数解，正确解不等式，求出解集是解答本题的关键．解不等式应根据不等式的基本性质．17、52【解析】【分析】（1）根据二次根式的性质计算即可；（2）根据二次根式除法运算法则计算即可．【详解】解：（1）2(5)5=；（2）1262÷=．故答案为：5；2．【点睛】此题主要考查了二次根式的性质和除法运算，正确掌握相关运算法则是解题关键．18、【解析】【分析】连接OE ，与DC 交于点F ，由四边形ABCD 为矩形得到对角线互相平分且相等，进而得到OD=OC ，再由两组对边分别平行的四边形为平行四边形得到OCED 为平行四边形，根据邻边相等的平行四边形为菱形得到四边形OCED 为菱形，得到对角线互相平分且垂直，求出菱形OCED 的面积即可．【详解】解：连接OE ，与DC 交于点F ，∵四边形ABCD 为矩形，∴OA=OC ，OB=OD ，且AC=BD ，即OA=OB=OC=OD ，AB=CD ，∵OD ∥CE ，OC ∥DE ，∴四边形ODEC 为平行四边形，∵OD=OC ，∴四边形OCED 为菱形，∴DF=CF ，OF=EF ，DC ⊥OE ，∵DE ∥OA ，且DE=OA ，∴四边形ADEO 为平行四边形，∵AD=，AB=2，∴OE=，CD=2，则S菱形OCED=OE•DC=××2=．故答案为：．【点睛】本题考查矩形的性质，菱形的判定与性质，以及勾股定理，熟练掌握矩形的性质是解题的关键．三、解答题（共78分）19、 (1)见解析；（2）①1；②102.【解析】试题分析：（1）根据平行四边形的性质得出四边形ADCE是平行四边形，根据垂直推出∠ADC=90°，根据矩形的判定得出即可；（2）①求出DC，根据勾股定理求出AD，根据矩形的面积公式求出即可；②要使ADCE是正方形，只需要AC⊥DE，即∠DOC=90°，只需要OD2+OC2=DC2，即可得到BC的长．试题解析：（1）证明：∵AE∥BC，∴∠AEO=∠CDO．又∵∠AOE=∠COD，OA=OC，∴△AOE≌△COD，∴OE=OD，而OA=OC，∴四边形ADCE是平行四边形．∵AD是BC边上的高，∴∠ADC=90°．∴□ADCE是矩形．（2）①解：∵AD是等腰△ABC底边BC上的高，BC=16，AB=17，∴BD=CD=8，AB=AC=17，∠ADC=90°，由勾股定理得：AD=22-=12，∴四边形ADCE的面积是AD×DC=12×8=1．178AC CD-=22②当BC=102时，DC=DB=52．∵ADCE是矩形，∴OD=OC=2．∵OD2+OC2=DC2，∴∠DOC=90°，∴AC⊥DE，∴ADCE是正方形．点睛：本题考查了平行四边形的判定，矩形的判定和性质，等腰三角形的性质，勾股定理的应用，能综合运用定理进行推理和计算是解答此题的关键，比较典型，难度适中．20、（1）确定共需租用6辆汽车；（2）最节省费用的租车方案是租用甲种客车4辆，乙种客车2辆．【解析】【分析】（1）首先根据总人数个车座确定租用的汽车数量，关键要注意每辆汽车上至少要有1名教师.（2）根据题意设租用甲种客车x 辆，共需费用y 元，则租用乙种客车(6)x -辆，因此可列出方程400280(6)y x x =+-，再利用不等式列出不等式组，即可解得x 的范围，在分类计算费用，选择较便宜的.【详解】解：（1）由使234名学生和6名教师都有座位，租用汽车辆数必需不小于234616453+=辆；每辆汽车上至少要有1名教师，租用汽车辆数必需不大于6辆．所以，根据题干所提供的信息，确定共需租用6辆汽车．（2）设租用甲种客车x 辆，共需费用y 元，则租用乙种客车(6)x -辆．6辆汽车载客人数为[]4530(6)x x +-人400280(6)y x x =+-=1201680x +∴ 4530(6)24012016802300x x x +-≥⎧⎨+≤⎩解得3146x ≤≤ ∴4x =，或5x =当4x =时，甲种客车4辆，乙种客车2辆，2160y =当5x =时，甲种客车5辆，乙种客车1辆，2300y =∴最节省费用的租车方案是租用甲种客车4辆，乙种客车2辆．【点睛】本题主要考查不等式组的应用问题，关键在于根据题意设出合理的未知数，特别注意，要取整数解，确定利润最小.21、（1）34m =-，52n =；（2）52x >；（3）7516 ． 【解析】【分析】 （1）先把P 点坐标代入23y x =-+求出n 的值，进而可得5(2P ，2)-，再把P 点坐标代入12y x m =-+可得m 的值； （2）根据函数图象可直接得到答案：直线12y x m =-+在直线23y x =-+上方的部分且即为所求； （3）首先求出A 、B 两点坐标，进而可得ABP ∆的面积．【详解】解：（1）23y x =-+过(,2)P n -．223n ∴-=-+，解得：52n =， 5(2P ∴，2)-， 12y x m =-+的图象过5(2P ，2)-． 15222m ∴-=-⨯+， 解得：34m =-； （2）不等式1232x m x -+>-+的解集为52x >； （3）当23y x =-+中，0x =时，3y =，(0,3)A ∴， 1324y x =--中，0x =时，34y =-， 3(0,)4B ∴-， 413345AB ⎛⎫∴=--= ⎪⎝⎭； ABP ∴∆的面积=151155752224216AB ⨯=⨯⨯=． 【点睛】 此题主要考查了一次函数图象上点的坐标特点，以及一次函数与不等式，关键是掌握函数图像上点的特征：函数图象经过的点必能满足解析式．22、（1）y=-30x+39200(0≤x ≤1);(2) 从甲库运往A 库1吨粮食，往B 库运送30吨粮食，从乙库运往A 库0吨粮食，从乙库运往B 库80吨粮食时，总运费最省为37100元【解析】试题分析：弄清调动方向，再依据路程和运费列出y （元）与x （吨）的函数关系式，最后可以利用一次函数的增减性确定“最省的总运费”．试题解析：（1）依题意有：若甲库运往A 库粮食x 吨，则甲库运到B 库（100－x ）吨，乙库运往A 库（1－x ）吨，乙库运到B 库（10+x ）吨．则010********x x x x ≥⎧⎪-≥⎪⎨-≥⎪⎪+≥⎩，解得：0≤x ≤1． y =12×20x +10×25（100－x ）+12×15（1－x ）+8×20×[110－（100－x ）]=－30x +39200（2）上述一次函数中k =－30＜0∴y 随x 的增大而减小∴当x =1吨时，总运费最省最省的总运费为：－30×1+39200=37100（元） 答：从甲库运往A 库1吨粮食，往B 库运送30吨粮食，从乙库运往A 库0吨粮食，从乙库运往B 库80吨粮食时，总运费最省为37100元．23、 (1)20;(2)0. 【解析】【分析】（1）先分别进行二次根式的化简，然后进行二次根式的乘除，最后再进行二次根式的加减即可得；（2）把x 的值代入进行计算即可得.【详解】（1）4÷=2-4410=+=（2）把x 1=，代入2x 2x 2+-，则原式))21212=+-3122=-+-0=.【点睛】本题考查了二次根式的混合运算，熟练掌握二次根式混合运算的去处顺序以及运算法则是解题的关键.24、见解析【解析】欲证明OE=OF ，只要证明△AOE ≌△COF （AAS ）即可．【详解】证明：∵四边形ABCD 是平行四边形，∴OA=OC ，∵AE ⊥BD 于点E ，CF ⊥BD 于点F ，∴∠AEO=∠CFO=90°，在△AOE 和△COF 中，AEO CFO AOE COF OA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AOE ≌△COF （AAS ），∴OE=OF ．【点睛】本题考查平行四边形的性质，全等三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．25、 (1)见解析;(2)见解析;(3)见解析.【解析】【分析】（1）先利用菱形的性质，得出ABD ∆是等边三角形，再利用等边三角形的性质，即可解答（2）设ABE α∠=，根据菱形的性质得出180120ABC ADC BAD ∠=∠=︒-∠=︒，由（1）可知120EBC α∠=︒-，即可解答（3）连接DE ，在AE 上取点F ，使AF EC =，延长AE 至G ，使EG EC =，连接GC ，连接DG ，设AE 与DC 的交点为O ，首先证明ADF CDE ∆≅∆，再根据全等三角形的性质得出CEG ∆是等边三角形，然后再证明DCG BCF ∆≅∆，即可解答【详解】（1）ABE ∆是等腰三角形；证明：∵四边形ABCD 是菱形，∴AB BC CD DA ===，∵60BAC ∠=︒，∴ABD ∆是等边三角形，∴AB BD =.∵BD BE =，∴AB BE =，∴ABE ∆是等腰三角形.（2）设ABE α∠=.∵四边形ABCD 是菱形，∴AD BC ∥，∴180120ABC ADC BAD ∠=∠=︒-∠=︒.由（1）知，AB BE =，同理可得：BC BE =.∴120EBC α∠=︒-， ∴()111809022AEB a α∠=︒-=︒-，∴()111801203022BEC αα∠=︒-+=︒+， ∴11903012022AEC AEB BEC αα∠=∠+∠=︒-+︒+=︒. ∴ADC AEC ∠=∠.（3）成立；证明：如图2，连接DE ，在AE 上取点F ，使AF EC =，延长AE 至G ，使EG EC =，连接GC ，连接DG ，设AE 与DC 的交点为O .∵ADC AEC ∠=∠，AOD COF ∠=∠，∴DAF DCE ∠=∠.∵AD DC =，∴ADF CDE ∆≅∆（ASA ），∴DF DE =，ADF CDE ∠=∠，∴120FDE ADC ∠=∠=︒，∴30DFE DEF ∠=∠=︒.∵150DEC ∠=︒，∵120AEC ∠=︒，∵60CEG ∠=︒，∴CEG ∆是等边三角形，∴EG CE GC ==.∵150DEG DEC ∠=∠=︒，∵DE DE =，∴DEC DEG ∆≅∆，∴DG DC =.∵BCD DCE ECG DCE ∠+∠=∠+∠，∴BCE DCG∠=∠，∴DCG BCF∆≅∆，∵BE DG=，∴BD BE=.【点睛】此题考查全等三角形的判定与性质，菱形的性质, 等边三角形的判定与性质，解题关键在于作辅助线26、（1）答案见解析；（2）甲组数据较稳定【解析】【分析】（1）根据图表按照平均数，众数，中位数的定义一一找出来填表即可．（2）此问先比较平均数，如果平均数相同再比较方差．【详解】（1）（2）∵甲、乙两组数据的平均数相同，且2S甲＜2S乙，∴甲组数据较稳定．【点睛】此题考查数据的收集和处理，包含内容有众数，中位数，平均数及方差．。

河南省信阳市平桥区羊山中学2023-2024学年八年级上学期期末数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列图形中，是轴对称图形的是（ ） A ． B ． C ． D ． 2．下列长度的三条线段组成三角形的是（ ）A ．2，11，13B ．5，12，13C ．5，5，11D ．5，12，7 3．点(3,2)M 关于y 轴对称的点的坐标为（ ）A ．(3,2)-B ．(3,2)--C ．(3,2)-D ．(2,3)- 4．如图，在折纸活动中，小明制作了一张△ABC 纸片，D ，E 分别是边AB ，AC 上的点，将△ABC 沿着DE 折叠压平，点A 与点A′重合，若∠A ＝70°，则∠1＋∠2的度数为( )A ．110°B ．140°C ．220°D ．70° 5．如图，在ABC V 中，90C ∠=︒，DE AB ⊥于点D ，BC BD =．如果3cm AC =，那么AE DE +=（ ）A ．2cmB ．4cmC ．3cmD ．5cm 6．如图，在Rt ABC △中，90ACB ∠=︒，根据尺规作图的痕迹，判断以下结论不一定成立的是（ ）二、填空题11．计算：()()3216842x x x x -+÷-=．12．冠状病毒是一类病毒的总称，其最大直径约为0.00000012米，数据0.00000012科学记数法表示为．13．已知，如图，在△ABC 中，CAD EAD ∠=∠，ADC ADE ∠=∠，5CB =cm ，BD ＝3cm ，则ED 的长为cm ．14．如图1，将一个长为2a ，宽为2b 的长方形沿图中虚线剪开分成四个完全相同的小长方形，然后将这四个完全相同的小长方形拼成一个正方形（如图2），设图2中的大正方形面积为1S ，小正方形面积为2S ，则12S S -的结果是（用含a ，b 的式子表示）．15．如图，在ABC V 中，90C ∠=︒，8cm BC =，6cm AC =，点E 是BC 的中点，动点P 从A 点出发，先以每秒2cm 的速度沿A →C 运动，然后以1cm /s 的速度沿C →B 运动．若设点P 运动的时间是t 秒，那么当t =时，APE V 的面积等于10？三、解答题(1)若A B C '''V 与ABC V 关于x 轴成轴对称，作出A B C '''V ；(2)若P 为y 轴上一点，使得APC △周长最小，在图中作出点P ，并写出P 点的坐标为______；(3)计算ABC V 的面积．19．某市为创建全国文明城市，开展“美化绿化城市”活动，计划经过若干年使城区绿化总面积新增360万平方米．自2018年初开始实施后，实际每年绿化面积是原计划的1.5倍，这样可提前4年完成任务．(1)实际每年绿化面积为多少万平方米？(2)为加大创建力度，市政府决定从2021年起加快绿化速度，要求不超过3年完成，那么实际平均每年绿化面积至少还要增加多少万平方米？20．如图，在ABC V 中，AB AC =，120BAC ∠=︒．(1)尺规作图：作ABC V 的高AD ，在AD 上取点P ，连接CP ，以点P 为圆心，PC 长为半径画弧，交BA 的延长线于点Q ，连接CQ （不写作法，保留作图痕迹）；(2)在上述的条件下，求证：CPQ V 为等边三角形．21．如图，在ABC V 和DBC △中，90ACB DBC ∠=∠=︒，E 是BC 的中点，DE AB ⊥于点F ，且AC EB =．(1)求证：V V ≌ACB EBD ；(2)若12DB =，求AC 的长．22．我国古代数学的许多发现都曾位居世界前列，“杨辉三角”就是其中一例，如图所示为这个“三角形”的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了()na b +（n 为正整数）的展开式（按a 的次数由大到小的顺序排列）的系数规律．例如，在“三角形”中，第三行的三个数121，，，恰好对应()2222a b a ab b +=++展开式中的系数；第四行的四个数1，3，3，1，恰好对应()3322333a b a a b ab b +=+++展开式中的系数．(1)根据上面的规律，写出()4a b +的展开式；(2)利用上面的规律计算：5432252102102521-⨯+⨯-⨯+⨯-；(3)()n a b +的展开式的系数和为；(4)运用：若今天是星期三，经过20242024天后是星期．23．(1)操作发现：如图①，D 是等边三角形ABC 边BA 上一动点(点D 与点B 不重合)，连接DC ，以DC 为边在DC 上方作等边三角形DCF ，连接AF .你能发现线段AF 与BD 之间的数量关系吗？并证明你发现的结论．(2)类比猜想：如图②，当动点D 运动至等边三角形ABC 边BA 的延长线上时，其他作法与(1)相同，猜想AF 与BD 在(1)中的结论是否仍然成立？(3)深入探究：Ⅰ.如图③，当动点D 在等边三角形ABC 边BA 上运动时(点D 与点B 不重合)，连接DC ，以DC 为边在DC 上方、下方分别作等边三角形DCF 和等边三角形DCF ′，连接AF 、BF ′，探究AF 、BF ′与AB 有何数量关系？并证明你探究的结论．Ⅱ.如图④，当动点D 在等边三角形边BA 的延长线上运动时，其他作法与图③相同，Ⅰ中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论．。

河南省信阳市2022-2023学年八年级上学期语文期末考试试卷一、积累与运用（共28分）1．阅读下面语段，回答问题。

秋雨洗涤．后的名苑新城，别有一番风味。

淡青的天空和灰白的屋顶勾勒出一幅宁静安适的水墨画。

墙角处，一丛杜鹃不折不náo____地傲立着。

我由zhōng____地感受到一股生命力正潜．滋暗长。

（1）给加点的字注音。

洗涤．（）潜．（）滋暗长（2）根据词语中的拼音写出相应的汉字。

不折不náo（）由zhōng（）2．下列说法有误的一项是（）A．《一着惊海天——目击我国航母舰载战斗机首架次成功着舰》采用现场特写的手法，生动再现了举世瞩目的我国航母舰载战斗机首次成功着舰那惊心动魄的一刻。

B．《美丽的颜色》节选自《居里夫人传》，该书详细叙述了居里夫人的一生。

作者艾芙·居里曾先后获1903年诺贝尔物理学奖和1911年诺贝尔化学奖。

C．《三峡》是北魏地理学家郦道元写的一篇散文，捕绘了三峡各具特色的四季风光，展现出了长江万里图中一帧挺拔隽秀的山水画。

D．《记承天寺夜游》是北宋文学家苏轼贬官黄州期间所写，描绘了一幅美丽月色图，创设了一种清冷皎洁的意境，表达了作者旷达的心境。

3．依次填入下面语段中横线处的句子，衔接最恰当的一项是（）散文素有“美文”之称，____，____。

____，____，____，提高自己的语言表达能力。

①不仅可以丰富知识，开阔眼界，培养高尚的思想情操②还有清新隽永、质朴无华的文采③它除了有精神的见解、优美的意境外④经常读一些好的散文⑤还可以从中学习选材立意、谋篇布局和遣词造句的技巧A．③②④①⑤B．④①⑤③②C．③⑤①②④D．①⑤③②④4．古诗文默写。

（1）采菊东蓠下，。

（《饮酒（其五）》）（2），家书抵万金。

（《春望》）（3）《使至塞上》中写诗人轻车简从，出使边塞的诗句是：，。

（4）《钱塘湖春行》中最能表现西湖春景美不胜收和诗人的喜爱与不舍之情的诗句是：，。