长方体体积计算公式推导
- 格式:ppt
- 大小:96.00 KB
- 文档页数:4

长方体计算体积的公式长方体是一种常见的立体几何体,它有六个面,每个面都是矩形。
计算长方体的体积是一个简单的数学问题,可以通过以下公式进行计算:体积=长×宽×高其中,长、宽和高分别代表长方体的三个相邻边长。
这个公式可以用来计算任意长方体的体积。
长方体体积的公式可以通过一个简单的图形理解:假设我们有一块三维的网格纸,每个小正方形的边长都是单位长度。
我们可以用这个网格纸来构建长方体。
首先,在纸上画一个矩形,它的长和宽分别为长方体的长和宽。
然后,在这个矩形的一个边上垂直地往上画一条直线,这条直线的长度就是长方体的高。
接下来,将这个矩形剪下来,沿着边缘将它折叠成一个长方体。
我们可以看到,在这个长方体中,有长×宽个单位正方形,每个单位正方形的高度都是长方体的高。
因此,长方体的体积就等于长×宽×高。
举例来说,假设我们有一个长方体,长为5个单位,宽为3个单位,高为2个单位。
根据公式,我们可以计算出这个长方体的体积:体积=5×3×2=30所以,这个长方体的体积为30个单位。
长方体的体积公式可以用于各种实际生活中的问题。
比如,在我们日常生活中,我们可能需要计算一个桌子、书柜或房间的体积。
这些都可以使用长方体体积的公式进行计算。
此外,长方体的体积公式还可以推广到其他立体几何体上。
其他立体几何体的体积计算也可以通过乘法运算来实现。
比如,正方体的体积可以用公式:体积=边长×边长×边长长方体体积的公式也可以应用于椎体、柱体等其他形状的几何体。
只要我们能够找到对应的边长或半径,以及相关的高度,就能够使用乘法运算来计算它们的体积。
总结起来,长方体的体积公式是一个简单且重要的立体几何计算工具。
它可以用来计算各种现实生活中的问题,而我们只需要知道长、宽和高的数值即可。
这个公式的应用简单而广泛,使得我们可以更方便地计算和解决各种几何体积相关问题。

推导公式体积公式的几何推导过程在几何学中,计算物体的体积是一项基本的任务。
根据物体的形状与特征,可以使用不同的公式来求解其体积。
本文将讨论推导公式体积公式的几何推导过程,以便更好地理解这些公式的来源与应用。
1. 推导正方体体积公式正方体是一种具有六个相等的正方形面的立体图形。
设正方体的边长为a,现在我们来推导正方体的体积公式。
由于正方体的六个面都是正方形,所以每个正方形的面积都等于边长a的平方。
因此,正方体的体积等于六个正方形的面积之和。
即体积(V) = 正方形面积 * 6 = a^2 * 6 = 6a^2。
2. 推导长方体体积公式长方体是一种具有六个面,其中相对面两两平行且相等的四边形的立体图形。
设长方体的长、宽、高分别为a、b、c,现在我们来推导长方体的体积公式。
根据长方体的性质,可以得知长方体可以看作是由两个等底且等高的矩形组成的。
其中,一个矩形的底边长为a,高为c;另一个矩形的底边长为b,高为c。
因此,长方体的体积等于这两个矩形的面积之和。
即体积(V) = 长方形1面积 + 长方形2面积 = ac + bc = c(a + b)。
3. 推导圆柱体体积公式圆柱体是由一个圆形底面与一个与底面平行的圆形顶面之间的曲面所围成的立体图形。
设圆柱体的底面半径为r,高为h,现在我们来推导圆柱体的体积公式。
首先,将圆柱体展开,可以得到一个高为h,底边周长为2πr的矩形,其中π是一个常数,约等于3.14159。
可以看出,这个矩形的面积等于底边周长乘以高。
即底矩形的面积 = 底边周长 * 高= 2πr * h。
因为底面是一个圆形,所以底面的面积为πr^2。
所以,圆柱体的体积等于底面的面积乘以高度。
即体积(V) = 底面积 * 高= πr^2 * h。
4. 推导球体体积公式球体是由所有与一个给定点的距离小于或等于一个给定数的点组成的立体图形。
设球体的半径为r,现在我们来推导球体的体积公式。
我们可以将球体切割成许多极小的圆柱体,然后将这些圆柱体的体积累加起来,来近似球体的体积。

长方体的体积计算方式长方体是一种具有六个矩形面的几何体,它的体积计算方式是将长、宽、高相乘。
在数学和几何学中,长方体是一个基本的三维图形,它在日常生活中有着广泛的应用。
长方体的体积计算方式非常简单,只需要将长、宽、高三个边长相乘即可得到体积。
具体计算公式为:体积 = 长× 宽× 高。
这个公式非常易于理解和应用,可以通过简单的乘法运算来得到长方体的体积。
长方体的体积计算方法可以通过具体的例子来加以说明。
假设有一个长方体,它的长为10厘米,宽为5厘米,高为3厘米。
那么根据体积计算公式,可以得到这个长方体的体积为:10厘米× 5厘米× 3厘米 = 150立方厘米。
因此,这个长方体的体积为150立方厘米。
长方体的体积计算方法也可以应用于实际生活中的问题。
比如,在装箱运输时,我们需要知道一个物体的体积,以确定它是否能够放入箱子中。
在建筑和设计领域,长方体的体积计算方法可以用来确定房间的容积,从而合理规划空间。
除了长方体,还有其他几何体的体积计算方式也是类似的。
例如,立方体和正方体的体积计算方式也是将边长相乘。
球体的体积计算方式是将4/3乘以π乘以半径的立方。
棱柱和棱锥的体积计算方式则需要分别计算底面积和高度,再相乘。
长方体的体积计算方法对于初学者来说非常重要,它是理解三维几何体的基础。
通过学习长方体的体积计算方法,我们可以更好地理解空间概念,并能够应用于实际问题中。
掌握了长方体的体积计算方法,我们可以更加准确地计算和测量物体的容积,为日常生活和工作带来便利。
长方体的体积计算方式是将长、宽、高三个边长相乘。
通过简单的乘法运算,我们可以得到长方体的体积。
长方体的体积计算方法在数学和几何学中有着重要的地位,对于理解和应用三维几何体非常关键。
掌握了长方体的体积计算方法,我们可以更好地理解空间概念,并能够应用于实际问题中。
通过实际的例子和应用,我们可以更深入地理解长方体的体积计算方式,为日常生活和工作带来便利。

长方体体积公式推导
长方体是一个立方体,它的体积可以通过计算它的长、宽和高的乘积得到。
假设长方体的长为l、宽为w、高为h,则其体积V可以表示为:
V = l * w * h
推导过程如下:
1. 假设长方体可以被划分为n层,每一层的体积都相同。
2. 第一层的体积为lw,第二层的体积也为lw,以此类推,直到第n层。
3. 将这些层的体积相加,得到总体积。
总体积 = lw + lw + lw + ... + lw (共有n个lw)
= nlw
4. 当n趋近于无穷大时,每一层的高度趋近于无穷小。
5. 此时,每一层的体积也趋近于无穷小。
6. 由于无穷小的体积是可以忽略的,我们可以认为每一层的体积为0。
7. 因此,长方体的体积在数学上可以表示为:
V = lim(n→∞) nlw = lwh
所以,长方体的体积公式为V = lwh。

体积重量计算公式单位体积重量计算公式的单位取决于所计算的物体或物质的属性和单位。
以下是一些常见的体积重量计算公式及其单位:1.长方体体积计算公式:体积=长度×宽度×高度单位:体积的单位可以是立方米(m³),立方厘米(cm³),立方英尺(ft³),立方英寸(in³)等。
2.圆柱体体积计算公式:体积=π×半径²×高度单位:体积的单位可以是立方米(m³),立方厘米(cm³),立方英尺(ft³),立方英寸(in³)等。
半径的单位可以是米(m),厘米(cm),英尺(ft),英寸(in)等。
高度的单位可以是米(m),厘米(cm),英尺(ft),英寸(in)等。
3.球体体积计算公式:体积=(4/3)×π×半径³单位:体积的单位可以是立方米(m³),立方厘米(cm³),立方英尺(ft³),立方英寸(in³)等。
半径的单位可以是米(m),厘米(cm),英尺(ft),英寸(in)等。
4.材料密度计算公式:密度=质量/体积单位:密度的单位可以是千克/立方米(kg/m³),克/立方厘米(g/cm³),磅/立方英尺(lb/ft³)等。
质量的单位可以是千克(kg),克(g),磅(lb)等。
体积的单位可以是立方米(m³),立方厘米(cm³),立方英尺(ft³),立方英寸(in³)等。
需要注意的是,在具体问题中,要根据实际情况选择合适的单位来计算和表示体积和重量。
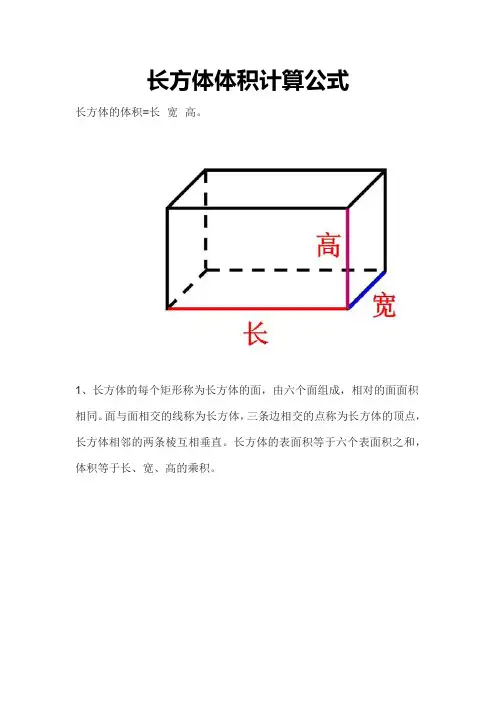
长方体体积计算公式
长方体的体积=长×宽×高。
1、长方体的每个矩形称为长方体的面,由六个面组成,相对的面面积相同。
面与面相交的线称为长方体,三条边相交的点称为长方体的顶点,长方体相邻的两条棱互相垂直。
长方体的表面积等于六个表面积之和,体积等于长、宽、高的乘积。
2、长方体的画法:先画一个平行四边形。
在平行四边形的四个顶点往下做垂线。
注意:左上角的顶点向下做的垂线要是虚线,因为在现实中的长方体是看不见那条棱的。
将四条垂线的下方点连接起来就画好了一个长方体。
3、长方体每个面都是长方形,有可能有2个相对的面是正方形。
长方体的体积用底面积乘以高,底面积可以是长方形可以是正方形,底面积等于长乘宽。
高就是竖的那条边,长方体的体积=底面积×高。

长方体体积的计算公式
长方体体积的计算公式:长方体的体积=长×宽×高。
长方体(又称矩体,cuboid)是底面为长方形的直四棱柱(或上、下底面为矩形的直平行六面体)。
其由六个面组成的,相对的面面积相等,可能有两个面(可能四个面是长方形,也可能是六个面都是长方形)是正方形。
长方体(cuboid)是底面是长方形的直棱柱。
正方体是特殊的长方体,正方体是六个面都是正方形的长方体。
长方体的每一个矩形都叫做长方体的面,面与面相交的线叫做长方体的棱,三条棱相交的点叫做长方体的顶点。
长方体六个面面积的和,叫作长方体的表面积。
长方体的体积是对长方体的一种度量,长方体的体积等于长、宽、高之积。
特征:
(1) 长方体有6个面。
每组相对的面完全相同。
(2) 长方体有12条棱,相对的四条棱长度相等。
按长度可分为三组,每一组有4条棱。
(3) 长方体有8个顶点。
每个顶点连接三条棱。
三条棱分别叫做长方体的长,宽,高。
(4) 长方体相邻的两条棱互相垂直。

长方体体积公式及外表积公式长方体是底面为长方形的直四棱柱〔或上、下底面为矩形的直平行六面体〕,其由六个面组成的,相对的面面积相等。
长方体是底面为长方形的直四棱柱〔或上、下底面为矩形的直平行六面体〕,其由六个面组成的,相对的面面积相等。
体积长方体的体积=长×宽×高。
设一个长方体的长、宽、高分别为a、b、c,那么它的体积:V=abc=Sh
因为长方体也属于棱柱的一种,所以棱柱的体积计算公式它也同样适用。
长方体体积=底面积×高,即V=Sh〔S是底面积〕外表积因为相对的2个面面积相等,所以先算上下两个面,再算前后两个面,最后算左右两个面。
设一个长方体的长、宽、高分别为a、b、c,那么它的外表积为S=(ab+bc+ca)×2,也等于2ab+2bc+2ca,还等于2〔ab+bc+ca〕;
公式:长方体的外表积=长×宽×2+宽×高×2+长×高×2,或:长方体的外表积=〔长×宽+宽×高+长×高〕×2。
性质(1)长方体有6个面。
每组相对的面完全一样。
(2)长方体有12条棱,相对的四条棱长度相等。
按长度可分为三组,每一组有4条棱。
(3)长方体有8个顶点。
每个顶点连接三条棱。
三条棱分别叫做长
方体的长,宽,高。
(4)长方体相邻的两条棱互相垂直。

长方体体积三个公式在我们的日常生活和学习中,长方体是一种常见的几何图形。
无论是在建筑、工程,还是在数学课堂上,了解长方体体积的计算都非常重要。
今天,咱们就来好好聊聊长方体体积的三个公式。
首先,咱们得清楚什么是长方体。
长方体是由六个长方形(特殊情况有两个相对的面是正方形)围成的立体图形。
它有 8 个顶点,12 条棱,相对的棱长度相等,还有 6 个面,相对的面面积相等。
那长方体体积到底怎么计算呢?这就引出了咱们要说的第一个公式:长方体体积=长×宽×高。
比如说,有一个长方体,长是 5 厘米,宽是 3 厘米,高是 2 厘米。
那它的体积就是 5×3×2 = 30 立方厘米。
这个公式很好理解,咱们可以把长方体想象成是由一层一层的小方块堆起来的。
长就代表着一行能放几个小方块,宽代表着能放几行,高则代表着能放几层。
这样一相乘,就得出了总的小方块数量,也就是长方体的体积。
接下来是第二个公式:长方体体积=底面积×高。
底面积怎么算呢?如果长方体底面的长是 a,宽是 b,那么底面积就是 a×b。
再乘以高 h,同样能得到体积。
这个公式其实和第一个公式是相通的。
还是拿刚才那个例子,底面积就是 5×3 = 15 平方厘米,高是 2 厘米,体积就是 15×2 = 30 立方厘米。
那这个公式有啥用呢?比如说,咱们知道一个长方体容器的底面积和里面液体的高度,就能很快算出液体的体积。
最后一个公式是:长方体体积=横截面面积×长。
这个公式在一些实际问题中也很有用。
比如一根长方体形状的柱子,咱们知道它横截面的面积,再知道它的长度,就能算出柱子的体积。
为了更好地理解这三个公式,咱们再来看几个例子。
假设要建造一个长方体形状的游泳池,长 20 米,宽 10 米,深 2 米。
用第一个公式来算,体积就是 20×10×2 = 400 立方米。

体积和重量计算公式体积和重量计算是在日常生活和工作中经常会遇到的问题。
无论是在购物、运输还是科学实验中,我们都需要准确地计算物体的体积和重量。
本文将介绍一些常见的计算公式,并通过实例来说明如何应用这些公式进行计算。
一、体积的计算公式1. 立方体体积计算公式:体积 = 边长³立方体是最简单的几何体之一,边长相等,因此只需要知道一个边长,就可以计算出立方体的体积。
2. 长方体体积计算公式:体积 = 长× 宽× 高长方体是我们常见的物体,如盒子、书本等,通过测量长、宽、高,就可以计算出长方体的体积。
3. 圆柱体体积计算公式:体积= π × 半径² × 高圆柱体是一个上底和下底都为圆形的几何体,通过测量底面圆的半径和高,就可以计算出圆柱体的体积。
4. 球体体积计算公式:体积= 4/3 × π × 半径³球体是一个完全由曲面构成的几何体,通过测量球的半径,就可以计算出球体的体积。
二、重量的计算公式重量是物体所受重力的大小,它与物体的质量有关。
在计算重量时,我们需要用到重力加速度的数值,通常取9.8 m/s²。
1. 质量和重力的关系:重量 = 质量× 重力加速度质量是物体所含物质的量,通过质量和重力加速度的乘积,就可以计算出物体的重量。
2. 体积和密度的关系:质量 = 体积× 密度密度是物体单位体积的质量,通过体积和密度的乘积,就可以计算出物体的质量。
三、实例演练为了更好地理解和应用上述计算公式,我们来看几个实际的例子。
例1:计算一个边长为5厘米的立方体的体积。
根据立方体体积计算公式,体积 = 边长³ = 5³ = 125立方厘米。
例2:计算一个长为10厘米、宽为5厘米、高为8厘米的长方体的体积。
根据长方体体积计算公式,体积 = 长× 宽× 高= 10 × 5 × 8 = 400立方厘米。
长方体表面积和体积计算公式长方体是一种常见的几何体,有着广泛的应用。
在工程、建筑、制造、物流等领域,长方体都扮演着重要的角色。
在计算长方体的体积和表面积时,我们需要使用相应的公式。
1. 长方体的体积公式长方体的体积是指其所占据的空间大小,通常用立方体积单位(如立方米、立方厘米等)来表示。
计算长方体的体积可以使用以下公式:体积 = 长× 宽× 高其中,长、宽、高分别表示长方体的三个相邻的棱长。
例如,一个长方体的长为3厘米、宽为4厘米、高为5厘米,则其体积为3 × 4 × 5 = 60立方厘米。
在实际应用中,我们可以使用尺子、卷尺等工具来测量长方体的三个边长,然后带入公式进行计算,得出长方体的体积。
2. 长方体的表面积公式长方体的表面积是指其六个面积之和,通常用平方面积单位(如平方米、平方厘米等)来表示。
计算长方体的表面积可以使用以下公式:表面积= 2 × (长× 宽 + 长× 高 + 宽× 高)其中,长、宽、高分别表示长方体的三个相邻的棱长。
例如,一个长方体的长为3厘米、宽为4厘米、高为5厘米,则其表面积为2 × (3 × 4 + 3 × 5 + 4 × 5) = 94平方厘米。
在实际应用中,我们可以使用尺子、卷尺等工具来测量长方体的三个边长,然后带入公式进行计算,得出长方体的表面积。
3. 长方体的应用长方体在生活中有着广泛的应用。
例如,我们常见的家具如衣柜、书柜、电视柜、餐桌等都是长方体的形状。
此外,在建筑、制造、物流等领域,长方体也扮演着重要的角色。
例如,在建筑工程中,我们需要计算房间的体积和表面积,以确定所需的建材数量;在制造业中,我们需要计算产品的体积和表面积,以确定所需的原材料数量;在物流行业中,我们需要计算货物的体积和表面积,以确定运输费用。
长方体是一种常见的几何体,其体积和表面积的计算公式十分简单易懂。
长方体体积公式的推导过程在我们日常生活中,长方体是一种常见的几何体。
当我们想要计算长方体的体积时,我们可以使用长方体体积公式来进行计算。
下面我们将详细探讨长方体体积公式的推导过程。
我们需要明确长方体的定义。
长方体是一种由六个矩形面组成的立体,其中相对的两个面的边长相等。
假设长方体的长、宽和高分别为L、W和H,我们的目标是推导出计算长方体体积的公式。
为了推导出长方体体积公式,我们可以利用长方体的性质和一些基本的几何知识。
首先,我们可以将长方体分解为多个小立方体,其中每个小立方体的边长相等。
这样,我们可以将整个长方体的体积表示为所有小立方体体积的总和。
假设我们将长方体分解为n个小立方体,每个小立方体的边长为a。
那么每个小立方体的体积为a^3。
我们可以表示长方体的体积V为:V = n * a^3接下来,我们需要找到一个与长方体的边长L、W和H有关的公式,以便将其与上述公式进行联系。
我们可以观察到,当我们将长方体沿着一条边进行切割时,得到的切面是一个矩形,其长和宽分别为长方体的宽和高。
我们可以假设我们将长方体沿着宽的方向切割,得到的切面的长为L,宽为H。
那么这个切面的面积可以表示为L * H。
同时,这个切面的面积也可以表示为所有小立方体的底面积之和,即n * a^2。
因此,我们可以得到以下等式:L * H = n * a^2通过上述等式,我们可以解出a的值:a = sqrt((L * H) / n)将a的值代入到长方体的体积公式中,我们可以得到:V = n * (sqrt((L * H) / n))^3= n * (L * H / n)^(3/2)= L * H * sqrt(L / n)接下来,我们需要确定n的值。
我们可以将长方体分解为许多小正方形,其中每个小正方形的边长为h。
那么,长方体的高H可以表示为h的n倍,即H = n * h。
将n的值代入到上述公式中,我们可以得到:V = L * H * sqrt(L / n)= L * (n * h) * sqrt(L / (n * h))= L * h * sqrt(L / h)我们得到了长方体体积公式的最终形式:V = L * h * sqrt(L / h)我们通过分解长方体、利用几何知识和推导过程,得到了长方体体积公式V = L * h * sqrt(L / h)。