长方体体积公式推导过程 PPT
- 格式:ppt
- 大小:212.00 KB
- 文档页数:11

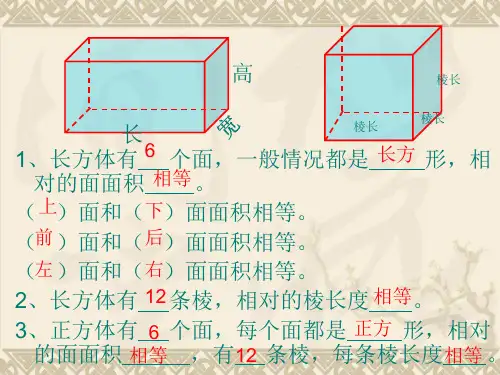

长方体体积推导公式一、长方体体积公式推导。
1. 用数小正方体个数的方法推导。
- 我们先想象一个长方体是由若干个小正方体组成的。
例如,一个长方体,它的长是a个小正方体的棱长长度,宽是b个小正方体的棱长长度,高是c个小正方体的棱长长度。
- 我们可以一层一层地数小正方体的个数。
先看最底层,沿着长的方向有a个小正方体,沿着宽的方向有b个小正方体,那么最底层小正方体的个数就是a× b个。
- 而这个长方体的高是c层,所以小正方体的总个数就是a× b× c个。
因为每个小正方体的体积是1(假设小正方体棱长为1单位长度),所以长方体的体积V = a× b× c。
2. 通过切割与拼接推导(从单位体积出发)- 我们取边长为1厘米的小正方体作为单位体积。
对于一个长方体,我们把它沿着长的方向切割成a个单位长度的部分,沿着宽的方向切割成b个单位长度的部分,沿着高的方向切割成c个单位长度的部分。
- 这样就相当于把这个长方体分割成了a× b× c个单位体积的小正方体。
- 由于长方体的体积就是这些小正方体体积之和,而每个小正方体体积是1立方厘米(因为棱长为1厘米),所以长方体的体积V=a× b× c。
3. 从长方体的底面积角度推导。
- 长方体的底面积S = a× b(底面积等于长乘以宽)。
- 而长方体的高是c,我们可以把长方体看作是由底面积为S,高为c的这样一个立体图形。
- 根据体积的意义,体积是物体所占空间的大小,那么这个长方体的体积就等于底面积乘以高,即V = S× c=(a× b)× c=a× b× c。



长方体和正方体的表面积和体积公式的推导
过程
长方体和正方体的表面积和体积公式的推导过程如下:
长方体的表面积S=2(lw+lh+wh),其中l、w、h分别为长方体的长、宽、高。
长方体的体积V=lwh。
正方体的表面积S=6s²,其中s为正方体的边长。
正方体的体积V=s³。
长方体推导过程:
长方体有6个面,每个面都是一个矩形,长方体的表面积等于它
所有面积之和。
设长方体的长、宽、高分别为l、w、h,那么长方体的表面积可以表示为S=2lw + 2lh + 2wh。
长方体的体积可以看成是一个长方体的六分之一,即V=lwh。
正方体推导过程:
正方体有6个面,每个面都是一个正方形,正方体的表面积等于6倍其中一个正方形的面积。
设正方体的边长为s,那么正方体的表面积可以表示为S=6s²。
正方体的体积可以表示为一个正方体的体积,即V=s³。
以上就是长方体和正方体的表面积和体积公式的推导过程。
当然,这些公式只适用于长方体和正方体,对于其他形状的立体,需要采用
其他公式来计算表面积和体积。

长方体体积的推导公式在咱们的数学世界里,长方体体积的推导公式可是个相当重要的知识点。
先来说说长方体吧,大家都见过,就像咱们的文具盒、书本啥的,很多都是长方体的形状。
那长方体的体积到底咋算出来的呢?这就得好好推导推导啦。
咱们想象一下,有一个大的长方体仓库,要知道能装多少东西,就得算出它的体积。
假设这个长方体仓库的长是 5 米,宽是 3 米,高是 2 米。
那怎么算出它的体积呢?咱们可以把这个长方体想象成是由一个个小的正方体拼成的。
就好像是用一块块小积木搭成了一个大房子。
如果这个小正方体的棱长是 1 米,那沿着长方体的长,能放 5 个这样的小正方体;沿着宽呢,能放 3 个;沿着高,能放 2 层。
这样一来,一共用的小正方体的个数就是 5×3×2 = 30(个)。
而每个小正方体的体积是 1×1×1 = 1(立方米),所以这个长方体仓库的体积就是 30×1 = 30(立方米)。
从这个例子咱们就能发现,长方体体积就等于长×宽×高。
这就好比咱们盖房子,长决定了能横着排多少块砖,宽决定了能竖着排多少块砖,高决定了能砌多少层砖。
我记得有一次,我带着学生们在教室里做一个小实验。
我给每个小组都发了一些小方块,让他们自己动手搭出不同大小的长方体,然后算出体积。
有个小组特别有意思,他们一开始手忙脚乱的,不知道该怎么下手。
我就在旁边稍微提示了一下,让他们先确定好长方体的长、宽、高分别要用几个小方块。
结果他们很快就搭好了,还兴奋地跟我汇报他们的成果。
通过这样的实践,孩子们对长方体体积的推导公式理解得可深刻了。
再回到咱们的数学学习中,明白了这个推导公式,做题目就容易多啦。
比如说,一个长方体的长是 8 厘米,宽是 6 厘米,高是 4 厘米,那它的体积就是 8×6×4 = 192(立方厘米)。
所以啊,同学们,只要咱们掌握了这个推导过程,不管遇到啥样的长方体体积问题,都能轻松搞定!总之,长方体体积的推导公式就是通过这样简单又有趣的方式得出来的。



归纳长方体正方体圆柱圆锥体积公式推导过程
推导长方体、正方体、圆柱和圆锥的体积公式
长方体体积公式推导过程:
我们知道长方体的体积等于底面积乘以高度。
设长方体的底面积为S,高度为h,则长方体的体积V=S*h。
正方体体积公式推导过程:
正方体是长方体的特殊情况,即长宽高相等。
设正方体的一边长为a,则底面积为a*a=a^2,高度也为a,所以正方体的体积V=a^2*a=a^3。
圆柱体积公式推导过程:
圆柱的底面为圆形,设底面半径为r,高度为h。
圆柱的底面积为π*r^2,高度为h,所以圆柱的体积V=π*r^2*h。
圆锥体积公式推导过程:
圆锥的底面为圆形,设底面半径为r,高度为h。
圆锥的底面积为π*r^2,高度为h,所以圆锥的体积V=1/3*π*r^2*h。
通过以上推导过程,我们得出了长方体、正方体、圆柱和圆锥的体积公式。
这些公式在几何学和工程学中都有广泛的应用,可以帮助我们计算和解决各种实际问题。
深入理解这些公式的推导过程,有
助于我们更好地掌握数学知识,提高解决问题的能力。
希望这篇文章能帮助读者更好地理解和运用这些几何体积公式。
