北航物理研究性报告 《氢原子光谱与里德伯常数测量》
- 格式:pdf
- 大小:264.57 KB
- 文档页数:19

基础物理实验研究性报告氢原子光谱实验中里德伯常数计算方法的探讨On different methods of estimating the Rydberg constant in the Hydrogen atoms spectrum experiment第一作者:彭志伟学号:10041189所在院系:能源与动力工程学院第二作者:贾林江学号:10041152所在院系:能源与动力工程学院目录氢原子光谱实验中里德伯常数计算方法的探讨 (1)摘要 (3)关键词 (3)Abstract (3)Key Words (4)一、引言 (1)二、氢原子光谱实验综述 (2)三、实验原理 (2)3.1 氢原子光谱 (2)3.2 光栅及其衍射分光原理 (3)四、里德伯常数数据处理方法 (3)4.1 可能的一些数据处理方法 (3)4.1.1 算数平均与加权平均 (3)4.1.2 一元线性回归法 (5)4.1.3 线性回归与最小二乘加权平均的比较 (8)4.2 结论 (10)五、结语 (11)六、参考文献 (12)七、附录——原始实验数据 (13)7.1 钠黄光校准光栅常数 (13)±级谱线校准光栅常数 (13)7.1.1 1±级谱线计算色分辨率 (13)7.1.2 27.2 氢光源测定里德伯常数 (13)7.2.1 红光原始数据 (13)7.2.2 蓝光原始数据 (13)7.2.3 紫光原始数据 (14)摘要本文讨论了氢原子光谱实验中里德伯常数的几种不同的数据处理方法。
理论上定量分析了不同算法的不确定度及置信水平,得出了应用不同波长求出里德伯常数后再采用加权最小二乘平均得到里德伯常数的最小方差无偏估计的算法较为合理的结论,并以原始实验数据进行了验证。
关键词:里德伯常数;数据处理;最小二乘法;加权平均AbstractThis paper discusses several data processing methods in the Hydrogen atoms spectrum experiment. By applying basic theory of mathematical statistics, the uncertainties and confidence levels of different methods are analyzed and compared. In conclus ion, it’s better to utilize Weighted Least Squares method (WLS) to get the minimum-variance unbiased estimate of the Rydberg constant after calculating the Rydberg constant of different wavelengths.Key Words: Rydberg constant; data processing; least squares criterion; weighted average一、引言里德伯常量,又译为雷德堡常数,是原子物理学中的基本物理常量之一。


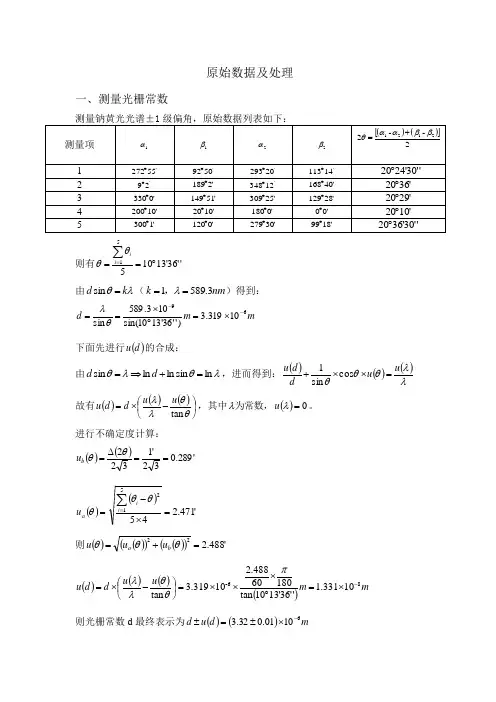
原始数据及处理一、测量光栅常数测量钠黄光光谱±1级偏角,原始数据列表如下: 测量项 1α1β2α2β()()[]2--22121ββααθ+=1 '55272︒'5092︒ '20293︒'14113︒ ''30'2420︒ 2 '29︒ '2189︒ '12348︒ '40168︒ '3620︒ 3 '0330︒ '51149︒ '25309︒ '28129︒ '2920︒ 4 '10200︒ '1020︒ '0180︒ '00︒'1020︒ 5'1300︒'0120︒'30279︒'1899︒''30'3620︒则有''36'1310551︒==∑=i iθθ由λθk d =sin (nm k 3.5891==λ,)得到:m m d 6910319.3)''36'1310sin(103.589sin --⨯=︒⨯==θλ下面先进行()d u 的合成:由λθλθln sin ln ln sin =+⇒=d d ,进而得到:()()()λλθθθu u d d u =⨯⨯+cos sin 1 故有()()()⎪⎭⎫⎝⎛-⨯=θθλλtan u u d d u ,其中()0=λλu 为常数,。
进行不确定度计算:()()'289.032'1322==∆=θθb u ()=θa u ()'471.245512=⨯-∑=i i θθ则()()()()()'488.222=+=θθθb a u u u()()()()m m u u d d u 86-10331.1''36'1310tan 18060488.210319.3tan -⨯=︒⨯⨯⨯=⎪⎭⎫ ⎝⎛-⨯=πθθλλ 则光栅常数d 最终表示为()()m d u d 61001.032.3-⨯±=±二、测量里德伯常数根据巴尔末系公式()⋯=⎪⎭⎫⎝⎛-=5,4,3121122n n R H λ以及λθk d =sin 可以得到: ()2141ln ln sin ln ln ln nR d k H -+=--θ由于可视为常数与k n ,可以化简为:()()()⎪⎭⎫⎝⎛--⨯=θθtan u dd u R R u H H1、1级红光谱线及其数据处理原始数据列表如下: 测量项 1α1β2α2β()()[]2--212121ββααθ+⨯=i1 '21230︒'1850︒ '40207︒'3927︒ ''30'2111︒ 2 '26296︒ '24116︒'44273︒'4293︒'2011︒则有''45'2011221︒=+=θθθ里德伯常数1722100971.11389.01sin 1312111-⨯=⨯=-⨯=m d R H θλ进行不确定度的计算:()()rad u b 4-10679.1'289.032'1322⨯===∆=θθ ()=θa u ()rad i i4-21210209.212⨯=⨯-∑=θθ()()()()()4-2210775.2⨯=+=θθθb a u u u则得到()()()141081.1tan -⨯=⎪⎭⎫ ⎝⎛--⨯=m u dd u R R u H H θθ里德伯常数最终表示为()1410)8.11.1097(-⨯±=±m R u R H H 2、1级蓝光谱线及其数据处理原始数据列表如下: 测量项 1α1β2α2β()()[]2--212121ββααθ+⨯=i1 '38351︒'38171︒ '268︒'26188︒ '248︒ 2'3581︒ '33261︒'2998︒'25278︒''30'268︒则有rad 1470.0''15'258221=︒=+=θθθ里德伯常数1722100958.11875.01sin 1412111-⨯=⨯=-⨯=m d R H θλ进行不确定度的计算:()()rad u b 4-10679.1'289.032'1322⨯===∆=θθ ()=θa u ()rad i i 4-21210040.212⨯=⨯-∑=θθ()()()()()4-2210642.2⨯=+=θθθb a u u u则得到()()()141002.1tan -⨯=⎪⎭⎫ ⎝⎛--⨯=m u dd u R R u H H θθ里德伯常数最终表示为()1410)0.18.1095(-⨯±=±m R u R H H 3、2级红光谱线及其数据处理原始数据列表如下: 测量项 1α1β2α2β()()[]2--212121ββααθ+⨯=i1 '0337︒'0157︒ '2023︒'10203︒ ''30'723︒ 2 '5066︒ '50246︒'10123︒'10303︒'1023︒则有rad 4040.0''45'823221=︒=+=θθθ里德伯常数1722100981.11389.01sin 2312111-⨯=⨯=-⨯=m d R H θλ进行不确定度的计算:()()rad u b 4-10679.1'289.032'1322⨯===∆=θθ ()=θa u ()rad i i 4-21210506.312⨯=⨯-∑=θθ()()()()()4-2210887.3⨯=+=θθθb a u u u则得到()()()141044.1tan -⨯=⎪⎭⎫ ⎝⎛--⨯=m u dd u R R u H H θθ里德伯常数最终表示为()1410)4.11.1098(-⨯±=±m R u R H H 4、通过加权平均值来获得H R 的最佳值:()()()()173123121009667.11-==⨯==∑∑m R u R u R R i Hi i Hi HiH()()()1431210741.011-=⨯==∑m R u R u i Hi H则获得里德伯常数的最佳表达式()()14107.07.1096-⨯±=±m R u R H H 与里德伯常数标准值534.10973731=H R 相比较,其相对误差为%0641.0%100=⨯-=HHH R R R E ,相对误差已经很小。

氢原子光谱和里德伯常量测定摘要:本文详细地介绍了氢原子光谱和里德伯常量实验的实验要求、实验原理、仪器介绍、实验内容和数据处理,并从钠黄双线无法区分的现象触发定量地分析了此现象的原因和由此产生的误差,结合光谱不够锐亮和望远镜转动带来的误差提出了创新的实验方案。
从理论上论证了实验方案的可行性,总结了基础物理实验的经验感想。
关键字:氢原子光谱里德伯常量钠黄双线Abstract:This paper introduced the hydrogen atoms spectrum and Rydberg constant experiment from experimental requirements, experimental principle, instruments required, content and Data processing. Considering that the wavelength difference of Na-light double yellow line is indistinguishable from human eyes, we analyze the cause of this phenomenon and the resulting errors quantitatively and propose an innovate experiment method combined with inadequate sharpness and lightness of the spectrum as well as the errors brought during the turning of telescope. We verify the feasibility of this method In theory and summarizes the experience and understanding of basic physics experiment.Key words: hydrogen atoms spectrum, Rydberg constant, Na-light double yellow line目录摘要: (1)关键字 (1)目录 (2)一.实验目的 (3)二.实验原理 (3)1.光栅衍射及其衍射 (3)2.光栅的色散本领与色分辨本领 (4)3.氢原子光谱 (5)4.测量结果的加权平均 (6)三.实验仪器 (7)四.实验内容 (7)五.实验数据及处理 (7)1.光栅常数测量 (8)2.氢原子光谱测里德波尔常数 (9)3.色散率和色分辨本领 (11)六.误差的定量分析 (11)1.人眼的分辨本领 (12)2.计算不确定度和相对误差: (12)七.实验方案的创新设想 (12)1.实验思路及理论验证 (12)2.实验光路 (13)3.方案理论评估 (13)八.实验感想与总结 (13)九.参考文献 (13)一.实验目的1. 巩固提高从事光学实验和使用光学仪器的能力; 2. 掌握光栅的基本知识和使用方法;3. 了解氢原子光谱的特点并用光栅衍射测量巴耳末系的波长和里德伯常数;4. 巩固与扩展实验数据的处理方法,及测量结果的加权平均,不确定度和误差计算,实验结果的讨论等。


氢原子光谱和里德伯常数的测定基础物理实验研究性报告一、实验目的1.掌握氢原子光谱测定方法。
2.理解和测定氢原子光谱系列。
3.通过测定氢原子光谱系列来计算里德伯常数。
4.分析实验结果并对其进行讨论。
二、实验原理1.氢原子光谱2.里德伯常数里德伯常数是描述氢原子光谱的重要物理常数,用于计算光谱线的频率和能级之间的能量差。
三、实验装置和材料1.光谱仪:用于测定氢原子光谱的波长。
2.氢放电装置:用于产生氢原子光谱。
3.高频电源:用于提供激发氢原子的电磁场。
4.精密光栅:用于分光。
5.光电倍增管:用于探测光信号。
四、实验步骤1.调整光谱仪和测定仪器,确保仪器的准确性和稳定性。
2.打开氢放电装置,产生氢原子光谱。
3.使用光谱仪测定不同波长的氢原子光谱,并记录光谱线的位置。
4.根据光谱线的位置和光谱系列的特点,确定氢原子光谱系列。
5.根据光谱系列和波长的关系,计算里德伯常数。
6.重复实验多次,计算平均值,并进行误差分析。
五、实验结果1.根据光谱线的位置,确定氢原子光谱系列为巴耳末系列。
2.根据巴耳末系列的波长和能级公式,计算里德伯常数的值。
六、实验分析和讨论七、实验结论通过本实验的研究,我们成功测定了氢原子的光谱并计算了里德伯常数。
实验结果与理论值相符,验证了实验方法的准确性和可靠性。
同时,根据实验结果可以进一步了解氢原子的能级结构,并研究光谱与能级之间的关系。
八、实验总结本实验通过测定氢原子光谱和计算里德伯常数的方法,深入研究了氢原子的光谱现象和能级结构。
通过实验的方法和结果,我们对氢原子的能级、波长和光谱系列有了更深入的理解。
同时,实验还进一步验证了实验方法的准确性和可靠性。
通过本次实验的学习,我们进一步掌握了基础物理实验的重要方法和技巧,并对物理实验的研究方法有了更深入的了解。

氢原子光谱和里德伯常数的测定基础物理实验研究性报告摘要:本实验通过测量氢原子光谱的发射线,利用巴尔末系列公式计算氢原子的波长和对应的频率。
通过计算求得里德伯常数。
实验结果显示,通过对氢原子光谱发射线的精确测量计算,我们得到了一个非常接近理论值的里德伯常数。
引言:在物理学中,氢原子光谱和里德伯常数是非常重要的研究内容。
氢原子的光谱可以通过精确测量发射线的波长和频率来研究。
里德伯常数是描述氢原子光谱的一个重要参数。
本实验通过测定氢原子光谱的发射线,计算出里德伯常数。
实验方法:1.实验仪器:用于测量光谱的光栅仪、频率计、电源等。
2.实验步骤:a.首先调整光谱仪的位置和角度,以确保获得清晰的光谱。
b.通过频率计测量氢原子光谱发射线的频率。
c.使用巴尔末系列公式计算波长,并计算对应的频率。
d.根据计算结果,得出里德伯常数。
实验结果与讨论:通过实验测量的氢原子光谱发射线的频率,我们计算得到了氢原子的波长和对应的频率。
利用计算结果,我们得到了里德伯常数的数值,并与理论值进行对比。
实验结果显示,我们得到的里德伯常数非常接近理论值。
结论:本实验通过测量氢原子光谱的发射线,计算出了里德伯常数。
实验结果显示,通过对氢原子光谱发射线的精确测量计算,我们得到了一个非常接近理论值的里德伯常数。
这个实验为研究氢原子的光谱和里德伯常数提供了有力的支持。
1. Griffiths, D. J. (2024). Introduction to quantum mechanics. Cambridge University Press.2. Cao, G. Z., Shu, S. B., & Gao, W. B. (1981). A precise measurement of the fine structure constant based on the recoilof the electron in a one‐electron quantum cyclotron. Applied Physics Letters, 39(8), 691-692.。

氢原子光谱和里德伯常数的测量Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】氢原子光谱和里德伯常数的测量第一作者 XXX第二作者 XXX指导老师:XXX一、实验要求实验重点○1巩固、提高从事光学实验和使用光学仪器的能力(分光仪的调整和使用)○2掌握光栅的基本知识和方法○3了解氢原子光谱的特点并使用光栅衍射测量巴尔末系的波长和里德伯常数○4巩固与扩展实验数据处理的方法——测量结果的加权平均,不确定度和误差的计算,实验结果的讨论等1、 预习思考题○1如何由()出发证明:在相邻的两个主极大之间由N-1个极小,N-1个次极大;N 越大,主极大的角宽度越小答:光栅衍射可以看作是单缝衍射和多缝干涉干涉的综合。
当平面单色光正入射到光栅上时,其衍射光振幅的角分布正比于单缝衍射因子sin αα和缝间干涉因子sin sin N ββ的乘积,及沿着 θ方向的的衍射光强220sin sin ()()()sin N I I αβθαβ=,式中sin sin ,,a d N θθαβλλ==是光栅的总缝数。
当sin 0β=时,sin N β也等于0,sin sin N N ββ=,()I θ形成干涉极大;当sin 0N β=但sin 0β≠时,()0I θ=,为干涉极小。
它说明:两个相邻的主极大之间有N-1个极小,N-2个次极大;N 数越多,主极大的角宽度越小。
○2 氢原子里德伯常数的理论值等于什么氢原子光谱的巴尔末系中对应的n=3,4,5的3条谱线应当是什么颜色答:理论值±)1m -。
谱线分别是红色、蓝色、与紫色。
○3 总结分光仪调整的关键步骤,在调整望远镜接受平行光、望远镜光轴垂直仪器主轴、平行光管射出平行光、平行光管主轴垂直仪器主轴的过程中应分别调整什么调整完成的标志又是什么答:分别应该调整目镜与载物台;载物台调平螺母;狭缝套筒与平行光管的水平调节螺母。

氢原子光谱摘 要:本实验用光栅光谱仪对氢原子光谱进行测量,测得了氢原子光谱巴尔末线系的波长,求出了里德伯常数。
最后对本实验进行了讨论。
关键词:氢原子光谱,里德伯常数,巴尔末线系,光栅光谱仪 1. 引言光谱线系的规律与原子结构有内在的联系,因此,原子光谱是研究原子结构的一种重要方式。
1885年巴尔末总结了人们对氢光谱测量的结果,发现了氢光谱的规律,提出了著名的巴尔末公式,氢光谱规律的发现为玻尔理论的成立提供了坚实的实验基础,对原子物理学和量子力学的发展起过重要作用。
1932年尤里按照里德伯常数随原子核质量不同而转变的规律,对重氢赖曼线系进行摄谱分析,发现氢的同位素氘的存在。
通过巴尔末公式求得的里德伯常数是物理学中少数几个最精准的常数之一,成为查验原子理论靠得住性的标准和测量其他大体物理常数的依据。
2. 氢原子光谱氢原子光谱是最简单、最典型的原子光谱。
用电激发氢放电管(氢灯)中的稀薄氢气(压力在102Pa 左右),可取得线状氢原子光谱。
瑞士物理学家巴尔末按如实验结果给出氢原子光谱在可见光区域的经验公式(1)式中λH 为氢原子谱线在真空中的波长。
λ0=364.57nm是一经验常数。
n取3,4,5等整数。
若用波数表示,则上式变成(2)式中RH 称为氢的里德伯常数。
按照玻尔理论,对氢和类氢原子的里德伯常数的计算,得4220-=n n H λλ⎪⎭⎫ ⎝⎛-==221211~n R v H H H λ(3)式中M为原子核质量,m为电子质量,e 为电子电荷,c 为光速,h 为普朗克常数,ε0为真空介电常数,z 为原子序数。
当M →∞时,由上式可得出相当于原子核不动时的里德伯常数(普适的里德伯常数)(4)所以R ∞=R ̅H (1+m/M H ) (5) 对于氢,有(6)这里MH 是氢原子核的质量。
由此可知,通过实验测得氢的巴尔末线系的前几条谱线的波长,借助(6)式可求得氢的里德伯常数。
里德伯常数R∞是重要的大体物理常数之一,对它的精密测量在科学上有重要意义,目前它的推荐值为R ∞=10973731.568549(83)/m 。

氢原子光谱实验报告一、实验目的与实验仪器1.学会并了解光栅的使用2.测定氢原子光谱3.计算氢氘原子核质量比及里德伯常数二、实验原理(要求与提示:限400字以内,实验原理图须用手绘后贴图的方式)氢原子光谱在可见光区域称为巴尔末线系式中n=3,4,5,6分别对应α β γ δ 谱线波长参数,若以波数表示谱线式中,109678 为氢的里德伯常量。
由波尔理论或量子力学得出的类氢离子的光谱规律为式中当 时,便得到里德伯常量所以还可以解出通过实验测出就可算出氢与氘的原子核质量比。
其中是电子质量和氢原子核质量之比为已知值。
三、实验步骤(要求与提示:限400字以内)1. 准备工作:选择光电倍增管接收方式,并启动软件同时初始化2. 校正光谱仪指示波长:使用汞灯三线作为标准值校正,调节合适的测量参数后开始测量汞灯谱线,并对测量结果进行修正。
3. 测量氢原子氘原子的巴尔末系4. 处理数据 四、数据处理(要求与提示:对于必要的数据处理过程要贴手算照片) 氢、氘原子的 α 谱线 n=3172292210096.1)3121(1086.6561)1-211m n R (177100959.171/1836.152 110096.1/1m M m R R HH1.906471/1836.152656.69656.86-656.69656.8671/1836.152/ H D H D H H H D M m M m M M177107095.11.90641836.15271/ 110096.1/1m M m R R HD )(氢、氘原子的 β 谱线 n=4172292210809.1)4121(10485.911)1-211m n R (177100979.171/1836.152 110098.1/1m M m R R HH1.966671/1836.152485.79485.92-485.79485.9271/1836.152/ H D H D H H H D M m M m M M177107095.11.96661836.15271/ 110096.1/1m M m R R HD )(氢、氘原子的 γ 谱线 n=5172292210809.1)5121(10433.471)1-211m n R (177100979.171/1836.152 110098.1/1m M m R R HH2.034971/1836.152433.35433.47-433.35433.4771/1836.152/ H D H D H H H D M m M m M M177107095.12.03491836.15271/ 110096.1/1m M m R R HD )(氢、氘原子的 δ 谱线 n=6172292210809.1)6121(10409.571)1-211m n R (177100979.171/1836.152 110098.1/1m M m R R HH1.289171/1836.152409.52409.57-409.52409.5771/1836.152/ H D H D H H H D M m M m M M177105095.11.28911836.15271/ 110096.1/1m M m R R HD )(1741100987.1m R R i不确定度:1710010.0 m9693.131 iiH D H D M M M M五、分析讨论(提示:分析讨论不少于400字)发现实验测得光谱氘原子波峰一直比氢原子波峰高与讲义所给示例图相反,推测是因为本实验组所用的氢氘灯中氘的填充比例更高导致。
氢原子光谱摘 要:本实验用光栅光谱仪对氢原子光谱进行测量,测得了氢原子光谱巴尔末线系的波长,求出了里德伯常数。
最后对本实验进行了讨论。
关键词:氢原子光谱,里德伯常数,巴尔末线系,光栅光谱仪1. 引言光谱线系的规律与原子结构有内在的联系,因此,原子光谱是研究原子结构的一种重要方法。
1885年巴尔末总结了人们对氢光谱测量的结果,发现了氢光谱的规律,提出了著名的巴尔末公式,氢光谱规律的发现为玻尔理论的建立提供了坚实的实验基础,对原子物理学和量子力学的发展起过重要作用。
1932年尤里根据里德伯常数随原子核质量不同而变化的规律,对重氢赖曼线系进行摄谱分析,发现氢的同位素氘的存在。
通过巴尔末公式求得的里德伯常数是物理学中少数几个最精确的常数之一,成为检验原子理论可靠性的标准和测量其他基本物理常数的依据。
2.实验目的(1)熟悉光栅光谱仪的性能和用法;(2)用光栅光谱仪测量氢原子光谱巴尔末系数的波长,求里德伯常数; 3. 氢原子光谱氢原子光谱是最简单、最典型的原子光谱。
用电激发氢放电管(氢灯)中的稀薄氢气(压力在102Pa 左右),可得到线状氢原子光谱。
瑞士物理学家巴尔末根据实验结果给出氢原子光谱在可见光区域的经验公式4220-=n n H λλ (1)式中ιH 为氢原子谱线在真空中的波长。
ι0=364.57nm是一经验常数。
n取3,4,5等整数。
若用波数表示,则上式变为⎪⎭⎫ ⎝⎛-==221211~n R v H H H λ (2)式中RH 称为氢的里德伯常数。
根据玻尔理论,对氢和类氢原子的里德伯常数的计算,得)/1()4(2320242M m ch z me R z +=πεπ (3)式中M为原子核质量,m为电子质量,e 为电子电荷,c 为光速,h 为普朗克常数,ε0为真空介电常数,z 为原子序数。
当M →∞时,由上式可得出相当于原子核不动时的里德伯常数(普适的里德伯常数)320242)4(2ch z me R πεπ=∞ (4)所以(5)对于氢,有)/1(H H M m R R +=∞(6)这里MH 是氢原子核的质量。
氢原子光谱实验报告---完成版解读氢原子光谱中文摘要:本实验用三棱镜对汞原子光谱进行测量,得出定标曲线;再对氢原子光谱进行测量,测得了氢原子光谱巴尔末线系的波长,求出了里德伯常数。
最后对本实验进行了讨论。
关键词:氢原子光谱,里德伯常数,巴尔末线系,三棱镜,汞原子光谱中图分类号:O433.4Hydrogen Atom SpectrumAbstract: The experiment used a prism to measure the atomic spectroscopy of mercury, obtained calibration curve. Then it measured the spectrum of the hydrogen atom, obtained the Balmer line system’s wavelength, finding the Rydberg constant. Finally, the experiment has some discussions.Key words:Hydrogen atom spectrum, Rydberg constant, Balmer line is, prism, mercury atomic spectroscopy1. 引言光谱线系的规律与原子结构有内在的联系,因此,原子光谱是研究原子结构的一种重要方法。
1885年巴尔末总结了人们对氢光谱测量的结果,发现了氢光谱的规律,提出了著名的巴尔末公式,氢光谱规律的发现为玻尔理论的建立提供了坚实的实验基础,对原子物理学和量子力学的发展起过重要作用。
1932年尤里根据里德伯常数随原子核质量不同而变化的规律,对重氢赖曼线系进行摄谱分析,发现氢的同位素氘的存在。
通过巴尔末公式求得的里德伯常数是物理学中少数几个最精确的常数之一,成为检验原子理论可靠性的标准和测量其他基本物理常数的依据。
氢原子光谱和里德伯常数测量综合探究第一作者:班级学号姓名第二作者:班级学号姓名日期:2013年5月22日目录摘要 (1)1实验目的 (2)2 实验原理 (3)2.1分光仪的调整 (3)2.2光栅及其衍射 (4)2.3光栅的色散本领与色分辨本领 (6)2.4 氢原子光谱 (8)3实验仪器 (10)4实验内容 (11)4.1调节分光仪 (11)4.2调节透射光栅 (13)4.3测光栅常数 (13)4.4测量氢原子里德伯常数 (13)5实验数据处理 (14)5.1光栅常数d的测量 (14)5.2氢原子光谱测里德伯常数 (15)5.3误差分析 (18)6实验数据处理再分析 (19)6.1波数为因变量的直线拟合 (19)6.2 等权平均法 (19)7总结与讨论 (21)7.1分光仪调节经验总结 (21)7.1.1 分光仪粗调方法 (21)7.1.2 十字反射像的寻找方法 (21)7.1.3调节望远镜光轴与分光仪轴垂直正交 (22)7.2固定透射光栅的技巧 (23)7.3实测谱线具有一定宽度的原因分析 (23)7.4钠黄双线能否被观测到分开的探讨以及不确定度进一步讨论 (23)8实验感想 (26)9 参考文献 (27)摘要:氢原子光谱是一种典型的线状光谱,是量子理论得以建立的最重要的实验基础之一。
该实验把作为分光元件的光栅和精密测角仪器的分光仪结合起来进行氢光谱的观察与测量。
本文通过介绍实验的原理、步骤、仪器,并对实验数据进行不同方式的处理与对比及最后结果的进一步探讨。
此外,还分析了分光仪调整方法、调整技巧以及在实验过程中未能观察到钠黄双线被分辨的原因等。
借助进一步研究该实验综合性地梳理了分光仪、光栅以及氢原子光谱的知识。
关键词:氢原子光谱分光仪钠黄光双线加权平均1巩固提高从事光学实验和使用光学仪器的能力;2掌握光栅的基本知识和使用方法;3了解氢原子光谱的特点并用光栅衍射测量巴耳末系的波长和里德伯常数;4巩固与扩展分光仪调节,实验数据的处理方法,及测量结果的加权平均,不确定度和误差计算,实验结果的讨论等。
氢原子光谱的测量一、试验目的(1)、了解小型棱镜摄谱仪的结构,掌握其分光原理。
(2)、学习用摄谱仪测量光谱波长的基本实验技术。
(3)、测量氢原子光谱巴尔末线系的波长,并计算里德伯常量.二、实验原理1、氢原子光谱的规律原子光谱与原子能级是密切相关的。
测量原子光谱的波长可推知原子能级的结构。
氢光谱中位于可见光区四条谱线的波长可用下面的经验公式表示:λ B (n=3,4,5,…) (2-232)式中,B是一恒量,值为364.56nm,是谱线系极限值,即n→∞时的波长值。
里德伯将此公式改为波数=1/λ表示=) (2—233)式中,R H 称为氢原子的里德伯常量,其实验测量值为109677.6cm-1。
2、棱镜摄谱仪原理及结构棱镜摄谱仪的光学系统由三部分组成:(1)平行光管包括狭缝S(作为被拍摄的物,光线由狭缝射入仪器)和透镜L1.S平面位于L1的焦面上,因而从S上每点发出的复色光经L1后变为平行光。
(2)、色散系统以棱镜作为色散元件。
不同波长的平行光经棱镜折射后变为不同方向的平行光。
(3)光谱接收部分包括透镜L2及放置在L2焦面上的照相感光板F.不同方向的平行光束L2聚焦,成像在不同位置,形成S的一系列单色像S1,S2,…。
F放在像面上,就在F上形成一排细线,每一条细线对应于一定的波长,叫光谱线。
图1 小型棱镜光路图2 摄谱仪光学系统原理图3、谱线波长的测量(1)、目测法用眼睛通过看谱镜直接观测。
先用已知波长λs的光谱作标准,通过读数鼓轮来确定待测各谱线的波长λx。
(2)、照相法将波长已知的光谱线(比较光谱)和波长未知的光谱线(待测谱线)拍摄在同一张感光板上。
拍摄时,不能移动狭缝和摄谱暗箱,只能通过抽动哈特曼光阑,使比较光谱和待测光谱中常用线性内插法测量.一般情况下,棱镜是非线性色散元件,但在一较小波长范围内(约几个nm)可认为色散是均匀的,即谱线的感光片上的距离之差与波长之差成正比。
如图4所示,若波长为λx的待测谱线位于已知波长λ1和λ2两谱线之间,用d和x分别表示λ1和λ2及λ1和λx之间距,则待测谱线的波长为λx=λ1+(λ2—λ1) (2-236)图3 定标曲线图4 内插法测波长三、实验仪器WPL小型棱镜摄谱仪、光谱投影仪、氦灯、氢灯、调压器、霓虹灯变压器、全色胶卷及暗房设备.四、实验步骤1、调试小型棱镜摄谱仪至工作状态(1)调整光源与聚光镜的位置,使其与平行光管等高、共轴;点燃氦灯,前后移动聚光灯,将光源成像于狭缝处,均匀照亮整个狭缝使通过摄谱仪的光通量达到最大.(2)调节狭缝宽度和调焦,使该谱线清晰.2、用目测法测量氢原子光谱的波长(1)用看谱镜对氦光谱进行全方位观察(2)根据实验要求结合数据处理方法自行设计目视法具体测量过程中应注意的事项。
北航氢原子光谱实验报告 -回复
敬启者:
随着现代化科技的不断发展和人们对于科学研究的追求,实验科研成为了人们实现全面开放的先行者,解决了科技瓶颈问题,推动了人类文明的飞跃。
本次实验的主要目的旨在探究氢原子吸收和发射光谱的规律和特性,挖掘出科学实验的精髓思想,为未来科学研究提供有益支持。
一、实验原理
氢原子光谱的研究,可以采用发射光谱和吸收光谱两种方式进行研究。
本次实验是采用氢原子吸收光谱,即通过光谱仪分析样品经过一定波长的电磁波后,所产生的吸收光谱来探究其性质。
二、实验器材
光源、氢气灯、凸透镜、光琴、望远镜、光谱仪、移动台
三、实验过程
1.实验前准备,调整仪器,打开光源,将氢气灯与凸透镜相联系。
2.将样品通过光源,通过凸透镜使氢原子射入灯管中。
3.将望远镜与光谱仪相联,调整使其垂直灯管。
4.目测望远镜的目视合法,使样品较明亮的氢原子能够射入。
慢慢调整光源,使其达到最佳状态。
5.调整光谱仪,寻找到氢原子的吸收峰值,并测量相应的光谱线强度和波长。
6.记录数据并制成数据图表,简要总结实验结果。
四、实验结果
在实验中,我们通过光谱仪检测了氢原子吸收光谱,并准确得到了吸收波长和吸收强度。
通过对实验数据的分析,得出了氢原子的光谱线,这也为之后氢原子的研究奠定了坚实的基础。
五、实验结论
本次实验研究氢原子吸收光谱,通过测得数据和分析数据,得出了氢原子的光谱线。
本次实验所得的结果符合以往实验的结果,也为之后的研究提供了参考。
同时,本次实验也显示出科学实验的重要性和必要性,令我们更加深刻理解科学实验的本质。