下载文档原格式
质量七大工具-柏拉图、排列图ParetoDiagram排列图(Pareto Diagram，柏拉图、帕累托图)什么是排列图法排列图法，又称主次因素分析法、帕累托（Pareto）图法，它是找出影响产品质量主要因素的一种简单而有效的图表方法。
1897年意大利经济学家帕累托（1848---1923）分析社会经济结构，发现80%的财富掌握在20%的人手里，后被称“帕累托法则”。
1907年美国经济学家劳伦兹使用累积分配曲线描绘了柏拉图法则，被称为“劳伦兹曲线”。
1930年美国品管泰斗朱兰博士将劳伦兹曲线应用到品质管理上。
20世纪60年代，日本品管大师石川馨在推行自己发明的QCC品管圈时使用了排列图法，从而成为品管七大手法。
排列图是根据“关键的少数和次要的多数”的原理而制做的。
也就是将影响产品质量的众多影响因素按其对质量影响程度的大小，用直方图形顺序排列，从而找出主要因素。
其结构是由两个纵坐标和一个横坐标，若干个直方形和一条折线构成。
左侧纵坐标表示不合格品出现的频数（出现次数或金额等），右侧纵坐标表示不合格品出现的累计频率（如百分比表示)，横坐标表示影响质量的各种因素，按影响大小顺序排列，直方形高度表示相应的因素的影响程度（即出现频率为多少），折线表示累计频率（也称帕累托曲线）。
通常累计百分比将影响因素分为三类：占0%～80%为A类因素，也就是主要因素；80%～90%为B类因素，是次要因素；90%～100%为C类因素，即一般因素。
由于A类因素占存在问题的80%，此类因素解决了，质量问题大部分就得到了解决。
为了方便理解，下面举个例子。
某酒杯制造厂对某日生产中出现的120个次品进行统计，做出排列图，如下图所示：排列图表明：酒杯质量问题的主要因素是划痕和气泡，一旦这些问题得到纠正，大部分质量问题即可消除。
排列图的作用1、作为降低不良依据。
2、决定改善的攻击目标。
3、确认改善效果。
4、用于发现现场的重要问题点5、用于整理报表或记录。
QC七大手法检查表(Data collection form)分层法(Stratification)散布图(Scatter)排列图(Pareto)直方图(Histogram)因果图(Cause-Effect diagram)控制图(Control Chart)1. 查检表（Check List）以简单的数据或容易了解的方式，作成图形或表格，只要记上检查记号，并加以统计整理，作为进一步分析或核对检查用，其目的在於『现状调查』。
2. 柏拉图（Pareto Diagram）根据所搜集之数据，以不良原因、不良状况、不良发生或客户抱怨的种类、安全事故等，项目别加以分类，找出比率最大的项目或原因并按照大小顺序排列，再加上累积值的图形。
用以判断问题症结之所。
3. 特性要因图（Characteristic Diagram）一个问题的特性（结果）受一些要因（原因）的影响时，将这些要因加以整理，而成为有相互关系而且有条且有系统的图形。
其主要目的在阐明因果关系，亦称『因果图』，因其形状与鱼骨图相似故又常被称作『鱼骨图』。
4. 散布图（Scatter Diagram）把互相有关连的对应数据，在方格上以纵轴表示结果，以横轴表示原因，然后用点表示分布形态，根据分析的形态未研判对应数据之间的相互关系。
5. 管制图（Control Chart）一种用於调查制造程序是否在稳定状态下，或者维持制造程序在稳定状态下所用的图。
管制纵轴表产品品质特性，以制程变化数据为分度；横轴代表产品的群体号码、制造曰期，依照时间顺序将点画在图上，再与管制界限比较，以判别产品品质是否安定的一种图形。
6. 直方图（Histogram）将搜集的数据特性值或结果值，在一定的范围横轴上加以区分成几个相等区间，将各区间内的测定值所出现的次数累积起来的面积用柱形画出的图形。
因此也叫柱形图。
7. 层别法（Stractification）针对部门别、人别、工作方法别、设备、地点等所搜集的数据，按照它们共同特徵加以分类、统计的一种分析方法.二： 8D 8D 的原名叫做 8 Disciplines，意思是8 个人人皆知解决问题的固定步骤。
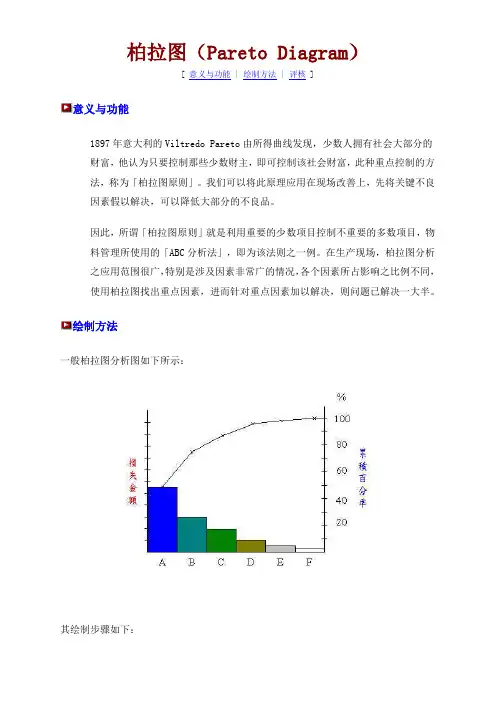
柏拉图（Pareto Diagram）[ 意义与功能 | 绘制方法 | 评核 ]意义与功能1897年意大利的Viltredo Pareto由所得曲线发现，少数人拥有社会大部分的财富，他认为只要控制那些少数财主，即可控制该社会财富，此种重点控制的方法，称为「柏拉图原则」。
我们可以将此原理应用在现场改善上，先将关键不良因素假以解决，可以降低大部分的不良品。
因此，所谓「柏拉图原则」就是利用重要的少数项目控制不重要的多数项目，物料管理所使用的「ABC分析法」，即为该法则之一例。
在生产现场，柏拉图分析之应用范围很广，特别是涉及因素非常广的情况，各个因素所占影响之比例不同，使用柏拉图找出重点因素，进而针对重点因素加以解决，则问题已解决一大半。
绘制方法一般柏拉图分析图如下所示：其绘制步骤如下：1.坐标取法A.横轴：用以代表材料别、机器别、缺点种类或其它分析的原因。
B.纵轴：不良百分率、故障次数、损失金额或其它因分析原因所造成的结果。
2.搜集资料依据既定所要分析的原因种别，搜集这些原因所造成的结果，通常是损失金额、损失时间等，这些数据有赖平常的纪录语汇整，并需要得到经营管理阶层与有关部门支持与提供情报，方能顺利达成目标。
3.制作柏拉图分析图A.按照横轴各可能原因所造成之影响大小，绘成直方图。
B.画出累积百方率曲线。
C.将改善目标值，以虚线画在图上，作为改进之准则。
D.将上期造成之影响总量标于图上，做为参考。
E.以一个月做为柏拉图分析的期间。
F.纵轴最好以损失金额取代不良品个数或其它非金额的影响，目的是使所有人均能一目了然。
G.精密机械加工业之柏拉图分析图范例，如下图所示：实施成效考核从每期得柏拉图分析中，可以知道主要因素在改善前后的效果，重点在于损失金额的减少多少，以此为评量绩效的依据。
目录1 –数据与图表2-常用统计分析方法概述3 -检查表（Check Sheets）4-柏拉图（Pareto Diagram）5-因果图（Cause & Effect Diagram）6 -散布图（Stratification）7 -分层法（Scatter Diagram）8 -直方图（Histogram）9 -控制图（Control Chart）柏拉图，排列图，帕累托图（Pareto Diagram）---发现问题的重心抓住一切，就等于失去所有；善用柏拉图，顺利掌握重点。
柏拉图的由来意大利经济学者V.Pareto分析其社会经济结构，发现一个规律“80%的社会财富掌握在20%的人手中”，称之为“柏拉法则”；柏拉法则---“关键的少数，次要的多数”美国经济学者M.O.Lorenz使用累积分配曲线来描绘“柏拉法则”，即经济学上所称之劳伦兹（Lorenz）曲线；美国J.M.Juran将Lorenz曲线应用到品质管理上，同时创出“Vital Few，Trivial Many”（重要的少数，琐细的多数）的名词，并将此现象定为“柏拉图原理”；品管圈创始人石川馨博士将柏拉图运用到品管圈活动中，使之成为品管七大手法之一；柏拉图的定义及使用时机1. 定义根据所搜集的数据，按不同区分标准加以整理、分类(按其大小顺序排列)，找出占最大比率之原因、状况或位置及其影响程度的图形；2. 柏拉图使用时机2.1 掌握问题点(抓住关键因素)2.2 找出原因（解决主要问题）2.3 效果确认（改善前、后之比较）柏拉图的应用品质管理：不良品数，损失金额，客诉项目，抱怨次数，返修品数……时间效率：作业的效率，故障率、修理时间……价格成本：材料单价，产品成本……社会治安：犯罪率、件数、年龄别……医疗保健：病因，职业病患，门诊科别……客户服务：客诉件数、处理时间、不良品数……业务销售：销售项目，销售区域……项目：电子件焊接不良分布柏拉图日期：2012.12.10～2013.1.14制图：###柏拉图的构成•确认柏拉图调查目的，决定数据的分类项目；•决定收集数据的期间及方法，并收集数据；•整理数据，制作统计表；•画出柱状图，绘制累计曲线；•记入必要的事项；•决定改善目标，找出问题点；1.确立调查目的，决定数据的分类项目（层别法）制作柏拉图时，首先确立柏拉图调查的目的或意图；一般的分类先从结果分类上着手，以便洞悉主要问题之所在；然后再进行原因分类，分析出问题产生之原因，以便采取有效的对策。
品质管理——柏拉图法第一篇：品质管理——柏拉图法品质管理工具之柏拉图（排列图）概述什么是柏拉图（排列图）？根据所搜集之数据，按不良原因、不良状况、不良发生位置等不同区分标准，以寻求占最大比率之原因，状况或位置的一种图形。
柏拉图又叫排列图。
它是将质量改进项目从最重要到最次要顺序排列而采用的一种图表。
柏拉图由一个横坐标、两个纵坐标、几个按高低顺序（“其他”项例外）排列的矩形和一条累计百分比折线组成。
柏拉图（排列图）格式柏拉图的主要用途(1)按重要顺序显示出每个质量改进项目对整个质量问题的作用；(2)识别进行质量改进的机会。
(即识别对质量问题最有影响的因素,并加以确认)作图步骤1)选择要进行质量分析的项目；2)选择用来进行质量分析的度量单位，如出现的次数（频数、件数）、成本、金额或其他；3)选择进行质量分析的数据的时间间隔；4)画横坐标； 5)画纵坐标；6)在每个项目上画长方形，它的高度表示该项目度量单位的量值，显示出每个项目的影响大小；7)由左到右累加每个项目的量值（以％表示），并画出累计频率曲线（帕累托曲线），用来表示各个项目的累计影响；8)利用柏拉图确定对质量改进最为重要的项目（关键的少数项目）。
注意事项1)一般来说，关键的少数项目应是本QC小组有能力解决的最突出的一个，否则就失去找主要矛盾的意义，要考虑重新进行项目的分类；2)纵坐标可以用“件数”或“金额”等来表示，原则是以更好地找到“主要项目”为准；3)不太重要的项目很多时，横轴会变得很长，通常都把这些列入“其他”栏内，因此“其他”栏总在最后；4)确定了主要因素，采取了相应的措施后，为了检查“措施效果”，还要重新画出排列图。
应用实例某公司QC小组在2001年对其电子产品的用户反馈单进行了统计，整理后的资料，如下：从图中可看出，该公司产品的“插头焊接缺陷”应作为“质量改进”的主要对象，应对它作进一步的调查研究与分析。
以上是对品质管理工具之一的柏拉图的介绍，其中柏拉图遵循二八原则，即：1、80%的问题由20%的原因引起；2、80%的索赔发生在20%的生产线上； 3、80%的销售额由20%的产品带来； 4、80%的品质成本由20%的品质问题造成；5、80%的品质问题由20%的人员引起做品质管理的工具除了柏拉图外，还有控制图、因果图等工具，其中企业在做品质管理时离不开SPC品质管理软件（SPC免费下载），SPC------(Statistical Process Control)译为统计制程管制，是指“在制程中去收集数据，并将所收集的数据加以统计分析，从分析中发现制程的异常，再通过问题的分析来挖掘异常的原因，并针对该原因采取适当有效的对策，使制程恢复正常状态，再透过制程能力的调查分析与标准化，不断提升制程能力的一种维护与改善的手法”。
第4章柏拉图 77第4章柏拉图(Pareto Diagram)排列图一、前言由生产现场所收集到的数据，有效的加以分析、运用，才能成为有价值的数据。
而将此数据加以分类、整理并作成图表，充分的掌握问题点及重要原因，则是目前不可或缺的管理工具。
而最为现场人员广泛使用于数据管理的图表为柏拉图。
二、柏拉图的由来意大利经济学家V.Pareto(1848-1923)在1897年分析社会经济结构时，赫然发现国民所得的大部份均集中于少数人身上，于是将所得的大小与拥有所得的关系加以整理。
发现有一定的方程式可以表示，称为[柏拉图法则]。
1907年美国经济学者M.O.Lorenz使用累积分配曲线来描绘[柏拉图法则]，也就是经济学所谓的劳伦兹(Lorenz)曲线。
美国品管专家J.M.Juran(朱兰博士)将劳伦兹曲线应用于品管上，同时创出[Vital Few, Trivial Many] (重要的少数，次要的多数)的见解，并借用Pareto的名字，将此现象定为[柏拉图原理]。
[柏拉图]方法，由品管圈(QCC)的创始人日本石川馨博士介绍到品管圈活动中使用，而成为品管七大手法之一。
三、柏拉图的定义1.根据所搜集的数据，按不良原因、不良状况、不良项目、不良发生的位置等不同区分标准而加以整理、分类，从中寻求占最大比率的原因、状况或位置，按其大小顺序排列，再加上累积值的图形。
2.从柏拉图可看出那一项目有问题，其影响度如何，以判断问题的症结所在，并针对问题点采取改善措施，故又称为ABC图。
（所谓ABC分析的重点是强调对于一切事务，依其价值的大小而付出不同的努力，以获至效果；亦即柏拉图分析前面2-3项重要项目的控制）。
78 品管七大手法3.又因图的排列系按大小顺序排列，故又可称为排列图。
四、柏拉图的制作步骤1.柏拉图的制作方法步骤1:决定数据的分类项目。
分类的方式有:(1)结果的分类包括不良项目别、场所别、时间别、工程别。
(2)原因的分类包括材料别(厂商、成份等)、方式别(作业条件、程序、方法、环境等)、人员别(年龄、熟练度、经验等)、设备别(机械、工具等)等。
分类的项目必须合乎问题的症结，一般的分类先从结果分类上著手，以便洞悉问题的所在，然后再进行原因分类，分析出问题产生的原因，以便采取有效的对策。
将此分析的结果，依其结果与原因分别绘制柏拉图。
步骤2:决定收集数据的期间，并按分类项目，在期间收集数据。
考虑发生问题的状况，从中选择恰当的期限(如一天、一周、一月、一季或一年为期间)来收集数据。
第4章柏拉图 79例:电气不良状况记录表期间:****年8月5日-9日步骤3:依分类项目别，做数据整理，并做成统计表。
(1)各项目按出现数据的大小顺序排列，其他项排在最后一项，并求求累积数(其他项不可大于前三项,若大于时应再细分)。
(2)求各项目数据所占比率及累计数的影响比率。
(3)其他项排在最后，若太大时，须检讨是否有其他重要项目还需细分出来。
80 品管七大手法不良率(%) =各项不良数÷总检查数×100影响比例(%) =各项不良数÷总不良数×100步骤4:记入图表用纸并依数据大小排列画出柱状图。
(1)于图表用纸记入纵轴及横轴。
纵轴左侧填不良数、不良率,或损失金额，纵轴右侧刻度表示累计影响度(比率)；在最上方刻100%，左方则依收集数据大小做适当刻度，横轴填分类项目名称，由左至右按照所占比率大小记入，其他项则记在最右边。
(2)横轴与纵轴应成适度比例，横轴不宜长于纵轴。
第4章 柏拉图 81步骤5:绘累计曲线。
(1)点上累计不良数(或累计不良率)。
(2)用折线连结。
步骤6:绘累计比率。
(1)纵轴右边绘折线终点为100%。
(2)将0~100%间分成10等分，把%的分度记上(即累计影响比例)。
(3)标出前三项(或四项)之累计影响比例是否>80%或接近80%。
不良数170 153 136119 102 85685134 17 0不良项目 收敛不良几何失真 白平衡 敲闪 无画面 画面倾斜 其他 不良不良数170 153 13611910285 6851 34 17 0不良项目 几何失真 白平衡 敲闪 无画面 画面倾斜 其他不良82 品管七大手法步骤7:记入必要的事项。
(1)标题(目的)。
(2)数据搜集期间。
(3)数据合计(总检查、不良数、不良率…等)。
(4)工程别。
(5)相关人员(包括记录者,绘图者…)。
2.绘制柏拉图应注意事项:(1)柏拉图的横轴是按项目别，按大小顺序由高而低排列，[其他]项排在最后一位。
(2)柏拉图的柱形图宽度要一致，纵轴与横轴比例为3:2。
(3)纵轴最高点为总不合格数，且所表示的间距应一致。
(4)次数少的项目太多时，可考虑将后几项归纳成[其他]项；其他项不应大于前几项，若大于时应再分析。
有时，改变层别或分类的方法，也可使分类的项目减少。
通常，项目别包括其他项在，以不要超过4-6项为原则。
累计 影 响比 例(%)不合格项目 不合格数 170 153 136 119 102 85 68 51 34 17 0 收敛 几何 白平衡 敲闪 无画面 画面 其他 不良 失真 不良 倾斜100%90% 80% 70% 60%50%40% 30% 20% 10% 不合格数 不合格项目 累 计影 响 比例 (%) 170 153136 119 102 85 68 51 34 17 0 收敛 几何 白平衡 敲闪 无画面 画面 其他 不良 失真 不良 倾斜100% 90%80% 70% 60% 50% 40% 30% 20% 10%工 程:电气检查 总检查数:1450总不合格数:170 期 间:82年8月5日~9日 检 验 者:王胜利 绘图者:李四第4章柏拉图 83(5)纵轴与横轴可表示下列容:a.纵轴:(a)品质—不合格数、退货数、不合格率。
(b)时间—维修时间、作业时间、运转时间。
(c)金额—销货金额、损失金额、人事费用。
(d)安全—灾害件数、故障件数。
(e)其他—缺席率、提案件数。
b.横轴:(a)现象—不合格项目别、位置别、区域别…等。
(b)时间—月、周、季、年别…等。
(c)设备—机械别、治具别…等。
(d)操作者—人别、年龄别、男女别、国别…等。
(e)其他—厂商、作业方法…等。
(6)每一不合格项目所引起的损失金额不同时，纵轴应以损失金额来表示。
(7)改善前后的比较时:a.改善后，横轴项目别依照出现大小顺序由高而低排列。
b.前后比较基准应一致，且刻度应相同。
c.各项目别以颜色来区分，则更易于比较。
(8)柏拉图中，连接各项目与纵轴对应点的线，名为“柏拉曲线”，但因各项次之数据分配并非连续分配，所以其连接线为折线而非曲线。
(9)一般而言，前三项不合格项目往往点累计影响比率的70~80%强；如能针对前三项做改善，便可得到70%以上的成效。
(10)柏拉图适用于计数值统计，而计量值则使用直方图。
84 品管七大手法例:某电子材料检验后，以不合格数及损失金额分别计算如下：第4章 柏拉图 85不 合格 数 不合格项次70 50 25100% 80 60 40 20累计不合格数(%)五、柏拉图的应用1. 作为降低不合格的依据：想降低不合格率，先绘柏拉图看看。
(1)全体的不合格有多少? (2)各种不合格占多少?(3)降低那些不合格，可将全体不合格降低70-80%以上? 真正影响不合格的大原因只2-3项而已,只要对2-3项主要原因把握住,整个不合格原因就减掉大半了. 2. 决定改善目标，找出问题点:柏拉图分析并不限于 “不合规格”的不合格，任何工厂的问题都可应用柏拉图分析，例如: (1)修理件数、费用、时间。
(2)客诉件数、处理时间及费用。
(3)不合格品数及所损失金额。
(4)效率损失。
3. 确认改善效果(改善前、后的比较):采取改善对策后，为确认其成效，需重绘一次柏拉图，如采取的对策有效，柱形图的高度会降低，且横轴的不合格项目及顺序会变动。
(1)把改善前、后的柏拉图排列在一起，即可评估其改善成效。
(2)确认改善效果时，应注意下列三点:a. 柏拉图收集数据的期间及对象要一致。
b.对季节性的变动应列入考虑。
5410 4410 3300 2200 1100100% 80 60 40 2086 品管七大手法c.对于对策外之要因，也应加以注意，以免疏忽。
4.应用于发掘现场的重要问题点。
一般数据可分为两大类:依结果的分类—将结果的数据加以分类绘柏拉图，可掌握住少数而重要的结果。
诸如:不良项目、工程别…等。
依要因的分类—将主要的结果找出后，再依特性要因图中的要因，搜集要因数据，作成柏拉图，即可找寻或掌握住重要的要因。
如此，先按结果分类，再从各类中找其要因，进而再对此要因寻求对策的话，则大部份的问题可获解决。
5.用于整理报告或记录。
若只用数据来写报告或记录，比较不容易了解问题点，若采用柏拉图来整理报告或记录时，则可使看者一目了然。
6.可作不同条件的评价。
对于同一过程前后不同时间的表现，用柏拉图来加以分析、评价。
7.验证或调整特性要因图。
对于凭经验或直觉绘制的特性要因图，可用柏拉图来加以验证或调整。
8.配合特性要因图使用。
把柏拉图上的项目当作质量特性加以要因分析，再用柏拉图整理重新分类，可以找出改善的方案。
改善前 改善后 A B C D EF A B C D E Fword 资料第4章 柏拉图 87六．应用柏拉图应注意的事项1. 柏拉图是按所选取的项目来分析；因此，只能针对所做项目加以比较,对于项目以外的分析无能为力。
例如:某产品不合格数中A 项占85%,减低A 项不合格数只能降低该产品的不合格率,并不代表此举最合乎经济效益原则。
2. 作成的柏拉图若发现各项目分配比例相关不多时,则不符合柏拉图法则,应从其他角度再作项目分类,再重新搜集资料来分析。
3. 制作柏拉图依据的数据应正确无误,方不致蒙敝事实真相。
4. 柏拉图仅是管理改善的手段而非目的;因此,对于数据类别重点已清楚明确的,则无必要再浪费时间作柏拉图分析。
5. 作成柏拉图后,如仍然觉得前面1~2项不够具体,无法据此采取对策时,可再做进一步之柏拉图,以便把握具体重点。
6. 柏拉图分析的主要目的是从柏拉图中获得情报,进而设法采取对策。
如果所得到的情报显示第一位的不合格项目并非本身工作岗位所能解决时,可以先避开第一位次,而从第二位次着手。
7. 先着手改善第一位次的项目,采取对策将不合格率降低;但过不久问题再出现时,则需考虑将要因重新整理分类,另作柏拉图分析。
8. [其他]项若大于最大的前面几项,则必须加对[其他]项再细分;检讨其中是否含有大的原因(以不超过前面三项为原则)。
9. 必要时,可作层别的柏拉图。
对有问题的项目,再进行层别作出柏拉图,直到原因别的柏拉图为止。
