酒杯中的解析几何问题

初中物理实验题讲解：“没底”的酒杯你把水注满到杯子的边上，杯子里完全装满了水。

在杯子旁边有一些大头针。

或许，杯子里还可能找得出一点点地方来安放一二枚大头针吧？试试看。

请你把大头针一枚一枚投进杯子里去，数着你投进去的数目。

投大头针的时候要谨慎小心：要小心地把针尖放进水里，然后轻轻把手放开，不让有一点震动，也不加一点压力。

你默默地数着：1枚、2枚、3枚，已经有3枚落到杯子底上了──可是水面并没有变动。

10枚、20枚、30枚了，杯里的水并没有溢出。

50枚、60枚、70枚……已经是整整100枚大头针丢在杯底了，可是杯里的水仍旧没有溢出一点来。

而且，还不只是没有水溢出来，甚至看不到水面有显著高出杯口的情形。

再加多些大头针看看。

200枚、300枚、400枚大头针已经沉到杯底了，可是，仍旧没有一滴水从杯口溢出来；只是现在已经可以看到水面比杯口略略高起一些了。

原来，这个奇怪现象的解答正在水面高起这一点。

玻璃只要略沾些油污，便很难沾水；在我们杯口的边上，也跟一切常用的器具一样，难免由于人手的接触留下一些油脂的痕迹。

杯口的边上既然不会沾水，那么，被杯里的大头针所排出的水就只好形成一个高起的凸面。

这个凸面的高出程度很不显著，这只要花一点时间算出一枚大头针的体积来，拿它跟这个高起部分的体积比较一下，就知道大头针的体积只有高起部分的体积的几百分之一，因此在这个装满水的杯子里才能找出容纳几百枚大头针的地方。

用的杯子杯口越大，可以容纳的大头针也越多，因为杯口越大，高起部分的体积也越大。

要更清楚地了解这个问题，让我们做一个计算，一枚大头针大约25毫米长、毫米粗。

这样一个圆柱体的体积不难依照几何学上的公式算出，等于53毫米。

再加上大头针的头，总体积大约不超过毫米。

现在来算一算杯口上高起部分的体积，假定杯口直径是9厘米。

这样的圆面积大约等于6400平方毫米。

如果我们把高起的水层的厚度算作1毫米，那么它的体积就是6400立方毫米，这就有大头针体积的1200倍。

一道光学赛题的解法（高二、高三）
陶汉斌
【期刊名称】《数理天地：高中版》
【年(卷),期】2005(000)004
【摘要】题一种高脚酒杯，如图1所示．杯内底面为一凸起的球面，球心在顶点O下方玻璃中的C点，球面的半径R=1．50cm，O点到杯口平面的距离为8．0cm．在杯脚底中心处P点紧贴一张画片，P点距O点6．3cm．这种酒杯未斟酒时，若在杯口处向杯底方向观看，看不出画片上的景物，但如果斟了酒，再在杯口处向杯底方向观看。

将看到画片上的景物．已知玻璃的折射率n1=1．56，酒的折射率n2=1．34．试通过分析计算与论证解释这一现象．
【总页数】2页(P40-41)
【作者】陶汉斌
【作者单位】浙江省武义县第一中学，321200
【正文语种】中文
【中图分类】O157.5
【相关文献】
1.探寻求解通法呈现最优解法r——一道不规则四边形赛题的解法探究
2.从一道高三题看向量解法
3.从一道高三题看向量解法
4.一道高三模考数列题的解法探究
5.一道高三调考导数压轴题的解法探析
因版权原因，仅展示原文概要，查看原文内容请购买。

形杯问题物理形杯问题是物理学中一个经典的问题，涉及到液体在不同形状的杯子中的高度和压强的关系。

在本文中，我们将探讨形杯问题的原理和相关理论。

形杯问题中的杯子可以是各种形状，如圆锥形、圆柱形、矩形等。

我们以圆锥形杯子为例进行分析。

假设圆锥形杯子的顶部是封闭的，底部是一个半径为R的圆形底部。

我们希望研究在不同高度处的液体压强与底部的关系。

我们需要了解液体的压强是如何产生的。

液体的压强是由于液体分子间的相互作用力造成的。

液体分子在受到重力的作用下，会受到上方液体层的压力，从而向下传递。

因此，在液体中的任何一点，都存在着液体分子对该点的压强。

根据形杯问题的假设条件，液体的密度是恒定的，并且液体是静止的。

根据静力学的原理，液体在不同高度处的压强与液体的高度以及液体的密度有关。

我们来推导液体在圆锥形杯子中的压强与高度的关系。

假设液体的高度为h，液体的密度为ρ。

我们知道，液体的压强等于液体的密度乘以重力加速度g再乘以液体的高度。

即P = ρg h。

根据圆锥形杯子的几何关系，我们可以得出液体在不同高度处的压强与底部的关系。

由于液体的密度和重力加速度都是恒定的，所以液体在不同高度处的压强只与液体的高度有关。

当液体的高度为0时，液体的压强为0。

当液体的高度为H时，液体的压强为P = ρgH。

在这之间的任何高度h处，液体的压强都可以用线性插值的方式计算。

即P = ρgh/H。

除了圆锥形杯子，其他形状的杯子也可以使用类似的方法进行分析。

不同形状的杯子会导致液体在不同高度处的压强与底部的关系不同。

因此，形杯问题在物理学中具有一定的复杂性。

形杯问题不仅在理论上有一定的研究价值，而且在实际生活中也有一定的应用。

例如，在工程设计中，我们需要考虑液体在不同形状的容器中的分布情况和压强分布情况，以确保容器的结构安全和液体的稳定性。

总结起来，形杯问题涉及到液体在不同形状的杯子中的高度和压强的关系。

通过分析液体的压强与液体的高度、液体的密度以及重力加速度的关系，我们可以得出液体在不同高度处的压强与底部的关系。

喝杯啤酒也有几何学？20世纪，心理学家Jean Piaget 曾提出了著名的认知发展理论。

他发现，小孩儿明显缺乏对物体体积的认知能力。

把缸子里的水倒进一个细杯子里，水位明显上升了，小孩子们便会手舞足蹈地说，哇，水变多了耶！不过，实际经验告诉我们，成年人似乎也好不到哪儿去。

在感知不同形状的物体体积时，人们似乎有一种天生的障碍。

如果用一个横截面积更小的杯子来喝酒，别人或许会真的以为你喝得更多呢！细而高的杯子看上去就是大些问题的关键在于半径与体积的关系上：半径扩大到原来的n倍，横截面积会扩大到原来的n2倍。

为了让圆柱体的体积保持不变，它的高度必须要缩小到原来的1/n2。

同样地，把一个圆柱体的半径缩小1/10，看上去似乎是微不足道的；然而，要想让圆柱体的体积保持不变，高度必须要增加到原来的1/(0.9*0.9)，大约是1.23倍。

从视觉上看，23%的高度变化要比10%的半径变化明显得多，于是乍看上去体积似乎变大了。

左边那个圆柱体的体积看上去是不是更大一些呢？其实，这三个圆柱体的体积是相同的。

杯子上部的空间比你想象的更大下图是一个酒杯，里面的酒没有倒满。

那么，你认为酒的体积占整个酒杯容积的百分之多少?如果酒杯没有装满的话，你可以少喝多少酒？为了解决这个问题，我们需要知道圆台体积的计算公式：—［下底面积+上底面积+ J下底面积X上底面积j因此，整个杯子的容积为：g j \-(兀 + 22r + \' }v 2^ JV j - 43.982.x.但液面高度只达到整个酒杯高度的5/6，因此液体体积为：5 |；t5)2I i5 \2~3^+(1+6)jr+V?r，［1 +6)32434两者一除，答案简直让人不敢相信：酒的体积竟然只有整个酒杯容积的73.74%,也就是说这样便能少喝超过1/4的酒！可是，为什么仅仅少了1/6的高度，就能少喝1/4的酒呢？这仍然是半径与体积的关系在作怪。

人们总是关注酒杯液面的高度，却忽视了倾斜的杯壁对体积的影响。

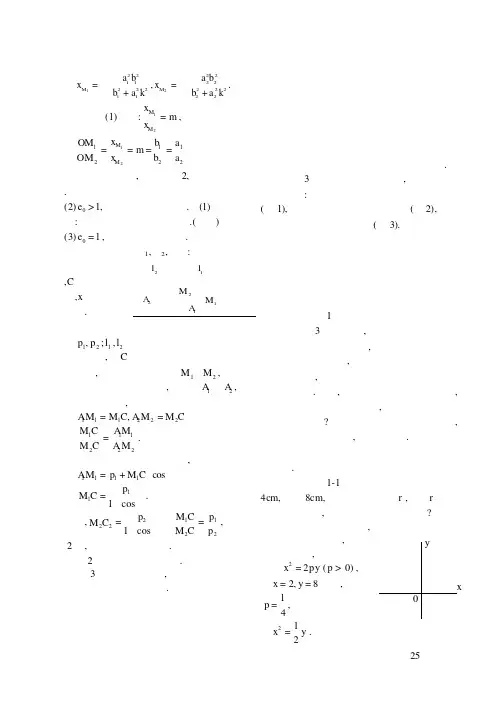
酒杯中的数学问题作者：葛晓光来源：《数学教学通讯(教师阅读)》2006年第08期近年来的高考模式一直处于不稳定的状态，但不管如何变化，数学对于所有的学生来说总是必考科目．在这一背景下，绝大多数的中学生都很重视数学这门学科，但不少学生却缺乏运用所学数学知识解决实际问题的意识与能力，如不重视并及时改变这一现状，那我们所培养出来的学生，将来的发展潜力是很有限的．因而，在平时的教学中，我们应该强化学生对数学知识的应用意识．其实只要细心观察就不难发现：在我们的生活中，数学的应用是无处不在的．本文就来谈谈圆锥曲线知识在酒杯系列问题中的应用．图1例1厨师李先生家中有一种酒杯（如图1）酒杯的轴截面为抛物线的一部分，杯口宽4 cm, 杯深4 cm，称之为抛物线型酒杯．若将一些大小不一的玻璃球放入该酒杯中，有些能触及酒杯底部，而有些则不能．你能用所学数学知识分析出，当玻璃球的半径r在什么范围内，玻璃球一定会触及酒杯底部？解：以杯底为原点建立直角坐标系．设抛物线方程为x2=2py (p＞0)，由题意，点（2，4）在抛物线上，将（2，4）代入抛物线方程，得p= 1 2 ，所以抛物线方程为x2=y．下面分3种思路来说明：思路1：设圆心在y轴正半轴并且过圆点的圆的方程为x2+(y-r)2=r2，将它代入抛物线方程，消去x，得 y2+(1-2r)y=0，解得y1=0,y2=2r-1．要使玻璃球能触及酒杯底部，需满足y2=2r-1≤0，即当0＜r≤ 1 2cm时，玻璃球一定会触及杯底．思路2：设p(a,a2)为抛物线上的动点，动圆B与抛物线x2=y相切，其中圆心B的坐标为(0,r)，当|PB|min=|OB|时，必然满足动圆B与抛物线相切于坐标原点O．记f(a)= a2+(a2-r)2 =(a2- 2r-1 2 )2+r2- (2r-1)2 4= 18 5 ．因为a2≥0，所以当且仅当 2r-1 2 ≤0 即 0＜r≤ 1 2 时，有f(a)min=f(0)=|OB|．所以当0＜r≤ 1 2 cm时，玻璃球能触及杯底．思路3：设P（a,a2)为抛物线x=y2上一动点，圆心为B（0,r)且过原点的圆的方程为x2+(y-r)2=r2，当满足|PB|≥r恒成立时，即 a2+(a2-r)2 ≥r恒成立，所以2r≤a2+1恒成立，因而2r≤(a2+1)min=1，即当0＜r≤ 1 2 cm时，玻璃球一定会触及杯底．说明：思路一主要是运用了方程的思想，思路二则体现了函数的思想，思路三则是运用了最值的思想．图2例2李先生工作的酒店里有一种轴截面为椭圆一部分的椭圆形酒杯（如图2），杯口宽3．6 cm，杯深为9 cm，中间最宽处宽6 cm．将一个半径为r的玻璃球放入酒杯中，问r在什么范围内可以使玻璃球触及酒杯底部？解：以椭圆的中心为原点建立直角坐标系．设椭圆方程为x2 a2 + y2 b2 =1 (a＞b＞0)，由题意，可得 b=3，且点（1．8，9-a)在椭圆上．将该点代入椭圆方程，解得a=5，则椭圆方程为y2 25 + x2 9 =1．设圆心为B（0，r-5)，半径为r的圆的方程为x2+(y+5-r)2=r2，与椭圆方程联立，消去x可得8y2+25(5-r)y+425-125r=0，解之得 y1=-5, y2= 25 8 r- 25 8 ，则当y2≤-5即0＜r＜1.8 cm时，圆B与椭圆相切于下顶点．又因为杯口半径为1．8 cm，则当0＜r＜1.8 cm时，玻璃球一定会触及酒杯底部．例3在例1的抛物线型酒杯中，放入一根长度为2 cm的粗细均匀的细棒．用细棒达到平衡状态时，它在酒杯中的位置如何？（细棒端点与酒杯壁之间的摩擦力忽略不计）分析：由于细棒粗细均匀而且摩擦力忽略不计，则细棒达到平衡状态时，其重心（细棒的中点）应最低，即细棒AB的中点M到x轴距离最短．图3解：如图3所示，抛物线的焦点为（0， 1 4 ），准线l的方程为y=- 1 4 过点A，B，M分别作l的垂线，垂足分别为A1，B1，M1，联结AF，BF．根据抛物线的定义可知：|AA1|=|AF|，|BB1|=|BF|，则|MM1|= 1 2 （|AA1|+|BB1|）= 1 2 （|AF|+|BF|）．由于|AB|=2，抛物线的通径2p=1即|AB|＞2p，因而在△ABF中，|AF|+|BF|≥|AB|，即|MM1|≥ 1 2 |AB|．当且仅当线段AB过焦点F时，等号成立．此时细棒AB的重心M到抛物线的顶点O所在水平面的距离取得最小值，为|MM1|- 1 4 = 1 2 |AB|- 1 4 =1- 1 4 = 3 4 ．即当细棒过抛物线的焦点时可以达到平衡状态．变题1：在例3中，若细棒长度为L，则对于不同的L值，细棒处于平衡状态的位置有何不同？解：由例3可知：（1）L≥2p=1，则当细棒过抛物线的焦点时可达到平衡状态；（2）若L＜2p=1，由于焦点在y轴上的抛物线的焦点弦长为 2p cos2α (α为焦点弦所在直线的倾斜角）．当α=0时，焦点弦长取得最小值2p=1．因为L＜2p=1，所以细棒不可能通过抛物线的焦点F．设方程AB为y=kx+b，A（x1,y1),B(x2,y2),M(x,y)，由 y=kx+b与x2=y 消去y得 x2-kx-b=0，所以 x= x1+x2 2 = k 2 k=2x, b=y-2x2(1)由 |AB|= 1+k2 |x1-x2|= 1+k2 · Δ =L, 可得（1+k2)(k2+4b)=L2 (2)将（1）代入（2）中并消去k、b可得 4(1+4x2)(y-x2)=L2y= L2 4(4x2+1) +x2= L2 4 · 1 4x2+1 + 1 4 (4x2+1)- 1 4 ．由 L2 4 · 1 4x2+1 = 1 4 (4x2+1)L=4x2+1≥1．而L＜1，则此时无法用均值定理来求y的最小值．因为函数y= 1 4 ( L2 t +t-1)在区间［L,+∞)上单调增，所以当x=0时y min= L2 4 ，此时当细棒滑到水平位置时，其重心最低，从而达到平衡状态．变题2：将该问题推广到其他形状的酒杯中．如果分别在轴截面是等腰直角三角形的圆锥形酒杯中，以及案例2的椭圆形酒杯中各放入一根长度为L粗细均匀的细棒，则细棒达到平衡状态时，它在酒杯中的位置分别是怎样的？图4解：（1）以等腰直角三角形的直角顶点为原点，以其底边上的高所在直线为y轴建立直角坐标系（如图4所示），则圆锥形酒杯壁所在射线方程为y=x或y=-x(y≥0)．设|AB|=L，M（x,y)为AB的中点A，B分别在两条射线上滑动．在Rt△AOB中，|OM|= 1 2 |AB|= 1 2 L，所以点M的轨迹是以O为圆心， 1 2 L为半径且位于两条射线y=±x (y≥0)之间的一段圆弧．显然，当点M在两条射线上，即细棒贴在酒杯壁上时，其重心最低，从而达到平衡状态．此时点M的坐标为（±24 L,24 L)．（2）椭圆形酒杯的轴截面所在椭圆方程为y2 25 + x2 9 =1 (-5≤y≤4)．通径为 2b2 a = 18 5 ．类似于变题1，若L≥ 18 5 ，则当AB过焦点F时，其重心最低，从而达到平衡状态；若L＜ 18 5 ，则当AB水平放置时，其重心最低，从而达到平衡状态．说明：以上例题及其变题所述结论都可以通过实验得到验证．注:本文中所涉及到的图表、注解、公式等内容请以PDF格式阅读原文。

酒杯中的数学九江市金安高级中学 宋俊浩教学内容：研究性学习——直线和抛物线的位置关系教学目标：1、通过分组试验，让学生观察，先后在抛物线型酒杯中放入长度不同、粗细均匀的牙签（假设牙签的端点与酒杯壁之间的摩擦忽略不计），充分摇动酒杯后，牙签最后到平衡状态时的位置。

2、分组探讨牙签最终平衡时的位置与牙签长短的关系，并通过定量计算对猜测的结论加以证明。

3、培养学生的自主探究与合作学习的意识，促进数学问题解决，感受成功的快乐。

教学过程：一、情境引入师：“同学们好”生：“老师好”师：“今天这节课非常有意思，我们要做一个数学试验，之前大家都做过物理和化学实验，有没有做过数学试验？”（板书试验）生：“没有”（异口同声）生甲：“老师，什么是数学试验？实验与试验有什么区别？”师：“这个问题问得好，那位学生能帮老师回答这个问题？”无声，学生犯难，不好解释。

师：“好吧，这个问题还是老师来回答吧，“实验”为了检验某种科学理论或假设而进行某种操作或从事某种活动。

“试验”为了察看某事的结果或某物的性能而从事某种活动。

今天我们所要进行的“数学试验”就是要大家观察酒杯中的数学问题。

今天老师带来8个形状和大小一样的酒杯，大家看这个酒杯的轴截面像什么曲线？”生：“抛物线”师：“对了，今天老师带来的酒杯轴截面曲线近似抛物线，下面我们分八个小组进行观察试验，每小组围一张桌子坐一起，下面按自然小组分组，动作快！”学生分小组环绕而坐。

师：“下面老师在每小组发三根牙签，长度分别为1cm、2cm和3cm，大家分别把这三根牙签放入杯中，充分摇匀杯子，最后把杯子静放在桌子上，观察牙签平衡时的位置状态，作好记录。

”学生分组操作，片刻师：“下面请第一组的学生代表发言，请问你们观察到牙签在平衡位置时是什么状态的？是水平放置还是倾斜的？”生：“最短的牙签近似水平放置，其余两根是倾斜的”师：“好的，请坐，其他组观察到什么现象？”生：“差不多”（异口同声）师：“既然大家所观察到现象差不多，下面有一个问题要大家思考：为什么最短的牙签在平衡位置时是水平放置的而较长的两根牙签却是倾斜的呢？为什么不也是水平放置的呢？”学生一脸疑惑师：“好的，暂时答不上没关系，下面大家再仔细看看，倾斜的两根牙签是平行的还是相交的？”生：“是相交的”（异口同声）师：“好的，老师先从物理学上给点提示：一个物体在平衡时它的重心是较高还是较低？”生：“较低”（异口同声）师：“这三根牙签的重心应该在什么位置？”生：“它们的中点”（异口同声）师：“不错，我们把杯子看作抛物线，牙签看作定长的线段，牙签在杯中运动可以看作定长的线段两端在抛物线上运动，牙签平衡时，其重心是不是相对其他位置时的重心要低？”学生点头赞同师：“我们怎么把这一现象抽象为抛物线的数学问题？关键是牙签的重心要最低怎么用数学语言来表达？”生：“老师是不是让线段AB 的中点到桌面距离最短？”师：“对了，但最好是把桌面换成与抛物线有关的水平线。

由沉到酒杯底部的球谈一类抛物线与圆的相关问题
高丰平
【期刊名称】《中学数学月刊》
【年(卷),期】2013(000)003
【摘要】酒杯中总可以放一个适当的小球，但只有当小球满足一定的条件时，方可触及酒杯底部，否则就会“搁”起来．通过数学计算，我们可以解决这类生活中的问题．以下辑录几例与此相关的抛物线与圆的问题，以期能够起到抛砖引玉的作用，对师生的教与学提供启发与帮助．
【总页数】2页(P53-54)
【作者】高丰平
【作者单位】湖北省孝昌县第二高级中学 432900
【正文语种】中文
【相关文献】
1.谈圆与圆的位置关系相关问题的处理 [J], 王俊胜
2.谈圆切于抛物线顶点的两个定理 [J], 汪海涛
3.谈圆与圆的位置关系相关问题的处理 [J], 王俊胜
4.乒乓球能沉在容器底部吗 [J], 李建;王小宇;李鸿
5.浅谈混凝土质量通病的产生和防治●张永冬期施工应关注的相关问题●杨力浅谈高层框剪结构住宅楼板开裂处理方法浅谈给水管道施工常见质量通病及防治中性线断线原因和危害分析及预防措沉厦因的分析及防治办法●韩卫东●李岩吴昊的质量控制●方芳卢新杨杨讨●范浩波中下析中探统基探程点系路因工几电头原桩的供
桥蚀注炉制交腐灌锅线立炉孔气四江锅钻燃相花业谈于三松工浅关浅谈混凝土质量通病的产生和防治 [J], 张永先
因版权原因，仅展示原文概要，查看原文内容请购买。

酒杯盛球问题探究
吕林兴
【期刊名称】《数理天地：高中版》
【年(卷),期】2008(000)002
【摘要】题目一个酒杯,它的轴截面是一个抛物线的一部分,方程是
x~2=y,y∈[0,10],在杯内放一个清洁球,要使清洁球能檫净酒杯的最底部,则清洁球的最大半径为多少?分析1可从函数的观点人手,建立以y为变量的函数,把实际问题转化为二次函数在y=0时求最小值的问题.
【总页数】1页(P3-3)
【作者】吕林兴
【作者单位】陕西省扶风高中;722200
【正文语种】中文
【中图分类】G634.6
【相关文献】
1.采用朗盛钕系BR生产的高尔夫球销售远超预期
2.采用朗盛顺丁橡胶生产的高尔夫球销售远超预期
3.“盛福名酒杯”落幕
4.巨鹫玉和金盛球两种仙人球静置水培适应性及营养液配方的研究
5.孙盛《晋阳秋》汤球辑本误收檀道鸾《续晋阳秋》考
因版权原因，仅展示原文概要，查看原文内容请购买。