下载文档原格式
试验设计与数据处理》第三章：统计推断3- 13解：取假设HO : u1-u2w 0和假设H1: u1-u2 > 0用sas 分析结果如下:Sample StatisticsGroupNMeanStd. Dev.Std. Errorx8 0.231875 0.0146 0.0051 y100.20970.00970.0031Hypothesis TestNull hypothesis:Mean 1 - Mean 2 = 0Alternative:Mean 1 - Mean 2 A= 0If Varianees Aret statistie DfPr > tEqual3.878 16 0.0013 Not Equal3.70411.670.0032由此可见p 值远小于0.05,可认为拒绝原假设，即认为2个作家所写的小品文中 由 3 个字母组成的词的比例均值差异显著。
3-14解：用sas 分析如下: Hypothesis TestNull hypothesis: Variance 1 / Variance 2 = 1 Alternative:Varia nee 1 / Varia nee 2 A = 1- Degrees of Freedom -FNumer. Denom.Pr > F第四章:方差分析和协方差分析4- 1 解:Sas 分析结果如下：Dependent Variable: ySum ofSouree DF Squares Mean Square F Value Pr > F Model 41480.823000370.20575040.88<.00012.27 7 由p 值为0.2501 > 0.05 （显著性水平） 9 0.2501，所以接受原假设， 两方差无显著差异Source DF Type I SS Mean Square F ValuePr > F m 2 44.33333333 22.16666667 4.09 0.0442 n 3 11.50000000 3.83333333 0.71 0.5657 m*n627.000000004.500000000.830.5684Source DF Type III SS Mean Square F ValuePr > F m 2 44.33333333 22.16666667 4.09 0.0442 n 3 11.50000000 3.83333333 0.71 0.5657 m*n 627.000000004.500000000.830.5684由结果可知， 在不同浓度下得率有显著差异， 在不同温度下得率差异不明显， 交 互作用的效应不显著。
《试验设计与数据处理》专业：机械工程班级：机械11级专硕学号：S110805035 姓名：赵龙第三章：统计推断3-13 解：取假设H0：u1-u2≤0和假设H1：u1-u2＞0用sas分析结果如下：Sample StatisticsGroup N Mean Std. Dev. Std. Error----------------------------------------------------x 8 0.231875 0.0146 0.0051y 10 0.2097 0.0097 0.0031Hypothesis TestNull hypothesis: Mean 1 - Mean 2 = 0Alternative: Mean 1 - Mean 2 ^= 0If Variances Are t statistic Df Pr > t----------------------------------------------------Equal 3.878 16 0.0013Not Equal 3.704 11.67 0.0032由此可见p值远小于0.05，可认为拒绝原假设，即认为2个作家所写的小品文中由3个字母组成的词的比例均值差异显著。
3-14 解：用sas分析如下：Hypothesis TestNull hypothesis: Variance 1 / Variance 2 = 1Alternative: Variance 1 / Variance 2 ^= 1- Degrees of Freedom -F Numer. Denom. Pr > F----------------------------------------------2.27 7 9 0.2501由p值为0.2501＞0.05（显著性水平），所以接受原假设，两方差无显著差异第四章：方差分析和协方差分析4-1 解：Sas分析结果如下：Dependent Variable: ySum ofSource DF Squares Mean Square F Value Pr > FModel 4 1480.823000 370.205750 40.88 <.0001Error 15 135.822500 9.054833Corrected Total 19 1616.645500R-Square Coeff Var Root MSE y Mean0.915985 13.12023 3.009125 22.93500Source DF Anova SS Mean Square F Value Pr > Fc 4 1480.823000 370.205750 40.88 <.0001由结果可知，p值小于0.001，故可认为在水平a=0.05下，这些百分比的均值有显著差异。
试验设计与数据处理课后习题试验设计与数据处理课后习题第三章3-7分别使用金球和铂球测定引力常数（单位：）1. 用金球测定观察值为 6.683，6.681, 6.676, 6.678, 6.679, 6.6722. 用铂球测定观察值为 6.661, 6.661，6.667, 6.667, 6.664设测定值总体为N（u，）试就1,2两种情况求u的置信度为0.9的置信区间，并求的置信度为0.9的置信区间。
用sas分析结果如下：第一组：第二组:3-13下表分别给出两个文学家马克吐温的8篇小品文以及斯诺特格拉斯的10篇小品文中由3个字母组成的词的比例：马克吐温： 0.225 0.262 0.217 0.240 0.230 0.229 0.235 0.217斯诺特格拉斯：0.209 0.205 0.196 0.210 0.202 0.207 0.224 0.223 0.220 0.201设两组数据分别来自正态总体，且两个总体方差相等，两个样本相互独立，问两个作家所写的小品文中包含由3个字母组成的词的比例是否有显著差异（a 0.05）取假设H0：u1-u2≤0和假设H1：u1-u2＞0用sas分析结果如下：Sample StatisticsGroup N Mean Std. Dev. Std. Errorx 8 0.231875 0.0146 0.0051y 10 0.2097 0.0097 0.0031Hypothesis TestNull hypothesis: Mean 1 - Mean 2 0Alternative: Mean 1 - Mean 2 ^ 0If Variances Are t statistic Df Pr tEqual 3.878 16 0.0013Not Equal 3.704 11.67 0.0032由此可见p值远小于0.05，可认为拒绝原假设，即认为2个作家所写的小品文中由3个字母组成的词的比例均值差异显著。
实验设计与数据处理(第二版部分答案)试验设计与数据处理学院班级学号学生姓名指导老师第一章4、相对误差18.20.1%0.0182x mg mg ∆=⨯=故100g 中维生素C 的质量范围为：18.2±0.0182mg 。
5、1）、压力表的精度为1.5级，量程为0.2MPa ，则 max 0.2 1.5%0.003330.3758R x MPa KPax E x ∆=⨯==∆=== 2）、1mm 的汞柱代表的大气压为0.133KPa ， 所以max 20.1330.1331.6625108R x KPax E x -∆=∆===⨯ 3）、1mm 水柱代表的大气压为gh ρ，其中29.8/g m s = 则：3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯ 6.样本测定值3.48 算数平均值 3.421666667 3.37 几何平均值 3.421406894 3.47 调和平均值 3.421147559 3.38 标准差s 0.046224092 3.4 标准差σ 0.04219663 3.43 样本方差S 2 0.002136667总体方差σ20.001780556算术平均误差△ 0.038333333 极差R 0.117、S ₁²＝3.733，S ₂²＝2.303F ＝S ₁²/ S ₂²＝3.733/2.303=1.62123而F 0.975 （9.9）=0.248386，F 0.025(9.9)=4.025994 所以F 0.975 （9.9）< F <F 0.025(9.9)两个人测量值没有显著性差异，即两个人的测量方法的精密度没有显著性差异。
分析人员A分析人员B8 7.5 样本方差1 3.733333 8 7.5 样本方差2 2.302778 10 4.5 Fa 值 0.248386 4.025994104F 值1.62123|||69.947|7.747 6.06p pd x =-=>6 5.56 84 7056 7.56 5.58 88.旧工艺新工艺2.69% 2.62%2.28% 2.25%2.57% 2.06%2.30% 2.35%2.23% 2.43%2.42% 2.19%2.61% 2.06%2.64% 2.32%2.72% 2.34%3.02%2.45%2.95%2.51%t-检验: 双样本异方差假设变量 1 变量 2平均0.025684615 2.291111111 方差0.000005861 0.031611111 观测值13 9 假设平均差0df 8t Stat -38.22288611P(T<=t) 单尾0t 单尾临界 1.859548033P(T<=t) 双尾0t 双尾临界 2.306004133F-检验双样本方差分析变量 1 变量 2平均0.025684615 2.291111111 方差0.000005861 0.031611111 观测值13 9 df 12 8 F 0.000185422P(F<=f) 单尾0F 单尾临界0.3510539349. 检验新方法是否可行，即检验新方法是否有系统误差，这里采用秩和检验。
《实验设计与数据处理》大作业《实验设计与数据处理》大作业及答案班级：姓名：学号：1、用Excel作出下表数据带数据点的折线散点图：（1）分别作出加药量和余浊、总氮T-N、总磷T-P、COD的变化关系图（共四张图，要求它们的格式大小一致，并以两张图并列的形式排版到Word中，注意调整图形的大小）；（2）在一张图中作出加药量和浊度去除率、总氮T-N去除率、总磷T-P去除率、COD去除率的变化关系折线散点图。
2、对离心泵性能进行测试的实验中，得到流量Qv、压头H和效率η的数据如表所示，绘制离心泵特性曲线。
将扬程曲线和效率曲线均拟合成多项式。
（要求作双Y 轴图）流量Qv、压头H和效率η的关系数据序号 1 2 3 4 5 6Q v(m3/h) H/m0.015.000.414.840.814.561.214.331.613.962.013.65η0.0 0.085 0.156 0.224 0.277 0.333序号7 8 9 10 11 12Q v(m3/h) H/mη2.413.280.3852.812.810.4163.212.450.4463.611.980.4684.011.300.4694.410.530.4313、用荧光法测定阿司匹林中的水杨酸（SA），测得的工作曲线和样品溶液的数据如下表:（1）列出一元线性回归方程，求出相关系数，并给出回归方程的精度；（2）求出未知液（样品）的水杨酸（SA）浓度。
4、对某矿中的13个相邻矿点的某种伴生金属含量进行测定，得到如下一组数据：试找出某伴生金属c与含量距离x之间的关系(要求有分析过程、计算表格以及回归图形)。
提示：⑴作实验点的散点图，分析c~x之间可能的函数关系，如对数函数y=a+blgx、双曲函数(1/y)=a+(b/x)或幂函数y=dx b等；⑵对各函数关系分别建立数学模型逐步讨论，即分别将非线性关系转化成线性模型进行回归分析，分析相关系数：如果R ≦0.553，则建立的回归方程无意义，否则选取标准差SD最小（或R最大）的一种模型作为某伴生金属c与含量距离x之间经验公式。
一．填空题1．反映两个连续变量间的相关性的指标可采用 相关系数 表示;反映一个连续变量和一组连续变量间的相关性的指标可采用 复相关系数 表示; 讨论一组连续变量和一组连续变量间的相关性可采用 典型相关系数 方法讨论。
2．在数据处理中概率可用 频率 近似;分布的数学期望可用 样本均值 近似; 分布的方差可用 样本方差 近似.3．配方试验中，若成分A 、B 、C 的总份数必须满足A+B+C=60份，采用正交试验的因素水平见表若正交)3(49L 的第9号试验条件 为（A 、B 、C ）=（3、3、2），请给出具体的试验方案(取小数点后一位)A= 6.7 份，B= 13.3 份，C= 40 份4．抽样调查不同阶层对某改革方案的态度,统计分析方法应为 方差分析法 ; 研究学历对收入的影响,统计分析方法应为 回归分析法/相关性分析法 。
5．设x1，x2，…，xn 是出自正态总体N （μ，σ2）的样本，其中σ2未知。
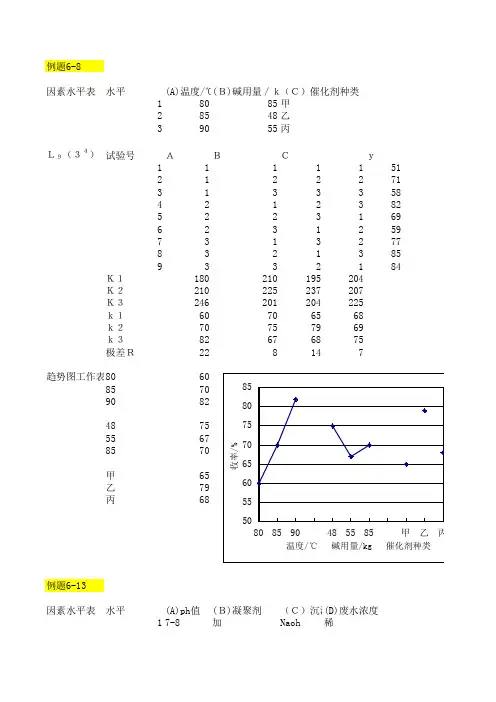
对假设检验H0∶μ=μ0， H1∶μ≠μ0，则当H0成立时，常选用的统计量是_ ns x T /0μ-=_，它服从的分布为__t(n-1)___.6．设有100件同类产品,其中20件优等品,30件一等品,30件二等品,20件三等品,则这四个等级的标准分依次为 1.28 、 0.39 、 -0.39 、 -1.28(记P(U u α≤)=α查标准正态表可得u65.0=0.39,u7.0=0.12,u8.0=0.84,u9.0=1.28)二．求解1．抗牵拉强度是硬橡胶的一项重要性能指标,现试验考察下列两个因素对该指标的影响.A(硫化时间): A 1(40秒), A 2(60秒)B(催化剂种类): B 1(甲种), B 2(乙种), B 3(丙种)以上六种水平组合下,各重复做了两次试验,测得数据(单位:kg/cm 2)如表:因素 B 1 B 2 B 3 A 1 390 380 440 420 370 350 A 2390 410450 430370 380试在显著性水平α=0.05下分析因素A 和因素B 对指标的主效应及交互效应是否显著?The GLM ProcedureDependent Variable: STRE A B C 水平1 18份 1.5倍A 1倍B 水平2 20份 1倍A 3倍B 水平3 22份 2倍A 2倍BSource DF Squares Mean Square F Value Pr > FModel 5 9866.66667 1973.33333 13.16 0.0035Error 6 900.00000 150.00000Corrected Total 11 10766.66667R-Square Coeff Var Root MSE STRE Mean0.916409 3.074673 12.24745 398.3333Source DF Type I SS Mean Square F Value Pr > FA 1 533.333333 533.333333 3.56 0.1083B 2 9316.666667 4658.333333 31.06 0.0007 A*B 2 16.666667 8.333333 0.06 0.9464Source DF Type III SS Mean Square F Value Pr > FA 1 533.333333 533.333333 3.56 0.1083B 2 9316.666667 4658.333333 31.06 0.0007 A*B 2 16.666667 8.333333 0.06 0.9464因为P值=0.1083>0.05，所以主效应A不显著；因为P值=0.0007<0.01，所以主效应B高度显著；因为P值=0.9464>0.05，所以交互效应不显著；2．以下是用SAS对三个指标的数据进行主成份分析的部分输出结果:(一) 在Proportion及Cumulative以下划线处填相应数值(二) 求第一主成份的表达式Z1=0.706330X1+0.043501X1+0.706544X3(三) 按85%阈值截取主成份并构造综合指标得Prin=0.667Z1+0.333Z2=0.667(0.706330X1+0.043501X1+0.706544X3)+0.333(-0.0356 89X1+0.99 9029X2-0.025830X3)=0.4592X1+0.362X2+0.462X33．在单纯形优化设计中，已知三因素的初始单纯形的试验方案及试验结果见下表（指标以大为好）试验点 A （4,2,1）B(3,4,2) C(2,1,3) D(1,3,4) 指标y14241820（一）以上初始单纯形的反射点E 的位置为E=（0，10/3，5 ）（二）若试验点E 的试验指标值Y E 为下表第一行中的各种情况，填表以表示下一推移动作名称及参数α的范围Y E 值 12 25 18 推移动作名称 内收缩 扩大 收缩 参数αα<0α>10<α<1（三）若需对初始单纯形“整体收缩”求新单纯形各点坐标。
A ’BC ’D ’ A ’((A+B)/2)=(7/2，3，3/2)，C ’((B+C)/2)=(5/2，5/2，5/2)，D ’((B+D)/2)=(2，7\2，3)4．利用SAS 在一次回归正交设计的输出部分结果如下:Sum of MeanSource DF Squares Square F Value Pr > FModel 4 543.10250 135.77562 4.38 0.0908 Error 4 123.94830 30.98708 Corrected Total 8 667.05080 ParameterVariable DF Estimate Pr > |t| Type I SS Intercept 1 56.46000 <.0001 28690 x1 1 2.92500 0.2675 51.33375 x2 1 5.27333 0.0811 166.84827 x3 1 7.28833 0.0327 318.71882 x4 1 -1.01667 0.6778 6.20167由于发现因子x1与x4不显著,故从回归方程中删去x1,x4.5．轴承硬度合格率y(%)与因素A （上升温度：℃）、因素B （保温时间：小时）、因素C （出炉温度：℃）有关，采用正交表)3(49L 安排试验，试验方案及试验结果见表：因素 试验号A B C指标y（1）填表 （2）指出3号试验的具体条件： 上升温度为820℃，保温时间为6h ，出炉温度为500℃ （3）指出可能好的水平组合 A3B3C3 （4）排出因素的主次顺序 B----A---C （5）画因素水平趋势图，并检验有无因素取值范围选偏的情况因素C 选偏，应选低于400℃的出炉温度6．测量圆柱体体积，体积公式为圆柱体高为底圆半径其中，h R h R V ,2π=。
若测得底圆周长C=40cm ，其均方差cm c 05.0=σ；测得高h=10cm ，其均方差cm h 2.0=σ，求圆柱体体积V 的均方差V σ。
解：π2c R = ππππ4222h c h c h R V =⎪⎭⎫⎝⎛== π2ch c v =∂∂ π42c h v =∂∂ 22422222164h c c h c σπσπσσ+== 66.2525.16202.044005.01024042322222222==⨯+⨯=+=ππσσπcm c h c hc7．10位专家对某类食品罐头的感官评定如下： 评语 指标较差 一般 良好 优 权重 色 0 2 6 2 0.20 味 1 4 3 2 0.40 香34210.201 1（800） 1（6） 3（400） 702 2（780） 1 1（450） 603 3（820） 1 2（500） 784 1 2（7） 2 745 2 2 3 906 3 2 1 927 1 3（8） 1 858 2 3 2 909 3 3 3 95 Ⅰ 229 208 237 Ⅱ240 256 242 Ⅲ265 270 255 极差R 3662 18形态 1 4 5 0 0.10 均匀性0 3 6 1 0.10试作综合评判（1）依据最大隶属原则；（2）依据秩加权平均原则；（3）若评语“优”对应分值100分，“良好”对应80分，“一般”对应60分“差”对应40分，问此类食品罐头可得评分值多少分？解：a=（0.20，0.40，0.20，0.10，0.10）R=Ar=（0.11，0.35，0.39，0.15）1：因为0.39最大，所以，依据最大隶属原则，可判定为良好2：加权平均1×0.15+2×0.39+3×0.35+4×0.11=2.42判定为良偏一般3：40×0.11+60×0.35+80×0.39+100×0.15=71.68．设对某多层次模糊指标评价的态度有赞成、不表态、反对,其分层的权向量和表态隶属向量见图,求模糊综合指标U的表态隶属向量。
