第18讲特殊的平行四边形复习课
- 格式:ppt
- 大小:750.50 KB
- 文档页数:29







人教版数学八年级下册-18.2-特殊的平行四边形-复习课-说课稿平行四边形复习课说课稿各位老师:大家好!今天我说课的内容是人教版数学八年级下册第十八章第二节特殊平行四边形的复习。
下面我从四个方面来谈谈我对本节课的理解和做法。
一、教材分析:1、地位与作用:本章是学生在掌握平行四边的性质和判定等有关知识,且具备初步的观察,操作等活动经验的基础上出现的。
通过本节的学习使学生清楚地理解各种特殊平行四边形的关系并掌握它们的性质与判定,进一步培养学生的合情推理能力,发展学生的逻辑思维能力与推理论证能力。
本节新课教学时共分5个教学课时,矩形性质与判定、菱形性质与判定、正方形性质、判定。
本课时是对前面5个教学课时知识内容的一次的系统复习。
本节是本章知识的重点之一,知识联系紧密,所以教学时作好认真复习,非常重要。
2、教学目标:根据中学生的心理特点与当前他们的认知基础及教学内容的特点,依据《数学课程标准》,我确定如下教学目标:知识与技能:(1)、掌握本节的知识体系,进一步理解各种特殊的平行四边形的关系并掌握它们的性质与判定。
(2)、通过设置问题探究的练习进一步培养学生的合情推理意识,增强学生的逻辑推理能力,使学生掌握说理的基本方法过程与方法:从问题出发有效组织学生独立思考,合作学习,通过综合的证明过程,体会证明的有关证明的思维方法,发展逻辑推理能力。
情感态度价值感:在活动中激发学生对数学的“好奇心”与“求知欲”,让学生在愉快的学习中不断获得成功的体验。
在数学思考活动中培养学生乐于探究、合作学习的习惯。
3、教学重点与难点:因为各种平行四边形概念交错,容易混淆,学生在应用时常会出现“张冠李戴”的现象,在应用它们的性质与判定的时候,也会常出现用错、多用、少用条件的错误。
因此我确定教学重点:各种特殊的平行四边形的性质和判定。
教学难点:各种特殊的平行四边形之间的联系和区别。
二、教法学法在许多人的印象中,复习课就是习题课。
本节课的教学设计为不落俗套,同时为让学生对学过的知识产生兴趣,能让学生在玩中学,乐中学,教学时我采用操作实践、判断归纳、探究联系为主线的探究式教学模式,充分体现老师的主导作用和学生的主体地位。



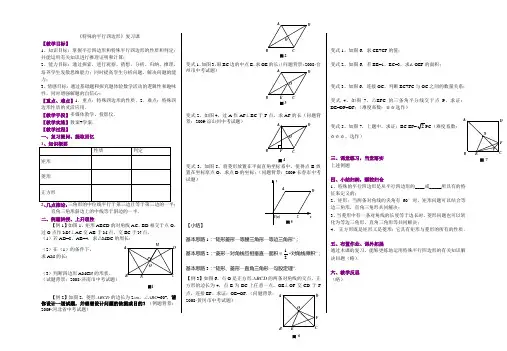
N M图1ODC B A 图 2AB CDOE O D C B A 图 3F ODC B A 图4图 6ABDE F图 7ABDE F 《特殊的平行四边形》复习课【教学目标】1、知识目标:掌握平行四边形和特殊平行四边形的性质和判定;并能运用有关知识进行推理证明和计算;2、能力目标:通过探索,进行观察、猜想、分析、归纳、推理,培养学生发散思维能力;同时提高学生分析问题,解决问题的能力;3、情感目标:通过基础题和探究题体验数学活动的逻辑性和趣味性,同时增强解题的自信心;【重点、难点】1.重点:特殊四边形的性质.2.难点:特殊四边形性质的灵活应用.【教学手段】多媒体教学、投影仪. 【教学实施】教案+学案. 【教学过程】一、复习提问、提取回忆2、几点推论:三角形的中位线平行于第三边且等于第三边的一半;直角三角形斜边上的中线等于斜边的一半. 二、例题讲授、上升理性【例1】如图1,矩形ABCD 的对角线AC 、BD 相交于点O ,过O 点作MN ⊥AC 交AB 于M 点,交BC 于N 点, (1)若AD=8,AB=4,求△MDC 的周长; (2)在(1)的条件下, 求AM 的长;(3)判断四边形AMCN 的形状。
(试题背景:2008·济南市中考试题)【例2】如图2,菱形ABCD 的边长为2cm ,∠ABC =60°,请你设计一道试题,并想想设计问题的依据或目的?(例题背景:2009·河北省中考试题)变式1、如图3,取BC 边的中点E ,求OE 的长;(问题背景:2008·台州市中考试题)变式2、如图4,过A 作AF ⊥BC 于F 点,求AF 的长(问题背景:2009·凉山州中考试题)变式3、如图5,将菱形放置在平面直角坐标系中,使得点B 放置在坐标原点O ,求点D 的坐标;(问题背景:2009·长春市中考试题)【小结】基本思路1:“矩形菱形—等腰三角形—等边三角形”; 基本思路2:“菱形—对角线互相垂直—面积=12×对角线乘积”; 基本思路3:“矩形、菱形—直角三角形—勾股定理”.【例3】如图6,点O 是正方形ABCD 的两条对角线的交点,正方形的边长为4,点E 为BC 上任意一点,OE ⊥OF 交CD 于F 点,连接EF 。
18.2特殊的平行四边形复习教案【教材分析】【教学流程】综合运用例1 如图,矩形ABCD中,O是对角线AC,BD的交点,过点O的直线EF与AB,CD的延长线分别交于点E,F.(1)求证:△BOE≌△DOF;(2)如图,当EF与AC满足什么关系时,以A,E,C,F为顶点的四边形是菱形?证明你的结论.[解析] (1)由矩形对角线互相平分及平行线的内错角相等得到△BOE≌△DOF.(2)当EF⊥AC时,四边形AECF是菱形,可先证四边形AECF是平行四边形再推出它是菱形.例2、如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.(1)求证:AF=BE;(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.分析:(1)根据正方形的性质可得教师出示例题1学生自主探究合作交流,展示评价教师适时点拨证明:(1)∵ OB=OD,AE∥CF,∴∠E=∠F,∠OBE=∠ODF,∴△BOE≌△DOF.(2)当EF⊥AC时,四边形AECF是菱形.证明:∵四边形ABCD是矩形,∴OA=OC.又由(1)△BOE≌△DOF,得OE=OF,∴四边形AECF是平行四边形.又∵EF⊥AC,∴四边形AECF是菱形.[归纳总结] 判定一个四边形是菱形,关键是把已知条件转化成判定方法所需要的那个(些)条件,本题是通过“对角线互相垂直的平行四边形是菱形”来证明的教师出示例2.教师要求学生先尝试独立思考,再小组讨论、交流.解:解答:(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°,∵AF⊥BE,AB=AD,∠BAE=∠D=90°,再根据同角的余角相等求出∠ABE=∠DAF,然后利用“角边角”证明△ABE和△DAF全等,再根据全等三角形的证明即可;(2)过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,然后与(1)相同.∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF,∵在△ABE和△DAF 中,,∴△ABE≌△DAF (ASA),∴AF=BE;(2)解:MP与NQ相等.理由如下:如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ 交AD于E,则与(1)的情况完全相同.矫正补偿⒈矩形、菱形、正方形都具有的性质是()A、对角线相等B、对角线互相平分C、对角线互相垂直D、四条边都相等⒉已知矩形的一条对角线与一边的夹角是40°,则两条对角线所成的锐角的度数()A、50°B、60°C、70°D、80°3.如图,矩形AEFG和矩形ABCD的大小、形状完全相同,把它们拼成如图所示的教师出示问题,学生自主探究、回答、师生共同纠正.1.B;2.D3.解:依题意可知:∠FAE=∠DCA=30 °,AF=AC∴∠DAC=60 °,∴∠FAC=90 °,∴∠1=45 °,∴∠2=∠ACF-∠ACD=15 °L型图案,已知∠FAE=30°,分别求∠1、∠2的度数.完善整合1.本节课我们复习了哪些知识点?2.你对本节课所复习的知识又有了哪些新的认识?师引导学生归纳总结.梳理知识,并建立知识体系.拓展提高4.如图,在正方形ABCD的对角线AC上取一点E,使CE=CD,过点E作EF⊥AC交AD于点F.求证:AE=EF=DF.[解析] 连接CF,证△CDF≌△CEF,得DF=EF.可证AE=EF,故AE=EF=DF.[点评] 本题考查的是正方形的性质,解题中易忽视△AEF是等腰直角三角形.解题的关键是证△AEF是等腰直角三角形,连接CF,证△CDF≌△CEF.教师出示问题,学生先自主探究,后小组同伴交流,最后展示,师生共同评价、纠正,教师点拨、强调。