材料力学实验电测实验

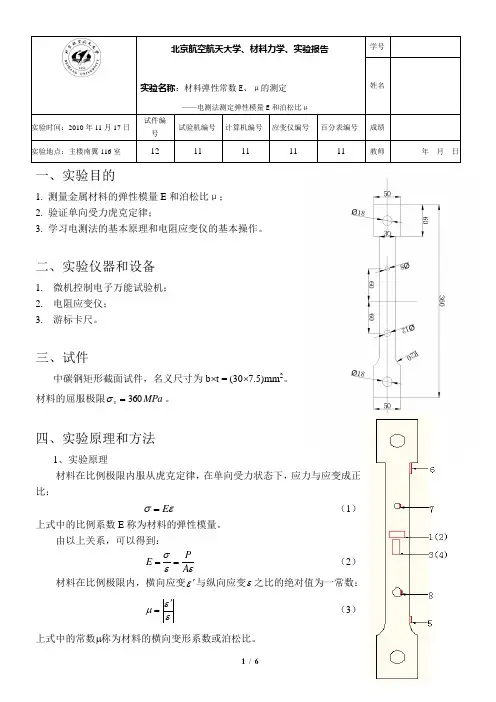
北京航空航天大学、材料力学、实验报告实验名称：材料弹性常数E 、μ的测定——电测法测定弹性模量E 和泊松比μ学号姓名实验时间：2010年11月17日 试件编号试验机编号 计算机编号 应变仪编号百分表编号成绩实验地点：主楼南翼116室12 11 11 11 11教师年 月 日一、实验目的1. 测量金属材料的弹性模量E 和泊松比μ；2. 验证单向受力虎克定律；3. 学习电测法的基本原理和电阻应变仪的基本操作。

二、实验仪器和设备1. 微机控制电子万能试验机；2. 电阻应变仪；3. 游标卡尺。

三、试件中碳钢矩形截面试件，名义尺寸为b ⨯t = (30⨯7.5)mm 2。

材料的屈服极限MPa s 360=σ。

四、实验原理和方法1、实验原理材料在比例极限内服从虎克定律，在单向受力状态下，应力与应变成正比：εσE = （1）上式中的比例系数E 称为材料的弹性模量。

由以上关系，可以得到：PE A σεε== （2）材料在比例极限内，横向应变ε'与纵向应变ε之比的绝对值为一常数：εεμ'=（3） 上式中的常数μ称为材料的横向变形系数或泊松比。

本实验采用增量法，即逐级加载，分别测量在各相同载荷增量∆P 作用下，产生的应变增量∆εi 。

于是式（2）和式（3）分别写为：ii A PE ε∆∆=0 （4） ii i εεμ∆'∆= （5）根据每级载荷得到的E i 和μi ，求平均值：n E E ni i∑==1（6）nni i∑==1μμ （7）以上即为实验所得材料的弹性模量和泊松比。

上式中n 为加载级数。

2、实验方法2.1电测法电测法基本原理：电测法是以电阻应变片为传感器，通过测量应变片电阻的改变量来确定构件应变，并进一步利用胡克定律或广义胡克定律确定相应的应力的实验方法。

试验时，将应变片粘贴在构件表面需测应变的部位，并使应变片的纵向沿需测应变的方向。

当构件该处沿应变片纵向发生正应变时，应变片也产生同样的变形。

电测法测定材料的弹性模量和泊松比 弹性模量E 和泊松比µ是各种材料的基本力学参数，测试工作十分重要，测试方法也很多，如杠杆引伸仪法、电测法、自动检测法，本次实验用的是电测法。

一、 实验目的在比例极限内，验证虎克定律，用应变电测法测定材料的弹性模量E 和泊松比µ。

二、 实验仪器设备和试样a) 多功能组合实验台b) 静态电阻应变仪c) 游标卡尺d) 矩形长方体扁试件三、 预习要求a) 预习本节实验内容和材料力学书上的相关内容。

b) 阅读并熟悉电测法基本原理和电阻应变仪的使用操作。

四、实验原理和方法材料在比例极限范围内，应力和应变呈线性关系，即：εσE =比例系数E 称为材料的弹性模量，可由下式计算，即：εσ=E （2－1） 设试件的初始横截面面积为o A ，在轴向拉力F 作用下，横截面上的正应力为： o A F =σ 把上式代入式（2－1）中可得：εo A F E = （2－2） 只要测得试件所受的荷载F 和与之对应的应变ε，就可由式（2－2）算出弹性模量E 。

受拉试件轴向伸长，必然引起横向收缩。

设轴向应变为ε，横向应变为ε′。

试验表明，在弹性范围内，两者之比为一常数。

该常数称为横向变形系数或泊松比，用µ表示，即：εεµ′=轴向应变ε和横向应变ε′的测试方法如下图所示。

在板试件中央前后的两面沿着试件轴线方向粘贴应变片1R 和′1R ，沿着试件横向粘贴应变片2R 和′2R 。

为了消除试件初曲率和加载可能存在偏心引起的弯曲影响，采用全桥接线法。

分别是测量轴向应变ε和横向应变ε′的测量电桥。

根据应变电测法原理基础，试件的轴向应变和横向应变是每台应变仪应变值读数的一半，即： r εε21= ′=′r εε21 实验时，为了验证胡克定律，采用等量逐级加载法，分别测量在相同荷载增量F ∆作用下的轴向应变增量ε∆和横向应变增量ε′∆。

若各级应变增量相同，就验证胡克定律。

五、 实验步骤（1）测量试件。

实验四：弯曲正应力电测实验一、实验目的和要求1．学习使用应变片和电阻应变仪测定静态应力的基本原理和方法。

2．用电测法测定纯弯曲钢梁横截面不同位置的正应力。

3．绘制正应力沿其横截面高度的的分布图，观察正应变（正应力）分布规律，验证纯弯曲梁的正应力计算公式。

二、实验设备、仪器和试件1.CLDS-2000型材料力学多功能实验台。

2.YJZ —8型智能数字静态电阻应变仪。

3.LY —5型拉力传感器。

4.直尺和游标卡尺。

三、实验原理和方法（1）理论公式：本实验的测试对象为低碳钢制矩形截面简支梁，实验台如图4-1所示，加载方式如图4-2所示。

图4-1 图4-2由材料力学可知，钢梁中段将产生纯弯曲，其弯矩大小为c PM 2∆=（1） 横截面上弯曲正应力公式为ZI My=σ （2） 式中y 为被测点到中性轴z 的距离，I z 为梁截面对z 轴的惯性矩。

123bh I Z =（3）横截面上各点正应力沿截面高度按线性规律变化，沿截面宽度均匀分布，中性轴上各点的正应力为零。

截面的上、下边缘上各点正应力为最大，最大值为WM =max σ。

（2）实测公式：实验采用螺旋推进和机械加载方法，可以连续加载，荷载大小可由电子测力仪读出。

当增加压力P ∆时，梁的四个点受力分别增加作用力2/P ∆，如图4-2所示。

为了测量梁纯弯曲时横截面上应变分布规律，在梁的纯弯曲段侧面布置了5片应变片，如4-2所示，各应变片的粘贴高度见梁上各点标注。

此外，在梁的上表面沿横向粘贴了第6片应变片，用以测定材料的泊松比μ；在梁的端部上表面零应力处粘贴了第7片温度补偿应变片，可对以上各应变片进行温度补偿。

在弹性范围内，如果测得纯弯曲梁在纯弯曲时沿横截面高度上的轴向应变，则由单向应力状态的胡克定律，即：σε=E （4） 由上式可求出各点处的应力实验值。

将应力实验值σε=E 与理论值ZI My=σ进行比较，以验证弯曲正应力公式。

如果测得应变片4和6的应变满足μεε=46/则证明梁弯曲时近似为单向应力状态，即梁的纵向纤维间无挤压的假设成立。

实验三 扭转实验一、实验目的1.测定低碳钢扭转时的强度性能指标：扭转屈服应力s τ和抗扭强度b τ。

2.测定灰铸铁扭转时的强度性能指标：抗扭强度b τ。

3.绘制低碳钢和灰铸铁的扭转图，比较低碳钢和灰铸铁的扭转破坏形式。

二、实验设备和仪器1.扭转试验机2.游标卡尺三、实验试样按冶金部标准采用圆形截面试件，两端成扁圆形。

如图1所示。

ldr图1 扭转试件图圆形截面试样的直径mm 10=d ，标距d l 5=或d l 10=，平行部分的长度为mm 20+l 。

若采用其它直径的试样，其平行部分的长度应为标距加上两倍直径。

试样头部的形状和尺寸应适合扭转试验机的夹头夹持。

由于扭转试验时，试样表面的切应力最大，试样表面的缺陷将敏感地影响试验结果，所以，对扭转试样的表面粗糙度的要求要比拉伸试样的高。

对扭转试样的加工技术要求参见国家标准GB10128—88。

四、实验原理与方法1.测定低碳钢扭转时的强度性能指标试样在外力偶矩的作用下，其上任意一点处于纯剪切应力状态。

随着外力偶矩的增加，测矩盘上的指针会出现停顿，这时指针所指示的外力偶矩的数值即为屈服力偶矩es M ，低碳钢的扭转屈服应力为1lpess 43W M =τ （１）式中：16/3p d W π=为试样在标距内的抗扭截面系数。

在测出屈服扭矩s T 后，改用电动加载，直到试样被扭断为止。

测矩盘上的从动指针所指示的外力偶矩数值即为最大力偶矩eb M ，低碳钢的抗扭强度为pebb 43W M =τ （２） 对上述两公式的来源说明如下：低碳钢试样在扭转变形过程中，利用扭转试验机上的自动绘图装置绘出的ϕ-e M 图如图12所示。

当达到图中A 点时，e M 与ϕ成正比的关系开始破坏，这时，试样表面处的切应力达到了材料的扭转屈服应力s τ，如能测得此时相应的外力偶矩ep M ，如图13a 所示，则扭转屈服应力为pep s W M =τ （３）经过A 点后，横截面上出现了一个环状的塑性区，如图2b 所示。

弯曲电测实验结论
弯曲电测实验结论
引言
弯曲电测实验是一种常见的材料力学测试方法，它可以用来研究材料在受力下的弯曲性能。

本文将介绍弯曲电测实验的基本原理、实验步骤及其结果分析。

一、弯曲电测实验原理
弯曲电测实验是基于电阻应变效应原理进行的，当材料发生弯曲时，其内部会产生应变，而应变会导致材料内部电阻发生变化。

因此，通过对材料内部电阻的监测，就可以得到材料在受力下的弯曲性能。

二、实验步骤
1. 准备工作：选取合适的试件和传感器，并进行校准。

2. 实验装置搭建：将试件固定在支架上，并将传感器连接到数据采集系统上。

3. 施加载荷：通过调节载荷施加装置，使试件产生一定程度的弯曲。

4. 数据采集：记录传感器输出的信号并进行处理。

5. 数据分析：根据数据分析得出相应结论。

三、结果分析
1. 强度与模量：通过对载荷-位移曲线的分析，可以得到材料的弯曲强度和弯曲模量。

弯曲强度是指材料在受力下发生破坏的最大载荷，而弯曲模量则是指材料在受力下产生应变时所表现出的刚度。

2. 材料性能：通过对载荷-位移曲线的形态进行分析，可以得到材料的韧性、脆性等性能。

3. 材料失效机理：通过对试件破坏部位进行观察和分析，可以得到材料失效的机理。

结论
通过对弯曲电测实验结果进行分析，我们可以得出相应结论。

例如，我们可以了解到材料在受力下的弯曲性能、韧性、脆性等特征，并进一步探究其失效机理。

这些结论对于我们进一步了解材料力学特性具有重要意义。

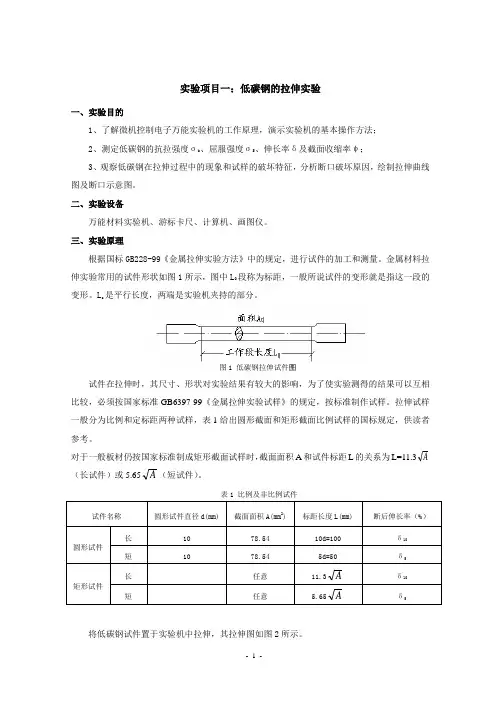
实验项目一：低碳钢的拉伸实验一、实验目的1、了解微机控制电子万能实验机的工作原理，演示实验机的基本操作方法；2、测定低碳钢的抗拉强度ζb、屈服强度ζS、伸长率δ及截面收缩率ψ；3、观察低碳钢在拉伸过程中的现象和试样的破坏特征，分析断口破坏原因，绘制拉伸曲线图及断口示意图。

二、实验设备万能材料实验机、游标卡尺、计算机、画图仪。

三、实验原理根据国标GB228-99《金属拉伸实验方法》中的规定，进行试件的加工和测量。

金属材料拉伸实验常用的试件形状如图1所示，图中L0段称为标距，一般所说试件的变形就是指这一段的变形。

L c是平行长度，两端是实验机夹持的部分。

图1 低碳钢拉伸试件图试件在拉伸时，其尺寸、形状对实验结果有较大的影响，为了使实验测得的结果可以互相比较，必须按国家标准GB6397-99《金属拉伸实验试样》的规定，按标准制作试样。

拉伸试样一般分为比例和定标距两种试样，表1给出圆形截面和矩形截面比例试样的国标规定，供读者参考。

对于一般板材仍按国家标准制成矩形截面试样时，截面面积A和试件标距L的关系为L=11.3A （长试件）或5.65A（短试件）。

表1 比例及非比例试件将低碳钢试件置于实验机中拉伸，其拉伸图如图2所示。

图2 低碳钢拉伸ζ-ε图 A 点以前，杆件仅有弹性变形，且P 和L 成线性关系，即遵守虎克定律：ΔL=EA PL （1-1） A 点以后，曲线不再保持直线，至B ´点开始屈服，以后成锯齿形，B 点为载荷下降的最低点。

B ´点的数值与试件加载速度、试件形式等有关，而B 点的数值比较稳定，工程上常取B 点的载荷作为屈服载荷。

因此屈服应力ζs =P s /A 。

到C 点，材料强化，曲线继续平滑上升，至D 点试件开始出现颈缩，载荷达到最大值P b ，抗拉强度为：ζb =0A P b （1-2） 试件断裂后，用游标卡尺量得标距间长度L 1和试件收缩处面积A 1,则可得试件的塑性性能：δ＝010L L L -×100% （1-3） ψ＝010A A A -×100% （1-4） 四、实验步骤1、试件准备1）在试件中段取标距L=10d(100mm)（低碳钢试件），用试样划线机将其划分为１０等份。

纯弯曲梁正应力电测实验报告纯弯曲梁正应力电测实验是一种常用的材料力学实验方法，用于测量梁在弯曲过程中的正应力分布情况。

本实验通过加载施加在金属横截面上的外力，测量由于弯曲产生的电势差，从而得到梁在各个截面上的正应力大小。

下面是一份纯弯曲梁正应力电测实验报告的参考内容。

实验目的：1. 理解材料在弯曲过程中的正应力分布特性；2. 掌握纯弯曲梁正应力电测实验的原理和方法；3. 学习使用实验仪器和数据处理软件。

实验仪器：1. 弯曲实验台；2. 弯曲应变计；3. 电压采集仪；4. 电压放大器；5. 计算机。

实验原理：在纯弯曲梁实验中，通过加载施加在梁上的外力，梁发生弯曲变形。

根据材料力学理论，梁在弯曲过程中会产生正应力。

实验中利用弯曲应变计测量梁在各个截面上的应变大小。

弯曲应变计通过压电效应将应变转化为电荷，产生电势差。

通过电压采集仪和电压放大器将电势差放大并记录下来，就可以得到梁在各个截面上的正应力大小。

实验步骤：1. 将要进行实验的梁固定在弯曲实验台上，调整梁的位置和姿态，使其能够正常受力并产生弯曲变形；2. 将弯曲应变计安装在梁的截面上，保证其能够准确测量应变；3. 连接弯曲应变计和电压采集仪，调整采集仪的参数，使其能够正常采集电势差；4. 将电压采集仪与电压放大器连接，调整放大器的增益，保证能够得到合适范围的电压信号；5. 开始加载外力，在加载过程中，实时记录电压采集仪采集到的电势差数据；6. 加载外力达到一定值后停止，记录下此时的电势差数据。

数据处理：1. 将采集到的电势差数据导入计算机；2. 对电势差数据进行处理，根据电压放大器的增益和弯曲应变计的灵敏度，将电势差数据转换为应变数据；3. 根据应变计的位置和梁的材料参数，计算出各个截面上的应变值；4. 利用梁的几何参数和材料参数，计算出各个截面上的正应力大小。

实验结果：根据数据处理的结果，可以得到梁在各个截面上的正应力大小的分布情况。

通过绘制应力-位置曲线，可以直观地观察梁在弯曲过程中正应力的变化趋势，并分析其特点和规律。

XL3418 多功能材料力学实验电测实验报告书秦皇岛市协力科技开发有限公司力学实验规则及要求一、作好实验前的准备工作（1）按各次实验的预习要求，认真阅读实验指导复习有关理论知识，明确实验目的，掌握实验原理，了解实验的步骤和方法。

（2）对实验中所使用的仪器、实验装置等应了解其工作原理，以及操作注意事项。

（3）必须清楚地知道本次实验须记录的数据项目及其数据处理的方法。

二、严格遵守实验室的规章制度（1）课程规定的时间准时进入实验室。

保持实验室整洁、安静。

（2）未经许可，不得随意动用实验室内的机器、仪器等一切设备。

（3）作实验时，应严格按操作规程操作机器、仪器，如发生故障，应及时报告，不得擅自处理。

（4）实验结束后，应将所用机器、仪器擦拭干净，并恢复到正常状态。

三、认真做好实验（1）接受教师对预习情况的抽查、质疑，仔细听教师对实验内容的讲解。

（2）实验时，要严肃认真、相互配合，仔细地按实验步骤、方法逐步进行。

（3）实验过程中，要密切注意观察实验现象，记录好全部所需数据，并交指导老师审阅。

四、实验报告的一般要求实验报告是对所完成的实验结果整理成书面形式的综合资料。

通过实验报告的书写，培养学习者准确有效地用文字来表达实验结果。

因此，要求学习者在自己动手完成实验的基础上，用自己的语言扼要地叙述实验目的、原理、步骤和方法，所使用的设备仪器的名称与型号、数据计算、实验结果、问题讨论等内容，独立地写出实验报告，并做到字迹端正、绘图清晰、表格简明。

目录第一章绪论 (1)§1-1实验的内容 (1)§1-2试验方法和要求 (1)第二章实验设备及测试原理 (2)§2-1组合式材料力学多功能实验台 (2)§2-2电测法的基本原理 (4)第三章材料力学电测实验 (8)实验一纯弯曲梁的正应力实验 (8)实验二薄壁圆筒在弯扭组合变形下主应力测定 (11)实验三材料弹性模量E、泊松比µ的测定 (16)实验四偏心拉伸实验 (20)实验五压杆稳定实验 (23)实验六电阻应变片灵敏系数标定 (26)实验七等强度梁实验 (29)第一章绪论§1-1实验的内容实验教学作为材料力学课程的一个重要组成部分，对于提高学生实践能力、设计能力具有重要意义，电测实验具体包含以下两个方面内容：1、验证理论材料力学常将实际问题抽象为理想模型，再由科学假设推导出一般公式，如纯弯曲梁和纯扭转圆轴（或筒）等的分析都使用了平面假设。

实验一、电测法测定材料弹性模量E、μ一、实验目的1．学习电测方法。

2．电测法测定材料的弹性模量E、μ。

二、实验仪器设备1．弯曲梁实验装置。

2．数字式电阻应变仪。

三、实验装置与实验原理图 1 图 2 1．实验装置见图1和图2，拔下销子3，卸下加载横梁8，卸下传感器9，从传感器上旋下加载压头7，然后将万向接头旋到加载系统5上，再将传感器旋到万向接头上，传感器下端与上夹头连接，下夹头安装在试验机架底座的孔内（注意：螺母不要旋紧，留有一定的活动距离，使其起到万向接头的作用；另外保护试件，以免试件被压弯），接着调整好上、下夹头之间的距离，将E、μ试件放入上、下夹头内，对准孔，插入销子，就可进行试验了。

图 3 图 42．实验原理试件上沿着试件轴向和横向各粘贴两片应变片，补偿块上粘贴四片应变片见图3，按图4接两个测量桥，对试件加载，记录载荷P ，并分别记录测得的轴向应变εP 和横向应变εP /，由公式P A P E ε= 计算出弹性模量E ，由公式 pp εεμ/=计算出泊松比μ。

实验一 电测法测定弹性模量E 和泊松比μ实验日期：： 室温 小组成员 （一）实验目的（二）实验设备、仪器（三）实验记录表1 测定E 和μ实验试件原始尺寸 试件材料宽度 b (mm) 厚度 t(mm)横截面面积A 0 (mm 2)长度 L (mm)152.5（四）结果处理弹性模量： 泊松比：（五）问题讨论1．电测法测定材料的E 和μ值时应测何值？2．电阻应变片的作用是什么？3．写出电阻应变仪的读数应变表达式εd ？4．温度补偿片的作用是什么？5．应变片在电桥中的接线方法有哪两种？6．根据逐级加载时载荷和变形的读数记录，作图验证虎克定律。

P E=εο∆A ∆=εεμ∆∆ O ε实验二、纯弯曲梁正应力电测实验一、实验目的1．电测法测定纯弯曲梁正应力分布规律。

2．验证纯弯曲梁正应力计算公式。

二、实验装置与仪器1．纯弯曲梁实验装置。

2．数字式电阻应变仪。

弯曲正应力电测实验报告弯曲正应力电测实验报告引言：弯曲正应力电测实验是一种常用的材料力学实验方法，通过施加外力使材料产生弯曲变形，进而测量材料在不同位置上的正应力分布情况。

本实验旨在探究不同材料在弯曲过程中的应力分布特点，并通过电测方法进行准确测量。

实验原理：弯曲正应力电测实验基于梁的弯曲理论，根据材料的弯曲变形情况，可以推导出弯曲梁上不同位置的应力分布。

在实验中，通过施加外力使梁产生弯曲，然后利用电测方法测量不同位置上的电势差，从而得到该位置上的正应力数值。

实验装置：本实验采用了一台弯曲正应力电测仪，该仪器由弯曲梁、电测电路和数据采集系统组成。

弯曲梁通常采用金属材料，如钢材或铝材，其形状可以是矩形、圆形或其他几何形状。

电测电路通过电极与弯曲梁连接，测量弯曲梁上不同位置的电势差。

数据采集系统用于记录和分析实验数据。

实验步骤：1. 准备工作：根据实验要求选择合适的弯曲梁材料，并将其固定在实验台上。

2. 施加外力：通过调节实验台上的施力装置，施加合适的外力使弯曲梁产生弯曲变形。

3. 连接电测电路：将电测电路与弯曲梁连接，确保电极与梁表面接触良好。

4. 测量电势差：打开数据采集系统，记录不同位置上的电势差数值。

5. 数据分析：根据电势差数值，计算得到不同位置上的正应力数值，并绘制应力分布曲线。

实验结果与讨论：根据实验数据，我们可以得到弯曲梁上不同位置的正应力分布情况。

通常情况下，弯曲梁的上表面受到压应力，下表面受到拉应力，而中性轴附近的应力为零。

应力分布曲线呈现出一定的对称性，符合弯曲梁的力学性质。

不同材料的弯曲正应力分布特点也有所不同。

例如，钢材的弯曲梁上应力分布相对均匀，且强度较高；而铝材的应力分布相对不均匀，容易出现应力集中现象。

这些差异可以通过实验数据进行比较和分析，为材料选择和工程设计提供参考。

实验误差与改进：在实验过程中，由于实验条件和仪器精度的限制，可能会产生一定的误差。

例如，电极与弯曲梁之间的接触电阻、电测电路的灵敏度等因素都会对实验结果产生影响。

(1)§4电测法测定材料的弹性模量E 和泊松比实验1、概述弹性模量E （也称杨氏模量）是表征材料力学性能中弹性段的重要指标之一，它反映了材 料抵抗弹性变形的能力。

泊松比反映了材料在弹性范围内，由纵向变形引起的横向变形的大小。

在对构件进行刚度稳定和振动计算、研究构件的应力和变形时，要经常用到E 和这两个弹性常 数。

而弹性模量E 和泊松比只能通过实验来测定。

2、实验目的验证胡克定律；了解电阻应变片的工作原理及贴片方式; 了解应变测试的接线方式。

3、实验原理 弹性模量E 和泊松比是反映材料弹性阶段力学性能的两个重要指标，在弹性阶段，给一个确定截而形状的试件施加轴向拉力，在截面上便产生了轴向拉应力，试件轴向伸 长，单位长度的 伸长量称之为应变，同样，当施加轴向压力时，试件轴向缩短。

在弹性阶 段，拉伸时的应力与应 变的比值等于压缩时的应力与应变的比值，且为一定值，称之为弹性模量E ，L/L在试件轴向拉伸仲长的同时，其横向会缩短，同样，在试件受压轴向缩短的同时，其横向会伸长，在弹性阶段，确定材质的试件拉仲时的横向应变与试件的纵向应变的比值等于 压缩时横向 应变与试件的 纵向应变的比值，且同样为一定值，称之为泊 松比，横纵L 横/ L0 压力的测量原理同拉、压实验，应变的测量采用电阻应变片电测法原理。

电阻应变片可形彖地理解为按一定规律排列有一定长度的电阻丝，实验前通过胶粘的 方式 将电阻应变片粘贴在试件的表而，试件受力变形时，电阻应变片中的电阻丝的长度也随 之发生相 应的变化，应变片的阻值也就发生了变化。

实验中我们采用的应变片是由两个单向应变片组成的 十字形应变花，所谓单向应变片，就是应变片的电阻值对沿某一个方向的变形最为敏感，称此 方向为应变片的纵向，而对垂直于该方向的变形阻值变化可忽略，称此方向为应变片的横向。

利用应变片的这个特性，在进行应变测试时，我们所测到只是试件沿应变 片纵向的应变，其不 包含试件垂直方向变形所引起的影响。