最新8.1-空间几何体的结构、三视图和直观图练习题

专题8.1空间几何体及其三视图和直观图练基础1.（2020·广西兴宁�南宁三中高一期末）已知一个几何体的三视图如图所示，则此几何体的组成方式为（）A．上面为圆台，下面为圆柱B．上面为圆台，下面为棱柱C．上面为棱台，下面为棱柱D．上面为棱台，下面为圆柱【答案】A【解析】结合图形分析知上面为圆台，下面为圆柱.故选：A.2.（2021·江西师大附中高二月考（理））如图是一个棱锥的正视图和侧视图，它们为全等的等腰直角三角形，则该棱锥的俯视图不可能是（）A．B．C．D．【答案】C【解析】根据棱锥的三视图想象原几何体的结构，可以在正方体中想象描出原几何体，确定其结构．【详解】若几何体为三棱锥，由其正视图和侧视图可知，其底面在下方且为直角三角形，故ABD 均有可能，若几何体是四棱锥，由其正视图和侧视图可知，其底面在下方，且为正方形，俯视图为正方形，但对角线应从左上到右下，C 不正确．故选：C ．3.（2021·江苏高一期末）已知一个圆锥的母线长为2，其侧面积为2π，则该圆锥的高为（）A ．1BC D ．2【答案】C【解析】由侧面积求出圆锥的底面圆半径，再根据勾股定理可求得其高.【详解】设圆锥的底面圆的半径为r ，母线为l ，则2l =，所以其侧面积为22rl r πππ==，解得1r =，==故选：C.4.（2020·河北易县中学高三其他（文））若圆台的母线与高的夹角为6π，且上、下底面半径之差为2，则该圆台的高为（）A ．233B ．2C ．22D ．3【答案】D【解析】设上、下底面半径分别为R ，r ，圆台高为h ，由题可知：tan 6R r h π-=，即233h =，所以23h =．故选：D5.（2020届浙江绍兴市诸暨市高三上期末）某几何体的正视图与侧视图如图所示：则下列两个图形①②中，可能是其俯视图的是（）A．①②都可能B．①可能，②不可能C．①不可能，②可能D．①②都不可能【答案】A【解析】若是①，可能是三棱锥；若是②，可能是棱锥和圆锥的组合；所以①②都有可能，故选：A.6．（2021·石家庄市第十七中学高一月考）如图，某沙漏由上、下两个圆锥组成，每个圆锥的底面直径和高均为12cm ，现有体积为396πcm 的细沙全部漏入下圆锥后，恰好堆成一个盖住沙漏底部的圆锥形沙堆，则此锥形沙堆的高度为（）A ．3cmB ．6cmC ．8cmD ．9cm【答案】C【解析】根据圆锥的体积公式列方程求出沙堆的高．【详解】解：细沙漏入下部后，圆锥形沙堆的底面半径为6r =，设高为h ，则沙堆的体积为216963V h ππ=⋅⋅=圆锥，解得()8h cm =，所以圆锥形沙堆的高度为8cm ．故选：C ．7.（2021·云南弥勒市一中高一月考）如图，正方形OABC 的边长为1，它是水平放置的一个平面图形的直观图，则原图形的周长是（）A ．8B ．6C ．(21D ．(21+【答案】A【解析】根据斜二测画法的规则，得到原图形的形状为平行四边形，进而求得其边长，即可求解.【详解】由斜二测画法的规则，可得原图形为O A B C ''''是一个平行四边形，如图所示，因为水平放置的一个平面图形的直观图OABC 的边长为1的正方形，可得1,OA OB ==1,O A O B ''''==在直角O A B '''△中，可得3A B ''==，所以原图形的周长为11338+++=.故选：A.8．（2021·浙江高三三模）如图，等腰直角三角形ABC 在平面α上方，90BAC ∠= ，若ABC 以BC 为旋转轴旋转，形成的旋转体在平面α内的投影不可能的是（）A ．B ．C ．D ．【答案】C【解析】对直线BC 与平面α的位置关系进行分类讨论，判断出投影的形状，即可得出合适的选项.【详解】若BC α⊥，则形成的旋转体在平面α内的投影如D 选项所示；若//BC α，则形成的旋转体在平面α内的投影为正方形；若BC 与α所成的角的取值范围是0,2π⎛⎫ ⎪⎝⎭时，则形成的旋转体在平面α内的投影如A 、B 选项所示.投影不可能如C 选项所示.故选：C.9．（2020·上海市进才中学高二期末）设MN 是半径为R 的球的直径，则,M N 两点的球面距离是________．【答案】Rπ【解析】MN 是半径为R 的球的直径，则,M N 两点所对的球心角为π，球面距离为R π．故答案为：R π．10．（2020·全国）如图为一几何体的平面展开图，按图中虚线将它折叠起来，画出它的直观图．【答案】见解析【解析】由题设中所给的展开图可以得出，此几何体是一个四棱锥，其底面是一个边长为2的正方形，垂直于底面的侧棱长为2，其直观图如图所示.练提升1.（2021·四川高一期末（理））某圆柱的高为1，底面周长为8，其三视图如图.圆柱表面上的点P在正视图上的对应点为A，圆柱表面上的点Q在左视图上的对应点为B，则在此圆柱侧面上，从P到Q的路径中，最短路径的长度为（）A17B5C．32D．1【答案】B【解析】根据三视图分析出,P Q所在的位置，然后结合圆柱的侧面展开图即可求出结果.【详解】由三视图还原几何体，如图：即点B在距离点A在底面投影的14圆弧处，沿A所在的母线得到如图所示的侧面展开图，圆柱的底面周长即为侧面展开图的长，圆柱的高即为侧面展开图的宽，而线段AB 的距离即为所求P 到Q 的路径中的最短路径，因为底面周长为8,所以1824A B '=⨯=，又因为高为1，则1A A '=，所以2222125AB A A A B ''=+=+=,故选：B.2.【多选题】（2021·宁波市北仑中学高一期中）如图，棱长为a 的正四面体形状的木块，点P 是ACD △的中心．劳动课上需过点P 将该木块锯开，并使得截面平行于棱AB 和CD ，则下列关于截面的说法中正确的是（）A ．截面不是平行四边形B ．截面是矩形C ．截面的面积为229a D ．截面与侧面ABC 的交线平行于侧面ABD【答案】BCD【解析】过点P 构建四边形，通过相关直线间的平行关系进一步证明为平行四边形，找对应线之间的垂直证明截面为矩形，从而计算截面面积【详解】解：如图所示，在正四面体中，4个面均为正三角形，由于点P 为ACD △的中心，所以P 位于CD 的中线的23外，分别取,,,BC AC AD BD 的三等分点，则EM ∥AB ，EF ∥CD ，FN ∥AB ，MN ∥CD ，所以EM ∥FN ，EF ∥MN ，所以截面EFNM 为平行四边形，所以A 错误，延长AP 交CD 于G ，连接BG ，由于P 为ACD △的中心，所以G 为CD 的中点，因为AC AD BC BD ===，所以,AG CD BG CD ⊥⊥，因为AG BG G = ，所以CD ⊥平面ABG ，所以CD AB ⊥，因为EM ∥AB ，EF ∥CD ，所以EM EF ⊥，所以截面EFNM 为矩形，所以B 正确，因为2211,3333MN CD a ME AB a ====，所以2212339S MN ME a a a =⋅=⋅=，所以C 正确，对于D ，截面EFNM ⋂平面ABC ME =，ME ∥AB ，ME ⊄平面ABD ，AB Ì平面ABD ，所以ME ∥平面ABD ，所以D 正确，故选：BCD3.（2021·湖北随州市·广水市一中高一月考）如图所示，矩形O A B C ''''是水平放置一个平面图形的直观图，其6O A ''=，2O C ''=，则原图形是（）A ．正方形B ．矩形C ．菱形D ．梯形【答案】C【解析】由已知得原图为平行四边形，OD BC ^，利用勾股定理计算边长得到OC OA =,可判断原图形的形状.【详解】因为//O A B C ''''，=O A B C ''''，所以直观图还原得//OA BC ，=6OA BC O A ''==，四边形OABC 为平行四边形，OD BC ^，则2C D O C ''''==，2CD ∴=，O D C ''''==2OD O D ''==6OC =，所以6OC OA ==，故原图形为菱形．故选：C.4．（2021·肇州县第二中学高一月考）如图是利用斜二测画法画出的Rt ABO 的直观图，已知4O B ''=，且ABO 的面积为16，过点A '作A C x '''⊥轴于点C '，则A C ''的长为（）A ．BC ．D ．1【答案】A【解析】利用面积公式，求出直观图的高，求出''A B ，然后在直角三角形'''A B C 中求解即可【详解】解：由直观图可知，在Rt ABO 中，2ABO π∠=，因为ABO 的面积为16，4O B OB ''==,所以1162AB OB ⋅=，所以8AB =，所以''4A B =，因为'''4A B C π∠=，A C x '''⊥轴于点C '，所以''''sin 44AC A B π=⋅==故选：A5．（2021·宁夏大学附属中学高一月考）三棱锥S ABC -及其三视图中的正视图和侧视图如图所示，则棱SB 的长为（）A ．B ．CD ．【答案】B【解析】根据几何体的三视图，结合几何体的数量关系，在直角SBD 中，即可求解.【详解】如图所示，根据三棱锥S ABC -及其三视图中的正视图和侧视图，可得底面ABC 中，点D 为AC 的中点，BD =SC ⊥底面ABC ，又由点D 为AC 的中点，且根据侧视图，可得BD AC ⊥，在直角BCD △中，可得4BC ===又由4SC =，在直角SBC 中，可得SB =故选：B.6．（2021·江苏省镇江中学）点P 是平面ABC 外一点，且PA PB PC ==，则点P 在平面ABC 上的射影一定是ABC 的（）A ．外心B ．内心C ．重心D ．垂心【答案】A【解析】过点P 作PO ⊥平面ABC ，因为PA PB PC ==，得到OA OB OC ==，即可求解.【详解】如图所示，过点P 作PO ⊥平面ABC ，可得222222,OA PA PO OB PB PO OC PC PO =-=-=-因为PA PB PC ==，可得OA OB OC ==，所以O 为ABC 的外心.故选：A.7.（2021·上海高二期末）圆锥的高为1，3则过圆锥顶点的截面面积的最大值为____________【答案】2【解析】求出圆锥轴截面顶角大小，判断并求出所求面积最大值．【详解】如图，SAB 是圆锥轴截面，SC 是一条母线，设轴截面顶角为θ，因为圆锥的高为1tan 2θ(0,)θπ∈，所以23θπ=，232ππθ=>，设圆锥母线长为l ，则2l =，截面SBC 的面积为211sin sin 22S SB SC BSC l BSC =⋅∠=∠，因为2(0,]3BSC π∠∈，所以2BSC π∠=时，2max 1222S =⨯=．故答案为：2．8．（2021·浙江绍兴市·高一期末）已知四面体ABCD 的所有棱长均为4，点O 满足OA OB OC OD ===，则以O ABCD 表面所得交线总长度为______.【答案】3【解析】根据正四面体的结构特征求得O 到面的距离，进而利用球的截面的性质求得各面所在平面与球的截面圆的半径，注意与各面的三角形内切圆的半径比较，确定此截面圆是否整个在面所在的三角形内，进而确定球与各面的交线，得到球与四面体表面所得交线总长度．【详解】已知四面体ABCD 的所有棱长均为4，所以四面体ABCD 是正四面体，因为点O 满足OA OB OC OD ===，所以O 为正四面体ABCD 的中心.设正三角BCD 的中心为F ，正三角ACD 的中心为G ，CD 的中点为E ，则连接,,,,AF BG AE BE 则,BG AF O BF AG E ⋂=⋂=．:::1:3,:1:4,OF OA GF AB EF EB OF AF ===∴=则224223BE AE =-=24333BF BE ==，224364()33AF =-，643AF OF ==．因为球O 2O 被平面BCD 截得圆半径为22623(2)()33r PF ==-=，因为正三角形BCD 的边长为4，所以正三角形内切圆半径为232tan 303︒=，故球O 与四面体ABCD 的每一个面所得的交线为正好为内切圆，每个内切圆的周长为4323r π，所以球与四面体ABCD 1633．故答案为：1633π．9.（2020届浙江杭州四中高三上期中）某几何体的三视图如图所示，且该几何体的体积是3，则正视图中的x 的值是_____，最长棱长为_____．【答案】3【解析】由已知中的三视图可得该几何体是一个以直角梯形为底面的四棱锥，且梯形上下边长为1和2，高为2，如图：2AD =，2AB =，1BC =，PA x =，//AD BC ，PA ⊥平面ABCD ，AD AB ⊥，∴底面的面积1(12)232S =⨯+⨯=，∴几何体的体积1333V x ==，可得3x =，最长棱长为：PC故答案为：3．10．（2019·全国高考真题（理））中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．【答案】共26个面.1-.【解析】由图可知第一层与第三层各有9个面，计18个面，第二层共有8个面，所以该半正多面体共有18826+=个面．如图，设该半正多面体的棱长为x ，则AB BE x ==，延长BC 与FE 交于点G ，延长BC 交正方体棱于H ，由半正多面体对称性可知，BGE ∆为等腰直角三角形，22,21)122BG GE CH x GH x x x ∴===∴=⨯+=+=，1x ∴==1．练真题1.（2021·全国高考真题）其侧面展开图为一个半圆，则该圆锥的母线长为（）A ．2B ．C ．4D ．【答案】B【解析】设圆锥的母线长为l ，根据圆锥底面圆的周长等于扇形的弧长可求得l 的值，即为所求.【详解】设圆锥的母线长为l ，由于圆锥底面圆的周长等于扇形的弧长，则2l ππ=l =.故选：B.2．（2021·北京高考真题）定义：24小时内降水在平地上积水厚度（mm ）来判断降雨程度．其中小雨（10mm <），中雨（10mm 25mm -），大雨（25mm 50mm -），暴雨（50mm 100mm -），小明用一个圆锥形容器接了24小时的雨水，如图，则这天降雨属于哪个等级（）A ．小雨B ．中雨C ．大雨D ．暴雨【答案】B【解析】计算出圆锥体积，除以圆面的面积即可得降雨量，即可得解.【详解】由题意，一个半径为()200100mm 2=的圆面内的降雨充满一个底面半径为()20015050mm 2300⨯=，高为()150mm 的圆锥，所以积水厚度()22150150312.5mm 100d ππ⨯⨯==⨯，属于中雨.故选：B.3.（2020·全国高考真题（理））如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为（）A．EB．F C．G D．H【答案】A【解析】根据三视图，画出多面体立体图形，14D D 上的点在正视图中都对应点M ,直线34B C 上的点在俯视图中对应的点为N,∴在正视图中对应M ,在俯视图中对应N 的点是4D ,线段34D D ,上的所有点在侧试图中都对应E ,∴点4D 在侧视图中对应的点为E .故选：A4．(2019年高考全国Ⅲ卷理)如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则()A．BM =EN ，且直线BM ，EN 是相交直线B．BM ≠EN ，且直线BM ，EN 是相交直线C．BM =EN ，且直线BM ，EN 是异面直线D．BM ≠EN ，且直线BM ，EN 是异面直线【答案】B【解析】如图所示，作EO CD ⊥于O ，连接ON ，BD ，易得直线BM ，EN 是三角形EBD 的中线，是相交直线.过M 作MF OD ⊥于F ，连接BF ，平面CDE ⊥平面ABCD ，,EO CD EO ⊥⊂平面CDE ，EO ∴⊥平面ABCD ，MF ⊥平面ABCD ，MFB ∴△与EON △均为直角三角形．设正方形边长为2，易知12EO ON EN ===,，5,,22MF BF BM ==∴=BM EN ∴≠，故选B．5.（2018·北京高考真题（文））某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（）A.1B.2C.3D.4【答案】C【解析】分析：根据三视图还原几何体，利用勾股定理求出棱长，再利用勾股定理逆定理判断直角三角形的个数.详解：由三视图可得四棱锥P ABCD -，在四棱锥P ABCD -中，2,2,2,1PD AD CD AB ====，由勾股定理可知：3,PA PC PB BC ====，则在四棱锥中，直角三角形有：,,PAD PCD PAB ∆∆∆共三个，故选C.6.（2021·全国高考真题（理））以图①为正视图，在图②③④⑤中选两个分别作为侧视图和俯视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为_________（写出符合要求的一组答案即可）．【答案】③④（答案不唯一）【解析】由题意结合所给的图形确定一组三视图的组合即可.【详解】选择侧视图为③，俯视图为④，如图所示，长方体1111ABCD A B C D -中，12,1AB BC BB ===，,E F 分别为棱11,BC BC 的中点，则正视图①，侧视图③，俯视图④对应的几何体为三棱锥E ADF -.故答案为：③④.。

高三数学空间几何体的三视图与直观图试题答案及解析1.一个多面体的三视图如图所示，则该多面体的体积为（）A．B．C．D．【答案】A【解析】由三视图可知，该多面体是由正方体截去两个正三棱锥所成的几何体，如图，正方体棱长为2，正三棱锥侧棱互相垂直，侧棱长为1，故几何体的体积为：V正方体-2V棱锥侧2×2×2−2×．故选：A．【考点】三视图求解几何体的体积．2.在长方体中割去两个小长方体后的几何体的三视图如图，则切割掉的两个小长方体的体积之和等于.【答案】24【解析】由题意割去的两个小长方体的体积为.【考点】三视图，几何体的体积..3.某几何体的三视图如图(其中侧视图中的圆弧是半圆)，则该几何体的表面积为()A．92＋14πB．82＋14πC．92＋24πD．82＋24π【答案】A【解析】由几何体的三视图，知该几何体的下半部分是长方体，上半部分是半径为2，高为5的圆柱的一半．长方体中EH＝4，HG＝4，GK＝5，所以长方体的表面积为(去掉一个上底面)2(4×4＋4×5)＋4×5＝92．半圆柱的两个底面积为π×22＝4π，半圆柱的侧面积为π×2×5＝10π，所以整个组合体的表面积为92＋4π＋10π＝92＋14π，选A．4.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图，可知该几何体为半圆锥和三棱锥的组合体，如图所示，可知左视图为等腰三角形，且轮廓线为实线，故选D．5.一个正方体截去两个角后所得几何体的正视图、侧视图如图所示，则其俯视图为()【答案】C【解析】依题意可知该几何体的直观图如图所示，故其俯视图应为C．6.某几何体的三视图如图所示，则该几何体的体积为A．12B．18C．24D．30【答案】C【解析】由三视图可知该几何体是一个底面为直角三角形的直三棱柱的一部分，其直观图如上图所示，其中,侧面是矩形，其余两个侧面是直角梯形，由于,平面平面,所以平面,所以几何体的体积为：故选C.【考点】1、空间几何体的三视图；2、空间几何体的体积.7.一块石材表示的几何体的三视图如图2所示，将石材切削、打磨、加工成球，则能得到的最大球的半径等于（）A．1B．2C．3D．4【答案】B【解析】由图可得该几何体为三棱柱,因为正视图,侧视图,俯视图的内切圆半径最小的是正视图(直角三角形)所对应的内切圆,所以最大球的半径为正视图直角三角形内切圆的半径,则,故选B.【考点】三视图内切圆球三棱柱8. [2013·四川高考]一个几何体的三视图如图所示，则该几何体可以是()A．棱柱B．棱台C．圆柱D．圆台【答案】D【解析】由正视图和侧视图可知，该几何体不可能是圆柱，排除选项C；又由俯视图可知，该几何体不可能是棱柱或棱台，排除选项A、B.故选D.9.[2013·宁波质检]如图，水平放置的三棱柱的侧棱长和底边长均为2，且侧棱AA1⊥平面A1B1C1，正视图是正方形，俯视图是正三角形，该三棱柱的侧视图面积为()A．2B．C．2D．4【答案】A【解析】由题意可知，该三棱柱的侧视图应为矩形，如图所示．在该矩形中，MM1＝CC1＝2，CM＝C1M1＝·AB＝.所以侧视图的面积为S＝2.10.某几何体的三视图如图所示,则该几何体的体积的最大值为 .【答案】【解析】该几何体是类似墙角的三棱锥，假设一条直角的棱长为x，则三条直角棱长分别为.所以体积为.当且仅当时取等号.【考点】1.三视图.2.函数最值问题.3.空间想象能力.11.（2012•广东）某几何体的三视图如图所示，它的体积为（）A．12πB．45πC．57πD．81π【答案】C【解析】由三视图可知，此组合体上部是一个母线长为5，底面圆半径是3的圆锥，下部是一个高为5，底面半径是3的圆柱故它的体积是5×π×32+π×32×=57π故选C12. (2014·咸宁模拟)某几何体的三视图如图所示(其中侧视图中的圆弧是半圆),则该几何体的表面积为( )A．92+14πB．82+14πC．92+24πD．82+24π【答案】A【解析】由几何体的三视图知该几何体的下半部分是长方体,上半部分是半径为2,高为5的圆柱的一半.所以长方体的表面积为(去掉一个上底面)2(4×4+4×5)+4×5=92.半圆柱的两个底面积为π×22=4π,半圆柱的侧面积为π×2×5=10π,所以整个组合体的表面积为92+4π+10π=92+14π. 13.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为【答案】D【解析】条件对应的几何体是由底面棱长为r的正四棱锥沿底面对角线截出的部分与底面为半径为r的圆锥沿对称轴截出的部分构成的。

高三数学空间几何体的三视图与直观图试题答案及解析1.已知某锥体的三视图（单位：cm）如图所示，则该锥体的体积为．【答案】２．【解析】由已知几何体的视图可知，几何体为四棱锥，其中SA垂直于平面ABCD，SA=2，四边形ABCD为直角梯形，AD=1，BC=2，AB=2，所以四棱锥的体积为【考点】三视图求几何体的体积.2.某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（）A．B．C．D．【答案】B【解析】由三视图知，原几何体是由一个长方体与一个三棱柱组成，其体积为，故选B.【考点】根据三视图还原几何体，求原几何体的体积，容易题.3.若某多面体的三视图（单位: cm）如图所示, 则此多面体的体积是（）A．cm3B．cm3C．cm3D．cm3【答案】C【解析】由三视图可得，该几何体相当于一个正方体切去一个三个侧棱长为1的三棱锥.所以该几何体的体积为.故选C.【考点】1.三视图.2.空间想象力.3.几何体的体积.4. (2014·孝感模拟)一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )A．16πB．14πC．12πD．8π【答案】A【解析】由三视图可知,该几何体是球挖去半球.其中两个半圆的面积为π×22=4π.个球的表面积为×4π×22=12π,所以这个几何体的表面积是12π+4π=16π.5.如图，某几何体的三视图都是等腰直角三角形，则几何体的体积是（）A．8B．7C．9D．6【答案】C【解析】由三视图可知,几何体是底面为等腰直角三角形,有一侧棱与底面垂直(垂足在非直角处)的三棱锥,其底面面积为×6×3=9,三棱锥的高为3,所以三棱锥的体积=×9×3=9．6.已知某几何体的三视图(如图),正视图和侧视图均为两个相等的等边三角形,府视图为正方形,则几何体的体积为（）A．B．4C．9D．9【答案】C【解析】由三视图可知,几何体由两个同底之正四棱锥组成所以其体积为V=2××32×3×=9 7.一空间几何体的三视图如图所示，该几何体的体积为12π＋，则正视图中x的值为( )A．5B．4C．3D．2【答案】C【解析】三视图，由正四棱锥和圆柱组成，故选C．8.如图，一个四棱锥的底面为正方形，其三视图如图所示，则这个四棱锥的体积为（）A．1B．2C．3D．4【答案】B【解析】由题意，棱锥的高为，底面面积为，∴.【考点】三视图，体积．9.某几何体的三视图如题（6）所示，其侧视图是一个边长为1的等边三角形，俯视图是两个正三角形拼成的菱形，则这个几何体的体积为（）A．1B．C．D．【答案】C【解析】这是由两个三棱锥拼成的几何体，其体积为.选C.【考点】三视图及几何体的体积.10.―个几何体的三视图如图所示(单位：)，则该几何体的体积为．【答案】18+9【解析】由三视图可知，此几何体为两个相切的球上方放了一个长方体组成的组合体，所以其体积为：V=3×6×1+2××=18+911.一个空间几何体的三视图如图所示，该几何体的表面积为__________.【答案】152【解析】几何体为一个三棱柱，底面为一个等腰三角形，底边长为6，底边上高为4，腰长为５.棱柱的高为8.因此表面积为【考点】三视图12.某三棱锥的三视图如图所示，则这个三棱锥的体积为；表面积为．【答案】；．【解析】由三视图知几何体如下图，为一个三棱锥，且三棱锥的一个侧面与底面垂直，底面三角形的一条边长为，该边上的高为，∴几何体的体积．它的表面积为．【考点】由三视图求面积、体积．13.已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是_______.【答案】【解析】由题意可得该几何体是一个三棱锥，体积.【考点】1.三视图的知识.2.立几中的线面关系.3.三棱锥的体积公式.14.一个空间几何体的三视图如图所示，其正视图、侧视图、俯视图均为等腰直角三角形，且直角边长都为1，则这个几何体的体积是【答案】【解析】由三视图，可知该几何体是三棱锥，并且侧棱，，，则该三棱锥的高是，底面三角形是直角三角形，所以这个几何体的体积＝＝．【考点】由三视图求几何体的体积．15.一个几何体的三视图如图所示,则该机合体的体积为( )A．B．C．D．【答案】B【解析】分析可得该几何体是底面为菱形的四棱锥,则高底面面积,所以.故选B【考点】三视图四棱锥体积16.一个几何体的三视图如图所示，则该几何体的体积是【答案】【解析】通过三视图的观察可得，该几何体是一个四棱柱，底面是一个直角梯形，其上下底分别为2,3，梯形的高为2.四棱柱的高为2.所以几何体的体积为.【考点】1.三视图的知识.2.几何体的体积.3.空间想象力.17.某长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为()A．4B．4C．6D．8【答案】D【解析】割补可得其体积为2×2×2＝8.18.某几何体的三视图如图所示，则该几何体的体积是________．【答案】16π－16【解析】由三视图知，该几何体是由一个底面半径为2，高为4的圆柱内挖去一个底面边长为2，高为4的正四棱柱后剩下的部分，∴V＝(π×22－22)×4＝16π－16.19.已知正方体ABCD-A1B1C1D1，M为棱A1B1的中点，N为棱A1D1的中点．如图是该正方体被M，N，A所确定的平面和N，D，C1所确定的平面截去两个角后所得的几何体，则这个几何体的正视图为()．【答案】B【解析】对于选项A，由于只是截去了两个角，此切割不可能使得正视图成为梯形．故A不对；对于B，正视图是正方形符合题意，线段AM的影子是一个实线段，相对面上的线段DC1的投影是正方形的对角线，由于从正面看不到，故应作成虚线，故选项B正确；对于C，正视图是正方形，符合题意，有两条实线存在于正面不符合实物图的结构，故不对；对于D，正视图是正方形，符合题意，其中的两条实线符合俯视图的特征，故D不对．20.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示，则该棱柱的体积为（）A．B．C．D．6【答案】B【解析】由三视图知该直三棱柱高为4，底面正三角形的高为3，所以正三角形边长为6，所以V＝×36×4＝36.故选B.【考点】1.三视图；2.柱体体积计算.21.某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为的扇形,则该几何体的体积为（）A．B．C．D．【答案】D【解析】由题意知道，该几何体体积是圆柱体积的，即.【考点】1、三视图；2、几何体体积.22.右图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为2和4，腰长为4的等腰梯形，则该几何体的侧面积是( )A．B．C．D．【答案】B【解析】由三视图可得该几何体是一个圆台，其两底直径分别为2和4，母线长为4，所以该几何体的侧面积是，选B..【考点】三视图，圆台的侧面积.23.如图是一个组合几何体的三视图，则该几何体的体积是 .A．B．C．D．【答案】A【解析】由三视图还原可知该几何体是一个组合体，下面是一个半径为4，高为8的圆柱，，上面是一个三棱柱，故所求体积为.【考点】三视图，圆柱、三棱柱的体积公式.24.已知一个几何体的三视图如图所示，则该几何体的体积为___________【答案】【解析】该几何体为圆柱中挖去半个球而得的组合体，其体积为.【考点】三视图.25.一个几何体的三视图如图所示（单位长度：），俯视图中圆与四边形相切，且该几何体的体积为，则该几何体的高为 .【答案】【解析】由如图所示的几何体的三视图知：这个几何体是一个半径为的球和一个直四棱柱的结合体，且这个直四棱柱的底面是对角线分别为和的棱形，这个直四棱柱的高为，∴这个几何体的体积：V=，解得h=.【考点】1.三视图；2.几何体的面积和体积26.一个几何体的三视图如图所示，则该几何体的直观图可以是（）【答案】D【解析】通过三视图的俯视图可知，该几何体是由两个旋转体组成，故选D.【考点】1.三视图的应用.27.如图为一个几何体的三视图正视图和侧视图均为矩形，俯视图中曲线部分为半圆，尺寸如图所示，则该几何体的表面积为（）A．B．C．D．【答案】D【解析】由三视图可知，这是一个由半个圆柱和一个三棱柱构成的组合体，这个组合体仍为一个柱体。

8.1 空间几何体的结构及其三视图和直观图五年高考考点1 空问几何体的结构 1．（2013天津，4，5分）已知下列三个命题：①若一个球的半径缩小到原来的,21则其体积缩小到原来的;81②若两组数据的平均数相等，则它们的标准差也相等； ③直线01=++y x 与圆2122=+y x 相切， 其中真命题的序号是 ( ).A ①②③ ①②.B ①③.C ②③.D2．（2013辽宁．10，5分）已知直三棱柱111A C B A BC -的6个顶点都在球O 的球面上，若4,AC 3,AB ==,12,1=⊥AA AC AB 则球O 的半径为( )2173.A 102.B 213.C 103.D 3．（2013课标全国I ，6，5分）如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm ，如果不计容器的厚度，则球的体积为 ( )33005.cm A π 33866.cm B π 331372.cm C π 332048.cm D π4．（2012福建．4.5分）一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是 ( ) A ．球 B ．三棱锥 C ．正方体 D ．圆柱5．(2011山东．11，5分 )如图是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱，其正（主）视图、俯视图如图；②存在四棱柱，其正（主）视图、俯视图如图；③存在圆柱，其正（主）视图、俯视图如图．其中真命题的个数是 ( )3.A 2.B 1.c 0.D6．（2013福建．12.4分）已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、侧视图、俯视图均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是7．（2010课标全国．14,5分）正视图为一个三角形的几何体可以是 ．（写出三种） 考点2三视图和直观图 1．（2013四川．3,5分）一个几何体的三视图如图所示，则该几何体的直观图可以是 ( )智力背景《九章算术》简介《九章算术》大约编于公元四、五十年间的东汉初期．这部书是采用问题集的形式 编成的，共有二百四十六个问题，分成方田、粟米、衰分、少广、商动、均输、盈不足、方程和勾股九章．方田章讲的是各种分数计算和方田、梯形田、斜方形田、圆田、半圆形田、弧田、环形田等的面积计算；粟米章讲的是粮食交易的简单比例计算， 2．（2013重庆，5，5分）某几何体的三视图如图所示，则该几何体的体积为 ( )3560.A 3580.B 200.C 240.D 3．（2013广东．5,5分）某四棱台的三视图如图所示，则该四棱台的体积是 ( )4.A 314.B 316.C 6.D 4．（2013湖南．7,5分）已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的正视图的面积不可能等于 ( )1.A2.B 212.-C 212.+D 5．（2013课标全国II ，7,5分）一个四面体的顶点在空间直角坐标系0 - xyz 中的坐标分别是(1，0，1)，(1，1，0)，(0，1，1)，(0，O ，O)，画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到的正视图可以为 ( )6．（2013课标全国I ，8,5分）某几何体的三视图如图所示，则该几何体的体积为 ( )π816.+A π88.+B π1616.+C π168.+D7．（2012课标全国．7,5分）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为( )6.A 9.B 12.C 18.D8．（2012湖北．4,5分）已知某几何体的三视图如图所示，则该几何体的体积为 ( )38.πA π3.B 310.πC π6.D 9．（2011课标．6,5分）在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为 ( )智力背景我可以创造 一个宇宙伽利略说：“给我空间、时间及对数，我可以创造一个宇宙…自然界的书是用数学的语言写成的．”哈尔莫斯说：“数学的创作绝不是单靠推论可以得到的，首先通常是一些模糊的猜测，揣摩着可能的推广，接着下了不十分有把握龅结论．然后整理想法，直到看出事实的端倪，往往还要费好大的劲儿，才能将一切特诸逻辑式的证明，这过程要经过许多失败、挫折，一再地猜测、揣摩，在试探中白花掉几个月的时间是常有的.”10.（2011广东．7，5分）如图，某几何体的正视图（主视图）是平行四边形，侧视图（左视图）和俯视图都是矩形，则该几何体的体积为 ( )36.A 39.B 312.C 318.D11.（2013辽宁，13.5分）某几何体的三视图如图所示，则该几何体的体积是12.（2013浙江．12.4分）若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积等于.3cm13.（2013陕西．12.5分）某几何体的三视图如图所示，则其体积为14.（2012浙江．11,4分）已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积等于 .3cm15.（2012辽宁，13.5分）一个几何体的三视图如图所示，则该几何体的表面积为解读探究智力背景什么是数学模型呢数学模型是指对于现实世界的某一特定对象，为了某个特定的目的，做出一些必要的简化和假设，运用适当的数学工具得到一个数学结构．数学结构是指数学符号、数学关系式、数学命题、图形图表等这些基于数学思想与方法的数学问题，总之，数学模型是对实际问题的一种抽象，基于数学理论和方法，用数学符号、数学关系式、数学命题、图形图表等来刻画客观事物的本质属性与其内在联系．知识清单1．棱柱的结构特征(1)棱柱的主要结构特征：有①面互相平行，其余各面都是②，并且每相邻③都互相平行，棱柱的两个互相平行的面叫棱柱的底面，其余各面叫棱柱的侧面，两侧面的公共边叫做棱柱的侧棱，如果棱柱的一个底面水平放置，则铅垂线与两底面的交点之间的线段或距离，叫做棱柱的高． (2)棱柱的分类：按侧棱与底面的关系可分为④、⑤；按底面多边形的边数可分为三棱柱、四棱柱、五棱柱等；底面是正多边形的⑥又称为正棱柱． 2．棱锥的结构特征(1)棱锥的定义：有一个面是多边形，其余各面是有一个⑦的三角形，这些面围成的几何体叫做棱锥．(2)正棱锥的定义：如果一个棱锥的底面是正多边形，并且顶点在底面内的射影是底面中心，这样的棱锥叫做正棱锥．(3)正棱锥的性质：a．各侧棱长度相等，各侧面都是全等的等腰三角形，各等腰三角形底边上的高相等，它叫做正棱锥的斜高．b．棱锥的高、斜高和斜足与底面中心连线组成一个直角三角形；棱锥的高、侧棱和侧棱在底面内的射影也组成一个直角三角形．3．圆柱、圆锥、圆台的结构特征分别以矩形一边、直角三角形一直角边、直角梯形中垂直于底边的腰所在的直线为旋转轴，其余各边旋转一周而形成的曲面所围成的几何体分别叫做圆柱、圆锥、圆台，其中旋转轴叫做所围成的几何体的轴；在轴上的这条边叫做这个几何体的高；垂直于轴的边旋转而成的圆面叫做这个几何体的底面；不垂直于轴的边旋转而成的曲面叫做这个几何体的侧面，无论旋转到什么位置，这条边都叫做侧面的母线．4．棱台、圆台的特征用平行于底面的平面去截棱锥、圆锥，截面与底面间的部分叫棱台、圆台．5．球(1)-个⑧围绕着它的直径所在的直线旋转一周所形成的曲面叫做球面，球面所围成的几何体叫做球．形成球的半圆的圆心叫做球心；连结球面上一点和球心的线段叫球的半径；连结球面上两点且通过球心的线段叫球的直径(2)球面被不经过球心的平面截得的圆叫做球的小圆，被经 过球心的平面截得的圆叫做球的大圆．球的截面性质：⑨ ，其中r 为截面圆的半径，R 为球的半径，d 为球心O 到截面圆心的距离． 6．几何体的三视图是指：⑩____、（11）____、（12）____．又称为主视图、左视图、俯视图． 7.三视图的画法要求(1)在画三视图时，重叠的线只画一条，被挡住的线要画成虚线．(2)三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线，画三视图的基本要求：（13） 、（14）____ 、（15） ．(3)由三视图想象几何体特征时要根据“长对正、宽相等、高平齐”的基本原则． 8．平行投影的投影线互相平行；中心投影的投影线交于一点． 9．水平放置的平面图形的直观图的斜二测画法的步骤(1)在已知图形中取互相垂直的x 轴和y 轴，两轴相交于0点，画直观图时，把它们画成对应的/x 轴与/y 轴，两轴相交于/O 且使,45///oy O x =∠用它们确定的平面表示水平面；(2)已知图形中平行于x 轴或y 轴的线段，在直观图中，分别画成平行于/x 轴或/y 轴的线段； (3)已知图形中平行于x 轴的线段，在直观图中保持原长度不变，平行于y 轴的线段，长度变为原来的一半． 【知识拓展】1．常见多面体及其关系、(1)平行六面体；直棱柱；正棱柱；长方体；正方体；正棱锥；正棱台．(2){正方体}≠⊂{正四棱柱}≠⊂{长方体}≠⊂{直平行六面体}≠⊂{平行六面体}≠⊂{四棱柱}．2.三视图在解题过程中，可以根据三视图的形状及图中所涉及的线段的长度，推出原几何图形中的点、线、面的位置关系及图中的一些线段的长度，从而解决其他有关问题，·知识清单答案智力背景石钟慈与中国计算数学的发展 中国计算数学家、中国科学院院士、中国科学院计算数学与科学工 程计算研究所研究员磊钟慈，曾任国家攀登项目“天规模科学与工程计算”首席科学家20世纪50年代 束，他建立了一种将变分原理和摄动理论相结合的新算法并算出氦原子最低能态的良好近似值；研究了 矩阵特征值的定位问题，得到精度很高的上下界估计公式．90年代后期，他研究弹性力学中闭锁问题的 有限元方法，成绩显著，居于国际前列.突破方法方法1几何体的三视图例1 （2012湖南,3,5分）某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是( )解题思路解析 A图是两个圆柱的组合体的俯视图；B图是一个四棱柱与一个圆柱的组合体的俯视图；C图是一个底面为等腰直角三角形的三棱柱与一个四棱柱的组合体的俯视图，采用排除法，故选D．答案 D【方法点拨】三视图的画法要坚持以下原则：(1)高平齐，即正视图和侧视图的高相等；(2)宽相等，即侧视图和俯视图的宽相等；(3)长对正，即正视图和俯视图的长相等；(4)看不见的轮廓线或棱要用虚线表示，方法2几何体的直观图例2（2012山东淄博三模．14，4分）有一块多边形的菜地，它的水平放置的平面图形的斜二测直观图是直角梯形（如图所示），,,1,45BCDCADABABC⊥===∠ 则这块菜地的面积为解题思路解析如图①，在直观图中，过点A作AElBC，垂足为E，则在Rt△ABE中，⋅=∴=∠=22,45,1BEABEAB而四边形AECD为矩形，AD =1，22.1=+=∴==∴ECBEBCADEC.1+由此可还原原图形如图②．在原图形中，===//////,2,1CBBADA,122+且,,//////////CBBACBDA⊥∴这块菜地的面积为//////)(21BACBDAs⋅+=⋅+=⨯++⨯=2222)2211(21答案 222+【方法点拨】 斜二测画法的注意事项：(1)对于几何体的直观图，一方面，要掌握斜二测画法规则，注意线线平行关系的不变性及长度的变化特征；另一方面，若能了解原图形面积S 与其直观图面积直S 之间的关系：,42s S =直还可以简化有关问题的计算．(2)把水平放置的直观图还原成原来的图形，基本过程就是逆用斜二测画法，使平行于/x 轴的线段长度不变，平行于/y 轴的线段长度变成原来的2倍，智力背景分解质因数的来源 1643年，欧洲殖民者在美洲大陆经历了一场恐怖：大量的蝉仿佛一夜之间从地底冒出，几周后销声匿迹，时隔17年，这现象再次出现到1991年共出现22次，周期很准确，科学家发现，蝉的生命周期大都为质数，如在北荑洲北部地区同濑为17年，在南部地区则为13年科学家说，蝉选择质数为生命周期，可降低与天敌遭遇的概率若它的生命周期是12年，则与生命周期为l 、2、3、4、6、的天教都可能遭遇，从而使种群生存受威胁.三年模拟A 组 2011-2013年模拟探究专项基础测试时间：35分钟 分值：40分 一、选择题（每题5分，共25分） 1．（2013北京通州高三上学期期末）一个几何体的三视图如图所示，该几何体的表面积是 ( )，2416.+A 2412.+B 248.+C 244.+D2．（2013广东云浮一模．3）如图，某几何体的正视图与侧视图都是边长为1的正方形，且体积为,21则该几何体的俯视图可以是( )3．（2013吉林长春5月，11）如图所示是一个几何体的三视图，则该几何体的体积为 ( )π216.+A π28.+B π+16.C π+8.D 4．（2012北京朝阳二模．8）有一个棱长为1的正方体，按任意方向正投影，其投影面积的最大值是 ( )1.A 223.B 2.C 3.D 5．（2011江西重点盟校二次联考．6）若某多面体的三视图(单位：cm)如图所示，则此多面体的体积是 ( )321.cm A 332.cm B 365.cm C 387.cm D 二、填空题（共5分）6．（2013河北石家庄二模,13）如图，矩形////C B A O 是水平放置的一个平面图形的直观图，其中,2,6////==C O A O 则原图形OABC 的面积为三、解答题（共10分）7．（2013北京大兴一模．17）用一个平行于圆锥底面的平面截这个圆锥，截得圆台的上、下底面的面积之比为1:16，截去的圆锥的母线长是3 cm ，求圆台的母线长，智力背景规矩和直尺（一） 古人云:“没有规矩，不成方圆，”可见在中国古代，就有了规和矩．我们知道，“规”是指画圆的圆规；“矩”是折成直角的曲尺，尺上有刻度，发明规矩的确切年代已无从查考．但在公元前15世纪的甲骨文中，已有规矩二字了．《史记》中有这样的记栽：夏禹治水的时候，是“左准绳，右规矩”．这意思是说，夏禹是左手拿着水准绳，右手拿规和矩进行测量，规划出治水方索的，由此说明在夏禹治水的年代就有了规和矩这两种几何工具了，B 组 2011-2013年模拟探究专项提升测试时间：50分钟 分值：50分 一、选择题（每题5分，共15分） 1．（2013北京昌平高三上学期期末）已知一个空间几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的全面积为 ( )243410.++A 243210.++B 243214.++C 243414.++D2．（2013山西阳泉一模．9）下列结论正确的是 ( )A ．各个面都是三角形的几何体是三棱锥B ．以三角形的一条边所在直线为旋转轴，其余两边旋转一周形成的曲面所围成的几何体叫圆锥C ．棱锥的侧棱长与底面多边形的边长相等，则此棱锥可能是六棱锥D ．圆锥的顶点与底面圆周上的任意一点的连线都是母线3．（2013甘肃西宁二模．4）将长方体截去一个四棱锥，得到的几何体如图所示，则该几何体的左视图为 ( )二、填空题（每题5分，共10分）4．（2013山东潍坊一模．13）等腰梯形ABCD ，上底CD =1，腰AD ,2⋅==CB 下底,3=AB 以下底所在直线为x 轴，则由斜二测画法画出的直观图////D C B A 的面积为5．（2013河南三门峡4月．14）如图，侧棱长为32的正三棱锥v-ABC 中，,40oCVA BVC AVB =∠=∠=∠ 过A 作截面△AEF，则截面△AEF 的周长的最小值为三、解答题（共25分）6．（2013东北八校一模．17）已知正三棱锥V-ABC 的正视图、侧视图和俯视图如图所示．(1)画出该三棱锥的直观图；(2)求出侧视图的面积．7．（2013四川西昌二模，18）如图所示，在正三棱柱111-ABC C B A 中，,2,21==AA AB 从顶点B 沿棱柱侧面（经过棱)AA 1到达顶点,1C 与1AA 的交点记为M 求：(1)正三棱柱侧面展开图的对角线长；(2)从B 经过M 到1C 的最短路线长及此时AMM A 1的值，智力背景规矩和直尺(二) 规矩的使用，对于我国古代几何学的发展有着很重要的意丸周代数学家商高曾把规 矩的用处作了总结：“平矩以正绳，偃矩以望高，覆矩以测深，卧矩以知远”这几句话，精炼地道出了矩的用途．希腊人作图只能从最基本的工具—一直尺和圆规开始，直尺还是没有刻度的尺．由于作图工具的限制，导致了历史上的三火几何不能作图问题：三等分任意角，倍立方，化圆为方，而在这三个难题的研究过程中又有许多发现，从而推动了数学的发展.。

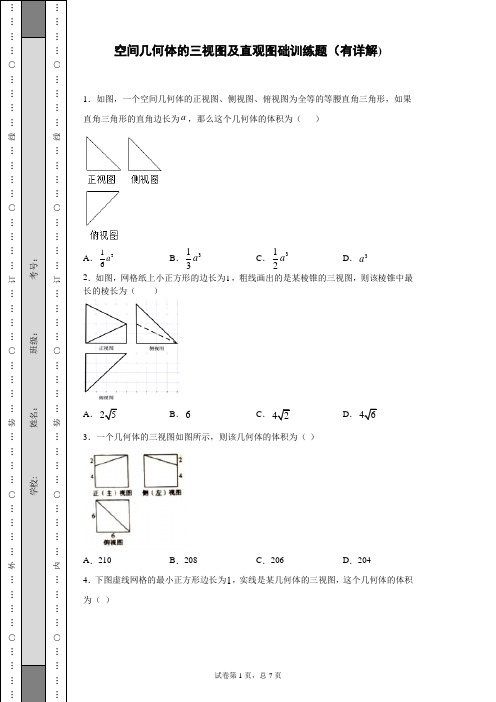
空间几何体的三视图及直观图础训练题（有详解) 1．如图，一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为a ，那么这个几何体的体积为（ ）A ．316aB ．313aC ．312aD ．3a 2．如图，网格纸上小正方形的边长为1，粗线画出的是某棱锥的三视图，则该棱锥中最长的棱长为（ ） A ．B ．6 C ．D ． 3．一个几何体的三视图如图所示，则该几何体的体积为（ ） A ．210 B ．208 C ．206 D ．204 4．下图虚线网格的最小正方形边长为1，实线是某几何体的三视图，这个几何体的体积为（ ）A ．4πB ．2πC ．43π D ．π 5．某多面体的三视图（单位：）如图所示，则此多面体外接球的表面积是（ ）A ．B ．C ．D ．6．如图是一个水平放置的正四棱柱被截掉一只角后的实物图形，则它的侧视图是( )A ．B ．C ．D ．7．某柱体的三视图如图所示（单位：），则该几何体的侧面积（单位：）是（ ）A ．6B ．C ．D ． 8．如图是某几何体的三视图，则这个几何体是（ ） A ．圆柱 B ．球 C ．圆锥 D ．棱柱9．如图所示，画出四面体AB 1CD 1三视图中的正视图，以面AA 1D 1D 为投影面，则得到的正视图可以为 ( ) A ． B ． C ． D ． 10．一几何体的直观图如右图，下列给出的四个俯视图中正确的是（ ） A ． B ． C ． D ．A ．B ．C ．D ． 12．某几何体的三视图如图所示，则其体积为（ ）A ．4B ．73. C ．43 D ．8313．若一个水平放置的平面图形的斜二测直观图是一个底角为45°，腰和上底均为1的等腰梯形，则原平面图形的周长为（ ）A ．4+B ．3C ．2D ．314．用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形，其中1OA OB ==，则原平面图形的面积为（ ）A ．1BC ．32 D ．215．如图，正方形////O A B C 的边长为1，它是水平放置的一个平面图形的直观图，则原图形的面积是（ ）A ．2B ．1C ．D ．16．如下图，是用“斜二测画法”画出的直观图，其中，那么是一个（ ）A ．等边三角形B ．直角三角形C ．钝角三角形D ．三边互不相等的三角形17．一个水平放置的平面图形，用斜二测画法画出了它的直观图，此直观图恰好是一个边长为2的正方形，如图所示，则原平面图形的面积为( ) A ．4 B ．8 C ．8 D ．8 18．斜二测图的轴间角分别为（ ） A ．， B ．， C ．， D ．，二、填空题 19．如图，网络纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的外接球的表面积为（________） 20．一个几何体的三视图及其尺寸如下图所示，其中主视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，则这个几何体的表面积是________．21．一个四棱锥的三视图如右图所示，已知该四棱锥的体积为20，则高h=____________.22．利用斜二测画法得到的结论正确的是_________①三角形的直观图是三角形③正方形的直观图是正方形 ④菱形的直观图是菱形； 23．若正ABC ∆的边长为a ，则ABC ∆的平面直观图A B C ∆'''的面积为=____________. 24．如图， '''O A B ∆是水平放置的ABC ∆的直观图，则ABC ∆的周长为 ______.三、解答题 25．画出如图所示几何体的三视图．参考答案1．A【解析】【分析】该几何体为三棱锥，且同一点出发的三条棱长度为1，可以以其中两条棱组成的直角三角形为底，另一棱为高，利用体积公式求得其体积【详解】根据几何体得三视图转换为几何体为：底面为直角边长为a 的等腰直角三角形，高为a 的三棱锥． 故：3111326V a a a a =⨯⨯⨯⨯=. 故选：A ．【点睛】本题考查简单的三视图问题，属于基础题2．B【解析】【分析】作出直观图，根据三视图的数据和勾股定理计算各棱长即可．【详解】解：作出四棱锥A ﹣BCDE 的直观图如图所示：由三视图可知底面BCDE 是直角梯形， DE ∥BC ，BC ⊥BE ，DE ⊥面ABE ，AE ⊥BE ，且AE ＝BE ＝DE ＝4，BC ＝2，∴AD ＝AB ＝，AC ＝6，CD =∴AC 为四棱锥的最长棱．故选：B ．【点睛】本题考查了棱锥的结构特征和三视图，考查空间想象能力与计算能力，属于中档题． 3．D【解析】【分析】根据三视图还原出原几何体，并得到各棱的长度，通过切割法求出其体积.【详解】由已知中的三视图可得：该几何体是由一个正方体切去一个三棱锥所得的组合体， 正方体的边长为6，切去一个三棱锥的底面是直角边长分别为6，6的等腰直角三角形，高为2， 故该几何体的体积为311666220432V =-⨯⨯⨯⨯=. 故选D 项.【点睛】本题考查三视图还原几何体，切割法求几何体体积，属于简单题.4．B【解析】【分析】画出几何体的直观图，利用三视图的数据，求解几何体的体积即可．【详解】解：应用可知几何体的直观图如图：是圆柱的一半， 可得几何体的体积为：211422ππ⨯⨯=． 故选：B ．【点睛】本题考查三视图求解几何体的体积的求法，判断几何体的形状是解题的关键．5．C【解析】【分析】通过三视图还原几何体，可得多面体为正方体去掉一个角。

§8.1空间几何体的结构及其三视图和直观图1.多面体的结构特征(1)棱柱的上下底面________，侧棱都________且____________，上底面和下底面是________的多边形.(2)棱锥的底面是任意多边形，侧面是有一个____________的三角形.(3)棱台可由________________________的平面截棱锥得到，其上下底面的两个多边形________.2.旋转体的结构特征(1)圆柱可以由矩形绕其________________旋转得到.(2)圆锥可以由直角三角形绕其________________________________旋转得到.(3)圆台可以由直角梯形绕直角腰所在直线或等腰梯形绕上下底中点的连线旋转得到，也可由______________________的平面截圆锥得到.(4)球可以由半圆或圆绕其________旋转得到.3.空间几何体的三视图空间几何体的三视图是用__________得到，这种投影下与投影面平行的平面图形留下的影子与平面图形的形状和大小是____________的，三视图包括____________、__________、________.4.空间几何体的直观图画空间几何体的直观图常用________画法，基本步骤是：(1)在已知图形中取互相垂直的x轴、y轴，两轴相交于点O，画直观图时，把它们画成对应的x′轴、y′轴，两轴相交于点O′，且使∠x′O′y′＝__________.(2)已知图形中平行于x轴、y轴的线段，在直观图中分别平行于____________.(3)已知图形中平行于x轴的线段，在直观图中长度____________，平行于y轴的线段，长度变为______________.(4)在已知图形中过O点作z轴垂直于xOy平面，在直观图中对应的z′轴也垂直于x′O′y′平面，已知图形中平行于z轴的线段，在直观图中仍平行于z′轴且长度________.[难点正本疑点清源]1.画空间几何体的三视图的两个步骤第一步，确定三个视图的形状；第二步，将这三个视图摆放在平面上.在绘制三视图时，分界线和可见轮廓线都用实线画出，被遮挡的部分的轮廓线用虚线表示出来，即“眼见为实、不见为虚”.2.三视图与空间几何体中的几何量的关系空间几何体的数量关系也体现在三视图中，正视图和侧视图的“高平齐”，正视图和俯视图的“长对正”，侧视图和俯视图的“宽相等”.其中，正视图、侧视图的高就是空间几何体的高，正视图、俯视图中的长就是空间几何体的最大长度，侧视图、俯视图中的宽就是空间几何体的最大宽度.要尽量按照这个规则画空间几何体的三视图.1.利用斜二测画法得到的以下结论，正确的是__________.(写出所有正确的序号)①三角形的直观图是三角形；②平行四边形的直观图是平行四边形；③正方形的直观图是正方形；④圆的直观图是椭圆；⑤菱形的直观图是菱形.2.如果圆锥的侧面展开图是半圆，那么这个圆锥的顶角(圆锥轴截面中两条母线的夹角)是________.3.一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号).①三棱锥；②四棱锥；③三棱柱；④四棱柱；⑤圆锥；⑥圆柱.4.以下命题：①直角三角形绕一边所在直线旋转得到的旋转体是圆锥；②夹在圆柱的两个平行截面间的几何体还是圆柱；③圆锥截去一个小圆锥后剩余部分是圆台；④棱锥截去一个小棱锥后剩余部分是棱台.其中正确的命题序号是________.5.(2011·浙江)若某几何体的三视图如图所示，则这个几何体的直观图可以是()题型一空间几何体的结构特征例1设有以下四个命题：①底面是平行四边形的四棱柱是平行六面体；②底面是矩形的平行六面体是长方体；③直四棱柱是直平行六面体；④棱台的相对侧棱延长后必交于一点.其中真命题的序号是________.探究提高解决该类题目需准确理解几何体的定义，要真正把握几何体的结构特征，并且学会通过反例对概念进行辨析，即要说明一个命题是错误的，设法举出一个反例即可.下面是关于四棱柱的四个命题：①若有两个侧面垂直于底面，则该四棱柱为直四棱柱；②若过两个相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱；③若四个侧面两两全等，则该四棱柱为直四棱柱；④若四棱柱的四条对角线两两相等，则该四棱柱为直四棱柱.其中，真命题的编号是________.题型二几何体的三视图例2已知三棱锥的正视图与俯视图如图所示，俯视图是边长为2的正三角形，则该三棱锥的侧视图可能为()探究提高根据几何体的直观图，画三视图，要根据三视图的画法规则进行.要严格按以下几点执行：①三视图的安排位置.正视图、侧视图分别放在左、右两边，俯视图放在正视图的下边.②注意实虚线的区别.一个长方体去掉一个小长方体，所得几何体的正视图与侧视图分别如图所示，则该几何体的俯视图为()题型三空间几何体的直观图例3已知△ABC的直观图A′B′C′是边长为a的正三角形，求原△ABC的面积.探究提高对于直观图，除了了解斜二测画法的规则外，还要了解原图形面积S与其直观图面积S′之间的关系S′＝24S，能进行相关问题的计算.如图所示，直观图四边形A ′B ′C ′D ′是一个底角为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积是________.题型四 几何体的截面问题例4 棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图所示，求图中三角形(正四面体的截面)的面积.探究提高 解决这类问题的关键是准确分析出组合体的结构特征，发挥自己的空间想象能力，把立体图和截面图对照分析，有机结合，找出几何体中的数量关系，为了增加图形的直观性，常常画一个截面圆作为衬托.在棱长为6的正四面体内有一个内切球(球与正四面体的四个面都相切)，经过四面体的一条棱及高作截面如图.求内切球的半径.8.三视图识图不准致误试题：(5分)一个空间几何体的三视图，如图所示，则这个空间几何体的表面积是________.学生答案展示审题视角 (1)由三视图还原成直观图，并注意数据的对应.(2)表面积包括哪些部分. 正确答案 4(π＋1)解析 这是一个由轴截面割开的半个圆柱与一个球的组合体，其表面积是圆柱的上下两个底面半圆、圆柱的侧面积的一半、圆柱的轴截面和球的表面积之和，故这个表面积是2×12×π×12＋12×2π×1×2＋2×2＋4π×⎝⎛⎭⎫122＝4(π＋1).批阅笔记 1.本题考查的是三视图和表面积计算问题.在由三视图还原为空间几何体的实际形状时，要从三个视图综合考虑，根据三视图的规则，空间几何体的可见轮廓线在三视图中为实线，不可见轮廓线为虚线.在还原空间几何体实际形状时一般是以正视图和俯视图为主，结合侧视图进行综合考虑.2.解本题易出现的错误有：(1)还原空间几何体形状时出错，不能判断出俯视图中的半圆所对应的几何体；(2)计算表面积时漏掉部分表面，如漏掉了半圆柱的截面矩形或是漏掉了上下两个半圆等.方法与技巧1.棱柱主要是理解、掌握基本概念和性质，并能灵活应用.2.正棱锥问题常归结到它的高、侧棱、斜高、底面正多边形内切圆半径或外接圆半径、底面边长的一半构成的直角三角形中解决.3.圆柱、圆锥、圆台、球应抓住它们是旋转体这一特点，弄清旋转轴、旋转面、轴截面. 失误与防范1.台体可以看成是由锥体截得的，但一定强调截面与底面平行.2.掌握三视图的概念及画法在绘制三视图时，若相邻两物体的表面相交，表面的交线是它们的分界线.在三视图中，分界线和可见轮廓线都用实线画出，被挡住的轮廓线画成虚线.并做到“正侧一样高、正俯一样长、俯侧一样宽”.3.掌握直观图的概念及斜二测画法在斜二测画法中，要确定关键点及关键线段.“平行于x轴的线段平行性不变，长度不变；平行于y轴的线段平行性不变，长度减半.”4.能够由空间几何体的三视图得到它的直观图；也能够由空间几何体的直观图得到它的三视图，提升空间想象能力.§8.1空间几何体的结构及其三视图和直观图(时间：60分钟)A组专项基础训练题组一、选择题1.给出四个命题：①各侧面都是全等四边形的棱柱一定是正棱柱；②对角面是全等矩形的六面体一定是长方体；③有两侧面垂直于底面的棱柱一定是直棱柱；④长方体一定是正四棱柱.其中正确的命题个数是()A.0B.1C.2D.32.如图是一个正方体的展开图，将其折叠起来，变成正方体后的图形是()3.(2011·课标全国)在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为()二、填空题4.如图所示，E、F分别为正方体ABCD—A1B1C1D1的面ADD1A1、面BCC1B1的中心，则四边形BFD1E在该正方体的面DCC1D1上的投影是______.(填序号)5.(2010·辽宁)如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为________.三、解答题6.已知圆锥的底面半径为r，高为h，且正方体ABCD—A1B1C1D1内接于圆锥，求这个正方体的棱长.B组专项能力提升题组一、选择题1.已知某一几何体的正视图与侧视图如图所示，则在下列图形中，可以是该几何体的俯视图的图形为()A.①②③⑤B.②③④⑤C.①②④⑤D.①②③④2.一个正方体截去两个角后所得几何体的正视图、侧视图如图所示，则其俯视图为()3.在棱长为1的正方体ABCD—A1B1C1D1中，过对角线BD1的一个平面交AA1于E，交CC1于F，得四边形BFD1E，给出下列结论：①四边形BFD1E有可能为梯形；②四边形BFD1E有可能为菱形；③四边形BFD1E在底面ABCD内的投影一定是正方形；④四边形BFD1E有可能垂直于平面BB1D1D；⑤四边形BFD1E面积的最小值为6 2.其中正确的是() A.①②③④ B.②③④⑤C.①③④⑤D.①②④⑤二、填空题4.如图，点O为正方体ABCD—A′B′C′D′的中心，点E为面B′BCC′的中心，点F为B′C′的中点，则空间四边形D′OEF在该正方体的各个面上的投影可能是________(填出所有可能的序号).5.对于四面体ABCD，下列命题正确的是________.(写出所有正确命题的编号)①相对棱AB与CD所在的直线异面；②由顶点A作四面体的高，其垂足是△BCD三条高线的交点；③若分别作△ABC和△ABD的边AB上的高，则这两条高所在的直线异面；④分别作三组相对棱中点的连线，所得的三条线段相交于一点；⑤最长棱必有某个端点，由它引出的另两条棱的长度之和大于最长棱.6.用半径为r的半圆形铁皮卷成一个圆锥筒，那么这个圆锥筒的高是________.三、解答题7.已知正三棱锥V—ABC的正视图、侧视图和俯视图如图所示.(1)画出该三棱锥的直观图；(2)求出侧视图的面积.答案1.(1)平行平行长度相等全等(2)公共顶点(3)平行于棱锥底面相似2.(1)一边所在直线(2)一条直角边所在直线(3)平行于圆锥底面(4)直径3.正投影完全相同正视图侧视图俯视图4.斜二测(1)45°(或135°)(2)x′轴、y′轴(3)保持不变原来的一半(4)不变基础自测1.①②④2.60°3.①②③⑤4.③5.D题型分类·深度剖析例1①④变式训练1②④例2B变式训练2 C例3解建立如图所示的坐标系xOy′，△A′B′C′的顶点C′在y′轴上，A′B′边在x轴上，把y′轴绕原点逆时针旋转45°得y轴，在y轴上取点C使OC＝2OC′，A、B点即为A′、B′点，长度不变.已知A′B′＝A′C′＝a，在△OA′C′中，由正弦定理得OC ′sin ∠OA ′C ′＝A ′C ′sin 45°， 所以OC ′＝sin 120°sin 45°a ＝62a ， 所以原三角形ABC 的高OC ＝6a ， 所以S △ABC ＝12×a ×6a ＝62a 2. 变式训练3 2＋2例4 解 如图所示，△ABE 为题中的三角形，由已知得AB ＝2，BE ＝2×32＝3， BF ＝23BE ＝233， AF ＝AB 2－BF 2＝ 4－43＝ 83， ∴△ABE 的面积为S ＝12×BE ×AF ＝12×3× 83＝ 2. ∴所求的三角形的面积为 2.变式训练4 解 AB 为正四面体的一条棱，所以AB ＝6. BD 为正四面体的一个面的高，所以BD ＝32×6＝33， 同理AD ＝33，又HD ＝13×BD ＝3， ∴AH ＝AD 2－HD 2＝26，又△AOE ∽△ADH ，∴AO AD ＝OE DH ，即26－OE 33＝OE 3，∴OE ＝62，∴内切球的半径为62.课时规范训练A 组1.A2.B3.D4.②5.2 36.解 如图所示，过内接正方体的一组对棱 作圆锥的轴截面，设圆锥内接正方体的棱 长为x ，则在轴截面中，正方体的对角面 A 1ACC 1的一组邻边的长分别为x 和2x . ∵△VA 1C 1∽△VMN ， ∴2x 2r ＝h－xh ，∴x ＝2rh2r ＋2h .即圆锥内接正方体的棱长为2rh2r ＋2h .B 组1.D2.C3.B4.①②③5.①④⑤6.32r7.解 (1)如图所示.(2)根据三视图间的关系可得BC ＝23， ∴侧视图中VA ＝42－⎝⎛⎭⎫23×32×232＝23，∴S △VBC ＝12×23×23＝6.。

高三数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图如图所示，则该几何体的体积是（）A．B．C．D．【答案】A【解析】由三视图可知，该几何体是圆锥的四分之一，其底半径为，高为，所以其体积为，故选.【考点】1.三视图；2.几何体的体积.2.若某三棱柱截去一个三棱锥后所剩几何体的三视图如下图所示，则此几何体的体积等于（）A．B．C．D．【答案】C【解析】由三视图可知，空间几体体的直观图如下图所示：所求几何体的体积故选C.【考点】1、三视图；2、空间几何体的体积.3.如图，一个几何体的三视图（正视图、侧视图和俯视图）为两个等腰直角三角形和一个边长为1的正方形，则其外接球的表面积为A．πB．2πC．3πD．4π【答案】C【解析】原几何体为有一条侧棱垂直于底面的四棱锥，且底面是边长为1的正方形，垂直于底面的侧棱长也为1，因此，该几何体可以补形为一个棱长为1的正方体，其外接球就是这个正方体的外接球，直径为正方体的对角线长，即2R＝，故R＝故外接球表面积为：4πR2＝3π.【考点】三视图，几何体的外接球及其表面积4.如图所示，一个三棱锥的三视图是三个直角三角形(单位： cm)，则该三棱锥的外接球的表面积为________cm2．【答案】29π【解析】从三棱锥的三视图可知，三棱锥有两侧面与底面垂直，把三棱锥补成长，宽，高分别为4,2,3的长方体，设外接球的半径为R，由42＋22＋32＝4R2得，S＝4πR2＝29π(cm2)．球5.某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为()A．4B．2C．D．8【答案】D【解析】由三视图可知，该几何体如图所示，其底面为正方形，正方形的边长为2．HD＝3，BF ＝1，将相同的两个几何体放在一起，构成一个高为4的长方体，所以该几何体的体积为×2×2×4＝8．6.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图，可知该几何体为半圆锥和三棱锥的组合体，如图所示，可知左视图为等腰三角形，且轮廓线为实线，故选D．7.一个几何体的三视图如图所示，已知这个几何体的体积为，= .【答案】【解析】由三视图知，原几何体是一个四棱锥，底面是面积为的矩形，高为，所以，解得.【考点】三视图，空间几何体的体积.8.如图，水平放置的正三棱柱的主视图是一边长为2的正方形，则该三棱柱的左视图的面积为．【答案】【解析】左视图为一个矩形，长宽分别为，因此面积为.【考点】三视图9.若一个正三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为() A．B．C．D．【答案】B【解析】依题意得，该正三棱柱的底面正三角形的边长为2，侧棱长为1．设该正三棱柱的外接球半径为R，易知该正三棱柱的底面正三角形的外接圆半径是2sin 60°×＝，所以R2＝＋＝，则该球的表面积为4πR2＝．10.图中的网格是边长为1的小正方形，在其上用粗线画出了某多面体的三视图，则该多面体的体积为________．【答案】16【解析】从三视图可知，这是一个四棱锥，.【考点】三视图.11.如图所示，一个空间几何体的正视图和左视图都是边长为的正方形，俯视图是一个直径为的圆，那么这个几何体的体积为 ( )A．B．C．D．【答案】B【解析】几何体是圆柱，.【考点】三视图，圆柱的体积.12.一个几何体的三视图如图所示，其中正视图是一个正三角形，则该几何体的体积为( )A．1B．C．D．【答案】B【解析】由三视图可知，此几何体为三棱锥，如图，其中正视图为，是边长为2的正三角形，，且，底面为等腰直角三角形，，所以体积为，故选B.13.已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的正视图的面积不可能等于（）A．1B．C．D．【答案】C【解析】由题意知，正视图的最大面积为对角面的面积，最小面积为，而，故选C．【考点】三视图.14.已知某几何体的三视图如右图所示，其中俯视图是圆，且该几何体的体积为；直径为2的球的体积为．则()A．B．C．D．【答案】C【解析】由题意，该几何体是一个圆柱挖去一个圆锥得到的几何体，，，∴.选B.【考点】三视图，体积.15.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为（）A．B．C．D．【答案】B【解析】过B作BD⊥AC于点D，则BD=2，CD=2，所以BC=,因为SC⊥平面ABC，所以SC⊥BC，所以SB=,故选B.【考点】三视图、直线与平面垂直的性质.16.一个几何体的三视图如图，则该几何体的体积为（）A．B．C．D．【答案】A【解析】由三视图可知，该几何体是由一个半圆柱和一个三棱锥拼接而成，且半圆柱的底面是半径为的半圆，高为，其底面积为，故其体积为，三棱锥的底面是一个直角三角形，三棱锥的高也为，其底面积为，故其体积为，所以该几何体的体积为，故选A.【考点】1.三视图；2.组合体的体积17.右图为某几何体的三视图，则该几何体的体积为 .【答案】【解析】所求几何体为一个底面半径为1，高为1的圆柱与半径为1的四分之一的球的组合体，所以体积为【考点】三视图18.一个空间几何体的三视图如图所示，该几何体的体积为______.【答案】96【解析】几何体为一个三棱柱，底面为一个等腰三角形，底边长为6，底边上高为4，棱柱的高为8.因此所求体积为【考点】三视图19.把边长为1的正方形ABCD沿对角线BD折起，形成三棱锥C－ABD，它的主视图与俯视图如右上图所示，则二面角 C－AB－D的正切值为．【答案】【解析】如图所示,做BD,AB的中点分别为点E,F.则有CE面ABD,由于EF为等腰直角三角形ABD的中位线,故EF AB,则为二面角 C－AB－D的代表角,所以,故填.【考点】二面角三视图20.已知水平放置的△ABC的直观图△A′B′C′(斜二测画法)是边长为a的正三角形，则原△ABC 的面积为()A．a2B．a2C．a2D．a2【答案】D【解析】斜二测画法中原图面积与直观图面积之比为1∶，则易知S＝ ( a)2，∴S＝a2.21.一个空间几何体的三视图如图所示,则该几何体的体积为()A．πcm3B．3πcm3C．πcm3D．πcm3【答案】D【解析】由三视图可知,此几何体为底面半径为1cm、高为3cm的圆柱上部去掉一个半径为1cm的半球,所以其体积为V=3π-π=π(cm 3).22. 右图为一简单组合体，其底面ABCD 为正方形，PD ⊥平面ABCD ，EC ∥PD ，且PD ＝AD ＝2EC ＝2.(1)请画出该几何体的三视图； (2)求四棱锥B-CEPD 的体积．【答案】(1)见解析 (2)2【解析】解：(1)该组合体的三视图如图所示．(2)∵PD ⊥平面ABCD ， PD ⊂平面PDCE ，∴平面PDCE ⊥平面ABCD. ∵四边形ABCD 为正方形，∴BC ⊥CD ，且BC ＝DC ＝AD ＝2. 又∵平面PDCE∩平面ABCD ＝CD ， BC ⊂平面ABCD. ∴BC ⊥平面PDCE.∵PD ⊥平面ABCD ，DC ⊂平面ABCD ， ∴PD ⊥DC.又∵EC ∥PD ，PD ＝2，EC ＝1，∴四边形PDCE 为一个直角梯形，其面积： S 梯形PDCE ＝ (PD ＋EC)·DC ＝×3×2＝3， ∴四棱锥B-CEPD 的体积V B-CEPD ＝S 梯形PDCE ·BC ＝×3×2＝2.23. 某几何体的三视图如图所示，则该几何体的体积为( )．A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π【答案】A【解析】将三视图还原成直观图为：上面是一个正四棱柱，下面是半个圆柱体．所以V＝2×2×4＋×22×π×4＝16＋8π.24.某几何体的三视图如图所示，则其体积为________．【答案】【解析】由三视图还原几何体为半个圆锥，高为2，底面半圆的半径r＝1.∴体积V＝×(π×12×2)＝.25.如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形，俯视图为正方形，侧视图为直角三角形)．(1)求四棱锥P-ABCD的体积；(2)若G为BC上的动点，求证：AE⊥PG.【答案】（1）（2）见解析【解析】(1)由几何体的三视图可知，底面ABCD是边长为4的正方形，PA⊥平面ABCD，PA∥EB，且PA＝4 ，BE＝2 ，AB＝4.∴VP-ABCD ＝PA·S四边形ABCD＝×4 ×4×4＝.(2)∵＝，∠EBA＝∠BAP＝90°，∴△EBA∽△BAP，∴∠BEA＝∠PBA.∴∠BEA＋∠BAE＝∠PBA＋∠BAE＝90°，∴PB⊥AE又∵BC⊥平面APEB，∴BC⊥AE.∵BC∩PB＝B，∴AE⊥平面PBC.∵PG⊂平面PBC，∴AE⊥PG.26.如图所示，网格上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为________．【答案】9【解析】由题意知，此几何体是三棱锥，其高h＝3，相应底面面积为S＝×6×3＝9，∴V＝Sh＝×9×3＝9.27.某几何体的三视图如图所示，主视图和侧视图为全等的直角梯形，俯视图为直角三角形.则该几何体的表面积为( )A. B. C. D【答案】B【解析】此几何体直观图如图所示。

214 §8.1 空间几何体的结构及其三视图和直观图基础自测1.下列不正确的命题的序号是 . ①有两个面平行，其余各面都是四边形的几何体叫棱柱 ②有两个面平行，其余各面都是平行四边形的几何体叫棱柱 ③有一个面是多边形，其余各面都是三角形的几何体叫棱锥 ④有一个面是多边形，其余各面都是有一个公共顶点的三角形的几何体叫棱锥答案 ①②③2.如果圆锥的侧面展开图是半圆，那么这个圆锥的顶角（圆锥轴截面中两条母线的夹角）是 . 答案 60°3.如果一个几何体的三视图如图所示（单位长度：cm ），则此几何体的表面积是 cm 2.答案 (20+42) 4.（2008·宁夏文，14）一个六棱柱的底面是正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的高为3，底面周长为3，那么这个球的体积为 .答案 34 5.已知正三角形ABC 的边长为a,那么△ABC 的直观图△A ′B ′C ′的面积为 .答案 166a 2 例题精讲例1 下列结论不正确的是 （填序号）.①各个面都是三角形的几何体是三棱锥②以三角形的一条边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫圆锥 ③棱锥的侧棱长与底面多边形的边长相等，则此棱锥可能是六棱锥④圆锥的顶点与底面圆周上的任意一点的连线都是母线答案 ①②③解析 ①错误.如图所示，由两个结构相同的三棱锥叠放在一起构成的几何体，各面都是三角形，但它不一定是棱锥.②错误.如下图，若△ABC 不是直角三角形或是直角三角形,但旋转轴不是直角边，所得的几何体都不是圆锥.215③错误.若六棱锥的所有棱长都相等，则底面多边形是正六边形.由几何图形知，若以正六边形为底面，侧棱长必然要大于底面边长.④正确.例2 已知△ABC 的直观图A ′B ′C ′是边长为a 的正三角形，求原三角形ABC 的面积.解 建立如图所示的xOy 坐标系，△ABC 的顶点C 在y 轴上，AB 边在x 轴上，OC 为△ABC 的高，把y 轴绕原点顺时针旋转45°得y ′轴，则点C 变为点C ′，且OC=2OC ′，A 、B 点即为A ′、 B ′点，AB=A ′B ，已知A ′B ′=A ′C ′=a ，在△OA ′C ′中， 由正弦定理得''sin C OA OC ∠=ο45sin ''C A ，所以OC ′=a οο45sin 120sin =a 26, 所以原三角形ABC 的高OC=6a ，所以S △ABC =21×a ×6a=a 262. 例3 一个正三棱柱的三视图如图所示，求这个三棱柱的表面积和体积.解 由三视图易知，该正三棱柱的形状如图所示：且AA ′=BB ′=CC ′=4cm,正三角形ABC 和正三角形A ′B ′C ′的高为23cm.∴正三角形ABC 的边长为|AB|=ο60sin 32=4.∴该三棱柱的表面积为S=3×4×4+2×21×42sin60°=48+83(cm 2). 体积为V=S 底·|AA ′|=21×42sin60°×4=163(cm 3). 故这个三棱柱的表面积为（48+83）cm 2,体积为163cm 3.例4 棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图所示， 求图中三角形（正四面体的截面）的面积.解 如图所示，△ABE 为题中的三角形，由已知得AB=2，BE=2×23=3, BF=32BE=332,AF=22BF AB -=344-=38,∴△ABE 的面积为216 S=21×BE ×AF=21×3×38=2.∴所求的三角形的面积为2. 巩固练习1.如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下四个命题中为真命题的是 （填序号）.①等腰四棱锥的腰与底面所成的角都相等②等腰四棱锥的侧面与底面所成的二面角都相等或互补③等腰四棱锥的底面四边形必存在外接圆④等腰四棱锥的各顶点必在同一球面上答案 ①③④2.一个平面四边形的斜二测画法的直观图是一个边长为a 的正方形,则原平面四边形的面积等于 . 答案 22a 23.已知某几何体的俯视图是如图所示的矩形，正视图（或称主视图）是一个底边长为8、高为4的等 腰三角形，左视图（或称侧视图）是一个底边长为6、高为4的等腰三角形.（1）求该几何体的体积V ；（2）求该几何体的侧面积S.解 （1）由该几何体的俯视图、正视图、左视图可知，该几何体是四棱锥，且四棱锥的底面ABCD 是边长为6和8的矩形，高VO=4，O 点是AC 与BD 的交点. ∴该几何体的体积V=31×8×6×4=64. （2）如图所示，侧面VAB 中，VE ⊥AB ，则VE=22OE VO +=2234+=5∴S △VAB =21×AB ×VE=21×8×5=20 侧面VBC 中，VF ⊥BC ，则VF=22OF VO +=2244+=42.∴S △VBC =21×BC ×VF=21×6×42=122∴该几何体的侧面积 S=2（S △VAB +S △VBC ）=40+242.4.（2007·全国Ⅱ文，15）一个正四棱柱的各个顶点在一个直径为2 cm 的球面上.如果正四棱柱的底面边长为1 cm ，那么该棱柱的表面积为 cm 2.答案 2+42 回顾总结知识方法思想课后作业一、填空题1.利用斜二测画法可以得到：①三角形的直观图是三角形，②平行四边形的直观图是平行四边形，③正方形的直观图是正方形，④菱形的直观图是菱形，以上正确结论的序号是 .217答案 ①②2.如图所示，甲、乙、丙是三个几何体图形的三视图，甲、乙、丙对应的标号是 . ①长方体；②圆锥；③三棱锥；④圆柱. 答案④③②3.下列几何体各自的三视图中，有且仅有两个视图相同的是 .答案 ②④4.用若干个大小相同，棱长为1的正方体摆成一个立体模型，其三视图如下：根据三视图回答此立体模型的体积为 .答案 55.棱长为1的正方体ABCD —A 1B 1C 1D 1的8个顶点都在球O 的表面上，E 、F 分别是棱AA 1、DD 1的中点，则直线EF 被球O 截得的线段长为 .答案 26.（2008·湖北理）用与球心距离为1的平面去截球，所得的截面面积为π，则球的体积为 . 答案 328π 7.用小立方块搭一个几何体，使得它的正视图和俯视图如图所示，这样的几何体至少要 个小立方块.最多只能用 个小立方块.答案 9 148.如图所示，E 、F 分别是正方体的面ADD 1A 1、面BCC 1B 1的中心，则四边形BFD 1E 在该正方体的面上的正投影可能是 .（把可能的图的序号都填上）218答案 ②③二、解答题9.正四棱台AC 1的高是17 cm ，两底面的边长分别是4 cm 和16 cm ，求这个棱台的侧棱长和斜高. 解 如图所示，设棱台的两底面的中心分别是O 1、O ，B 1C 1和BC 的中点分别是E 1和E ，连接O 1O 、E 1E 、O 1B 1、OB 、O 1E 1、OE ，则四边形OBB 1O 1和OEE 1O 1都是直角梯形.∵A 1B 1=4 cm ，AB=16 cm ， ∴O 1E 1=2 cm ，OE=8 cm ，O 1B 1=22 cm ，OB=82 cm ，∴B 1B 2=O 1O 2+（OB-O 1B 1)2=361 cm 2，E 1E 2=O 1O 2+（OE-O 1E 1)2=325 cm 2，∴B 1B=19 cm ，E 1E=513cm.答 这个棱台的侧棱长为19 cm ，斜高为513cm.10.圆台的一个底面周长是另一个底面周长的3倍，轴截面的面积等于392 cm 2,母线与轴的夹角是45°，求这个圆台的高、母线长和两底面半径.解 圆台的轴截面如图所示，设圆台上下底面半径分别为x cm,3x cm.延长AA 1交OO 1的延长线于S ， 在Rt △SOA 中，∠ASO=45°, 则∠SAO=45°，∴SO=AO=3x ，∴OO 1=2x ，又S 轴截面=21（6x+2x ）·2x=392，∴x=7. 故圆台的高OO 1=14 (cm)，母线长l=2O 1O=142 (cm)，两底面半径分别为7 cm,21 cm.11.正四棱锥的高为3，侧棱长为7，求侧面上斜高（棱锥侧面三角形的高）为多少？解 如图所示，正棱锥S-ABCD 中高OS=3，侧棱SA=SB=SC=SD=7，在Rt △SOA 中， OA=22OS SA =2，∴AC=4.∴AB=BC=CD=DA=22.作OE ⊥AB 于E ，则E 为AB 中点.连接SE ，则SE 即为斜高，则SO ⊥OE.在Rt △SOE 中，∵OE=21BC=2，SO=3，∴SE=5，即侧面上的斜高为5.12. 如图所示的几何体中，四边形AA 1B 1B 是边长为3的正方形，CC 1=2，CC 1∥AA 1，这个几何体是棱柱吗？若是，指出是几棱柱.若不是棱柱，请你试用一个平面截去一部分，使剩余部分是一个棱长为2的三棱柱，并指出截去的几何体的特征，在立体图中画出截面.解 这个几何体不是棱柱；在四边形ABB 1A 1中，在AA 1上取点E ，使AE=2；在BB 1上取F 使BF=2；连接C 1E ，EF ，C 1F ，则过C 1EF 的截面将几何体分成两部分，其中一部分是棱柱ABC —EFC 1，其棱长为2；截去的部分是一个四棱锥C1—EA1B1F.219。

§8.1 空间几何体的三视图、直观图、表面积与体积第1讲空间几何体的结构、三视图和直观图考纲考情1.能画出柱、锥、台、球等简易组合体的三视图，并能识别三视图所表示的立体模型．会用斜二测画法画出它们的直观图．2.了解平行投影与中心投影，了解空间图形的不同表示形式．主干知识·整合知识点一空间几何体的结构特征1．多面体(1)棱柱的侧棱都________，上下底面是______且______的多边形．(2)棱锥的底面是任意多边形，侧面是有一个________的三角形．(3)棱台可由________________的平面截棱锥得到，其上下底面是________且_____的多边形．2．旋转体(1)圆柱可以由______绕其任一边旋转得到．(2)圆锥可以由直角三角形绕其__________________旋转得到．(3)圆台可以由直角梯形绕直角腰或等腰梯形绕上下底中点连线旋转得到，也可由______于圆锥底面的平面截圆锥得到．(4)球可以由半圆或圆绕____________旋转得到．对点快练1．下列说法正确的是()A．有两个平面互相平行，其余各面都是平行四边形的多面体是棱柱B．四棱锥的四个侧面都可以是直角三角形C．有两个平面互相平行，其余各面都是梯形的多面体是棱台D．棱台的各侧棱延长后不一定交于一点2．下图所示的几何体中，是棱柱的为________(填写所有正确的序号)．知识点二空间几何体的三视图1．三视图的名称几何体的三视图包括________、________、________.2．三视图的画法(1)画三视图时，重叠的线只画一条，挡住的线要画成虚线．(2)三视图的正视图、侧视图、俯视图分别是从几何体的______方、______方、______方观察几何体得到的正投影图．对点快练3．将一个长方体沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧(左)视图为()4．如图所示，图①②③是图④所示的几何体的三视图，若图①是正视图，则图②是________，图③是________．知识点三空间几何体的直观图空间几何体的直观图常用________画法来画，其规则是：1．原图形中x轴、y轴、z轴两两垂直，直观图中，x′轴、y′轴的夹角为____，z′轴与x′轴和y′轴所在平面______．2．原图形中平行于坐标轴的线段，直观图中仍分别____________．平行于x轴和z轴的线段在直观图中保持原长度________，平行于y轴的线段在直观图中长度变为__________．对点快练5．用斜二测画法画一个水平放置的水平图形的直观图为如图所示的一个正方形，则原来的图形是()热点命题·突破热点一空间几何体的结构特征例1给出下列命题：①棱柱的侧棱都相等，侧面都是全等的平行四边形；②若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直；③在四棱柱中，若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱；④存在每个面都是直角三角形的四面体；⑤棱台的侧棱延长后交于一点．其中正确命题的序号是________．变式训练给出下列命题：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线；②有一个面是多边形，其余各面都是三角形的几何体是棱锥；③直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥；④棱台的上、下底面可以不相似，但侧棱长一定相等．其中正确命题的个数是()A．0 B．1C．2 D．3热点二空间几何体的三视图考向1由直观图判断三视图例2如图所示，四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形，起辅助作用)，则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)()A．①②⑥B．①②③C．④⑤⑥D．③④⑤考向2由三视图还原直观图例3某三棱锥的三视图如图所示，则该三棱锥的体积为()A. 16 B.13 C.12D．1考向3由部分视图确定剩余视图例4已知某组合体的正视图与侧视图相同，如图所示，其中AB＝AC，四边形BCDE为矩形，则该组合体的俯视图可以是________(把你认为正确的图的序号都填上)．总结反思三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图．注意正视图、侧视图和俯视图的观察方向，注意看到的部分用实线表示，不能看到的部分用虚线表示．(2)由几何体的部分视图画出剩余的部分视图．先根据已知的一部分三视图，还原、推测直观图的可能形式，然后再找其剩下部分三视图的可能形式．当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是否符合．(3)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图.变式训练(1)如图，在正四棱柱ABCD－A1B1C1D1中，点P是平面A1B1C1D1内一点，则三棱锥P－BCD 的正视图与侧视图的面积之比为()A．1 1 B．21C．2 3 D．32(2)一个锥体的正视图和侧视图如图所示，下面选项中，不可能是该锥体的俯视图的是()(3)已知三棱锥的四个面都是腰长为2的等腰三角形，该三棱锥的正视图如图所示，则该三棱锥的体积是________．热点三空间几何体的直观图例5如图所示，四边形A′B′C′D′是一平面图形的水平放置的斜二测画法的直观图，在斜二测直观图中，四边形A′B′C′D′是一直角梯形，A′B′∥C′D′，A′D′⊥C′D′，且B′C′与y′轴平行，若A′B′＝6，D′C′＝4，A′D′＝2.求这个平面图形的实际面积．变式训练已知平面△ABC的直观图A′B′C′是边长为a的正三角形，求原△ABC的面积．课堂总结1．对于基本概念和能用公式直接求棱柱、棱锥、棱台与球的表面积的问题，要结合它们的结构特点与平面几何知识来解决，这种题目难度不大．2．在绘制三视图时，若相邻两物体的表面相交，表面的交线是它们的分界线．在三视图中，分界线和可见轮廓线都用实线画出，被挡住的轮廓线画成虚线．并做到“长对正、高平齐、宽相等”．3．能够由空间几何体的三视图得到它的直观图；也能够由空间几何体的直观图得到它的三视图．提升空间想象能力．参考答案主干知识·整合知识点一空间几何体的结构特征1．(1)互相平行互相平行全等(2)公共顶点(3)平行于棱锥底面相互平行相似2．(1)矩形(2)一条直角边所在直线(3)平行(4)直径所在直线对点快练1．【答案】B【解析】A错，如图1；B正确，如图2，其中底面ABCD是矩形，可证明∠P AB，∠PCB 都是直角，这样四个侧面都是直角三角形；C错，如图3；D错，由棱台的定义知，其侧棱必相交于同一点．2．【答案】③⑤【解析】根据棱柱的结构特征可知③⑤是棱柱．知识点二空间几何体的三视图1．正视图侧视图俯视图2．(2)正前正左正上对点快练3．【答案】B【解析】由正视图、俯视图得原几何体的形状如图所示，则该几何体的侧视图为B.4．【答案】侧视图俯视图【解析】根据三视图的概念知图②是侧视图，图③是俯视图．知识点三空间几何体的直观图斜二测1. 45°或135°垂直2. 平行于坐标轴不变原来的一半对点快练5．【答案】A【解析】由直观图的画法可知，落在y轴上的对角线的长度为2 2.热点命题·突破热点一空间几何体的结构特征例1【答案】②③④⑤【解析】①不正确，根据棱柱的定义，棱柱的各个侧面都是平行四边形，但不一定全等；②正确，若三棱锥的三条侧棱两两垂直，则三个侧面构成的三个平面的二面角都是直二面角；③正确，因为两个过相对侧棱的截面的交线平行于侧棱，又垂直于底面；④正确，如图，正方体AC 1中的三棱锥C 1－ABC ，四个面都是直角三角形；⑤正确，由棱台的概念可知．变式训练 【答案】A【解析】①不一定，只有当这两点的连线平行于轴时才是母线；②不一定，因为“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”，如图1所示；③不一定，当以斜边所在直线为旋转轴时，其余两边旋转形成的面所围成的几何体不是圆锥，如图2所示，它是由两个同底圆锥组成的几何体；④错误，棱台的上、下底面相似且是对应边平行的多边形，各侧棱延长线交于一点，但是侧棱长不一定相等．例2 【答案】 B【解析】 正视图应该是边长为3和4的矩形，其对角线左下到右上是实线，左上到右下是虚线，因此正视图是①；侧视图应该是边长为5和4的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此侧视图是②；俯视图应该是边长为3和5的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此俯视图是③. 例3 【答案】 A【解析】 由三视图可得该几何体的直观图为三棱锥A －BCD ，将其放在长方体中如图所示，其中BD ＝CD ＝1，CD ⊥BD ，三棱锥的高为1，所以三棱锥的体积为13×12×1×1×1＝16.故选A .例4 【答案】 ①②③④【解析】 直观图如图1的几何体(上部是一个正四棱锥，下部是一个正四棱柱)的俯视图为①；直观图如图2的几何体(上部是一个正四棱锥，下部是一个圆柱)的俯视图为②；直观图如图3的几何体(上部是一个圆锥，下部是一个圆柱)的俯视图为③；直观图如图4的几何体(上部是一个圆锥，下部是一个正四棱柱)的俯视图为④.变式训练【答案】(1)A (2)C (3)33【解析】(1)根据题意，三棱锥P －BCD 的正视图是三角形，且底边为正四棱柱的底面边长、高为正四棱柱的高；侧视图是三角形，且底边为正四棱柱的底面边长、高为正四棱柱的高，故三棱锥P －BCD 的正视图与侧视图的面积之比为11.(2)A ，B ，D 选项满足三视图作法规则，C 不满足三视图作法规则中的宽相等，故C 不可能是该锥体的俯视图．(3)由正视图知，底面三角形是腰长为2，底边为23的等腰三角形，三棱锥的高为1，所以该三棱锥的体积V ＝13×(12×23×1)×1＝33.例5 解：根据斜二测直观图画法规则可知该平面图形是直角梯形，且AB ＝6，CD ＝4保持不变． 由于C ′B ′＝2A ′D ′＝2 2.所以CB ＝4 2. 故平面图形的实际面积为12×(6＋4)×42＝20 2.变式训练 解：如图所示，△A ′B ′C ′是边长为a 的正三角形，作C ′D ′∥A ′B ′交y ′轴于点D ′，则D ′到x ′轴的距离为32a ，∵∠D ′A ′B ′＝45°，∴A ′D ′＝62a ， 由斜二测画法的法则知，在△ABC 中，AB ＝A ′B ′＝a ，AB 边上的高是A ′D ′的二倍，即为6a ，∴S △ABC ＝12a ·6a ＝62a 2.。

高三数学空间几何体的三视图与直观图试题答案及解析1.已知某锥体的三视图（单位：cm）如图所示，则该锥体的体积为．【答案】２．【解析】由已知几何体的视图可知，几何体为四棱锥，其中SA垂直于平面ABCD，SA=2，四边形ABCD为直角梯形，AD=1，BC=2，AB=2，所以四棱锥的体积为【考点】三视图求几何体的体积.2.右图为某几何体的三视图，则该几何体的体积为【答案】【解析】由三视图知，该几何体是底面半径为1，高为1的圆柱与半径为1的球体组成的组合体，其体积为=．【考点】简单几何体的三视图，圆柱的体积公式，球的体积公式3.一个几何体的三视图及尺寸如图所示，则该几何体的外接球半径为（）A．B．C．D．【答案】C【解析】由三视图可知：该几何体是一个如图所示的三棱锥P-ABC，它是一个正四棱锥P-ABCD 的一半，其中底面是一个两直角边都为6的直角三角形，高PE=4．设其外接球的球心为O，O点必在高线PE上，外接球半径为R，则在直角三角形BOE中，BO2=OE2+BE2=（PE-EO）2+BE2，即R2=（4-R）2+（3）2，解得：R=，故选C.【考点】三视图，球与多面体的切接问题，空间想象能力4.如图是一个几何体的三视图，则该几何体的表面积是____________【答案】28＋12【解析】这是一个侧放的直三棱柱，底面是等腰直角三角形，侧棱长为6故表面积为2×(×2×2)＋(2＋2＋2)×6＝28＋12.【考点】三视图，几何体的表面积.5.在长方体中割去两个小长方体后的几何体的三视图如图，则切割掉的两个小长方体的体积之和等于.【答案】24【解析】由题意割去的两个小长方体的体积为.【考点】三视图，几何体的体积..6.某空间几何体的正视图是三角形，则该几何体不可能是（）圆柱圆锥四面体三棱柱【答案】A【解析】由于圆柱的三视图不可能是三角形所以选A.【考点】三视图.7.某几何体的三视图如图所示，其中正视图是腰长为2的等腰三角形，侧视图是半径为1的半圆，则该几何体的表面积是________．【答案】2(π＋)【解析】由三视图可知此几何体的表面积分为两部分：底面积即俯视图的面积为2；侧面积为一个完整的圆锥的侧面积，且圆锥的母线长为2，底面半径为1，所以侧面积为2π．两部分加起来即为几何体的表面积，为2(π＋)．8.一个锥体的主(正)视图和左(侧)视图如图所示，下面选项中，不可能是该锥体的俯视图的是()【答案】C【解析】俯视图是选项C的锥体的正视图不可能是直角三角形．另外直观图如图1的三棱锥(OP⊥面OEF，OE⊥EF，OP＝OE＝EF＝1)的俯视图是选项A，直观图如图2的三棱锥(其中OP，OE，OF两两垂直，且长度都是1)的俯视图是选项B，直观图如图3的四棱锥(其中OP⊥平面OEGF，底面是边长为1的正方形，OP＝1)的俯视图是选项D．9.如图所示，正方形O′A′B′C′的边长为1，它是水平放置的一个平面图形的直观图，则原图形的周长是()A．6B．8C．2＋3D．2＋2【答案】B【解析】如图，OB＝2，OA＝1，则AB＝3．∴周长为8．10.某几何体的三视图如图所示，且该几何体的体积是2，则正(主)视图的面积等于()A．2B．C．D．3【答案】A【解析】由三视图可知该几何体是一个四棱锥，其底面积就是俯视图的面积S＝(1＋2)×2＝3，其高就是正(主)视图以及侧(左)视图的高x，因此有×3×x＝2，解得x＝2，于是正(主)视图的面积S＝×2×2＝2．11.如图，三棱柱的侧棱长和底边长均为2，且侧棱AA1⊥底面A1B1C1，正视图是边长为2的正方形，俯视图为一个等边三角形，则该三棱柱的侧视图的面积为( )A. C.4 D.【答案】A【解析】侧视图也为矩形，底宽为原底等边三角形的高，侧视图的高为侧棱长，所以侧视图的面积为,故选B.【考点】三视图12.一个几何体的三视图如图所示，则该几何体内切球的体积为 .【答案】【解析】依题意可得该几何体是一个正三棱柱，底面边长为2，高为.由球的对称性可得内切球的半径为.由已知计算得底面内切圆的半径也为.所以内切球的体积为.【考点】1.三视图.2.几何体内切球的对称性.3.球的体积公式.4.空间想象力.13.已知一个正三棱柱的所有棱长均等于2，它的俯视图是一个边长为2的正三角形，那么它的左视图面积的最小值是________．【答案】【解析】如图，正三棱柱中，分别是的中点，则当面与侧面平行时，左视图面积最小，且面积为.【考点】三视图.14.某几何体的三视图如图3所示，则其体积为________．【答案】【解析】原几何体可视为圆锥的一半，其底面半径为1，高为2，∴其体积为×π×12×2×＝.15.已知正△ABC的边长为2，那么用斜二测画法得到的△ABC的直观图△A′B′C′的面积为（）A．B．C．D．【答案】D【解析】∵正△ABC的边长为2，故正△ABC的面积S==设△ABC的直观图△A′B′C′的面积为S′则S′=S=•=故选D16.一个体积为12的正三棱柱的三视图如图所示，则这个三棱柱的侧视图的面积为（）A．B．C．D．【答案】A【解析】依题意可得三棱柱的底面是边长为4正三角形.又由体积为.所以可得三棱柱的高为3.所以侧面积为.故选A.【考点】1.三视图的知识.2.棱柱的体积公式.3.空间想象力.17.某几何体的三视图如题（6）所示，其侧视图是一个边长为1的等边三角形，俯视图是两个正三角形拼成的菱形，则这个几何体的体积为（）A．1B．C．D．【答案】C【解析】这是由两个三棱锥拼成的几何体，其体积为.选C.【考点】三视图及几何体的体积.18.一个四面体的顶点在空间直角坐系O－xyz中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx平面为投影面，则得到的正视图可以为（）A．B．C．D．【答案】A【解析】设O(0，0，0)，A(1，0，1)，B(1，1，0)，C(0，1，1)，将以O，A，B，C为顶点的四面体补成一正方体后，因为OA⊥BC，所以补成的几何体以zOx平面为投影面的正视图为A．19.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几体的体积为（）A．6B．9C．12D．18【答案】B【解析】由三视图可知，此几何体为如图所示的三棱锥，其底面△ABC为等腰三角形且AB=BC，AC=6，AC边上的高为3，SB⊥底面ABC，且SB=3，因此此几体的体积为V=××6×3×3=920.如图所示，一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的表面积为 .【答案】【解析】由三视图知，该几何体是一个圆柱，其表面积为.【考点】三视图及几何体的表面积.21.在三棱锥中，，平面ABC,.若其主视图，俯视图如图所示，则其左视图的面积为【答案】【解析】左视图是一个直角三角形，其直角边分别是2与.所以面积为.【考点】1.三视图知识.2.三角形面积的计算.22.一个几何体的三视图如图所示,则这个几何体的体积是_________.【答案】【解析】由三视图还原几何体，该几何体为底面半径为，高为的圆柱，去掉底面半径为，高为的圆锥的剩余部分，则其体积为．【考点】1、三视图；2、几何体的体积.23.棱长为2的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是( ).A．B．4C．D．3【答案】B【解析】如图，红色虚线表示截面，可见这个截面将正方体分为完全相同的两个几何体，则所求几何体的体积即是原正方体的体积的一半，.【考点】1.三视图；2.正方体的体积24.如图，一个四棱锥的底面为正方形，其三视图如图所示，则这个四棱锥的体积为（）A．1B．2C．3D．4【答案】Ｂ【解析】由题设及图知，此几何体为一个四棱锥，其底面为一个对角线长为的正方形，故其底面积为，由三视图知其中一个侧棱为棱锥的高，其相对的侧棱与高及底面正方形的对角线组成一个直角三角形，由于此侧棱长为，对角线长为，故棱锥的高为，此棱锥的体积为，故选B．【考点】由三视图求面积、体积．25.已知某几何体的三视图如右图所示，其中，正视图，侧视图均是由三角形与半圆构成，俯视图由圆与内接三角形构成，根据图中的数据可得此几何体的体积为（）A．B．C．D．【答案】C【解析】由已知的三视图可知原几何体是上方是三棱锥,下方是半球,∴，故选C.【考点】1.三视图；2.几何体的体积.26.如图是一个组合几何体的三视图,则该几何体的体积是.【答案】36+128π【解析】由三视图还原可知该几何体是一个组合体,下面是一个圆柱,上面是一个三棱柱,故所求体积为V=×3×4×6+16π×8=36+128π.27.某几何体的三视图如图所示，其中俯视图为扇形，则该几何体的体积为（）A．B．C．D．【答案】D【解析】由三视图可知，该几何体是三分之一个圆锥，其体积为.【考点】三视图及几何体的体积.28.某几何体的三视图(图中单位：cm)如图所示，则此几何体的体积是()A．36 cm3B．48 cm3C．60 cm3D．72 cm3【答案】B【解析】由三视图可知几何体上方是一长方体，下方是一放倒的直四棱柱，且四棱柱底面是等腰梯形，上底长为2 cm，下底长为6 cm，高为2 cm，故几何体的体积是2×2×4＋×(2＋6)×2×4＝48(cm3)，故选B.29.如图是某三棱柱被削去一个底面后的直观图、侧(左)视图与俯视图．已知CF＝2AD，侧视图是边长为2的等边三角形，俯视图是直角梯形，有关数据如图所示．求该几何体的体积．【答案】3【解析】解：取CF中点P，过P作PQ∥CB交BE于Q，连接PD，QD，则AD∥CP，且AD＝CP.所以四边形ACPD为平行四边形，所以AC∥PD.所以平面PDQ∥平面ABC.该几何体可分割成三棱柱PDQ－CAB和四棱锥D－PQEF，所以V＝V－CAB＋V D－PQEFPDQ＝×22sin 60°×2＋××＝3.30.一个几何体的三视图如图所示，则该几何体的表面积是()A．6＋8B．12＋7C．12＋8D．18＋2【答案】C【解析】该空间几何体是一个三棱柱．底面为等腰三角形且底面三角形的高是1，底边长是2 ，两个底面三角形的面积之和是2，侧面积是(2＋2＋2)×3＝12＋6，故其表面积是12＋8.31. 已知四棱锥P-ABCD 的三视图如右图所示，则四棱锥P-ABCD 的四个侧面中的最大面积是( )．A ．6B ．8C ．2D ．3【答案】A【解析】四棱锥如图所示：PM ＝3，S △PDC ＝×4×＝2，S △PBC ＝S △PAD ＝×2×3＝3，S △PAB ＝×4×3＝6，所以四棱锥P-ABCD 的四个侧面中的最大面积是6.32. 若某几何体的三视图如图所示，则这个几何体的直观图可以是( )．【答案】B【解析】分别从三视图中去验证、排除．由正视图可知，A 不正确；由俯视图可知，C ，D 不正确，所以选B.33. 一个几何体的三视图如图所示，已知这个几何体的体积为，则h________.【答案】【解析】依题意可得四棱锥的体积为.所以可得.解得.故填.本小题的是常见的立几中的三视图的题型，这类题型关键是要能还原几何体的直观图形.所以培养空间的思想很重要.【考点】1.三视图的识别.2.空间几何体的直观图.34.图中的网格纸是边长为的小正方形，在其上用粗线画出了一四棱锥的三视图，则该四棱锥的体积为（）A．B．C．D．【答案】C【解析】由三视图知，该几何体是一个四棱锥，且其底面为一个矩形，底面积，高为，故该几何体的体积，故选C.【考点】1.三视图；2.锥体的体积35.已知某几何体的三视图如图，其中主视图中半圆直径为2，则该几何体的体积____________【答案】24-【解析】由三视图可知，该几何体是有长方体里面挖了一个半圆柱体，可知，长方体的长为4，宽为3，高为2，那么圆柱体的高位3，底面的半径为1，则可知该几何体的体积为，故答案为．【考点】由三视图求面积、体积．36.把边长为的正方形沿对角线折起，连结，得到三棱锥，其正视图、俯视图均为全等的等腰直角三角形（如图所示），则其侧视图的面积为（）A．B．C．D．【答案】B【解析】在三棱锥中，在平面上的射影为的中点，∵正方形边长为，∴，∴侧视图的面积为.【考点】1.三视图；2.三角形的面积.37.一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的（）A．外接球的半径为B．体积为C．表面积为D．外接球的表面积为【答案】D．【解析】由题意设外接球半径为，则，A错误；外接球的表面积为，D正确；此几何体的体积为，故B错误；此几何体的表面积为，C错误．【考点】三视图及球的表面积公式.38.一个几何体的三视图如图所示，则该几何体的体积为( )A．4B．8C．D．【答案】B【解析】有三视图可以看出，该几何体是一个三棱锥，它的体积为．【考点】三视图，几何体的体积．39.如图，直三棱柱的侧棱长和底面边长均为2，正视图和俯视图如图所示，则其侧视图的面积为（）A．B．C．4D．2【答案】A【解析】由题意易知，直三棱柱的底面是边长为2的正三角形.其侧视图为矩形，矩形的高为2，宽为底面正三角形的高.易知边长为2的正三角形的高为.所以面积为.【考点】三视图40.如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是( )A．B．21C．D．24【答案】A【解析】还原几何体，得棱长为2的正方体和高为1的正四棱锥构成的简单组合体，如图所示，=，选A.【考点】1、几何体的表面积；2、三视图.41.某几何体的三视图如图所示，则它的表面积为（）A．B．C．D．【答案】A【解析】易知该三视图的直观图是倒立的半个三棱锥，其表面积由底面半圆，侧面三角形和侧面扇形，所以，故选A.【考点】1.立体几何三视图；2.表面积和体积的求法.42.一几何体的三视图如图所示，则该几何体的体积为（）A．200＋9πB．200＋18πC．140＋9πD．140＋18π【答案】A【解析】通过观察三视图，易知该几何体是由半个圆柱和长方体组成的，则半个圆柱体积；长方体的体积为,所以该几何体的最终体积，故选A.【考点】1.三视图的应用；2.简单几何体体积的求解.43.一个几何体的三视图如图所示，其中主视图和左视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为( )A．B．C．D．【解析】把原来的几何体补成以为长、宽、高的长方体，原几何体四棱锥与长方体是同一个外接球，，，.【考点】1.补体法；2.几何体与外接球之间的元素换算.44.一个几何体的三视图如图所示，其中府视图为正三角形，则侧视图的面积为（）A．8B．C．D．4【答案】B【解析】由三视图可知：该几何体是一个正三棱柱，高为4，底面是一个边长为2的正三角形．因此，侧视图是一个长为４，宽为的矩形，．【考点】三视图与几何体的关系、几何体的侧面积的求法能力．45.某几何体的三视图如图所示，则它的侧面积为（）A．B．C．24D．【答案】A【解析】由三视图得,这是一个正四棱台,由条件，侧面积.【考点】1.三视图；2.正棱台侧面积的求法.46.一个几何体的三视图如图所示，其中正视图与侧视图都是底边长为6、腰长为5的等腰三角形，则这个几何体的全面积为（）A．B．C．D．【解析】由三视图知，该几何体是一个圆锥，且圆锥的底面直径为，母线长为，用表示圆锥的底面半径，表示圆锥的母线长，则，，故该圆锥的全面积为.【考点】三视图、圆锥的表面积47.一个空间几何体的三视图如右图所示，其中主视图和侧视图都是半径为的圆，且这个几何体是球体的一部分，则这个几何体的表面积为( )A．3πB．4πC．6πD．8π【答案】B【解析】此空间几何体是球体切去四分之一的体积，表面积是四分之三的球表面积加上切面面积，切面面积是两个半圆面面积.故这个几何体的表面积是.【考点】1、几何体的三视图; 2、球的表面积公式.48.右图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为和，腰长为的等腰梯形，则该几何体的表面积是．【答案】【解析】从三视图可以看出：几何体是一个圆台，上底面是一个直径为4的圆，下底面是一个直径为2的圆，侧棱长为4．上底面积，下底面积，侧面是一个扇环形，面积为，所以表面积为．【考点】空间几何体的三视图、表面积的计算．49.某零件的正（主）视图与侧（左）视图均是如图所示的图形（实线组成半径为的半圆，虚线是等腰三角形的两腰），俯视图是一个半径为的圆（包括圆心），则该零件的体积是 ( )A．B．C．D．【解析】由题意易知该几何体为一半球内部挖去一圆锥所成，故体积为.故选C.【考点】1.体积； 2.三视图.50.某四棱台的三视图如图所示,则该四棱台的体积是 ( )A．B．C．D．【答案】B【解析】由三视图可知,该四棱台的上下底面边长分别为和的正方形,高为,故,故选B．【考点】三视图与四棱台的体积51.若一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为（）A．B．C．D．【答案】B【解析】由已知底面是正三角形的三棱柱的正视图,我们可得该三棱柱的底面棱长为2，高为1,则底面外接圆半径，球心到底面的球心距,则球半径,则该球的表面积，故选B.【考点】由三视图求面积、体积．点评：本题考查的知识点是由三视图求表面积，其中根据截面圆半径、球心距、球半径满足勾股定理计算球的半径，是解答本题的关键．52.如图所示是某一容器的三视图，现向容器中匀速注水，容器中水面的高度随时间变化的可能图像是（）A． B． C． D．【答案】B【解析】由三视图可知该几何体是圆锥，顶点在下，底面圆在上，在匀速注水过程中水面高度随着时间的增大而增大，且刚开始时截面积较小，所以高度变化较快，随着水面的升高，截面圆面积增大，高度变化速度减缓，因此函数的瞬时变化率逐渐减小，导数减小，图像为B项【考点】函数导数的定义点评：本题通过高度的瞬时变化率的变化情况得到函数的导数的大小，从而通过做出的切线斜率的变化得出正确图像53.已知一个三棱锥的主视图与俯视图如图所示，则该三棱锥的侧视图面积为（）A．B．C．D．【答案】B【解析】根据题意，由于三棱锥的俯视图为直角三角形，正视图为直角三角形，且斜边长为2，直角边长为，那么结合图像可知其侧视图为底面边长为1，高为的三角形，因此其面积为，故选B.【考点】三棱锥点评：解决的关键是根据三棱锥的三视图来得到底面积和高进而求解侧视图，属于基础题。