2016-2017郑州期末考试题(1)

2016—2017学年度郑州市上期期末考试高一英语参考答案一、选择题（1-60）：1.C2.B3.B4.A5.C6.A7.B8.C9.A 10.C 11.C 12.B 13.A 14.C 15.C 16.B 17.B 18.C 19.B 20.A 21.A 22.C 23.D 24.B 25.C 26.A 27.D 28.B 29.D 30.B 31.C 32.B 33.D 34.A 35.C 36.A 37.C 38.G 39.D 40.E 41.C 42.D 43.B 44.A 45.B 46.A 47.C 48.D 49.B 50.C 51.D 52.A 53.D 54.C 55.A 56.B57.C 58.B 59.A 60.D二、英语知识运用第二节（61-70）：61. successful 62. where/that 63. days 64. gradually 65. myself66. but 67. in 68. to learn 69. that/and 70. have reached三、短文改错：Hello Tina,I’m very pleased to know you were coming to visit us here in China. I know you are reallyareinteresting in animals, so I suggest that we visit Chengdu, a beautiful and attractively city in interested attractive Sichuan Province. We can see pandas in the park near of Chengdu. We can also visit Du Fu’sThatched Cottage (Du Fu Caotang), that is one of my favourite places. Du Fu was one of a mostwhich the famous poets (诗人) in Chinese history. He lived there for several year. After he died, it becomes ayears became place for people to remember him. It is a traditional Chinese garden as well ∧a beautiful andasquiet place, excellent for reading and thought.thinkingI hope you like my suggestions.Love,Weiwei（注：第4处错误，若把of改为to亦可。

郑州市2016-2017学年下期期末考试七年级数学试题卷注意:本试卷分试题卷和答题卡两部分，考试时间90分钟，满分100分，考生应首先阅读答题卡上的文字信息，然后在答题卡上作答，在试题卷上作答无效，交卷时只交答题卡。

一、选择题（每小题3分，共30分）1.以下是回收、绿色包装、节水、低碳四个标志，其中是轴对称图形的是2.下列计算正确的是A ()222242y xy x y x ++=+ B ()73482x x = C 32622x x x -=÷- D ()()()32y x x y y x -=--3.如图，下列条件中，不能判断直线1l ∥2l 的是A ∠1=∠3B ∠2=∠3C ∠4=∠5D ∠2+∠4=180°4.下列事件中，属于不确定事件的是A 在△ABC 中，∠A+∠B+∠C=180°B 如果a 、b 为有理数，那么a+b=b+aC 两个负数的和是正数D 若∠a=∠B ，则∠a 和∠B 是一对对顶角5.如图，在折纸活动中，聪聪制作了一张△ABC 纸片，点D 、E 分别在边AB 、AC 上，将△ABC 沿着DE 折叠压平，A 与A 重合，若∠A=65°，则∠1+∠2=A 120°B 130°C 105°D 75°6.小茗同学骑自行车去上学，一开始以某一速度匀速行进，途中车子发生故障，只好停下来修车，车修好后，因怕耽误上课时间，于是加快车速.如图所示的四个图象中(S 表示距离，t 表示时间)符合以上情况的图象是7.如图，一扇窗户打开后，用窗钩AB 可将其固定，这里所运用的几何原理是A 三角形的稳定性B 两点之间线段最短C 两点确定一条直线D 垂线段最短8.如图，在一个等边三角形纸片中取三边的中点，以虚线为折痕折叠纸片，图中阴影部 分的面积是整个图形面积的 A 41 B 31 C 32 D 83 9.两个正方形的面积分别为25，16，两阴影部分的面积分别为a ，b(a>b)，则b a 等于A 9B 8C 7D 610. 如图，锐角△ABC 中，D 、E 分别是AB 、AC 边上的点，△ADC ≌△ADC ，△AEB ≌△AEB ′，且CD ∥EB'∥BC ，BE 、CD 交于点F ，若∠BAC=36°，则∠BFC 的大小是A 106°B 108C 110°D 112°二、填空题（每小题3分，共15分）11.英国两位物理学家安德烈和康斯坦丁成功地从石墨中分离出石墨烯，荣获了诺贝尔物理学奖.石墨烯目前是世界上最薄也是最坚硬的纳米材料，同时还是导电性最好的材料，其理论厚度仅0.00000000034米，将0.00000000034用科学记数法可表示为12.已知∠A=35°，则∠A 的余角的3倍是13.一只蚂蚁在如图所示的七巧板上任意爬行，已知它停在这副七巧板上的任何一点的可能性都相同，那么它停在3号板上的概率是14.任意写下一个三位数(三位数字都不相同).重新排列各位数字，使其组成一个最大的数和一个最小的数，然后用最大的数减去最小的数，得到差.不断重复这个过程，最后一定会得到相同的结果，这个结果是15.若m+n=17，mn=70，则m-n=三、解答题(本大题共7个小题，共55分)16.(6分)先化简，再求值[(x+2y)2-(x+y)(3x-y)-5y 2]÷(2x)，其中32-=x17.(7分)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有两个格点A 、B 和直线l 。

2016-2017学年上期期末考试高二数学（理）试题卷第I 卷（选择题，共60分）一、选择题（本大题共12个小题，每题5分，共60分. 在每个小题所给出的四个选项中，只有一项是符合题目要求的） 1. 不等式11x>的解集为（ ） A. (),1-∞ B. ()01， C. ()1+∞， D. ()0+∞， 2. a b >的一个充分不必要条件是（ ） A. 1,0a b == B.11a b< C. 22a b > D. 33a b > 3. ABC ∆中，若1,2,cos a b A ===，则sin B =（ ）A.B. 13C. D.234. 等比数列{}n a 中，243520,40a a a a +=+=，则6a =（ ）A. 16B. 32C. 64D. 1285. 两座灯塔A 和B 与海洋观测站C 的距离分别是km a 和2km a ，灯塔A 在观测站C 的北偏东20︒，灯塔B 在观测站C 的南偏东40︒，则灯塔A 与灯塔B 之间的距离为（ ）A.km B. 2km aC. kmD. km6. 在正方体1111ABCD A BC D -中，点,E F 满足11113,3A E EB C F FD ==，则BE 与DF 所成角的正弦值为（ ） A.817 B. 917 C. 1217 D. 15177. 等差数列{}n a 的前n 项和为n S ，若10091a =，则2017S =（ ）A. 1008B. 1009C. 2016D. 2017 8. 过24y x =的焦点作直线交抛物线于,A B 两点，若O 为坐标原点，则OA OB ⋅=（ ） A. 1- B. 2- C. 3- D. 4-9. 设椭圆()2222:10x y C a b a b+=>>的左、右焦点分别为12,,F F P 是C 上的点，212PF F F ⊥，1260F PF ∠=︒，则C 的离心率为（ ）A.6 B. 13 C. 12 D. 310. ABC ∆中，若=2,120BC A =︒，则AB CA ⋅的最大值为（ ）A.23 B. 23- C. 43 D. 43- 11. 正数,a b 满足121a b+=，则()()24a b ++的最小值为（ ）A. 16B. 24C. 32D. 4012. 圆O 的半径为定长，A 是平面上一定点，P 是圆上任意一点，线段AP 的垂直平分线l 和直线OP 相交于点Q ，当点P 在圆上运动时，点Q 的轨迹是（ ）A. 一个点B. 椭圆C. 双曲线D.以上选项都有可能第II 卷（非选择题，90分）二、选择题：本大题共4小题，每题5分，共20分. 13. 命题“,,tan 43x x m ππ⎡⎤∃∈-≤⎢⎥⎣⎦”的否定是 14. 若,x y 满足21x y xx y ≤≤⎧⎨+≤⎩，则2Z x y =+的取值范围是15. 已知F 是双曲线22:1412x y C -=的左焦点，()1,4A ，P 是C 右支上一点，当APF ∆周长最小时，点F 到直线AP 的距离为16．数列{}n a 满足()1121nn n a a n ++-=-，则{}n a 的前40项的和三、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤. 17. 设()()211f x m x mx m =+-+-.（I ）当1m =时，求不等式()0f x >的解集；（II ）若不等式()10f x +>的解集为332⎛⎫⎪⎝⎭，，求m 的值.18. 在ABC ∆中，,,a b c 分别为角,,A B C 的对边，2228,65bca cb a -=-=,ABC ∆的面积为24.（I ）求角A 的正弦值；（II ）求边,b c19. n S 为数列{}n a 的前n 项和. 已知0n a >，22n n n a a S +=.（I ）求{}n a 的通项公式；（II ）若12n nn a a b -=，求数列{}n b 的前n 项和n T .20. 已知命题:p 函数()()2lg 2f x x x a =-+的定义域为R ；命题:q 对于[]1,3x ∈，不等式260ax ax a --+<成立，若p q ∨为真命题，p q ∧为假命题，求实数a 的取值范围.21. 如图，四棱柱1111ABCD A BC D -中，1A D ⊥平面ABCD ，底面ABCD 是边长为1的正方形，侧棱12AA =.（I ）求直线DC 与平面1ADB 所成角的大小；（II ）在棱上1AA 是否存在一点P ，使得二面角11A B C P --的大小为30︒，若存在，确定P 点位置；若不存在，说明理由.22. 在圆223x y +=上任取一动点P ，过P 作x 轴的垂线PD ，D 为垂足，3PD MD =，动点M 的轨迹为曲线C .（I ）求C 的方程及其离心率；（II ）若直线l 交曲线C 于,A B 两点，且坐标原点到直线l ，求AOB ∆面积的最大值.2016—2017学年度郑州市上期期末考试 高二数学（理科） 参考答案1-12 BADCD ADCDA CD 13. ,,tan ;43x x m ππ⎡⎤∀∈->⎢⎥⎣⎦14. 5[0,];3 15. 32;5 16. 820. 17.解：（1）当1=m 时，不等式0)(>x f 为220,x x ->………….2分因此所求解集为1(,0)(,).2-∞⋃+∞………….4分（2）不等式01)(>+x f ，即2(1)0,m x mx m +-+>………….6分由题意知3,23是方程0)1(2=+-+m mx x m 的两根，………….8分因此33,921.37321m m m m m ⎧+=⎪⎪+⇒=-⎨⎪⨯=⎪+⎩………….10分 18.（1）由59222bc b c a -=-，可得2224cos ,25b c a A bc +-==………….2分 3sin .5A ==…………..4分（2）因为24sin 21==A bc S ,所以80,bc =…………..6分将80,6==bc a 带入可得22164,b c +=…………..8分与80=bc 联立解得8,10==c b 或者8,10.b c ==…………..12分19.解：（Ⅰ）由题得211122,2,n n n n n n a a S a a S +++⎧+=⎪⎨+=⎪⎩两式子相减得：()()111.n n n n n n aa a a a a ++++-=+…………..2分结合0n a >得11,n n a a +-= …………..4分令n =1得2111122a a S a +==，即1 1.a =所以{}n a 是首项为1，公差为1的等差数列，即.n a n =…………..6分 （Ⅱ）因为n b =11,22n n a n a n--=(n ≥2) 所以121211...,2222n n n n n n n T ---+=++++ ①2111211...,22222n n n n n n n T -+-+=++++ ② …………..8分 ① - ②得211111111331 (2222222)n n n n n n n T -++++=++++-=-，所以数列{}n b 的前n 项和33.2n n n T +=- …………..12分20.解：当P 真时，2()lg(2)f x x x a =-+的定义域为R ， 有440a ∆=-<,解得1,a > .………..2分当q 真时，即使06)1()(2<-+-=x x a x f 在[]3,1∈x 上恒成立，则有162+-<x x a 在[]3,1∈x 上恒成立， 而当[]3,1∈x 时，22666,1317()24x x x =≥-+-+ 6.7a ∴< .………..5分又因为“q p ∨”为真，“q p ∧”为假，所以p,q 一真一假， …………..6分当p 真q 假时，1,1,67a a a >⎧⎪⇒>⎨≥⎪⎩ .………..8分 当p 假q 真时，1,6.677a a a ≤⎧⎪⇒<⎨<⎪⎩………..10分 所以实数a 的取值范围是6(,)(1,).7-∞⋃+∞ .……..12分21.解：（I ）以点D 为坐标原点O ，1,,DA DC DA 分别为,,x y z 轴， 建立空间直角坐标系，则 ,…………..2分有1(1,0,0),(0,1DA DB ==设平面的法向量为),,(z y x m =，由10,0,m DA m DB ⎧⋅=⎪⎨⋅=⎪⎩取(0,3,1),m =-………..4分 又(0,1,0),DC =设直线DC 与平面所成角为,θ则3sin cos ,DC m DC m DC mθ⋅===xyz O -()()()()()()()3,1,1,3,0,1,3,1,0,3,0,0,0,1,1,0,0,1,0,0,01111--C D B A B A D 1ADB 1ADB因为0,2πθ⎡⎤∈⎢⎥⎣⎦，所以.3πθ= 即直线DC 与平面所成角的大小为.3π…………..6分（II ）假设存在点P ，使得使得二面角的大小为， 设1,AP PA λ=111AP PA P λλ⎛=∴ +⎝⎭，1111(1,0,0),,1,,1B C B P λ⎛=-=- +⎝⎭平面的法向量为(,,)n a b c =，由1110,0,n B C n B P ⎧⋅=⎪⎨⋅=⎪⎩取0,,1.1n λ⎛⎫=- ⎪ ⎪+⎝⎭ …….9分 由（I ）知，平面11AB C D的法向量(0,m =311cos300, 2.m nm nλλ+⋅∴==>∴=所以棱上存在一点，且12AP PA = 使得二面角的大小为.…..12分22.解：（Ⅰ）设(,)M x y ，00(,)P x y ，由3PD MD =得0,,x x y =⎧⎪⎨=⎪⎩ …………..2分因为22003x y +=，所以22)3x +=，即22: 1.3x C y += 其离心率e =…………..4分 （Ⅱ）当AB 垂直x轴时，AB =当AB 不垂直x 轴时，设直线AB 的方程为,y kx m =+2=，即223(1).4m k =+ …………..6分联立22,13y kx m x y =+⎧⎪⎨+=⎪⎩ 得222(13)6330.k x km m +++-= 1ADB P C B A --11︒30P C B 111AA P P C B A --11︒30设1122(,),(,)A x y B x y ，由求根公式得：12221226,1333,130,km x x k m x x k -⎧+=⎪+⎪-⎪=⎨+⎪∆>⎪⎪⎩…………..8分 所以222222121222633(1)()4(1)()41313km m AB k x x x x k k k ⎡⎤--⎡⎤=++-=+-⎢⎥⎣⎦++⎣⎦()()()()22222222242212(1)133(1)19123.1691313k k m k k k k kkk ++-++===+++++ 当0k =时，AB =； 当0k ≠时，2221233 4.196AB k k=+≤+=++…………..10分当且仅当2219k k =即k =时，取等号，此时满足0∆>. 综上所述，max 2AB =，此时AOB S ∆的最大值为12AB ⨯= ………..12分。

2016-2017学年河南省郑州市高二(上)期末数学试卷(理科)一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.1.(5分)不等式＞1的解集为()A.(﹣∞，1)B.(0，1)C.(1，＋∞)D.(0，＋∞)2.(5分)a＞b的一个充分不必要条件是()A.a＝1，b＝0B.＜C.a2＞b2D.a3＞b33.(5分)在△ABC中，若a＝1，b＝2，cosA＝，则sinB＝()A. B. C. D.4.(5分)等比数列{a n}中，a2＋a4＝20，a3＋a5＝40，则a6＝()A.16B.32C.64D.1285.(5分)两座灯塔A和B与海洋观测站C的距离分别是akm和2akm，灯塔A在观测站C的北偏东20°，灯塔B在观测站C的南偏东40°，则灯塔A与灯塔B之间的距离为()A.akmB.2akmC.akmD.akm6.(5分)在正方体ABCD﹣A1B1C1D1中，点E，F满足＝3，＝3，则BE与DF所成角的正弦值为()A. B. C. D.7.(5分)等差数列{a n}的前n项和为S n，若a1009＝1，则S2017()A.1008B.1009C.2016D.20178.(5分)过抛物线y2＝4x的焦点作直线交抛物线于A，B两点，若O为坐标原点，则•＝()A.﹣1B.﹣2C.﹣3D.﹣49.(5分)设椭圆C：＝1(a＞b＞0)的左、右焦点分别为F1、F2，P是C上的点PF2⊥F1F2，∠PF1F2＝30°，则C的离心率为()A. B. C. D.10.(5分)在△ABC中，若BC＝2，A＝120°，则•的最大值为()A. B.﹣ C. D.﹣11.(5分)正实数ab满足＋＝1，则(a＋2)(b＋4)的最小值为()A.16B.24C.32D.4012.(5分)圆O的半径为定长，A是平面上一定点，P是圆上任意一点，线段AP的垂直平分线l和直线OP相交于点Q，当点P在圆上运动时，点Q的轨迹为() A.一个点 B.椭圆C.双曲线D.以上选项都有可能二、填空题：本大题共4小题，每小题5分，共20分.13.(5分)命题“∃x∈[﹣，]，tanx≤m”的否定为.14.(5分)若x，y满足，则z＝x＋2y的取值范围为.15.(5分)已知F为双曲线C：﹣＝1的左焦点，A(1，4)，P是C右支上一点，当△APF周长最小时，点F到直线AP的距离为.16.(5分)若数列{a n}满足a n＋1＋(﹣1)n•a n＝2n﹣1，则{a n}的前40项和为.三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明或推理、验算过程.17.(10分)设f(x)＝(m＋1)x2﹣mx＋m﹣1.(1)当m＝1时，求不等式f(x)＞0的解集；(2)若不等式f(x)＋1＞0的解集为，求m的值.18.(12分)在△ABC中，a，b，c的对角分别为A，B，C的对边，a2﹣c2＝b2﹣，a＝6，△ABC的面积为24.(1)求角A的正弦值；(2)求边b，c.19.(12分)S n为数列{a n}的前n项和，已知a n＞0，a n2＋a n＝2S n.(1)求数列{a n}的通项公式；(2)若b n＝，求数列{b n}的前n项和T n.20.(12分)已知命题p：函数f(x)＝lg(x2﹣2x＋a)的定义域为R，命题q：对于x∈[1，3]，不等式ax2﹣ax﹣6＋a＜0恒成立，若p∨q为真命题，p∧q为假命题，求实数a的取值范围.21.(12分)如图，四棱柱ABCD﹣A1B1C1D1中，A1D⊥平面ABCD，底面为边长为1的正方形，侧棱AA1＝2(1)求直线DC与平面ADB1所成角的大小；(2)在棱上AA1是否存在一点P，使得二面角A﹣B1C1﹣P的大小为30°，若存在，确定P的位置，若不存在，说明理由.22.(12分)在圆x2＋y2＝3上任取一动点P，过P作x轴的垂线PD，D为垂足，＝动点M的轨迹为曲线C.(1)求C的方程及其离心率；(2)若直线l交曲线C交于A，B两点，且坐标原点到直线l的距离为，求△AOB 面积的最大值.2016-2017学年河南省郑州市高二(上)期末数学试卷(理科)参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.1.(5分)不等式＞1的解集为()A.(﹣∞，1)B.(0，1)C.(1，＋∞)D.(0，＋∞)【解答】解：不等式可化为x(x﹣1)＜0，∴0＜x＜1，∴不等式＞1的解集为(0，1)，故选B.2.(5分)a＞b的一个充分不必要条件是()A.a＝1，b＝0B.＜C.a2＞b2D.a3＞b3【解答】解：A.当a＝1，b＝0时，满足a＞b，反之不成立，则a＝1，b＝0是a ＞b的一个充分不必要条件.B.当a＜0，b＞0时，满足＜，但a＞b不成立，即充分性不成立，C.当a＝﹣2，b＝1时，满足a2＞b2，但a＞b不成立，即充分性不成立，D.由a3＞b3得a＞b，即a3＞b3是a＞b成立的充要条件，故选：A3.(5分)在△ABC中，若a＝1，b＝2，cosA＝，则sinB＝()A. B. C. D.【解答】解：∵0＜A＜π，且cosA＝，∴sinA＝＝，由正弦定理得，，则sinB＝＝＝，故选D.4.(5分)等比数列{a n}中，a2＋a4＝20，a3＋a5＝40，则a6＝()A.16B.32C.64D.128【解答】解：∵等比数列{a n}中，a2＋a4＝20，a3＋a5＝40，∴，解得a＝2，q＝2，∴a6＝2×25＝64.故选：C.5.(5分)两座灯塔A和B与海洋观测站C的距离分别是akm和2akm，灯塔A在观测站C的北偏东20°，灯塔B在观测站C的南偏东40°，则灯塔A与灯塔B之间的距离为()A.akmB.2akmC.akmD.akm【解答】解：根据题意，△ABC中，∠ACB＝180°﹣20°﹣40°＝120°，∵AC＝akm，BC＝2akm，∴由余弦定理，得cos120°＝，解之得AB＝akm，即灯塔A与灯塔B的距离为akm，故选：D.6.(5分)在正方体ABCD﹣A1B1C1D1中，点E，F满足＝3，＝3，则BE与DF所成角的正弦值为()A. B. C. D.【解答】解：如图，以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，设正方体ABCD﹣A1B1C1D1中棱长为4，∵点E，F满足＝3，＝3，∴B(4，4，0)，E(4，3，4)，D(0，0，0)，F(0，1，4)，＝(0，﹣1，4)，＝(0，1，4)，设异面直线BE与DF所成角为θ，则cosθ＝＝＝.sinθ＝＝，∴BE与DF所成角的正弦值为.故选：A.7.(5分)等差数列{a n}的前n项和为S n，若a1009＝1，则S2017()A.1008B.1009C.2016D.2017【解答】解：∵等差数列{a n}的前n项和为S n，a1009＝1，∴S2017＝(a1＋a2017)＝2017a1009＝2017.故选：D.8.(5分)过抛物线y2＝4x的焦点作直线交抛物线于A，B两点，若O为坐标原点，则•＝()A.﹣1B.﹣2C.﹣3D.﹣4【解答】解：由题意知，抛物线y2＝4x的焦点坐标为(1，0)，∴直线AB的方程为y＝k(x﹣1)，由，得k2x2﹣(2k2＋4)x＋k2＝0，设A(x1，y1)，B(x2，y2)，x1＋x2＝，x1＋x2＝1，y1•y2＝k(x1﹣1)•k(x2﹣1)＝k2[x1•x2﹣(x1＋x2)＋1]'则•＝x1•x2＋y1•y2＝x1•x2＋k(x1﹣1)•k(x2﹣1)＝﹣3.故选：C.9.(5分)设椭圆C：＝1(a＞b＞0)的左、右焦点分别为F1、F2，P是C上的点PF2⊥F1F2，∠PF1F2＝30°，则C的离心率为()A. B. C. D.【解答】解：|PF2|＝x，∵PF2⊥F1F2，∠PF1F2＝30°，∴|PF1|＝2x，|F1F2|＝x，又|PF1|＋|PF2|＝2a，|F1F2|＝2c∴2a＝3x，2c＝x，∴C的离心率为：e＝＝.故选D.10.(5分)在△ABC中，若BC＝2，A＝120°，则•的最大值为()A. B.﹣ C. D.﹣【解答】解：∵，∴⇒4＝AC2＋AB2﹣2AC•ABcosA⇒4＝AC2＋AB2＋AC•AB≥2A•CAB＋AC•AB＝3AC•AB⇒AC•AB≤∴•＝AC•ABco s120°≤，则•的最大值为，故选：A.11.(5分)正实数ab满足＋＝1，则(a＋2)(b＋4)的最小值为()A.16B.24C.32D.40【解答】解：正实数a，b满足＋＝1，∴1≥2，解得ab≥8，当且仅当b＝2a＝4时取等号.b＋2a＝ab.∴(a＋2)(b＋4)＝ab＋2(b＋2a)＋8＝3ab＋8≥32.故选：C.12.(5分)圆O的半径为定长，A是平面上一定点，P是圆上任意一点，线段AP的垂直平分线l和直线OP相交于点Q，当点P在圆上运动时，点Q的轨迹为() A.一个点 B.椭圆C.双曲线D.以上选项都有可能【解答】解：∵A为⊙O外一定点，P为⊙O上一动点线段AP的垂直平分线交直线OP于点Q，则QA＝QP，则QA﹣QO＝QP﹣QO＝OP＝R，即动点Q到两定点O、A的距离差为定值，根据双曲线的定义，可知点Q的轨迹是：以O，A为焦点，OP为实轴长的双曲线故选：C.二、填空题：本大题共4小题，每小题5分，共20分.13.(5分)命题“∃x∈[﹣，]，tanx≤m”的否定为∀x∈[﹣，]，tanx ＞m.【解答】解：命题“∃x∈[﹣，]，tanx≤m”的否定为命题“∀x∈[﹣，]，tanx＞m”，故答案为：∀x∈[﹣，]，tanx＞m14.(5分)若x，y满足，则z＝x＋2y的取值范围为[0，] .【解答】解：x，y满足，不是的可行域如图：z＝x＋2y化为：y＝﹣＋，当y＝﹣＋经过可行域的O时目标函数取得最小值，经过A时，目标函数取得最大值，由，可得A(，)，则z＝x＋2y的最小值为：0；最大值为：＝.则z＝x＋2y的取值范围为：[0，].故答案为：[0，].15.(5分)已知F为双曲线C：﹣＝1的左焦点，A(1，4)，P是C右支上一点，当△APF周长最小时，点F到直线AP的距离为.【解答】解：设双曲线的右焦点为F′(4，0)，由题意，A，P，F′共线时，△APF 周长最小，直线AP的方程为y＝(x﹣4)，即4x＋3y﹣16＝0，∴点F到直线AP的距离为＝，故答案为：16.(5分)若数列{a n}满足a n＋1＋(﹣1)n•a n＝2n﹣1，则{a n}的前40项和为820.＋(﹣1)n a n＝2n﹣1，【解答】解：由于数列{a n}满足a n＋1故有a2﹣a1＝1，a3＋a2＝3，a4﹣a3＝5，a5＋a4＝7，a6﹣a5＝9，a7＋a6＝11，…a50﹣a49＝97.从而可得a3＋a1＝2，a4＋a2＝8，a7＋a5＝2，a8＋a6＝24，a9＋a7＝2，a12＋a10＝40，a13＋a11＝2，a16＋a14＝56，…从第一项开始，依次取2个相邻奇数项的和都等于2，从第二项开始，依次取2个相邻偶数项的和构成以8为首项，以16为公差的等差数列.{a n}的前40项和为10×2＋(10×8＋×16)＝820，故答案为：820三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明或推理、验算过程.17.(10分)设f(x)＝(m＋1)x2﹣mx＋m﹣1.(1)当m＝1时，求不等式f(x)＞0的解集；(2)若不等式f(x)＋1＞0的解集为，求m的值.【解答】(本题12分)解：(1)当m＝1时，不等式f(x)＞0为：2x2﹣x＞0⇒x(2x﹣1)＞0⇒x＞，x＜0；因此所求解集为；…(6分)(2)不等式f(x)＋1＞0即(m＋1)x2﹣mx＋m＞0∵不等式f(x)＋1＞0的解集为，所以是方程(m＋1)x2﹣mx＋m＝0的两根因此⇒. …(12分)18.(12分)在△ABC中，a，b，c的对角分别为A，B，C的对边，a2﹣c2＝b2﹣，a＝6，△ABC的面积为24.(1)求角A的正弦值；(2)求边b，c.【解答】解：(1)由在△ABC中，a2﹣c2＝b2﹣①，整理得cosA＝＝，则sinA＝＝；(2)∵S＝bcsinA＝24，sinA＝，∴bc＝80，将a＝6，bc＝80代入①得：b2＋c2＝164，与bc＝80联立，解得：b＝10，c＝8或b＝8，c＝10.19.(12分)S n为数列{a n}的前n项和，已知a n＞0，a n2＋a n＝2S n.(1)求数列{a n}的通项公式；(2)若b n＝，求数列{b n}的前n项和T n.【解答】解：(1)由题得a n2＋a n＝2S n，a n＋12＋an＋1＝2S n＋1，两式子相减得：结合a n＞0得a n＋1﹣a n＝1 …..(4分)令n＝1得a12＋a1＝2S1，即a1＝1，所以{a n}是首项为1，公差为1的等差数列，即a n＝n…..(6分)(2)因为b n＝＝(n≥2)所以T n＝＋…＋①T n＝＋…＋＋②…..(8分)①﹣②得T n＝1＋＋…＋﹣＝﹣，所以数列{b n}的前n项和T n＝3﹣.…..(12分)20.(12分)已知命题p：函数f(x)＝lg(x2﹣2x＋a)的定义域为R，命题q：对于x∈[1，3]，不等式ax2﹣ax﹣6＋a＜0恒成立，若p∨q为真命题，p∧q为假命题，求实数a的取值范围.【解答】解：当P真时，f(x)＝lg(x2﹣2x＋a)的定义域为R，有△＝4﹣4a＜0，解得a＞1.…..(2分)当q真时，即使g(x)＝ax2﹣ax﹣6＋a在x∈[1，3]上恒成立，则有a＜在x∈[1，3]上恒成立，而当x∈[1，3]时，＝≥，故a＜.…..(5分)又因为p∨q为真命题，p∧q为假命题，所以p，q一真一假，…..(6分)当p真q假时，a＞1.…..(8分)当p假q真时，a＜…..(10分)所以实数a的取值范围是(﹣∞，)∪(1，＋∞)…..(12分)21.(12分)如图，四棱柱ABCD﹣A1B1C1D1中，A1D⊥平面ABCD，底面为边长为1的正方形，侧棱AA1＝2(1)求直线DC与平面ADB1所成角的大小；(2)在棱上AA1是否存在一点P，使得二面角A﹣B1C1﹣P的大小为30°，若存在，确定P的位置，若不存在，说明理由.【解答】解：(1)∵四棱柱ABCD﹣A1B1C1D1中，A1D⊥平面ABCD，底面为边长为1的正方形，侧棱AA1＝2，∴以点D为坐标原点O，DA，DC，DA1分别为x，y，z轴，建立空间直角坐标系，…..(2分)D(0，0，0)，A(1，0，0)，B1(0，1，)，C(0，1，0)，，＝(0，1，)，＝(0，1，0)，的法向量为，设平面ADB则，取z＝1，得＝(0，﹣，1)，…..(4分)设直线DC与平面所ADB1成角为θ，则sinθ＝|cos＜＞|＝＝，∵θ∈[0，]，∴θ＝，∴直线DC与平面ADB1所成角的大小为.…..(6分)(2)假设存在点P(a，b，c)，使得二面角A﹣B1C1﹣P的大小为30°，设＝，由A1(0，0，)，得(a﹣1，b，c)＝λ(﹣a，﹣b，)，∴，解得，B1(0，1，)，C1(﹣1，1，)，＝(﹣1，0，0)，＝(，﹣1，﹣)，设平面的法向量为＝(x，y，z)，则，取z＝1，得＝(0，﹣，1)，….(9分)由(1)知，平面AB1C1D的法向量为＝(0，﹣，1)，∵二面角A﹣B1C1﹣P的大小为30°，∴cos30°＝＝＝.由λ＞0，解得λ＝2，所以棱AA1上存在一点P，使得二面角A﹣B1C1﹣P的大小为30°，且AP＝2PA1.22.(12分)在圆x2＋y2＝3上任取一动点P，过P作x轴的垂线PD，D为垂足，＝动点M的轨迹为曲线C.(1)求C的方程及其离心率；(2)若直线l交曲线C交于A，B两点，且坐标原点到直线l的距离为，求△AOB 面积的最大值.【解答】解：(Ⅰ)设M(x，y)，P(x0，y0)，由＝得x0＝x，y0＝y …..(2分)因为x02＋y02＝3，所以x2＋3y2＝3，即＝1，其离心率e＝.…..(4分)(Ⅱ)当AB与x轴垂直时，|AB|＝.(5分)②当AB与x轴不垂直时，设直线AB的方程为y＝kx＋m，A(x1，y1)，B(x2，y2)，由已知，得.(6分)把y＝kx＋m代入椭圆方程，整理得(3k2＋1)x2＋6kmx＋3m2﹣3＝0，∴x1＋x2＝，x1x2＝(7分)∴k≠0，|AB|2＝(1＋k2)(x2﹣x1)2＝3＋≤4，当且仅当9k2＝，即k＝时等号成立，此时|AB|＝2.(10分)当k＝0时，|AB|＝.(11分)综上所述：|AB|max＝2，此时△AOB面积取最大值＝(12分)。

郑州市2016-2017学年下期期末考试高二语文试题(含答案)2016—2017学年度郑州市下期期末考试高中二年级语文参考答案一、现代文阅读（35分）（一）论述类文本阅读（9分，每小题3分）1.B（曲解文意。

原文意思是，据瓷器专家考证，三只瓷器为明朝宣德至成化年间之物。

认为画中的瓷器应是欧洲大航海初期，甚至更早的时候由中国传入西方的，是文章作者的推测。

）2.A（强加因果。

原文并没有提到“诸多流派流传时间短”是“西方油画中最初出现东方元素的时间无法确定”的原因。

）3.D（理解有误。

根据文意，艺术上的文化自信应是在保存本民族传统文化特色的基础上，研究、吸纳其他文化艺术的精华，而在努力适应现代化和国际化发展潮流的同时，加强对本民族文化传统的保护也是它的应有之意。

）（二）文学类文本阅读（14分）4.C（A项村主任“像牛一样号啕起来”，其实是因为后怕、无奈等；B项“老鼠冷不防会弄下一大团灰尘”不是拟人；D项“突出了小说关爱农村留守儿童的主旨”理解有误。

）5.①关爱学生，心地仁慈。

看到孩子为刚到的他抬水而倍感温暖；阻止了孩子们轮流为他抬水；留下几个家离校较远的孩子与他一同分享玉米棒和山药蛋。

②讲授有方，善于激励。

运用“顺水行舟”法，引导学生用本人的眼睛和耳朵观察、倾听大自然；奇妙地鼓励学生表达出本人的观察所得；让学生经由过程画画学写汉字，让一向被以为很难的字写起来简单；率领学生观察天体、唱歌、升国旗，使缄默沉静已久的孩子们像春天夙起的鸟儿叽叽喳喳地欢叫开来。

③聪明睿智，坚韧乐观。

经由过程观察老鼠搬家，预知校舍将要倒塌；校舍将要倒塌时，他告诉孩子们将幸运地见证奇迹，并相信会有一所新学校拔地而起。

④酷爱（献身）教育，矢志不移。

掉臂乡村小学条件简陋，想方设法改动那里教育落后的现状；当村里盖起了新校舍、学校分配来了新老师，他又选择去另外一所更偏僻的学校。

（5分；一点2分，其中概括、分析各1分；“概括部分”两个短语答出任何一个即可得1分，“分析部分”答出分号前后的任意一点即可得1分，概括与分析须一致；答出任意三点，意思对即可）6.①小说开头描写天下着小雨，照应题目“湿漉漉的雨”，点明了人物活动的环境特点；营造出下雨天湿寒阴郁的氛围，衬托出孩子们对新来的XXX老师的热情。

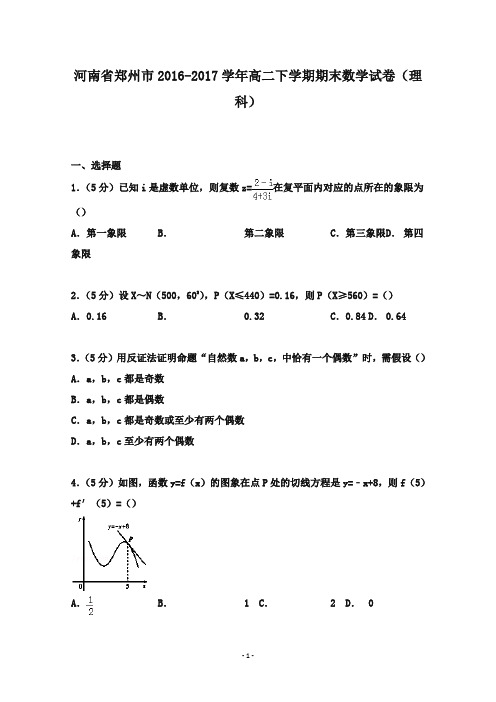
河南省郑州市2016-2017学年高二下学期期末数学试卷（理科）一、选择题1．（5分）已知i是虚数单位，则复数z=在复平面内对应的点所在的象限为（）A．第一象限B．第二象限C．第三象限D．第四象限2．（5分）设X～N（500，602），P（X≤440）=0.16，则P（X≥560）=（）A．0.16 B．0.32 C．0.84 D．0.643．（5分）用反证法证明命题“自然数a，b，c，中恰有一个偶数”时，需假设（）A．a，b，c都是奇数B．a，b，c都是偶数C．a，b，c都是奇数或至少有两个偶数D．a，b，c至少有两个偶数4．（5分）如图，函数y=f（x）的图象在点P处的切线方程是y=﹣x+8，则f（5）+f′（5）=（）A．B． 1 C． 2 D．05．（5分）某餐厅的原料费支出x与销售额y（单位：万元）之间有如下数据，根据表中提供的全部数据，用最小二乘法得出y与x的线性回归方程为=8.5x+7.5，则表中的m的值为（）x 2 4 5 6 8y 25 35 m 55 75A．50 B．55 C．60 D．656．（5分）若函数f（x）=，则f′（x）是（）A．仅有最小值的奇函数B．仅有最大值的偶函数C．既有最大值又有最小值的偶函数D．非奇非偶函数7．（5分）由曲线y=，直线y=x﹣2及y轴所围成的图形的面积为（）A．B． 4 C． D． 68．（5分）函数f（x）=x3﹣3x+1在闭区间[﹣3，0]上的最大值、最小值分别是（）A．1，﹣1 B．1，﹣17 C．3，﹣17 D．9，﹣199．（5分）某班级要从4名男士、2名女生中选派4人参加某次社区服务，如果要求至少有1名女生，那么不同的选派方案种数为（）A．14 B．24 C．28 D．4810．（5分）设f′（x）是函数f（x）的导函数，将y=f（x）和y=f′（x）的图象画在同一个直角坐标系中，不可能正确的是（）A．B．C．D．11．（5分）口袋里放有大小相同的2个红球和1个白球，有放回的每次摸取一个球，定义数列{an }：，如果Sn为数列{an}的前n项之和，那么S7=3的概率为（）A．B．C．D．12．（5分）若函数f（x）=x3+ax2+bx+c有极值点x1，x2，且f（x1）=x1，则关于x的方程3（f（x））2+2af（x）+b=0的不同实根个数是（）A．3B． 4 C． 5 D． 6二、填空题13．（5分）的展开式中x3的系数是．14．（5分）设ξ是一个离散型随机变量，其概率分布列如下：ξ﹣1 0 1P 0.5 q2则q=．15．（5分）设A、B为两个事件，若事件A和B同时发生的概率为，在事件A发生的条件下，事件B发生的概率为，则事件A发生的概率为．（i=1，2，3，4），P 16．（5分）设面积为S的平面四边形的第i条边的边长为ai是该四边形内一点，点P到第i条边的距离记为，类比上述结论，体积为V的三棱锥的第i个面的面积记为S（i=1，2，3，4），Q是该三棱锥内的一点，点Q到第i，若等于．i个面的距离记为di三、解答题17．（10分）设复数z=，若z2+az+b=1+i，求实数a，b的值．18．（12分）已知（n∈N*）的展开式中第五项的系数与第三项的系数的比是10：1．（1）求展开式中各项系数的和；（2）求展开式中含的项．19．（12分）某市随机抽取一年（365天）内100天的空气质量指数API的监测数据，结果统计如下：API [0，50] （50，100] （100，150] （150，200]（200，250] （250，300] ＞300空气质量优良轻微污染轻度污染中度污染中度重污染重度污染天数 4 13 18 30 9 11 15记某企业每天由于空气污染造成的经济损失为S（单位：元），空气质量指数API 为ω，在区间[0，100]对企业没有造成经济损失；在区间（100，300]对企业造成经济损失成直线模型（当API为150时造成的经济损失为500元，当API为200时，造成的经济损失为700元）；当API大于300时造成的经济损失为2000元．（1）试写出S（ω）表达式；（2）试估计在本年内随机抽取一天，该天经济损失S大于500元且不超过900元的概率；（3）若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染，完成下面2×2列联表，并判断能否有95%的把握认为该市本年空气重度污染与供暖有关？P（K2≥k）0.25 0.15 0.10 0.05 0.025 0.010 0.005c0.001K1.3232.072 2.7063.841 5.024 6.635 7.879 10.828cK2=非重度污染重度污染合计供暖季非供暖季合计10020．（12分）学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）（Ⅰ）求在1次游戏中获奖的概率；（Ⅱ）求在2次游戏中获奖次数X的分布列及数学期望E（X）．21．（12分）当n∈N*时，，Tn=+++…+．（Ⅰ）求S1，S2，T1，T2；（Ⅱ）猜想Sn 与Tn的关系，并用数学归纳法证明．22．（12分）已知函数f（x）=lnx+x2．（Ⅰ）求h（x）=f（x）﹣3x的极值；（Ⅱ）若函数g（x）=f（x）﹣ax在定义域内为增函数，求实数a的取值范围；（Ⅲ）设F（x）=2f（x）﹣3x2﹣k，k∈R，若函数F（x）存在两个零点m，n（0＜m＜n），且满足2x0=m+n，问：函数F（x）在（x，F（x））处的切线能否平行于x轴？若能，求出该切线方程，若不能，请说明理由．河南省郑州市2016-2017学年高二下学期期末数学试卷（理科）参考答案与试题解析一、选择题1．（5分）已知i是虚数单位，则复数z=在复平面内对应的点所在的象限为（）A．第一象限B．第二象限C．第三象限D．第四象限考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：利用复数的运算法则及其几何意义即可得出．解答：解：复数z====在复平面内对应的点所在的象限为第四象限．故选：D．点评：本题考查了复数的运算法则及其几何意义，属于基础题．2．（5分）设X～N（500，602），P（X≤440）=0.16，则P（X≥560）=（）A．0.16 B．0.32 C．0.84 D．0.64考点：正态分布曲线的特点及曲线所表示的意义．分析：利用正态分布的对称性即可得出．解答：解：∵μ=500，σ2=602，即σ=60．根据正态分布的对称性P（X≥μ﹣3σ）=P（X≤μ﹣3σ）=0.16．故选A．点评：正确理解正态分布的对称性是解题的关键．3．（ 5分）用反证法证明命题“自然数a，b，c，中恰有一个偶数”时，需假设（）A．a，b，c都是奇数B．a，b，c都是偶数C．a，b，c都是奇数或至少有两个偶数D．a，b，c至少有两个偶数考点：反证法．专题：推理和证明．分析：直接利用反证法的定义，写出结果即可．解答：解：用反证法证明命题“自然数a，b，c，中恰有一个偶数”时，需假设：a，b，c都是奇数或至少有两个偶数．故选：C．点评：本题考查反证法的定义，利用反证法证明命题的步骤，基本知识的考查．4．（5分）如图，函数y=f（x）的图象在点P处的切线方程是y=﹣x+8，则f（5）+f′（5）=（）A．B． 1 C． 2 D．0考点：导数的运算．专题：导数的概念及应用．分析：利用函数在切点处的导数值是切线的斜率求出f′（5），将切点坐标代入切线方程求出f（5）．解答：解：f′（5）=﹣1将x=5代入切线方程得f（5）=﹣5+8=3，所以f（5）+f′（5）=3+（﹣1）=2，故选：C点评：本题考查导数的几何意义：函数在切点处的导数值是切线的斜率．5．（5分）某餐厅的原料费支出x与销售额y（单位：万元）之间有如下数据，根据表中提供的全部数据，用最小二乘法得出y与x的线性回归方程为=8.5x+7.5，则表中的m的值为（）x 2 4 5 6 8y 25 35 m 55 75A．50 B．55 C．60 D．65考点：线性回归方程．专题：应用题；概率与统计．分析：计算样本中心点，根据线性回归方程恒过样本中心点，列出方程，求解即可得到结论．解答：解：由题意，==5，==38+，∵y关于x的线性回归方程为=8.5x+7.5，根据线性回归方程必过样本的中心，∴38+=8.5×5+7.5，∴m=60．故选：C．点评：本题考查线性回归方程的运用，解题的关键是利用线性回归方程恒过样本中心点，这是线性回归方程中最常考的知识点．属于基础题．6．（5分）若函数f（x）=，则f′（x）是（）A．仅有最小值的奇函数B．仅有最大值的偶函数C．既有最大值又有最小值的偶函数D．非奇非偶函数考点：简单复合函数的导数．专题：导数的概念及应用．分析：先求导，转化为二次函数型的函数并利用三角函数的单调性求其最值，再利用函数的奇偶性的定义进行判断其奇偶性即可．解答：解：∵函数f（x）=，∴f′（x）=cos2x+cosx=2cos2x+cosx﹣1=，当cosx=时，f′（x）取得最小值；当cosx=1时，f′（x）取得最大值2．且f′（﹣x）=f′（x）．即f′（x）是既有最大值，又有最小值的偶函数．故选C．点评：熟练掌握复合函数的导数、二次函数型的函数的最值、三角函数的单调性及函数的奇偶性是解题的关键．7．（5分）由曲线y=，直线y=x﹣2及y轴所围成的图形的面积为（）A．B． 4 C． D． 6考点：定积分在求面积中的应用．专题：计算题．分析：利用定积分知识求解该区域面积是解决本题的关键，要确定出曲线y=，直线y=x﹣2的交点，确定出积分区间和被积函数，利用导数和积分的关系完成本题的求解．解答：解：联立方程得到两曲线的交点（4，2），因此曲线y=，直线y=x﹣2及y轴所围成的图形的面积为：S=．故选C．点评：本题考查曲边图形面积的计算问题，考查学生分析问题解决问题的能力和意识，考查学生的转化与化归能力和运算能力，考查学生对定积分与导数的联系的认识，求定积分关键要找准被积函数的原函数，属于定积分的简单应用问题．8．（5分）函数f（x）=x3﹣3x+1在闭区间[﹣3，0]上的最大值、最小值分别是（）A．1，﹣1 B．1，﹣17 C．3，﹣17 D．9，﹣19考点：函数的最值及其几何意义．专题：计算题．分析：求导，用导研究函数f（x）=x3﹣3x+1在闭区间[﹣3，0]上的单调性，利用单调性求函数的最值．解答：解：f′（x）=3x2﹣3=0，x=±1，故函数f（x）=x3﹣3x+1[﹣3，﹣1]上是增函数，在[﹣1，0]上是减函数又f（﹣3）=﹣17，f（0）=1，f（1）=﹣1，f（﹣1）=3．故最大值、最小值分别为3，﹣17；故选C．点评：本题考点是导数法求函数最值．此类解法的步骤是求导，确定极值点，研究单调性，求出极值与区间端点的函数值，再比较各数的大小，选出最大值与最小值．9．（5分）某班级要从4名男士、2名女生中选派4人参加某次社区服务，如果要求至少有1名女生，那么不同的选派方案种数为（）A．14 B．24 C．28 D．48考点：排列、组合的实际应用．专题：计算题；转化思想．分析：法一：用直接法，4人中至少有1名女生包括1女3男及2女2男两种情况，计算各种情况下的选派方案种数，由加法原理，计算可得答案；法二：用排除法，首先计算从4男2女中选4人的选派方案种数，再计算4名都是男生的选派方案种数，由排除法，计算可得答案．解答：解：法一：4人中至少有1名女生包括1女3男及2女2男两种情况，故不同的选派方案种数为C12•C34+C22•C24=2×4+1×6=14；法二：从4男2女中选4人共有C46种选法，4名都是男生的选法有C44种，故至少有1名女生的选派方案种数为C46﹣C44=15﹣1=14．故选A．点评：本题考查简单的排列组合，建议如果分类讨论太复杂的题目最好用间接法即排除法，以避免直接的分类不全情况出现．10．（5分）设f′（x）是函数f（x）的导函数，将y=f（x）和y=f′（x）的图象画在同一个直角坐标系中，不可能正确的是（）A．B．C．D．考点：利用导数研究函数的单调性；导数的几何意义．专题：压轴题．分析：本题可以考虑排除法，容易看出选项D不正确，因为D的图象，在整个定义域内，不具有单调性，但y=f（x）和y=f′（x）在整个定义域内具有完全相同的走势，不具有这样的函数．解答：解析：检验易知A、B、C均适合，不存在选项D的图象所对应的函数，在整个定义域内，不具有单调性，但y=f（x）和y=f′（x）在整个定义域内具有完全相同的走势，不具有这样的函数，故选D．点评：考查函数的单调性问题．11．（5分）口袋里放有大小相同的2个红球和1个白球，有放回的每次摸取一个球，定义数列{an }：，如果Sn为数列{an}的前n项之和，那么S7=3的概率为（）A．B．C．D．考点：等可能事件的概率．专题：常规题型；概率与统计．分析： S7=3说明共摸球七次，只有两次摸到红球，由于每次摸球的结果数之间没有影响，故可以用独立事件的概率乘法公式求解．解答：解：由题意S7=3说明共摸球七次，只有两次摸到红球，因为每次摸球的结果数之间没有影响，摸到红球的概率是，摸到白球的概率是所以只有两次摸到红球的概率是=故选B点评：本题考查独立事件的概率乘法公式，考查学生分析解决问题的能力，确定S7=3说明共摸球七次，只有两次摸到红球是关键．12．（5分）若函数f（x）=x3+ax2+bx+c有极值点x1，x2，且f（x1）=x1，则关于x的方程3（f（x））2+2af（x）+b=0的不同实根个数是（）A．3B． 4 C． 5 D． 6考点：函数在某点取得极值的条件；根的存在性及根的个数判断．专题：综合题；压轴题；导数的综合应用．分析：求导数f′（x），由题意知x1，x2是方程3x2+2ax+b=0的两根，从而关于f（x）的方程3（f（x））2+2af（x）+b=0有两个根，作出草图，由图象可得答案．解答：解：f′（x）=3x2+2ax+b，x1，x2是方程3x2+2ax+b=0的两根，不妨设x2＞x1，由3（f（x））2+2af（x）+b=0，则有两个f（x）使等式成立，x1=f（x1），x2＞x1=f（x1），如下示意图象：如图有三个交点，故选A．点评：考查函数零点的概念、以及对嵌套型函数的理解，考查数形结合思想．二、填空题13．（5分）的展开式中x3的系数是24．考点：二项式系数的性质．专题：计算题．分析：求出的通项公式为 Tr+1=，令，求出r的值，即可求得x3的系数．解答：解：由于的展开式的通项公式为Tr+1==，令，解得 r=2，故 T4=24 x3，故展开式中x3的系数是24，故答案为：24．点评：本题考查二项展开式的通项公式，求展开式中某项的系数，二项式系数的性质，求出通项公式为=，是解题的关键，属于中档题．Tr+114．（5分）设ξ是一个离散型随机变量，其概率分布列如下：ξ﹣1 0 1P 0.5 q2则q=．考点：离散型随机变量及其分布列．专题：计算题；阅读型．分析：根据随机变量的概率非负不大于1，且随机变量取遍所有可能值时相应的概率之和等于1，列出方程和不等式，解方程组即可．解答：解：因为随机变量的概率非负且随机变量取遍所有可能值时相应的概率之和等于1，0.5+1﹣q+q2=1 ①0≤1﹣q≤1 ②q2≤1③∴解一元二次方程得q=或1，而1代入②③不合题意，舍去，故答案为：．点评：本题主要考查了分布列的简单应用，通过解方程组得到要求的变量，这与求变量的分布列是一个相反的过程，但是两者都要用到分布列的性质，属于中档题．15．（5分）设A、B为两个事件，若事件A和B同时发生的概率为，在事件A 发生的条件下，事件B发生的概率为，则事件A发生的概率为．考点：条件概率与独立事件．专题：计算题；概率与统计．分析：根据题意，结合条件概率公式加以计算即可得到事件A发生的概率．解答：解：根据题意，得∵P（A|B）=，P（AB）=，P（A|B）=∴=，解得P（B）==故答案为：点评：本题给出事件A、B同时发生的概率和A发生的条件下B发生的概率，求事件A的概率，着重考查了条件概率及其应用的知识，属于基础题．16．（5分）设面积为S的平面四边形的第i条边的边长为a（i=1，2，3，4），Pi是该四边形内一点，点P到第i条边的距离记为，类比上述结论，体积为V的三棱（i=1，2，3，4），Q是该三棱锥内的一点，点Q到第锥的第i个面的面积记为Si，若等于．i个面的距离记为di考点：类比推理．专题：计算题．分析：由可得a=ik，P是该四边形内任意一点，将P与四边i形的四个定点连接，得四个小三角形，四个小三角形面积之和为四边形面积，即采用分割法求面积；同理对三棱值得体积可分割为5个已知底面积和高的小棱锥求体积．解答：解：根据三棱锥的体积公式得：，即S1H1+2S2H2+3S3H3+4S4H4=3V，∴，即．故答案为：．点评：本题主要考查三棱锥的体积计算和运用类比思想进行推理的能力．解题的关键是理解类比推理的意义，掌握类比推理的方法．平面几何的许多结论，可以通过类比的方法，得到立体几何中相应的结论．当然，类比得到的结论是否正确，则是需要通过证明才能加以肯定的．三、解答题17．（10分）设复数z=，若z2+az+b=1+i，求实数a，b的值．考点：复数代数形式的混合运算；复数的基本概念．专题：计算题．分析：先将z按照复数代数形式的运算法则，化为代数形式，代入 z2+az+b=1+i，再根据复数相等的概念，列出关于a，b的方程组，并解即可．解答：解：z=====1﹣iz2+az+b=（1﹣i）2+a（1﹣i）+b=a+b﹣（a+2）i=1+i∴解得点评：本题考查了复数代数形式的混合运算，复数相等的概念，属于基础题．18．（12分）已知（n∈N*）的展开式中第五项的系数与第三项的系数的比是10：1．（1）求展开式中各项系数的和；（2）求展开式中含的项．考点：二项式系数的性质．专题：计算题．分析：（1）利用二项展开式的通项公式求出二项展开式的通项，求出第五项的系数与第三项的系数，根据已知条件列出方程，求出n的值，将n的值代入二项式，给二项式中的x赋值1，求出展开式中各项系数的和．（2）令二项展开式的通项中的x的指数为，求出r的值，将r的值代入通项求出展开式中含的项．解答：解：由题意知，展开式的通项为则第五项系数为Cn 4•（﹣2）4，第三项的系数为Cn2•（﹣2）2则有，化简，得n2﹣5n﹣24=0解得n=8或n=﹣3（舍去）（1）令x=1，得各项系数的和为（1﹣2）8=1（2）令，则r=1故展开式中含的项为点评：求二项展开式的特定项问题一般借助的工具是二项展开式的通项公式；求二项展开式的各项系数和问题，一般通过观察，通过赋值的方法来解决．19．（12分）某市随机抽取一年（365天）内100天的空气质量指数API的监测数据，结果统计如下：API [0，50] （50，100] （100，150] （150，200]（200，250] （250，300] ＞300空气质量优良轻微污染轻度污染中度污染中度重污染重度污染天数 4 13 18 30 9 11 15记某企业每天由于空气污染造成的经济损失为S（单位：元），空气质量指数API 为ω，在区间[0，100]对企业没有造成经济损失；在区间（100，300]对企业造成经济损失成直线模型（当API为150时造成的经济损失为500元，当API为200时，造成的经济损失为700元）；当API大于300时造成的经济损失为2000元．（1）试写出S（ω）表达式；（2）试估计在本年内随机抽取一天，该天经济损失S大于500元且不超过900元的概率；（3）若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染，完成下面2×2列联表，并判断能否有95%的把握认为该市本年空气重度污染与供暖有关？）0.25 0.15 0.10 0.05 0.025 0.010 0.005P（K2≥kc0.0011.3232.072 2.7063.841 5.024 6.635 7.879 10.828KcK2=非重度污染重度污染合计供暖季非供暖季合计100考点：独立性检验．专题：综合题；概率与统计．分析：（1）根据在区间[0，100]对企业没有造成经济损失；在区间（100，300]对企业造成经济损失成直线模型（当API为150时造成的经济损失为500元，当API为200时，造成的经济损失为700元）；当API大于300时造成的经济损失为2000元，可得函数关系式；（2）由500＜S≤900，得150＜ω≤250，频数为39，即可求出概率；（3）根据所给的数据，列出列联表，根据所给的观测值的公式，代入数据做出观测值，同临界值进行比较，即可得出结论．解答：解：（1）根据在区间[0，100]对企业没有造成经济损失；在区间（100，300]对企业造成经济损失成直线模型（当API为150时造成的经济损失为500元，当API为200时，造成的经济损失为700元）；当API大于300时造成的经济损失为2000元，可得S（ω）=；（2）设“在本年内随机抽取一天，该天经济损失S大于500元且不超过900元”为事件A；由500＜S≤900，得150＜ω≤250，频数为39，∴P（A）=；（2）根据以上数据得到如表：非重度污染重度污染合计供暖季 22 8 30非供暖季63 7 70合计85 15 100K2的观测值K2=≈4.575＞3.841所以有95%的把握认为空气重度污染与供暖有关．点评：本题考查概率知识，考查列联表，观测值的求法，是一个独立性检验，我们可以利用临界值的大小来决定是否拒绝原来的统计假设，若值较大就拒绝假设，即拒绝两个事件无关．20．（12分）学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）（Ⅰ）求在1次游戏中获奖的概率；（Ⅱ）求在2次游戏中获奖次数X的分布列及数学期望E（X）．考点：离散型随机变量的期望与方差；古典概型及其概率计算公式．专题：计算题；概率与统计．分析：（I）设“在X次游戏中摸出i个白球”为事件Ai（i=，0，1，2，3），“在1次游戏中获奖”为事件B，则B=A2∪A3，求出相应的概率，再相加即可求得结果；（II）在2次游戏中获奖次数X的取值是0、1、2，根据上面的结果，代入公式得到结果，写出分布列，求出数学期望．解答：（I）解：设“在X次游戏中摸出i个白球”为事件Ai（i=，0，1，2，3），“在1次游戏中获奖”为事件B，则B=A2∪A3，又P（A3）=，P（A2）==，且A2，A3互斥，所以P（B）=P（A2）+P（A3）=+=；（II）解：由题意可知X的所有可能取值为0，1，2.所以X的分布列是X 0 1 2PX的数学期望E（X）=0×+1×+2×=．点评： 本题考查古典概型及共概率计算公式，离散型随机变量的分布列数学期望、互斥事件和相互独立事件等基础知识，考查运用概率知识解决实际问题的能力．21．（12分）当n ∈N *时，，T n =+++…+．（Ⅰ）求S 1，S 2，T 1，T 2；（Ⅱ）猜想S n 与T n 的关系，并用数学归纳法证明．考点： 数学归纳法；数列的求和． 专题： 点列、递归数列与数学归纳法．分析： （Ⅰ）由已知直接利用n=1，2，求出S 1，S 2，T 1，T 2的值；（Ⅱ）利用（1）的结果，直接猜想S n =T n ，然后利用数学归纳法证明，①验证n=1时猜想成立；②假设n=k 时，S k =T k ，通过假设证明n=k+1时猜想也成立即可． 解答： 解：（Ⅰ）∵当n ∈N *时，，T n =+++…+．∴S 1=1﹣=，S 2=1﹣+﹣=，T 1==，T 2=+=（2分） （Ⅱ）猜想：S n =T n （n ∈N *），即：1﹣+﹣+…+﹣=+++…+（n ∈N *）（5分） 下面用数学归纳法证明： ①当n=1时，已证S 1=T 1（6分） ②假设n=k 时，S k =T k （k≥1，k ∈N *），即：1﹣+﹣+…+﹣=+++…+（8分）则：S k+1=S k +﹣=T k +﹣（10分）=+++…++﹣（11分）=++…+++（﹣）=++…++=T k+1，由①，②可知，对任意n ∈N *，S n =T n 都成立．（14分）点评： 本题是中档题，考查数列递推关系式的应用，数学归纳法证明数列问题的方法，考查逻辑推理能力，计算能力．22．（12分）已知函数f （x ）=lnx+x 2． （Ⅰ）求h （x ）=f （x ）﹣3x 的极值；（Ⅱ）若函数g （x ）=f （x ）﹣ax 在定义域内为增函数，求实数a 的取值范围； （Ⅲ）设F （x ）=2f （x ）﹣3x 2﹣k ，k ∈R ，若函数F （x ）存在两个零点m ，n （0＜m ＜n ），且满足2x 0=m+n ，问：函数F （x ）在（x 0，F （x 0））处的切线能否平行于x 轴？若能，求出该切线方程，若不能，请说明理由．考点： 利用导数研究函数的极值；利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．专题： 综合题；导数的综合应用．分析： （Ⅰ）求导数，利用极值的定义，求h （x ）=f （x ）﹣3x 的极值； （Ⅱ）根据题意写出g （x ）再求导数，由题意知g′（x ）≥0，x ∈（0，+∞）恒成立，转化为a≤2x+，再利用基本不等式求右边的最小值，即可求得实数a 的取值范围；（Ⅲ）先假设F （x ）在（x 0，F （x 0））的切线平行于x 轴，其中F （x ）=2lnx ﹣x 2﹣kx ．结合题意列出方程组，利用换元法导数研究单调性，证出ln ＜在（0，1）上成立，从而出现与题设矛盾，说明原假设不成立．由此即可得到函数F （x ）在（x 0，F （x 0））处的切线不能平行于x 轴．解答：解：（Ⅰ）由已知，，令=0，得，所以h（x）极小值=h（1）=﹣2，（Ⅱ）因为g（x）=f（x）﹣ax=lnx+x2﹣ax，属于g′（x）=+2x﹣a由题意知，g′（x）≥0，x∈（0，+∞）恒成立，即a≤（2x+）min又x＞0，2x+≥2，当且仅当x=时等号成立故（2x+）min=2，所以a≤2（Ⅲ）设F（x）在（x0，F（x））的切线平行于x轴，其中F（x）=2lnx﹣x2﹣kx结合题意，有①﹣②得2ln﹣（m+n）（m﹣n）=k（m﹣n）所以k=﹣2x，由④得k=﹣2x所以ln=…⑤设u=∈（0，1），得⑤式变为lnu﹣=0（u∈（0，1）），设y=lnu﹣（u∈（0，1）），可得y′=＞0，所以函数y=lnu﹣在（0，1）上单调递增，因此，y＜y|u=1=0，即lnu﹣＜0，也就是ln＜此式与⑤矛盾所以函数F（x）在（x0，F（x））处的切线不能平行于x轴．点评：本题给出含有对数符号的基本初等函数函数，讨论了函数的单调性并探索函数图象的切线问题，着重考查了导数的几何意义和利用导数研究函数的单调性等知识，属于中档题．。

河南省郑州市2016-2017学年高一上学期期末考试数学试题 Word版含答案数学试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.若$\{1,2\}\subset A\subset\{1,2,3,4,5\}$，则满足条件的集合$A$的个数是（）A。

6B。

8C。

7D。

92.设$a,b\in\mathbb{R}$，集合$A=\{1,a+b,a\},B=\{0,\frac{b}{a},b\}$，若$A=B$，则$b-a=$（）A。

2B。

$-1$C。

1D。

$-2$3.下列各组函数中$f(x)$与$g(x)$的图象相同的是（）A。

$f(x)=x,g(x)=|x|$B。

$f(x)=x^2,g(x)=\begin{cases}x,&(x\geq 0)\\-x,&(x<0)\end{cases}$C。

$f(x)=1,g(x)=x$D。

$f(x)=x,g(x)=\begin{cases}x,&(x\geq0)\\0,&(x<0)\end{cases}$4.下列函数中，既是偶函数又在$(-\infty,0)$内为增函数的是（）A。

$y=-\frac{1}{2}$B。

$y=x^2$C。

$y=x+1$D。

$y=\log_3(-x)^2$5.三个数$a=0.32,b=\log_2 0.3,c=2^0.3$之间的大小关系为（）A。

$a<c<b$B。

$a<b<c$C。

$b<a<c$D。

$b<c<a$6.下列叙述中错误的是（）A。

若点$P\in\alpha,P\in\beta$且$\alpha\cap\beta=l$，则$P\in l$B。

三点$A,B,C$能确定一个平面C。

若直线$a\parallel b$，则直线$a$与$b$能够确定一个平面D。

若点$A\in l,B\in l$且$A\in\alpha,B\in\alpha$，则$l\subset\alpha$7.方程$\log_3 x+x=3$的解所在区间是（）A。

理科数学2019—2019学年度郑州市下期期末考试高中二年级数学（理科）参照答案一、选择题:1. C．2. B. ．4. D．5. D．6. B．8. D．9.B. 10.B. 11. C ．12. A.二、填空题:13. 60；14. 4 2; 15. 2 33; 16.38.三、解答题：17.证明：因为a 0，所以方程最少有一个实根bx . .................2 分a假设方程不仅一个实根，没关系设x1, x2 是它的两个不一样的实根，即a x1 b，ax2 b .两式相减得a(x1 x2 )0. ..................6 分因为x1 x2 ，所以x1 x2 0，所以应有 a 0，这与已知矛盾，故假设错误...................8 分所以，当 a 0，方程ax b有且只有一个根..................10 分18. 解：（I ）由2 103 9 3 2 2 3 34 4 9 9(1 x x )(1 x) (1 x )(1 x) (1 x )(1 9x C x C x C x L C x )9 9 9 9所以 4x 的系数为4C9 9 135.................6 分（II ）因为5555 55 1 54 54 55 1 54 5455 6 56 1 (56 C 56 L C 56 1) 6 (56 C 56 L C 56 ) 755 55 55 55..................10 分所以5555 6 除以8 的余数为 1. . ................12 分19. 解：（I）由题意，K2= ≈＜50. 708，........3 分∴没有60%的掌握以为“微信控”与“性别”有关；.................4 分（II ）从参加检查的女性用户中按分层抽样的方法，比率为3：2，选出 5 人赠予营养面膜 1 份，由题知X=1 ，2，3，则.................7 分P（X=1 ）= ，P（X=2 ）= ，P（X=3 ）= ．.................10 分X 的分布列为：X 1 2 3P.................11 分随机变量X 的数学希望为EX =1×0.3+2×0.6+3×0.1=1．.8 .................12 分20.解：（I）当x 0时，f x e x a f x e x a2 ..................2 分x 3, 2 x2因为y f x 在x2处获得极值，所以 f (2) 0 ，解得 2a 2 e .. ................3 分经考据满足题意，所以 2a 2 e . .................5 分(II) 由题意知y f x 的图像上存在两点关于原点对称，即y x2e x a 2x30 图象上存在一点, 0x0 y x ，使得0 02 ax a2 xx0, y 在y x 3 3 0 的图象上0y 0 y2x3axx2e 0 x a2a2 33消去x 2 2 2y ，得2e 0 x a 3 x 3ax a 30 0 0 0，化简得ax2e 0x...................8 分则由题意关于x 的方程0 ax2e在0, 上有解.当x1时，h x 0，h x 在1,为增函数；第5 页当0 x 1时，h x 0，h x 在0,1 为减函数. ..................10 分所以h x h 1 2e,且x 时，h x ; x 0时，h x ，即h x 的值域为2e, .所以当 a 2e时，方程ax2ex在0, 上有解.即当a 2e时，函数y f x 的图像上存在两点关于原点对称. ..................12 分21. 解：（Ⅰ）1 1 1a2 ,a ,a...............3 分3 42 3 3 4 4 51*（Ⅱ）由（Ⅰ）猜想a n (n N ），..................4 分n(n 1)下用数学归纳法证明之证明：（1）当n 1时，猜想成立.（2）假设n k 时，猜想成立，即 ak1k(k 1),那么n k 1时，2 2S 1 (k 1) a 1,即S a 1 (k 1) a 1.k k k k k12 ( 1)2 2k a k a k a k a ，..................6 分k 1 k 1 k 1k(k 1)得1a k ，即n k 1时成立.1 k k( 1) (2)由（1）（2）知猜想正确，1a n . ..................8 分n(n 1)1 1 1 12所以i n1bi1 1 1 1 1 1 3 1 1 1（1 ) ( ),L2 3 2 4 n n 2 4 2 n 1 n 2第6 页所以i n13b .................12 分i4x ,则f (x) e x k ,................1 分22 解：（I）由f (x) e kx k (k R)若k0,则f (x) 0 ,故y f (x) 在( , ) 上单调递加；,................3 分若k 0,令 f (x) 0 ,解得x ln k ;令 f (x) 0 ,解得x ln k ,所以单调递加区间为(ln k, ) , 单调递减区间为( ,ln k) .................5 分(II) （i)由题意:由(1) 可知, 当k 0时,函数至多只有一个零点,不吻合题意,舍去;ln k k k k , 解得k e2 , 此时 f (1) e 0 ; x 时, k 0 时, 令 f (ln k) e ln 0f (x) 0 ,所以会有两个零点,吻合题意.2综上:实数k的取值范围是( , )e ................8 分(ii) 由（2）可知： 22 kk e 时，此时f (1) e 0;x 时，f (x) 0,且f (2) e 0,x x所以(1,2), (2, ),x1 x 由e 1 kx k,e 2 kx k ，相除后获得2 1 2xe2x1x2x111两边取对数得ln( 1) ln( 1)x2 x x x ，1 2 1令1,1, y2 x y x 即2 1 1y2y2 y ln y ln y ln ，1 2 1y12( y y ) y要证x1 x2 4,即证y1 y2 2，即证ln ,2 1 2y y y..................10 分即证构造函数( 1)t 1, h(t ) ln t t y t 1 t 1121 2(t 1) 2(t 1) (t 1)由h (t ) 0 , y h(t ) 单调递加,则h(t) h (1) 0 ,2 t t2tt 1 1故不等式成立,综上即原不等式成立. .................12 分第7 页。

2016—2017学年度郑州市下期期末考试八年级思想品德参考答案二、辨别与分析（10分）18.（1）信息泄露会侵害个人隐私，影响生活的自由与安宁，甚至危及财产安全。

（3分）（2）扫码支付已成为不可抗拒的潮流（或深受人们欢迎），不能因其存在一定风险而简单叫停。

（2分）（3）只要不断提高防伪技术，加强监管，消费者提高警惕，就可以有效防控扫码风险。

（2分）（4）我们既应看到扫码支付的优势，支持其发展；又应重视其存在的风险，不断完善改进，共同分享其方便快捷、省时省力的服务。

（3分）三、观察与思考（26分）19.（1）侵犯了他人的人格尊严；违反道德和法律；滥用言论自由权；是缺乏责任意识的表现；扰乱社会秩序；未能合理调控情绪。

（两方面即可，4分）（2）没有珍惜自身人格尊严；是一种扭曲的价值观（或：是一种急功近利的思想）；污染了网络环境。

（两方面即可，6分）（3）示例：利用网络查找自己需要的资料信息；利用网络与朋友沟通交流。

（两方面即可，4分）20.①保障公民财产安全（或：保障公民的合法财产所有权；保护消费者的安全权）。

②保障公民的隐私权。

③保障公共安全；维护人民群众生命健康权。

④保护知识产权；尊重他人的劳动和创造。

（每个要点3分，共12分）四、活动与探索（13分）21.（1）崇尚正义、英勇无畏（不怕牺牲）、助人为乐、勇于担当、无私奉献等等。

（答出一条给2分，两条给3分）（2）见义勇为者可能因此陷入困境，需要法律救助和“护身”；权利义务具有一致性，见义勇为者为社会作出贡献，理应受到尊重和认可；为见义勇为者“护身”体现了社会公平正义，是法律的价值与追求；法律与社会主义道德相互促进，法律“护身”有利于培育社会主义核心价值观；等等。

（两方面即可，6分）（3）开展道德模范评选，表彰见义勇为者；对见义勇为牺牲人员家属及子女进行安置；对讹诈、诬陷或打击报复见义勇为人员的行为，依法予以严惩；因见义勇为而受伤的，政府要给予资金进行治疗；见义勇为人员贷款、创业时，给予支持和照顾；企业优先聘用见义勇为人员；等等。