等腰梯形小练习1
- 格式:doc
- 大小:71.00 KB
- 文档页数:2

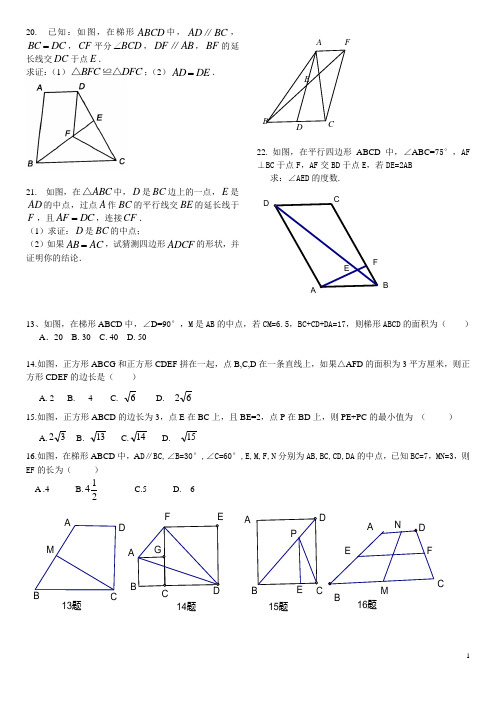
20. 已知:如图,在梯形ABCD 中,AD BC ∥, B C D C =,CF 平分BCD ∠,DF AB ∥,BF 的延长线交DC 于点E .求证:(1)BFC DFC △≌△;(2)AD DE =.21. 如图,在ABC △中,D 是BC 边上的一点,E 是AD 的中点,过点A 作BC 的平行线交BE 的延长线于F ,且AF DC =,连接CF . (1)求证:D 是BC 的中点;(2)如果AB AC =,试猜测四边形ADCF 的形状,并证明你的结论.22. 如图,在平行四边形ABCD 中,∠ABC=75°,AF⊥BC 于点F ,AF 交BD 于点E ,若DE=2AB 求:∠AED 的度数.F EDCBA13、如图,在梯形ABCD 中,∠D=90°,M 是AB 的中点,若CM=6.5,BC+CD+DA=17,则梯形ABCD 的面积为( ) A .20 B. 30 C. 40 D. 5014.如图,正方形ABCG 和正方形CDEF 拼在一起,点B,C,D 在一条直线上,如果△AFD 的面积为3平方厘米,则正方形CDEF 的边长是( ) A. 2 B. 4 C.6 D. 6215.如图,正方形ABCD 的边长为3,点E 在BC 上,且BE=2,点P 在BD 上,则PE+PC 的最小值为 ( ) A.32 B.13 C.14 D. 1516.如图,在梯形ABCD 中,A D ∥BC,∠B=30°,∠C=60°,E,M,F,N 分别为AB,BC,CD,DA 的中点,已知BC=7,MN=3,则EF 的长为( ) A .4 B.214C.5D. 6 16题15题14题13题GF ED C BA MD CBA PEDCBANM F ED CBABA FCED一 选择题1.下面10个命题中的正确个数为( )(1)只有一组对边平行的四边形是梯形;(2)梯形的内角最多有两个是锐角;(3)等腰梯形的两条对角线相等; (4)等腰梯形的对角互补;(5)我们通常把梯形中较短的底叫上底,较长的底叫下底;(6)梯形的高一定小于腰的长度;(7)如果一个梯形是轴对称图形,则它一定是等腰梯形;(8)对角互补的梯形为等腰梯形;(9)如果梯形的一组对角互补,则另一组对角也互补;(10)延长等腰梯形的两腰交于一点后形成的图形中的三角形一定是等腰三角形。

2017年中考数学专项复习《梯形(1)》练习(无答案)浙教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017年中考数学专项复习《梯形(1)》练习(无答案)浙教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017年中考数学专项复习《梯形(1)》练习(无答案)浙教版的全部内容。
梯形(01)一、选择题1.如图的灰色小三角形为三个全等大三角形的重迭处,且三个大三角形各扣掉灰色小三角形后分别为甲、乙、丙三个梯形.若图中标示的∠1为58°,∠2为62°,∠3为60°,则关于甲、乙、丙三梯形的高的大小关系,下列叙述何者正确?( )A.乙>甲>丙B.乙>丙>甲C.丙>甲>乙D.丙>乙>甲2.如图,梯形ABCD中,AD∥BC,E点在BC上,且AE⊥BC.若AB=10,BE=8,DE=6,则AD 的长度为( )A.8 B.9 C.6D.63.如图,梯形ABCD中,AD∥BC,AB=,BC=4,连结BD,∠BAD的平分线交BD于点E,且AE∥CD,则AD的长为()A.B.C.D.24.如图,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O,则下列判断不正确的是()A.△ABC≌△DCB B.△AOD≌△COB C.△ABO≌△DCO D.△ADB≌△DAC5.装有一些液体的长方体玻璃容器,水平放置在桌面上时,液体的深度为6,其正面如图1所示,将容器倾斜,其正面如图2所示.已知液体部分正面的面积保持不变,当AA1=4时,BB1=( )A.10 B.8 C.6 D.46.如图,已知等腰梯形ABCD中,AD∥BC,AB=CD=AD=3,梯形中位线EF与对角线BD相交于点M,且BD⊥CD,则MF的长为()A.1.5 B.3 C.3.5 D.4。

人教版小学四年级数学上册同步练习5.2平行四边形和梯形(含答案)一、填空题1.等腰梯形周长35cm ,上底5cm ,一条腰长7cm ,它的下底长是( )厘米。
2.一个平行四边形的周长是32cm ,其中一条边长是10cm 。
把它拉成一个长方形(如图)这个长方形的宽是( )cm ,这个长方形的面积是( )cm 2。
(第2题) (第3题) 3.下图四边形ABCD 是一个梯形,它的高是( )cm ;如果把点D 向( )平移( )格,这个梯形就变成一个平行四边形。
4.从平行四边形一条边上的一点向对边引一条( ),这点和( )之间的线段叫做平行四边形的高,( )所在的边叫做平行四边形的底。
5.通过动手拉平行四边形框架的活动,我们知道,平行四边形有( )的特性,生活中( )运用了这一特性。
6.在等腰梯形中画一条高,可以将它分割成两个完全一样的( )形;也可以将它分割成一个( )形和一个( )形。
7.已知四边形ABCD 是等腰梯形,用量角器量一量,你发现了什么? A ∠=( )° B ∠=( )° C ∠=( )° D ∠=( )° 我发现:______________________________________________________。
(第7题) (第8题) 8.如图,在给定的正方形点子图上,找一点D (D 在格点上),使ABCD 成为梯形。
那么符合条件的D点的位置有( )个。
二、选择题9.平行四边形的两组对边()。
A.分别平行B.分别垂直C.相交D.以上答案都不对10.一个等腰梯形上底3米,下底5米,腰4米,这个等腰梯形的周长是()米。
A.12B.15C.1611.把一个平行四边形任意分割成两个梯形,这两个梯形中()总是相等的。
A.高B.面积C.上下两底的和12.平行四边形的高有()条。
A.无数B.2C.413.把一个平行四边形框架拉成长方形,这个长方形和原来的平行四边形比,面积()。

梯形(1)
梯形的定义:
一组对边平行而另一组对边不平行的四边形叫做梯形
梯形的相关概念
一组对边平行而另一组对边不平行的四边形叫做梯形ABCD 底边底边腰腰平行的两边叫做梯形的底边
不平行的两边叫做梯形的腰
夹在两底之间的垂线段叫做梯形的高
特殊的梯形
有一个角是直角
有两条腰相等的梯形叫做等腰梯形
一腰和底垂直的梯形叫做直角梯形
等腰梯形的性质结论:(3)等腰梯形同一底上的两个内角相等
(1)两腰相等。
(4)等腰梯形是轴对称图形
∵四边形ABCD 是等腰梯形,AD∥BC∴AB=CD∴∠BAD= ∠CDA,
∠ABC= ∠BCD
(2)对角线相等∴AC=BD 请你证明上面的性质
等腰梯形的性质定理
等腰梯形同一底上的两个底角相等,两条对角线相等。
已知:在梯形ABCD 中,AD∥BC,AB=DC。
求证:(1)∠ABC=∠DCB,∠BAD=∠CDA
(2)AC=BDEEF 议一议。

关于梯形的练习题一、选择题:1. 梯形的上底和下底平行,以下哪个图形不是梯形?A. 平行四边形B. 长方形C. 菱形D. 正方形2. 梯形的面积公式是:A. \( \frac{1}{2} \times (上底 + 下底) \times 高 \)B. \( (上底 + 下底) \times 高 \)C. \( \frac{1}{2} \times 上底 \times 高 \)D. \( 下底 \times 高 \)3. 一个梯形的上底为5厘米,下底为10厘米,高为4厘米,其面积是:A. 20平方厘米B. 30平方厘米C. 40平方厘米D. 50平方厘米4. 如果一个梯形的上底和下底分别增加2厘米,高不变,那么面积会增加多少?A. 4平方厘米B. 6平方厘米C. 8平方厘米D. 10平方厘米5. 以下哪个选项不是梯形的性质?A. 梯形的中位线等于两底边长的一半之和。
B. 梯形的对角线相等。
C. 梯形的两底边平行。
D. 梯形的两腰不一定相等。
二、填空题:6. 一个梯形的上底是8厘米,下底是12厘米,高是3厘米,其面积是________平方厘米。
7. 梯形的中位线长度等于________。
8. 如果一个梯形的上底是10厘米,下底是20厘米,高是6厘米,那么这个梯形的中位线长度是________厘米。
9. 梯形的内角和为________度。
10. 一个等腰梯形的两腰相等,其上底和下底的长度分别是6厘米和12厘米,如果这个等腰梯形的高是4厘米,那么这个等腰梯形的面积是________平方厘米。
三、简答题:11. 描述如何利用梯形的面积公式计算梯形的面积。
12. 解释为什么梯形的对角线不一定相等。
四、计算题:13. 一个梯形的上底是15厘米,下底是25厘米,高是7厘米,求这个梯形的面积。
14. 一个梯形的上底是12厘米,下底是18厘米,高是5厘米,如果将这个梯形分成两个小梯形,其中一个小梯形的上底是原梯形上底的一半,求这个小梯形的面积。
等腰梯形性质练习题 姓名: 1.填空(1)在梯形ABCD 中,已知AD ∥BC ,∠B=50°,∠C=80°,AD=a ,BC=b ,,则DC= . (2)直角梯形的高为6cm ,有一个角是30°,则这个梯形的两腰分别是 和 . (3)等腰梯形 ABCD 中,AB ∥DC ,A C 平分∠DAB ,∠DAB=60°,若梯形周长为8cm ,则AD= .2.已知:如图,在等腰梯形ABCD 中,AB ∥CD ,AB >CD ,AD=BC ,BD 平分∠ABC ,∠A=60°,梯形周长是20cm ,求梯形的各边的长.3.下列命题中,真命题是( )A 、有一组对边平行但不相等的四边形是梯形B 、直角梯形中只有一个直角C 、等腰梯形的对角线相等且互相垂直D 、等腰梯形是轴对称图形,有两条对称轴4.在梯形ABCD 中,∠D =90°,AD =DC =4,AB =1,E 为AD 的中点,则点E 到BC 的距离为__________.5.已知等腰梯形的锐角等于60°它的两底分别为15cm 和49cm ,求它的腰长和面积. 6.已知,如图,梯形ABCD 中,AD ∥BC ,E 是AB 的中点,DE ⊥CE ,求证:AD+BC=DC .(延长DE 交CB 延长线于点F ,由全等可得结论)7.已知:如图,梯形ABCD 中,CD//AB ,∠=A 40 ,∠=B 70 . 求证:AD=AB —DC .8、梯形ABCD 中,AD ∥BC ,AB =CD =AD =1,∠B =60°,直线MN 为梯形ABCD 的对称轴,P 为MN 上一点,那么PC +PD 的最小值为______.等腰梯形判定练习 姓名:1.等腰梯形一底角60,上、下底分别为8,18,则它的腰长为_____,高为______,面积是_____.2.梯形两条对角线分别为15,20,高为12,则此梯形面积为_________. 3.已知:如图,在四边形ABCD 中,∠B=∠C ,AB 与CD 不平行,且AB=CD . 求证:四边形ABCD 是等腰梯形.4、已知,如图,在四边形ABCD 中,AB >DC ,∠1=∠2,AC=BD ,求证:四边形ABCD 是等腰梯形5.如图4.9-9,梯形ABCD 中,AB ∥CD ,AD=BC ,CE ⊥AB 于E ,若AC ⊥BD 于G . 求证:CE=21(AB+CD ).梯形中位线练习题1.已知梯形中位线长是5cm ,高是4cm ,则梯形的面积是 。