1-2 信源熵-习题答案
- 格式:ppt
- 大小:1.73 MB
- 文档页数:61

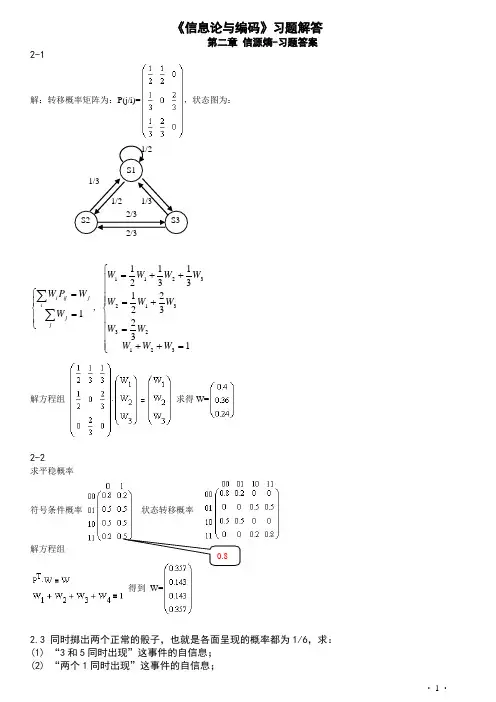
《信息论与编码》习题解答第二章 信源熵-习题答案2-1解:转移概率矩阵为:P(j/i)=,状态图为:⎪⎩⎪⎨⎧==∑∑j jj ij ii W W P W 1,⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=++=+=++=1323221313121321233123211W W W W W W W W W W W W 解方程组求得W=2-2求平稳概率符号条件概率状态转移概率解方程组得到 W=2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求: (1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
解: (1)bitx p x I x p i i i 170.4181log )(log )(18161616161)(=-=-==⨯+⨯=(2)bitx p x I x p i i i 170.5361log )(log )(3616161)(=-=-==⨯=(3)共有21种组合:其中11,22,33,44,55,66的概率是3616161=⨯ 其他15个组合的概率是18161612=⨯⨯symbol bit x p x p X H ii i / 337.4181log 18115361log 3616)(log )()(=⎪⎭⎫ ⎝⎛⨯+⨯-=-=∑(4)参考上面的两个点数的排列,可以得出两个点数求和的概率分布如下:symbolbit x p x p X H X P Xii i / 274.3 61log 61365log 365291log 912121log 1212181log 1812361log 3612 )(log )()(36112181111211091936586173656915121418133612)(=⎪⎭⎫ ⎝⎛+⨯+⨯+⨯+⨯+⨯-=-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡∑(5)bit x p x I x p i i i 710.13611log)(log )(3611116161)(=-=-==⨯⨯=2-4(4)2.5 居住某地区的女孩子有25%是大学生,在女大学生中有75%是身高160厘米以上的,而女孩子中身高160厘米以上的占总数的一半。


5.1设有信源⎭⎬⎫⎩⎨⎧=⎪⎪⎭⎫ ⎝⎛01.01.015.017.018.019.02.0)(7654321a a a a a a a X P X (1)求信源熵H(X)(2)编二进制香农码(3)计算其平均码长及编码效率解:(1)H(X)=-)(log )(21i ni i a p a p ∑=H(X)=-0.2log 20.2-0.19log 20.19-0.18log 20.18-0.17log 20.17-0.15log 20.15-0.log 20.1-0.01log 20.01H(X)=2.61(bit/sign)(2)ia i P(ai)jP(aj)ki码字a 001a 10.210.0030002a 20.1920.2030013a 30.1830.3930114a 40.1740.5731005a 50.1550.7431016a 60.160.89411107a 70.0170.9971111110(3)平均码长:-k =3*0.2+3*0.19+3*0.18+3*0.17+3*0.15+4*0.1+7*0.01=3.14(bit/sign)编码效率:η=R X H )(=-KX H )(=14.361.2=83.1%5.2对习题5.1的信源二进制费诺码,计算器编码效率。
⎭⎬⎫⎩⎨⎧=⎪⎪⎭⎫ ⎝⎛0.01 0.1 0.15 0.17 0.18 0.19 2.0 )(7654321a a a a a a a X P X 解:Xi)(i X P 编码码字ik 1X 0.2000022X 0.191001033X 0.18101134X 0.17101025X 0.151011036X 0.110111047X 0.01111114%2.9574.2609.2)()(74.2 01.0.041.0415.0317.0218.0319.032.02 )(/bit 609.2)(1.5=====⨯+⨯+⨯+⨯+⨯+⨯+⨯===∑KX H R X H X p k K sign X H ii i η已知由5.3、对信源⎭⎬⎫⎩⎨⎧=⎪⎪⎭⎫ ⎝⎛01.01.015.017.018.019.02.0)(7654321x x x x x x x X P X 编二进制和三进制赫夫曼码,计算各自的平均码长和编码效率。

第二章习题:补充题:掷色子,(1)若各面出现概率相同(2)若各面出现概率与点数成正比试求该信源的数学模型 解: (1)根据61()1ii p a ==∑,且16()()p a p a ==,得161()()6p a p a ===,所以信源概率空间为123456111111666666⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P (2)根据61()1i i p a ==∑,且126(),()2,()6p a k p a k p a k ===,得121k =。
123456123456212121212121⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P 2-2 由符号集{}0,1组成的二阶马尔可夫链,其转移概率为P(0/00)=0.8,P(0/11)=0.2,P(1/00)=0.2, P(1/11)=0.8,P(0/01)=0.5,P(0/10)=0.5,P(1/01)=0.5,P(1/10)=0.5。
画出状态图,并计算各状态的稳态概率。
解:由二阶马氏链的符号转移概率可得二阶马氏链的状态转移概率为: P(00/00)=0.8 P(10/11)=0.2 P(01/00)=0.2 P(11/11)=0.8 P(10/01)=0.5 P(00/10)=0.5 P(11/01)=0.5 P(01/10)=0.5二进制二阶马氏链的状态集S={,1S 432,,S S S }={00,01,10,11}0.80.20.50.50.50.50.20.8⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦P 状态转移图各状态稳定概率计算:⎪⎪⎩⎪⎪⎨⎧==∑∑==41411i jij i j j WP W W 即 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=++++++=+++=+++=+++=143214443432421414434333232131342432322212124143132121111W W W W P W P W P W P W W P W P W P W P W W P W P W P W P W w P W P W P W P W W0.80.8得:14541==W W 14232==W W 即:P(00)=P(11)=145 P(01)=P(10)=1422-6掷两粒骰子,当其向上的面的小圆点数之和是3时,该消息所包含的信息量是多少?当小圆点数之和是7时,该消息所包含的信息量又是多少? 解:2211111(3)(1)(2)(2)(1)666618(3)log (3)log 18()P P P P P I p ⎧=⋅+⋅=⨯+⨯=⎪⎨⎪=-=⎩比特 226(7)(1)(6)(2)(5)(3)(4)(4)(3)(5)(2)(6)(1)36(7)log (7)log 6()P P P P P P P P P P P P P I p ⎧=⋅+⋅+⋅+⋅+⋅+⋅=⎪⎨⎪=-=⎩比特2-72-7设有一离散无记忆信源,其概率空间为⎥⎥⎦⎤⎢⎢⎣⎡=====⎥⎦⎤⎢⎣⎡81,41,41,833,2,1,04321x x x x P X该信源发出的消息符号序列为(202 120 130 213 001 203 210 110 321 010 021 032 011 223 210),求此消息的自信息量是多少及平均每个符号携带的信息量?解:消息序列中,“0”个数为1n =14,“1”个数为2n =13,“2”个数为3n =12,“3”个数为4n =6. 消息序列总长为N =1n +2n +3n +4n =45(个符号)(1) 消息序列的自信息量: =I ∑==41)(i iix I n -)(log 412i i ix p n∑== 比特81.87)3(log 6)2(log 12)1(log 13)0(log 142222=----p p p p(2) 平均每个符号携带的信息量为:)/(95.14571.87符号比特==N I 2-14 在一个二进制信道中,信息源消息集X={0,1},且P(1)=P(0),信宿的消息集Y={0,1},信道传输概率P (1/0)=1/4,P (0/1)=1/8。


2.4 设离散无记忆信源⎭⎬⎫⎩⎨⎧=====⎥⎦⎤⎢⎣⎡8/14/1324/18/310)(4321x x x x X P X ,其发出的信息为(202120130213001203210110321010021032011223210),求 (1) 此消息的自信息量是多少?(2) 此消息中平均每符号携带的信息量是多少?解:(1) 此消息总共有14个0、13个1、12个2、6个3,因此此消息发出的概率是:62514814183⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛=p此消息的信息量是:bit p I811.87log =-=(2) 此消息中平均每符号携带的信息量是:bitn I 951.145/811.87/==41()()log () 2.010i i i H X p x p x ==-=∑2.6 设信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡17.016.017.018.019.02.0)(654321x x x x x x X P X ,求这个信源的熵,并解释为什么H(X) > log6不满足信源熵的极值性。
解:585.26log )(/ 657.2 )17.0log 17.016.0log 16.017.0log 17.018.0log 18.019.0log 19.02.0log 2.0( )(log )()(26=>=+++++-=-=∑X H symbol bit x p x p X H ii i 不满足极值性的原因是107.1)(6>=∑iix p 。
2.7 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求: (1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
解:(1)用随机事件i x 表示“3和5同时出现”,则bitx p x I x p i i i 170.4181log )(log )(18161616161)(=-=-==⨯+⨯=(2) 用随机事件i x 表示“两个1同时出现”,则bitx p x I x p i i i 170.5361log )(log )(3616161)(=-=-==⨯=(3)两个点数的排列如下: 11 12 13 14 15 16 21 22 23 24 25 26 31 32 33 34 35 36 41 42 43 44 45 46 51 52 53 54 55 56 61 6263646566共有21种组合:其中11,22,33,44,55,66的概率是3616161=⨯ 其他15个组合的概率是18161612=⨯⨯symbol bit x p x p X H ii i / 337.4181log 18115361log 3616)(log )()(=⎪⎭⎫ ⎝⎛⨯+⨯-=-=∑(4)参考上面的两个点数的排列,可以得出两个点数求和的概率分布如下:sym bolbit x p x p X H X P X ii i / 274.3 61log 61365log 365291log 912121log 1212181log 1812361log 3612 )(log )()(36112181111211091936586173656915121418133612)(=⎪⎭⎫ ⎝⎛+⨯+⨯+⨯+⨯+⨯-=-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡∑(5)bitx p x I x p i i i 710.13611log )(log )(3611116161)(=-=-==⨯⨯=2.10 对某城市进行交通忙闲的调查,并把天气分成晴雨两种状态,气温分成冷暖两个状态,调查结果得联合出现的相对频度如下:忙晴雨冷 12暖 8暖 16冷 27闲晴雨冷 8暖 15暖 12冷 5若把这些频度看作概率测度,求: (1) 忙闲的无条件熵;(2) 天气状态和气温状态已知时忙闲的条件熵;(3) 从天气状态和气温状态获得的关于忙闲的信息。

第二章信息的度量2.1信源在何种分布时,熵值最大?又在何种分布时,熵值最小?答:信源在等概率分布时熵值最大;信源有一个为1,其余为0时熵值最小。
2.2平均互信息量I(X;Y)与信源概率分布q(x)有何关系?与p(y|x)又是什么关系?答:若信道给定,I(X;Y)是q(x)的上凸形函数;若信源给定,I(X;Y)是q(y|x)的下凸形函数。
2.3熵是对信源什么物理量的度量?答:平均信息量2.4设信道输入符号集为{x1,x2,……xk},则平均每个信道输入符号所能携带的最大信息量是多少?答:kk k xi q xi q X H i log 1log 1)(log )()(2.5根据平均互信息量的链规则,写出I(X;YZ)的表达式。
答:)|;();();(Y Z X I Y X I YZ X I 2.6互信息量I(x;y)有时候取负值,是由于信道存在干扰或噪声的原因,这种说法对吗?答:互信息量)()|(log );(xi q yj xi Q y x I ,若互信息量取负值,即Q(xi|yj)<q(xi),说明事件yi 的出现告知的是xi 出现的可能性更小了。
从通信角度看,视xi 为发送符号,yi 为接收符号,Q(xi|yj)<q(xi),说明收到yi 后使发送是否为xi 的不确定性更大,这是由于信道干扰所引起的。
2.7一个马尔可夫信源如图所示,求稳态下各状态的概率分布和信源熵。
答:由图示可知:43)|(41)|(32)|(31)|(41)|(43)|(222111110201s x p s x p s x p s x p s x p s x p 即:43)|(0)|(41)|(31)|(32)|(0)|(0)|(41)|(43)|(222120121110020100s s p s s p s s p s s p s s p s s p s s p s s p s s p 可得:1)()()()(43)(31)()(31)(41)()(41)(43)(210212101200s p s p s p s p s p s p s p s p s p s p s p s p得:114)(113)(114)(210s p s p s p )]|(log )|()|(log )|()[()]|(log )|()|(log )|()[()]|(log )|()|(log )|()[(222220202121211111010100000s s p s s p s s p s s p s p s s p s s p s s p s s p s p s s p s s p s s p s s p s p H 0.25(bit/符号)2.8一个马尔可夫信源,已知:0)2|2(,1)2|1(,31)1|2(,32)1|1(x x p x x p x x p x x p 试画出它的香农线图,并求出信源熵。


· 1 ·2.1 试问四进制、八进制脉冲所含信息量是二进制脉冲的多少倍? 四进制脉冲可以表示4个不同的消息,例如:{0, 1, 2, 3}八进制脉冲可以表示8个不同的消息,例如:{0, 1, 2, 3, 4, 5, 6, 7} 二进制脉冲可以表示2个不同的消息,例如:{0, 1} 假设每个消息的发出都是等概率的,则:四进制脉冲的平均信息量symbol bit n X H / 24log log )(1=== 八进制脉冲的平均信息量symbol bit n X H / 38log log )(2=== 二进制脉冲的平均信息量symbol bit n X H / 12log log )(0=== 所以:四进制、八进制脉冲所含信息量分别是二进制脉冲信息量的2倍和3倍。
2.2 居住某地区的女孩子有25%是大学生,在女大学生中有75%是身高160厘米以上的,而女孩子中身高160厘米以上的占总数的一半。
假如我们得知“身高160厘米以上的某女孩是大学生”的消息,问获得多少信息量?设随机变量X 代表女孩子学历X x 1(是大学生) x 2(不是大学生)P(X)0.250.75设随机变量Y 代表女孩子身高 Y y 1(身高>160cm )y 2(身高<160cm )P(Y)0.50.5已知:在女大学生中有75%是身高160厘米以上的 即:bit x y p 75.0)/(11=求:身高160厘米以上的某女孩是大学生的信息量 即:bit y p x y p x p y x p y x I 415.15.075.025.0log)()/()(log )/(log )/(11111111=⨯-=-=-=2.3 一副充分洗乱了的牌(含52张牌),试问 (1) 任一特定排列所给出的信息量是多少?(2) 若从中抽取13张牌,所给出的点数都不相同能得到多少信息量?(1) 52张牌共有52!种排列方式,假设每种排列方式出现是等概率的则所给出的信息量是:!521)(=i x pbit x p x I i i 581.225!52log )(log )(==-=(2) 52张牌共有4种花色、13种点数,抽取13张点数不同的牌的概率如下: bitCx p x I C x p i i i 208.134log)(log )(4)(135213135213=-=-==· 2 ·2.4 设离散无记忆信源⎭⎬⎫⎩⎨⎧=====⎥⎦⎤⎢⎣⎡8/14/1324/18/310)(4321x x x x X P X,其发出的信息为(202120130213001203210110321010021032011223210),求 (1) 此消息的自信息量是多少?(2) 此消息中平均每符号携带的信息量是多少?(1) 此消息总共有14个0、13个1、12个2、6个3,因此此消息发出的概率是: 62514814183⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛=p 此消息的信息量是:bit p I 811.87log =-=(2) 此消息中平均每符号携带的信息量是:bit n I 951.145/811.87/==2.5 从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%,如果你问一位男士:“你是否是色盲?”他的回答可能是“是”,可能是“否”,问这两个回答中各含多少信息量,平均每个回答中含有多少信息量?如果问一位女士,则答案中含有的平均自信息量是多少?男士: symbolbit x p x p X H bitx p x I x p bit x p x I x p ii i N N N Y Y Y / 366.0)93.0log 93.007.0log 07.0()(log )()( 105.093.0log )(log )(%93)( 837.307.0log )(log )(%7)(2=+-=-==-=-===-=-==∑女士:symbol bit x p x p X H ii i / 045.0)995.0log 995.0005.0log 005.0()(log )()(2=+-=-=∑2.6 设信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡17.016.017.018.019.02.0)(654321x x x x x x X P X,求这个信源的熵,并解释为什么H(X) >log6不满足信源熵的极值性。

《通信原理》习题参考答案第一章1-1. 设英文字母E 出现的概率为0.105,x 出现的概率为0.002。
试求E 及x 的信息量。
解: )(25.3105.01)(log 2bit E I ==)(97.8002.01)(log 2bit X I == 题解:这里用的是信息量的定义公式)(1log x P I a =注:1、a 的取值:a =2时,信息量的单位为bita =e 时,信息量的单位为nita =10时,信息量的单位为哈特莱2、在一般的情况下,信息量都用bit 为单位,所以a =21-2. 某信息源的符号集由A ,B ,C ,D 和E 组成,设每一符号独立出现,其出现概率分别为1/4,1/8,1/8,3/16和5/16。
试求该信息源符号的平均信息量。
解:方法一:直接代入信源熵公式:)()()()()(E H D H C H B H A H H ++++=516165316163881881441log log log log log 22222++++=524.0453.083835.0++++= 符号)/(227.2bit =方法二:先求总的信息量I)()()()()(E I D I C I B I A I I ++++= 516316884log log log log log 22222++++= 678.1415.2332++++= )(093.12bit =所以平均信息量为:I/5=12.093/5=2.419 bit/符号题解:1、方法一中直接采用信源熵的形式求出,这种方法属于数理统计的方法求得平均值,得出结果的精度比较高,建议采用这种方法去计算2、方法二种采用先求总的信息量,在取平均值的方法求得,属于算术平均法求平均值,得出结果比较粗糙,精度不高,所以尽量不采取这种方法计算注:做题时请注意区分平均信息量和信息量的单位:平均信息量单位是bit/符号,表示平均每个符号所含的信息量,而信息量的单位是bit ,表示整个信息所含的信息量。
《信息理论与编码》习题参考答案1. 信息是什么?信息与消息有什么区别和联系?答:信息是对事物存在和运动过程中的不确定性的描述。
信息就是各种消息符号所包含的具有特定意义的抽象内容,而消息是信息这一抽象内容通过语言、文字、图像和数据等的具体表现形式。
2. 语法信息、语义信息和语用信息的定义是什么?三者的关系是什么? 答:语法信息是最基本最抽象的类型,它只是表现事物的现象而不考虑信息的内涵。
语义信息是对客观现象的具体描述,不对现象本身做出优劣判断。
语用信息是信息的最高层次。
它以语法、语义信息为基础,不仅要考虑状态和状态之间关系以及它们的含义,还要进一步考察这种关系及含义对于信息使用者的效用和价值。
三者之间是内涵与外延的关系。
第2章1. 一个布袋内放100个球,其中80个球是红色的,20个球是白色的,若随机摸取一个球,猜测其颜色,求平均摸取一次所能获得的自信息量?答:依据题意,这一随机事件的概率空间为120.80.2X x x P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦其中:1x 表示摸出的球为红球事件,2x 表示摸出的球是白球事件。
a)如果摸出的是红球,则获得的信息量是()()11log log0.8I x p x =-=-(比特)b)如果摸出的是白球,则获得的信息量是()()22log log0.2I x p x =-=-(比特)c) 如果每次摸出一个球后又放回袋中,再进行下一次摸取。
则如此摸取n 次,红球出现的次数为()1np x 次,白球出现的次数为()2np x 次。
随机摸取n 次后总共所获得信息量为()()()()1122np x I x np x I x +d)则平均随机摸取一次所获得的信息量为()()()()()()()()()112211221log log 0.72 H X np x I x np x I x n p x p x p x p x =+⎡⎤⎣⎦=-+⎡⎤⎣⎦=比特/次2. 居住某地区的女孩中有25%是大学生,在女大学生中有75%是身高1.6米以上的,而女孩中身高1.6米以上的占总数的一半。
第1章 绪论1-2 设信源X 由4个符号a,b,c,d 组成,各符号出现概率分别为3/8,1/4,1/8,1/4,每个符号的出现是独立的,求(1)信源熵H(X);(2)一个消息babcacaddabbcdcaabdcb 的信息量I 。
解:(1)符号/bit .log log log log )x (p log )x (p )x (H i i i 906141418181414183832222241=----=-=∑= (2)4148154168362222412log log log log )x (p log N I i i i ----=-=∑=bit ..494381512498=+++=若 bit ..)x (H 0264021906121=⨯=⨯个符号 是统计平均,与题意不符,为错的。
1-4 八进制数字信号在3分钟内共传送72000个码元,求码元速率和每个码元所含的信息量。
解:码元速率: B R B 40060372000=⨯=每个码元所含的信息量:bit log I 382==1-5 已知信源X 含有两个符号x 1,x 2,它们的出现概率分别为p(x 1)=q ,p(x 2)=1-q ,设信源每秒向信道发出1000个符号,求此无扰离散信道的信道容量。
解:符号/bit )q (log )q (q log q )x (p log)x (p )x (H i i i----=-=∑=1122212当21=q 时,信源熵有最大值:符号/bit H max 1= 每秒发送1000个符号,所以最大信息速率:s /bit R max b =⨯=10001信道容量:s /bit R C max b 1000==第2章 预备知识2-4 (a )试写出图P2-3(a )所示方波波形的复数傅里叶级数表示式;(b )用(a )中所得结果写出图P2-3(b )所示三角形波的复数傅里叶级数表示式。
解:(a )t n j n e n Aj t f 0)12(1)12(2)(ωπ+∞-∞=∑⋅+= (b )∑∞-∞=+⋅++=n t n j e n AT AT t f 0)12(22002)12(4)(ωπ2-9 已知)(t f 的频谱函数如图P2-5所示,画出t t fcos )(ω的频谱函数图,设τωω50=。