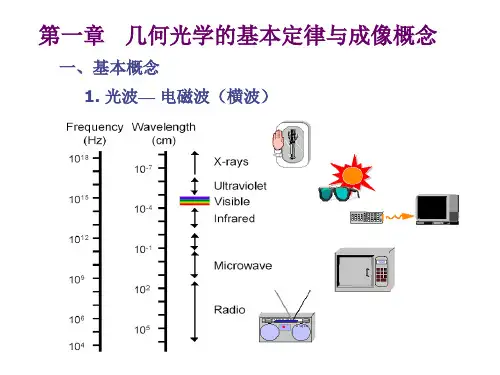
应用光学第一章总结知识点一、基本概念1. 光的本质光是一种电磁波，具有双重性质，既能像波一样传播，又能像粒子一样照射。
2. 光的特性光具有波长、频率、速度和偏振等特性，光的波长决定了它的颜色，频率决定了它的亮度，速度取决于介质的折射率，偏振决定了光的方向性。
3. 光的传播光在真空中的传播速度是光速，而在不同介质中传播的速度和方向都会发生变化。
光的传播遵循光线理论和波动理论。
4. 光的干涉和衍射光的干涉和衍射是光学现象的重要表现形式，它们揭示了光的波动性。
干涉是指两束波相遇时相互干扰的现象，衍射是指波通过孔隙或物体边缘时发生的扩散和弯曲。
5. 光的吸收和发射光与物质相互作用时会发生吸收和发射，物质的吸收和发射特性与光的波长有关。
二、光学元件1. 透镜透镜是光学系统的重要组成部分，它能够折射光线，使光线汇聚或发散。
透镜有凸透镜和凹透镜之分，可以用在光学仪器中进行成像。
2. 镜面镜面是能够反射光线的表面，具有平面镜、球面镜等形式。
镜面的反射特性与入射角和反射角有关，根据镜子的曲率不同，反射出的光线会发生聚焦或发散。
3. 棱镜棱镜是一种类似透镜的光学元件，它能够使光线发生色散，将不同波长的光线分散成不同的方向。
4. 光栅光栅是一种利用周期性的结构使光发生衍射的光学元件，它可以分解光线，用于光谱仪等领域。
5. 波片波片是一种能够改变光线偏振状态的光学元件，常用于偏振光学和激光器件中。
6. 光阑光阑是一种用于控制光线传播的光学元件，它能够限制光线的传播范围，提高光学系统的分辨率。
7. 光学滤波器光学滤波器是一种通过选择性吸收或透射特定波长光线的光学元件，它可以应用于激光器件、摄像头和光学测量中。
8. 光学偏振元件光学偏振元件是一种能够改变光线偏振状态的光学元件，包括偏振片、偏光镜和偏振棱镜等。
三、光学系统1. 成像系统成像系统是由透镜、镜面和光学滤波器等组成，它能够将物体上的信息投影到成像平面上，形成清晰的图像。
