当前位置：文档之家 › 应用光学课件第六章.

应用光学课件第六章.

  • 格式：ppt
  • 大小：2.97 MB
  • 文档页数：122

下载文档原格式

  / 122

合集下载

应用光学课件-PPT

应用光学课件-PPT
4)若视阑为长方形或正方形,其线视场按对角线计算。
5)入射窗、出射窗、视阑之间得相互共轭关系。
大家应该也有点累了,稍作休息
大家有疑问得,可以询问与交流
10
例:有一光学系统,透镜O1、O2得口径D1=D2=50mm,焦距 f1′= f2′=150mm,两透镜间隔为300mm,并在中间置一光 孔O3,口径D3=20mm,透镜O2右侧150mm处再置一光孔O4,口 径D4=40mm,平面物体处于透镜O1左侧150mm处。求该系统 得孔径光阑、入瞳、出瞳、视场光阑、入窗、出窗得位 置与大小。
两正薄透镜组L1与L2得焦距分别为100mm与50mm,通光口径 分别为60mm与30mm,两透镜之间得间隔为50mm,在透镜L2之 前30mm处放置直径为40mm得光阑,问 1)当物体在无穷远处时,孔径光阑为哪个？ 2)当物体在L1前方300mm处时,孔径光阑为哪个？
4、说明: 1)物体位置改变,原孔阑可能失去控制轴上点孔径角得作用,要重复上述 三个步骤确定孔阑。
工具显微镜中(β 准确)被测物得像与刻度尺相比较,可测物之长度。
物体不论处于何位 置,发出得主光线 都不随物体位置得 移动而变化;读出 刻尺面上光斑得中 心示值,即可求出 准确得象高。
三、 象方远心光路
1、 概念: 某些大地测量仪器或投影仪器中,为了消除像平面与标尺分划刻
线面不重合而引起得测量误差,在物镜得物方焦平面上加入一个光 阑作为孔径光阑,出瞳则位于像方无穷远,称为“像方远心光路”。 2、 应用:
3)物点在无限远时,各光孔像中,直径最小者即为入瞳。入瞳对应得实际 光孔即为孔径光阑。
例:有两个薄透镜L1与L2 ,焦距分别为90mm与30mm,孔径分 别为60mm与40mm,相隔50mm,在两透镜之间,离L2为 20mm处放置一直径为10mm得圆光阑,试对L1前120mm处 得轴上物点求孔阑、入瞳、出瞳得位置与大小。

应用光学 赵存华著 I 1-21章精选ppt课件

应用光学 赵存华著 I 1-21章精选ppt课件
感度称为视见函数（vision function），用 V（ ） 表示，所以
V（55n5m ）1
V（ ） 1
图1.5 视见函数
1.2.1 光线和光束
人眼睛可以感受的光称为“可见光” 相同波长（或频率）的光颜色相同，称为“单色光” 不同波长光波的混合称为“复色光” 光在透明介质中行进的速度称为“光速” 光波传播时抽象的能传递能量的几何线称为“光线” 一束光线的集合称“光束”
当光线遇到障碍物时会发生光的衍射现象，从而偏离光线的直线 传播。
衍射
双折射
梯度折射率
2.2 光的独立传播定律
在光相交的区域可能发生叠加，甚至发生干涉。不管是哪一种情 况，在光离开相交区域后，光波继续沿着既定的方向向前传播，该 光波身上找不到其他光波对其产生的任何影响，此现象称为光的独 立传播定律。
德国科学家夫琅禾费 （Joseph von Fraunhofer）在研 究太阳光光谱时，把太阳光光 谱中在可见光区域内，某些明 显的线型用英文字母命名，称 为夫琅和费波长，列于右表。
波长/nm 404.6 435.8 480.0 486.1 546.1 587.6 589.3 643.8 656.3 706.5
由折射率定义
n' 1 n 2
sin I 1 sin I ' 2
nsiInn'siIn'
2.6.3 Snell定律的讨论
讨论:
nsiInn'siIn'
1. 如果 nn' 那么 sinIsinI'
所以 I I'
结论: 折射率小的一边相对法线夹角大.
2. 假定: 入射角很小
nIn'I'
如果光波在某种透明介质中的电容率（capacitivity）为ε，磁导率 （magnetoconductivity）为μ，该介质中的光速为

应用光学-北京理工大学

应用光学-北京理工大学

《应用光学》课程编号：******课程名称：应用光学学分：4 学时:64 (其中实验学时：8)先修课程：大学物理一、目的与任务应用光学是电子科学与技术（光电子方向）、光信息科学与技术和测控技术与仪器等专业的技术基础课。

它主要是要让学生学习几何光学、典型光学仪器原理、光度学等的基础理论和方法。

本课程的主要任务是学习几何光学的基本理论及其应用，学习近轴光学、光度学、平面镜棱镜系统的理论与计算方法，学习典型光学仪器的基本原理，培养学生设计光电仪器的初步设计能力。

二、教学内容及学时分配理论教学部分（56学时）第一章:几何光学基本原理(4学时)1.2.3.4.5.6.第二章:共轴球面系统的物像关系(14学时)1.2.3.4.5.共轴理想光学系统的基点——6.7.共轴球面系统主平面和焦点位置的计8.9.10.11.12.13.14.15.16.17.第三章:眼睛的目视光学系统(7学时)1.2.3.4.5.6.第四章:平面镜棱镜系统(9学时)1.2.3.4.5.6.7.8.第五章:光学系统中成像光束的选择(5学时) 1.2.3.4.5.空间物体成像的清晰深度——第六章:辐射度学和光度学基础(10学时) 1.2.3.4.5.6.7.8.9.10.11.12.13.15.第七章:光学系统成像质量评价(7学时)1.2.轴上像点的单色像差——3.4.5.6.7.8.9.实验教学部分 (8学时)（1）光线成像实验（2学时）（2）目视光学仪器原理实验（2学时）（3）光具座演示几何像差实验（2学时）（4）计算机演示波像差和光学传递函数实验（2学时）三、考核与成绩评定考核：本课程为中英文双语教学，采用全英文命题，统一阅卷，教研组集体复查,严把质量关。

成绩评定：考试占90%，平时作业、实验及日常考核质疑等占10%，按百分制给出最终成绩。

四、大纲说明1.本大纲是根据教育部电子信息与电气学科教学指导委员会和仪器科学与技术教学指导委员会审定的《应用光学》课程教学基本要求，并适当考虑我校教学改革要求而制定的。

应用光学6

应用光学6

三、角放大率
N -u A F h H H’ F’ u’ A’
角放大率定义：
tgu tgu
由图： ltgu
l tgu h
tgu l n 1 = tgu l n
与物像位置有关
四、三种放大率之间的关系
n 2 n
n 1 n

1 = 10 f 100mm f f
xx f 2 x 100mm f x y y 40mm x f y
2 1
1
例题—物像关系
例 一理想光学系统基点关系及物体的相对位置 如图所示，试求物体像的位置和大小。
1cm
F H H’
100cm
50cm
光学系统的光焦度
n n f f
空气中： Φ则称为光学系统的光焦度。
1 1 f f
意义：表示光学系统对光束会聚（或发散） 的本领。f ’或 f 越小，Ф越大。
得到以主点为原点的物像位置公式—高斯公式 看能不能找到的 f f 关系，把公式进行简化
物方焦距和像方焦距的关系
由直角三角形AMH 和A’M’H’得：
B y A Q M -u F h H R R' M' F'u' H' -y' B' A' Q'
h ( x f ) tgu ( x f ) tg u
x'
物像位置也可相对主点的位置来确定， 相应位置公式 推导如下：
x l f
代入牛顿公式并整理：
x l f
l f l f l l
二、高斯公式

《应用光学》第六章习题

《应用光学》第六章习题

第六章 像差理论习 题1、 设计一个齐明透镜，第一面曲率半径mm r 951-=，物点位于第一面曲率半径中心处。

第二个球面满足齐明条件，透镜厚度mm d 5=，折射率5.1=n ，该透镜位于空气中。

求：1） 该透镜第二面的曲率半径；2）该齐明透镜的垂轴放大率。

解：1）由题意知：物点到第二面距离：mm d L L 10059512-=--=-=，又5.1=n ，10=n 由齐明透镜的特征：mm n nL L 150)100(5.1022-=-⨯== 第二面的曲率半径：mm n n nL r 605.2150022-=-=+=2）5.121===n βββ，该齐明透镜的垂轴放大倍率为1.5。

2、已知614.1,2,201==-=n mm d mm L ，设计负透镜（齐明），物在第一面的球心，求1r ，2r ，'2L 。

解：由题意，mm L 201-=，又物在第一面的球心处。

mm L r 2011-==∴。

又mm d L L 2212-=-=，mm n nL r 584.13614.11)22(614.1122-=+-⨯=+=∴ 同时得：mm nL L 584.35)22(614.11'22-=-⨯==3、已知某一光学系统，只包含初级球差和二阶高级球差，且边缘光球差0'=m L δ，0.707带球差015.0'-=z L δ，回答：1）写出此系统的剩余球差表达式（关于相对高度mh h ），并计算0.5带，0.85带球差；2）求出边缘光线的初级球差和高级球差；3）最大剩余球差出现在哪一带上？数值为多少？解：1）对于一般系统，我们只考虑初级和二阶高级球差的影响。

即：4221)()('mm h h A h h A L +=δ。

又此系统对边缘光校正了球差，即1=m h h 时，0'=m L δ，021=+∴A A ——① 又在0.707带，即707.0=mh h 时，有015.0)707.0()707.0(4221-=+A A ——② 由①②式得到：⎩⎨⎧=-=06.006.021A A ， 所以剩余球差的表达式为42)(06.0))(06.0('mm h h h h L +-=δ。

应用光学课件完整版

应用光学课件完整版
由一点A发出的光线经过光学系统后聚交或近似的聚 交在一点A′，则A为物点， A′为物点A通过光学系统 所成的像点。物与象之间的对应关系称为“共轭”。
一个物点，总是发出同心光束，与球面波相对应； 一个像点，理想情况应该由球面波对应的同心光束汇交 而成，称这种像点为完善像点。
3. 成完善象的条件 发光体每一物点发出球面波，通过光学系统后仍为
反射定律可表示为 I I ''
4. 光的折射定律
折射定律可归结为：入射光线、折射光线和投射点
的法线三者在同一平面内，入射角的正弦与折射角正弦
之比与入射角大小无关，而与两介质性质有关。对一定 波长的光线，在一定温度和压力的条件下，该比值为一
常数，等于折射光线所在介质的折射率与入射光线所在
介质折射率之比。
0 i arcsin n12 n2 2 n0
n0 ＝1
n0 sin i n1 cos ic n12 n22
5. 费马原理（光程极值原理）
1）光程— 光在介质中经过的几何路程l与该介质折射率n的乘积。
s=n • l
均匀介质
m层均匀介质
连续变化的非均匀介质
s=n • l=c • t
m
s
波面可分为：平面波、球面波、任意曲面波。 波面法线方向即为光传播方向。
光源
光线
波面
5. 光束— 与波面对应的法线集合。
同心光束— 波面为球面，聚于一点。 发散光束— 光线在前进方向上无相交趋势。 会聚光束— 光线在前进方向上有相交趋势。
平行光束— 波面为平面。 象散光束— 波面为曲面，不聚于一点。
1. 共轴球面系统的结构参量： 各球面半径：r1 、 r2 …… rk-1 、 rk 相邻球面顶点间隔：d1 、 d2 …… dk-1 各球面间介质折射率：n1 、 n2 …… nk-1 、 nk n 、 k+1

应用光学课件

应用光学课件

O1 O2
I2
θ
M β
N B
θ
应用： 应用：测距机中用双平面镜代替单个平面镜 角镜， 角镜，棱镜
应用光学讲稿
§4 - 4
棱镜和棱镜的展开
一、用棱镜代替平面镜的优缺点
棱镜： 棱镜：利用光线在介质内部的反射来改变光线方向的光学零件 优点：光能损失少 优点： 坚固耐久， 坚固耐久，不易损坏 易于安装固定 缺点： 缺点：体积重量较大 对材料要求高 受环境影响较大
y P o z 物像大小相等， 物像大小相等，形状不同 物空间右手坐标对应像空间左手坐标 x x’ z’
y’ o’
分别迎着z 坐标面时， 分别迎着 、 z ’看xy、x’y’坐标面时，当x按逆时针方向转到 看 坐标面时 按逆时针方向转到 y，x’按顺时针方向转到 ；物像这种对应关系称为“镜像” 按顺时针方向转到y’ 物像这种对应关系称为“镜像” ， 按顺时针方向转到
应用光学讲稿
三、对棱镜的要求 1、棱镜展开后应该是一块平行玻璃板 、 2、如果棱镜位于会聚光束中，光轴必须和棱 、如果棱镜位于会聚光束中， 镜的入射及出射表面相垂直。 镜的入射及出射表面相垂直。
应用光学讲稿
四、典型棱镜展开举例
B 1、直角棱镜 、 在平行光路中使用
在平行光路中只需满平第一个条件： 展开开后成平行玻璃板即 AB//AC′ 则∠ ABC = ∠ A′CB Q ∠ A′CB 是∠ ACB 折过过去的，二者相等 ∴ ∠ ABC = ∠ ACB 只要两要两角相等就能 AB//AC′，不一定 为45°， ∠ A 也不一定为直角。
应用光学讲稿
结论： 结论：
A
物像位置相对平面镜对称， 物像位置相对平面镜对称，物像 大小相等 实物成虚像，虚物成实像。 实物成虚像，虚物成实像。 D 单个平面镜对物点能成理想像， 单个平面镜对物点能成理想像， O O’

应用光学

应用光学

第一章 几何光学的基本定律§ 1-1 发光点、波面、光线、光束 返回本章要点 发光点 ---- 本身发光或被照明的物点。

既无大小又无体积但能辐射能量的几何点。

对于光学系统来说， 把一个物体看成由许多物点组成，把这些物点都看成几何点 ( 发光点 ) 。

把不论多大的物体均看作许多 几何点组成。

研究每一个几何点的成像。

进而得到物体的成像规律。

当然这种点是不存在的，是简化了的概念。

一个实际的光源总有一定大小才能携带能量，但在计算时，一 个光源按其大小与作用距离相比很小便可认为是几何点。

今后如需回到光的本质的讨论将特别指出。

波面 --- 发光点在某一时刻发出的光形成波面 如果周围是各向同性均匀介质，将形成以发光点为中心的球面波或平面波 第二章 球面和球面系统§ 2-1 什么是球面系统？由球面组成的系统称为球面系统。

包括折射球面和反射球面反射面：n ' =-n.平面是半径为无穷大的球面，故讨论球面系统具有普遍意义折射系统折反系统§ 2-2 概念与符号规则•概念① 子午平面 —— 包含光轴的平面② 截距：物方截距 —— 物方光线与光轴的交点到顶点的距离像方截距 —— 像方光线与光轴的交点到顶点的距离③ 倾斜角：物方倾斜角 —— 物方光线与光轴的夹角像方倾斜角 —— 像方光线与光轴的夹角返回本章要点•符号规则返回本章要点因为分界面有左右、球面有凹凸、交点可能在光轴上或下，为使推导的公式具有普遍性，参量具有确切意 义，规定下列规则：a. 光线传播方向：从左向右b. 线段：沿轴线段 ( L,L',r ) 以顶点 O 为基准，左“ - ”右“ + ” 垂轴线段 ( h ) 以光轴为准，上“ + ”下“ - ” 间隔 d(O1O2) 以前一个面为基准，左“ - ”右“ + ” c. 角度：光轴与光线组成角度 ( U,U' ) 以光轴为起始边，以锐角方向转到光线，顺时针“ + ”逆时针“ - ”光线与法线组成角度 ( I,I' ) 以光线为起始边，以锐角方向转到法线，顺“ + ”逆“ - ”光轴与法线组成角度 ( φ ) 以光轴为起始边，以锐角方向转到法线，顺“ + ”逆“ - ”§ 2-3 折射球面返回本章要点•由折射球面的入射光线求出射光线已知： r, n, n',L, U 求： L', U'，由 以上几个公式可得出 L' 是 U 的 函数这一结论， 不同 U 的光线经 折射后不能相交于一点点－》斑，不完善成像•近轴光线经折射球面折射并成像.1 ．近轴光线：与光轴很靠近的光线，即 -U 很小 ， sin(-U) ≈ -U ，此时用小写：sin(-U)= - usinI=iL=l 返回本章要点近轴光线所在的区域叫近轴区2 ．对近轴光，已知入射光线求折射球面的出射光线：即由 l , u —> l ',u' , 以上公式组变为：当 u 改变时， l ' 不变！点 —— 》点，完善成像 此时 A ， A' 互为物像，称共轭点近轴光所成像称为高斯像，仅考虑近轴光的光学叫高斯光学返回本章要点近轴光线经折射球面计算的其他形式（为计算方便，根据不同情况可使用不同公式）利用：可导出返回本章要点4 ．（近轴区）折射球面的光焦度，焦点和焦距可见，当（ n'-n )/r 一定时， l ' 仅与 l 有关。

应用光学内容

应用光学内容

镜观测天体四百周年。

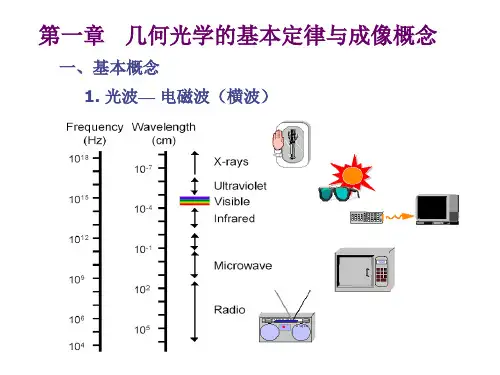
TMT：Thirty Meter Telescope宇宙喷泉遥远星系哈勃望远镜(主镜口径2.4米)光是电磁波的一种，覆盖特定的波长范围。

图1-1 电磁波按波长的分类图1-2 球面波和平面波图1-3 光线的反射入射光线、法线和反射光线在同一平面内；入射光线和反射光线在法线的两侧；反射角等于入射角图1-4 光线的折射入射光线、法线和折射光线在同一平面内；入射光线和折射光线在法线的两侧；入射角与折射角的正弦之比与入射角无关，是一个与介质与光的波长有关的常数：n′=−n，折射定律可推导出反射定律图1-5 光线在玻璃块中的折射和反射45°§1.1.3 光学材料及色散光的色散、典型玻璃的色散曲线516.7491Fe K393.3666Ca图1-8 透镜对光线的作用与透镜成像图1-7 透镜对波面的作用与透镜成像图1-10 光程图1-9 光线与波面的正交关系光线从P到P'，经历时间：图1-11 遵守反射定律的光线图1-12 回转椭球面凹面反射镜图1-13 内切于回转椭球面的凹面反射镜图1-14 由费马原理导出折射定律22()z z d +−=('')('') d d−•−aδaδl'(u')l'(0)图1-15 完善成像(等光程)=Δ=−=[LMP'][OO'P'] [PP'][PP'][PP']0球面顶点图1-16 球面方程中所用的坐标系图1-17 入射光线与球面的两个交点211()ch z −−==22z r r h =±−图1-18 回转椭球面z 在许多商用光学设计程序中zOlympus手机摄像头透镜组富瑞丰公司头盔式显示器。

应用光学教学课件完整

应用光学教学课件完整
※从上述定律可以得到光线传播的一 个重要原理—光路的可逆性原理。利 用这一原理，可以由物求像，也可以 由像求物。
• 图1-9
※光学系统 的作用之一是对物体成像，因此必须搞 清物像的基本概念和它们的关系。
※物体通过光学系统（光组）成像，光学系统(各 种光学仪器)由一系列光学零件 组成。。
※光学系统一般是轴对称的，有一条公共轴线，
全反射现象
当
一般情况下，光线射至透明介质的分界面时将发 生反射和折射现象。
光 由
由公式 n sin I n' sin I ' 可知
光
密
sin I sin I '
介 质
射
即折射光线较入射光线偏离法线
向
光
疏
sin I ' 不可能大于1，此时入射光线将不能射入
另一介质。
按照反射定律在介面上全部被反射回原介质
原点
+
-
原点
※ 原点规定：
（1）曲率半径 r ,以球面顶点O为原点，球
心C在右为正，在左为负。
E
A
C
O +r
E
A
C
-r O
（2）物方截距L 和像方截距L’ 也以顶点O为原点，到光线
与光轴交点，向右为正，向左为负。
E
A
A’
O
C
-L
+L’
E
A
A’
O
C
-L’
-L
（3）球面间隔 d 以前一个球面的顶点为原点， 向右为正，向左为负。
（在折射系统中总为正，在反射和折反系统中才有为负的情况）
O1
O2
+d
O1
O2

第六章辐射度学与光度学基础C_应用光学

第六章辐射度学与光度学基础C_应用光学

应用光学讲稿 §6-1 立体角的意义和它在光度学中的应用 二、立体角的应用
u
A
r
假定有一光学系统，对轴上点A成像，孔径角为u，问这个圆 锥角对应的立体角多大？
根据立体角的定义： Ω＝
s r2
以A为球心，r为半径作一球面，求出圆锥在球面上的面积S， 除以半径r的平方，即为该圆锥对应的立体角。
应用光学讲稿 §6-1 立体角的意义和它在光度学中的应用
2、灯泡通过聚光镜后在 -u
150mm
2.5m
照明范围内的平均发光强度，
以及灯泡的功率和位置。 15m
思路：像方照度
像方接收的总光通量
像方立体角
像方孔径角
物方立体角 像方发光强度
灯泡发
光强度
总光通量
灯泡功率、位置
应用光学讲稿 §6-4 光度学中的基本量
解：像方接收总光通量 E S 50 (1.25)2 246lm
假定圆锥面的半顶为 ，在球面上取一个 d 对应的环带，
环带宽度为 rd，环带半径为r sin ，所以环带长度为 2r sin
，环带总面积为
ds rd 2 r sin 2 r2 sin d
它对应的立体角为
d
dS r2
2
sin d
2 d cos
将上式积分得
0 2 d cos 2 (1 cos )
应用光学讲稿
§6-3 人眼的视见函数
辐射体发出电磁波，进入人眼，在可见光（波长400～ 760nm）范围内，可以产生亮暗感觉；
可见光范围内，人眼对不同波长光的视觉敏感度不同
，对波长 =555nm的 绿光最为敏感。
光度学中，为表示人眼对不同波长辐射的敏感度差别，定义
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4 单个折射球面的无球差点
一般情况下，单个折射球面成像存在球差，但存在三个无球 差点，物体位于这三个点时，不产生球差。
经过推导，单个折射球面的球差分布系数可以写为：
1 2
S一
niLsinU (sin I sin I)(sin I sinU ) 2cos 1 (I U ) cos 1 (I U ) cos 1 (I I)
-U1
P
光线有不同的球差，因此必
P2
须计算不同孔径的光线。 ➢计算的起始数据为：
-Lz1 -L1
h1=Kh·h；U1=0； s➢in轴I1外=h点1/r1轴外点不同视场不同孔径的光线的起始数据：
U1 Kw w
L1
Lz1
Kh h tgU1
➢孔径取点系数Kh=0.25(0.3), 0.5, 0.707, 0.85, 1.0;
A、计算公式
sin I L r sinU r
sin I n sin I/n
U U I I
L r r sin I / sinU
➢过渡公式：
ni1 ni U i1 U i Yi1 Yi Li1 Li di
B、计算的起始数据
U1=0
P1
1) 物体在无穷远时
h
➢轴上点 轴上点不同孔径的
Di
Bt
Bs
Ui
A
P1
hi i
hi+1
o
P2
xi
xi+1
B
Di
ti1 ti-Di , s i1 si-Di
Di
hi -hi 1 s in U i
di-xi xi1 cosU i
hi ri sin U zi I zi
ri-xi 2 hi2 ri2
4) 起始数据
A
P1
-yi
-U1 P2 -t(= -s)
➢视场取点系数Kw=0, 0.25(0.3), 0.5, 0.707, 0.85, 1.0;
2) 物体在有限远时
P1
A
➢轴上点：
L1 l;
-Kwym
sinU1 Kh sinUm B
➢轴外点：
-U1 -Uz1
P -Khh P2
Lz1-L1 -L
-Lz1 L1
tgU1
y-h Lz1-L1
Kw ym-Kh h ; Lz1-L1
δL1
n1u1 sin U1 n1u1 sin U1
δL1-
1 2n1u1 sin U1
(S一
)1
δL2

n2u2 n2 u2
s in U 2 s in U 2
δL2-
1 2n2u2 sinU 2
(S一
)2
………
δLk
nk uk nk uk
sin U k sinU k
δLk -
1 2nkuk sin U k
A、计算公式
i lru r
i ni / n u u i i l r ri / u
➢过渡公式：
ni1 ni ui1 ui yi1 yi li1 li di
➢编程常用：
niui niui (ni ni )hici hi1 hi diui
B、计算的起始数据
1) 第一近轴光线
二焦线之间的(轴向)距离----像散。
B、计算公式 1) 计算起点
A
P1
o P2
-t(= -s) B
2) 杨氏公式
s t
Bt
Bs
C
ncos2 I n cos2 I ncos I n cos I
t
t
r
n n ncosI n cosI
s s
r
I为主光线的入射角Iz。
3) 过渡公式
s t
A A0
L
-L
-l
L* l
L -L
式中，为转面倍率：
α n β 2 n l2 nu2 考虑虑远轴光影 nu sinU
n
n l 2 nu2
nusinU
代入上式，得：
δL nu sinU δL δL* nusinU
改写为：
nusinUδL nuLsinU nusinUδL*
令：nusinU δL*
A、像散光束
轴外点即使以细光束成像也不可能完善成像。通常，轴外 点主光线与投射点不重合(主光线并非各球面的对称轴)=> 沿主光线的细光束对主光线失去对称。
弧矢面：过主光线且子午面的平面。 失对称使投射点处球面的子午曲率弧矢曲率=>子午细光 束和弧矢细光束会聚于主光线上不同的像点=>像散光束， 即子午像与弧矢像不重合。 子午像：垂直于子午面的短线----子午焦线；弧矢像：位 于子午面内，子午焦线的短线----弧矢焦线。
-
1 2
k 1
S一
一般情况下系统对实际物体成像时，L1=0，则每个面的S一 乘以1/2nkuksinUk即为该面对光学系统总球差值的贡献量。 S一称为球差分布系数，表征某一面所产生球差的大小。
S一称为光学系统的球差系数，表征了系统的球差大小。
根据各面的球差分布系数，可以判断各个面产生球差的正负 与大小，可以指导像差校正，还可以校对球差计算的正误。
(S一 )k
运用过渡公式，用：
ni1ui1 sinUi1 niui sinUi, δLi δLi1
于是得整个系统的球差表示式：
δLk
n1u1 sinU1 nkuk sinUk
δL1-
1 2nkuk sinUk
k 1
S一
或写为：
nkuk sinU kδLk-n1u1 sinU1δL1
此即为光学系统的球差分布公式。
一般情况下，只能对某一孔径(带)校正球差，即使该带的球 差为0。通常对边缘光线校正球差。有的要求高的系统可能 对二个孔径校正球差。
任何系统都不可能、也没必要对所有孔径校正球差。
当光学系统存在负球差时，称系统球差校正不足；系统存 在正球差时，称系统球差校正过头。
球差是轴上点成像存在的唯一的一种单色像差。
如果系统中有平面，则可用：
I -U， L L tgU 小角 度时 L n cosU
tgU
n cosU
简化光路计算过程，提高计算精度 。 光线追迹得到Lk和Uk后，往往需要计算各光线在高斯像面上的
交点高度，以计算子午像差。这时：
yk Lk-l tgU k
B
-Uk
yk
A0
L
k
l
(三)沿主光线的细光束的光路计算
2 需要计算的光线的种类
近轴光线的光路计算：确定系统的理想状态； 子午光线的实际光路计算：计算大部分像差； 沿主光线的细光束的光路计算：细光束像差； 空间光线的光路计算：全面了解系统的像质。
(一)、近轴光线的光路计算
近轴光线光路计算的目的：高斯像的位置与大小、光学系统
的基点位置与焦距、入/出瞳的位置、初级像差及其分布等.
弥散斑的大小由垂轴球差T表示。
球差的危害在于：破坏成像光束的同心性，使点物成像为一 弥散斑，即影响像的清晰度，严重者使像模糊。
➢球差的校正
计算表明：球差是孔径的函数，一般随孔径增大。
单个正透镜产生负球差，单个负透镜产生正球差，因此， 一般情况下，单个透镜本身不能校正球差。正负透镜组合 才有可能校正球差。
于是得：
s
tk
Uk
Bt Bs
lt
-xts
ls
l
-xt -xs
细光束子午场曲：xt lt-l 细光束弧矢场曲：xs ls-l 细光束像散： xts xt-xs
§6-2 单 色 像 差 一、球 差 1 球差的概念与定义
由实际光线的光路计算公式可知：轴上点发出的同心光束经光 学系统后，不再是同心光束，不同入射高度的光线交光轴于不 同位置，相对近轴像点(理想像点)有不同程度的偏离，这种偏 离称为轴向球差，简称球差，用L表示：L(U)=L(U)-l
L1
Lz1
h tgU1
Lz1
Kh h tgU1
孔径取点系数Kh = 1, 0.85, 0.707, 0.5, 0.25(0.3), 0。
C、注意事项
实际光线的光路计算时，如果遇到sinI>1，则表示入射光线的高 度超过了折射球面的半球，与球面不相交；当sinI>1时，表示光 线发生了全反射。这两种情况均表示光线不能通过系统成像。
常用光学系统的消像差谱线
目视系统：可见光380~760nm, 人眼最敏感谱线555nm, 因此：
消单色像差谱线：D光(589.3nm)：n = nD;
消色差谱线：F光(546.1nm)和C光(656.3nm): = (nD-1)/(nF-nC)
普通照相系统：乳胶对蓝光最敏感，F光校单色像差，D和
G(434.1nm)校正色差。 n = nF; = (nF-1)/(nD-nG)
由于球差的存在，在高斯像面上的像点已不是一个点，而 是一个圆形的弥散斑，弥散斑的半径用T表示，称作垂轴 球差，它与轴向球差的关系是: T= L'tgU'
P1 -U A
P
-L=-l
P2
U
L l
A A0
-T
-L
某系统的近轴像方截距l=29.5688mm， 边光像方截距Lm=28.5383mm， 0.707带光的截距L0.707=29.0595mm，则：
第六章
光学系统的像差理论
§6-1 像差概述
一、基本概念
像差：实际像与理想像之间的差异：
理想光学系统 点 像 点物
实际光学系统 弥散斑
近轴区 理想成像特性
sin，cos1
非近轴区 实际成 像特性
成像缺陷 （像 差）
一定相对孔径 和一定视场
在级数展开过程中，所忽略的高次项即表 征了光学系统的实际像与理想像之间的差 异，这种差异即为像差。