余弦定理1

三角形的余弦定理三角形的余弦定理，也称作Cosine定理，是解决三角形问题时常用的重要定理之一。

它可以用来计算三角形中缺失的一边长度，或者计算三个角中的某一个角的大小。

通过余弦定理，我们可以更加灵活地处理三角形相关的计算和分析。

余弦定理可以用于任意一个三角形，不仅限于直角三角形。

该定理的表达方式如下：在一个三角形中，设边长分别为a、b、c，对应的角度为A、B、C，则余弦定理可以表述为：c² = a² + b² - 2ab * cosC （1）a² = b² + c² - 2bc * cosA （2）b² = a² + c² - 2ac * cosB （3）在这三个表达式中，c是第三边的长度，A、B、C是三个角的大小，a、b、c是对应的边长。

通过这三个方程，我们可以互相推导计算。

通过余弦定理，我们可以解决各种与三角形相关的问题。

首先，我们可以计算三角形的某个边的长度，只要已知其他两边的长度和夹角的大小即可。

其次，我们也可以计算三角形中某个角的大小，只要已知其他两条边的长度和这个角的对边即可。

在实际问题中，余弦定理经常被用来解决测量和计算问题。

例如，当我们需要测量一个不规则的三角形中的一条边时，可以利用余弦定理进行计算。

又或者，当我们需要计算两个天线之间的距离时，如果我们知道了两个天线之间的夹角，以及与这个夹角对应的两边长度，就可以利用余弦定理进行计算。

此外，余弦定理也常常与正弦定理结合使用。

这两个定理配合使用可以解决更为复杂的三角形问题，例如计算一个三角形的面积。

正弦定理可以用来计算三角形的面积，而余弦定理则可以用来计算三角形的边长和角度。

总结而言，余弦定理是解决三角形问题时非常有用的工具之一。

它可以应用于各种类型的三角形，并且可以计算三角形的边长和角度。

通过掌握和应用这个定理，我们可以更加方便地解决与三角形相关的计算和分析问题。

余弦定理公式
余弦定理公式：cosA=（b²+c²-a²）/2bc，cosA=邻边比斜边。

余弦定理是描述三角形中三边长度与一个角的余弦值关系的数学定理。

运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个
边求角的问题。

1余弦定理性质
对于任意三角形，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的两倍积，若三边为a，b，c三角为A，B，C，则满足性质：
a^2=b^2+c^2-2·b·c·cosA
b^2=a^2+c^2-2·a·c·cosB
c^2=a^2+b^2-2·a·b·cosC
cosC=（a^2+b^2-c^2）/（2·a·b）
cosB=（a^2+c^2-b^2）/（2·a·c）
cosA=（c^2+b^2-a^2）/（2·b·c）
（物理力学方面的平行四边形定则以及电学方面正弦电路向量
分析也会用到）
第一余弦定理（任意三角形射影定理）
设△ABC的三边是a、b、c，它们所对的角分别是A、B、C，则有
a=b·cosC+c·cosB，b=c·cosA+a·cosC，c=a·cosB+b·cosA。

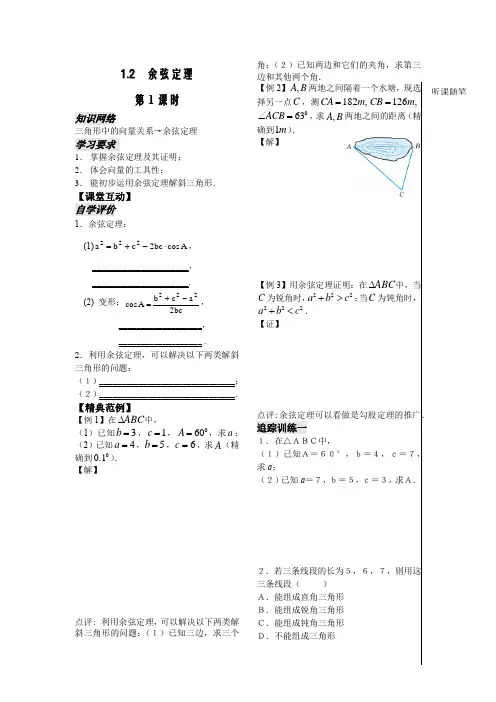
听课随笔1.2 余弦定理第1课时知识网络三角形中的向量关系→余弦定理学习要求1．掌握余弦定理及其证明；2．体会向量的工具性；3．能初步运用余弦定理解斜三角形．【课堂互动】自学评价1．余弦定理：(1)Acosbc2cba222⋅-+=，______________________，______________________.(2)变形：bc2acbAcos222-+=，___________________，___________________ .2．利用余弦定理，可以解决以下两类解斜三角形的问题：（１）_______________________________；（２）_______________________________．【精典范例】【例1】在ABC∆中，（1）已知3b=，1c=，060A=，求a；（2）已知4a=，5b=，6=c，求A（精确到00.1）．【解】点评: 利用余弦定理，可以解决以下两类解斜三角形的问题：（１）已知三边，求三个角；（２）已知两边和它们的夹角，求第三边和其他两个角．【例2】,A B两地之间隔着一个水塘，现选择另一点C，测182,CA m=126,CB m=63ACB∠=，求,A B两地之间的距离（精确到1m）．【解】【例3】用余弦定理证明：在ABC∆中，当C为锐角时，222a b c+>；当C为钝角时，222a b c+<．【证】点评:余弦定理可以看做是勾股定理的推广．追踪训练一１．在△ＡＢＣ中，（１）已知Ａ＝６０°，ｂ＝４，ｃ＝７，求a；（２）已知a＝７，ｂ＝５，ｃ＝３，求Ａ．２．若三条线段的长为５，６，７，则用这三条线段（）Ａ．能组成直角三角形Ｂ．能组成锐角三角形Ｃ．能组成钝角三角形Ｄ．不能组成三角形听课随笔３．在△ＡＢＣ中，已知222c ab b a =++，试求∠Ｃ的大小．４．两游艇自某地同时出发，一艇以１０ｋｍ／ｈ的速度向正北行驶，另一艇以７ｋｍ／ｈ的速度向北偏东４５°的方向行驶，问：经过４０ｍｉｎ，两艇相距多远？【选修延伸】【例4】在△ABC 中，BC =a ，AC =b ，且a ，b 是方程02322=+-x x 的两根，()1cos 2=+B A 。

课题 余弦定理1.余弦定理在三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍，即a 2＝b 2＋c 2－2bc cos A ，b 2＝c 2＋a 2－2ac cos B ，c 2＝a 2＋b 2－2ab cos C ．2．余弦定理的推论根据余弦定理，可以得到以下推论：cos A ＝b 2＋c 2－a 22bc ，cos B ＝a 2＋c 2－b 22ac ，cos C ＝a 2＋b 2－c 22ab. 3．余弦定理与勾股定理的关系在△ABC 中，由余弦定理，得c 2＝a 2＋b 2－2ab cos C ，若角C ＝90°，则cos C ＝0，于是c 2＝a 2＋b 2－2a ·b ·0＝a 2＋b 2，这说明勾股定理是余弦定理的特例，余弦定理是勾股定理的推广．规律：设c 是△ABC 中最大的边(或C 是△ABC 中最大的角)，则a 2＋b 2<c 2⇔△ABC 是钝角三角形，且角C 为钝角；a 2＋b 2＝c 2⇔△ABC 是直角三角形，且角C 为直角；a 2＋b 2>c 2⇔△ABC 是锐角三角形，且角C 为锐角．在△ABC 中，AB ＝4，BC ＝3，B ＝60°，则AC 等于________． 13.边长为5、7、8的三角形中，最大角与最小角的和是________．1200在△ABC 中，sin A ：sin B ：sin C ＝3：5：7，则△ABC 是( )cA ．锐角三角形B ．直角三角形C ．钝角三角形D ．无法确定题型1 已知两边及其一角解三角形例1 △ABC 中，已知b ＝3，c ＝33，B ＝30°，解此三角形．解析：方法一 由余弦定理b 2＝a 2＋c 2－2ac cos B.得32＝a 2＋(33)2－2a ×33×cos 30°，∴a 2－9a ＋18＝0，得a ＝3或6.当a ＝3时，A ＝30°，∴C ＝120°.当a ＝6时，由正弦定理sin A ＝a sin B b ＝6×123＝1.∴A ＝90°，∴C ＝60°. 变式1：已知△ABC 中，a ＝1，b ＝1，C ＝120°，则边c ＝________. 3题型2 已知三边解三角形例2 已知△ABC 中，a ∶b ∶c ＝2∶6∶(3＋1)，求△ABC 的各内角度数．分析：由比例的性质可以引入一个字母k ，用k 表示a 、b 、c ，再由余弦定理求解各角．解析：∵a ∶b ∶c ＝2∶6∶(3＋1)，∴令a ＝2k ，b ＝6k ，c ＝(3＋1)k.由余弦定理，有cos A ＝b 2＋c 2－a 22bc ＝6k 2＋（3＋1）2k 2－4k 22·6k ·（3＋1）k＝22，∴A ＝45°. cos B ＝a 2＋c 2－b 22ac ＝4k 2＋（3＋1）2k 2－6k 22×2k （3＋1）k＝12，∴B ＝60°. ∴C ＝180°－A －B ＝180°－45°－60°＝75°.变式2：在△ABC 中，已知a －b ＝4，a ＋c ＝2b ，且最大角为120°，求三边的长．解析：由⎩⎪⎨⎪⎧a －b ＝4，a ＋c ＝2b 得⎩⎪⎨⎪⎧a ＝b ＋4.c ＝b －4. ∴a ＞b ＞c ，∴a 2＝b 2＋c 2－2bc cos 120°，即(b ＋4)2＝b 2＋(b －4)2－2b (b －4)×⎝⎛⎭⎫－12， 即b 2－10b ＝0. 解得b ＝0(舍去)或b ＝10，此时a ＝14，c ＝6.题型3 判断三角形的形状例3在△ABC 中，若b 2sin 2C ＋c 2sin 2B ＝2bc cos B cos C ，试判断△ABC 的形状．[解析] 解法一：∵b 2sin 2C ＋c 2sin 2B ＝2bc cos B cos C ，∴利用正弦定理可得 sin 2B sin 2C ＋sin 2C sin 2B ＝2sin B ·sin C ·cos B ·cos C ，∵sin B sin C ≠0，∴sin B ·sin C ＝cos B cos C ，∴cos(B ＋C )＝0，∴cos A ＝0，∵0<A <π，∴A ＝π2，∴△ABC 为直角三角形． 解法二：已知等式可化为b 2－b 2cos 2C ＋c 2－c 2·cos 2B ＝2bc cos B cos C ，由余弦定理可得b 2＋c 2－b 2·⎝⎛⎭⎫a 2＋b 2－c 22ab 2－c 2(a 2＋c 2－b 22ac )2＝2bc ·a 2＋b 2－c 22ab ·a 2＋c 2－b 22ac ∴b 2＋c 2＝a 2，∴△ABC 为直角三角形．变式3： 在△ABC 中，已知c ＝a cos B ，b ＝a sin C ，判断三角形形状．解析：由余弦定理知cos B ＝a 2＋c 2－b 22ac ，代入c ＝a cos B 得：c ＝a·a 2＋c 2－b 22ac，∴c 2＋b 2＝a 2， ∴△ABC 是以A 为直角的直角三角形．又∵b ＝a sin C ，∴b ＝a·c a，∴b ＝c ， ∴△ABC 也是等腰三角形．综上所述，△ABC 是等腰直角三角形．题型四：正弦、余弦定理的综合应用例4：(2013·广东东莞第五中学高二期中测试)在四边形ABCD 中，已知AD ⊥CD ，AD ＝10，AB ＝14，∠BDA ＝60°，∠BCD ＝135°，求BC 的长．[解析] 在△ABD 中，设BD ＝x ，由余弦定理：BA 2＝BD 2＋AD 2－2BD ·AD ·cos ∠BDA即142＝x 2＋102－2·10x ·cos60°，整理得：x 2－10x －96＝0，解得x 1＝16，x 2＝－6(舍去)，由正弦定理，得BC sin ∠CDB ＝BD sin ∠BCD， ∴BC ＝16sin135°·sin30°＝8 2.变式4：如图，在△ABC 中，已知BC ＝15，AB AC ＝78，sin B ＝437，求BC 边上的高AD 的长． [解析] 在△ABC 中，由已知设AB ＝7x ，AC ＝8x ，由正弦定理，得7x sin C ＝8x sin B， ∴sin C ＝7x sin B 8x ＝78×437＝32，∴C ＝60°(C ＝120°舍去，否则由8x >7x ，知B 也为钝角，不符合要求)． 由余弦定理，得(7x )2＝(8x )2＋152－16x ×15cos60°，∴x 2－8x ＋15＝0，＝43AB 123，或20 3.。

对于任意三角形，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的两倍积，若三边为a,b,c 三角为A,B,C ，则满足性质——a^2 = b^2 + c^2 - 2·b·c·c os Ab^2 = a^2 + c^2 - 2·a·c·c os Bc^2 = a^2 + b^2 - 2·a·b·cos Cc os C = (a^2 + b^2 - c^2) / (2·a·b)c os B = (a^2 + c^2 - b^2) / (2·a·c)c os A = (c^2 + b^2 - a^2) / (2·b·c)（物理力学方面的平行四边形定则中也会用到）第一余弦定理（任意三角形射影定理）设△ABC的三边是a、b、c，它们所对的角分别是A、B、C，则有a＝b·cos C＋c·cos B， b＝c·cos A＋a·cos C， c＝a·cos B＋b·cos A。

编辑本段余弦定理证明两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)cot(A+B)=(cotAcotB-1)/(cotB+cotA)cot(A-B)=(cotAcotB+1)/(cotB-cotA)倍角公式tan2A=2tanA/[1-(tanA)^2]cos2a=(cosa)^2-(sina)^2=2(cosa)^2 -1=1-2(sina)^2sin2A=2sinA*cosA三倍角公式sin3a=3sina-4(sina)^3cos3a=4(cosa)^3-3cosatan3a=tana*tan(π/3+a)*tan(π/3-a)半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA)) cot(A/2)=√((1+cosA)/((1-cosA)) cot(A/2)=-√((1+cosA)/((1-cosA)) tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA)和差化积2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B) )2cosAcosB=cos(A+B)+cos(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosB积化和差公式sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(pi/2-a)=cos(a)cos(pi/2-a)=sin(a)sin(pi/2+a)=cos(a)cos(pi/2+a)=-sin(a)sin(pi-a)=sin(a)cos(pi-a)=-cos(a)sin(pi+a)=-sin(a)cos(pi+a)=-cos(a)tgA=tanA=sinA/cosA万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))其它公式a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中，tan(c)=b/a] a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中，tan(c)=a/b] 1+sin(a)=(sin(a/2)+cos(a/2))^21-sin(a)=(sin(a/2)-cos(a/2))^2。

余弦定理公式6个余弦定理是解决三角形中边长和角度之间关系的重要工具。

它可以帮助我们计算未知的边长或角度，从而更好地理解和分析三角形。

1. 第一个余弦定理公式是用于计算三角形边长的公式。

若三角形的边长分别为a、b和c，而对应的内角为A、B和C，则余弦定理可以表达为：c = a + b - 2abcos(C)。

这个公式可以帮助我们计算未知边长，只需要已知两个边长和它们之间的夹角即可。

2. 第二个余弦定理公式是用于计算三角形内角的公式。

若三角形的边长分别为a、b和c，而对应的内角为A、B和C，则余弦定理可以表达为：cos(C) = (a + b - c) / 2ab。

这个公式可以帮助我们计算未知角度，只需要已知三个边长即可。

3. 第三个余弦定理公式是用于计算三角形面积的公式。

若三角形的边长分别为a、b和c，而对应的内角为A、B和C，则余弦定理可以表达为：Area = 0.5 * ab * sin(C)。

这个公式可以帮助我们计算未知面积，只需要已知两个边长和它们之间的夹角即可。

4. 第四个余弦定理公式是用于判断三角形形状的公式。

若三角形的边长分别为a、b和c，则余弦定理可以表达为：c < a + b，如果等号成立，则表示三角形是直角三角形；如果等号不成立，则表示三角形是锐角三角形；如果等号反向成立，则表示三角形是钝角三角形。

5. 第五个余弦定理公式是用于计算三角形的高度的公式。

若三角形的边长分别为a、b和c，而对应的内角为A、B和C，则余弦定理可以表达为：h = b * sin(A)，其中h表示三角形的高度。

这个公式可以帮助我们计算未知高度，只需要已知一个边长和它对应的角度即可。

6. 第六个余弦定理公式是用于计算三角形的周长的公式。

若三角形的边长分别为a、b和c，则余弦定理可以表达为：Perimeter = a + b + c。

这个公式可以帮助我们计算未知周长，只需要已知三个边长即可。

综上所述，余弦定理提供了多种公式和方法来解决三角形中的边长和角度之间的关系。

余弦定理的十一种证明方法余弦定理和勾股定理一样，证明方法也有很多种,下面给出比较经典的十一种证明方法，供大家参考！余弦定理：三角形任一边的平方等于另外两边的平方和减去这两边与其夹角余弦的积的二倍。

如图1所示，在△ABC中，若AB＝c，BC＝a，CA＝b，则有：c2＝a2＋b2－2ab cosCa2＝b2＋c2－2bc cosAb2＝c2＋a2－2c a cosB.【证法1】如图2，在锐角△ABC中，作AD⊥BC于D，则CD＝b cosC，AD＝b sinC，在△ABD中，由勾股定理，得AB2＝BD2＋AD2，即AB2＝(a－b cosC)2＋(b sinC)2＝a2－2ab cosC＋b2cos2C＋b2sinC2＝a2－2ab cosC＋b2，即c2＝a2＋b2－2ab cosC。

当C重合于D时，在Rt△ABC中，∠C＝90°，因cosC＝0，所以c2＝a2＋b2。

当C在D左侧时，△ABC为钝角三角形，如图3所示，∠ACD＝180°－C，cos∠ACD＝cos(180°－C)＝－cosC，sin∠ACD＝sin(180°－C)＝sinC，所以CD＝b cos(180°－C)＝－b cosC，AD＝b sin(180°－C)＝b sinC，在Rt△ABD中，由勾股定理，得AB2＝BD2＋AD2，即AB2＝(a－b cosC)2＋(b sinC)2＝a2－2ab cosC＋b2cos2C＋b2sinC2＝a2－2ab cosC＋b2，即c2＝a2＋b2－2ab cosC。

【证法2】将△ABC 的顶点C 置于原点，CA 落在x 轴的正半轴上，如图4所示，则A ，B ，C 三点的坐标分别为A (b ，0)，B (a cosC ，a sinC)，C (0，0).由此得|AB|2＝(a cosC －b )2＋(a sinC －0)2＝a 2cos 2C －2ab cosC ＋b 2＋a 2sin 2C＝a 2＋b 2－2ab cosC ，即c 2＝a 2＋b 2－2ab cosC 。

解三角形 余弦定理1、余弦定理：在中，有，，C ∆AB 2222cos a b c bc =+-A 2222cos b a c ac =+-B ．2222cos c a b ab C =+-余弦定理：三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.2、余弦定理的推论：，，．222cos 2b c a bc +-A =222cos 2a c b ac +-B =222cos 2a b c C ab+-=3、设、、是的角、、的对边，则：①若，则a b c C ∆AB A B C 222a b c +=；90C = ②若，则；③若，则．222a b c +>90C < 222a b c +<90C > 余弦定理的应用范围：②知三边求三角；②已知两边及它们的夹角，求第三边.用余弦定理，得到：=+⇔⇔∆>+⇔⇔∆<+⇔⇔222222222是直角是直角三角形是钝角是钝角三角形是锐角a b c A AB Ca b c A A B C ab c A∆是锐角三角形A B C 例题：1、在ABC 中，已知，，求b 及A .∆=a c 060=B 2、在ΔABC 中，已知a ＝7，b ＝10，c ＝6，求A 、B 和C .3、在ΔABC 中，已知a ＝2，b ＝3，C ＝60°，解这个三角形.4、在ABC 中，若，求角A .∆222a b c bc =++1、在△ABC 中，，，，那么等于（）3a =b =2c =B ∠A 、30°B 、45°C 、60°D 、120°2、已知△ABC 的三边长，则△ABC 的面积为（ ）6,5,3===c b a A 、B 、C 、D 、14142151523、在△ABC 中，，则△ABC 是（ ）31,4a b c =-== A 、锐角三角形 B 、直角三角形 C 、钝角三角形 D 、任意三角形4．在△ABC 中， ，则A 等于（ ）222a b c bc =++ A ．60° B ．45° C ．120° D ．30°5．在△ABC 中，b cos A ＝a cos B ，则三角形的形状为（ ）A ．直角三角形B ．锐角三角形C ．等腰三角形D ．等边三角形6．在△ABC 中，sin A :sin B :sin C =3:2:4，则cos C 的值为（ ） A ． B ．－ C ．　D ．－232314147．在△ABC 中，已知a ＝7，b ＝8，cos C ＝，则最大角的余弦值是1413________．8．在△ABC 中，若AB ＝，AC ＝5，且cos C ＝，则BC ＝________．51099、在△ABC 中，，求及。

余弦定理的十种证明方法余弦定理是解决任意三角形的重要定理之一，可以用来求解三角形的边长、角度等问题。

下面将介绍十种证明余弦定理的方法。

1.平面向量法：设三角形的三边向量分别为a、b、c，则有a²=b²+c²-2bc*cosA，b²=a²+c²-2ac*cosB，c²=a²+b²-2ab*cosC。

将这些公式转化为三角形的边长形式即为余弦定理。

2.向量的模长法：设向量a、b、c的模长分别为A、B、C，夹角分别为α、β、γ，则有A²=B²+C²-2BC*cosα，B²=A²+C²-2AC*cosβ，C²=A²+B²-2AB*cosγ。

令边长等于向量的模长，将这些公式转化为三角形的边长形式即为余弦定理。

3.正弦定理扩展法：在一个三角形的条边上延长一边，并在延长边上取一点，使得三角形分为两个相似三角形。

利用相似三角形的关系可以推导出余弦定理。

4.科学结算法：这种方法将余弦定理看作三角形面积公式的一种特殊情况。

通过证明三角形的面积公式和余弦定理是等价的，就证明了余弦定理的正确性。

5.高中数学综合证明法：利用高中教材中的已知定理和公式，如三角形内角和定理、三角形的面积公式等，可以通过一系列的推导和变形，最终得到余弦定理。

6.解析几何法：将三角形的顶点与坐标系关联，根据顶点的坐标，可以得到三角形的边长、角度等信息。

通过求解三角形的边长和角度，可以得到余弦定理。

7.直角三角形法：将三角形分解为两个直角三角形，利用直角三角形的性质和勾股定理，可以推导出余弦定理。

8.球面三角形法：在球面上考虑三角形的问题，利用球面三角形的性质和球面上的几何关系，可以推导出余弦定理。

9.微积分法：将三角形分解为一组小三角形，并使用微积分的方法求解这些小三角形的边长和角度。

余弦定理余弦定理（第二余弦定理）余弦定理是揭示三角形边角关系的重要定理，直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题，若对余弦定理加以变形并适当移于其他知识，则使用起来更为方便、灵活.直角三角形的一个锐角的邻边和斜边的比值叫做这个锐角的余弦值.余弦定理性质三角形中，任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍，若三角形三边分别为a ，b ，c ，三角分别为A ，B ，C ，则满足性质：a 2=b 2+c 2-2bccosA ，b 2=c 2+ a 2-2cacosB ，c 2= a 2+b 2-2abcosC ，推论：2222cos b c a bc A +-= 2222cos c a b ca B +-= 2222cos a b c ab C +-=（物理力学方面的平行四边形定则中也会用到）.第一余弦定理（任意三角形射影定理）.设△ABC 的三边是a ，b ，c ，它们所对的角分别是A ，B ，C ，则有a=b·cos C+c·cos B， b=c·cos A+a·cos C， c=a·cos B+b·cos A .余弦定理证明平面向量证法∵如图，有a+b=c(平行四边形定则：两个邻边之间的对角线代表两个邻边大小）.∴|c2|=(a+b)·(a+b)，∴|c2|=a·a+2a·b+b·b.∴c2=a2+b2+2|a||b|cos(π-θ).（以上粗体字符表示向量）又∵cos(π-θ)=-cosθ，∴c2=a2+b2-2|a||b|cosθ，（注意：这里用到了三角函数公式）再拆开，得c2=a2+b2-2·a·b·cosC，即222 cos2+-=a b cCab同理可证其他.平面几何证法在任意△ABC中，∠C所对的边为c，∠B所对的边为b，∠A所对的边为a，作AD⊥BC.则有BD=cosB·c，AD=sinB·c，DC=BC-BD=a-cosB·c，根据勾股定理可得：AC2=AD2+DC2b2=(sinB·c)2+(a-cosB·c)2，b2=(sinB·c)2+a2-2ac·cosB+(cosB)2·c2，b2=(sin2B+cos2B)·c2-2ac·cosB+a2，b2=c2+a2-2ac·cosB，222Bcos+-=c a b作用(1)已知三角形的三条边长，可求出三个内角.(2)已知三角形的两边及夹角，可求出第三边.(3)已知三角形两边及其一边对角，可求其他的角和第三条边.(见解三角形公式，推导过程略)判定定理一(两根判别法)：若记m(c1,c2)为c的值为正根的个数，c1为c的表达式中根号前取加号的值，c2为c的表达式中根号前取减号的值，①若m(c1,c2)=2,则有两解；②若m(c1,c2)=1,则有一解；③若m(c1,c2)=0,则有零解(即无解).注意：若c1等于c2且c1或c2大于0，此种情况算第二种情况，即有一解.判定定理二(角边判别法):（1）当a>bsinA时，①当b>a且cosA>0(即A为锐角)时，则有两解；②当b>a且cosA≤0(即A为直角或钝角)时,则有零解(即无解)；③当b=a且cosA>0(即A为锐角)时，则有一解；④当b=a且cosA≤0(即A为直角或钝角)时,则有零解(即无解)；⑤当b<a时，则有一解.（2）当a=bsinA时，①当cosA>0(即A为锐角)时,则有一解；②当cosA≤0(即A为直角或钝角)时，则有零解(即无解).（3）当a<bsinA时,则有零解(即无解)，其他从余弦定理和余弦函数的性质可以看出，如果一个三角形两边的平方和等于第三边的平方，那么第三边所对的角一定是直角；如果小于第三边的平方，那么第三边所对的角是钝角；如果大于第三边的平方，那么第三边所对的角是锐角.即，利用余弦定理，可以判断三角形的形状.同时，还可以用余弦定理求三角形边长的取值范围.解三角形时，除了用到余弦定理外还常用到正弦定理.。

一、正弦定理和余弦定理 1、正弦定理和余弦定理 定理 正弦定理余弦定理内容2sin sin sin a b c RABC===2222222222cos ,2cos ,2cos .a b c bc A b c a ac B c a b ab C =+-=+-=+-变形形式①a=2RsinA,b=2RsinB,c=2RsinC;②sinA=2a R ,sinB=2b R ,sinC=2cR ;③a:b:c=sinA: sinB: sinC;④sin sin sin sin a b c aA B C A ++=++222222222cos ;2cos ;2cos .2b c a A bc a c b B ca a b c C ab +-=+-=+-=解决的问题已知两角和任一边，求另一角和其他两条边； 已知两边和其中一边的对角，求另一边和其他两角。

已知三边，求各角；已知两角和它们的夹角，求第三边和其他两个角。

注：在ΔABC 中，sinA>sinB 是A>B 的充要条件。

（∵sinA>sinB ⇔22a b R R >⇔a>b ⇔A>B ）2、在在ΔABC 中，已知a,b 和A 时，解的情况如下：3、三角形中的一些常用结论在⊿ABC 中，设角A 、B 、C 的对边长度分别为（1）三角形内角和定理 A+B+C=π（2）三角形中的诱导公式Sin(A+B)=sinC,cos(A+B)=-cosC,tan(A+B)=-tanC,（3）三角形中的边角关系三角形中等边对等角，大边对大角，反之亦然；三角形中任意两边之和大于第三边，任意两边之差小于第三边。

（4）三个重要结论①A＞B＞C⇔sinA＞sinB＞sinC;②sinA:sinB:sinC=a:b:c.③二、应用举例1、实际问题中的常用角（1）仰角和俯角在视线和水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下文的叫俯角（如图①）（2）方位角从指北方向顺时针转到目标方向线的水平角，如B点的方位角为α（如图②）注：仰角、俯角、方位角的区别是：三者的参照不同。

余弦定理编辑
余弦定理，是描述三角形中三边长度与一个角的余弦值关系的数学定理。

是勾股定理在一般三角形情形下的推广模式。

余玄定理
表达式
cos A=(b²+c²-a²)/2bc[1]
欧几里得
余弦定理是解三角形中的一个重要定理，可应用于以下两种需求：
当已知三角形的两边及其夹角，可由余弦定理得出已知角的对边。

当已知三角形的三边，能够由余弦定理得到三角形的三个内角。

求边
余弦定理公式可变换为以下形式所以，如果知道了三角形的两边及其夹角，可由余弦定理得出已知角的对边。

求角
余弦定理公式可变换为以下形式所以，如果已知三角形的三条边，能够由余弦定理得到三角形的三个内角。

证明编辑
三角函数证明
如上图所示，△ABC，在c上做高，根据射影定理，可得到：
将等式同乘以c得到：
使用同样的方式能够得到：
将两式相加：
向量证明
中，
，
，
：。

第一余弦定理推导我们可以根据正弦定理和余弦定理推导出第一余弦定理。

正弦定理：在任意三角形ABC中，有：sin(A)/a=sin(B)/b=sin(C)/c其中，a、b、c分别是三角形ABC的三个边长，A、B、C分别是三个角的度数。

余弦定理：在任意三角形ABC中，有：c²=a²+b²-2abcos(C)其中，c、a、b分别是三角形ABC的三个边长，C是C角的度数。

根据正弦定理和余弦定理，可以推导出第一余弦定理：cos(A)=(b²+c²-a²)/(2bc)其中，a、b、c分别是三角形ABC的三个边长，A是A角的度数。

证明：根据正弦定理，有：sin(A)/a=sin(B)/b=sin(C)/c两边同时乘以abc，得到：sin(A)b+sin(A)c=a[sin(B)+sin(C)]即：sin(A)b+sin(A)c=a[sin(B)+sin(C)]根据余弦定理，有：c²=a²+b²-2abcos(C)将cos(C)替换为[1-sin²(C)]/2，得到：c²=a²+b²-2ab[1-sin²(C)]/2即：c²=a²+b²-ab[1-2sin²(C)]将上述两个公式联立，得到：sin(A)b+sin(A)c=a[sin(B)+sin(C)] c²=a²+b²-ab[1-2sin²(C)]将上述两个公式联立，得到：sin(A)b+sin(A)c=a[sin(B)+sin(C)] c²=a²+b²-ab[1-2sin²(C)]将上述两个公式联立，得到：cos(A)=(b²+c²-a²)/(2bc)。