北师大版五年级上册分数的意义
- 格式:ppt
- 大小:1.86 MB
- 文档页数:11

初二下半期语文试题及答案一、选择题(每题2分,共10分)1. 下列词语中,注音全部正确的一组是:A. 倔强(jué jiàng)B. 锲而不舍(qiè ér bù shě)C. 迸溅(bèng jiàn)D. 剽悍(piāo hàn)2. 下列句子中,没有语病的一句是:A. 通过这次活动,使我们的团队合作能力得到了提高。
B. 他虽然年纪大了,但是仍然保持着一颗年轻的心。
C. 这本书的内容非常丰富,值得一读。
D. 我们不能因为一次失败就放弃追求。
3. 下列句子中,使用了拟人修辞手法的是:A. 春风又绿江南岸。
B. 明月松间照,清泉石上流。
C. 落霞与孤鹜齐飞,秋水共长天一色。
D. 黄河远上白云间,一片孤城万仞山。
4. 下列关于文学常识的表述,正确的一项是:A. 《红楼梦》是清代作家曹雪芹所著,是中国古典小说的巅峰之作。
B. 《水浒传》是明代作家施耐庵所著,是中国四大名著之一。
C. 鲁迅是中国现代文学的奠基人,代表作有《呐喊》、《彷徨》等。
D. 《诗经》是我国最早的一部诗歌总集,共有305篇。
5. 下列句子中,使用了排比修辞手法的是:A. 他勤奋好学,乐于助人,诚实守信。
B. 春天来了,万物复苏,大地回春。
C. 他不仅学习优秀,而且体育也很棒。
D. 窗外的雨,淅淅沥沥,如丝如缕。
答案:1. B 2. C 3. A 4. C 5. A二、填空题(每题2分,共10分)6. “但愿人长久,千里共婵娟”出自宋代词人苏轼的《________》。
7. 《三国演义》中,曹操的“________”是其著名的政治手腕之一。
8. “春眠不觉晓,处处闻啼鸟”是唐代诗人孟浩然的《________》中的名句。
9. 鲁迅的《朝花夕拾》是他的________作品集。
10. “路漫漫其修远兮,吾将上下而求索”出自屈原的《________》。
答案:6. 《水调歌头》7. “挟天子以令诸侯” 8. 《春晓》 9. 散文 10. 《离骚》三、阅读理解(共20分)阅读下面的文段,完成11-15题。

第五单元分数的意义㈠分数的再认识知识点:在具体情境中,进一步认识分数.分数对应的“整体”不同,分数所表示的部分的大小或具体数量也不一样,也就是分数具有相对性.㈡分饼(真分数与假分数)知识点:理解真分数、假分数、带分数的意义. 1123像2、4、3、4,…这样的分数叫作真分数3359像 2、3、4、4,…这样的分数叫作假分数像 211,5这样的分数叫作带分数54带分数的读法:2读作:二又四分之一.★补充知识点:分子是分母倍数的假分数可以化成整数.分子不是分母倍数的假分数可以化成带分数.㈢分数与除法知识点:被除数理解分数与除法的关系:被除数÷除数=除数(除数不为0).分数的分母不能是0.因为在除法中,0不能做除数,因此根据分数与除法的关系,分数中的分母相当于除法中的除数,所以分母也不能是0.运用分数与除法的关系解决实际问题.用分数来表示两数相除的商.根据分数与除法的关系把假分数化成带分数的方法:用分子除以分母,把所得的商写在带分数的整数位置上,余数写在分数部分的分子上,仍用原来的分母作分母.把带分数化成假分数的方法:将整数与分母相乘的积加上原来的分子作分子,分母不变.㈣分数基本性质知识点:理解分数的基本性质:分数的分子和分母都乘或除以相同的数(0除外),分数的大小不变.联系分数与除法的关系以及“商不变”的规律,来理解分数的基本性质. 分子相当于被除数,分母相当于除数,被除数和除数同时乘或除以相同的数(0除外),商不变.因此分数的分子和分母都乘或除以相同的数(0除外),分数的大小也是不变的.运用分数的基本性质,把一个分数化成指定分母(或分子)而大小不变的分数. ㈤找最大公因数知识点:理解公因数和最大公因数的意义. 找两个数的公因数和最大公因数的方法:1、列举法:运用找因数的方法先分别找到两个数各自的因数,再找出两个数的因数中相同的因数,这些数就是两个数的公因数;再看看公因数中最大的是几,这个数就是两个数的最大公因数.补充知识点:其他找最大公因数的方法:2、找两个数的公因数和最大公因数,可以先找出两个数中较小的数的因数,再看看这些因数中有哪些也是较大的数的因数,那么这些数就是这两个数的公因数.其中最大的就是这两个数的最大公因数.例如:找15和50的公因数和最大公因数:可以先找出15的因数:1,3,5,15.再判断4个数中,哪几个也是50的因数,只有1和5,1和5就是15和50的公因数.5就是它们的最大公因数. 3、如果两个数是不同的质数,那么这两个数的公因数只有1.4、如果两个数是连续的自然数(0除外),那么这两个数的公因数只有1.5、如果两个数具有倍数关系,那么较小的数就是这两个数的最大公因数.6、短除法偶数与所有奇数的最大公因数是1;一个数与它的的倍数的最大公因数是它本身.㈥约分知识点:理解约分的含义:理解最简分数的含义: 13掌握约分的方法:约分的方法一般有两种,一种是用两个数的公因数一个一个去除,另一种是直接用两个数的最大公因数去除.补充知识点:比较分数大小时,分母相同的、分子相同的可以直接比较,有些时候分子分母都52不相同可以采用约分后进行比较的方法.例如:○ 612㈦找最小公倍数知识点:理解公倍数和最小公倍数的含义. 找两个数的公倍数和最小公倍数的方法:1、先找出两个数各自的倍数(限制一定的范围内),再找出公有的倍数,找出两个数公有的倍数,看看这些公倍数中最小的是几,这个数就是两个数的最小公倍数.两个数公倍数的个数是无限的,因此只有最小公倍数没有最大的公倍数. 补充知识点:其他找公倍数和最小公倍数的方法:2、找两个数的公倍数和最小公倍数,可以先找出两个数中较大的数的倍数(限制一定的范围内),再看看这些倍数中有哪些也是较小的数的倍数,那么这些数就是这两个数的公倍数.其中最小的就是这两个数的最小公倍数.例如:找6和9的公倍数和最小公倍数.(50以内)可以先找出9的倍数(50以内)有:9,18,27,36,45,再从这些数中找出6的倍数18,36,18和36就是6和9的公倍数,18是最小公倍数.3、如果两个数是不同的质数,那么这两个数的最小公倍数是两个数的乘积.4、如果两个数是连续的自然数(0除外),那么这两个数的最小公倍数是两个数的乘积.5、如果两个数具有倍数关系,那么较大的数就是这两个数的最小公倍数.6、短除法求最小公倍数㈧分数的大小知识点:理解通分的含义:■分数大小比较:分子分母都不相同的分数相比较的方法:........补充知识点:通分一般以最小公倍数作分母.。


北师大版五年级上册数学《5.1 分数的意义》说课稿 (1)一. 教材分析分数的意义是北师大版五年级上册数学的一节课,本节课的主要内容是让学生理解分数的概念,掌握分数的表示方法,以及理解分数与整数之间的关系。
通过本节课的学习,学生能够运用分数解决实际问题,提高他们的数学素养。
二. 学情分析五年级的学生已经学习了整数的概念和运算,他们对数的认识有一定的基础。
但是,分数的概念对学生来说是一个新的学习内容,需要他们进行一定的理解和消化。
在学生的认知过程中,他们可能会对分数的概念产生困惑,例如分数与整数的关系,分数的表示方法等。
因此,教师需要通过具体的教学活动,帮助学生理解和掌握分数的概念。
三. 说教学目标1.知识与技能目标:学生能够理解分数的概念,掌握分数的表示方法,能够运用分数解决实际问题。
2.过程与方法目标:学生通过观察、操作、思考等活动,培养他们的观察能力、动手能力和思维能力。
3.情感态度与价值观目标:学生能够积极参与数学学习,体验数学学习的乐趣,增强他们的自信心。
四. 说教学重难点1.教学重点:学生能够理解分数的概念,掌握分数的表示方法。
2.教学难点:学生能够理解分数与整数之间的关系,能够运用分数解决实际问题。
五. 说教学方法与手段在本节课的教学中,我将采用启发式教学法和情境教学法。
启发式教学法能够激发学生的思维,培养他们的观察能力和动手能力。
情境教学法能够激发学生的学习兴趣,使他们能够主动参与数学学习。
此外,我还将运用多媒体教学手段,如课件、动画等,帮助学生形象地理解分数的概念。
六. 说教学过程1.导入:通过一个具体的情境,如分蛋糕,引入分数的概念,让学生观察和思考如何用数来表示分蛋糕的方法。
2.探究:学生分组讨论,分享各自的想法,教师引导学生用分数来表示分蛋糕的方法,并解释分数的含义。
3.讲解:教师通过讲解和示例,让学生理解分数的概念,掌握分数的表示方法,并引导学生理解分数与整数之间的关系。

北师大分数的意义教案【篇一:最新北师大版五年级数学上册第五单元分数的意义优秀教学设计含反思】本单元教材是在学生初步了解分数的基础上,引导学生进一步认识和理解分数,学习分数的再认识、分数与除法的关系、真分数与假分数、分数的基本性质、公因数与约分、公倍数与通分、分数的大小比较等知识。
这些知识的学习是进一步学习分数四则运算、运用分数知识解决实际问题的基础。
教材通过创设具体的问题情境,丰富学生对分数的认识,让学生在实际操作中进一步理解分数 ;在观察比较中发现分数与除法的关系 ,探索假分数与带分数的互化方法 ,让学生经历知识的形成过程 ,探索分数的基本性质 ; 在探索活动中理解公因数与公倍数的含义 ,掌握约分与通分的方法。
学生已经结合情境和直观操作 ,体验了分数产生的过程 ,初步理解了分数的意义 ,能认、读、写简单的分数 ,已经会计算简单的同分母分数加减法 ,能初步运用分数表示一些事物 ,解决一些简单的实际问题 ,为进一步深入理解分数的再认识中的知识点打下了基础。
1.结合具体情境与直观操作 ,体验分数产生的实际背景 ,进一步理解分数,能正确用分数描述图形和简单的生活现象。
2.认识真分数、假分数 ,理解分数与除法的关系 ,能正确进行假分数与带分数、整数的互化。
3.探索分数的基本性质 ,会进行分数的大小比较。
4. 能找出 10 以内两个自然数的公倍数和最小公倍数,能找出 100 以内两个自然数的公因数和最大公因数,会正确进行约分和通分。
5.体会分数与现实生活的联系 ,初步了解分数在实际生活中的应用 ,提高综合运用数学知识和方法解决具体问题的能力 ,能运用分数知识解决一些简单的实际问题。
6.能积极参与操作活动 ,主动地观察、操作、分析和推理 ,体验数学问题的探索性与挑战性。
1.在教学中 ,通过创设情境 ,可以激发学生学习数学的兴趣 ,启发学生积极思维 ,引导学生主动地探索。
2.主动探索、合作交流是学生学习数学的重要方式。



五年级上册数学教案第五单元《分数的意义》北师大版今天,我要为大家分享的是五年级上册数学教案,第五单元《分数的意义》,这是北师大版的教材。
一、教学内容我们今天要学习的教材章节是第五单元的《分数的意义》。
具体内容包括:理解分数的概念,掌握分数的表示方法,理解分数的性质,以及学会分数的加减法运算。
二、教学目标通过本节课的学习,我希望学生们能够理解分数的概念,掌握分数的表示方法,熟练运用分数进行加减法运算,并能够运用分数解决实际问题。
三、教学难点与重点本节课的重点是分数的概念和分数的加减法运算,而难点则是理解分数的性质和运用分数解决实际问题。
四、教具与学具准备为了帮助学生们更好地理解分数的概念,我准备了一些实物,如苹果、饼干等,以及一些分数的图片。
同时,我还会使用多媒体教具,如PPT等,来展示分数的加减法运算。
五、教学过程1. 实践情景引入:我会给学生们展示一些实物,如苹果和饼干,然后让学生们试着将这些实物分成几份,并用自己的方式来表示这些份数。
2. 讲解分数的概念:通过展示分数的图片,我会向学生们解释分数的概念,即分数是用来表示一个整体被分成几份中的一份的数量。
3. 分数的表示方法:我会教学生们如何用符号来表示分数,如分子表示几份,分母表示整体被分成几份。
4. 分数的性质:我会通过示例来讲解分数的性质,即分数的大小不变,无论分子和分母的大小如何变化。
5. 分数的加减法运算:我会用PPT展示分数的加减法运算的步骤,并让学生们跟着一起练习。
6. 随堂练习:我会给出一些分数的题目,让学生们自己试着解答,然后我会进行讲解和解析。
六、板书设计板书设计如下:分数的概念:整体÷ 份数 = 分数分数的表示方法:分子÷ 分母分数的性质:分子和分母的大小变化,分数的大小不变分数的加减法运算:同分母分数加减法、异分母分数加减法七、作业设计答案:答案:八、课后反思及拓展延伸重点和难点解析在今天的五年级上册数学教案中,我们学习了第五单元《分数的意义》,这是北师大版的教材。

重点提示:分数中要强调把一个整体“平均分”。
易错题:判断:有甲、乙两个正方形,乙正方形面积的12一定大于甲正方形面积的14。
(√)错因分析:虽然1 2>14,但是两个正方形的大小不确定,也就是单位“1”不确定,所以无法比较。
答案:✕易错题:判断:56的分数单位是15。
(√)错因分析:把一个整体平均分成几份,其中的1份就是这个分五、分数的基本性质1. 分数的基本性质.......:.分数的分子和分母同时乘或除.............以一个不为零的数........,.分数的大小不变。
........25=2×45×4=8201232=12÷432÷4=382. 分母和分子同时扩大到原来的.............n .(.n .>1..).倍.,.分子和分....母同时增加原来的........(.n .-.1.).倍.,.分数值不变。
......3. 运用分数的基本性质.........,.要想保持分数的大小不变...........,.必须使分数的分子和分母都乘或除以相同的数....................(.0.除外..).。
.如果是分子.....(.分母..).加上或减去一个数........,.看是把原分子......(.分.母.).乘或除以几得到新的分子...........(.分母..),..然后分母....(.分子..).也随..着乘或除以几得到新分母...........(.分子..).。
观察由原分数到新分数...........的分母...(.分子..).增加或减少了几。
........ 六、找最大公因数1. 几个数相同的因数,叫作这几个数的公因数;其中最大的一个叫作它们的最大公因数。
2. 求两个数的公因数和最大公因数的方法:先分别找出两个数各自所有的因数,再从中找出两个数的公因数,其中最大的一个就是这两个数的最大公因数。

五年级上册数学学案第五单元分数的意义分数与除法北师大版一、分数的意义分数是数学中的一个重要概念,它表示一个整体被等分成若干份,取其中的一份或几份。
在五年级上册数学的学习中,我们将深入学习分数的意义,并掌握分数的基本运算。
分数由分子和分母组成,分子表示取的份数,分母表示整体被等分成的份数。
例如,分数 3/4 表示将整体分成 4 份,取其中的 3 份。
分数可以表示具体的数量,也可以表示比例关系。
分数的意义在生活中有着广泛的应用。
例如,在分割食物、分配资源、计算百分比等方面,分数都发挥着重要的作用。
通过学习分数的意义,学生可以更好地理解和应用分数,提高解决问题的能力。
二、分数与除法分数与除法有着密切的关系。
在数学中,分数可以表示两个数的除法关系。
具体来说,分数 a/b 表示 a 除以 b 的结果。
例如,分数 4/2 表示 4 除以 2 的结果,即 2。
分数与除法的关系可以通过以下两个方面来理解:1. 分数表示除法的结果:当一个数除以另一个数时,可以表示为一个分数。
例如,8 除以 4 可以表示为分数 8/4,其结果为 2。
2. 分数运算与除法运算的关系:分数的乘法和除法运算与除法运算有着密切的关系。
具体来说,分数的乘法运算可以表示为除法运算的乘法逆运算,分数的除法运算可以表示为除法运算的除法逆运算。
通过学习分数与除法的关系,学生可以更好地理解除法的意义,并掌握分数的乘除运算。
这将有助于提高学生的数学运算能力和解决问题的能力。
三、总结在五年级上册数学的学习中,我们将深入学习分数的意义和分数与除法的关系。
通过学习分数的意义,学生可以更好地理解和应用分数,提高解决问题的能力。
通过学习分数与除法的关系,学生可以更好地理解除法的意义,并掌握分数的乘除运算。
这将有助于提高学生的数学运算能力和解决问题的能力。
在以上的内容中,分数与除法的关系是需要重点关注的细节。
分数与除法的关系是分数学习的重点和难点,理解它们之间的关系对于掌握分数的运算和应用至关重要。
一、分数的意义1、分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数,叫做分数。
2、分数单位:把单位“1”平均分成若干份,表示这样的一份的数叫做分数单位。
3、分数与除法的关系:除法中的被除数相当于分数的分子,除数相当于分母。
被除数÷除数 = 除数被除数 用字母表示:a÷b= ba (b≠0)。
4、分数未带单位表示两个量之间的倍数关系;分数带有单位表示一个具体的数量。
二、真分数和假分数1、真分数和假分数:① 分子比分母小的分数叫做真分数,真分数小于1。
② 分子比分母大或分子和分母相等的分数叫做假分数,假分数大于1或等于1。
③ 由整数部分和分数部分组成的分数叫做带分数。
2、假分数与带分数的互化:① 把假分数化成带分数,用分子除以分母,所得商作整数部分,余数作分子,分母不变。
② 把带分数化成假分数,用整数部分乘分母加上分子作分子,分母不变。
三、分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变,这叫做分数的基本性质。
四、约分1、最大公因数:几个数公有的因数叫做它们的公因数,其中最大的一个叫做最大公因数。
2、两个数的公因数和它们最大公因数之间的关系:所有的公因数都是最大公因数的因数,最大公因数是它们的倍数。
3、互质数:公因数只有1的两个数叫做互质数。
4、两个数互质的特殊判断方法:① 1和任何大于1的自然数互质。
② 2和任何奇数都是互质数。
③ 相邻的两个自然数是互质数。
④ 相邻的两个奇数互质。
⑤ 不相同的两个质数互质。
⑥当一个数是合数,另一个数是质数时(除了合数是质数的倍数情况下),一般情况下这两个数也都是互质数。
5、求最大公因数的方法:① 倍数关系: 最大公因数就是较小数。
② 互质关系: 最大公因数就是1。
6、最简分数:分子和分母只有公因数1的分数叫做最简分数。
7、约分:把一个分数化成和它相等,但分子和分母都比较小的分数,叫做约分。
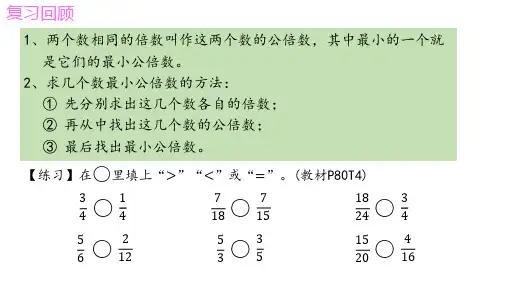
五、通分1、最小公倍数:几个数公有的倍数叫做它们的公倍数,其中最小的一个叫最小公倍数。
北师大版五年级上册数学《5.1 分数的意义》说课稿一. 教材分析《5.1 分数的意义》这一节内容是北师大版五年级上册数学的重要内容,主要让学生理解分数的概念,掌握分数的表示方法,以及理解分数之间的关系。
通过这一节内容的学习,使学生能够初步理解分数的含义,为以后学习分数的运算和其他相关知识打下基础。
二. 学情分析五年级的学生已经具备了一定的数学基础,他们对数的认识已经比较成熟,但对分数的理解还是相对陌生。
因此,在教学过程中,我需要结合学生的实际情况,从他们的生活经验出发,让他们能够更好地理解分数的意义。
三. 说教学目标1.知识与技能目标:让学生理解分数的概念,掌握分数的表示方法,能够正确地读写分数。
2.过程与方法目标:通过观察、操作、思考等过程,培养学生解决问题的能力。
3.情感态度与价值观目标:激发学生学习分数的兴趣,培养学生的自信心,使学生感受到数学与生活的紧密联系。
四. 说教学重难点1.教学重点:让学生理解分数的概念,掌握分数的表示方法。
2.教学难点:让学生理解分数之间的关系,以及如何正确地读写分数。
五. 说教学方法与手段在本节课的教学中,我将采用情境教学法、引导发现法、分组合作法等多种教学方法,以激发学生的学习兴趣,提高学生参与课堂的积极性。
同时,利用多媒体课件、实物模型等教学手段,帮助学生更好地理解分数的意义。
六. 说教学过程1.导入新课:通过一个分水果的生活情境,引入分数的概念,激发学生的学习兴趣。
2.探究新知:让学生观察、操作,发现分数的表示方法,理解分数之间的关系。
3.巩固新知:通过一些练习题,让学生运用所学的分数知识解决问题。
4.课堂小结:让学生总结本节课所学的分数知识,加深对分数的理解。
5.课后作业:布置一些有关分数的家庭作业,让学生巩固所学知识。
七. 说板书设计板书设计要简洁明了,能够突出本节课的主要内容。
可以设计一个分数的框架,包括分数的定义、表示方法、读写方法等,让学生一目了然。
一、分数的意义1、分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数,叫做分数。
2、分数单位:把单位“1”平均分成若干份,表示这样的一份的数叫做分数单位。
二、真分数与假分数1、真分数与假分数:①分子小于分母的分数叫做真分数,真分数<1。
②分子大于或等于分母的分数叫做假分数,假分数≥1。
③由整数部分和真分数部分组成的分数叫做带分数,带分数>1。
2、假分数与带分数的互化:①把假分数化成带分数,用分子除以分母,所得商作整数部分,余数作分子,分母不变。
15 3(如:= 3 )4 4②把带分数化成假分数,用整数部分乘分母加上分子作分子,分母不变。
1 2×3+1 7(如:2 = = )3 3 3三、分数与除法的关系1、除法中的被除数相当于分数的分子,除数相当于分母。
被除数 a被除数÷除数= , 用字母表示:a÷b= (b≠0)。
除数 b2、分数未带单位表示两个量之间的倍数关系;分数带有单位表示一个具体的数量。
四、分数的基本性质分数的分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变,这叫做分数的基本性质。
五、找最大公因数、约分1、最大公因数:几个数相同的因数叫做它们的公因数,其中最大的一个叫做最大公因数。
2、两个数的公因数和它们的最大公因数之间的关系:所有的公因数都是最大公因数的因数,最大公因数是它们的倍数。
3、互质数:公因数只有1的两个数叫做互质数。
4、两个数互质的特殊判断方法:① 1和任何大于1的自然数互质。
② 2和任何奇数互质。
③相邻的两个自然数互质。
④相邻的两个奇数互质。
⑤不相同的两个质数互质。
⑥当一个数是合数,另一个数是质数时(除了合数是质数的倍数情况下),一般情况下这两个数也互质。
5、求最大公因数的方法:①倍数关系:最大公因数就是较小数。
②互质关系:最大公因数就是1 。
③一般关系:从大到小看较小数的因数是否是较大数的因数。
6、最简分数:分子和分母只有公因数1的分数叫做最简分数。
一、分数的意义1、分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数,叫做分数.2、分数单位:把单位“1”平均分成若干份,表示这样的一份的数叫做分数单位.二、真分数与假分数1、真分数与假分数:①分子小于分母的分数叫做真分数,真分数<1.②分子大于或等于分母的分数叫做假分数,假分数≥1.③由整数部分和真分数部分组成的分数叫做带分数,带分数>1.2、假分数与带分数的互化:①把假分数化成带分数,用分子除以分母,所得商作整数部分,余数作分子,分母不变.15 3(如:= 3 )4 4②把带分数化成假分数,用整数部分乘分母加上分子作分子,分母不变.1 2×3+1 7(如:2 = = )3 3 3三、分数与除法的关系1、除法中的被除数相当于分数的分子,除数相当于分母.被除数 a被除数÷除数= , 用字母表示:a÷b= (b≠0).除数 b2、分数未带单位表示两个量之间的倍数关系;分数带有单位表示一个具体的数量.四、分数的基本性质分数的分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变,这叫做分数的基本性质.五、找最大公因数、约分1、最大公因数:几个数相同的因数叫做它们的公因数,其中最大的一个叫做最大公因数.2、两个数的公因数和它们的最大公因数之间的关系:所有的公因数都是最大公因数的因数,最大公因数是它们的倍数.3、互质数:公因数只有1的两个数叫做互质数.4、两个数互质的特殊判断方法:① 1和任何大于1的自然数互质.② 2和任何奇数互质.③相邻的两个自然数互质.④相邻的两个奇数互质.⑤不相同的两个质数互质.⑥当一个数是合数,另一个数是质数时(除了合数是质数的倍数情况下),一般情况下这两个数也互质.5、求最大公因数的方法:①倍数关系:最大公因数就是较小数.②互质关系:最大公因数就是1 .③一般关系:从大到小看较小数的因数是否是较大数的因数.6、最简分数:分子和分母只有公因数1的分数叫做最简分数.7、约分:把一个分数的分子、分母同时除以公因数,分数的值不变,这个过程叫做约分.(并不是一定要把分数化成与它相等的最简分数才叫约分;但一般要约到最简分数为止.)六、找最小公倍数、通分1、最小公倍数:几个数相同的倍数叫做它们的公倍数,其中最小的一个叫做最小公倍数.2、两个数的公倍数和它们的最小公倍数之间的关系:几个数的公倍数是它们最小公倍数的倍数.3、通分:把异分母分数分别化成和原来分数相等的同分母分数,这个过程叫做通分.(通分时,公分母一般为几个数的公倍数或最小公倍数).4、求最小公倍数的方法:①倍数关系:最小公倍数就是较大数.②互质关系:最小公倍数就是它们的乘积.③一般关系:大数翻倍(从小到大看较大数的倍数是否是较小数的倍数).5、用短除法求最大公因数和最小公倍数:(18,24)=2×3=6[18,24] =2×3×3×4=72【注】约分和通分的依据都是分数的基本性质.七、分数的大小比较①同分母分数,分子大的分数就大,分子小的分数就小;②同分子分数,分母大的分数反而小,分母小的分数反而大.③异分母分数,先化成同分母分数(分数单位相同),再进行比较.八、分数和小数的互化1、小数化分数:一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几……,去掉小数点作分子,能约分的必须约成最简分数;2、分数化小数:用分子除以分母,除不尽的按要求保留几位小数.(一般保留两位小数.)3、判断分数是否能化成有限小数的方法:①判断分数是否是最简分数;如果不是最简分数,先把它化成最简分数;②把分数的分母分解质因数:如果分母中除了2和5以外,不含有其他质因数,这个分数就能化成有限小数;如果分母中含有2和5以外的质因数,这个分数就不能化成有限小数.。