变化曲线的识别.
- 格式:doc
- 大小:36.00 KB
- 文档页数:3

曲线的五大要素一、引言在众多图表中,曲线图是一种非常直观、易于理解的表达方式。
无论是描述产品销售量、经济发展、股价波动等数据变化,曲线图都能清晰地展示出其中的规律和趋势。
要深入了解曲线图,我们需要了解构成曲线的五大要素。
二、曲线的定义和作用1.定义曲线是用一组有序数据(x,y)描绘出来的,在平面直角坐标系中呈现出的一种连续、光滑的轨迹。
2.作用曲线能够直观地反映数据间的变化关系,有助于分析和预测未来的发展趋势。
通过曲线,我们可以快速发现数据的变化规律、极值点和拐点,为决策提供依据。
三、曲线的五大要素1.起点和终点起点和终点决定了曲线在坐标系中的位置和方向。
它们是曲线的基本要素,对于分析曲线具有重要意义。
在实际应用中,我们需要关注起点和终点所表示的实际含义,以便正确理解曲线所反映的问题。
2.拐点拐点是曲线在某一区间内趋势发生变化的点。
识别拐点有助于我们判断曲线的走势,预测未来的发展方向。
拐点的分析方法有多种,如求导数、二阶导数等。
3.曲线的斜率曲线的斜率表示曲线在某一点处的切线斜率,反映了数据变化的速度。
通过计算曲线的斜率,我们可以了解曲线在某一时期内的变化情况。
同时,斜率的变化也能揭示曲线趋势的转变。
4.曲线的波动范围曲线的波动范围是指曲线在某一时间段内的最大值和最小值之差。
了解曲线的波动范围有助于我们评估曲线的稳定性,以及在波动过程中可能产生的影响。
5.曲线的趋势曲线的趋势分为上升、下降和波动三种。
分析曲线的趋势,可以让我们更好地了解数据的变化规律,为决策提供依据。
趋势分析的方法有多种,如线性回归、指数平滑等。
四、各要素的分析和应用1.起点和终点(1)重要性:起点和终点是曲线的基础,决定了曲线在坐标系中的位置和方向。
(2)应用:通过比较不同曲线的起点和终点,我们可以初步判断曲线所表示的数据之间的大小关系和变化趋势。
2.拐点(1)识别拐点的方法:求导数、二阶导数等。
(2)拐点对曲线走势的影响:拐点的出现意味着曲线趋势的转变,对于分析曲线的未来发展具有重要意义。


霍夫变换检测曲线
霍夫变换是一种在图像处理中常用的技术,主要用于检测直线、圆或其他简单形状。
在检测曲线时,霍夫变换通常通过将图像空间参数化,然后利用参数空间中的直线来逼近原始曲线。
具体步骤如下:
1. 边缘检测:首先对图像进行边缘检测,提取出可能的曲线段。
2. 参数化:将每个曲线段参数化,通常使用曲线的弧长或角度作为参数。
3. 霍夫变换:对参数空间中的每个点应用霍夫变换,生成霍夫空间的直方图。
4. 峰值检测:在霍夫空间中寻找峰值,这些峰值对应于原始图像中的曲线。
5. 拟合:对每个检测到的曲线,使用参数空间中的直线进行拟合,得到曲线的参数。
值得注意的是,霍夫变换检测曲线的精度取决于参数化的精度和霍夫空间的维数。
对于更复杂的曲线,可能需要更精细的参数化方法。
此外,对于噪声较多的图像,可能需要结合其他技术(如滤波)来改善检测效果。
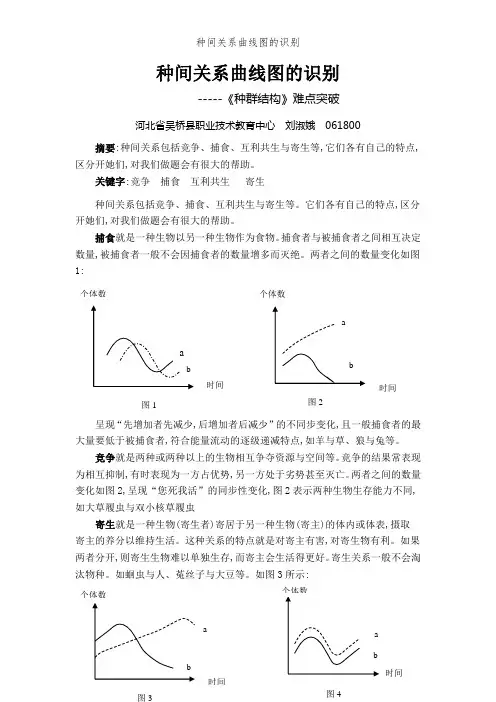
种间关系曲线图的识别-----《种群结构》难点突破河北省吴桥县职业技术教育中心 刘淑娥 061800摘要:种间关系包括竞争、捕食、互利共生与寄生等,它们各有自己的特点,区分开她们,对我们做题会有很大的帮助。
关键字:竞争 捕食 互利共生 寄生种间关系包括竞争、捕食、互利共生与寄生等。
它们各有自己的特点,区分开她们,对我们做题会有很大的帮助。
捕食就是一种生物以另一种生物作为食物。
捕食者与被捕食者之间相互决定数量,被捕食者一般不会因捕食者的数量增多而灭绝。
两者之间的数量变化如图1:的不同步变化,且一般捕食者的最大量要低于被捕食者,符合能量流动的逐级递减特点,如羊与草、狼与兔等。
竞争就是两种或两种以上的生物相互争夺资源与空间等。
竞争的结果常表现为相互抑制,有时表现为一方占优势,另一方处于劣势甚至灭亡。
两者之间的数量变化如图2,呈现“您死我活”的同步性变化,图2表示两种生物生存能力不同,如大草履虫与双小核草履虫寄生就是一种生物(寄生者)寄居于另一种生物(寄主)的体内或体表,摄取 寄主的养分以维持生活。
这种关系的特点就是对寄主有害,对寄生物有利。
如果两者分开,则寄生生物难以单独生存,而寄主会生活得更好。
寄生关系一般不会淘互利共生就是两种生物共同生活在一起,相互依存,彼此有利。
如果分开,则双方或者一方不能独立生存。
数量上两种生物同时增加,同时减少,呈现出“同生共死”的同步性变化,曲线呈“同升同降”特点。
如地衣内的真菌与单细胞藻类、大豆与根瘤菌等。
如图4所示:小试牛刀:1、如图所示为3组生物,A、根瘤菌与豆科植物;B、农作物与杂草;C、狐与兔的种间关系示意图(纵轴表示个体数,横轴表示时间)。
请据图回答:(1)判断A-C三组生物对应的曲线:A______, B________, C_______。
(2)造成图②现象就是由于________________________________。
(3)若3种种间关系中的b死亡,对a有利的就是________________。

2022届高考生物一轮复习必修二技能专项训练:(二)减数分裂及有丝分裂的图像及曲线的识别与判断1.如图是三种二倍体高等动物的细胞分裂模式图,下列相关叙述中,正确的是( )A.图乙细胞中含有姐妹染色单体,图甲细胞中含有同源染色体B.图甲细胞处于有丝分裂后期,也可能处于减数第二次分裂后期C.图乙细胞处于减数第二次分裂中期,属于次级精母细胞D.图丙细胞中若①上有A基因,④上有a基因,则该细胞一定发生了基因突变2.图1表示某二倍体动物细胞分裂过程中同源染色体对数的变化曲线,图2为细胞分裂某时期模式图。
下列叙述正确的是( )A.图1中CD段细胞内含有2条X染色体,4 个染色体组B.图1中AB段、FG段均可发生同源染色体的联会C.图2所示细胞进入分裂后期不会发生等位基因分离D.图2所示细胞进入分裂后期对应图1中的FG段3.下图表示某生物细胞分裂过程,两对等位基因A、a和B、b分别位于两对同源染色体上,若不考虑互换,则下列叙述正确的是( )A.细胞Ⅱ可能是次级卵母细胞,无同源染色体B.细胞Ⅳ中有2个B 基因和2个b 基因C.细胞Ⅴ中可能含有2条染色体,1个b 基因D.细胞Ⅲ中的染色体数目与核DNA 数目的比例始终为1∶24.某生物兴趣小组观察了几种二倍体生物不同分裂时期的细胞,并根据观察结果绘制出如下图形。
下列与图形有关的说法正确的是( )A.甲图所示细胞处于有丝分裂后期,在此时期之前细胞中央出现了赤道板B.甲图所示细胞处于有丝分裂后期,可对应于丙图中的B 组细胞C.乙图所示细胞可能处于减数第一次分裂后期,此阶段发生同源染色体的分离D.如果丙图表示精巢内的几种细胞,则C 组细胞可发生同源染色体分离5.如图为某高等动物 (2n)在细胞分裂过程中染色体与核DNA 数目比值的 变化。
正常情况下,cd 段细胞中不可能出现的现象是( )A.同源染色体交叉互换B.染色体着丝点排列在赤道板上C.染色体着丝点分裂,染色体数2n nD.同源染色体分离,非同源染色体自由组合6.甲、乙、丙三图分别表示某二倍体高等动物细胞分裂图像,下列说法正确的是( )A.依图可判定该个体为雌性B.图甲和图丙可发生同源染色体交又互换C.若乙图中的2、3表示两条X染色体,则说明该细胞分裂方式是减数分裂D.重组性状要在后代中表现出来,一般要通过精子与卵细胞结合产生新个体来实现7.某二倍体高等雌性动物体内有些细胞正处于分裂状态,比如细胞①内有同源染色体,着丝点刚断裂;细胞②内有同源染色体,细胞质正在进行不均等分裂;细胞③内无同源染色体,着丝点整齐排列在赤道板上;细胞④内无同源染色体,着丝点刚断裂。
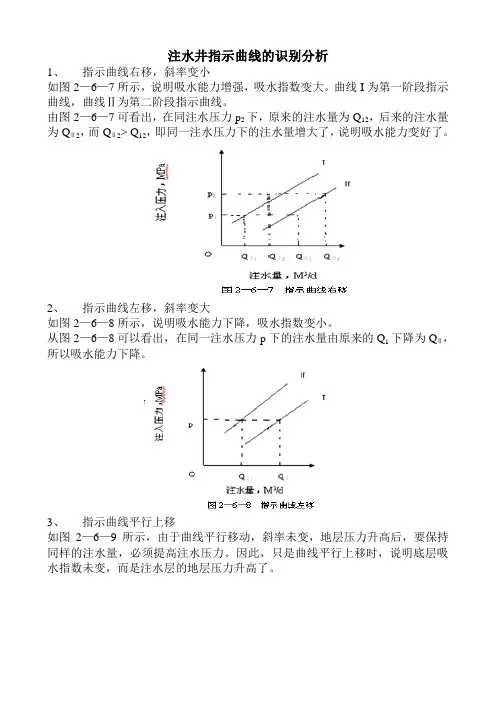
注水井指示曲线的识别分析1、指示曲线右移,斜率变小如图2—6—7所示,说明吸水能力增强,吸水指数变大。
曲线I为第一阶段指示曲线,曲线Ⅱ为第二阶段指示曲线。
由图2—6—7可看出,在同注水压力p2下,原来的注水量为Q12,后来的注水量为QⅡ2,而QⅡ2> Q12,即同一注水压力下的注水量增大了,说明吸水能力变好了。
2、指示曲线左移,斜率变大如图2—6—8所示,说明吸水能力下降,吸水指数变小。
从图2—6—8可以看出,在同一注水压力p下的注水量由原来的Q1下降为QⅡ,所以吸水能力下降。
3、指示曲线平行上移如图2—6—9所示,由于曲线平行移动,斜率未变,地层压力升高后,要保持同样的注水量,必须提高注水压力。
因此,只是曲线平行上移时,说明底层吸水指数未变,而是注水层的地层压力升高了。
4、指示曲线平行下移如图2—6—10所示,曲线平行下移,其地层吸水指数未变。
但同一注水量所需要的注水压力由原来的p1下降为pⅡ,说明地层压力下降了。
一般在采取酸化、压裂等增注措施后出现这种情况。
以上仅就直线只是曲线情况比较复杂,但基本是这四种变化情况的不同组合。
5、分析吸水能力变化要注意的问题(1)分析地层吸水能力的变化,必须用有效压力来绘制地层真实曲线。
若用井口实测注水压力绘制指示曲线,必须是在同一管柱所测指示曲线对比吸水能力的变化。
不同管柱结构所测的指示曲线,由于井内压力损失不同,用来进行对比和分析地层吸水能力的变化误差较大。
(2)由于井下工具工作状况的变化,也会影响指示曲线。
因此,用指示曲线分析地层吸水能力时,应该考虑井下工具工作状况对指示曲线的影响。

有丝分裂中遗传物质数量变化曲线 1、染色体数目何时增加,增加多少? 亲本细胞染色体在细胞分裂间期进行了复制,使每条染色体含有两条染色单体,但染色体的数目并未改变。
只有进入细胞分裂后期时,伴随染色体着丝点的分裂,才使每条染色体上的两条染色单体分别成为一条子染色体,使染色体数目增加一倍(图3)。
2、染色体数目何时减半? 染色体数目增加一倍后,什么时候恢复正常,即何时由4N→2N。
常见两种看法,一种认为染色体数目减半发生在后期结束时(图4-甲),另一种认为发生在末期结束时(图4-乙),两种图形均未明确其含义。
第一种图形可理解为:进入末期时,出现“一胞两核”的特殊现象,此时每个核内的染色体数目只有核出现前细胞内染色体数目的一半(图4-甲);第二种图形可理解为:细胞分裂结束时才形成两个独立的子细胞,此时每个细胞内的染色体数目只相当于形成前亲本细胞的一半(图4-乙)。
如果不明确的给所画图形赋予其特定含义,学生难以明白其内涵。
因此,笔者以为,对所绘之图形进行说明是很有必要的。
对DNA含量减半的时间及意义可与染色体减半行为作相同理解(图5)。
3.关于染色单体的变化情况对染色单体的变化,各种资料比较统一,均认为在分裂间期随着染色体复制结束而产生,0→4N;后期由于着丝点的分裂每条染色单体变成一条子染色体而消失,由4N→0,见图6。
4.结合上述讨论,建议使用两种图形 4.1 第一种为图7,其意义为DNA分子的复制为S期,DNA含量因复制由2a→4a,末期伴随着子细胞形成而减半;染色体数目于后期加倍,末期时形成两个独立的子细胞,每个细胞内的染色体仅相当于形成子细胞前亲本细胞的一半;染色单体于分裂间期结束前产生、分裂后期着丝点分裂形成子染色体而消失。
4.2 第二种为图8,与图7的主要区别在于DNA含量和染色体数目的减少不在末期,而在后期结束时。
意义为:伴随着新核的形成每个核内的DNA含量和染体数目相当于前一时刻亲本细胞的一半。

曲线凹凸性的判断方法
曲线凹凸性判断是识别函数曲线处处向量切线方向的重要方法,用于求解微积分、动力学等重要问题,也是检测函数曲线任意点处变化状态的依据。
曲线凹凸性的判断方法有以下几种:
1、利用积分法:将曲线上的每一片分段折线积分,由积分结果得出曲线的凹
凸性,即根据积分结果的符号大小来确定曲线的凹凸性:若积分结果为正,则曲线向上凸出,上升趋势明显;若积分结果为负,则曲线向下凹陷,下降趋势明显。
2、利用微分法:以曲线上任一点为中心,考察它及其附近的某点处方向与曲
线段的夹角大小及趋势,从而判断曲线凹凸性:若夹角大于零,则曲线向上凸出,上升趋势明显;若夹角小于零,则曲线向下凹陷,下降趋势明显。
3、利用数值分析法:画出曲线的网格折线,采用直接数值法求出曲线的凹凸性,即根据曲线上点之间的数值大小比较结果来判断曲线的凹凸性:若曲线点值持续上升,则曲线向上凸出,上升趋势明显;若曲线点值持续下降,则曲线向下凹陷,下降趋势明显。
4、利用图象识别法:观察曲线的图象,根据曲线的连续变化特点来确定曲线
的凹凸性,即观察曲线的拐点位置及方向确定曲线的凹凸性:若拐点持续向上,则曲线向上凸出,上升趋势明显;若拐点持续向下,则曲线向下凹陷,下降趋势明显。
以上便是曲线凹凸性判断的主要方法,各种方法有各种优缺点,在实际应用中,以上四种方法相互之间可以结合使用,以达到合理判断曲线凹凸性的效果,使曲线凹凸性判断得以正确与准确地实现。


串并联电路的识别方法
串联电路是指所有电子元件依次连接在一个电路中,串联电路中的电流大小相同,电压共享。
而并联电路是指所有电子元件平行连接在一个电路中,并联电路中的电压大小相同,电流分流。
下面是识别串并联电路的方法:
1. 分析电路图:观察电路图上元件的连接方式。
如果元件依次连接在一起,没有分支,则为串联电路。
如果元件有平行连接的情况,则为并联电路。
2. 测量电流和电压:使用电表测量电路中的电流和电压。
串联电路中,电流值在各个元件间保持不变;而并联电路中,各个分支中的电流之和等于总电流。
如果电流在各个元件之间没有变化,则为串联电路。
3. 检查电阻:可以通过测量电阻值来判断电路的连接方式。
串联电路中,电阻值相加等于总电阻;而并联电路中,总电阻的倒数等于各分支电阻的倒数和。
通过测量电阻值并进行计算,可以确定电路的连接方式。
4. 观察特征曲线:某些电子元件的特征曲线在串并联电路中会显示出不同的特点。
例如,二极管在串联电路中会表现出阻抗递增的特征,而在并联电路中阻抗递减。
观察特征曲线的变化,可以判断电路的连接方式。
通过以上方法,可以准确识别串并联电路的连接方式。

曲线检测算法
曲线检测算法是一种用于检测图像中曲线的方法。
曲线检测算法可以应用于许多领域,如计算机视觉、图像处理和模式识别等。
常见的曲线检测算法包括:
1. 边缘检测:边缘是图像中颜色、亮度或纹理变化的地方,边缘检测算法可以找到图像中的边缘,从而间接得到曲线的位置。
2. 霍夫变换:霍夫变换是一种常用的曲线检测算法,它可以在参数空间中找到与曲线对应的累加器峰值,并根据峰值的位置和强度提取出曲线的参数。
3. 曲率计算:曲率是曲线在某点上的弯曲程度,曲线的曲率可以通过计算曲线在每个点处的切线解算出来。
曲率计算算法可以根据曲线的切线角度和曲线的弯曲程度来确定曲线的位置和形状。
4. 活动轮廓模型:活动轮廓模型是一种基于能量泛函的曲线检测算法。
它根据曲线的能量泛函和附加约束条件,通过优化求解得到曲线的位置和形状。
这些曲线检测算法可以根据具体的应用场景和需求进行选择和组合使用,以达到准确和高效地检测曲线的目的。
dirca哈曼曲线-概述说明以及解释1.引言1.1 概述dirca哈曼曲线是一种特殊的数学曲线,其特点是能够描述物体的运动规律和变化趋势。
它是由法国数学家dirca和德国物理学家哈曼共同发现和研究的,因此得名dirca哈曼曲线。
dirca哈曼曲线具有独特的形态和性质,其数学表达式为一组复杂的方程。
它是一条连续的曲线,通常呈现出光滑的弯曲和变化。
曲线的形状和轨迹随着参数的不同而变化,可以呈现出各种曲线形式,例如圆弧、螺旋等。
dirca哈曼曲线的应用范围广泛。
在物理学领域,它可以用于描述物体运动的轨迹和速度变化,帮助科学家理解和预测物体的运动规律。
在工程学领域,dirca哈曼曲线可以用于设计和优化轨迹规划算法,提高自动化系统的运动效率和精度。
此外,dirca哈曼曲线还可以应用于图像处理、数据拟合等领域,具有广泛的实际应用价值。
然而,dirca哈曼曲线也存在一些不足之处。
首先,由于其数学表达式复杂,计算和求解过程较为繁琐,需要借助计算机和专业软件进行计算。
其次,dirca哈曼曲线的参数选择和调节对曲线形态和特性具有重要影响,需要经验和技巧进行调试。
总之,dirca哈曼曲线是一种重要的数学工具,具有丰富的特性和广泛的应用价值。
深入研究和应用dirca哈曼曲线,有助于我们更好地理解和掌握物体运动规律,推动科学技术的发展与创新。
在接下来的文章中,我们将详细介绍dirca哈曼曲线的定义、特点、应用以及其优缺点,并对其进行进一步的总结和展望。
1.2 文章结构文章结构部分的内容可以包括对整篇文章的章节分布和每个章节的概述。
下面是一个可能的编写范例:文章结构:本篇文章将按照以下章节进行讨论。
首先,引言部分将介绍dirca哈曼曲线的概述、文章的结构、目的以及总结。
接下来,正文部分将详细阐述dirca哈曼曲线的定义、特点、应用以及优缺点。
最后,结论部分将对dirca哈曼曲线进行总结,并展望未来的研究方向。
同时,我们也会提及研究的局限性。
曲线拐点识别算法简介曲线拐点识别算法是一种用于识别曲线数据中的拐点(即曲线发生突变或转折的点)的方法。
在很多领域中,如金融、工程、医学等,对于曲线的拐点进行准确的识别和分析具有重要意义。
通过识别拐点,可以帮助人们发现异常情况、预测趋势变化等。
本文将介绍曲线拐点识别算法的原理、常用方法以及应用场景,并对其中一种经典算法进行详细说明。
原理曲线拐点识别算法基于以下原理:在平滑连续的曲线上,当曲线发生突变或转折时,其导数也会出现明显的变化。
因此,通过分析曲线上某个点处导数的变化情况,可以判断该点是否为拐点。
常用方法1. 线性回归线性回归是一种常见且简单的方法,用于找到最佳直线以逼近给定数据集。
在曲线拐点识别中,可以通过适当选择数据集的子集,并对其进行线性回归分析来确定拐点位置。
具体步骤如下:1.将曲线数据集分成多个子集(通常是相等长度的窗口);2.对每个子集进行线性回归,得到拟合直线的斜率;3.计算每个子集的斜率变化,找到最大变化的子集对应的位置,即为拐点位置。
2. 方差分析方差分析是一种统计方法,用于比较两个或多个样本之间的差异。
在曲线拐点识别中,可以通过方差分析来确定曲线上某个点是否为拐点。
具体步骤如下:1.将曲线数据按照某种方式划分成若干组(如等间距划分);2.对每组数据进行方差分析,计算组内方差和组间方差;3.比较组内方差和组间方差的大小关系,如果组内方差较小且组间方差较大,则该点可能是一个拐点。
3. 斜率变化法斜率变化法是一种直观且简单的方法,通过计算曲线上相邻两点之间斜率的变化情况来确定拐点位置。
具体步骤如下:1.计算相邻两点的斜率,即曲线在该点处的导数;2.计算相邻两点斜率的变化情况,如差值、百分比变化等;3.找到斜率变化最大的位置,即为拐点位置。
应用场景曲线拐点识别算法在许多领域中都有广泛的应用,以下列举几个常见的应用场景:1. 股票市场分析股票价格曲线中的拐点往往代表着股票价格发生重大变化的时刻。
各类型几何图图形识别技巧各类型几何图形识别技巧一、引言几何图形识别是计算机视觉和图像处理领域的一个重要研究方向。
通过对各类型几何图形的识别,可以实现对现实世界中物体的分类、检测和识别。
本文将介绍几种常见几何图形的识别技巧,帮助读者更好地理解和应用这一领域。
二、点、线、面的识别1.点的识别:点是最基本的几何图形,其识别主要依据像素强度和邻域特性。
常用的方法有:–零交叉法:通过寻找图像梯度的零交叉点来检测边缘,进一步确定点的位置。
–局部极值法:在图像中寻找局部最大值和最小值,作为点的候选位置。
2.线的识别:线的识别通常基于边缘检测算法,如Canny、Sobel和Prewitt等。
线的特征主要包括:–方向:利用边缘检测算子计算线条的倾斜角度。
–长度:通过积分图像或线段检测算法测量线段的长度。
–宽度:线段的横向尺寸。
3.面的识别:面的识别主要基于区域的生长和连通性。
常用的方法有:–四连通性:通过判断相邻像素间的相似性,生长出完整的目标区域。
–八连通性:在四连通性的基础上,考虑对角线相邻像素的相似性。
三、圆形和椭圆的识别1.圆形的识别:圆形识别的关键在于圆心和半径的确定。
常用的方法有:–Hough变换:将圆的方程参数化,通过投票机制检测图像中的圆。
–模板匹配:预先准备圆形模板,与图像中的候选圆形区域进行匹配。
2.椭圆的识别:椭圆的识别与圆形类似,主要区别在于椭圆的长轴和短轴。
常用的方法有:–Hough变换:将椭圆的方程参数化,通过投票机制检测图像中的椭圆。
–模板匹配:预先准备椭圆模板,与图像中的候选椭圆区域进行匹配。
四、矩形和多边形的识别1.矩形的识别:矩形识别的关键在于四个顶点的确定。
常用的方法有:–霍夫变换:将矩形的方程参数化,通过投票机制检测图像中的矩形。
–角点检测:检测图像中的角点,通过角点对构建矩形。
2.多边形的识别:多边形识别的关键在于顶点的确定和边的连接。
常用的方法有:–边界跟踪:通过边缘检测算法跟踪多边形的边界。
人工智能识别曲线
人工智能可以通过图像识别技术来识别曲线。
图像识别是一种通过算法识别和理解图像的技术。
对于曲线识别,人工智能可以通过提取图像中的曲线特征,然后利用深度学习等方法对这些特征进行分析和识别。
在曲线识别中,通常需要使用边缘检测算法来提取图像中的曲线边界,并将其转换为数学上的曲线表示。
然后,可以使用特定的曲线拟合算法来拟合这些曲线,并对其进行分类或识别。
人工智能可以学习和训练,通过大量带有标签的曲线图像样本,学习曲线的特征和模式,从而能够在未知图像中自动识别曲线。
曲线识别在许多应用中都有广泛的应用,例如医学影像分析中的血管识别、工程中的曲线检测与测量等。
人工智能的发展使得曲线识别变得更加准确和高效。
波长变化的曲线通常指的是光谱曲线,它是描述光(或电磁波)波长与强度(或功率、能量)关系的图表。
在不同的领域,光谱曲线可以有不同的表现形式和应用。
以下是几种常见的波长变化曲线:
1. 吸收光谱曲线:在化学和物理领域,吸收光谱曲线用于描述物质对不同波长光的吸收情况。
横坐标是波长,纵坐标是吸光度(无单位)或吸光强度。
这种曲线常用于分析物质的组成和结构。
2. 发射光谱曲线:在原子和分子物理学中,发射光谱曲线描述了原子或分子在特定能级跃迁时发射光子的波长和强度。
这种曲线有助于了解原子的能级结构和光谱特性。
3. 反射光谱曲线:在光学和材料科学中,反射光谱曲线用于描述材料对不同波长光的反射能力。
这种曲线对于了解材料的颜色和光学特性非常重要。
4. 透过光谱曲线:在光学领域,透过光谱曲线描述了光通过不同材料时波长与透过率的关系。
透过率是指光通过材料后剩余的强度与入射光强度的比值。
5. 散射光谱曲线:在粒子物理学和大气科学中,散射光谱曲线用于描述光在介质中传播时因散射而改变波长和强度的现象。
这种曲线对于了解光的传播特性和粒子的大小分布非常重要。
6. 干涉光谱曲线:在光学和光谱学中,干涉光谱曲线描述了光波经过干涉现象后的波长与强度关系。
这种曲线可以用于精确测量光的波长。
7. 光谱能量分布曲线:在太阳物理学和天文学中,光谱能量分布曲线用于描述太阳光或其他恒星光在不同波长范围内的能量分布。
这种曲线对于了解恒星的光谱类型和能量输出非常重要。
每种光谱曲线都有其特定的应用背景和意义,通过分析这些曲线,可以获取有关光、物质和现象的详细信息。
基于CMPSO算法的永磁同步电机转动惯量识别研究田峰; 林荣文; 吴雅琳【期刊名称】《《电机与控制应用》》【年(卷),期】2019(046)010【总页数】6页(P14-18,65)【关键词】永磁同步电机; 改进粒子群优化算法; 柯西变异; 矢量控制; 转动惯量识别【作者】田峰; 林荣文; 吴雅琳【作者单位】福州大学电气工程与自动化学院福建福州 350108【正文语种】中文【中图分类】TM3510 引言永磁同步电机(PMSM)是一个非线性、时变、大延时的复杂系统,存在转子惯量变化扰动等多种扰动,对系统的精度、稳定性、动静态性能等造成了影响。
为了识别转动惯量,研究者提出了基于朗道离散时间递推算法[1]、递推最小二乘法[2]等,但是PMSM工作环境复杂多变,难以准确地、实时地识别出转动惯量。
为此,有学者提出引进智能算法[3],如粒子群优化算法(PSO)、遗传算法(GA)等。
但是,标准智能算法各有不足之处,如标准PSO容易局部最优[4],GA算法实现复杂、耗时长[5]。
文献[6]提出采用柯西变异的策略,较好地解决了标准PSO容易陷入局部最优的问题。
文献[7-8]虽然采用智能算法识别PMSM参数,但是缺少对于PMSM转动惯量识别的研究。
本文采用模型参考自适应方法的基本原理,无需设计自适应率迭代识别算法,利用柯西变异粒子群优化(CMPSO)算法代替自适应律,通过迭代更新粒子值从而识别得到转动惯量。
利用仿真和试验验证了CMPSO辨识算法的可行性、正确性和准确性。
1 PMSM d-q数学模型在理想化条件下,能够简化PMSM数学模型[9]。
本文PMSM采用的控制策略是id=0的双闭环矢量控制[10]。
该控制策略简单,没有去磁效应,所有电流均用来产生电磁转矩。
本质是控制PMSM的直轴电流id和交轴电流iq,可等效为直流电机控制。
因此,本文给出在d-q坐标系下PMSM数学方程。
PMSM结构图如图1所示。
图1 PMSM结构图在d-q坐标系下,PMSM电压方程为(1)磁链方程为(2)电磁转矩方程为当Ld=Lq时,式(3)可变为(4)机械运动方程为(5)式中: Ud、Uq——d、q轴电压;Rs——定子绕组的电阻;id、iq——d、q轴电流;ψd、ψq——定子磁链d、q分量;ωr——转子电角速度;Ld、Lq——d、q轴等效电感;ψf——转子磁极磁链;p——极对数;J——电机转动惯量;ωm——机械角速度;Bm——黏滞系数。