北大高微讲义第4章 需求
- 格式:pdf
- 大小:148.17 KB
- 文档页数:39


四、偏好关系与选择规则之间的关系1. Question :Can the choice structure be generated (or rationalized) by a rational preference relation? In other words, can we find some rational preference relation such that *()(,)C C =i i ? A natural candidate of such a is the * that is implied by C(•). ()**(,*)C C →→i i Question: ()*(,*)?C C =i iIn order for C to be rationalized by some preference relation, we need C to satisfy:and ', , and ',(),(')B B x y B B x C B y C B ∀∈∈∈(i.e. x is chosen when y is also available and y is chosen when x is also available), then (),(')y C B x C B ∈∈.Another way of expressing this is:定义6:(WARP or Weak Axiom of Revealed Preference )Suppose B ∈B ,,, and ()x y B x c B ∈∈. Then B ′∀∈B ,with , and ()x y B y c B ′′∈∈, we must have ()x c B ′∈.In the two earlier examples, C 1 satisfies WARP but C 2 does not.Recall the definition of C*, the choice rule implied by :B ∀∈B {}*(, ): for every assumeC B x x y y B φ=∈≠ Q :If is rational, does *(, C i satisfy WARP?A :Yes, i.e., WARP is a necessary condition for C to be rationalized by a rational preference relation. 证明:假定,,*(),,,,*()x y B x C B B x y B y C B ∈∈Β∈′′′∈Β∈∈且 要证:*(x C B ′∈) *(),,*(), , for all *()x C B x y y C B y z for z B x z z B x C B ∈⇒′′∈⇒∀∈′∴∈′∈ 由即 利用了理性偏好的传递性2、 Question: Is WARP also a sufficient condition? (choice rule →preference relation)Suppose C satisfies WARP, can we always find a s.t *()(,)C C =i i ?A: No!Counter example :{}{}{}{}{}x z z y z y x X ,,,,y,x,B ,,=={}{}{}(,){}(,){}(,){}.C x y x C y z y C z x z ===可以证明这样的()C i 是满足WARP 的,但是它所产生的* 却是非理性的:but .x y y x x y ≥⇒ Similarly, and ,y z z x contradictory to rationality.3、 命题3:给定choice structure (B ,()C i ),假定a) Satisfy WARP ;b) B contains all subsets of X with three or less elements 。



北大测试全套课件和教案 9. 第4章第3讲《软件测试基础》授课教案授课内容:第四章白盒测试技术授课课次:第9次课授课时数:2学时授课日期: 上课教室: 目的与要求:掌握白盒测试中基本路经测试的概念和方法;了解程序插桩的概念和方法。
教学重点:基本路经测试教学难点:程序插桩教学方式:1. 运用《白盒测试技术》课件进行课堂讲授,让学生理解基本路径测试的概念,掌握基本路径测试方法;2. 进行课堂练习,加深对基本路径测试的理解和使用。
教学内容:1.程序结构分析 2.DD路径测试 3.基本路径测试 4.程序插桩内容提要及时间分配:1、课前引导(8分钟)? 回顾6种覆盖法的基本思想。
? 白盒测试中有哪些常用方法?2、本课内容(75分钟)? 程序结构分析 ? DD路径测试 ? 基本路径测试 ? 程序插桩3、课后小结(5分钟)4、布置作业(2分钟)教学参考书:1. 软件测试方法和技术朱少民清华大学出版社2. 软件测试Paul C.Jorgensen 机械工业出版社讨论与思考:把第2章的NextDate问题的伪代码转换成为控制流图,并简化。
作业:1.请把下面的程序流程图转化成控制流图。
12364791181052.重新编写程序片断14~20,用嵌套if-then-else语句替代复合条件。
14. if(a=b)AND (b=c) 15. T hen Output(“Equilateral”)16. Else If(a<>b)AND(a<>c)AND(b<>c) 17. Then Output(“Scalence”) 18. Else Output(“Isosecles”) 19. EndIf 20. EndIf比较你改写后的程序和上面程序片断的圈复杂度。
复问题目:序号 1 2 3 题目学生成绩教学内容与方法步骤4.2.3程序结构分析引言:程序的结构形式是白盒测试的主要依据。
这一部分将从控制流分析和数据流分析的不同方面讨论如何分析程序结构。


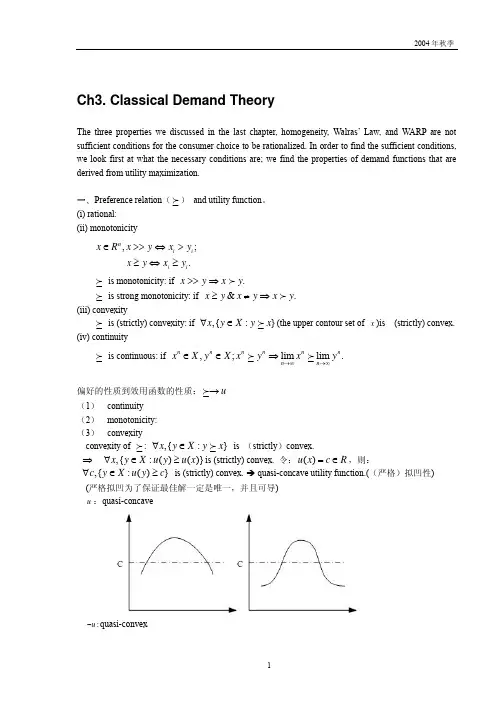
Ch3. Classical Demand TheoryThe three properties we discussed in the last chapter, homogeneity, Walras’ Law, and WARP are not sufficient conditions for the consumer choice to be rationalized. In order to find the sufficient conditions, we look first at what the necessary conditions are; we find the properties of demand functions that are derived from utility maximization.一、Preference relation ( ) and utility function 。
(i) rational: (ii) monotonicity,; .n i i i i x R x y x y x y x y ∈>>⇔>≥⇔≥is monotonicity: if .x y x y >>⇒is strong monotonicity: if &.x y x y x y ≥≠⇒(iii) convexityis (strictly) convexity: if ,{:}x y X y x ∀∈ (the upper contour set of x )is (strictly) convex. (iv) continuityis continuous: if ,;lim lim .nnnnnnn n x X y X x y x y →∞→∞∈∈⇒偏好的性质到效用函数的性质:u → (1) continuity (2) monotonicity:(3) convexity convexity of : ,{:}x y X y x ∀∈ is (strictly )convex.⇒ ,{:()()}x y X u y u x ∀∈≥is (strictly) convex. 令:()u x c R =∈,则:,{:()}c y X u y c ∀∈≥ is (strictly) convex. Î quasi-concave utility function.((严格)拟凹性)(严格拟凹为了保证最佳解一定是唯一,并且可导) u :quasi-concave:u −quasi-convexQuasi-concave and quasi-convex: monotone function; special e.g. line functionAnother proposition: if u is concave (convex) , f is strictly increasing, then f u is quasi-concave (quasi-convex).二、效用最大化问题(utility maximization problem )(UMP)1、 效用最大化问题 给定p ,w ,11max ()s.t. or (budget constraint)xn n u x px w px p x p x ≤=+⋅⋅⋅+性质1:只要u 是连续的,UMP 有解重写UMP {},max ()s.t. :,0xp w u x x B x px w x ∈=≤≥解的存在性和唯一性: B p,w 是闭集,并且有上下界,⇒B p,w 是紧集(compact set ),紧集上的连续函数最大化问题一定有解。

第1部分消费者行为理论•第1章消费者的最优决策•第2章比较静态分析•第3章显示偏好理论•第4章需求•第5章消费者的福利变化•第6章库恩---塔克条件•第7章不确定条件下的个人选择1第6章库恩---塔克条件(Kuhn —Tucker condition)一、K —T 条件•在最优化问题中,若–选择变量要求非负–约束条件是不等式则需要用K —T 条件来解决问题。
1、K —T 条件初步理解(1)关于选择变量非负的要求Max y =f (xs .. t x ≥0f ' (x ≤0, x ≥0, and f ' (x ⋅x =02第6章库恩---塔克条件(2)关于约束条件是不等式的要求:P1在(1)的基础上加入不等约束的要求Max x y =f (x 1, x 2, x 3 s . t . g 1(x 1, x 2, x 3 ≤r 1g 2(x 1, x 2, x 3 ≤r 2且x 1, x 2, x 3≥03()第6章库恩---塔克条件(3)关于(P1)最优解的推导第一步:加入两个虚设变量s 1、s 2 ≥0,将(P1)处理成以下的等价形式(P2)。
(即:去掉不等式约束条件)Max y =f (x 1, x 2, x 3 x , s(P2)s . t . g (x 1, x 2, x 3 +s 1=r 1g (x 1, x 2, x 3 +s 2=r 221且x 1, x 2, x 3, s 1, s 2≥04第6章库恩---塔克条件(3)关于(P1)最优解的推导第二步:假设去掉选择变量的非负要求,于是有:Z (x 1, x 2, x 3, s 1, s 2, λ1, λ2=f (x 1, x 2, x 3 +λ1(r 1−g (x1, x 2, x 3 −s 1 +λ2(r 2−g (x 1, x 2, x 3 −s 2 (P2' )∂z ∂z ∂z F . O . C . ===0∂x 1∂x 2∂x 3∂z ∂z ==0∂s 1∂s 2∂z ∂z ==0∂λ1∂λ2512第6章库恩---塔克条件(3)关于(P1)最优解的推导第三步:加上选择变量非负的要求。

