第2课时垂线一、教学目标：知识目标：表述垂线的概念，会用三角尺或量角器过一点画已知直线的垂线。
能力目标：通过垂线的画法，进一步提高实际动手操作能力。
情感目标：通过垂线，进一步体会到几何图形的对称美。
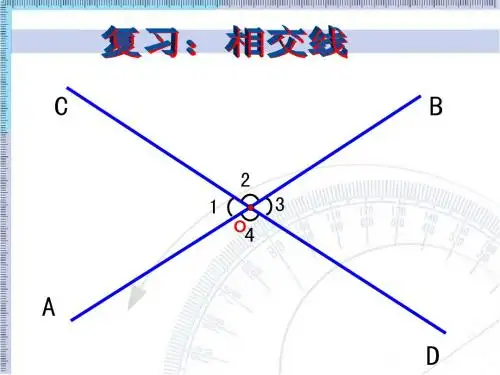
二、教学重难点：重点：垂线的概念和性质；难点：垂线的判断和性质的理解运用；三、教学过程：（一）导入新课：把一张正方形纸片按下图方式折叠，得到∠1，∠1是什么角？把这张纸片展开，如下图，AB、CD是两条折痕，相交于点O，则∠AOC、∠AOD、∠BOC、∠BOD与∠1有什么关系？它们是什么角？由此发现这两条相交直线是一种怎样的特殊情况？（二）探究新知：1．垂直的概念垂直是相交的一种特殊情形，当两条直线相交所成的四个角中有一个是直角时，我们就说这两条直线互相垂直（perpendicuLar），其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足。
在下图中，AB⊥CD，垂足为O。
注意：（1）两条直线相交，只要有一个角是直角，即说这两条直线互相垂直。
但是，由对顶角的性质可知，两条直线垂直时，相交成的四个角都是直角。
（2）两条直线互相垂直，每一条都叫做另一条的垂线。
符号表示：两条直线互相垂直，怎样用符号和几何语言表示呢？如下图，记作AB⊥CD，读作“AB垂直于CD”。
AB是CD的垂线，也可以说CD是AB 的垂线。
它们的交点O叫做垂足。
日常生活中，两条直线互相垂直的情形很常见，说出下图中的一些互相垂直的线条。
你能再举出其他例子吗?例如：（出示图片）请同学们找出图中相互垂直的直线，再举一些生活中的例子。
由于定义既可以当性质用，又可以当判定用，因此可以有以下两个方向的推理过程。
（1）已知垂直关系，可得所成的角为90°（性质）．即：∵AB⊥CD于O（已知）∴∠AOD=90°（垂直的定义）注：写∠AOC=90°、∠COB=90°、∠BOD=90°均可。
（2）已知两直线相交有一个角为90°，可得两直线垂直（判定）。
