当前位置：文档之家 › 屈服与破坏准则 便宜版27页PPT

屈服与破坏准则 便宜版27页PPT

  • 格式：ppt
  • 大小：2.94 MB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

l08-第3.4节-屈服准则-0102PPT精品文档35页

l08-第3.4节-屈服准则-0102PPT精品文档35页


12xy
2yz
2zx
26
2
2
2
xy
yz
zx

12122232312
C
单向应力状态下
1 s ; 2 3 0 ;C s
x y 2 y z2 z x 2 6 x y 2 y z 2 z x 2 2 S 2
(3)弹塑性材料 2)弹塑性硬化材料。在塑性变形时，既要考虑塑性 变形之前的弹性变形．又要考虑加工硬化的材料， 见图3—40d。这种材料在进入塑性状态后，如应力 保持不变，则不能进一步变形。只有在应力不断增 加，也即在加载条件下才能连续产生塑性变形。
有关材料性质的几点说明
(4)刚塑性材料 不考虑塑性变形之前的弹性变形的材料。 1)理想刚塑性材料。在研究塑性变形时既不考虑弹 性变形，又不考虑变形过程中的加工硬化的材料
p r3 5 3 0 0
1 tt ; 2 z 2 t 2 t; 3 p 0
1 3 s ;3 5 t3 0 0 7 0 0 ;t 3 5 7 0 3 0 0 0 m m 1 5 m m
2K
三、 Mises屈服准则
1913年，Mises屈服准则 — 当质点的等效应力到达某定 值时，材料屈服，该定值与应力状态无关。
一.屈服准则的基本概念 ★
屈服准则：
变形体内质点由弹性状态过渡到塑性状态，并 维持继续进行塑性变形所需满足的力学条件， 即各应力分量与材料性能之间必须符合的一定 关系。(塑性条件、屈服条件)
根据屈服准则的定义，可用如下数学模型概括
f(ij) C (i,jx ,y ,z)
fJ1,J2,J3C

3-3屈服准则

3-3屈服准则

3-3屈服准则第16章屈服准则yield criteria本章内容：屈服准则本章重点：两个屈服准则的表达及应用单向应力时：只要单向应力达到屈服极限，材料就屈服，进入塑性状态。

多向应力时：各应力分量—（屈服准则）—材料性能即?()ijσ=C材料性质：实际材料（理想弹塑性elastic-perfectly plastic，理想刚塑性rigid-perfectly plastic，弹塑性硬化harding plastic，刚塑性硬化）符合各向同性理想塑性材料perfectly plastic material的Tresca 和Mises 屈服准则16．1 Tresca 屈服准则（最大切应力不变条件）最大切应力达到一定值时，材料屈服。

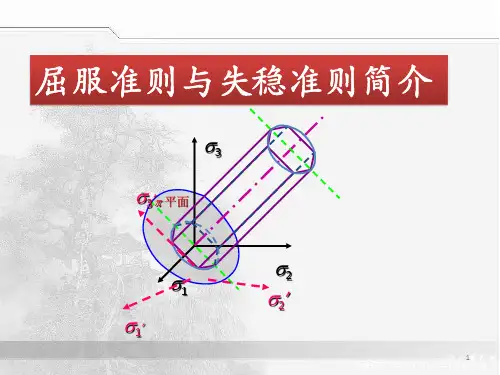
由于()3212m ax 31σσστσσ>>±=-Tresca 屈服准则为：C =-31σσ（C 为常数，与材料有关）单向拉伸时由于0,321===σσσσs 有：s C σ=因此Tresca 准则为：s σσσ=-31或者=-=-=-s ssσσσσσσσσσ13平面问题中任意坐标系应力分量表示的Tresca准则为：()222m ax xyy x ττσσ+=-或者：()2s224στσσ=+-xyy x16．2 Mises 屈服准则（弹性形变能elastic strain energy 不变条件）等效应力σ达到一定值时，材料屈服。

()()()[]21323222121σσσσσσσ-+-+-=()()()()C zx yz xy x z z y y x =+++-+-+-=222216τττσσσσσσ单向拉伸时s σσσ==1 032==σσ 有s C σ=Mises 准则为：()()()22132322212sσσσσσσσ=-+-+-或()()()()222222226szxyzxyx z z y y xστττσσσσσσ=+++-+-+-平面应力状态：()003====σττσxz yz z Mises:=+-=+-+222212122223s s xy y x y x σσσσσστσσσσ 平面应变状态：0==zy yz ττ()23221σσσσσσ++==yx zMises:()?=++=-2342232214s xyy x s στσσσσσ 轴对称状态：0==z θρθττ()θρσσ= Mises:()??=-=+-s s z z σσσστσσρρ312223 ()()()2222226szz z στσσσσσσγγθθγ=+-+-+-16．3 屈服轨迹和屈服表面yield locus and yield surface 16．3．1 平面应力状态（03=σ）Tresca:s σσσ=-21 s σσ=2s σσ=1Mises:2222121sσσσσσ=+-两准则图上相同点：A 、C 、E 、G 、I 、K ，相差最大点：B 、D 、F 、H 、J 、L其中：A 、E 、G 、K ，单向应力状态。

屈服准则与失稳准则介绍ppt课件

屈服准则与失稳准则介绍ppt课件

ij ,
ij , t,T ) 0
在不考虑时间效应(如应变率)和温 度的条件下：
F ( ij ,ij ) 0
考虑屈服前应力和应变的对应关 系，可进一步简化为：
2020/1/6
3
3.各向同性屈服准则
3.1Tresca 屈服条件(最大剪应力不变条件)
1864年Tresca根据Coulomb对土力学的研究和他自己对金属挤压试验中得到的结果，提出 以下假设：
如 2.屈何服建准立则一的个特统征一的函数表达屈服条件
F ( ①屈服与坐标选一择般无情关况，下屈，屈服服函条数件是与一应个不变量；
②③屈屈服服与与球应应力力而为、 且 屈力的应 是 服无是变 它 函关拉、 们 数，还时 的 。迭是间 函加压、 数球无温 ，度这应关等个力。有函不关数改，称变原来的状态；
)m

( 2bi 90
)m

/
2

( 2bi 45
)m
m bi
m
( 2bi )m 45
1
m

ln 2(1 r45 ) ln 2bi
45
式中， 为纯剪时的屈服应力，0、 45、90分别为沿与轧制方向成 0o, 45o,90o 进行单向拉伸
时的屈服应力， bi 为液压胀形屈服时的顶点应力，m值的意义同Hill79屈服准则。
那么： R11 1, R22
r90 (r0 1) r0 (r90 1)
,
R33

r90 (r0 r0
1) ,
r90
R22

3r90 (r0 1) (2r45 1)(r0 r90 )
其中 r0 , r45 , r90 分别为沿着轧制方向、与轧制方向成45°、以及横截面方向拉伸试样宽

屈服准则

屈服准则
第三章 屈服准则 Chapter 3 Yield Criterion
1
1 2 3 4
预备知识 屈雷斯加屈服准则 米塞斯屈服准则
两种屈服准则的几何描述
2
1
Preliminary knowledge
单拉时材料达到 s 时，材料由弹性阶段进入塑性阶 段，而在多向应力下，必须考虑所有的应力分量，在一 定变形条件（温度、变形温度）下，只有各个应力分量 之间符合一定关系时，质点才进入塑性状态，该关系即 屈服准则，也称塑性条件，可表示为：
f ( ij ) C
式中C——与材料性质有关而与应力状态无关的常 数，可通过试验求得。
3
1
Preliminary knowledge
对于各向同性材料，坐标选取时与屈服准则无关， 故可用主应力表示为
f (1 , 2 , 3 ) C
当 f ( ij ) C 时，质点处于弹性状态，f ( ij )=C 时质 点处于塑性状态，不会出现 f ( ij ) C 的状况
如果不知道主应力大小顺序时，则屈雷斯加屈服准则表达式为：
7
3
米塞斯屈服准则
Description
在一定的变形条件下，当受力物体内一点的应力偏张量的第 二不变量J2’达到某一定值时，该点就进入塑性状态，即
f ( 'ij ) J '2 C
用应力分量表示为
1 2 2 2 2 2 2 J '2 ( ) ( ) ( ) 6( x y y z z x xy yz zx ) C 6
10
Summary
屈雷斯加 PK 米塞斯
Similarities
（1）屈服准则的表达式都和坐标的选择无关， 等式左边都是不变量的函数； （2）三个主应力可以任意置换而不影响屈服； 同时，认为拉应力和压应力的作用是一样的； （3）各表达式都和应力球张量无关。（静水 压力不影响屈服）

第03章 第03节 屈服准则

第03章 第03节 屈服准则
不同点：
Tresca屈服准则没有考虑中间应力的影响，三个主应力大 小顺序不知时，使用不便；而Mises屈服淮则考虑了中间应 力的影响，使用方便。
本节小结
• Tresca，Mises准则的数学表达； • Tresca，Mises准则物理意义； • Tresca，Mises准则的比较；
每日一练
• 1、考虑材料的弹性，也考虑材料硬化的材 料模型称为 。 • A、理想弹塑性材料 B、理想刚塑性材料 C、硬化刚塑性材料 D、硬化弹塑性材料
(110 10)2 (10 0)2 (0 110)2 2 s2
1 100 20 100 20 2 110 302 = 3 2 2 10
Tresca:
s =1 3 =110-0=110
例题２
一圆柱体，直径φ100mm，且为理想塑性材料，服从屈雷斯加准则， 屈服应力为σs=160N/mm2,在外载荷作用下内部形成一定的应力场。现设 所有应力分量和θ及z坐标无关（即轴对称状态，且在高度方向应力均 布），而且应力分量σr，σθ，σz都是主应力。 a)试判断下列两种应力场是否有可能存在；如有可能存在，则进而判 断试样内各部分质点处于什么状态（弹性或塑性）； 1）σr=σθ=3r -180, σz=-200N/mm2; 2) σr=σθ=3r-180, σz=-190N/mm2。

Mises准则又可表述为：在一定的变形条件下，当受力物 体内一点的等效应力达到某一定值时，该点就开始进入 塑性状态。
Mises屈服准则
2、Mises准则的物理意义 在一定的变形条件下，当材料的单位体积形状改变的弹性位能(又称 弹性形变能)达到某一常数时，材料就屈服。
说明:
弹性变形位能包括体积变化位能和形状变化位能

07第七章 屈服准则

07第七章 屈服准则
2 2 2
Mises刚提出这一准则时，认为是对Tresca准则的一种数学处理，是近似的，而Tresca 准则是准确的。但大量试验证明，对大多数材料， Mises准则更准确。
将单向拉伸时的屈服强度： 1 s 代入上式得： C 2 s 2 。
令
c ( C 2 ) s

1 2
(
主应力空间中的任一点对应物体某点的应力状态则主应力空间中的任一曲线表示某点上的应力的变化过程称为加载路径材料开始进入塑性变形状态产生不可恢复的变形称为屈服相应的在主应力空间中的点为屈服点
?
第七章 屈服准则
目标： 1) 掌握屈服、屈服强度和屈服准则等基本概念 2) 了解等向强化、随动强化的物理意义 3) 熟练运用Tresca、 Mises屈服准则
主应力空间的屈服曲面（续）
?
根据Mises准则，当
MP
2 3
s
时，材料就进入屈服。可以看出，在
主应力空间中，屈服曲面是一个以等倾线为轴线的圆柱面。顺着等倾线
看过去，屈服曲面成为一个圆。
2
这个圆被坐标轴分成六个等价的部
单向应力
分。每个和坐标轴重合的点表示单
向应力(或迭加一个求张量) ；而 相距最远的点为纯剪(平面应变) 状态。
MP OP OM
2 2 2 2
1 2 3 1 ( 1 2 3 ) 3
2 1 3 2 3 2 2
2
O
2
[( 1 2 ) ( 2 3 ) ( 3 1 ) ]

2
1

则等倾线上各点都表示一个球应力(静水压力)状态。其中OM代表该应力 状态中的球应力张量，MP代表造成形状变化的偏应力张量。

屈服与破坏准则


图1-7 单向拉压时的硬化模型
结论：S-D校应是岩土材料的固有属性，包辛格改变了材料的内部结构。在经过拉伸塑性变 形后改变了材料内部的微观结构，使拉伸屈服应力提高压缩屈服应力降 低；同样经过压缩塑 性变形后压缩应力提高，拉伸应力降低的现象叫包辛格（Bauschinger）效应。当然这是以 金属材料为试验标本。
② D-P准则表达式
图4-1 Mises与D-P准则的屈服曲面及屈服曲线
2. 评价结果
表4-1 Mises屈服破坏准则评价结果
表4-2
D-P屈服破坏准则评价结果
五． Mises 准则与 Drucker-Prager准则
Coulomb-Mohr条件
smooth
Z-P准则
Mises准则
Tresca准则
图1-3
应力张量的分解
3. 单纯的静水压力可以产生屈服。
图1-4
岩土材料的各种屈服面图形
如何判断单纯静水压力可以产生屈服？
4. 具有S-D效应，即岩土材料的拉压强度不同。例如砂土，粘土，混凝 土和岩石等。
S-D校应与包辛格（Bauschinger）校应的区别？
图1-5
有包辛格校应
图1-6
无包辛格校应
岩土塑性力学中的基本假设： 连续性假设 忽略温度与时间或应变速率影响的假设
9. 数学函数连续。 10. 适用性好，相关系数易于测定。
二．Coulomb-Mohr 准则
C-M准则考虑了正应力或平均应力作用的最大主剪应力或单一剪应力屈服理论。
1. 表达式
Coulomb形式与Mohr形式的关系？
拟合C-M得系数
D-P准则
广义Tresca准则
1
式4-3-5
两者在偏平面上的图（图3）可见设置 g ( ) 就是将C-M准则在偏平面上的六角抹去。 C-M

l08-第3.4节-屈服准则-0102

和轴对称应力状态，两准则一致。 两个轨迹六个点B( (
1 3 1 3 2 3 1 3 2 3 1 3 2 3 1 3
S,


S
) 、D (
1 3
S,

S
) 、F
2 3
S,
1 3

1
S
)、H(

S
S,

S
) 、J(
S,

S
)、
L(
S,
) ，为纯剪切应力状态和平面应变应力状态，

z

p r
2
2 r t

pr 2t
;

p2r 2t

pr t
;


p 0
1
pr t

35 300 t s;
;

2

z

pr 2t

35 300 2t
;

3

p
0
1
35 300 t
3
7 0 0;
t
35 300 700
应力达到某一定值（材料的性能：剪切屈服强度）时，材 料就发生屈服。（最大切应力不变条件）
m ax K
单向应力状态
m ax
1 3
2
K
1 2
0
3

3


2
s
1
s
2

2
s
K
2K
m ax K
1
3
s
一般应力条件下
f J1, J 2 C

3屈服与破坏准则

如果我们并不知道主应力的大小顺序，则可表示为： 如果我们并不知道主应力的大小顺序，则可表示为：
f = {(σ 1 − σ 2 ) 2 − [(σ 1 + σ 2 ) sin ϕ − 2c ⋅ cos ϕ ]2 } {(σ 2 − σ 3 ) 2 − [(σ 2 + σ 3 )sin ϕ − 2c ⋅ cos ϕ ]2 } {(σ 3 − σ 1 ) 2 − [(σ 3 + σ 1 ) sin ϕ − 2c ⋅ cos ϕ ]2 } = 0
§3.1 概述
一、基本概念 2. 屈服条件、加载条件与破坏条件 屈服条件、 对于简单应力条件，我们很容易判定材料何时屈服、 对于简单应力条件，我们很容易判定材料何时屈服、何 时破坏，以及是加载还是卸载，它们都与应力或应变相关。 时破坏，以及是加载还是卸载，它们都与应力或应变相关。 在复杂应力条件下，就必须有一个判定材料屈服 屈服、 在复杂应力条件下，就必须有一个判定材料屈服、破坏 的条件和 卸载条件。 的条件和加、卸载条件。 一般地，屈服条件是应力（应变）状态的函数； 一般地，屈服条件是应力（应变）状态的函数；破坏条 件是破坏应力（应变）与破坏参量的函数； 件是破坏应力（应变）与破坏参量的函数；加卸载条件是加 卸载应力和硬化参量的函数。 卸载应力和硬化参量的函数。 因此，屈服条件也称屈服函数 屈服准则； 屈服函数或 因此，屈服条件也称屈服函数或屈服准则；破坏条件也 破坏函数或 破坏准则； 卸载条件一般称加载函数或 称破坏函数或破坏准则；加、卸载条件一般称加载函数或加 加载函数 载准则。 载准则。
（c） σ 2 = 0 子午面 ）
C-M准则图像 准则图像
§3.2 C-M准则 准则
二、C-M准则的其它形式 准则的其它形式
1. p-q- θσ 形式：（ − π ≤ θσ ≤ π ） 形式： 6 6

屈服与破坏准则 便宜版


§3.1 概述
一、基本概念 3. 屈服曲面、加载曲面与破坏曲面 对屈服函数在应力空间内的图像即为屈服曲面（在二维 应力空间内即为屈服曲线）。 屈服曲面上所有的点都表示介质初次屈服时的应力状态。 屈服曲面把应力空间分成两个部分：应力点在屈服面内属弹 性状态；在屈服面上的点材料开始屈服。 对于理想塑性材料，应力点不可能跑出屈服面之外；对 于硬化材料，在屈服面外则属塑性状态的继续，此时屈服函 数将是变化的，这种屈服函数一般叫做加载函数，亦称后继 屈服面或加载曲面。加载曲面的极限就是破坏曲面。
一、L-D屈服准则
在 平面上的投影为一套随静水压力不断扩大的曲边三角 形。随着静水压力减小，曲边三角形曲率变大并接近圆形， 最后当p=0时收缩为一点。 在子午面上，屈服曲线为一族通过原点的射线。
§3.5 L-D准则和Lade准则
二、Lade屈服准则
虽然L－D屈服准则反映了三个主应力，特别是中间主
§3.2 C-M准则
一、C-M准则
即Coulomb-Mohe准则，我们已经很熟悉了。当知道主 应力的大小，即 1 2 3 时，表示为：
f tan c 0
f (1 3 ) (1 3 )sin 2c cos 0
§3.5 L-D准则和Lade准则
二、Lade屈服准则
Lade 屈 服 函 数 的 几 何 与 物理意义为：在主应力空间，
剪胀屈服面是以等倾线为对称
轴，母线为三次曲线的不通过 原点的一族开口曲边三角锥体， k值增大，剪胀屈服面扩大； 压缩屈服面在主应力空间是一 个以原点为球心，以r为半径 的一族同心球面。
如果我们并不知道主应力的大小顺序，则可表示为：
f {( 1 2 )2 [( 1 2 )sin 2c cos ]2 } {( 2 3 )2 [( 2 3 )sin 2c cos ]2 } {( 3 1 )2 [( 3 1 )sin 2c cos ]2 } 0
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。