材料屈服与强度理论
- 格式：ppt
- 大小：980.50 KB
- 文档页数：39
下载文档原格式
合集下载
材料力学四大强度准则
材料力学四大强度准则材料力学的强度准则就像是建筑的“生死簿”，这些准则告诉我们，啥时候材料能撑得住，啥时候就要“打退堂鼓”。
想象一下，你在盖房子，突然发现材料一旦承载超出它的能力，就像是给它施加了“过重的包袱”，结果可想而知，房子就得闹脾气了，哐当一声倒下去，那场面可真是心疼啊。
第一个强度准则，叫做“最大应力理论”。
这玩意儿就像个“保镖”，随时随地守护着材料。
它告诉你，材料能承受的最大拉力和压强就像你能吃的最大份儿的火锅，超出这个范围，那可真是撑不住的。
如果你拿着一根细细的铁丝，往上提，轻轻一扯就没事，但要是你使劲，嘿嘿，那可就“翻车”了。
材料承受的压力太大，结果就是“应力集中”，就像是给材料聚集了太多不必要的烦恼，最后它就会“罢工”。
然后说说“屈服强度理论”。
这个就有点像你在职场上遇到的那些无良老板，给你加班加点，结果你也会有一天受不了，直接“辞职”。
材料也是一样，屈服强度就像是一个材料的“底线”，当你施加的力量超过它的承受能力，它就会变形，哪怕不碎，也得“扭曲”一下。
这种变形可不是普通的捏捏，简直就是“折磨”，一旦开始变形，就像是你和老板之间的关系，再也回不去了。
接下来是“强度极限理论”，这玩意儿就像是赛车的极速表，告诉你材料的“极限”。
要知道，材料在承受极大的负载时，就会像是在冲刺，最后一旦达到极限，就会直接崩溃，发出“轰”的一声，简直就是“英雄惜英雄”，瞬间变成碎片。
这就让人想起那些极限运动，冲得太猛，最后摔得“头破血流”。
所以，在设计的时候，得留点余地，给自己留条后路，不然真是“骑虎难下”。
最后是“疲劳强度理论”，这就有点像是人长时间加班，精疲力尽的状态。
你知道吗，材料在长期的重复载荷下，可能会悄悄地“累坏”，没啥征兆，突然就“垮了”。
就像你熬夜，第二天起床时，感觉四肢无力，脑袋重得像块石头。
材料也是如此，经过无数次的“折腾”，最终在某个瞬间就会因为“疲劳”而失去耐力，轻松就折断。
这个理论提醒我们，在设计的时候，得考虑到材料的“心情”，不要一味追求极限，得给它“喘口气”的时间。
13-3四个强度理论-材料力学
体，求主应力。 4、强度分析：选择适当的强度理论，计算相当应力，进行
强度计算。
例1 图示几种单元体，分别按第三和第四强度理论 求相当应力（单位MPa)
60
100
（1）
40 100
40
（2）
10
60
30 （3）
例2 直径为d=0.1m的圆杆受力如图,T=7kNm,P=50kN, 为铸铁构
件，[]=40MPa,试用第一强度理论校核杆的强度。
7.7
0
0
所以，此容器不满足第三强度理论。不安全。
第三强度理论（第三相当应力） xd3 1 3
第四强度理论（第四相当应力）
xd 4
1 2
1
2
2
2
3
2
3
1
2
三、强度计算的步骤：
1、外力分析：确定所需的外力。 2、内力分析：画内力图，确定可能的危险面。 3、应力分析：画危险截面应力分布图，确定危险点并画出单元
2
1
2 2
2
3 2
3
1 2
3、实用范围：实用于破坏形式为屈服的构件。
第一、第二强度理论适合于脆性材料； 第三、第四强度理论适合于塑性材料。 1、伽利略1638年提出了第一强度理论； 2、马里奥特1682年提出了第二强度理论；
3、杜奎特（C.Duguet)提出了最大剪应力理论；也有一说是库 伦1773年提出，特雷斯卡1868完善的。
到单向拉伸的强度极限时，构件就发生断裂。
1、破坏判据： 1 b ;( 1 0)
2、强度准则： 1 ; ( 1 0)
3、实用范围：实用于破坏形式为脆断的构件。
强度计算。
例1 图示几种单元体，分别按第三和第四强度理论 求相当应力（单位MPa)
60
100
（1）
40 100
40
（2）
10
60
30 （3）
例2 直径为d=0.1m的圆杆受力如图,T=7kNm,P=50kN, 为铸铁构
件，[]=40MPa,试用第一强度理论校核杆的强度。
7.7
0
0
所以，此容器不满足第三强度理论。不安全。
第三强度理论（第三相当应力） xd3 1 3
第四强度理论（第四相当应力）
xd 4
1 2
1
2
2
2
3
2
3
1
2
三、强度计算的步骤：
1、外力分析：确定所需的外力。 2、内力分析：画内力图，确定可能的危险面。 3、应力分析：画危险截面应力分布图，确定危险点并画出单元
2
1
2 2
2
3 2
3
1 2
3、实用范围：实用于破坏形式为屈服的构件。
第一、第二强度理论适合于脆性材料； 第三、第四强度理论适合于塑性材料。 1、伽利略1638年提出了第一强度理论； 2、马里奥特1682年提出了第二强度理论；
3、杜奎特（C.Duguet)提出了最大剪应力理论；也有一说是库 伦1773年提出，特雷斯卡1868完善的。
到单向拉伸的强度极限时，构件就发生断裂。
1、破坏判据： 1 b ;( 1 0)
2、强度准则： 1 ; ( 1 0)
3、实用范围：实用于破坏形式为脆断的构件。
材料力学强度理论
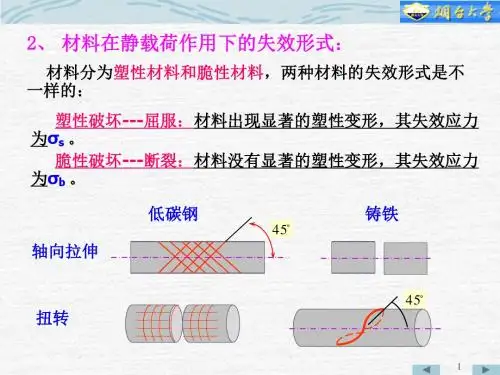
9 强度理论1、 脆性断裂和塑性屈服脆性断裂:材料无明显的塑性变形即发生断裂，断面较粗糙，且多发生在垂直于最大正应力的截面上，如铸铁受拉、扭，低温脆断等。
塑性屈服:材料破坏前发生显著的塑性变形，破坏断面较光滑，且多发生在最大剪应力面上，例如低碳钢拉、扭，铸铁压。
2、四种强度理论(1)最大拉应力理论（第一强度理论）材料发生脆性断裂的主要因素是最大拉应力达到极限值,即：01σσ= (2)最大伸长拉应变理论（第二强度理论）：无论材料处于什么应力状态,只要发生脆性断裂,都是由于最大拉应变（线变形）达 到极限值导致的,即： 01εε=(3)最大切应力理论（第三强度理论）无论材料处于什么应力状态,只要发生屈服,都是由于最大切应力达到了某一极限 值,即： 0max ττ=(4)形状改变比能理论（第四强度理论）无论材料处于什么应力状态,只要发生屈服,都是由于单元体的最大形状改变比能达到一个极限值,即：u u 0dd =强度准则的统一形式 [] σσ≤*其相当应力: r11σ=σr2123()σ=σ-μσ+σ r313σ=σ-σ222r41223311()()()2⎡⎤σ=σ-σ+σ-σ+σ-σ⎣⎦ 3、摩尔强度理论的概念与应用； 4、双剪强度理论概念与应用。
9.1图9.1所示的两个单元体，已知正应力σ =165MPa ，切应力τ=110MPa 。
试求两个单元体的第三、第四强度理论表达式。
图9.1[解] （1）图9.1（a ）所示单元体的为空间应力状态。
注意到外法线为y 及－y 的两个界面上没有切应力，因而y 方向是一个主方向，σ是主应力。
显然，主应力σ 对与y 轴平行的斜截面上的应力没有影响，因此在xoz 坐标平面内可以按照平面应力状态问题对待。
外法线为x 、z 轴两对平面上只有切应力τ，为纯剪切状态，可知其最大和最小正应力绝对值均为τ,则图9.1（a ）所示单元体的三个主应力为：τστσσσ-===321、、,第三强度理论的相当应力为解题范例r4σ=()eq313165110275a σσσστ=-=+=+=MPa第四强度理论的相当应力为：()eq4a σ==252.0== MPa(2)图9.1(b)所示单元体,其主应力为第三强度理论的相当应力为：()eq31322055275b σσσ=-=+=MPa第四强度理论的相当应力为：()eq4a σ=252.0==MPa9.2一岩石试件的抗压强度为[]σ=14OMPa,E=55GPa, μ=0.25, 承受三向压缩。
四大强度理论
六、例题： 例题1、薄壁容器，厚度 δ<< 平均直径D，在容器中贮满
水，水结冰后，将容器涨破，而冰不碎，解释原因。
解：⑴、水结冰时，发生膨胀，容器将受到内压作用，其单 元体的应力状态为二向拉应力状态。
15
p
李禄昌
p
1
p
1
2
1
由纵向截面上的静力平衡条件
Y 0 2 l p D l 0
轴向拉伸时
1 s , 2 3 0 ud 1 2 s2
6E
11
李禄昌
3、强度条件：
1 s 2 1 1 2 2 2 2 22 2 s uf (21 3 3 ) (3 ) u 1 2( 2 6 f 2) 3 11 E n 2 6E s
1
b
n
4、存在问题：⑴、该理论只考虑σ1 ，而没有考虑σ2 、σ3的 影响。⑵、当σ1＜0，即没有拉应力的应力状态时，它不能对 材料的压缩破坏作出合理解释。⑶、 σ1必须是拉应力。
4
李禄昌 试验证明，这一理论与铸铁、岩石、砼、陶瓷、玻璃等脆 性材料的拉断试验结果相符，这些材料在轴向拉伸时的断裂 破坏发生于拉应力最大的横截面上。 脆性材料的扭转破坏，也是沿拉应力最大的斜面发生断裂， 这些都与最大拉应力理论相符。
x
x
得主应力
1 =14.5 103 F ( MPa) 2 0 3 1.8 10 F ( MPa)
3
19
李禄昌
⑶、对于钢材，利用第三强度理论强度条件：
r 3 1 3 [ ]
代入有关参数得：
[ ] F 9.8 KN 3 16.3 10
材料力学第9章 强度理论
由于物体在外力作用下所发生的弹性变形既包括 物体的体积改变，也包括物体的形状改变，所以可推 断，弹性体内所积蓄的变形比能也应该分成两部分： 一部分是形状改变比能（畸变能） ，一部分是体积改 变比能 。 在复杂应力状态下，物体形状的改变及所积蓄的 形状改变比能是和三个主应力的差值有关；而物体体 积的改变及所积蓄的体积改变比能是和三个主应力的 代数和有关。
注意：图示应力状态实际上为弯扭组合加载对 应的应力状态，其相当应力如下：
r 3 2 4 2 [ ] 2 2 [ ] r 4 3
可记住，便于组合变形的强度校核。
例1 对于图示各单元体,试分别按第三强度理论及第四强度理论 求相当应力。
120 MPa 140 MPa
r4
1 2 2 2 [(0 120) ( 120 120) ( 120 0) ] 120MPa 2
140 MPa
（2）单元体（b）
σ1 140MPa
σ 2 110MPa
σ3 0
110 MPa
σr 3 σ1 σ 3 140MPa 1 2 2 2 σr 4 [30 110 ( 140) ] 128MPa 2
1u
1u
E
b
E
1 1 1 2 3 E
1u
1u
E
b
E
1 2 3 b
强度条件为： 1 2 3
b
n
[ ]
实验验证： a) 可解释大理石单压时的纵向裂缝； b) 脆性材料在双向拉伸-压缩应力状态下,且压应 力值超过拉应力值时,该理论与实验结果相符合。
σ1 94 .72MPa σ 3 5 .28MPa
材料力学四大强度理论
材料力学四大强度理论材料力学是研究材料在外力作用下的力学性能和变形规律的学科，其中强度理论是材料力学中的重要内容之一。
材料的强度是指材料在外力作用下抵抗破坏的能力，而强度理论则是用来描述和预测材料在不同应力状态下的破坏规律和强度值的理论体系。
在材料力学中，有四大经典的强度理论，分别是极限强度理论、绝对最大剪应力理论、莫尔-库伊特理论和最大应变能理论。
首先，极限强度理论是最早被提出的强度理论之一，它是根据材料的屈服条件来描述材料的破坏规律。
极限强度理论认为材料在受到外力作用时，只要应力达到了材料的屈服强度，材料就会发生破坏。
这种理论简单直观，易于应用，但在实际工程中往往存在一定的局限性，因为它忽略了材料在屈服之前的变形过程。
其次，绝对最大剪应力理论是基于材料的最大剪应力来描述材料的破坏规律。
这种理论认为，材料在受到外力作用时，只要材料中的最大剪应力达到了材料的抗剪强度，材料就会发生破坏。
这种理论在一些特定情况下具有较好的适用性，但在一些复杂应力状态下往往难以准确描述材料的破坏规律。
接下来，莫尔-库伊特理论是基于材料的主应力来描述材料的破坏规律。
这种理论认为，材料在受到外力作用时，只要材料中的任意一个主应力达到了材料的抗拉强度或抗压强度，材料就会发生破坏。
莫尔-库伊特理论相对于前两种理论来说，更加全面和准确，因为它考虑了材料在不同应力状态下的破坏规律。
最后，最大应变能理论是基于材料的应变能来描述材料的破坏规律。
这种理论认为，材料在受到外力作用时，只要材料中的应变能达到了材料的抗拉强度或抗压强度，材料就会发生破坏。
最大应变能理论在描述材料的破坏规律时考虑了材料的变形能量，因此在一些复杂应力状态下具有较好的适用性。
综上所述，材料力学中的强度理论是描述和预测材料在外力作用下的破坏规律和强度值的重要理论体系。
四大强度理论分别是极限强度理论、绝对最大剪应力理论、莫尔-库伊特理论和最大应变能理论，它们各自具有一定的适用范围和局限性，工程应用中需要根据具体情况进行选择和应用。
屈服准则简要说明
屈服准则简要说明屈服准则是指在表面或内部应力作用下，物质开始发生变形或破坏的临界条件。
当物体受到外界力的作用时，会引起内部应力的产生，若这些应力超过了物体的屈服准则，就会导致物体的塑性变形或破坏。
屈服准则是材料力学中一个重要的概念，对于材料的设计和使用具有重要的意义。
在材料力学中，常用的屈服准则有两种，分别是塑性屈服准则和破坏屈服准则。
塑性屈服准则是指材料开始发生塑性变形的应力状态。
常用的塑性屈服准则有屈服强度理论和Tresca准则。
屈服强度理论a（YS）是指材料在受力过程中发生塑性变形的特征应力状态，是材料强度的一个重要参数。
它可以通过材料的抗拉强度或者屈服强度等进行表征。
塑性屈服准则是指当材料受力达到屈服强度时，就会发生可见的塑性变形。
Tresca准则是指当材料受力时，如果材料中任意剪切面上的最大剪应力达到屈服强度时，就会引起材料的塑性变形。
破坏屈服准则是指材料在受到极限载荷时发生破坏的应力状态。
常用的破坏屈服准则有最大剪应力理论、最大正应力理论和最大扭矩理论。
最大剪应力理论是指当材料中任何一个剪应力达到或超过破坏强度时，材料就会发生破坏。
最大正应力理论是指当材料中任何一个正应力达到或超过破坏强度时，材料就会发生破坏。
最大扭矩理论是指当材料中任何一个扭矩达到或超过破坏强度时，材料就会发生破坏。
不同的材料在不同的条件下可能采用不同的屈服准则。
例如对于金属材料来说，常用的屈服准则是屈服强度理论或Tresca准则。
而对于混凝土材料来说，常用的屈服准则是最大剪应力理论。
此外，不同的材料也可能根据具体情况选择不同的屈服准则，以满足特定的工程需求。
总的来说，屈服准则是材料力学的重要概念，用于描述材料的塑性变形和破坏行为。
掌握和了解不同材料的屈服准则对于材料的设计和使用至关重要，可以帮助我们选择合适的材料和确定合理的设计方案。
材料力学强度理论
纵截面裂开，这与第
二强度理论旳论述
基本一致。
例6、填空题
危险点接近于三向均匀受拉旳塑性材
料，应选用 第一 强度理论进行计算，
因为此时材料旳破坏形式
为
脆性断。裂
例8、圆轴直径为d，材料旳弹性模量为E，泊松比为 ，为了测得轴端旳力偶m之值，但只有一枚电阻片。 （1）试设计电阻片粘贴旳位置和方向； （2） 若按照你所定旳位置和方向，已测得线应变为
（一）、有关脆断旳强度理论
1、最大拉应力理论（第一强度理论）
假定：不论材料内各点旳应力状态怎样， 只要有一点旳主应力σ1 到达单向拉伸断裂时旳 极限应力σu，材料即破坏。
在单向拉伸时，极限应力 σu =σb
失效条件可写为 σ1 ≥ σb
第一强度理论强度条件：
1 [ ]
[ ] b
n
第一强度理论—最大拉应力理论
（二）强度校核 先绘出C截面正应力分布图和剪应力分布图。
C截面
a．正应力强度校核（K1）点
max
k1
MC WZ
32 103 237 106
135Mpa 150Mpa
b．剪应力强度校核(K2)点
C截面
max
k2
FS hb
(200
100 103 22.8) 103 7 103
1 , 2 0, 3
第三强度理论旳强度条件为：
1 3 ( ) 2 [ ]
由此得： [ ]
2
剪切强度条件为： [ ]
按第三强度理论可求得： [ ] [ ]
2
第四强度理论旳强度条件为：
1
2
( 1 2 )2
( 2
3)2
( 3
1)2
3 [ ]
材料学 强度理论
σ3
[σt ] 2
O3O2
σ1
2
σ3
[σc ] 2
M´
[c]
L´ T´ [t]
1
代入 O1N O3O1 O2F O3O2
强度条件
1
[ [
t c
]
]
3
[ t ]
三、 各种强度理论的适用范围及其应用（The appliance range and application for all failure criteria）
阿托?莫尔(O.Mohr),1835～1918
二、莫尔强度理论（Mohr’s failure criterion）
任意一点的应力圆若与极限曲线
M
L
相接触,则材料即将屈服或剪断.
F N
公式推导
O2 O O1
T
O3
O1 N
[σt ] 2
σ1
σ3 2
O2F
[σc ] 2
σ1
σ3 2
O3O1
σ1
2
基本假说:最大伸长线应变1 是引起材料脆断破坏的因素.
脆断破坏的条件:
1
σb E
最大伸长线应变:
1
1 E [σ1
(σ2
σ3 )]
强度条件:
σ1 (σ2 σ3 ) [σ]
五、第二类强度理论
（The second types of failure criterion）
1.最大切应力理论 （第三强度理论）
（3）单元体（c）
σ1 80MPa σ2 -70MPa σ3 -140MPa
70 MPa
σr3 220MPa σr4 195MPa
（4）单元体（d）
140 MPa
强度理论
Mmax 56kN m
⑴ 最大弯曲正应力强度校核
max
Mmax 56 103 0.25 133.3MPa 5 Wz 2 5.25 10
⑵ 最大弯曲切应力强度校核 根据第三强度理论
0.5 80MPa
0.5 80MPa
116.7 2 3 46.32 141.6MPa
所以无论采用第三强度理论或第四强度理论进行强度校核， 危险点的强度满足要求
例：试按强度理论确定塑性材料的许用切应力。 解：纯剪切应力状态的主应力 3 1 2 0 第三强度理论的强度条件 r3 1 3 2 第四强度理论的强度条件 1 r4 [( 1 2 )2 ( 2 3 )2 ( 3 1 )2 ] 3 2 剪切强度条件 按第三强度理论确定塑性材料的许用切应力 0.5 按第四强度理论确定塑性材料的许用切应力 3 0.6
⑴ 应用：材料的屈服失效形式。
⑵ 局限：与第三强度理论相比更符合实际，但公式过 于复杂。
五、强度理论的应用
1. 各强度理论的适用范围
·断裂失效
第一强度理论（脆性材料的单、二向应力状态，塑 性材料的三向应力状态）。
·屈服失效
第三、四强度度理论（脆性材料的三向应力状态， 塑性材料的单、二向应力状态）。
三、最大切应力理论（第三强度理论）
材料发生屈服是最大切应力引起，即最大切应力达到某 一极限值时材料发生屈服。 1．第三强度理论的计算准则 单向应力状态 s (材料屈服失效)
max
2
s
2
max
1 3
2
⑴ 最大弯曲正应力强度校核
max
Mmax 56 103 0.25 133.3MPa 5 Wz 2 5.25 10
⑵ 最大弯曲切应力强度校核 根据第三强度理论
0.5 80MPa
0.5 80MPa
116.7 2 3 46.32 141.6MPa
所以无论采用第三强度理论或第四强度理论进行强度校核， 危险点的强度满足要求
例：试按强度理论确定塑性材料的许用切应力。 解：纯剪切应力状态的主应力 3 1 2 0 第三强度理论的强度条件 r3 1 3 2 第四强度理论的强度条件 1 r4 [( 1 2 )2 ( 2 3 )2 ( 3 1 )2 ] 3 2 剪切强度条件 按第三强度理论确定塑性材料的许用切应力 0.5 按第四强度理论确定塑性材料的许用切应力 3 0.6
⑴ 应用：材料的屈服失效形式。
⑵ 局限：与第三强度理论相比更符合实际，但公式过 于复杂。
五、强度理论的应用
1. 各强度理论的适用范围
·断裂失效
第一强度理论（脆性材料的单、二向应力状态，塑 性材料的三向应力状态）。
·屈服失效
第三、四强度度理论（脆性材料的三向应力状态， 塑性材料的单、二向应力状态）。
三、最大切应力理论（第三强度理论）
材料发生屈服是最大切应力引起，即最大切应力达到某 一极限值时材料发生屈服。 1．第三强度理论的计算准则 单向应力状态 s (材料屈服失效)
max
2
s
2
max
1 3
2
工程力学四大强度理论的基本内容
工程力学中四大强度理论的基本内容一、四大强度理论基本内容介绍：1、最大拉应力理论（第一强度理论）：这一理论认为引起材料脆性断裂破坏的因素是最大拉应力，无论什么应力状态，只要构件内一点处的最大拉应力σ1达到单向应力状态下的极限应力σb，材料就要发生脆性断裂。
于是危险点处于复杂应力状态的构件发生脆性断裂破坏的条件是：σ1=σb。
σb/s=[σ] ，所以按第一强度理论建立的强度条件为：σ1≤[σ]。
2、最大伸长线应变理论（第二强度理论）：这一理论认为最大伸长线应变是引起断裂的主要因素，无论什么应力状态，只要最大伸长线应变ε1达到单向应力状态下的极限值εu，材料就要发生脆性断裂破坏。
εu=σb/E；ε1=σb/E。
由广义虎克定律得：ε1=[σ1-u(σ2+σ3)]/E 所以σ1-u(σ2+σ3)=σb。
按第二强度理论建立的强度条件为：σ1-u(σ2+σ3)≤[σ]。
3、最大切应力理论（第三强度理论）：这一理论认为最大切应力是引起屈服的主要因素，无论什么应力状态，只要最大切应力τmax达到单向应力状态下的极限切应力τ0，材料就要发生屈服破坏。
依轴向拉伸斜截面上的应力公式可知τ0=σs/2（σs——横截面上的正应力）由公式得：τmax=τ1s=（σ1-σ3）/2。
所以破坏条件改写为σ1-σ3=σs。
按第三强度理论的强度条件为：σ1-σ3≤[σ]。
4、形状改变比能理论（第四强度理论）：这一理论认为形状改变比能是引起材料屈服破坏的主要因素，无论什么应力状态，只要构件内一点处的形状改变比能达到单向应力状态下的极限值，材料就要发生屈服破坏。
二、四大强度理论适用的范围1、各种强度理论的适用范围及其应用（1）、第一理论的应用和局限应用：材料无裂纹脆性断裂失效形势（脆性材料二向或三向受拉状态；最大压应力值不超过最大拉应力值或超过不多）。
局限：没考虑σ2、σ3对材料的破坏影响，对无拉应力的应力状态无法应用。
（2）、第二理论的应用和局限应用：脆性材料的二向应力状态且压应力很大的情况。
20.四个常用的强度理论
七、相当应力：（强度准则的统一形式）。
σ ≤[σ ] 其中，σ
∗
*—相当应力。
{ σ b ,σ 0.2 ,σ s } [σ ] =
n
σ r1 = σ 1
σ r2 = σ 1 − µ (σ 2 + σ 3 )
σ r3 = σ 1 − σ 3
σ r4 =
1 (σ 1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ 1 )2 2
[
u xmax = u xs
]
1、破坏判据： 2、强度准则
1 (σ1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ1 )2 = σ s 2
1 (σ 1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ 1 )2 ≤ [σ ] 2
[
]
σ r4 =
[
]
3、适用范围：实用于破坏形式为屈服的构件。（塑性材料） 4、局限性：无法解释脆性材料的破坏现象
六、形状改变比能（第四强度）理论： 认为构件的屈服是由形状改变比能引起的。当形状改变比 能达到单向拉伸试验屈服时形状改变比能时，构件就破坏了。
ux = 1+ µ (σ 1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ 1 )2 ≤ 1 + µ ( 2σ 12 ) 6E 6E
四、最大伸长线应变（第二强度）理论： 认为构件的断裂是由最大拉应变引起的。当最大伸长线应变 达到单向拉伸试验下的极限应变时，构件就断了。 σb 1 ( ) [ ] = − + = ε σ μ σ σ ε1 = εb ;(ε1 > 0) 1 1 2 3 E E 1、破坏判据： σ1 − μ (σ 2 + σ 3 ) = σ b 2、强度准则： σ r2 = σ1 − μ (σ 2 + σ 3 ) ≤ [σ ] 3、适用范围：适用于破坏形式为脆断的构件。（石料等材料） 4、局限性：无法解释脆性材料的二向拉伸等破坏现象 无法解释塑性材料的破坏
《强度理论 》课件
《强度理论》PPT课件
CATALOGUE
目录
强度理论概述强度理论的类型强度理论的计算方法强度理论的应用实例强度理论的未来发展
01
强度理论概述
机械工程
用于飞机、火箭等复杂结构的强度分析。
航空航天
土木工程
材料科学
01
02
04
03
用于研究材料的力学性能和失效机制。
用于设计和分析机械零件、结构件等。
总结词
03
强度理论的计算方法
静力计算方法是强度理论中常用的一种方法，主要用于分析结构在静力载荷作用下的响应。
静力计算方法概述
基于牛顿第二定律和弹性力学的基本原理，通过建立平衡方程和应力应变关系来求解结构的内力和位移。
基本原理
适用于分析结构在静力载荷作用建筑结构的强度分析是确保建筑物安全的重要环节，通过强度理论的运用，对建筑物的各个组成部分进行受力分析、稳定性评估和抗震性能研究。
总结词
在建筑结构的强度分析中，强度理论同样发挥了重要作用。通过对建筑物的梁、柱、板等各个组成部分进行受力分析，了解其在各种工况下的应力分布和承载能力。同时，结合建筑物的功能需求和地理环境，对建筑物的稳定性、抗震性能等进行评估。通过合理的强度分析，可以有效地避免建筑物在自然灾害或意外事故中发生倒塌或损坏，保障人们的生命财产安全。
详细描述
第二强度理论认为，材料在受到外力作用时，其破坏是由于最大剪应力达到材料屈服极限所引起的。当最大剪应力达到材料的屈服极限时，材料发生屈服破坏，即丧失了承载能力。
VS
形状改变比能达到材料屈服极限时发生屈服破坏。
详细描述
第三强度理论认为，材料在受到外力作用时，其破坏是由于形状改变比能达到材料屈服极限所引起的。当形状改变比能达到材料的屈服极限时，材料发生屈服破坏，即丧失了承载能力。
CATALOGUE
目录
强度理论概述强度理论的类型强度理论的计算方法强度理论的应用实例强度理论的未来发展
01
强度理论概述
机械工程
用于飞机、火箭等复杂结构的强度分析。
航空航天
土木工程
材料科学
01
02
04
03
用于研究材料的力学性能和失效机制。
用于设计和分析机械零件、结构件等。
总结词
03
强度理论的计算方法
静力计算方法是强度理论中常用的一种方法，主要用于分析结构在静力载荷作用下的响应。
静力计算方法概述
基于牛顿第二定律和弹性力学的基本原理，通过建立平衡方程和应力应变关系来求解结构的内力和位移。
基本原理
适用于分析结构在静力载荷作用建筑结构的强度分析是确保建筑物安全的重要环节，通过强度理论的运用，对建筑物的各个组成部分进行受力分析、稳定性评估和抗震性能研究。
总结词
在建筑结构的强度分析中，强度理论同样发挥了重要作用。通过对建筑物的梁、柱、板等各个组成部分进行受力分析，了解其在各种工况下的应力分布和承载能力。同时，结合建筑物的功能需求和地理环境，对建筑物的稳定性、抗震性能等进行评估。通过合理的强度分析，可以有效地避免建筑物在自然灾害或意外事故中发生倒塌或损坏，保障人们的生命财产安全。
详细描述
第二强度理论认为，材料在受到外力作用时，其破坏是由于最大剪应力达到材料屈服极限所引起的。当最大剪应力达到材料的屈服极限时，材料发生屈服破坏，即丧失了承载能力。
VS
形状改变比能达到材料屈服极限时发生屈服破坏。
详细描述
第三强度理论认为，材料在受到外力作用时，其破坏是由于形状改变比能达到材料屈服极限所引起的。当形状改变比能达到材料的屈服极限时，材料发生屈服破坏，即丧失了承载能力。
几种屈服准则的差异性和适用性
几种屈服准则的差异性和适用性
屈服准则是衡量材料或结构出现变形或破坏的标准，是通过对结构的受力状态和破坏机制的分析，从而确定结构安全性的方法。
不同的屈服准则基于不同的假设和条件，因此在不同的应用环境下具有差异性和适用性。
以下是几种常见的屈服准则的差异性和适用性：
1.极限强度理论：极限强度理论认为，当材料或结构达到其最大强度时，即为屈服。
该理论假设材料的应变和应力之间存在线性的关系，并且强度在材料的全截面上都是均匀分布的。
这种屈服准则比较简单且易于计算，适用于强度均匀且线性的材料，如金属材料。
2.钢铁理论：钢铁理论是一种屈服准则，用于考虑材料的塑性变形。
该理论假设材料在达到屈服点时，继续加载会导致材料的塑性变形，直到出现破坏。
这种屈服准则适用于大多数金属材料，尤其是钢铁。
3.衰减理论：衰减理论是一种屈服准则，考虑了材料在长期加载下的疲劳破坏。
衰减理论假设材料的疲劳寿命是基于它的强度随时间的衰减。
这种屈服准则适用于需要经历长期加载的结构，如桥梁和飞机。
4.弹性准则：弹性准则是一种屈服准则，假设材料在达到其弹性极限时发生屈服。
这种准则适用于弹性材料，如橡胶和塑料。
弹性准则也可以用于计算结构在正常工作条件下的应力和变形。
不同的屈服准则具有不同的适用性，可根据具体的工程需求和材料特性选择。
需要考虑材料的强度、刚度、加载方式、应变速率等因素。
在实践中，通常会使用组合屈服准则，以综合考虑材料的多个方面和应对复杂加载条件。
高分子物理-第七章-屈服和强度
银纹和剪切带
均有分子链取向，吸收能量，呈现屈服现象
主要区别
形
变
曲线特征
体
积
力
结
果
剪切屈服
45o
90o
a
抵抗外力的方式
两
种
抗张强度：抵抗拉力的作用
0
aan
aas
0 /2
抗剪强度：抵抗剪力的作用
0o
45o
90o
抗张强度什么面最大？ a=0， an=0
抗剪强度什么面最大？ a=45， as=0/2
当应力0增加时，法向应力和切向应力增大的幅度不同
在45o时, 切向应力最大
泊松比: 在拉伸实验中，材料横向应变
与纵向应变之比值的负数
m
v
l
m0
l0
T
常见材料的泊松比
泊松比数值
解
释
0.5
不可压缩或拉伸中无体积变化
0.0
没有横向收缩
0.49~40
塑料的典型数值
E, G, B and
E2
G
(1
)
EB
3 (1
2
第 一 期 的 入 党积极 分子培 训课将 要结束 了，在 培训期 间，通 过尊敬 的合江 县府王
督 学 、 学 院 党委王 书记及 学院党 办邬主 任和相 关领导 、教授 对党章 ，党课 及现阶
段 国 内 外 形 式的讲 解，以 及通过 参加学 院开展 的颂歌 献给党 、喜迎 十八大 歌咏比
赛 及 参 观 了 武警合 江中队 和合江 县清代 考试院 、合江 县汉代 石棺陈 列馆等 活
韧性断裂 ductile fracture
各种情况下的应力-应变曲线
20.四个常用的强度理论
7.35
[
]
八、强度计算的步骤： 1、外力分析：确定所需的外力值。 2、内力分析：画内力图，确定可能的危险面。 3、应力分析：画危面应力分布图，确定危险点并画出单元体， 求主应力。 4、强度分析：选择适当的强度理论，计算相当应力，然后进行 强度计算。
九、强度理论的选用原则：依破坏形式而定。 1、脆性材料：使用第一、第二强度理论；
三、最大拉应力（第一强度）理论： 认为构件的断裂是由最大拉应力引起的。当最大拉应力达到 单向拉伸的强度极限时，构件就断了。 1、破坏判据： σ1 = σ b ; (σ1 > 0) 2、强度准则： σ r1 = σ 1 ≤ [σ ] ; ( σ 1 > 0) 3、适用范围：适用于破坏形式为脆断的构件。（脆性材料） 4、局限性：当σ1＜0 时无法解释破坏现象 没有考虑其他两个主应力的影响 无法解释塑性材料的破坏
五、最大剪应力（第三强度）理论： 认为构件的屈服是由最大剪应力引起的。当最大剪应力达 到单向拉伸试验的极限剪应力时，构件就破坏了。
τ max = τ s
τ max =
σ1 − σ 3 σ s = = τs 2 2
1、破坏判据： σ 1 − σ 3 = σ s 2、强度准则： σ r3 = σ 1 − σ 3 ≤ [σ ] 3、适用范围：适用于破坏形式为屈服的构件。（塑性材料） 4、局限性：无法解释脆性材料的破坏现象 偏于安全
当时无法解释破坏现象没有考虑其他两个主应力的影响无法解释塑性材料的破坏四最大伸长线应变第二强度理论
20.四个常用的强度理论
一、强度理论：是关于“构件发生强度失效（failure by lost strength）起因”的假说。 二、材料的破坏形式：⑴ 屈服； ⑵ 断裂 。 1、伽利略播下了第一强度理论的种子； 2、马里奥特关于变形过大引起破坏的论述，是第二强度理论的 萌芽； 3、杜奎特（C.Duguet)提出了最大剪应力理论； 4、麦克斯威尔最早提出了最大畸变能理论（maximum distortion energy theory）；这是后来人们在他的书信出版后才知道的。
[
]
八、强度计算的步骤： 1、外力分析：确定所需的外力值。 2、内力分析：画内力图，确定可能的危险面。 3、应力分析：画危面应力分布图，确定危险点并画出单元体， 求主应力。 4、强度分析：选择适当的强度理论，计算相当应力，然后进行 强度计算。
九、强度理论的选用原则：依破坏形式而定。 1、脆性材料：使用第一、第二强度理论；
三、最大拉应力（第一强度）理论： 认为构件的断裂是由最大拉应力引起的。当最大拉应力达到 单向拉伸的强度极限时，构件就断了。 1、破坏判据： σ1 = σ b ; (σ1 > 0) 2、强度准则： σ r1 = σ 1 ≤ [σ ] ; ( σ 1 > 0) 3、适用范围：适用于破坏形式为脆断的构件。（脆性材料） 4、局限性：当σ1＜0 时无法解释破坏现象 没有考虑其他两个主应力的影响 无法解释塑性材料的破坏
五、最大剪应力（第三强度）理论： 认为构件的屈服是由最大剪应力引起的。当最大剪应力达 到单向拉伸试验的极限剪应力时，构件就破坏了。
τ max = τ s
τ max =
σ1 − σ 3 σ s = = τs 2 2
1、破坏判据： σ 1 − σ 3 = σ s 2、强度准则： σ r3 = σ 1 − σ 3 ≤ [σ ] 3、适用范围：适用于破坏形式为屈服的构件。（塑性材料） 4、局限性：无法解释脆性材料的破坏现象 偏于安全
当时无法解释破坏现象没有考虑其他两个主应力的影响无法解释塑性材料的破坏四最大伸长线应变第二强度理论
20.四个常用的强度理论
一、强度理论：是关于“构件发生强度失效（failure by lost strength）起因”的假说。 二、材料的破坏形式：⑴ 屈服； ⑵ 断裂 。 1、伽利略播下了第一强度理论的种子； 2、马里奥特关于变形过大引起破坏的论述，是第二强度理论的 萌芽； 3、杜奎特（C.Duguet)提出了最大剪应力理论； 4、麦克斯威尔最早提出了最大畸变能理论（maximum distortion energy theory）；这是后来人们在他的书信出版后才知道的。
四个强度理论
第 二 类强度理论
三、 最大剪应力理论 (第三强度理论)
根据：当作用在构件上的外力过大时，其危险点处的材料就会
沿最大剪应力所在截面滑移而发生屈服失效。 基本假说： 最大剪应力 max 是引起材料屈服的因素。
屈服条件：
τ max τ u
σs 2
在复杂应力状态下一点处的最大剪应力为
τ max 1 2 ( 1 3)
四个强度理论及其相当应力
在常温、静载荷下，常用的四个强度理论分两类
第 一类强度理论——以脆断作为破坏的标志
包括：最大拉应力理论和最大伸长线应变理论
第 二类强度理论——以出现屈服现象作为破坏的标志
包括：最大剪应力理论和形状改变比能理论
第 一类强度理论
一、 最大拉应力理论（第一强度理论） 根据：当作用在构件上的外力过大时，其危险点处的材 料就会沿最大拉应力所在截面发生脆性断裂。
77.5MPa
例题 9-2 两种应力状态分别如图所示，试按第四强度理论, 比较两者的危险程度。 解：一、定性分析 由于各向同性材料，正应力仅产生线应变，剪应力 仅产生剪 应变。而两种情况下的正应力和剪应力分 别相 等，因此， 其形状改变比能也相等，故两种情况下的危险程度相 等。 σ σ
τ τ
(a)
基本假说：最大拉应力1是引起材料脆断破坏的因素。
脆断破坏的条件： 1 = u （材料极限应力值） 强度条件为： r1 = 1 [ (9-2-1)
注意：无拉应力时，该理论无法应用。
二、 最大伸长线应变理论（第二强度理论）
根据：当作用在构件上的外力过大时，其危险点处的材料 就会沿垂直于最大伸长线应变方向的平面发生 脆断破坏。 基本假说：最大伸长线应变 1 是引起材料脆断破坏的因素。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
➢ 它的特性是：在变形过程中应力和应变关系不再是 一一对应关系，而是随载荷点变化的路径和加载的 过程而变化，因此，应力应变关系是增量关系，从 而就有增量理论，又称流动理论。
➢ 一般的金属材料当应力状态满足屈服条件时，即进 入塑性阶段。在外力作用下，任何一点的应变为：
ij
e ij
ijp
当外载有微小变量时，有：
dijp dsij
此即为塑性材料的本构方程，其中所引进的参数 dλ，为一非负的比例常数，它只有在应力满足屈 服条件时才不等于零。
根据以上几式子有：
dij 21Gdsij dsij
即为Prandtl-Reuss方程。
如果在上式中将塑性应变增量换成总应变增 量，即忽略弹性应变部分，则得Levy-Mises方 程：
➢ 从弹性力学中我们知道，材料的应变能为:
Ue UovUod
• Von Mises的屈服条件就是畸变能条件，它认 为如物体中某点应力相应的畸变能达到某一 数值时，该点就屈服。就应力和应变表示的 总应变能为:
Ue1 2112233
上式可化为：
U e 1 2 m s 1 m e 1 m s 2 m e 2 m s 3 m e 3
➢ 强度理论是一个很独特和奇妙的研究主题.它的命题很简单，但 问题很复杂。它是Da Vinci(1452年、1519年)、 GalileoGalilei(1564年、1642年)、Coulomb(1736年、1806年)和 OttoMolir(1835年、1918年)等最早研究过的经典课题之一但至 今仍在不断发展。人们对强度理论已进行了大量的理论研究和 实验验证。至目前为止，已经提出了上百个模型或准则，但没 有一个模型或准则能够被所有人所接受。强度理论就像中国古 语所说的那样:“百花齐放，百家争鸣”。这在自然科学中并不 多见。
➢ 对于一般的三维应力系统或一方向为拉应力， 另一方向为压应力，第三方向为零，最大切 应力为：
max13/2
➢ 在单轴拉伸情况，只有一个主应力σ1(σ2= σ3) ， 因此其最大切应力为:
max 1 /2
➢在屈服时就为 :
Y Y / 2
1.2 Von Mises 屈服条件
➢ Huber在1904年提出材料微元内的弹性应变 可当作由体积变化储存的能量和形状变化 储存的能量之和。后者亦称畸变形，被认 为可作为复杂塑性变形的判据。Maxwell， Von Mises和Henchy也单独地提出了这一观 念，但习惯上均称为Von Mises判据。
材料的屈服与强度理论
前言
➢ 强度理论研究材料在复杂应力下的屈服和破坏的规律。强度理 论是一个总称，它包括屈服准则、破坏准则、多轴疲劳准则、 多轴蠕变条件，以及计算力学和计算程序中的材料模型。
➢ 强度理论是材料强度和结构强度研究的重要基础，它在物理、 力学、材料科学、地球科学和工程中得到广泛的应用。强度理 论在理论研究、工程应用和有效利用材料等方面都具有很重要 的意义。特别在各种结构设计中，对多轴应力的合理的强度预 计是一个实际问题.强度理论是物理学家、材料学家、地球科学 家，以及土木工程师、机械工程师等共同相关的交叉研究的领 域。
1.3 材料屈服的其它事项
➢ 其他因素，如材料的强化问题和各向异性问题都会给 材料的屈服条件带来影响。由单向拉伸试验的应力应 变关系曲线可知，对于人们假定的理想弹塑性材料， 应力超过屈服应力之后，随应变的继续增加，应力则 保持为常值。但对强化材料则不然，应力超过初始屈 服应力之后，随着应变的继续增加，应力值也增加； 只有继续加载才能产生后续的塑性屈服变形。此外， 一旦发生塑性屈服，再除去外力，应力将按弹性规律 减小。因此，塑性力学与弹性力学不同之处还在于， 需要这个判定准则来判明材料是否处于加载或重复加 载的情况下卸载，才能正确使用计算理论分析应力。 这类问题对于计算一个结构的疲劳问题和寿命问题评 估极为重要。
1
➢ 法国工程师Tresca提出，材料屈服的条件为最 大切应力达到一个临界值，这就是材料在单 轴拉伸试验屈服时的最大切应力。在复杂应 力系统中的最大切应力则三个主应力的相对 值和符合有关，总是等于其最大和最小差值 的1/2。需要留意的是这最小的应力可能等于 零或压应力，这时它为负值。
强度理论的历史
1 材料的屈服条件
➢ 从材料的简单拉伸试验可以看出它的屈服 应力，材料到达了屈服应力就到达了从弹 性到塑性的过渡。但对于复杂的三维应力 状态则不那么简单，需要在试验的基础上 来驱动屈服条件。
1.1 H.Tresca 屈服条件
➢ 屈服理论一般以主应力为依据，因为由它们 可确定材料应力的一般状态。下图1所示为 一个材料单元受三个主应力作用，且令 ：
关于各向异性材料，如复合材料，则有正交 各向异性材料的屈服条件可供参考：
F (y z ) 2 G (z x ) 2 H (x y ) 2 2 L y 2 z 2 M z 2 x 2 N x 2 y 1
其中，F，G，H，L，M，N需由试验确定。
2 塑性材料的本构方程
➢ 塑性材料也是固体材料的一种理想模型。
其中：
因此：
U e1 23mm (s1 e 1 s2 e2 s3 e3) U o v U o d
以上介绍的Tresca和Mises屈服条件是塑性力学最早 提出的屈服条件，也是塑性力学中对大多数金属材 料迄今适用的屈服条件。在这一情况下，畸变能条 件更接近于实际。但是由于具有一定的局限性，例 如，没有计入拉压强度不等的情况及没有考虑体积 变形对屈服的影响等，所以后来又提出了一些其他 更广泛的屈服条件，如最大偏应力屈服条件，广义 双剪应力屈服条件，莫尔－库伦屈服准则等。这里 不作一一介绍。
dijp dij diej
在塑性状态，材料不可压缩，即体积变形等 于零，则：
因此
d
i
p j
0
dm 13diej dme
故应变偏量增量为
deij dij-dmij
可以导出增量形式的广义胡克定律为
dm2kdm
d
e ij
1 2G
dsij
从而可得
dijpdijdie j dij21 Gdsij
塑性应变增量与瞬时应力偏量成正比，于是有：
➢ 一般的金属材料当应力状态满足屈服条件时，即进 入塑性阶段。在外力作用下，任何一点的应变为：
ij
e ij
ijp
当外载有微小变量时，有：
dijp dsij
此即为塑性材料的本构方程，其中所引进的参数 dλ，为一非负的比例常数，它只有在应力满足屈 服条件时才不等于零。
根据以上几式子有：
dij 21Gdsij dsij
即为Prandtl-Reuss方程。
如果在上式中将塑性应变增量换成总应变增 量，即忽略弹性应变部分，则得Levy-Mises方 程：
➢ 从弹性力学中我们知道，材料的应变能为:
Ue UovUod
• Von Mises的屈服条件就是畸变能条件，它认 为如物体中某点应力相应的畸变能达到某一 数值时，该点就屈服。就应力和应变表示的 总应变能为:
Ue1 2112233
上式可化为：
U e 1 2 m s 1 m e 1 m s 2 m e 2 m s 3 m e 3
➢ 强度理论是一个很独特和奇妙的研究主题.它的命题很简单，但 问题很复杂。它是Da Vinci(1452年、1519年)、 GalileoGalilei(1564年、1642年)、Coulomb(1736年、1806年)和 OttoMolir(1835年、1918年)等最早研究过的经典课题之一但至 今仍在不断发展。人们对强度理论已进行了大量的理论研究和 实验验证。至目前为止，已经提出了上百个模型或准则，但没 有一个模型或准则能够被所有人所接受。强度理论就像中国古 语所说的那样:“百花齐放，百家争鸣”。这在自然科学中并不 多见。
➢ 对于一般的三维应力系统或一方向为拉应力， 另一方向为压应力，第三方向为零，最大切 应力为：
max13/2
➢ 在单轴拉伸情况，只有一个主应力σ1(σ2= σ3) ， 因此其最大切应力为:
max 1 /2
➢在屈服时就为 :
Y Y / 2
1.2 Von Mises 屈服条件
➢ Huber在1904年提出材料微元内的弹性应变 可当作由体积变化储存的能量和形状变化 储存的能量之和。后者亦称畸变形，被认 为可作为复杂塑性变形的判据。Maxwell， Von Mises和Henchy也单独地提出了这一观 念，但习惯上均称为Von Mises判据。
材料的屈服与强度理论
前言
➢ 强度理论研究材料在复杂应力下的屈服和破坏的规律。强度理 论是一个总称，它包括屈服准则、破坏准则、多轴疲劳准则、 多轴蠕变条件，以及计算力学和计算程序中的材料模型。
➢ 强度理论是材料强度和结构强度研究的重要基础，它在物理、 力学、材料科学、地球科学和工程中得到广泛的应用。强度理 论在理论研究、工程应用和有效利用材料等方面都具有很重要 的意义。特别在各种结构设计中，对多轴应力的合理的强度预 计是一个实际问题.强度理论是物理学家、材料学家、地球科学 家，以及土木工程师、机械工程师等共同相关的交叉研究的领 域。
1.3 材料屈服的其它事项
➢ 其他因素，如材料的强化问题和各向异性问题都会给 材料的屈服条件带来影响。由单向拉伸试验的应力应 变关系曲线可知，对于人们假定的理想弹塑性材料， 应力超过屈服应力之后，随应变的继续增加，应力则 保持为常值。但对强化材料则不然，应力超过初始屈 服应力之后，随着应变的继续增加，应力值也增加； 只有继续加载才能产生后续的塑性屈服变形。此外， 一旦发生塑性屈服，再除去外力，应力将按弹性规律 减小。因此，塑性力学与弹性力学不同之处还在于， 需要这个判定准则来判明材料是否处于加载或重复加 载的情况下卸载，才能正确使用计算理论分析应力。 这类问题对于计算一个结构的疲劳问题和寿命问题评 估极为重要。
1
➢ 法国工程师Tresca提出，材料屈服的条件为最 大切应力达到一个临界值，这就是材料在单 轴拉伸试验屈服时的最大切应力。在复杂应 力系统中的最大切应力则三个主应力的相对 值和符合有关，总是等于其最大和最小差值 的1/2。需要留意的是这最小的应力可能等于 零或压应力，这时它为负值。
强度理论的历史
1 材料的屈服条件
➢ 从材料的简单拉伸试验可以看出它的屈服 应力，材料到达了屈服应力就到达了从弹 性到塑性的过渡。但对于复杂的三维应力 状态则不那么简单，需要在试验的基础上 来驱动屈服条件。
1.1 H.Tresca 屈服条件
➢ 屈服理论一般以主应力为依据，因为由它们 可确定材料应力的一般状态。下图1所示为 一个材料单元受三个主应力作用，且令 ：
关于各向异性材料，如复合材料，则有正交 各向异性材料的屈服条件可供参考：
F (y z ) 2 G (z x ) 2 H (x y ) 2 2 L y 2 z 2 M z 2 x 2 N x 2 y 1
其中，F，G，H，L，M，N需由试验确定。
2 塑性材料的本构方程
➢ 塑性材料也是固体材料的一种理想模型。
其中：
因此：
U e1 23mm (s1 e 1 s2 e2 s3 e3) U o v U o d
以上介绍的Tresca和Mises屈服条件是塑性力学最早 提出的屈服条件，也是塑性力学中对大多数金属材 料迄今适用的屈服条件。在这一情况下，畸变能条 件更接近于实际。但是由于具有一定的局限性，例 如，没有计入拉压强度不等的情况及没有考虑体积 变形对屈服的影响等，所以后来又提出了一些其他 更广泛的屈服条件，如最大偏应力屈服条件，广义 双剪应力屈服条件，莫尔－库伦屈服准则等。这里 不作一一介绍。
dijp dij diej
在塑性状态，材料不可压缩，即体积变形等 于零，则：
因此
d
i
p j
0
dm 13diej dme
故应变偏量增量为
deij dij-dmij
可以导出增量形式的广义胡克定律为
dm2kdm
d
e ij
1 2G
dsij
从而可得
dijpdijdie j dij21 Gdsij
塑性应变增量与瞬时应力偏量成正比，于是有：