电路的过渡过程介绍
- 格式:ppt
- 大小:2.20 MB
- 文档页数:32

第3章电路的过渡过程及换路定律本书此前所讨论的电路,不论是直流还是交流,电路的联接方式和参数值是不变的,电源的输出是恒定的或周期性变化的,电路中的各部分电压也是恒定的或周期性变化的。
电路的这种状态称之为稳定状态,简称稳态。
当电路接通、断开或电路各元件的参数变化时,电路中的电压、电流等都在发生改变,从原来的稳定状态变化到另一个新的稳定状态,这个过程称过渡过程。
它不能瞬间完成,需要一定的时间(尽管往往是极短暂的),又称暂态过程。
电路在过渡过程中的工作状态称暂态。
3.1 过渡过程的产生与换路定律3.1.1.电路中产生过渡过程的原因电路中之所以出现过渡过程,是因为电路中有电感、电容这类储能元件的存在。
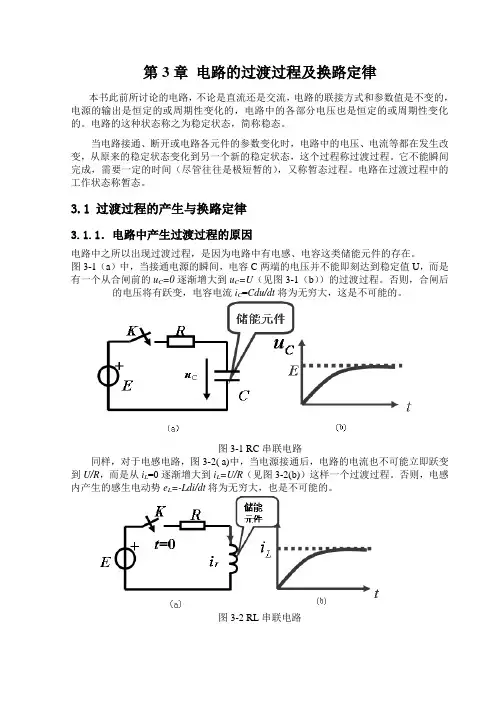
图3-1(a)中,当接通电源的瞬间,电容C两端的电压并不能即刻达到稳定值U,而是有一个从合闸前的u C=0逐渐增大到u C=U(见图3-1(b))的过渡过程。
否则,合闸后的电压将有跃变,电容电流i C=Cdu/dt将为无穷大,这是不可能的。
图3-1 RC串联电路同样,对于电感电路,图3-2( a)中,当电源接通后,电路的电流也不可能立即跃变到U/R,而是从i L=0逐渐增大到i L=U/R(见图3-2(b))这样一个过渡过程。
否则,电感内产生的感生电动势e L=-Ldi/dt将为无穷大,也是不可能的。
图3-2 RL串联电路过渡过程产生的实质是由于电感、电容元件是储能元件,能量的变化是逐渐的,不能发生突变,需要一个过程。
而电容元件储有的电场能W C =C 2/2C u ,电感元件储有的磁场能W L =L 2/2Li ,所以电容两端电压u C 和通过电感的电流i L 只能是连续变化的。
因为能量的存储和释放需要一个过程,所以有电容或电感的电路存在过渡过程。
产生过渡过程的内因:电路中存在储能元件 ,C L u i ;外因:电路出现换路时,储能元件能量发生变化。
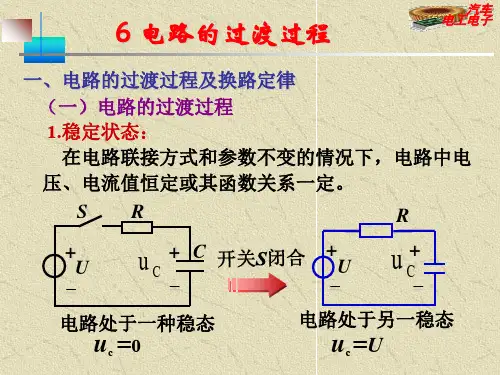
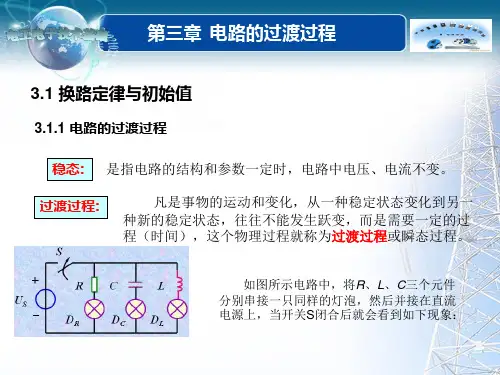
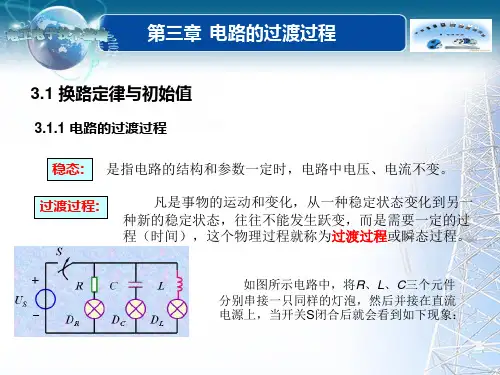
3.1.2.换路定律电路工作状态的改变如电路的接通、断开、短路、改路及电路元件参数值发生变化等,称换路。






电路的过渡过程简介引言电路过渡过程是指在开关电路中,从一个稳定状态到另一个稳定状态的切换过程。
在现代电子设备中,电路过渡过程的速度和稳定性对设备的性能和可靠性至关重要。
本文将介绍电路过渡过程的定义、重要性以及常见的过渡过程控制方法。
电路过渡过程的定义电路过渡过程是指电路在切换输入条件或内部状态时,电流和电压随时间的变化。
过渡过程通常发生在电路初始状态和目标状态之间,时间长度取决于电路的响应速度和输入信号的变化速度。
电路过渡过程的目标是尽快达到目标状态,并保持稳定。
电路过渡过程的重要性电路过渡过程的速度和稳定性对电子设备的性能和可靠性有着重要影响。
以下是电路过渡过程的几个重要方面:1. 响应时间电路过渡过程的响应时间是指从切换开始到电路达到目标状态所需的时间。
响应时间较短可以提高电路的性能和效率。
2. 峰值电压在过渡过程中,电路中可能会出现峰值电压。
过高的峰值电压可能导致电路元件损坏,因此需要控制峰值电压。
3. 震荡电路过渡过程中可能会出现震荡现象,即电流和电压在稳定状态之间不断变化。
震荡会增加功耗和噪声,影响电路的性能。
过渡过程控制方法为了控制电路过渡过程,提高电路性能和可靠性,有几种常见的方法可以采取:1. 信号延迟信号延迟可以通过添加合适的延迟电路来实现。
延迟电路可以使输入信号的变化更平缓,减少电路响应的速度,从而控制过渡过程的速度。
2. 滤波器滤波器可以用来控制电路的频率响应,滤除过渡过程中的高频噪声。
常见的滤波器包括低通滤波器和带通滤波器。
3. 反馈控制反馈控制是一种常见的过渡过程控制方法。
通过检测电路的输出,并通过反馈回路调整输入信号,可以使电路更快地达到稳定状态。
4. 优化设计优化电路设计可以提高电路的速度和稳定性。
优化设计包括选取合适的元件、调整电路拓扑结构以及优化电路参数等。
结论电路过渡过程在现代电子设备中起着重要的作用。
通过合适的过渡过程控制方法,可以提高电路的性能和可靠性。
我们可以采取信号延迟、滤波器、反馈控制和优化设计等方法来控制电路过渡过程。
二阶电路过渡过程二阶电路是指由两个储能元件(电感和电容)和一个阻抗元件(电阻)组成的电路。
在电路中,储能元件存储着电能,而阻抗元件则控制着电路的电流和电压。
当电路发生变化时,比如电源的切换或者电路参数的调整,电路中的电流和电压会发生过渡过程,即从一个稳态到另一个稳态的过程。
二阶电路过渡过程是一个动态的过程,涉及到电流和电压的变化。
在过渡过程中,电路中的电感和电容会储存和释放电能,从而导致电流和电压的变化。
具体来说,当电路的输入信号发生变化时,储存在电感和电容中的电能会被释放或吸收,从而导致电流和电压的变化。
在二阶电路中,过渡过程的特点取决于电路的参数和初始条件。
电路的参数包括电感的大小、电容的大小和电阻的大小,而初始条件包括电流和电压的初始值。
这些参数和初始条件决定了电路的响应特性,即电流和电压的变化速度和幅度。
在过渡过程中,电路会逐渐趋向于一个新的稳态。
稳态是指电路中的电流和电压达到了一个恒定的数值,不再发生变化。
在过渡过程中,电路的响应特性会逐渐趋近于稳态的特性,即电流和电压的变化速度会逐渐减小,幅度会逐渐稳定下来。
为了描述电路的过渡过程,可以使用一些指标来衡量电路的响应特性。
常用的指标包括上升时间、下降时间和超调量。
上升时间是指电路从初始值到达稳态值所需要的时间,下降时间是指电路从稳态值返回到初始值所需要的时间,而超调量则是电路响应超过稳态值的幅度。
在二阶电路中,过渡过程的时间常常会受到电路的阻尼比的影响。
阻尼比是指电路中电阻元件对电感和电容元件的影响程度。
当阻尼比为零时,电路为无阻尼振荡;当阻尼比小于一时,电路为欠阻尼过程;当阻尼比等于一时,电路为临界阻尼过程;当阻尼比大于一时,电路为过阻尼过程。
不同的阻尼比会导致电路过渡过程的速度和幅度不同。
二阶电路的过渡过程是一个动态的过程,涉及到电流和电压的变化。
电路的响应特性在过渡过程中会逐渐趋近于稳态的特性,而过渡过程的特点取决于电路的参数和初始条件。
RL电路的过渡过程过渡过程是指从一个稳态状态到另一个稳态状态的中间过程。
在RL 电路中,R代表电阻,L代表电感,过渡过程是指当电路中的电流或电压发生变化时,电阻和电感之间的相互作用导致电路中电流或电压逐渐向新的稳态状态变化的过程。
在RL电路中,当电压源或电流源发生突变时,电感上的电压和电流以及电阻中的电流和电压会逐渐的变化直到最终达到新的稳态。
这个过程可以通过欧姆定律和基尔霍夫电压定律来进行分析和计算。
当电压源突然变化时,电感中的电流发生变化。
根据欧姆定律和基尔霍夫电压定律,电流变化会导致电感中的电压也发生变化。
由于电感的特性,电流的变化是缓慢的,因此电感中的电压也是缓慢变化的。
电流和电压的变化服从指数函数的规律,其具体形式取决于电路中的电阻和电感的数值。
过渡过程可以分为两个阶段:自由响应和强迫响应。
自由响应是指在没有外加电源情况下,电路中的电感和电阻之间的相互作用导致的电流或电压的变化。
在自由响应阶段,电流和电压的变化是由电感的特性决定的。
根据基尔霍夫电压定律和欧姆定律可以得到自由响应的微分方程。
将这个微分方程带入求解,可以得到电流和电压随时间的变化规律。
强迫响应是指在有外加电源情况下,电路中的电感和电阻之间的相互作用导致的电流或电压的变化。
在强迫响应阶段,外加电源的作用使得电流和电压的变化更加复杂。
强迫响应可以通过将外加电源视为输入信号,将电感和电阻视为系统响应,应用输入输出关系进行分析。
在整个过渡过程中,电感中的电流和电压的变化逐渐减小,最终达到新的稳态。
这个过程的时间取决于电路中的电感和电阻的数值,以及外加电源变化的速度。
通过计算和模拟可以得到过渡过程的详细特性。
总之,RL电路的过渡过程是指从一个稳态到另一个稳态之间的中间过程,其中电流和电压的变化是由电感和电阻之间的相互作用导致的。
过渡过程可以分为自由响应和强迫响应两个阶段,并且最终会达到新的稳态。
通过分析欧姆定律和基尔霍夫电压定律,可以得到过渡过程的微分方程并进行求解。
电路从一种稳态变化到另一种稳态的过渡过程电路从一种稳态变化到另一种稳态的过渡过程,是指在电路中一些参数的变化导致电路的工作状态从一种稳定状态逐渐变化到另一种稳定状态的过程。
这种过渡过程在电路设计和分析中是非常重要的,它可以通过分析电路的动态响应来获取电路的稳态特性和动态特性。
电路的稳态即电路在没有任何外部扰动的情况下,各个元件的电压和电流分布呈稳定的状态。
在稳态下,电路中的各个元件的电压和电流值不随时间变化。
而电路的动态则指的是当电路受到外部干扰或者自身参数变化时,电路中的元件电压和电流发生变化的过程。
在电路的过渡过程中,一般可以通过数学模型或者进行实验观测来分析电路的动态行为。
下面将以一个简单的RLC电路作为例子,来说明电路从一种稳态变化到另一种稳态的过渡过程。
考虑一个由电源、电感和电容组成的串联RLC电路,电源的电压为V(t),电感的电流为iL(t),电容的电压为VC(t)。
假设初始时刻电路处于稳态,电感中的电流为零,电容的电压为零。
现在突然扫描电源的直流电压,使得电源电压从初始时刻开始以一定的变化速率逐渐增加。
在这种情况下,电路的稳态将会发生改变,电感中的电流和电容的电压将随时间逐渐变化。
根据电路的基本定律,我们可以得到电感和电容的动态方程:LdiL(t)/dt + RiL(t) + 1/C ∫V(t)dt = 01/C dVC(t)/dt + 1/R ∫iL(t)dt + Vc(t) = 0这是一组常微分方程,可以通过求解来得到电感电流和电容电压随时间的变化情况。
一般情况下我们可以采用数值解法(如欧拉法、Runge-Kutta法)来求解这个方程组。
解得电感电流和电容电压随时间的变化曲线即可描述电路从一种稳态到另一种稳态的过渡过程。
在实际过渡过程中,电路中的各个元件的响应速度是不同的。
电感对电流的响应时间常数较小,一般来说会比电容对电压的响应时间常数小很多。
因此,在初始时刻,由于电容的电压为零,电感的电流为零,电压变化很大的电源将会首先产生电感中的电流。