装配尺寸链计算

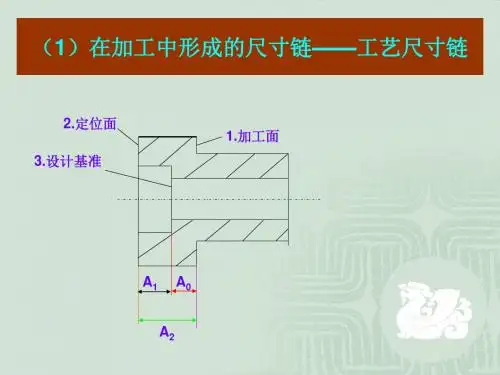
装配尺寸链计算-例1一个键装入轴的槽中，根据设计要求，需要保持一定的间隙。

设201=A mm ，202=A mm ，20.005.000++=A mm（设计要求）。

要求根据生产类型和具体条件确定装配方法，并计算出1A 和2A 的上下偏差。

解：（1）完全互换法首先考虑完全互换法，计算平均精度：()075.01305.020.010=−−=−=n A T T 平均mm 因为尺寸1A 是外尺寸，2A 为内尺寸，前者比后者容易加工，故将公差按生产经验分配，先确定()1.02=A T mm ，然后试计算出()1A T ：()()()()05.01.015.0201=−=−=A T A T A T mm因为涉及上对2A 的公差分布并无规定要求，故可按加工的“入体”习惯方法，即内尺寸采用单向正公差，所以尺寸2A 及其偏差可预先确定为：1.00220+=A mm 画尺寸链：0A 为封闭环，2A 为增环，1A 为减环因为()()()120A EI A ES A ES −=所以()()()()10.020.010.0021−=−=−=A ES A ES A EI mm 因为()()()120A ES A EI A EI −=所以()()()()05.005.00021−=−=−=A EI A EI A ES mm 于是得到05.010.0120−−=A mm因为用了经济公差，所以不论哪一种生产类型，这种装配方法都是合适的。

下面按概率计算法来估计实际生产中的间隙0A 的分布范围。

()()()()112.01.005.02222211120≈+=+==∑−=A T A T A T A T n i imm ()()()[]075.021.005.021111−=−−=+=∆A EI A ES A mm ()()()[]05.0201.021222=+=+=∆A EI A ES A mm ()()()()[]125.0075.005.0120=−−=∆−∆=∆A A A mm()()()181.02112.0125.02000=⎟⎠⎞⎜⎝⎛+=+∆=A T A A ES mm ()()()069.02112.0125.02000=⎟⎠⎞⎜⎝⎛−=−∆=A T A A EI mm 即按概率法计算时，间隙尺寸的实际分布是：181.0069.000++=A mm这说明：在实际中，尺寸0A 的波动范围要比按极大极小计算的范围小一些（图3）。

尺寸链计算及公差分析一、尺寸链计算1.确定基准尺寸：首先需要确定产品的基准尺寸，这是其他尺寸的参考值。

2.确定功能尺寸：根据产品的功能要求，确定与之相关的尺寸。

例如，一个机械零件的功能要求是与其他组件配合，那么相关的尺寸即为功能尺寸。

3.确定辅助尺寸：辅助尺寸是与功能尺寸无关的尺寸，通常用于产品的加工和装配。

例如，孔的直径和深度就是辅助尺寸。

4.确定公差：在确定各个尺寸之后，需要为它们设置公差。

公差是指允许的尺寸变化范围，它的大小取决于产品的制造工艺和功能要求。

5.进行尺寸链计算：根据产品的功能和制造要求，依次计算各个尺寸的数值。

计算时需要考虑公差的影响，确保产品在允许的范围内可以正常工作。

二、公差分析公差分析是确定产品尺寸的变化范围，即各个尺寸的上下限。

公差分析可以帮助工程师评估产品的质量，确定工艺参数，并优化产品设计。

1.确定公差类型：公差分为基本公差和几何公差两种类型。

基本公差是根据工艺要求和产品功能确定的，例如直径公差、平行度公差等；几何公差是根据产品的形状和配合要求确定的，例如圆度公差、轴线位置公差等。

2.进行公差叠加：公差叠加是将各个尺寸的公差叠加在一起，得到产品整体的公差。

这可以通过数学模型或专业软件进行计算。

3.进行公差分析：在确定产品整体的公差后，可以进行公差分析。

公差分析可以通过模拟或实验的方式进行，用于评估产品在实际使用中尺寸变化的影响。

4.优化设计：通过公差分析可以了解产品尺寸变化的情况，如果发现一些尺寸变化太大，可能会导致产品的功能受到影响，需要对设计进行优化。

优化设计可以包括调整公差、改变加工工艺等。

总结起来，尺寸链计算及公差分析是确定产品尺寸和形状的重要方法，它可以帮助工程师评估产品的质量和性能，指导产品的制造和装配。

在实际应用中，需要充分考虑产品的功能要求、制造工艺和使用环境等因素，合理确定尺寸链和公差，以确保产品的质量和性能达到要求。

一、尺寸链及尺寸链计算公式1、尺寸链的定义在工件加工和机器装配过程中，由相互联系的尺寸,按一定顺序排列成的封闭尺寸组，称为尺寸链。

尺寸链示例2、工艺尺寸链的组成环：工艺尺寸链中的每一个尺寸称为尺寸链的环。

工艺尺寸链由一系列的环组成。

环又分为：（1）封闭环（终结环）：在加工过程中间接获得的尺寸，称为封闭环。

在图b所示尺寸链中，A0是间接得到的尺寸，它就是图b所示尺寸链的封闭环。

（2）组成环：在加工过程中直接获得的尺寸，称为组成环。

尺寸链中A1与A2都是通过加工直接得到的尺寸，A1、A2都是尺寸链的组成环。

1）增环：在尺寸链中，自身增大或减小，会使封闭环随之增大或减小的组成环，称为增环。

表示增环字母上面用--> 表示。

2）减环：在尺寸链中，自身增大或减小，会使封闭环反而随之减小或增大的组成环，称为减环。

表示减环字母上面用<-- 表示。

3）怎样确定增减环：用箭头方法确定，即凡是箭头方向与封闭环箭头方向相反的组成环为增环，相同的组成环为减环。

在图b所示尺寸链中，A1是增环，A2是减环。

4）传递系数ξi：表示组成环对封闭环影响大小的系数。

即组成环在封闭环上引起的变动量对组成环本身变动量之比。

对直线尺寸链而言，增环的ξi＝1，减环的ξi＝－1。

3.尺寸链的分类4.尺寸链的计算尺寸链计算有正计算、反计算和中间计算等三种类型。

已知组成环求封闭环的计算方式称作正计算；已知封闭环求各组成环称作反计算；已知封闭环及部分组成环，求其余的一个或几个组成环，称为中间计算。

尺寸链计算有极值法与统计法（或概率法）两种。

用极值法解尺寸链是从尺寸链各环均处于极值条件来求解封闭环尺寸与组成环尺寸之间关系的。

用统计法解尺寸链则是运用概率论理论来求解封闭环尺寸与组成环尺寸之间关系的。

5.极值法解尺寸链的计算公式（4）封闭环的中间偏差（5）封闭环公差（6）组成环中间偏差Δi＝(ES i＋EI i)/2（7）封闭环极限尺寸（8）封闭环极限偏差6.竖式计算法口诀：封闭环和增环的基本尺寸和上下偏差照抄；减环基本尺寸变号；减环上下偏差对调且变号。

内容提纲1、装配尺寸链1装配尺寸链2、保证机器装配精度的方法2保证机器装配精度的方法当遇到有些要求较高的装配精度，如果完全靠相关零件的制造精度来直接保证，则零件的加工精度将会很高，给加工带来较大困难。

一、装配尺寸链1.装配尺寸链的概念装配尺寸链是以某项装配精度指标（或装配要求）作为封闭环，查找所有与该项精度指标（或装配要求）有关零件的尺寸（或位置要求）作为组成环而形成的尺寸链。

☞装配尺寸链的封闭环、组成环●封闭环：是间接保证的。

装配尺寸链的封闭环→产品或部件的装配精度要求。

如装配间隙、过盈量、装配后的位置要求。

一个装配精度要求就可以建立一个装配尺寸链。

●组成环：对装配精度要求有直接影响的那些零、部件上的尺寸和位置关系。

分为增环和减环（定义及判断方法同工艺尺寸链）。

2. 装配尺寸链的分类◆分类：根据各环的几何特征及所处的空间位置线性尺寸链→所有环为长度或精度的尺寸链，各环→所有环为长度或精度的尺寸链各环位于同一平面且彼此平行。

角度尺寸链→垂直度、平行度等平面尺寸链空间尺寸链装配尺寸链的建立步骤建3. 装配尺寸链的建立步骤一般按下列步骤建立尺寸链。

1、确定封闭环2、查找组成环(1)查找相关零件(2)确定相关零件上的相关尺寸3、画尺寸链图并确定组成环的性质（1）几何公差环的特点何差几何公差环可看做公称尺寸为零的尺寸环。

若几何公差的上、下极限偏差对称分布，如同轴度和对称度等那么无论把该环定为增环是减环它们对封称度等，那么无论把该环定为增环还是减环，它们对封闭环的影响将是相同的。

因此，上、下极限偏差对称分布的几何公差环，可以不必判定其是增环还是减环，任意假定都可以。

若几何公差的上下极限偏差虽是对称分布而若几何公差的上、下极限偏差虽是对称分布，而实际上是只允许单向极限偏差的环，那么就必须判定其是增环还是减环并限制其出现另一方向的极限偏差还是减环，并限制其出现另一方向的极限偏差。

判定方法见角度尺寸链。

（2）配合间隙环的特点间隙配合间隙环是指间隙配合时，因轴比孔小，引起轴的轴线和孔的轴线的偏移量。

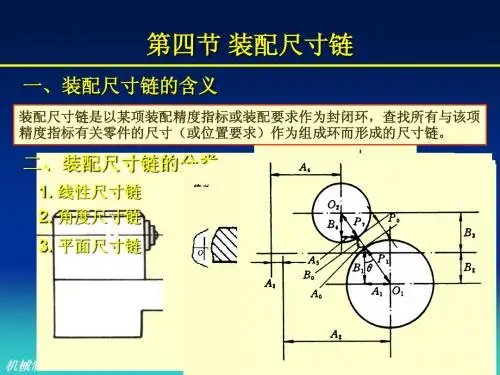
尺寸链计算方法及案例详解尺寸链计算方法是指根据产品的尺寸要求和特定的工艺流程，通过一系列的计算和分析来确定产品各个部件的尺寸和配合关系的方法。

尺寸链计算方法主要应用于机械设计、工程制图、零部件加工等领域，是确保产品尺寸精度和装配质量的重要手段。

首先，尺寸链计算方法需要明确产品设计的功能要求和工艺要求，包括产品的使用环境、受力情况、材料特性等。

然后，根据这些要求，确定产品各个部件之间的配合关系和尺寸范围。

接着，通过计算和分析，确定各个部件的尺寸，并建立尺寸链，保证各个部件在装配时能够满足设计要求。

在实际应用中，尺寸链计算方法通常涉及到几个方面的内容，包括尺寸配合计算、公差分配、尺寸链分析等。

在尺寸配合计算中，需要根据配合要求和公差要求，确定配合尺寸的上限和下限。

公差分配则是根据产品功能和装配要求，合理地分配公差，确保产品的性能和装配质量。

尺寸链分析则是通过建立尺寸链图，分析各个部件之间的尺寸关系，找出影响产品尺寸精度的关键因素，从而指导产品设计和加工。

举个简单的案例来说明尺寸链计算方法的应用。

比如，某机械零件的装配要求是要求两个轴承孔的中心距离在一定范围内，并且轴承孔的直径要求在一定的公差范围内。

在这种情况下，就需要通过尺寸链计算方法来确定轴承孔的尺寸和配合关系。

首先根据轴承的尺寸和公差要求，确定轴承孔的上限和下限尺寸。

然后根据轴承孔的位置和受力情况，确定轴承孔中心距离的范围。

最后通过尺寸链计算方法，确定轴承孔的尺寸和配合关系，以保证产品的装配质量和性能。

总之，尺寸链计算方法是一种重要的工程技术方法，通过合理的计算和分析，能够确保产品的尺寸精度和装配质量，对于提高产品的质量和竞争力具有重要意义。

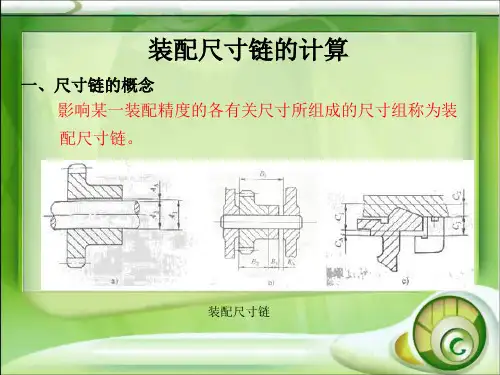
装配尺寸链的计算方法
装配尺寸链是指将多个零件按照一定规律组装在一起时所需要
的尺寸链，也称为装配尺寸序列。

它是用来确保装配质量的重要工具，通过计算装配尺寸链可以帮助工程师预测和解决零件装配过程中可
能出现的问题，从而提高装配质量和效率。

计算装配尺寸链的方法如下：
1. 确定装配关系：首先确定零件的装配关系，即哪些零件应该放在一起装配，哪些零件先装配，哪些后装配。

2. 确定重要特征：确定装配过程中的重要特征，如轴承孔、轴承外径等。

3. 确定公差：根据设计要求和实际情况确定零件和重要特征的公差。

4. 计算尺寸链：按照装配关系逐步计算各个零件和重要特征的尺寸链，即从一个零件的基准面到下一个零件的基准面的距离。

5. 验证尺寸链：对计算出来的尺寸链进行验证，确保其符合设计要求并且能够实现装配。

除了以上的方法，还有一些常用的计算尺寸链的工具和软件，如CATIA、Pro/E、SolidWorks等，它们能够帮助工程师更快速、更准确地计算出尺寸链。

总之，计算装配尺寸链是一个非常重要的工作，它能够帮助工程师预测和解决零件装配过程中可能出现的问题，从而提高装配质量和效率。