马尔科夫链例题

马尔可夫链例题讲解
马尔可夫链是一个数学模型，用于描述一系列状态之间的随机转移。

每个状态的未来只取决于其当前状态，而与过去的状态无关。

以下是一个马尔可夫链的简单例题及其讲解：
例题：求销售状态的转移概率矩阵
题目描述：记录了某抗病毒药的6年24个季度的销售情况，得到表1。

试求其销售状态的转移概率矩阵。

表1 某抗病毒药24个季度的销售情况
季度销售状态
Q1 畅销
Q2 畅销
Q3 畅销
... ...
Q24 畅销
分析表中的数据，其中有15个季度畅销，9个季度滞销，连续出现畅销和
由畅销转入滞销以及由滞销转入畅销的次数均为7，连续滞销的次数为2。

由此，可得到下面的市场状态转移情况表（表2）。

表2 市场状态转移情况表
下季度药品所处的市场状态 1（畅销） 2（滞销）本季度药品所处的市
场状态
1（畅销） 7 7 1（畅销）
2（滞销） 7 2 2（滞销）
现计算转移概率：以频率代替概率，可得连续畅销的概率：P(连续畅销) =
7/15。

同样得由畅销转入滞销的概率：P(畅销→滞销) = 7/15。

滞销转入畅销的概率：P(滞销→畅销) = 7/15。

连续滞销的概率：P(连续滞销) = 2/15。

综上，得销售状态转移概率矩阵为：P=(P(连续畅销) P(畅销→滞销) P(滞销→畅销) P(连续滞销))=(7/15 7/15 7/15 2/15)。

从上面的计算过程知，所求转移概率矩阵P的元素其实可以直接通过表2中的数字计算而得到，即将表中数分母中的数为15减1是因为第24季度是
畅销，无后续记录，需减1。

选择题在离散时间马尔可夫模型中，如果状态转移概率矩阵P的某一行所有元素之和不为1，这意味着什么？A. 该模型是稳态的B. 存在吸收状态C. 存在状态转移概率的误差（正确答案）D. 模型是周期性的设有一个三状态（S1, S2, S3）的离散时间马尔可夫模型，若从S1到S2的转移概率为0.4，从S1到S3的转移概率为0.5，则从S1到自身的转移概率是多少？A. 0.9B. 0.1（正确答案）C. 0.4D. 0.5在一个离散时间马尔可夫链中，如果一个状态是常返的，那么它满足什么条件？A. 平均返回时间为无穷大B. 在有限步内一定会返回到该状态（正确答案）C. 转移概率矩阵的对应行全为0D. 该状态是吸收状态假设一个离散时间马尔可夫模型有两个状态（A和B），从A到B的转移概率是0.7，从B 到A的转移概率是0.4，那么状态A是哪种类型的状态？A. 吸收状态B. 瞬时状态C. 常返状态（正确答案）D. 周期状态在离散时间马尔可夫链中，如果一个状态是瞬时的，那么它满足什么条件？A. 从该状态出发，最终会回到该状态B. 从该状态出发，永远不会回到该状态（正确答案）C. 该状态是链的起始状态D. 该状态是链的终止状态设有一个四状态（S1, S2, S3, S4）的离散时间马尔可夫模型，如果S1是吸收状态，那么从S1到其他状态的转移概率应该是多少？A. 大于0B. 小于1C. 等于0（正确答案）D. 无法确定在一个离散时间马尔可夫链中，如果状态转移概率矩阵P的某一列所有元素之和为1，这意味着什么？A. 存在一个吸收状态（正确答案）B. 模型是稳态的C. 存在状态转移概率的误差D. 模型是周期性的假设一个离散时间马尔可夫模型有三个状态（X, Y, Z），从X到Y的转移概率是0.3，从X到Z的转移概率是0.4，从X到自身的转移概率是0.2，那么从X状态出发，下一步不可能发生的情况是？A. 转移到Y状态B. 转移到Z状态C. 转移到一个新的未知状态（正确答案）D. 保持在X状态在离散时间马尔可夫模型中，如果一个状态是周期性的，且周期为2，那么这意味着什么？A. 该状态每隔一步就会返回到自身B. 该状态在两步之后才能返回到自身（正确答案）C. 该状态是吸收状态D. 该状态是瞬时状态。

马尔科夫计算例题
马尔科夫链蒙特卡洛（Markov Chain Monte Carlo，MCMC）是一种统计模拟方法，用于从复杂的分布中抽样。

以下是一个简单的马尔科夫链蒙特卡洛计算例题：
假设我们有一个随机变量 \(X\)，其分布是 \(P(X)\)。

我们的目标是计算
\(P(X)\) 的期望值，也就是：
\(\text{E}[X] = \int x P(x) dx\)
但是，直接计算这个积分是非常困难的。

因此，我们使用马尔科夫链蒙特卡洛方法来近似这个积分。

步骤如下：
1. 初始化一个随机数 \(x_0\) 作为当前状态。

2. 生成一个随机数 \(r\) 服从均匀分布 \(U(0,1)\)。

3. 计算接受率 \(A = \min(1, \frac{P(x_i)}{P(x_j)})\)，其中 \(j\) 是 \(r\) 落入的区间中的状态。

4. 以概率 \(A\) 接受 \(x_j\) 作为新的状态 \(x_{i+1}\)。

5. 如果接受，回到步骤 2；否则，令 \(i = i+1\) 并回到步骤 2。

6. 重复步骤 2-5，直到达到足够的样本数量。

然后，我们可以用这些样本的平均值来近似期望值。

这是一个简单的例子，实际上马尔科夫链蒙特卡洛方法可以用于更复杂的问题，如高维积分、优化问题等。

离散时间马氏链例题离散时间马氏链（离散时间马尔科夫链）是一种随机过程，其中每个状态的未来转变仅依赖于其当前状态，而不依赖于过去的状态或转变。

以下是离散时间马氏链的一个简单例题：天气预报问题假设明天的天气仅与今天的天气有关，而与过去的天气无关。

如果今天下雨，那么明天下雨的概率为0.7；如果今天不下雨，那么明天下雨的概率为0.4。

我们要求出今天下雨并且四天后仍然下雨的概率（假设α=0.7，β=0.4）。

解：定义状态：我们可以定义两个状态，状态0表示不下雨，状态1表示下雨。

建立转移概率矩阵：根据题目描述，我们可以得到以下的转移概率矩阵P：P = [0.6 0.4; 0.3 0.7]其中，P(i, j)表示从状态i转移到状态j的概率。

3. 应用马氏链的性质：我们知道马氏链的性质是未来的状态只与当前状态有关，与过去的状态无关。

因此，我们可以使用转移概率矩阵来计算四天后仍然下雨的概率。

我们从今天下雨（状态1）开始，想要知道四天后仍然下雨的概率。

我们可以通过连续应用转移概率矩阵来计算这个概率：今天下雨并且四天后仍然下雨的概率= P(1, 1)^4但是这是错误的，因为我们不能直接取四次方。

正确的做法是，考虑所有可能的路径，即在这四天中，天气可能如何变化。

例如，它可能一直保持下雨，或者可能在中间某天下雨然后再次下雨等等。

我们需要考虑所有这些可能性。

但是，对于较大的n值，直接计算所有路径是不切实际的。

我们可以使用一种称为“稳态概率”的概念来简化计算。

稳态概率是指，当时间趋于无穷大时，马氏链处于某个特定状态的概率。

在这个例子中，我们可以计算出稳态概率，然后用它来估计四天后下雨的概率。

然而在这个特定的例子中，由于转移概率矩阵不是对称的，因此没有简单的公式可以直接计算出n步转移概率。

我们需要使用矩阵的n次幂来计算这个概率。

但是注意，我们不能简单地取P(1,1)的四次幂，因为那将假设每天都独立地下雨，而实际上每天的天气都依赖于前一天的天气。

连续时间马尔可夫链例题假设有一个连续时间马尔可夫链，描述一个人的健康状态。

该马尔可夫链包含三个状态：健康、生病和康复。

人的健康状态可以根据以下转移概率进行模拟：1. 在任何时间点，一个健康的人以0.1的速率生病。

2. 在任何时间点，一个生病的人以0.2的速率康复。

3. 在任何时间点，一个康复的人以0.05的速率重新生病。

现在假设一个人的初始状态是健康，我们可以使用连续时间马尔可夫链模型来模拟他的健康状态随时间的变化。

假设每个时间单位是一周，我们希望模拟他一年内的健康状态。

根据上面的转移概率，我们可以得到如下的转移矩阵：```| 健康 | 生病 | 康复 |----------------------------健康 | 0.9 | 0.1 | 0 |生病 | 0.05 | 0.75 | 0.2 |康复 | 0 | 0.05 | 0.95|```该矩阵中的每个元素表示从当前状态转移到下一个状态的概率。

例如，一个健康的人在一周后仍然健康的概率为0.9，在一周后生病的概率为0.1，在一周后康复的概率为0。

使用该转移矩阵，我们可以模拟一个人一年内的健康状态。

假设每个时间单位是一周，则一年共有52个时间单位。

我们可以使用随机数生成器来生成每个时间单位的状态。

假设生成的随机数在[0,1)之间，我们可以根据转移概率进行状态转移。

例如，如果生成的随机数小于0.9，则人在下一个时间单位仍然健康；如果生成的随机数介于0.9和0.95之间，则人在下一个时间单位康复；如果生成的随机数大于等于0.95，则人在下一个时间单位重新生病。

使用这种方法，我们可以模拟一个人一年的健康状态，并观察他在这段时间内的状态变化。

这可以帮助我们更好地了解和预测一个人的健康动向。

连续时间马尔可夫链连续时间马尔可夫链（Continuous-time Markov Chain）是马尔可夫链在连续时间下的一种模型。

它受到时间的连续性限制，可以用于描述一些随机过程。

马尔可夫链基本概念马尔可夫链是指具有“无记忆性”的随机过程。

在离散时间中，马尔可夫链指的是一个随机变量序列，其中每个随机变量的取值依赖于其前一时刻的取值。

这个过程可以用一个状态转移概率矩阵来描述。

在连续时间中，马尔可夫链则是一个具有无记忆性的连续随机过程。

与离散时间不同，连续时间马尔可夫链的状态在一定时间段内可以发生任意多次的改变。

连续时间马尔可夫链的定义连续时间马尔可夫链是一个随机过程，其状态空间为有限个数。

该过程在任意时刻处于某个状态，并且满足无记忆性的马尔可夫性质。

连续时间马尔可夫链的演变是通过指数分布来描述的。

在每个状态之间的转移时间服从指数分布，转移时间的参数与当前状态有关。

连续时间马尔可夫链的转移速率矩阵与离散时间马尔可夫链中的状态转移矩阵类似，连续时间马尔可夫链使用转移速率矩阵来描述状态之间的转换关系。

设连续时间马尔可夫链的状态空间为{1, 2, …, n}，转移速率矩阵为Q。

矩阵Q的元素qij表示从状态i到状态j的速率，且满足以下条件：•qij≥0, i≠j;•对于每一个状态i，有qii = -∑qij（i≠j）。

在连续时间马尔可夫链中，从状态i到状态j的转移概率为pij(t)，t表示时间。

转移概率在给定时间段内满足以下等式：equation1其中X(t)表示在时刻t的状态，P表示概率。

连续时间马尔可夫链的性质连续时间马尔可夫链有许多属性与离散时间马尔可夫链类似。

•遍历性：如果状态空间中的每一个状态在有限时间内是可达的，则称连续时间马尔可夫链是遍历的。

•稳态概率分布：马尔可夫链可能存在稳态概率分布，对于连续时间马尔可夫链也是如此。

稳态概率分布表示在长时间内各个状态的概率分布。

•等距离转换概率：等距离转换概率描述了在任意的相同时间间隔内，从一个状态转移到另一个状态的概率。

马尔科夫链是一种随机过程，具有“马尔科夫性质”，即未来状态的概率仅仅取决于当前状态，而与过去状态无关。

转移概率是指从一个状态转移到另一个状态的概率。

下面是一个简单的马尔科夫链的例子，包含一些状态和它们之间的转移概率。

假设有三个天气状态：晴天（Sunny）、多云（Cloudy）和雨天（Rainy）。

状态之间的转移概率如下：
- 如果今天是晴天，明天是晴天的概率为0.7，多云的概率为0.2，雨天的概率为0.1。

- 如果今天是多云，明天是晴天的概率为0.3，多云的概率为0.4，雨天的概率为0.3。

- 如果今天是雨天，明天是晴天的概率为0.2，多云的概率为0.3，雨天的概率为0.5。

这些转移概率可以用矩阵表示，该矩阵称为转移矩阵。

假设状态按照晴天（S）、多云（C）、雨天（R）的顺序排列，则转移矩阵如下：
```
P = | 0.7 0.2 0.1 |
| 0.3 0.4 0.3 |
| 0.2 0.3 0.5 |
```
其中，P(i, j) 表示从状态i 转移到状态j 的概率。

如果当前是晴天，我们可以使用转移矩阵来计算明天各种天气的概率。

假设今天是晴天（S），我们想知道明天是晴天（S）、多云（C）或雨天（R）的概率，可以将转移矩阵与当前状态向量相乘：
```
State vector today: | 1 |
| 0 |
| 0 |
State vector tomorrow = P * State vector today
```
计算结果将给出明天各种天气的概率。

这个过程可以一直迭代下去，得到未来时间点的状态概率。

应用随机过程markov链经典例题
随机过程是指随机事件随时间的推移而发生的过程，而马尔可夫过程则是一种特殊的随机过程，其特点是未来状态的概率只取决于当前状态，而与过去状态无关。

经典的马尔可夫链例题是假设某个小球在三个盒子之间随机跳跃，每次跳跃只能移动到相邻的盒子，且概率相等。

问当小球在盒子1时，经过n次跳跃后恰好回到盒子1的概率是多少
首先，我们可以用矩阵表示小球在不同盒子之间跳跃的概率。

假设矩阵P表示小球从一个盒子跳到另一个盒子的概率，即：
P = [0 1/2 1/2; 1/2 0 1/2; 1/2 1/2 0]
其中，第i行第j列的元素表示小球从盒子i跳到盒子j的概率。

例如，P(1,2)表示小球从盒子1跳到盒子2的概率为1/2。

接下来，我们需要用这个矩阵来计算小球从盒子1跳跃n次后回到盒子1的概率。

假设矩阵P的n次方为P^n，则小球从盒子1跳跃n次后回到盒子1的概率为P^n(1,1)。

例如，当n=2时，P^2为：
P^2 = [1/2 1/4 1/4; 1/4 1/2 1/4; 1/4 1/4 1/2]
则小球从盒子1跳跃2次后回到盒子1的概率为P^2(1,1)=1/2。

因此，当小球在盒子1时，经过n次跳跃后恰好回到盒子1的概率为P^n(1,1)。

我们可以通过不断计算矩阵P的幂来得到不同次数下的概率。

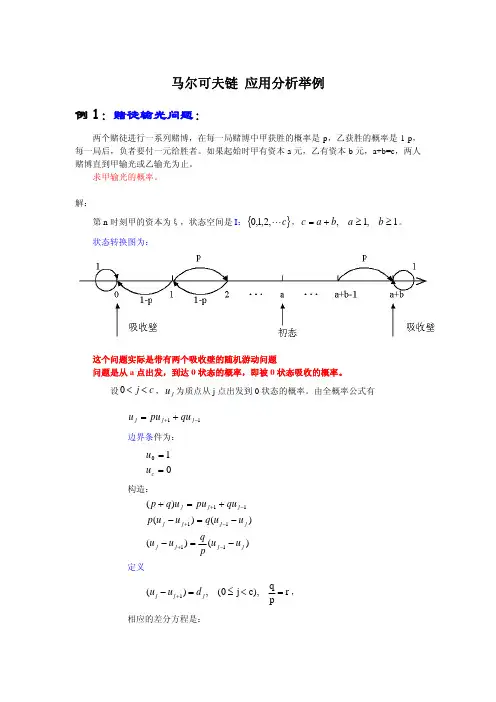
练习四：马尔可夫链 随机过程练习题1．设质点在区间[0，4]的整数点作随机游动，到达0点或4点后以概率1停留在原处，在其它整数点分别以概率31向左、右移动一格或停留在原处。

求质点随机游动的一步和二步转移的概率矩阵。

2．独立地重复抛掷一枚硬币，每次抛掷出现正面的概率为p ，对于2≥n 求，令n X =0，1，2或3，这些值分别对应于第1-n 次和第n 次抛掷的结果为（正，正），（正，反），（反，正）或（反，反）。

求马尔可夫链},2,1,0,{ =n X n 的一步和二步转移的概率矩阵。

3．设}0,{≥n X n 为马尔可夫链，试证： （1）},,,|,,,{11002211n n m n m n n n n n i X i X i X i X i X i X P ======++++++ }|,,,{2211n n m n m n n n n n i X i X i X i X P =====++++++（2）}|,,,,,,{11221100++++++======n n m n m n n n n n i X i X i X i X i X i X P}|,,,{111100++=====n n n n i X i X i X i X P ==⋅+++m n n n X i X P ,,{22 }|11+++=n n m n i X i4．设}1,{≥n X n 为有限齐次马尔可夫链，其初始分布和转移概率矩阵为==0{X P p i4,3,2,1,41}==i i ，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=4/14/14/14/18/34/18/14/14/14/14/14/14/14/14/14/1P ，试证 }41|4{}41,1|4{12102<<=≠<<==X X P X X X P5．设}),({T t t X ∈为随机过程，且)(11t X X =，,),(22 t X X = ),(n n t X X =为独立同分布随机变量序列，令2,,)(,011110≥=+===-n X cY Y X t Y Y Y n n n ，试证}0,{≥n Y n 是马尔可夫链。

随机过程的马尔可夫链当然，请看以下的20道试题：1. 什么是马尔可夫链？- A. 一个随机过程- B. 一个确定过程- C. 一个线性过程- D. 一个非随机过程2. 马尔可夫链具有什么样的记忆特性？- A. 有限记忆- B. 无限记忆- C. 完全没有记忆- D. 部分记忆3. 马尔可夫链的状态空间是指什么？- 空格填空：__________4. 马尔可夫链状态的转移概率是指什么？- 空格填空：__________5. 马尔可夫链状态转移概率的性质是什么？- A. 非负性- B. 可加性- C. 归一性- D. 全部正确6. 马尔可夫链的平稳分布是指什么？- 空格填空：__________7. 马尔可夫链收敛到平稳分布的条件是什么？- A. 非周期性- B. 非简并性- C. 正常性- D. 所有选项都是8. 马尔可夫链的平稳分布可以通过什么方法求解？- 空格填空：__________9. 马尔可夫链的平稳分布与其初始分布之间的关系是什么？- A. 线性关系- B. 非线性关系- C. 比例关系- D. 无关系10. 马尔可夫链的遍历性质指的是什么？- 空格填空：__________11. 马尔可夫链的马尔可夫性质是指什么？- A. 状态的独立性- B. 未来状态只依赖于当前状态- C. 状态转移是确定的- D. 初始状态不影响最终状态12. 马尔可夫链的时间反转性质是指什么？- 空格填空：__________13. 马尔可夫链的条件转移概率公式是什么？- 空格填空：__________14. 马尔可夫链的转移概率矩阵具有什么性质？- A. 非负性- B. 可加性- C. 归一性- D. 所有选项都是15. 马尔可夫链的瞬时状态概率是指什么？- 空格填空：__________16. 马尔可夫链的延迟时间是指什么？- 空格填空：__________17. 马尔可夫链的重现时间是指什么？- 空格填空：__________18. 马尔可夫链的复发时间是指什么？- 空格填空：__________19. 马尔可夫链的周期性质是指什么？- A. 完全周期性- B. 非周期性- C. 部分周期性- D. 无关20. 马尔可夫链的平稳分布可以通过什么方法求解？- A. 特征向量法- B. 特征值法- C. 特征分布法- D. 特征过程法。

1.假设某地有1600户居民，某产品只有甲乙丙三家厂家在该地销售，经调查，8月份购买甲乙丙三层的户数分别为480,320,800. 9月份里，原买甲的有48户转买乙产品，有96户转买丙产品。

原买乙的有32户转买甲产品，有64户转买丙产品，原买丙的有64户转买甲产品，有32户转买乙产品。

用状态1,2,3分别表示甲乙丙三厂。

试求：
<!--[if !supportLists]-->a)<!--[endif]-->一步转移概率矩阵。

<!--[if !supportLists]-->b)<!--[endif]-->10月份市场占有率的分布。

<!--[if !supportLists]-->c)<!--[endif]-->稳定状态下的市场占有率的分布。

若甲厂考虑采用不同的策略来增加市场占有率，策略I为通过广告宣传等策略占领其他厂家的市场，则在原来的基础上改变为：原买乙的有45户转买甲产品，原买丙的有80户转买丙产品。

策略II为采用提高服务质量以挽留顾客减少顾客外流，则原买甲的减少为有40户转买乙产品，有50户转买丙产品。

采用这两种策略的成本分别为15万，和8万元。

请问甲厂为了在长期经营中获取最大利润，应采取哪种策略？假定策略一经采取就不再改变。

截止日期2014年12月17日下午11时59分00秒。