四面体外接球表面积公式

四面体外接球的球心、在立体几何中，几何体外接球是一个常考的知识点，对于学生来说这是一个难点，一方面图形不会画，另一方面在画出图形的情况下无从下手，不知道球心在什么位置，半径是多少而无法解题。

本文章在给出图形的情况下解决球心位置、半径大小的问题。

、出现“墙角”结构利用补形知识，联系长方体。

【原理】：长方体中从一个顶点出发的三条棱长分别为a,b,c，则体对角线长为________ / 2 . b2 + ~2I = J a2+b2+C2，几何体的外接球直径2R为体对角线长I即R = ---------- --【例题】：在四面体ABCD中，共顶点的三条棱两两垂直, 其长度分别为1, V6,3，若该四面体的四个顶点在一个球面上，求这个球的表面积。

解:因为：长方体外接球的直径为长方体的体对角线长所以：四面体外接球的直径为AE的长即：4R2=AB2+AC2+AD2C 4R2 =12+32+ 府=16 所以R =2球的表面积为S=4；IR2=16；I二、出现两个垂直关系，利用直角三角形结论。

【原理】：直角三角形斜边中线等于斜边一半。

球心为直角三角形斜边中点。

【例题】：已知三棱锥的四个顶点都在球0的球面上，AB丄BC且PA =7，PB=5, PC =751，AC =10,求球0 的体积。

解：AB 丄BC 且PA =7，PB=5，P C=妬，AC =10,!_ 2因为=102所以知AC2=PA2+ PC2设球心坐标为O(x, y,z)贝U AO=BO=CO =DO ,由空间两点间距离公式知x 2 +y 2 +z 2 =(x -1)2 +(y -73)2 +z 2J 3解得 “1 y=- z =1所以PA 丄PC 所以可得图形为:在RtAABC 中斜边为AC 在RU PAC 中斜边为AC取斜边的中点0 , 在 RUABC 中 0A = 0B = 0C在 RtiPAC中 OP = OB =OC 所以在几何体中OP = OB =OC =OA ，即O 为该四面体的外接球的球心1R = — AC = 52 所以该外接球的体积为V 丄职―500工3 3 【总结】斜边一般为四面体中除了直角顶点以外的两个点连线。

几何体外接球表面积及体积的求法答案1.D【考点】由三视图求面积、体积．【专题】数形结合；转化法；空间位置关系与距离．【分析】根据三视图得出该几何体是圆柱，求出圆柱体的表面积和它外接球的表面积即可得出结论．【解答】解：根据三视图得，该几何体是底面半径为3，高为4的圆柱体，所以该圆柱体的表面积为S1=2π×32+2π×3×8=66π；根据球与圆柱的对称性，得它外接球的半径R满足（2R）2=62+82=100，所以外接球的表面积为S2=4πR2=100π；所以剩余几何体的表面积是S=S1+S2=66π+100π=166π．故选：D．【点评】本题考查了三视图的应用问题，也考查了利用三视图研究直观图的性质，球与圆柱的接切关系，球的表面积计算问题，是基础题目．2.D【考点】球的体积和表面积．【专题】计算题；空间位置关系与距离．【分析】由长方体的对角线公式，算出正四棱柱体对角线的长，从而得到球直径长，得球半径R=1，最后根据球的体积公式，可算出此球的体积．【解答】解：∵正四棱柱的底面边长为1，侧棱长为，∴正四棱柱体对角线的长为=2又∵正四棱柱的顶点在同一球面上，∴正四棱柱体对角线恰好是球的一条直径，得球半径R=1根据球的体积公式，得此球的体积为V=πR3=π．故选：D．【点评】本题给出球内接正四棱柱的底面边长和侧棱长，求该球的体积，考查了正四棱柱的性质、长方体对角线公式和球的体积公式等知识，属于基础题．3.C【考点】球内接多面体；球的体积和表面积．【专题】空间位置关系与距离．【分析】先画出图形，正四棱锥外接球的球心在它的底面的中心，然后根据勾股定理列方程，解出球的半径即可．【解答】解：如图，设正四棱锥底面的中心为E，过点A，B，C，D，S的球的球心为O，半径为R，则在直角三角形AEO中，AO=R，AE=BD=4，OE=SE﹣AO=8﹣R由AO2=AE2+OE2得R2=42+（8﹣R）2，解得R=5球半径R=5，故选C．【点评】本题主要考查球，球的内接体问题，考查计算能力和空间想象能力，属于中档题．4.D考点：球的体积和表面积．专题：计算题．分析：由AB=BC=CA=2，求得△ABC的外接圆半径为r，再由R2﹣（R）2=，求得球的半径，再用面积求解．解答：解：因为AB=BC=CA=2，所以△ABC的外接圆半径为r=．设球半径为R，则R2﹣（R）2=，所以R2=S=4πR2=．故选D点评：本题主要考查球的球面面积，涉及到截面圆圆心与球心的连垂直于截面，这是求得相关量的关键．5.C【考点】棱柱、棱锥、棱台的体积．【专题】计算题；空间位置关系与距离．【分析】根据题意作出图形，利用截面圆的性质即可求出OO1，进而求出底面ABC上的高SD，即可计算出三棱锥的体积．【解答】解：根据题意作出图形：设球心为O，过ABC三点的小圆的圆心为O1，则OO1⊥平面ABC，延长CO1交球于点D，则SD⊥平面ABC．∵CO1==，∴OO1==，∴高SD=2OO1=，∵△ABC是边长为1的正三角形，∴S△ABC=，∴V三棱锥S﹣ABC==．故选：C．【点评】本题考查棱锥的体积，考查球内接多面体，解题的关键是确定点S到面ABC的距离．6.C【考点】球的体积和表面积．【专题】空间位置关系与距离．【分析】将四面体补成长方体，通过求解长方体的对角线就是球的直径，然后求解外接球的表面积．【解答】解：由题意可采用割补法，考虑到四面体ABCD的四个面为全等的三角形，所以可在其每个面补上一个以，，为三边的三角形作为底面，且以分别x，y，z长、两两垂直的侧棱的三棱锥，从而可得到一个长、宽、高分别为x，y，z的长方体，并且x2+y2=29，x2+z2=34，y2+z2=37，则有（2R）2=x2+y2+z2=50（R为球的半径），得R2=，所以球的表面积为S=4πR2=50π．故选：C．【点评】本题考查几何体的外接球的表面积的求法，割补法的应用，判断外接球的直径是长方体的对角线的长是解题的关键之一．7.B【考点】球的体积和表面积．【专题】计算题；空间位置关系与距离．【分析】三棱锥A﹣BCD的三条侧棱两两互相垂直，所以把它扩展为长方体，它也外接于球，对角线的长为球的直径，然后解答即可．【解答】解：三棱锥A﹣BCD的三条侧棱两两互相垂直，所以把它扩展为长方体，它也外接于球，对角线的长为球的直径，d==，它的外接球半径是外接球的表面积是4π（）2=14π故选：B．【点评】本题考查球的表面积，考查学生空间想象能力，是基础题．8.B【考点】球内接多面体．【专题】计算题；方程思想；综合法；空间位置关系与距离．【分析】三棱锥A﹣BCD的三条侧棱两两互相垂直，所以把它扩展为长方体，它也外接于球，对角线的长为球的直径，然后解答即可．【解答】解：三棱锥A﹣BCD的三条侧棱两两互相垂直，所以把它扩展为长方体，它也外接于球，对角线的长为球的直径，d==，它的外接球半径是，外接球的表面积是4π（）2=14π故选：B．【点评】本题考查球的表面积，考查学生空间想象能力，是基础题．9.D【考点】棱柱、棱锥、棱台的体积．【专题】计算题；空间位置关系与距离．【分析】设该球的半径为R，则AB=2R，2AC=AB=，故AC=R，由于AB是球的直径，所以△ABC在大圆所在平面内且有AC⊥BC，由此能求出球的体积．【解答】解：设该球的半径为R，则AB=2R，2AC=AB=，∴AC=R，由于AB是球的直径，所以△ABC在大圆所在平面内且有AC⊥BC，在Rt△ABC中，由勾股定理，得：BC2=AB2﹣AC2=R2，所以Rt△ABC面积S=×BC×AC=，又PO⊥平面ABC，且PO=R，四面体P﹣ABC的体积为，∴V P﹣ABC==，即R3=9，R3=3，所以：球的体积V球=×πR3=×π×3=4π．故选D．【点评】本题考查四面体的外接球的体积的求法，解题时要认真审题，仔细解答，注意合理地化空间问题为平面问题．10.B【考点】球的体积和表面积；球内接多面体．【专题】计算题；空间位置关系与距离．【分析】以PA、PB、PC为过同一顶点的三条棱，作长方体如图，则长方体的外接球同时也是三棱锥P﹣ABC外接球．算出长方体的对角线即为球直径，结合球的表面积公式，可算出三棱锥P﹣ABC外接球的体积．【解答】解：以PA、PB、PC为过同一顶点的三条棱，作长方体如图则长方体的外接球同时也是三棱锥P﹣ABC外接球．∵长方体的对角线长为2，∴球直径为2，半径R=，因此，三棱锥P﹣ABC外接球的体积是πR3=π×（）3=4π故选：B．【点评】本题给出三棱锥的三条侧棱两两垂直，求它的外接球的表面积，着重考查了长方体对角线公式和球的表面积计算等知识，属于基础题．11.D12.考点：球的体积和表面积；球内接多面体．专题：空间位置关系与距离．分析：求出BC，利用正弦定理可得△ABC外接圆的半径，从而可求该三棱锥的外接球的半径，即可求出三棱锥的外接球表面积．解答：解：∵AC=2，AB=1，∠BAC=120°，∴BC==，∴三角形ABC的外接圆半径为r，2r=，r=，∵SA⊥平面ABC，SA=2，由于三角形OSA为等腰三角形，则有该三棱锥的外接球的半径R═=，∴该三棱锥的外接球的表面积为S=4πR2=4π×（）2=．故选：D．点评：本题考查三棱锥的外接球表面积，考查直线和平面的位置关系，确定三棱锥的外接球的半径是关键．12.A考点：球内接多面体；棱柱、棱锥、棱台的体积．专题：压轴题．分析：先确定点S到面ABC的距离，再求棱锥的体积即可．解答：解：∵△ABC是边长为1的正三角形，∴△ABC的外接圆的半径∵点O到面ABC的距离，SC为球O的直径∴点S到面ABC的距离为∴棱锥的体积为故选A．点评：本题考查棱锥的体积，考查球内角多面体，解题的关键是确定点S到面ABC的距离．13.【考点】棱柱、棱锥、棱台的体积．【专题】计算题；空间位置关系与距离．【分析】由于面SAB⊥面ABC，所以点S在平面ABC上的射影H落在AB上，根据球体的对称性可知，当S 在“最高点”，也就是说H为AB中点时，SH最大，棱锥S﹣ABC的体积最大．【解答】解：由题意画出几何体的图形如图由于面SAB⊥面ABC，所以点S在平面ABC上的射影H落在AB上，根据球体的对称性可知，当S在“最高点”，也就是说H为AB中点时，SH最大，棱锥S﹣ABC的体积最大．∵△ABC是边长为2的正三角形，所以球的半径r=OC=CH=．在RT△SHO中，OH=OC=OS∴∠HSO=30°，求得SH=OScos30°=1，∴体积V=Sh=××22×1=．故答案是．【点评】本题考查锥体体积计算，根据几何体的结构特征确定出S位置是关键．考查空间想象能力、计算能力．14.12π【考点】球的体积和表面积．【专题】计算题；空间位置关系与距离．【分析】利用平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，求出球的半径，然后求解球O的表面积．【解答】解：因为平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，所以球的半径为： =．所以球O的表面积为4π×3=12π．故答案为：12π．【点评】本题考查球的表面积的求法，考查空间想象能力、计算能力．15.【考点】球的体积和表面积．【专题】计算题．【分析】正方体的内切球的直径为正方体的棱长，外接球的直径为正方体的对角线长，设出正方体的棱长，即可求出两个半径，求出两个球的面积之比．【解答】解：正方体的内切球的直径为，正方体的棱长，外接球的直径为，正方体的对角线长，设正方体的棱长为：2a，所以内切球的半径为：a；外接球的直径为2a，半径为：a，正方体的内切球与外接球的面积之比：==．故答案为：．【点评】本题是基础题，考查正方体的外接球与内切球的面积之比，求出外接球的半径，是解决本题的关键．16.16π【考点】球的体积和表面积．【专题】计算题；方程思想；数形结合法；立体几何．【分析】正四棱锥P﹣ABCD的五个顶点在同一球面上，则其外接球的球心在它的高PO1上，记为O，如图．求出AO1，OO1，解出球的半径，求出球的表面积．【解答】解：正四棱锥P﹣ABCD的外接球的球心在它的高PO1上，记为O，PO=AO=R，PO1=3，OO1=3﹣R，在Rt△AO1O中，AO1=AC=，由勾股定理R2=3+（3﹣R）2得R=2，∴球的表面积S=16π故答案为：16π．【点评】本题考查球的表面积，球的内接体问题，解答关键是确定出球心的位置，利用直角三角形列方程式求解球的半径．需具有良好空间形象能力、计算能力．17.36π【考点】球的体积和表面积．【专题】计算题．【分析】由题意推出MN⊥平面SAC，即SB⊥平面SAC，∠ASB=∠BSC=∠ASC=90°，将此三棱锥补成正方体，则它们有相同的外接球，正方体的对角线就是球的直径，求出直径即可求出球的表面积．【解答】解：∵三棱锥S﹣ABC正棱锥，∴SB⊥AC（对棱互相垂直）∴MN⊥AC，又∵MN⊥AM而AM∩AC=A，∴MN⊥平面SAC即SB⊥平面SAC，∴∠ASB=∠BSC=∠ASC=90°，将此三棱锥补成正方体，则它们有相同的外接球，∴2R=2 ，∴R=3，∴S=4πR2=4π•（3）2=36π，故答案为：36π．【点评】本题是中档题，考查三棱锥的外接球的表面积，考查空间想象能力；三棱锥扩展为正方体，它的对角线长就是外接球的直径，是解决本题的关键．18.；。

立体几何专题：外接球问题中常见的8种模型1.知识梳理一、墙角模型适用范围：3组或3条棱两两垂直；可在长方体中画出该图且各顶点与长方体的顶点重合直接用公式(2R )2=a 2+b 2+c 2，即2R =a 2+b 2+c 2，求出R【补充】图1为阳马，图2和图4为鳖臑二、麻花模型适用范围：对棱相等相等的三棱锥对棱相等指四面体的三组对棱分别对应相等，且这三组对棱构成长方体的三组对面的对角线。

推导过程：三棱锥(即四面体)中，已知三组对棱分别相等，(AB =CD ，AD =BC ，AC =BD )第一步：画出一个长方体，标出三组互为异面直线的对棱；第二步：设出长方体的长宽高分别为a ,b ,c ，AD =BC =x ，AB =CD =y ，AC =BD =z ，列方程组，a 2+b 2=x 2b 2+c 2=y 2c 2+a 2=z 2⇒(2R )2=a 2+b 2+c 2=x 2+y 2+z 22，补充：V A −BCD =abc −16abc ×4=13abc 第三步：根据墙角模型，2R =a 2+b 2+c 2=x 2+y 2+z 22，R 2=x 2+y 2+z 28，R =x 2+y 2+z 28，求出R .三、垂面模型适用范围：有一条棱垂直于底面的棱锥。

推导过程：第一步：将ABC 画在小圆面上，A 为小圆直径的一个端点，作小圆的直径AD ,连接PD ,则PD 必过球心O .第二步：O 1为ABC 的外心，所以OO 1⊥平面ABC ，算出小圆O 1的半径O 1D =r(三角形的外接圆直径算法:利用正弦定理a sin A =b sin B=csin C =2r ,OO 1=12PA .第三步：利用勾股定理求三棱锥的外接球半径：(1)(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2；(2)R 2=r 2+OO 21⇔R =r 2+OO 21.公式：R 2=r 2+h 24四、切瓜模型适用范围：有两个平面互相垂直的棱锥推导过程：分别在两个互相垂直的平面上取外心O 1、O 2过两个外心做两个垂面的垂线，两条垂线的交点即为球心0，取B C 的中点为E ，连接OO 1、OO 2、O 2E 、O 1E 为矩形由勾股可得|OC |2=|O 2C |2+|OO 2|2=|O 2C |2+|O 1C |2-|CE |2∴R 2=r 21+r 22-l 24公式：R 2=r 21+r 22-l 24五、斗笠模型适用于：顶点的投影在底面的外心上的棱锥推导过程：取底面的外心01，连接顶点与外心，该线为空间几何体的高h ，在h 上取一点作为球心0，根据勾股定理R 2=(h -R )2+r 2⇔R =r 2+h 22h公式：R =r 2+h 22h六、矩形模型适用范围：两个直角三角形的斜边为同一边，则该边为球的直径推导过程：图中两个直角三角形ΔPAB 和ΔQAB ，其中∠APB =∠AQB =90°，求外接圆半径取斜边AB 的中点O ，连接OP ,OQ ，则OP =12AB =OA =OB =OQ 所以O 点即为球心，然后在ΔPOQ 中解出半径R 公式：R 2=l22(l 为斜边长度)七、折叠模型适用范围：两个全等三角形或等腰三角形拼在一起，或菱形折叠.推导过程：两个全等的三角形或者等腰拼在一起，或者菱形折叠，设折叠的二面角∠A EC =α,CE =A E =h .如图，作左图的二面角剖面图如右图：H 1和H 2分别为△BCD ,△A BD 外心，分别过这两个外心做这两个平面的垂线且垂线相交于球心O CH 1=r =BD 2sin ∠BCD,EH 1=h -r ,OH 1=(h -r )tanα2由勾股定理可得：R 2=OC 2=OH 21+CH 21=r 2+(h -r )2tan 2α2.公式：R 2=r 2+(h -r )2tan 2α2八、鳄鱼模型适用范围：所有二面角构成的棱锥，普通三棱锥方法：找两面外接圆圆心到交线的距离m ,n ，找二面角α，找面面交线长度l 推导过程：取二面角两平面的外心分别为O 1,O 2并过两外心作这两个面的垂线，两垂线相交于球心O ，取二面角两平面的交线中点为E ，则O ,O 1,E ,O 2四点共圆，由正弦定理得：OE =2r =O 1O 2sin α①在ΔO 1O 2E 中，由余弦定理得：O 1O 2 2=O 1E 2+O 2E 2-2O 1E O 2E cos α②由勾股定理得：OD 2=O 1O 2+O 1D 2③由①②③整理得：OD2=O 1O 2+O 1D 2=OE 2-O 1E 2+O 1D 2=O 1O 2sin α2-O 1E 2+O 1D 2=O 1E2+O 2E 2-2O 1E O 2E cos αsin 2α-O 1E 2+O 1D 2=O1E2+O2E2-2O1EO2Ecosαsin2α-O1E2+O1B2记O1E=m,O2E=n,AB=l,则R2=m2+n2-2mn cosαsin2α+l22公式：R2=m2+n2-2mn cosαsin2α+l222.常考题型3.题型精析题型一:墙角模型1(2023·高一单元测试)三棱锥A-BCD中，AD⊥平面BCD，DC⊥BD，2AD=BD=DC=2，则该三棱锥的外接球表面积为()A.3π2B.9π2C.9πD.36π1.(2022秋·陕西西安·高一统考期末)在《九章算术》中，将四个面都为直角三角形的三棱锥称之为鳖臑．已知在鳖臑A-BCD中，满足AB⊥平面BCD，且AB=BD=5，BC=3，CD=4，则此鳖臑外接球的表面积为()A.25πB.50πC.100πD.200π2.(2023·高一课时练习)《九章算术》是我国古代数学名著，它在几何学中的研究比西方早1000多年．在《九章算术》中，将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马．如图P-ABCD是阳马，PA⊥平面ABCD，PA=5，AB=3，BC=4．则该阳马的外接球的表面积为()A.1252π3B.50πC.100πD.500π33.(2023·广西南宁·统考二模)在《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑，在鳖臑A -BCD 中，AB ⊥平面BCD ，CD ⊥AD ，AB =BD =2，已知动点E 从C 点出发，沿外表面经过棱AD 上一点到点B 的最短距离为10，则该棱锥的外接球的体积为.4.(2023春·辽宁朝阳·高二北票市高级中学校考阶段练习)已知四棱锥P -ABCD 的外接球O 的表面积为64π，PA ⊥平面ABCD ，且底面ABCD 为矩形，PA =4，设点M 在球O 的表面上运动，则四棱锥M -ABCD 体积的最大值为.题型二:麻花模型1(2023春·广东梅州·高二统考期中)已知三棱锥S -ABC 的四个顶点都在球O 的球面上，且SA =BC =2，SB =AC =7，SC =AB =5，则球O 的体积是()A.83π B.3223π C.423π D.823π1.(2022春·江西景德镇·高一景德镇一中校考期中)在△ABC 中，AB =AC =2，cos A =34，将△ABC 绕BC 旋转至△BCD 的位置，使得AD =2，如图所示，则三棱锥D -ABC 外接球的体积为．2.(2023秋·吉林·高一吉林一中校考阶段练习)如图，在△ABC 中，AB =25,BC =210,AC =213，D ，E ，F 分别为三边中点，将△BDE ,△ADF ,△CEF 分别沿DE ,EF ,DF 向上折起，使A ，B ，C 重合为点P ，则三棱锥P -DEF 的外接球表面积为()A.72π B.7143π C.14π D.56π3.(2023·江西·统考模拟预测)在三棱锥P -ABC 中，已知PA =BC =213,AC =BP =41,CP =AB =61，则三棱锥P -ABC 外接球的表面积为()A.77πB.64πC.108πD.72π4.(2022·全国·高三专题练习)已知四面体ABCD 的棱长满足AB =AC =BD =CD =2，BC =AD =1，现将四面体ABCD 放入一个轴截面为等边三角形的圆锥中，使得四面体ABCD 可以在圆锥中任意转动，则圆锥侧面积的最小值为．题型三:垂面模型1(2023·高一单元测试)在三棱锥P -ABC 中，PA ⊥平面ABC ，PA =6，BC =3，∠CAB =π6，则三棱锥P -ABC 的外接球半径为()A.3B.23C.32D.61.(2023·全国·高一专题练习)已知A ，B ，C ，D 在球O 的表面上，△ABC 为等边三角形且边长为3，AD ⊥平面ABC ，AD =2，则球O 的表面积为()A.4πB.8πC.16πD.32π2.(2020春·天津宁河·高一校考期末)在三棱锥P -ABC 中，AP =2,AB =3,PA ⊥面ABC ，且在△ABC 中，C =60°，则该三棱锥外接球的表面积为()A.20π3B.8πC.10πD.12π3.(2023·全国·高一专题练习)已知A ，B ，C ，D 在球O 的表面上，△ABC 为等边三角形且其面积为334，AD ⊥平面ABC ，AD =2，则球O 的表面积为()A.πB.2πC.4πD.8π4.(2022春·山东聊城·高一山东聊城一中校考阶段练习)在四棱锥P -ABCD 中，PA ⊥平面ABCD ，四边形ABCD 为矩形，BC =2，PC 与平面PAB 所成的角为30o ，则该四棱锥外接球的体积为()A.433π B.43πC.823πD.833π题型四:切瓜模型1(2023·贵州贵阳·校联考模拟预测)在三棱锥A -BCD 中，已知AC ⊥BC ,AC =BC =2,AD =BD =6，且平面ABD ⊥平面ABC ，则三棱锥A -BCD 的外接球表面积为()A.8πB.9πC.10πD.12π1.(2023·四川达州·统考二模)三棱锥A -BCD 的所有顶点都在球O 的表面上，平面ABD ⊥平面BCD ，AB =AD =6，AB ⊥AD ，∠BDC =2∠DBC =60°，则球O 的体积为()A.43πB.32π3C.49π3D.323π2.(2023春·陕西西安·高一长安一中校考期中)在直三棱柱ABC -A 1B 1C 1中，AB ⊥BC ，AB =BC =AA 1=4，点P 为B 1C 1的中点，则四面体PABC 的外接球的体积为()A..41416π B.41413π C.41412π D.4141π3.(2022·高一单元测试)四棱锥P -ABCD 的顶点都在球O 的表面上，△PAD 是等边三角形，底面ABCD 是矩形，平面PAD ⊥平面ABCD ，若AB =2，BC =3，则球O 的表面积为()A.12πB.16πC.20πD.32π4.(2021·高一课时练习)在四棱锥P -ABCD 中，平面PAD ⊥平面ABCD ，且ABCD 为矩形，∠DPA =π2，AD =23，AB =2，PA =PD ，则四棱锥P -ABCD 的外接球的体积为()A.163π B.323π C.643π D.16π5.(2023春·全国·高一专题练习)在四棱锥P-ABCD中，ABCD是边长为2的正方形，AP=PD=10，平面PAD⊥平面ABCD，则四棱锥P-ABCD外接球的表面积为()A.4πB.8πC.136π9D.68π3题型五:斗笠模型1(2023·全国·高一专题练习)正四面体S-ABC内接于一个半径为R的球，则该正四面体的棱长与这个球的半径的比值为()A.64B.33C.263D.31.(2022·高一专题练习)已知正四棱锥P-ABCD(底面四边形ABCD是正方形，顶点P在底面的射影是底面的中心)的各顶点都在同一球面上，底面正方形的边长为10，若该正四棱锥的体积为50 3，则此球的体积为()A.18πB.86πC.36πD.323π2.(2022·全国·高一专题练习)某四棱锥的底面为正方形，顶点在底面的射影为正方形中心，该四棱锥内有一个半径为1的球，则该四棱锥的表面积最小值是()A.16B.8C.32D.243.(2022春·安徽·高三校联考阶段练习)在三棱锥P-ABC中，侧棱PA=PB=PC=10，∠BAC=π4，BC=22，则此三棱锥外接球的表面积为．题型六:矩形模型1(2022春·全国·高一期末)已知三棱锥A-BCD中，CD=22，BC=AC=BD=AD=2，则此几何体外接球的表面积为()A.2π3B.2π C.82π3D.8π1.(2022春·广东惠州·高一校考期中)在矩形ABCD中，AB=6,BC=8，现将△ABC沿对角线AC翻折，得到四面体DABC，则该四面体外接球的体积为()A.1963π B.10003π C.4003π D.5003π2.(2022春·河北沧州·高一校考阶段练习)矩形ABCD中，AB=4,BC=3，沿AC将三角形ABC折起，得到的四面体A-BCD的体积的最大时，则此四面体外接球的表面积值为()A.25πB.30πC.36πD.100π3.(2022春·四川成都·高一统考期末)在矩形ABCD 中，AB =6，AD =8，将△ABC 沿对角线AC 折起，则三棱锥B -ACD 的外接球的表面积为()A.36πB.64πC.100πD.与二面角B -AC -D 的大小有关题型七:折叠模型1(2022春·陕西西安·高一长安一中校考期末)已知菱形ABCD 的边长为3，∠ABC =60°，沿对角线AC 折成一个四面体，使平面ACD 垂直平面ABC ，则经过这个四面体所有顶点的球的体积为()．A.5152π B.6πC.515πD.12π1.已知等边△ABC 的边长为2，将其沿边AB 旋转到如图所示的位置，且二面角C -AB -C 为60°，则三棱锥C -ABC 外接球的半径为2.(2023·广西南宁·统考二模)蹴鞠，又名“蹴球”“蹴圈”等，“蹴”有用脚蹴、踢的含义，鞠最早系外包皮革、内饰米糠的球，因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动，类似今日的足球，现已知某“鞠”的表面上有四个点A ,B ,C ,D 满足AB =BC =CD =DA =DB =433cm ，AC =23cm ，则该“鞠”的表面积为cm 2.3.(2022秋·福建泉州·高三校考开学考试)在三棱锥S -ABC 中，SA =SB =AC =BC =2,SC =1，二面角S -AB -C 的大小为60°，则三棱锥S -ABC 的外接球的表面积为.4.(2022秋·山东德州·高二统考期中)已知在三棱锥中，S -ABC 中，BA ⊥BC ，BA =BC =2，SA =SC =22，二面角B -AC -S 的大小为5π6，则三棱锥S -ABC 的外接球的表面积为()A.56π3B.58π3C.105π4D.124π9题型八:鳄鱼模型1(2022春·四川成都·高一树德中学校考期末)已知在三棱锥S-ABC中，AB⊥BC，AB=BC=2，SA =SC=22，二面角B-AC-S的大小为2π3，则三棱锥S-ABC的外接球的表面积为()A.124π9B.105π4C.105π9D.104π91.(2023春·全国·高一专题练习)如图，在三棱锥P-ABC，△PAC是以AC为斜边的等腰直角三角形，且CB=22，AB=AC=6，二面角P-AC-B的大小为120°，则三棱锥P-ABC的外接球表面积为()A.5103π B.10π C.9π D.4+23π2.(2023·陕西榆林·统考三模)在三棱锥A-BCD中，AB⊥BC,BC⊥CD,CD=2AB=2BC= 4，二面角A-BC-D为60°，则三棱锥A-BCD外接球的表面积为()A.16πB.24πC.18πD.20π3.(2023春·安徽阜阳·高三阜阳市第二中学校考阶段练习)如图1，四边形ABCD中，AB=AD =2，CB=CD=2，AB⊥AD，将△ABD沿BD翻折至△PBD，使二面角P-BD-C的正切值等于2，如图2，四面体PBCD的四个顶点都在同一个球面上，则该球的表面积为()A.4πB.6πC.8πD.9π4.(2023·江西南昌·校联考模拟预测)在平面四边形ABCD中，AD=CD=3，∠ADC=∠ACB =90°，∠ABC=60°，现将△ADC沿着AC折起，得到三棱锥D-ABC，若二面角D-AC-B的平面角为135°，则三棱锥D-ABC的外接球表面积为.5.(2023春·广东广州·高三统考阶段练习)在三棱锥P-ABC中，△ABC为等腰直角三角形，AB=AC=2，△PAC为正三角形，且二面角P-AC-B的平面角为π6，则三棱锥P-ABC的外接球表面积为．。

内接球和外接球半径计算公式
内接球和外接球是几何学中的概念，它们分别是指一个多面体内部最大的（最小的）球和一个多面体外部最小的（最大的）球。

下面是内接球和外接球的半径计算公式。

（以下解释中，我们以正四面体为例）
内接球半径计算公式：
正四面体的内接球是四面体内部最大的球，它的半径可以通过正四面体的棱长计算得出。

设正四面体的棱长为a，则正四面体的内接球半径R为：
R = a / (2√3)
其中√3表示根号下3，也就是3的平方根。

该公式适用于所有正多面体内接球的半径计算。

外接球半径计算公式：
正四面体的外接球是四面体外部最小的球，它的半径可以通过正四面体的边长计算得出。

设正四面体的边长为a，则正四面体的外接球半径r为：
r = a / (2√6)
其中√6表示根号下6，也就是6的平方根。

该公式同样适用于所有正多面体外接球的半径计算。

需要注意的是，以上公式仅适用于正多面体，对于其他不规则多面体，内接球和外接球的半径计算需要用到其他方法。

空间几何体的表面积与体积公式大全一、全（表）面积（含侧面积）1、①棱柱②圆柱2、①②3、①②4、①球：②③二、1、①棱柱②圆柱2、①棱锥②圆锥3、①棱台②圆台4、①球：②③三、1、2、则+=即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和 3、台体体积公式公式：)(31S SS S h V 下下上上台++=证明：如图过台体的上下两底面中心连线的纵切面为梯形ABCD 。

延长两侧棱相交于一点P 。

则∴V 即：)(33)(31S SS S h h S S S hS V 下下上上下上下上台++=++=∴)(31S S S S h V 下下上上台++=4、球体体积公式推导分析：将半球平行分成相同高度的若干层（层n ），n 越大，每一层越近似于圆柱，+∞→n 时，每一层都可以看作是一个圆柱。

这些圆柱的高为nr，则：每个圆柱的体积h S V i i ==nrr i 2π……=2r nr ⨯π=[3r n n π=[3r n n π当→n ∴V 半球5、 ∴S =球6、（1则其体积为：a V 3=正方体四个角上切下的每一个三棱锥体积为：中间剩下的正四面体的体积为：a a a a hSV 322231]60sin 21[3131)32232()2()2(=-⨯︒⨯⨯⨯==⨯⨯正三棱锥这样一个即：61（2 (a)(b)(c)(d)(e)（3（a ） 正方体内切球直径=正方体棱长（b ） 正方体内切球与正四面体的四条棱相切。

（c ） 与正四面体四条棱相切的球半径=正方体棱长的一半 （d ） 设正四面体棱长为a ，则与其棱都相切的球半径为r 1有：aar 422211=⨯= 7、利用祖暅原理推导球体体积。

构造一个几何体，使其截面与半球截面处处相等，根据祖暅原理可得两物体体积相等。

证明：作如下构造：在底面半径和高都是r 的圆柱内挖去一个与圆柱等底等高的圆锥。

如图：R ，∴S 1π=即：S 1 8、 正方体与球（1） 正方体的内切球正方体的棱长=a 球体的直径d （2） 正方体的外接球正方体的体对角线=a 3球体的直径d（3） 规律：①正方体的内切球与外接球的球心为同一点； ②正方体的内切球与外接球的球心在体对角线上； ③正四面体的内切球与外接球的的半径之比为：3:1 ④正四面体内切球与外接球体积之比为：1：339（∴a h r 12641==即：a a r V 33321663434)126(πππ===球∴π3:18=V V 球正四机体： （2）正四面体的外接球 外接球的半径=)2332(224343a a⨯-⨯=⨯高=a 46 ∴2:33122:86:33ππ==aaV V 正四面体球 （310、 （1 球体直径、圆柱的高、圆柱底面直径构成直角三角形。

例1。

若棱长为3的正方体的顶点都在同一球面上，求该球的表面积和体积。

分析：①334R V π=球（R 为球半径） ②24R S π=球 （R 为球半径) 需要求出半径。

正方体的棱长为a ，则:正方体的内切球、棱切球、外接球半径分别为:a 21，a 22，a 23。

变式：一个长方体的各顶点均在同一球面上，且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为。

【解析】关键是求出球的半径,因为长方体内接于球，所以它的体对角线正好为球的直径。

长方体体对角线长为14,故球的表面积为14π。

变式：（已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积为( ）.A 。

16π B 。

20π C 。

24π D 。

32π解题关键：通过多面体的一条侧棱和球心，或接点作出截面图。

棱锥与球例题：求棱长为1的正四面体ABCD 的外接球体积. 分析:作出合适的球的轴截面图，找准球心位置，构造三角形求解半径。

常用结论：正四面体外接球的球心在高线上，半径是正四面体高的43解法一、 解法二、如何求正四面体的外接球半径法1.补成正方体法2.勾股定理法例题：求棱长为a 的正四面体的内切球半径。

分析：并非所有多面体都有内切球，正多面体存在内切球，且正多面体的中心为内切球球心。

常用结论：正多面体内切球半径是高的41；31⋅⋅=内切表多R S V 1、正三棱锥的高为1，底面边长为62，内有一个球与它的四个面都相切．求：（1）外接球的表面积和体积;(2）内切球的表面积与体积．设正四面体的棱长为a ，则：正四面体的内切球、棱切球、外接球半径分别为: a 126、a 42、a 46. 构造长方体变式 P 、A 、B 、C 是球O 面上的四个点,PA 、PB 、PC 两两垂直，PA=PB=PC=a,求这个球的体积。

例 已知点A 、B 、C 、D 在同一个球面上,B BCD A ⊥平面,BC DC ⊥,若6,AC=213,AD=8AB =，则B 、C 两点间的球面距离是____。

高一数学（必修2）百所名校速递分项汇编专题04 空间几何体的外接球与内切球一、选择题1．【2017-2018学年辽宁省抚顺二中高一（上）期末】在三棱锥中，，，则该三棱锥的外接球的表面积为A．B．C．D．【答案】D∴外接球的表面积为S=4π×DG2=43π．故选：D．2．【黑龙江省实验中学2017-2018学年高一下学期期末】四面体中，，，，则此四面体外接球的表面积为A．B．C．D．【答案】A【解析】由题意，△BCD中，CB=DB=2，∠CBD=60°，可知△BCD是等边三角形，BF=∴△BCD的外接圆半径r==BE，FE=∵∠ABC=∠ABD=60°，可得AD=AC=，可得AF=∴AF⊥FB∴AF⊥BCD，∴四面体A﹣BCD高为AF=．设：外接球R，O为球心，OE=m可得：r2+m2=R2……①，（）2+EF2=R2……②由①②解得：R=．四面体外接球的表面积：S=4πR2=．故选：A．3．【四川省泸州市泸化中学2017-2018学年高一5月月考】三棱柱中，，、、，则该三棱柱的外接球的表面积为( )A．4πB．6πC．8πD．10π【答案】C【解析】由题意得三棱柱为直三棱柱，且正好是长方体切出的一半，所以外接球半径为，，选C.4．【四川省泸州市泸化中学2017-2018学年高一5月月考】三棱柱中，，、、，则该三棱柱的外接球的体积( )A．B．C．D．【答案】B【解析】为直角三角形，斜边为，球心与该斜边的中点的连线垂直于平面，故球的半径，故球的体积为，故选B.5．【2018年人教A版数学必修二】棱长分别为2、、的长方体的外接球的表面积为（）A．B．C．D．【答案】B【解析】设长方体的外接球半径为，由题意可知：，则：，该长方体的外接球的表面积为.本题选择B选项.6．【浙江省嘉兴市第一中学2018-2019学年高二上学期期中】在四面体中，，二面角的余弦值是，则该四面体外接球的表面积是（）A．B．C．D．【答案】C【解析】取中点，连接，，平面，为二面角，在中，，，取等边的中心，作平面，过作平面，（交于），因为二面角的余弦值是，，，点为四面体的外接球球心，其半径为，表面积为，故选C.7．【安徽省黄山市屯溪第一中学2018-2019学年高二上学期期中考试】三棱锥P ­ABC中，PA⊥平面ABC，Q是BC边上的一个动点，且直线PQ与面ABC所成角的最大值为则该三棱锥外接球的表面积为( )A．B．C．D．【答案】C【解析】三棱锥P﹣ABC中，PA⊥平面ABC，直线PQ与平面ABC所成角为θ，如图所示；则sinθ==，且sinθ的最大值是，∴（PQ）min=2，∴AQ的最小值是，即A到BC的距离为，∴AQ⊥BC，∵AB=2，在Rt△ABQ中可得，即可得BC=6；取△ABC的外接圆圆心为O′，作OO′∥PA，∴=2r，解得r=2；∴O′A=2，取H为PA的中点，∴OH=O′A=2，PH=，由勾股定理得OP=R==，∴三棱锥P﹣ABC的外接球的表面积是S=4πR2=4×=57π．故答案为：C8．【广东省佛山市第一中学2018-2019学年高二上学期第一次段考】三棱锥的三视图如图所示，则该三棱锥外接球的体积为（）A．B．C．D．【答案】A则球的半径R为，所以球的体积为.本题选择A选项.9．【内蒙古鄂尔多斯市第一中学2018-2019学年高二上学期期中考试】已知一个三棱锥的三视图如图所示，其中俯视图是等腰直角三角形，则该三棱锥的外接球体积为（）A．B．C．D．【答案】C【解析】由三视图知几何体是一个侧棱与底面垂直的三棱锥，底面是斜边上的高为的等腰直角三角形，与底面垂直的侧面是个等腰三角形，底边长为，高为，故三棱锥的外接球与以棱长为的正方体的外接球相同，其直径为，半径为三棱锥的外接球体积为故选10．【四川省遂宁市2017-2018学年高二上学期教学水平监测】已知长方体中，,则长方体外接球的表面积为A．B．C．D．【答案】C11．【山西省朔州市应县第一中学2018-2019学年高二上学期期中考试】在三棱锥中，三侧面两两互相垂直，侧面的面积分别为，则此三棱锥的外接球的表面积为（）A．B．C．D．【答案】A【解析】由题意得，侧棱两两垂直，设，则都是以为直角顶点的直角三角形，得，解之得，即，侧棱两两垂直，以为过同一顶点的三条棱作长方体，该长方体的对角线长为，恰好等于三棱锥外接球的直径，由此可得外接球的半径，可得此三棱锥外接球表面积为，故选A.12．【重庆市铜梁一中2018-2019学年高二10月月考】棱长分别为2，，的长方体的外接球的表面积为( )A．B．C．D．【答案】B13．【黑龙江省大庆中学2018-2019学年高二10月月考】长方体的三个相邻面的面积分别为2，3，6，则该长方体外接球的表面积为A．B．C．D．【答案】C【解析】设长方体的棱长分别为，则，所以，于是，设球的半径为，则，所以这个球面的表面积为．本题选择C选项.14．【重庆市万州三中2018-2019学年高二上学期第一次月考】已知一个表面积为44的长方体,且它的长、宽、高的比为3 21,则此长方体的外接球的体积为（）A．B．C．D．【答案】D【解析】设长方体的长、宽、高分别为，则，解得，即，即长方体的棱长分别为，所以长方体的对角线长为，所以球的半径为，即，所以球的体积为，故选D.二、填空题15．【江西省赣州市十四县（市）2018-2019学年高二上学期期中联考】在三棱锥中，，，，，，则三棱锥的外接球的表面积为_______________．【答案】【解析】由题意，在三棱锥中，平面，以为长宽高构建长方体，则长方体的外接球是三棱锥的外接球，所以三棱锥的外接球的半径为，所以三棱锥的外接球的表面积为.16．【贵州省遵义市南白中学2018-2019学年高二上学期第一次月考】正四面体内切球半径与外接球半径之比为__________．【答案】【解析】由正四面体的对称性可得正四面体的内切球与外接球球心重合且在正四面体的高上，设正四面体的内切球与外接球球心为，正四面体的高为，将正四面体分成以为顶点，以四面体的四个面为底面的四个正四棱锥，这四个正四棱锥的底面积是正四面体的底面积，高为内切球的半径，设四面体外接球半径为，则，由四个正四棱锥的体积和等于正四面体的体积可得，故答案为.17．【山西省长治市第二中学2017-2018学年高二下学期期末考试】已知三棱锥中，,，则三棱锥的外接球的表面积为________________.【答案】【解析】如图：∵AD=2，AB=1，BD=，满足AD2+AB2=SD2∴AD⊥AB，又AD⊥BC，BC∩AB=B，∴AD⊥平面ABC，∵AB=BC=1，AC=，∴AB⊥BC，∴BC⊥平面DAB，∴CD是三棱锥的外接球的直径，∵AD=2，AC=，∴CD=，∴三棱锥的外接球的表面积为4π（）2=6π．故答案为：6π18．【高二人教版必修2 第一章本章能力测评】已知正六棱柱的底面边长为4，高为6，则它的外接球的表面积为__________.【答案】【解析】根据正六棱柱的对称性可得，正六棱柱的体对角线就是球的直径，由高为，底面边长为，结合正六边形的性质，可得，即，所以外接球的表面积为，故答案为．19．【江西省南昌市第十中学2017-2018学年高二下学期期末考试】在三棱锥中，，，，，且三棱锥的体积为，则该三棱锥的外接球半径是_________【答案】3【解析】取的中点，连接，因为，，，，所以，且，所以平面，且是外接球的直径，设,所以为正三角形，则,则，解得．20．【山东省潍坊市2017-2018学年高二5月份统一检测】如图，在三棱锥中，平面，,,，则三棱锥外接球的表面积为__________．【答案】。

多面体的外接球专题模型总结终极版题型一、长方体的外接球1.长方体外接球半径R=√a2+b2+c22a2.正方体外接球半径R=√323.长方体外接球的切割体（从长方体八个顶点中任取四个顶点）（1）三条侧棱两两垂直的三棱锥简称墙角型（2）一条侧棱垂直于底面，底面是直角三角形的三棱锥（双垂直）（3）各棱相等的三棱锥（正四面体）（4）对棱相等的三棱锥专题练习例1.在三棱锥BCD A −中，侧棱AB 、AC 、AD 两两垂直，ABC ∆、ACD ∆、ADB ∆的面积分别为22、32、62，则三棱锥BCD A −的外接球的体积为（ ）A ．6πB ．26πC ．36πD ．46π例2. 如图所示，已知球O 的面上有四点A 、B 、C 、D ，2===⊥⊥BC AB DA BC AB ABC DA ，，面,则球O 的体积等于 ．例 3.已知三棱锥BCD A −的所有棱长都为2，则该三棱锥外接球的体积为_________例4.四面体BCD A −中，5==CD AB ，34==BD AC ，41==BC AD ，则四面体BCD A −外接球的表面积为（ ）A ．π50B ．π100C ．π150D ．π200变式练习1.在三棱锥ABC P −中，4==BC PA ，5==AC PB ，11==AB PC ，则三棱锥ABC P −的外接球的表面积为（ ）A ．π8B ．π12C ．π26D ．π242.已知三棱锥ABC P −的顶点都在球O 的表面上，若PA ，PB ，PC 两两互相垂直，且2===PC PB PA ，则球O 的体积为（ ） A ．π312 B ．π28 C ．π34 D ．π43.《九章算术》中，将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥ABC P −为鳖臑，⊥PA 平面ABC ，2==AB PA ，4=AC ，三棱锥ABC P −的四个顶点都在球O 的球面上，则球O 的表面积为（ ） A ．π8 B ．π12 C ．π20 D ．π244．已知三棱锥ABC S −的各顶点都在一个半径为r 的球面上，且1===SC SB SA ，2===AC BC AB ，则球的表面积为（ ）A ．π12B ．π8C ．π4D ．π35．已知三棱锥ABC P −的各顶点都在同一球面上，且⊥PA 平面ABC ，若该棱锥的体积为332，2=AB ，1=AC ，︒=∠60BAC ，则此球的表面积等于（ ） A ．π5 B ．π8 C ．π16 D ．π206．三棱锥ABC P −的四个顶点都在球O 的球面上，已知PA ，PB ，PC 两两垂直，1=PA ，4=+PC PB ，当三棱锥的体积最大时，球O 的体积为（ ） A ．π36 B ．π9C ．29π D ．49π7．如图所示，平面四边形ABCD 中，2===CD AD AB ，22=BD ，CD BD ⊥，将其沿对角线BD 折成四面体ABCD ，使平面ABD ⊥平面BCD ，若四面体ABCD 的顶点在同一个球面上，则该球的体积为（ ）A ．π328B ．π24C ．π34题型二、上下对称几何体外接球（直棱柱）直棱柱外接球半径R=√r 2+h 24,其中r 是底面外接圆半径，h 是直棱柱的高 r =a 2sinA(正弦定理)例1.设三棱柱的侧棱垂直于底面，所有棱长都为a ，顶点都在一个球面上，则该球的表面积为（ ）A.πa 2B.73.πa 2 C. 113πa 2 D. 5πa 2例2.如图，网格纸上小正方形的边长为 1，粗线画出的是某几何体的三视图，则该几何体的外接球的表面积为 ．例3.如图，三棱锥的所有顶点都在一个球面上，在ABC ∆中，3=AB ，︒=∠60ACB ，︒=∠90BCD ，CD AB ⊥，22=CD ，则该球的体积为 ．例4. 如图是某几何体的三视图，正视图是等边三角形，侧视图和俯视图为直角三角形，则该几何体外接球的表面积为（ ） A ．320πB ．π8C ．π9D ．319π例5. 如图，某三棱锥的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和等边三角形，若该三棱锥的顶点都在同一球面上，则该球的表面积为（ ） A ．π27 B ．π48 C ．π64D ．π81变式练习1.已知A ，B ，C ，D 是同一球面上的四个点，其中ABC ∆是正三角形，⊥AD 平面ABC ，62==AB AD ，则该球的体积为（ ） A ．π332 B ．π48 C ．π24 D ．π162.四面体ABCD 的四个顶点都在球O 的表面上，⊥AB 平面BCD ，三角形BCD 是边长为3的等边三角形，若4=AB ，则球O 的表面积为（ ） A ．π36B ．π28C ．π16D ．π43.已知一个三棱锥的三视图如下图所示，其中俯视图是顶角为32π的等腰三角形，则该三棱锥外接球的表面积为（ ） A ．π20B ．π17C ．π16D ．π8题型三、正N 棱锥外接球正N 棱锥外接球半径R=l 22ℎ,其中l 是侧棱长度，h 是正棱锥的高例1. 正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（ ） A.81π4B. 16πC. 9πD.27π4题型四、等腰三角形底边与一直角三角形斜边构成二面角的四面体如上图中，ABC △为等腰三角形，且AC AB =，DBC △是以BC 为斜边的△Rt ，D BC A −−二面角为α，令ABC △的外接圆半径为2r ，BC 边上的高为21h AO =，12r BC =，F 为ABC △的外心，则根据剖面图可知，外接球半径R 满足以下恒等式()21222221212sin r r h R E O OO OE +⎪⎭⎫ ⎝⎛−==+=α．例1在四面体ABC S −中，BC AB ⊥，2==BC AB ，SAC △为等边三角形，二面角B AC S −−的余弦值为33−，则四面体ABC S −的外接球表面积为 ．CB图3图4图5作二面角剖面⇒例2.在四面体ABCD 中，AB=AD=2,∠BAD =60。

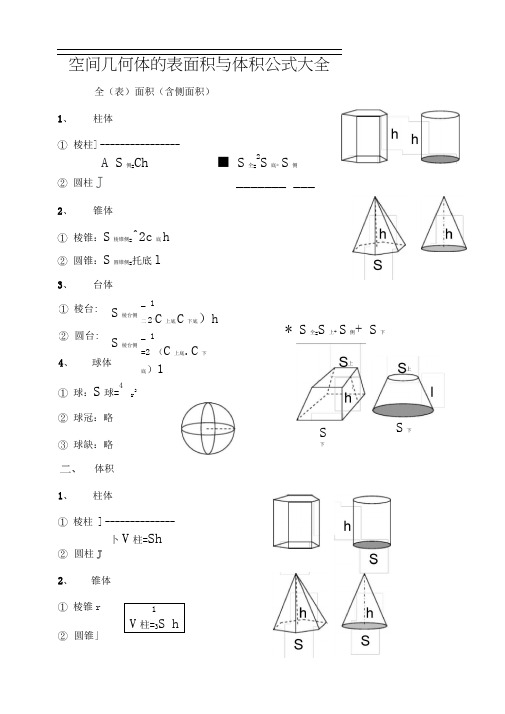
空间几何体的表面积与体积公式大全全（表）面积（含侧面积）1、柱体①棱柱]----------------A S侧=Ch ■ S全=2S底* S侧②圆柱J _______ ___2、锥体①棱锥：S棱锥侧=^2c底h②圆锥：S圆锥侧=托底l3、台体①棱台:②圆台:S棱台侧S棱台侧_ 1二2（C上底C下底）h_ 1=2 （C上底.C下底）1* S全=S上+ S侧+ S下4、球体①球：S球=4r2②球冠：略③球缺：略S下S下体积1、柱体①棱柱]--------------卜V柱=Sh②圆柱J2、锥体①棱锥r②圆锥」1V柱=3S h3、台体1①棱台］V台=gh （S上NS上S^ +S下）②圆台J V圆台=3兀h （r上+Q r上r下+ r下）4、球体①球：V球=4二r'②球冠：略③球缺：略说明：棱锥、棱台计算侧面积时使用侧面的斜高h计算；而圆锥、圆台的侧面积计算时使用母线I计算。

三、拓展提高1、祖暅原理：（祖暅：祖冲之的儿子）夹在两个平行平面间的两个几何体，如果它们在任意高度上的平行截面面积都相等，那么这两个几何体的体积相等。

最早推导出球体体积的祖冲之父子便是运用这个原理实现的2、阿基米德原理：（圆柱容球）圆柱容球原理：在一个高和底面直径都是2r的圆柱形容器内装一个最大的球体，则该球体的全面积等于圆柱的侧面积，体积等于圆柱体积的-。

3分析：圆柱体积：V圆柱=Sh =（二「2）2r=2^r'圆柱侧面积：S圆柱侧=C h =（2 r） 2r = 4二「因此：球体体积：V球=2 2二J=4二r33 3球体表面积：S球=4 r2即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和3、台体体积公式公式：V台=1h （S上+ S下）证明：如图过台体的上下两底面中心连线的纵切面为梯形ABCD 延长两侧棱相交于一点P设台体上底面积为S上,下底面积为S下P 高为h。

易知：PDC s .>PAB ,设PE = h i，则PF =h i h由相似三角形的性质得:CD PEAB PFA整理得：h 1 ： =S上hPS 下-VS上又因为台体的体积=大锥体体积一小锥体体积1 11 1 二V台=3S 下(h 1h K3S 上h^3h 1(S下一S上) 下h代入：h= i S 上芬得: V台=3胪L(S下—S"3S 下hJS下3*SrS31 ___ I ------ ------ 1即: V 台=3 S上h (S下S上)3S下人二 V 台=3h （S 上S 上S 下S下）球体体积公式推导即：ShiS 下-h lh （相似比等于面积比的算术平方根）1 ______________=3h (S上S 上S 下S下)4、分析：将半球平行分成相同高度的若干层（ n 层），n 越大，每一层越近似于圆柱，n “ •「时，每一层都可以看作是个圆柱。

外接球半径求法
外接球半径是指一个几何体的外接球的半径，它可以通过该几何体的某些特征来求解。

以下是几种常见的求解方法：
1. 对于正四面体、正六面体、正八面体等正多面体，其外接球半径可以直接通过公式计算得出。

例如，对于正四面体，其外接球半径R等于边长a乘以根号2除以4，即R=a√2/4。

2. 对于任意三角形ABC，其外接圆的半径R可以通过三角形的三边长度a、b、c来计算。

具体而言，可以使用海伦公式计算三角形的面积S，然后通过公式R=abc/4S求解外接圆半径R。

其中a、b、c分别为三角形的三边长度。

3. 对于任意四面体ABCD，其外接球半径可以通过四个顶点之间的距离来计算。

具体而言，假设四个顶点分别为A、B、C和D，则可以先计算出任意两个顶点之间的距离（如AB、AC等），然后使用这些距离来计算四面体各个侧面上三角形的面积，并使用这些面积来计算四面体总表面积S。

最后使用公式R=abc/4S求解出外接球半径R。

以上是几种常见的求解外接球半径的方法，不同的几何体可能需要使
用不同的方法来求解。

在实际应用中，可以根据具体情况选择合适的方法来计算外接球半径。

9.3 空间几何外接球和内切球一．公式1.球的表面积：S ＝4πR 22.球的体积：V ＝43πR 3二．概念1.2.考向一 长（正）方体外接球【例1】若一个长、宽、高分别为4，3，2的长方体的每个顶点都在球O 的表面上，则此球的表面积为__________． 【答案】29π【解析】因为长方体的顶点都在球上，所以长方体为球的内接长方体，其体对角线l ==为球的直径，所以球的表面积为24292l S ππ⎛⎫== ⎪⎝⎭，故填29π.【举一反三】1.已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为________． 【答案】92π【解析】设正方体棱长为a ，则6a 2＝18，∴a ＝ 3.设球的半径为R ，则由题意知2R ＝a 2＋a 2＋a 2＝3，∴R ＝32.故球的体积V ＝43πR 3＝43π×⎝ ⎛⎭⎪⎫323＝92π.2.如图是一个空间几何体的三视图，则该几何体的外接球的表面积是________.【答案】48π【解析】由几何体的三视图可得该几何体是直三棱柱ABC A B C '-''，如图所示：其中，三角形ABC 是腰长为4的直角三角形，侧面ACC A ''是边长为4的正方形，则该几何体的外接球的半径为2=∴该几何体的外接球的表面积为(2448ππ⨯=.故答案为48π.考向二 棱柱的外接球【例2】直三棱柱AAA −A ′A ′A ′的所有棱长均为2√3，则此三棱柱的外接球的表面积为（ ） A ．12π B ．16π C ．28π D ．36π【答案】C【解析】由直三棱柱的底面边长为2√3，得底面所在平面截其外接球所成的圆O 的半径r =2， 又由直三棱柱的侧棱长为2√3，则球心到圆O 的球心距d =√3，根据球心距，截面圆半径，球半径构成直角三角形，满足勾股定理，我们易得球半径R 满足：R 2＝r 2+d 2=7，∴外接球的表面积S ＝4πR 2=28π．故选：C ．【举一反三】1. 设直三棱柱ABC-A 1B 1C 1的所有顶点都在一个球面上，且球的表面积是40π，AB=AC=AA 1，∠BAC=120°，则此直三棱柱的高是________.【答案】【解析】设三角形BAC 边长为a ，则三角形BAC外接圆半径为122sin 3a π⋅=，因为2244010R R ππ=∴=所以22210,2a R a a ⎛⎫=+== ⎪⎝⎭即直三棱柱的高是.2.直三棱柱AAA −A 1A 1A 1中，已知AA ⊥AA ，AA =3，AA =4，AA 1=5，若三棱柱的所有顶点都在同一球面上，则该球的表面积为__________． 【答案】50π【解析】AAA −A 1A 1A 1是直三棱柱，∴A 1A ⊥AA ，又三棱柱的所有顶点都在同一球面上，A 1A 是球的直径，∴A =A 1A2；∵AA ⊥AA ，∴AA =√32+42=5 ，∴A 1A 2=52+52=50 ；故该球的表面积为A =4AA 2=4A (A 1A 2)2=AA 1A 2=50A考向三 棱锥的外接球类型一：正棱锥型【例3-1】已知正四棱锥P ABCD -的各顶点都在同一球面上，体积为2，则此球的体积为 （ ）A.1243π B. 62581π C. 50081π D. 2569π【答案】C【解析】如图所示，设底面正方形ABCD 的中心为O '，正四棱锥P ABCD -的外接球的球心为O1O D ∴'=正四棱锥的体积为22123P ABCDV PO -⨯⨯'∴==，解得3PO '=3OO PO PO R ∴-'=='-在 Rt OO D '中，由勾股定理可得： 222OO O D OD '+='即()22231R R -+=，解得53R =2344550033381V R πππ⎛⎫∴==⨯= ⎪⎝⎭球故选C【举一反三】1.已知正四棱锥P ABCD -的各条棱长均为2，则其外接球的表面积为( ) A. 4π B. 6π C. 8π D. 16π 【答案】C【解析】设点P 在底面ABCD 的投影点为O ',则12,2AO AC PA PO ==''=⊥平面ABCD,故PO =='而底面ABCD 所在截面圆的半径AO '=故该截面圆即为过球心的圆，则球的半径,故外接球的表面积为248,S R ππ==故选C.2．如图，正三棱锥D ABC -的四个顶点均在球O 的球面上，底面正三角形的边长为3，侧棱长为则球O 的表面积是( )A ．4πB ．323πC ．16πD ．36π【答案】C【解析】如图，设OM x =，OB OD r ==，3AB =，BM ∴=DB =3DM ∴=，在Rt OMB ∆中，22(3)3x x -=+，得：1x =，2r ∴=，16O S π∴=球，故选：C ．类型二：侧棱垂直底面型【例3-2】在三棱锥P ABC -中， 2AP =， AB = PA ⊥面ABC ，且在三角形ABC 中，有()cos 2cos c B a b C=-（其中,,a b c 为ABC ∆的内角,,A B C 所对的边），则该三棱锥外接球的表面积为（ ） A. 40π B. 20π C. 12π D.203π【答案】A【解析】设该三棱锥外接球的半径为R .在三角形ABC 中， ()cos 2cos c B a b C =-（其中,,a b c 为ABC ∆的内角,,A B C 所对的边）. ∴cos cos 2cos c B b C a C +=∴根据正弦定理可得sin cos sin cos 2sin cos C B B C A C +=，即()sin 2sin cos B C A C +=.∵sin 0A ≠∴1cos 2C =∵()0,C π∈∴3C π= ∴由正弦定理，332sin3r π=，得三角形ABC 的外接圆的半径为3r =.∵PA ⊥面ABC∴()()()22222PA r R +=∴210R =∴该三棱锥外接球的表面积为2440S R ππ==故选A.【举一反三】1.已知几何体的三视图如图所示，则该几何体的外接球的表面积为（ ）A.214π3 B. 127π3 C. 115π3 D. 124π3【答案】D【解析】根据几何体的三视图可知，该几何体为三棱锥A −AAA 其中AA =AA =2，AA =4且AA ⊥底面AAA ，∠AAA =120° 根据余弦定理可知：AA 2−AA 2+AA 2−2AA ∙AA ∙AAA 120°=42+22−2×4×2×(−12)=28可知AA =2√7根据正弦定理可知∆AAA 外接圆直径2A =AAAAA ∠AAA=2√7AAA 120°=4√7√3∴A =2√213，如图，设三棱锥外接球的半径为A ，球心为A ，过球心A 向AA 作垂线，则垂足A 为AA 的中点AA =1，在AA ∆AAA 中，A 2=AA 2=(2√213)2+1=313∴外接球的表面积A =4AA 3=4A ×313=124A3故选A2.已知三棱锥S ABC －中， SA ⊥平面ABC ，且30ACB ∠=︒， 21AC AB SA ===.则该三棱锥的外接球的体积为( )B. 13π 【答案】D【解析】∵30ACB ∠=︒， 2AC AB ==ABC 是以AC 为斜边的直角三角形其外接圆半径2ACr ==，则三棱锥外接球即为以ABC C 为底面，以SA 为高的三棱柱的外接球∴三棱锥外接球的半径R 满足R ==故三棱锥外接球的体积34.3V R π== 故选D. 类型三：侧面垂直与底面型【例3】已知四棱锥A −AAAA 的三视图如图所示，则四棱锥A −AAAA 外接球的表面积是（ ）A. 20AB. 101A5C. 25AD. 22A【答案】B【解析】由三视图得，几何体是一个四棱锥A-BCDE,底面ABCD是矩形，侧面ABE⊥底面BCDE.如图所示，矩形ABCD的中心为M,球心为O,F为BE中点，OG⊥AF.设OM=x,由题得AA=√5,在直角△OME中，A2+5=A2(1)，又MF=OG=1,AF=√32−22=√5,AA=√A2−1,AA=A,∴√A2−1+A=√5(2)，解（1）（2）得A2=10120,∴A=4AA2=1015A.故选B.【举一反三】1.《九章算术》是我国古代数学名著，它在几何学中的研究比西方早一千多年，其中有很多对几何体外接球的研究，如下图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的外接球的表面积是（）A. 81AB. 33AC. 56AD. 41A 【答案】D【解析】由三视图可得，该几何体是一个如图所示的四棱锥A −AAAA ，其中AAAA 是边长为4的正方形，平面AAA ⊥平面AAAA ．设A 为AA 的中点，A 为正方形AAAA 的中心，A 为四棱锥外接球的球心，A 1为AAAA 外接圆的圆心，则球心A 为过点A 且与平面AAAA 垂直的直线与过A 1且与平面AAA 垂直的直线的交点． 由于AAAA 为钝角三角形，故A 1在AAAA 的外部，从而球心A 与点P 在平面AAAA 的两侧． 由题意得AA =1,AA =A 1A ,AA 1=AA ， 设球半径为A ，则A 2=AA 2+AA 2=AA 2+A 1A 2, 即AA 2+(2√2)2=22+(1+AA )2，解得AA =32， ∴A 2=(32)2+(2√2)2=414， ∴A 球表=4AA 2=41A ．选D ．2．已知如图所示的三棱锥D ABC -的四个顶点均在球O 的球面上，ABC ∆和DBC ∆所在平面相互垂直，3AB =，AC =BC CD BD ===O 的表面积为( )A ．4πB ．12πC ．16πD ．36π【答案】C【解析】3AB =，AC =BC =222AB AC BC ∴+=，AC AB ∴⊥，ABC ∴∆ ABC ∆和DBC ∆所在平面相互垂直，∴球心在BC 边的高上，设球心到平面ABC 的距离为h ，则2223()2h R h +==， 1h ∴=，2R =，∴球O 的表面积为2416R ππ=．故选：C ．3．三棱锥P ABC -的底面是等腰三角形，120C ∠=︒，侧面是等边三角形且与底面ABC 垂直，2AC =，则该三棱锥的外接球表面积为( ) A ．12π B ．20πC ．32πD ．100π【答案】B【解析】 如图， 在等腰三角形ABC 中， 由120C ∠=︒，得30ABC ∠=︒， 又2AC =，设G 为三角形ABC 外接圆的圆心， 则22sin sin 30AC CG ABC ==∠︒，2CG ∴=．再设CG 交AB 于D ，可得1CD =，AB =1DG =． 在等边三角形PAB 中， 设其外心为H ， 则223BH PH PD ===． 过G 作平面ABC 的垂线， 过H 作平面PAB 的垂线， 两垂线相交于O ，则O 为该三棱锥的外接球的球心， 则半径R OB ===∴该三棱锥的外接球的表面积为2420ππ⨯=．故选：B ．类型四：棱长即为直径【例3-4】已知底面边长为√2，各侧面均为直角三角形的正三棱锥A −AAA 的四个顶点都在同一球面上，则此球的表面积为（ ）A. 3AB. 2AC. 43A D. 4A 【答案】A【解析】由题意得正三棱锥侧棱长为1，将三棱锥补成一个正方体（棱长为1），则正方体外接球为正三棱锥外接球，所以球的直径为√1+1+1=√3，故其表面积为A =4×A ×(√32)2=3A ．选A ．【举一反三】1．已知三棱锥P ABC -的所有顶点都在球O 的球面上，PC 是球O 的直径．若平面PCA ⊥平面PCB ，PA AC =，PB BC =，三棱锥P ABC -的体积为a ，则球O 的体积为( )A ．2a πB ．4a πC ．23a πD ．43a π【答案】B【解析】如下图所示，设球O 的半径为R ，由于PC 是球O 的直径，则PAC ∠和PBC ∠都是直角，由于PA AC =，PB BC =，所以，PAC ∆和PBC ∆是两个公共斜边PC 的等腰直角三角形，且PBC ∆的面积为212PBC S PC OB R ∆==， PA AC =，O 为PC 的中点，则OA PC ⊥，平面PAC ⊥平面PBC ，平面PAC ⋂平面PBC PC =，OA ⊂平面PAC ，所以，OA ⊥平面PBC ， 所以，三棱锥P ABC -的体积为23111333PBC OA S R R R a ∆⨯⨯=⨯==，因此，球O 的体积为33414433R R a πππ=⨯=，故选：B ．考向四 墙角型【例4】某几何体的三视图如图所示，则该几何体的外接球的体积是（ ）A B ．2 C ．3π D ．【答案】B【解析】根据几何体的三视图，该几何体是由一个正方体切去一个正方体的一角得到的．故：该几何体的外接球为正方体的外接球，所以：球的半径2r ==则：343V π=⋅⋅=⎝⎭.故选：B ．【举一反三】1.已知四面体AAAA 的四个面都为直角三角形，且AA ⊥平面AAA ，AA =AA =AA =2，若该四面体的四个顶点都在球A 的表面上，则球A 的表面积为（ ） A ．3AB ．2√3AC ．4√3AD ．12A【答案】D【解析】∵AA =AA =2且AAAA 为直角三角形 ∴AA ⊥AA 又AA ⊥平面AAA ，AA ⊂平面AAA ∴AA ⊥AA ∴AA ⊥平面AAA 由此可将四面体AAAA 放入边长为2的正方体中，如下图所示：∴正方体的外接球即为该四面体的外接球A正方体外接球半径为体对角线的一半，即A =12⋅√22+22+22=√3 ∴球A 的表面积：A =4AA 2=12A 本题正确选项：A2．已知一个棱长为2的正方体被两个平面所截得的几何体的三视图如图所示，则该几何体外接球的表面积是( )A ．24πB ．20πC ．16πD ．12π【答案】D【解析】该几何体是把正方体1AC 截去两个四面体111AA B D 与111CC B D ， 其外接球即为正方体1AC 的外接球，由1AC ==∴外接球的半径R =∴该几何体外接球的表面积是2412ππ⨯=．故选：D ．3．在三棱锥P 一ABC 中，1PA PB PC ===，PA 、PB 、PC 两两垂直，则三棱锥P ABC -的外接球的表面积为( ) A ．12π B ．6πC ．4πD ．3π【答案】A 【解析】在三棱锥P 一ABC 中，1PA PB PC ===，PA 、PB 、PC 两两垂直，∴以PA 、PB 、PC 为棱构造棱长为1的正方体，则这个正方体的外接球就是三棱锥P ABC -的外接球，∴三棱锥P ABC -的外接球的半径2r ==∴三棱锥P ABC -的外接球的表面积为：2412S r ππ==．故选：A ．考向五 内切球【例5】正三棱锥的高为1，底面边长为62，正三棱锥内有一个球与其四个面相切．求球的表面积与体积．【答案】πππ)625(8)26(4422-=-==R S 球，33)26(3434-==ππR V 球．∴R R ⨯⨯+⨯⨯⨯=⨯⨯36313233113631得：2633232-=+=R ， ∴πππ)625(8)26(4422-=-==R S 球．∴33)26(3434-==ππR V 球． 【举一反三】1．球内切于圆柱， 则此圆柱的全面积与球表面积之比是( ) A ．1:1 B ．2:1C ．3:2D ．4:3【答案】C【解析】设球的半径为R ，则圆柱的底面半径为R ，高为2R ，222226S R R R R πππ∴=⨯+⨯=圆柱，24S R π=球．∴此圆柱的全面积与球表面积之比是：226342S R S R ππ==圆柱球．故选：C ．2．若三棱锥A BCD -中，6AB CD ==，其余各棱长均为 5 ，则三棱锥内切球的表面积为 ．【答案】6316π【解析】由题意可知三棱锥的四个面全等， 且每一个面的面积均为164122⨯⨯=． 设三棱锥的内切球的半径为r ，则三棱锥的体积14163ABC V S r r ∆==， 取CD 的中点O ，连接AO ，BO ，则CD ⊥平面AOB ，4AO BO ∴==，162AOB S ∆=⨯=12233A BCD C AOB V V --∴==⨯⨯=，16r ∴=，解得r =． ∴内切球的表面积为263416S r ππ==． 故答案为：6316π．3．一个几何体的三视图如图所示， 三视图都为腰长为 2 的等腰直角三角形， 则该几何体的外接球半径与内切球半径之比为( )A BC D 【答案】A【解析】 由题意可知几何体是三棱锥， 是正方体的一部分， 如图： 正方体的棱长为 2 ，内切球的半径为r ，可得：21111222(322)3232r ⨯⨯⨯⨯=⨯⨯⨯⨯，解得r ==故选：A ．考向六 最值问题【例6】已知球O 的内接长方体ABCD A B C D -''''中，2AB =，若四棱锥O ABCD -的体积为2，则当球O 的表面积最小时，球的半径为( )A．B ．2 CD ．1【答案】B【解析】由题意，球O 的内接长方体ABCD A B C D -''''中，球心O 在T 对角线交点上， 可得：四棱锥O ABCD -的高为1(2h h 是长方体的高）， 长方体的边长2AB =，设BC a =，高为h ， 可得：112223a h ⨯⨯⨯⨯=，即6ah =，6h a∴=那么：23614222R ==+=，（当且仅当a =故选：B ． 【举一反三】1．已知A ，B 是球O 的球面上两点，90AOB ∠=︒，C 为该球面上的动点，若三棱锥O ABC -体积的最大值为36，则球O 的表面积为( )A ．36πB ．64πC ．144πD ．256π【答案】C【解析】如图所示，当点C 位于垂直于面AOB 的直径端点时，三棱锥O ABC -的体积最大，设球O 的半径为R ，此时2311136326O ABC C AOB V V R R R --==⨯⨯⨯==，故6R =，则球O 的表面积为24144R ππ=， 故选：C ．1．已知正三棱柱111ABC A B C -的底面边长为3，外接球表面积为16π，则正三棱柱111ABC A B C -的体积为（ ）A ．4B ．2C D ．2【答案】D【解析】正三棱柱111ABC A B C -的底面边长为3,故底面的外接圆的半径为：03,2sin 60r r r =⇒=外接球表面积为16π242R R π=⇒=外接球的球心在上下两个底面的外心MN 的连线的中点上，记为O 点，如图所示在三角形1OMB 中，22211112MB r OB R MB OM OB ===+=解得1,2OM MN h ===故棱柱的体积为：133222V Sh ==⨯⨯⨯= 故答案为：D. 2．已知P ，A ，B ，C ，D 是球O 的球面上的五个点，四边形ABCD 为梯形，//AD BC ，2AB DC AD ===，4BC PA ==，PA ⊥面ABCD ，则球O 的体积为（ ）A ．3B C ．D ．16π【答案】A【解析】取BC 中点E ，连接,,AE DE BD//AD BC 且12AD BC EC ==∴四边形ADCE 为平行四边形AE DC ∴=，又12DC BC =12DE BC ∴=AE DE BE EC ∴===E ∴为四边形ABCD 的外接圆圆心设O 为外接球的球心，由球的性质可知OE ⊥平面ABCD 作OF PA ⊥，垂足为F ∴四边形AEOF 为矩形，2OF AE == 设AF x =，OP OA R ==则()22444x x +-=+，解得：2x =R ∴==∴球O 的体积：3433V R π==本题正确选项：A3．已知三棱锥S ABC -的各顶点都在一个球面上，球心O 在AB 上，SO ⊥底面ABC ，球的体积与三棱锥体积之比是4π，AC = （ ）A ．πB ．2πC ．3πD ．4π【答案】D 【解析】由于OA OB OC OS ===，且SO ⊥平面ABC ，所以π2ACB ∠=，设球的半径为R ，根据题目所给体积比有34π114π332R R =⋅⋅，解得1R =，故球的表面积为4π.4．某三棱锥的三视图如图所示，则此三棱锥的外接球表面积是（ ）A ．163π B ．283πC ．11πD ．323π【答案】B【解析】根据几何体得三视图转换为几何体为：该几何体为：下底面为边长为2的等边三角形，有一长为2的侧棱垂直于下底面的三棱锥体，故：下底面的中心到底面顶点的长为：3，所以：外接球的半径为：R =故：外接球的表面积为：27284433S R πππ==⋅=．故选：B ． 5．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，已知其俯视图是正三角形，则该几何体的外接球的体积是（ ）A B C ．193πD ．223π【答案】A的四棱锥，且侧面PAB 垂直底面ABCD ，如图所示：还原长方体的长是2，宽为1设四棱锥的外接球的球心为O ，则过O 作OM 垂直平面PAB ，M 为三角形PAB 的外心，作ON 垂直平面ABCD ，则N 为矩形ABCD 的对角线交点，11,233OM ON ===所以外接球的半径222221912R ON AN R =+=+=∴=所以外接球的体积343V R π== 故选A 6．《九章算术》中将底面为长方形，且有一条侧棱与底面垂直的四棱锥称之为“阳马”现有一阳马，其正视图和侧视图是如图所示的直角三角形.若该阳马的顶点都在同一个球面上，则该球的表面积为（ ）A ．√6AB ．6AC ．9AD ．24A【答案】B【解析】如图所示，该几何体为四棱锥A −AAAA ．底面AAAA 为矩形，其中AA ⊥底面AAAA ．AA =1，AA =2，AA =1．则该阳马的外接球的直径为AA =√1+1+4=√6．∴该阳马的外接球的表面积为：4A ×(√62)2=6A ．故选：A ．7．如图，边长为2的正方形AAAA 中，点A、A 分别是AA、AA 的中点，将AAAA ，AAAA ，AAAA分别沿AA ，AA ，AA 折起，使得A 、A 、A 三点重合于点A ′，若四面体A ′AAA 的四个顶点在同一个球面上，则该球的表面积为( )A ．5AB ．6AC ．8AD ．11A【答案】B【解析】由题意可知△A′AA 是等腰直角三角形，且A′A ⊥平面A′AA ． 三棱锥的底面A′AA 扩展为边长为1的正方形，然后扩展为正四棱柱，三棱锥的外接球与正四棱柱的外接球是同一个球， 正四棱柱的对角线的长度就是外接球的直径，直径为：√1+1+4=√6． ∴球的半径为√62，∴球的表面积为4A ·(√62)2=6A ．故选：A ．8．某简单几何体的三视图如图所示，若该几何体的所有顶点都在球A 的球面上，则球A 的表面积是：（ ）A ．8AB ．12√3AC ．12AD ．48A【答案】C【解析】由三视图还原几何体如图，可知该几何体为直三棱柱，底面为等腰直角三角形，直角边长为2，侧棱长为2． 把该三棱柱补形为正方体，则正方体对角线长为√22+22+22．∴该三棱柱外接球的半径为：√3．则球O 的表面积是：4A ×(√3)2=12π．故选：C ．9．已知三棱锥A −AAA 的底面AAAA 的顶点都在球A 的表面上，且AA =6，AA =2√3，AA =4√3，且三棱锥A −AAA 的体积为4√3，则球A 的体积为（ ） A ．32A3B ．64A3C ．128A3D ．256A3【答案】D【解析】由O 为球心，OA ＝OB ＝OC ＝R ，可得O 在底面ABC 的射影为△ABC 的外心，AB ＝6，AA =2√3，AA =4√3，可得△ABC 为AC 斜边的直角三角形，O 在底面ABC 的射影为斜边AC 的中点M ，可得13•OM •12AB •BC =16OM •12√3=4√3，解得OM ＝2， R 2＝OM 2+AM 2＝4+12＝16，即R ＝4，球O 的体积为43πR 3=43π•64=2563π．故选：D ．10．我国古代数学名著《九章算术》中有这样一些数学用语，“堑堵”意指底面为直角三角形，且侧棱垂直于底面的三棱柱.现有一如图所示的堑堵，AC BC ⊥，若12A A AB ==，则堑堵111ABC A B C -的外接球的体积为（ ）AB ．8πCD ．43π 【答案】C【解析】由题意，在直三棱柱111ABC A B C -中，因为AC BC ⊥，所以ABC ∆为直角三角形，且该三角形的外接圆的直径22r AB ==， 又由12AA =，所以直三棱柱111ABC A B C -的外接球的直径2R ==所以R =，所以外接球的体积为334433V R ππ==⨯=C. 11．在三棱锥P ABC -中.2PA PB PC ===.1AB AC ==，BC =则该三棱锥的外接球的表面积为（ ）A ．8πB ．163π C ．43π D【答案】B【解析】因为1,AB AC BC ===，由余弦定理可求得23BAC π∠=， 再由正弦定理可求得ABC ∆的外接圆的半径122sin3BCr π==， 因为2PA PB PC ===，所以P 在底面上的射影为ABC ∆的外心D，且PD =，设其外接球的半径为R，则有2221)R R =+，解得R =24164433S R πππ==⨯=，故选B.12．一个各面均为直角三角形的四面体有三条棱长为2，则该四面体外接球的表面积为（ ） A ．6π B ．12πC ．32πD ．48π【答案】B【解析】由题得几何体原图如图所示，其中SA ⊥平面ABC,BC ⊥平面SAB,SA=AB=BC=2,所以SC =设SC 中点为O,则在直角三角形SAC 中，在直角三角形SBC 中，OB=12SC =所以,所以点O所以四面体外接球的表面积为4=12ππ.故选：B13．已知在三棱锥P ABC -中，1PA PB BC ===，AB =，AB BC ⊥，平面PAB ⊥平面ABC ，若三棱锥的顶点在同一个球面上，则该球的表面积为（ ）A ．2B C ．2π D ．3π【答案】D【解析】根据题意, AC 为截面圆的直径, AC =设球心到平面ABC 的距离为d ,球的半径为R 。

§2长方体外接球及正四面体公式秒杀知识点知识点1：（长方体外接球半径公式）长方体外接球半径为R ，a ，b ，c 为长方体的长、宽、高． 则22224R a b c =++．（外接球表面积()222πS a b c =++球） 特别：当a b c ==（正方体）时，2243R a =或2234R a =．知识点2：（正四面体公式）设正四面体棱长为a ，则：（1）3V =正四面体．（2）外接球半径R =．（3）内切球半径r =（:3:1R r =）．秒杀思路分析球的计算是考纲中的一个重要知识点．对特殊几何体特别是长方体或正四面体及其外接球的计算更是高考中的一个高频考点．这类试题秒杀思路一般是直接套用公式，或进行转化为长方体或正四面体后套用公式直接计算．后一种情况要求能力较高．【示例1】（2017年全国卷Ⅱ文15）长方体的长、宽、高分别为3，2，1，其顶点都在球O 的球面上，则球O 的表面积为______．【示例2】（2013年辽宁卷理10）已知直三棱柱111ABC A B C -的6个顶点都在球O 的球面上．若3AB =，4AC =，AB AC ⊥，112AA =，则球O 的半径为（）AB ．C ．132D ．【示例3】（2003年全国卷）一个四面体所有棱长都为2，四个顶点在同一球面上，则此球的表面积为（ ）A ．3πB ．4πC ．D ．6π方法对比【例1】（2013年新课标全国卷Ⅱ文15）已知正四棱锥O ABCD -O为球心，OA 为半径的球的表面积为______．【例2】（2013年湖北预赛）已知四面体P ABC -的体积为1，G ，K 分别是ABC △，PBC △的重心，过G 作直线分别与AB ，AC 交于点M ，N ，则四棱锥K MNCB -体积的最大值为______．【例3】（清华2018年高三11月标准学术能力诊断测试（理）15）已知正四面体ABCD 的棱长为个顶点都在球心为O 的球面上，点P 为棱BC 的中点，过P 作球O 的截面，则截面面积的最小值为______秒杀训练【试题1】已知正四面体的俯视图如图所示，其中四边形ABCD 是边长为2的正方形，则这个正四面体的体积为______．【试题2】在三棱锥A BCD -中，侧棱AB ，AC ，AD 两两垂直，ABC △，ACD △，ADB △的面积分别为，则该三棱锥外接球的表面积为（ ）A ．2πB ．6πC ．D ．24π【试题3】设长方体长、宽、高分别为2a ，a ，a ，其顶点都在同一个球面上，则该球的表面积为（ ）A ．23πaB ．26πaC ．212πaD ．224πa【试题4】如图是一个体积为72的正四面体，连接两个面的重心E ，F ，则线段EF 的长为______．【试题5】在平面上，若两个正三角形边长的比为:21，则它们的面积比为:41．类似地，空间中，若两个正四面体的棱长之比为:21，则它们的体积比为______．真题回放【试题1】（2017年天津卷文11）已知一个正方体的所有顶点都在一个球面上，若这个正方体的表面积为18，则这个球的体积为______．【试题2】（2014年河南高二预赛）棱长为1的正四面体的四个面的中心所组成的小正四面体的外接球的体积为______．【试题3】（2017~2018学年度沈阳市郊联体高三一模文11）已知三棱锥S ABC -的所有顶点都在球O 的球面上，SA ⊥平面ABC ，SA =，1AB =，2AC =，60BAC ∠=︒，则球O 的表面积为（ ）A ．4πB ．8πC ．12πD ．16π求异面直线所成角的正弦公式【公式】：如图，平面MCD ⊥平面NCD ．直线AB 与两平面分别相交于A ，B ，且直线AB 与平面MCD 所成角为α，直线AB 与平面NCD 所成角为β，记异面直线AB 与CD 所成角为θ，则222sin sin sin θαβ=+．【示例】（2014年新课标全国Ⅱ卷理11）直三棱柱111ABC A B C -中，90BCA ∠=︒，M ，N 分别是11A B ，11A C 的中点，1BC CA CC ==，则BM 与AN 所成角的余弦值为（ ）A ．110B ．25C D§2 长方体外接球及正四面体公式秒杀知识点知识点1：（长方体外接球半径公式）长方体外接球半径为R ，a ，b ，c 为长方体的长、宽、高． 则22224R a b c =++．（外接球表面积()222πS a b c =++球） 特别：当a b c ==（正方体）时，2243R a =或2234R a =．知识点2：（正四面体公式）设正四面体棱长为a ，则：（1）3V =正四面体．（2）外接球半径R =．（3）内切球半径r =（:3:1R r =）．【证明】这里只证明知识点2中的公式（2），其余请同学自行完成．设正四面体外接球球心为O ，BCD △的中心为1O ，则1OO D △为直角三角形．可知12233O D MD ===，222211233AO a a a =-=，∴1AO =，∴1OO R -．在直角1OO D △中，由勾股定理得22213R a R ⎫=+-⎪⎭，∴R =．（也可转化为正方体证明，略）记忆方法：（1）长方体外接球直径平方（对角线平方）等于三边平方和．（2有关：即313V =．（3有关，共四个面．即R =，13r =． 秒杀思路分析球的计算是考纲中的一个重要知识点．对特殊几何体特别是长方体或正四面体及其外接球的计算更是高考中的一个高频考点．这类试题秒杀思路一般是直接套用公式，或进行转化为长方体或正四面体后套用公式直接计算．后一种情况要求能力较高．【示例1】（2017年全国卷Ⅱ文15）长方体的长、宽、高分别为3，2，1，其顶点都在球O 的球面上，则球O 的表面积为______．这是典型长方体外接球问题，直接用公式即可“秒杀”． 【秒杀方法】由知识点1得()222321π14πS =++=球．【示例2】（2013年辽宁卷理10）已知直三棱柱111ABC A B C -的6个顶点都在球O 的球面上．若3AB =，4AC =，AB AC ⊥，112AA =，则球O 的半径为（ ）AB ．C ．132D ．由已知分析，直三棱柱恰为一个长方体的一半，即可转化为长方体“秒杀”．【秒杀方法】直三棱柱外接球恰为长方体外接球，由知识点1得22222434125R =++=+221213=，即213R =，故132R =．即选择C ．【示例3】（2003年全国卷）一个四面体所有棱长都为2，四个顶点在同一球面上，则此球的表面积为（ ） A ．3πB ．4πC ．D ．6π正四面体可以放入正方体中，利用长方体公式求解．若利用正四面体公式即可速解． 【秒杀方法1】把正四面体放入正方体中，如图所示． 图中11D A BC -即为正四面体，可知正方体棱长为1．∴外接球表面积()222111π3πS =++=球．故选择A ．【秒杀方法2】直接用知识点2公式：R ==则234π4π3π4S R ==⨯=球．故选择A ．方法对比【例1】（2013年新课标全国卷Ⅱ文15）已知正四棱锥O ABCD -O为球心，OA 为半径的球的表面积为______．【例2】（2013年湖北预赛）已知四面体P ABC -的体积为1，G ，K 分别是ABC △，PBC △的重心，过G 作直线分别与AB ，AC 交于点M ，N ，则四棱锥K MNCB -体积的最大值为______．BC 时，59MNCB '=⨯153394⨯⨯（注：棱长为a 的正四面体高【例3】（清华2018年高三11月标准学术能力诊断测试（理）15）已知正四面体ABCD 的棱长为个顶点都在球心为O 的球面上，点P 为棱BC 的中点，过P 作球O 的截面，则截面面积的最小值为______秒杀训练【试题1】已知正四面体的俯视图如图所示，其中四边形ABCD 是边长为2的正方形，则这个正四面体的体积为______．【解析】把四面体放入正方体中，可得正四面体棱长为∴3883V ==⨯=．【试题2】在三棱锥A BCD -中，侧棱AB ，AC ，AD 两两垂直，ABC △，ACD △，ADB △的面积分别为，则该三棱锥外接球的表面积为（ ） A ．2π B ．6π C． D ．24π【解析】构造长方体，如图，设长、宽、高分别为x ，y ，z ．由题意得121212xy xz yz ⎧⎪⎪⎪⎨⎪⎪⎪===⎩①②③，②解得1,x y z =⎧⎪=⎨⎪=⎩，∴()221236R =++=，即246R =．∴24π6πS R ==球．故选择B ．【试题3】设长方体长、宽、高分别为2a ，a ，a ，其顶点都在同一个球面上，则该球的表面积为（ ）A ．23πaB ．26πaC ．212πaD ．224πa 【解析】设球半径为R ，则()22222246R a a a a =++=，∴2232R a =．则224π6πS R a ==球．故选择B ．【试题4】如图是一个体积为72的正四面体，连接两个面的重心E ，F ，则线段EF 的长为______．【解析】∵372=，∴()136a =⨯．设EF x =，∵2232x a =，∴13x a =．∴()132x =⨯=EF的长为【试题5】在平面上，若两个正三角形边长的比为:21，则它们的面积比为:41．类似地，空间中，若两个正四面体的棱长之比为:21，则它们的体积比为______． 【解析】由公式2：31V =，32V =．∵:1:2a b =，∴31218VV ==．故体积比为1:8．真题回放【试题1】（2017年天津卷文11）已知一个正方体的所有顶点都在一个球面上，若这个正方体的表面积为18，则这个球的体积为______．【解析】设正方体的棱长为a ，则2618a =，∴a =设球半径为R ，则()22239R a ==，∴32R =．故球的体积为249ππ32V R R =⋅=．【试题2】（2014年河南高二预赛）棱长为1的正四面体的四个面的中心所组成的小正四面体的外接球的体积为______． 【解析】如图，1122MN BD ==，∴1223O O MN =，∴12211323O O =⨯=．由公式2得，外接球半径13r =．∴34π3V r ==球．【试题3】（2017~2018学年度沈阳市郊联体高三一模文11）已知三棱锥S ABC -的所有顶点都在球O 的球面上，SA ⊥平面ABC，SA =，1AB =，2AC =，60BAC ∠=︒，则球O 的表面积为（ ）A ．4πB ．8πC ．12πD ．16π【解析】把三棱锥S ABC -放入如图所示的长方体中，易知BC = 则()(222222221121316R a b c =++=++=++=．即16πS =球．故选择D ．求异面直线所成角的正弦公式【公式】：如图，平面MCD ⊥平面NCD ．直线AB 与两平面分别相交于A ，B ，且直线AB 与平面MCD 所成角为α，直线AB 与平面NCD 所成角为β，记异面直线AB 与CD 所成角为θ，则222sin sin sin θαβ=+．【证明】：如图，作AE CD ⊥于E ，BF CD ⊥于F ，过E 作//EG BF ，且//GB CD ，连接AF ，AG ，则ABG θ∠=，ABE α∠=，BAF β∠=． 则2222222222sin sin sin AE BF AE BF AG AB AB AB AB αβθ+⎛⎫⎛⎫+=+=== ⎪ ⎪⎝⎭⎝⎭． 故222sin sin sin θαβ=+．【示例】（2014年新课标全国Ⅱ卷理11）直三棱柱111ABC A B C -中，90BCA ∠=︒，M ，N 分别是11A B ，11A C 的中点，1BC CA CC ==，则BM 与AN 所成角的余弦值为（ ）A ．110B ．25C D 【秒杀方法】令正方体1111AA BC A A B C ''-的棱长为2，易知平面AA N N ''⊥平面11A BB A ''，则sin sinMN N BM MB α''∠=== 过B 作BK A N ''⊥于K ，易求得BK =sin sin BK BMK MB β∠===．∴2221167sin sin sin 63010θαβ=+=+=．则273cos 11010θ=-=，故cos θ=，选择C ．。

几类特殊的多面体的外接球问题沈清臣(湖南省长沙市长郡中学㊀４１００００)摘㊀要:本文主要通过空间球体的截面性质引入ꎬ介绍几类锥体㊁柱体的外接球问题的求解策略.关键词:多面体ꎻ外接球ꎻ截面ꎻ补体中图分类号:Ｇ６３２㊀㊀㊀㊀㊀㊀文献标识码:Ａ㊀㊀㊀㊀㊀㊀文章编号:１００８－０３３３(２０２０)２８－００６１－０３收稿日期:２０２０－０７－０５作者简介:沈清臣(１９７９.１１－)ꎬ男ꎬ湖南省沅陵人ꎬ本科ꎬ中学一级教师ꎬ从事高中数学教学研究.基金项目:本文系长沙市教育科学规划重点资助课题«高中数学必修模块易错点提前干预策略的研究»成果.㊀㊀空间几何体与球的组合问题是近几年高考中的一个频考点ꎬ且考查形式灵活多样ꎻ要正确求解此类问题ꎬ学生必须通过读㊁想㊁画㊁转㊁算五个基本环节ꎬ找准熟悉的基本几何模型及相应的求解策略.此类问题可划分为旋转体㊁多面体的内切㊁外接球问题ꎻ而旋转体的内切㊁外接球问题ꎬ通过轴截面可转化为平面几何问题求解ꎻ多面体的内切球问题ꎬ利用等体法可直接求解.因此ꎬ本文主要介绍多面体(棱柱㊁棱锥)的外接球问题ꎬ在此之前ꎬ我们先熟悉空间球体的截面性质及其应用.㊀㊀一㊁球的截面性质及其应用如图１ꎬ空间球体有如下性质:(１)用一个平面去截球ꎬ所得截面是一个圆面ꎻ(２)球心与截面圆心的连线与截面垂直ꎬ且满足:Ｒ２＝ｒ２＋ｄ２(其中Ｒ表示球的半径ꎬｒ表示截面圆的半径ꎬｄ表示球心到截面的距离).图１㊀㊀㊀㊀㊀㊀㊀㊀图２例１㊀(２０１８年全国卷Ⅲ理第１０题)设ＡꎬＢꎬＣꎬＤ是同一个半径为４的球的球面上四点ꎬәＡＢＣ为等边三角形且其面积为９３ꎬ则三棱锥Ｄ－ＡＢＣ体积的最大值为(㊀㊀).Ａ.１２３㊀Ｂ.１８３㊀Ｃ.２４３㊀Ｄ.５４３分析㊀如图２ꎬ设等边三角形әＡＢＣ外接圆圆心为Ｏ１ꎬ则易知当Ｏ１㊁Ｏ㊁Ｄ共线ꎬ即ＤＯ１为高时ꎬ棱锥体积最大.又由等边三角形әＡＢＣ的面积可求得边长ＡＢ＝６ꎬ所以ＡＯ１＝１２ ＡＢｓｉｎ６０ʎ＝２３ꎬ所以ＯＯ１＝ＡＯ２－ＡＯ２１＝２ꎬ即可得三棱锥Ｄ－ＡＢＣ体积的最大值为１３ＳΔＡＢＣ ＤＯ１＝１３ˑ９３ˑ(４＋２)＝１８３ꎬ故选答案Ｂ.上例的求解过程ꎬ充分利用球体的截面性质ꎬ即球心与截面圆圆心的连线与截面垂直ꎬ使得求解难度大大降低.类似的问题还在高考试题中曾多次出现ꎬ如２０１３年新课标Ⅰ(理)第６题㊁２０１３年新课标Ⅰ卷(文)第１５题㊁２０１３年大纲卷(文)第１６题㊁２０１３年大纲卷(理)第１６题等.其实ꎬ更多几何体的外接球问题的求解均需要利用到球体的截面性质ꎬ在后面的问题中将作介绍.㊀㊀二㊁棱柱的外接球问题此处我们主要介绍直棱柱(侧棱垂直于底面)的外接球问题.因为正方体㊁长方体的外接球直径即为体对角线ꎬ因此遇到直棱柱的外接球问题ꎬ首先可以考虑将该直棱柱补体为长方体或正方体ꎻ若不能补体ꎬ再考虑利用球体的截面性质确定球心位置ꎬ再由勾股定理求解.图３如图３ꎬ设直三棱柱ＡＢＣ－Ａ１Ｂ１Ｃ１上㊁下底面的外接圆圆心分别为Ｈ１㊁Ｈꎬ连接Ｈ㊁Ｈ１ꎬ则易知ＨＨ１的中点Ｏ即为该棱柱外接球的球心ꎬＡＨ即为底面外接圆的半径ꎬＡＯ即为球的半径Ｒ.利用平面几何知识求出ＡＨꎬ再结合球的截面性质可直接求解.例２㊀(２０１３年辽宁文㊁理第１０题)已知三棱柱ＡＢＣ－Ａ１Ｂ１Ｃ１的６个顶点都在球Ｏ的球面上ꎬ若ＡＢ＝３ꎬＡＣ＝４ꎬＡＢʅＡＣꎬＡＡ１＝１２ꎬ则球Ｏ的半径为(㊀㊀).１６Ａ.３１７２㊀㊀Ｂ.２１０㊀㊀Ｃ.１３２㊀㊀Ｄ.３１０分析１㊀由题设条件ꎬ可将该三棱柱补成长㊁宽㊁高分别为３ꎬ４ꎬ１２的长方体ꎬ则长方体的对角线长为１３ꎬ即外接球的直径为１３ꎬ半径为１３２ꎬ故选答案Ｃ.分析２㊀易知底面әＡＢＣ为Ｒｔәꎬ所以其外接圆半径ｒ＝ＢＣ２＝５２ꎬ球心到底面的距离ｄ＝ＡＡ１２＝６ꎬ因此由球的截面性质可得所求球的半径Ｒ＝ｒ２＋ｄ２＝１３２ꎬ故选答案Ｃ.直接考查正方体㊁长方体的外接球问题ꎬ在高考试题中曾多次出现ꎬ如２０１３年天津文第１０题㊁２０１４年陕西理第５题㊁２０１６全国Ⅱ文第４题㊁２０１７年天津文㊁理第１０题㊁２０１７年全国Ⅱ文第１５题等ꎬ此类问题难度不大.补体的策略在后面的锥体的外接球问题中将进一步详细介绍.㊀㊀三㊁棱锥的外接球问题球与锥体的组合问题ꎬ在高考真题及各地的模拟试题中出现频率最高ꎬ试题形式多样ꎬ灵活多变.类似于柱体的求解策略ꎬ我们首先考虑补体ꎬ再者利用截面性质确定球心ꎬ进而可得解.下面将按四种类型进行详细阐述.１.有条侧棱垂直于底面的棱锥若棱锥的一条侧棱垂直于底ꎬ则补体为直棱柱求解ꎬ如图４ꎬ三棱锥Ｓ－ＡＢＣ中ꎬ侧棱ＳＡʅ底面ＡＢＣꎬ则可补体成直棱柱ＳＱＰ－ＡＢＣ(如图５)ꎬ即转化为直棱柱的外接球问题.图４㊀㊀㊀㊀㊀㊀㊀㊀图５例３㊀(２０１９年全国Ⅰ理第１０题)已知三棱锥Ｐ－ＡＢＣ的四个顶点在球Ｏ的球面上ꎬＰＡ＝ＰＢ＝ＰＣꎬәＡＢＣ是边长为２的正三角形ꎬＥꎬＦ分别是ＰＡꎬＡＢ的中点ꎬøＣＥＦ＝９０ʎꎬ则球Ｏ的体积为(㊀㊀).Ａ.８６π㊀Ｂ.４６π㊀Ｃ.２６π㊀Ｄ.６π分析㊀如图６ꎬ易知三棱锥Ｐ－ＡＢＣ为正棱锥ꎬ故对棱相互垂直ꎬ即ＰＢʅＡＣꎬ又由题设条件知ＥＦʅＥＣꎬＰＢʊＥＦꎬʑＰＢʅＥＣꎬ即ＰＢʅ平面ＰＡＣ.结合正三棱锥的结构特征ꎬ可知ＰＡꎬＰＢꎬＰＣ两两垂直ꎬ且ＰＡ＝ＰＢ＝ＰＣ＝２.将三棱锥Ｐ－ＡＢＣ补成正方体ꎬ如图７.所以外接球的半径Ｒ＝３２ˑ２＝６２ꎬ体积为Ｖ＝４３πＲ３＝４３π(６２)３＝６πꎬ故选答案Ｄ.图６㊀㊀㊀㊀㊀㊀㊀㊀图７在三棱锥中ꎬ若共顶点的三条棱两两垂直ꎬ则将棱锥补体为正方体或长方体ꎬ可迅速求解.类似问题再如ꎬ２０１２年辽宁文理第１６题.２.对棱相等的锥体正方体或长方体中ꎬ相对面的对角线相等ꎬ因此当三棱锥的对棱相等的时候ꎬ可以将该三棱锥放于正方体或长方体内ꎬ即补体为正方体或长方体.例４㊀三棱锥Ｄ－ＡＢＣ中ꎬＡＢ＝ＣＤ＝６ꎬ其余四条棱均为２ꎬ则三棱锥Ｄ－ＡＢＣ的外接球的表面积为.图８分析㊀如图８ꎬ将三棱锥Ｄ－ＡＢＣ放入到长方体中ꎬ并设该长方体的长㊁宽㊁高分别为ａꎬｂꎬｃꎬ则ａ２＋ｂ２＝６ꎬｂ２＋ｃ２＝４ꎬｃ２＋ａ２＝４{⇒ａ２＋ｂ２＋ｃ２＝７ꎬʑ球的半径Ｒ满足４Ｒ２＝ａ２＋ｂ２＋ｃ２＝７ꎬ故表面积为Ｓ＝４πＲ２＝７π.本例也可以取ＡＢ或ＣＤ的中点ꎬ作出截面ꎬ根据几何体的对称特征ꎬ确定球心的位置ꎬ利用球的截面性质列出方程组求解.但两种解法对比ꎬ可体现上述解法的简便快捷.特别是准确熟悉正四面体与正方体之间的联系ꎬ可快速解决正四面体的外接球问题ꎬ比如下面的例题.３.正棱锥(底面为正三角形ꎬ顶点在底面的射影为底面的中心)由正棱锥的结构特征可知ꎬ其外接球的球心一定在图９其高线上.如图９ꎬ在正三棱锥Ｓ－ＡＢＣ中ꎬ设底面边长为ａꎬ侧棱长为ｂꎬ高为ｈꎬ外接球球心为Ｏꎬ半径为Ｒꎬ则ＡＨ即为底三角形的外接圆半径ꎬ且ＡＨ＝３３ａꎬｈ＝ｂ２－(３３ａ)２ꎬ再由ＡＯ２＝ＡＨ２＋ＯＨ２得ꎬＲ２＝(３３ａ)２＋(ｈ－Ｒ)２ꎬ即可求出外接球半径Ｒ的值.２６例５㊀(２０１４年大纲文第１０题㊁理第８题)正四棱锥的顶点都在同一球面上ꎬ若该棱锥的高为４ꎬ底面边长为２ꎬ则该球的表面积为(㊀㊀).Ａ.８１π４㊀Ｂ.１６π㊀Ｃ.９π㊀Ｄ.２７π４图１０分析㊀如图１０ꎬ正四棱锥Ｐ－ＡＢＣＤ的高为ＰＥꎬ则ＰＥ＝４ꎬＡＢ＝２ꎬＡＥ＝１２ＡＣ＝２.设外接球的球心为Ｏꎬ半径为Ｒꎬ连接ＡＯꎬ则在ＲｔәＡＯＥ中ꎬ有ＡＯ２＝ＡＥ２＋ＯＥ２ꎬ即Ｒ２＝(２)２＋(４－Ｒ)２ꎬ解得Ｒ＝９４.ʑ球的表面积为Ｓ＝４πＲ２＝４πˑ(９４)２＝８１４πꎬ故选择答案Ａ.上述例题的求解过程ꎬ还是利用球体的截面性质.前述例３(２０１９年全国Ⅰ理第１０题)亦可利用上述方法求解.４.有两个面垂直的棱锥如图１１ꎬ已知球Ｏ１㊁Ｏ２的两个截面圆所在平面垂直ꎬ则四边形ＯＯ１ＨＯ２为矩形ꎬ且әＯＡＯ１ꎬәＯＢＯ２均为ＲｔәꎬＡＯ＝ＢＯ＝Ｒ.利用勾股定理结合已知条件列出方程组ꎬ即可求解.例６㊀四面体Ａ－ＢＣＤ中ꎬøＡＢＣ＝øＡＢＤ＝øＣＢＤ＝６０ʎꎬＡＢ＝３ꎬＣＢ＝ＤＢ＝３ꎬ则此四面体外接球的表面积为(㊀㊀).Ａ.１９π２㊀Ｂ.１９３８π２４㊀Ｃ.１７π㊀Ｄ.１７１７π６图１１㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀图１２分析㊀如图１２ꎬ由题设条件知әＢＣＤ是边长为３的正三角形ꎬ设Ｅ为其外接圆圆心ꎬ则其外接圆半径ｒ１ＢＥ＝２３ＢＦ＝２３３ꎬ且ＥＦ＝３３.又ȵøＡＢＣ＝øＡＢＤ＝６０ʎꎬＡＢ＝３ꎬＣＢ＝ＤＢ＝３ꎬ由余弦定理可得ＡＤ＝ＡＣ＝７ꎬＣＤ边上高ＡＦ＝６ꎬ则ＡＦ２＋ＢＦ２＝ＡＢ２ꎬʑＡＦʅＢＦꎬ即可得ＡＦʅ平面ＢＣＤꎬ即有平面ＡＣＤʅ平面ＢＣＤ.设әＢＣＤꎬәＡＣＤ的外接圆圆心分别为Ｅ㊁Ｈꎬ四面体Ａ－ＢＣＤ的外接球球心为Ｏꎬ则ＯＥʅ平面ＢＣＤꎬＯＨʅ平面ＡＣＤꎬＯＥＦＨ为矩形ꎬʑＯＥ＝ＨＦꎬＯＨ＝ＥＦ.连接ＡＯ㊁ＢＯꎬ并设外接球半径为ＲꎬＯＥ＝ＨＦ＝ｘꎬ则分别在ＲｔәＢＯＥꎬＲｔәＡＯＨ中可得:ＢＯ２＝ＢＥ２＋ＯＥ２ꎬＡＯ２＝ＡＨ２＋ＯＨ２ꎬ{即Ｒ２＝(２３３)２＋ｘ２ꎬＲ２＝(６－ｘ)２＋(３３)２ìîíïïïï解得Ｒ２＝１９８.ʑ四面Ａ－ＢＣＤ的外接球的表面积Ｓ＝４πＲ２＝１９π２ꎬ故选答案为Ａ.上述例题的求解过程ꎬ还是利用球的截面性质(过截面圆圆心且与截面垂直的直线一定过球心)ꎬ通过两个截面来确定球心的位置ꎬ再利用勾股定理求解.其实ꎬ一般情况下ꎬ并要求两个截面圆所在平面垂直.如下例:例７㊀(２０２０年广州市一模文第１２题)在三棱锥Ａ－ＢＣＤ中ꎬәＡＢＤ和әＣＢＤ均为边长为２的等边三角形ꎬ且二面角Ａ－ＢＤ－Ｃ的平面角为１２０ʎꎬ则此三棱锥的外接球的表面为(㊀㊀).Ａ.７π㊀㊀Ｂ.８π㊀㊀Ｃ.１６π３㊀㊀Ｄ.２８π３图１３分析㊀如图１３ꎬ取ＢＤ的中点为Ｅꎬ并连结ＡＥꎬＣＥꎬ易知øＡＥＣ＝１２０ʎ.设әＡＢＤ和әＣＢＤ的外心分别为Ｈ２ꎬＨ１ꎬ并过Ｈ２ꎬＨ１作平面ＡＢＤ和平面ＣＢＤ的垂线交于点Ｏꎬ则Ｏ即为三棱锥Ａ－ＢＣＤ的外接球的球心ꎬ且ＥＨ１＝ＥＨ２＝１３ＣＥ＝３３ꎬʑＲｔәＯＥＨ１≅ＲｔәＯＥＨ２ꎬøＯＥＨ１＝øＯＥＨ２＝１２øＡＥＣ＝６０ʎꎬＯＥ＝２ＥＨ１＝２３３ꎬ故所求外接球半径为Ｒ＝ＯＢ＝ＯＥ２＋ＢＥ２＝２１３.ʑ三棱锥Ａ－ＢＣＤ的外接球的表面积Ｓ＝４πＲ２＝２８π３ꎬ故选答案Ｄ.以上内容是对常见的棱柱㊁棱锥的几类外接球问题及其求解策略的归纳.因为题型可以灵活多变ꎬ问题的求解途径多种多样ꎬ以上肯定有阐述不全面不到位的地方ꎬ期盼读者去补充完善.㊀㊀参考文献:[１]周瑜芽.对一道三棱外接球高考题的解法探究[Ｊ].中学数学研究(华南师范大学版)ꎬ２０２０(０２):５７－５９.[２]熊向前ꎬ杨墁.例析破解三棱锥外接球问题的六种方法[Ｊ].中学数学研究ꎬ２０２０(０３上):３８－４０.[责任编辑:李㊀璟]３６。

外接球与内切球问题解题技巧梳理一．外接球8大模型秒杀公式推导r α说明：为底面外接圆的半径，R 为球的半径，l 为两面公共边的长度 为两个面的二面角，h 是空间几何体的高，H 为某一面的高1.墙角模型(1) 使用范围：3组或3条棱两两垂直；或可在长方体中画出该图且各顶点与长方体的顶点重合 （2）推导过程：长方体的体对角线就是外接球的直径(2) 秒杀公式：222222a b c 3a R (a b c R (a 44++==、、为长方体的长宽高）正方体的边长）（4）图示过程(3) 秒杀公式：2.汉堡模型（1）使用范围：有一条侧棱垂直与底面的柱体或椎体 （2）推导过程第一步：取底面的外心O 1,，过外心做高的的平行且长度相等，在该线上中点为球心的位置第二步：根据勾股定理可得222h R r 4=+（3）秒杀公式：222h R r 4=+（4）图示过程3.斗笠模型（1）使用范围：正棱锥或顶点的投影在底面的外心上 （2）推导过程第一步：取底面的外心O 1,，连接顶点与外心，该线为空间几何体的高h 第二步：在h 上取一点作为球心O第三步：根据勾股定理22222r h R (h R)r R 2h+=-+⇔=（3）秒杀公式：22r h R 2h+=（4）图示过程4.折叠模型（1）使用范围：两个全等三角形或等腰三角形拼在一起，或菱形折叠 （2）推导过程第一步：过两个平面取其外心H 1、H 2，分别过两个外心做这两个面的垂线且垂线相交于球心O第二步：计算2222222111OH H E tan=(CE-H E)tan (H r)tan (222ααα==-α为两个平面的二面角） 第三步：22222211OC OH CH (H r)tanr 2α=+=-+ （3）秒杀技巧：2222R (H r)tanr 2α=-+ （4）图示过程5.切瓜模型（1）使用范围：有两个平面互相垂直的棱锥 （2）推导过程：第一步：分别在两个互相垂直的平面上取外心F 、N ，过两个外心做两个垂面的垂线，两条垂线的交点即为球心O ，取BC 的中点为M ，连接FM 、MN 、OF 、ON第二步：22222222212l ONMF OA AN ON AN MF R r r 4∴=+=+∴=+-为矩形由勾股可得（3）秒杀公式：222212l R r r 4=+-（4）图示过程6.麻花模型（1）使用范围：对棱相等的三棱锥（2）推导过程：设3组对棱的长度分别为x 、y 、z,长方体的长宽高分别为a 、b 、c2222222222222x a b x y z y b c R 8z a c ⎧=+⎪++⎪=+⇔=⎨⎪=+⎪⎩（3）秒杀公式：2222x y z R 8++=（4）图示过程7.矩形模型（1）使用范围：棱锥有两个平面为直角三角形且斜边为同一边（2）推导过程：根据球的定义可知一个点到各个顶点的距离相等该点为球心可得，斜边为球的直径（3）秒杀公式：22l R 4=（4）图示过程8.鳄鱼模型（1）使用范围：适用所有的棱锥 （2）推导过程：121212222121221212221122211O O O O O O OO E r (1sin O O E O O =O E O E 2O E O E cos 2 OD O O O D 3OD O O O D∴α∆+-α=+=+第一步：在两个平面上分别找外心、两外心做这两面的垂线相交于球心第二步：四点共圆，正弦定理可得OE=2=）在中，（）（）第三步：由（1）（2）（3)整理可得 且 过 2221122212112222221211122221212 =OE O E O DO O O EO Dsin O E O E 2O E O E cos O E O D sin O E O E 2O E O E cos =sin -+=-+α+-α=-+α+-α=2211O E O B-+α2122222O E=m O E=n AB=l,m n2mncos lR=+sin4α+-αα第四步：设，，两个面的二面角为由第三步可得（3）秒杀公式：22222m n2mncos lR=+sin4+-αα（4）图示过程二．内切球的半径---等体积法1.推导过程P ABC PAB PAC PBC ABCPAB PAC PBC ABC11111V S h RS RS RS RS 333331=R(S S S S)31=RS33VR=S-∆∆∆∆∆∆∆∆==++++++∴底面表面积几何体表面积以三棱锥P-ABC为例2.秒杀公式：3VR=S几何体表面积3.图示过程技巧1 外接球之墙角模型【例1】已知长方体''''ABCD A B C D -中，''A B =''1B C =，'A B 与平面''ACC A 所成角的正）A ．4πB ．16πC ．163π D ．323π 【举一反三】1．棱长为2的正方体的外接球的表面积为（ ）A ．4πB ．43π C ．12πD ．2．球面上有,,,A B C D 四个点，若,,AB AC AD 两两垂直，且4AB AC AD ===，则该球的表面积为（ ） A ．803πB ．32πC ．42πD ．48π技巧2 外接球之汉堡模型【例2】已知四棱锥A BCDE -中，四边形BCDE 是边长为2的正方形，3AB =且AB ⊥平面BCDE ，则该四棱锥外接球的表面积为（ ） A ．4π B ．174πC ．17πD ．8π【举一反三】1．各顶点都在一个球面上的正四棱柱（底面是正方形，侧棱垂直于底面）高为2，体积为8，则这个球的表面积是（ ） A ．16πB ．12πC ．10πD ．8π2．如图，在三棱锥A ﹣BCD 中，BD ⊥平面ADC ，BD ＝1，AB ＝2，BC ＝3，AC A ﹣BCD 外接球的体积为（ ）A ．4πB ．3πC ．D ．3．在长方体1111ABCD A B C D -中，1AB CC ==1BC =，点M 在正方形11CDD C 内，1C M ⊥平面1ACM ，则三棱锥11M ACC -的外接球表面积为（ ）A ．11π2B ．7πC ．11πD ．14π4．（2020·全国高三月考（文））三棱柱111ABC A B C -中，1AA ⊥平面ABC ，AC AB ⊥，1AC =，AB =12AA =，则该三棱柱111ABC A B C -的外接球的体积为（ ）A ．3B ．3C ．3D ．8π技巧3 外接球之斗笠模型【例3】正三棱锥S ABC -中，2SA =，AB = ）A ．B ．4πC ．12πD ．6π【举一反三】1．已知正三棱锥S ABC -的侧棱长为6，则该正三棱锥外接球的表面积是________. 2．正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（ ） A ．814πB ．16πC ．9πD ．274π技巧4 外接球之折叠模型【例4】在三棱锥A ﹣BCD 中，△ABD 与△CBD 均为边长为2的等边三角形，且二面角A BD C --的平面角为120°，则该三棱锥的外接球的表面积为（ ） A ．7π B ．8πC ．163πD ．283π【举一反三】 1．已知二面角PAB C 的大小为120°，且90PAB ABC ∠=∠=︒，AB AP =，6AB BC +=.若点P 、A 、B 、C 都在同一个球面上，则该球的表面积的最小值为______.2．如图所示，三棱锥S 一ABC 中，△ABC 与△SBC 都是边长为1的正三角形，二面角A ﹣BC ﹣S 的大小为23π，若S ，A ，B ，C 四点都在球O 的表面上，则球O 的表面积为（ ）A ．73π B ．133π C ．43π D ．3π技巧5 外接球之切瓜模型【例5】已知三棱锥P ABC -中，1PA =，3PB =，AB =CA CB ==面PAB ⊥面ABC ，则此三棱锥的外接球的表面积为（ ） A ．143πB ．283πC ．11πD ．12π【举一反三】1．已知三棱锥A BCD -中，平面ABD ⊥平面BCD ，且ABD △和BCD △都是边长为2的等边三角形，则该三棱锥的外接球表面积为（ ） A ．4πB ．163πC ．8πD ．203π技巧6 外接球之麻花模型【例6】在四面体ABCD 中，若AB CD ==2==AC BD ，AD BC ==ABCD 的外接球的表面积为（ ） A ．2πB ．4πC ．6πD ．8π技巧7 外接球之矩形模型【例7】在四面体ABCD 中，AB =，1DA DB CA CB ====，则四面体ABCD 的外接球的表面积为( ) A ．π B ．2πC ．3πD ．4π【举一反三】1．四面体SABC 中，AC BC ⊥，SA ⊥平面ABC ，SA =AC =BC =，则该四面体外接球的表面积为（ ） A ．323πB ．163πC ．16πD ．32π2．已知四面体ABCD 满足：1AB BC CD DA AC =====，BD =，则四面体ABCD 外接球的表面积为_______.技巧8 内切球半径【例8】正四面体的外接球与内切球的表面积比为（ ） A ．9: 1 B ．27: 1C ．3: 1D ．不确定【举一反三】1．如图所示，球内切于正方体．如果该正方体的棱长为a ，那么球的体积为（ ）A ．343a πB ．3aC 3aD ．316a π2．已知直三棱柱ABC -A 1B 1C 1的底面ABC 为等边三角形，若该棱柱存在外接球与内切球，则其外接球与内切球表面积之比为（ ） A ．25︰1B ．1︰25C ．1︰5D ．5︰13的内切球，则此棱柱的体积是（ ）.A ．3B ．354cmC ．327cmD ．3巩固练习1．直三棱柱111ABC A B C -的所有顶点都在同一球面上，且2AB AC ==，90BAC ∠=︒，1AA =则该球的表面积为（ ） A ．40πB ．32πC ．10πD ．8π2．在三棱锥P ABC -中，AB AC ==120BAC ∠=，PB PC ==，PA =棱锥的外接球的表面积为（ ） A ．40πB ．20πC ．80πD ．60π3．已知四棱锥A BCDE -中，AB ⊥平面BCDE ，底面BCDE 是边长为2的正方形，且3AB =，则该四棱锥外接球的表面积为（ ） A ．4πB ．174πC ．17πD ．8π4．已知点P ，A ，B ，C 在同一个球的球表面上，PA ⊥平面ABC ，AB ⊥AC ，PB BC ，PC =2，则该球的表面积为（ ） A ．6πB ．8πC ．12πD ．16π5．四面体A BCD -中，AB ⊥底面BCD ，AB BD ==1CB CD ==，则四面体A BCD -的外接球表面积为（ ） A ．3πB ．4πC ．6πD ．12π6．平行四边形ABCD 中，AB BD ⊥，且2224AB BD +=，沿BD 将四边形折起成平面ABD ⊥平面BDC ，则三棱锥A BCD -外接球的表面积为（ ）A ．2π B ．2πC ．4πD ．16π7．张衡(78年~139年)是中国东汉时期伟大的天文学家､文学家､数学家.他的数学著作有《算罔论》，他曾经得出结论：圆周率的平方除以十六等于八分之五.已知正方体的外接球与内切球上各有一个动点A ，B ，若线段AB 1，利用张衡的结论可得该正方体的外接球的表面积为（ ）A ．30B ．C ．D ．368．已知直三棱柱111ABC A B C -的顶点都在球O 上，且4AB =，16AA =，30ACB ∠=︒，则此直三棱柱的外接球O 的表面积是（ ） A ．25πB ．50πC ．100πD ．500π39．已知三棱柱111ABC A B C -(侧棱1AA ⊥底面111A B C ，底面111A B C △是正三角形)内接于球O ，1AB 与底面111A B C 所成的角是45°.若正三棱柱111ABC A B C -的体积是3，则球O 的表面积是（ ） A ．228π c m 3B ．256π c m 3C ．27π c m 3D ．214π c m 310．在四棱锥P ABCD -中，//BC AD ，AD AB ⊥，AB =6AD =，4BC =，PA PB PD ===P BCD -外接球的表面积为（ ）A ．60πB ．40πC ．100πD ．80π11．已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是（ ） A ．10B ．20πC ．24πD ．32π12．我国古代数学名著《九章算术》中，将底面是直角三角形的直三棱柱（侧棱垂直于底面的三棱柱）称之为“堑堵”．如图，三棱柱111ABC A B C -为一个“堑堵”，底面ABC 是以AB 为斜边的直角三角形且5AB =，3AC =，点P 在棱1BB 上，且1PC PC ⊥，当1APC 的面积取最小值时，三棱锥P ABC -的外接球表面积为（ ）A ．45π2B C ．30π D ．45π13．已知正三棱柱111ABC A B C -的体积为54，6AB =，记三棱柱111ABC A B C -的外接球为球1O ，则外接球1O 的表面积是__________．14．在三棱锥P ABC -中，侧棱PA ⊥底面,120,1ABC BAC AB AC ∠===且2,PA BC =则该三棱锥的外接球的体积为__________．15．如图所示，在三棱锥B ACD -中，3ABC ABD DBC π∠=∠=∠=，3AB =，2BC BD ==，则三棱锥B ACD -的外接球的表面积为______.16．鳖臑（bi ē n ào ）出自《九章算术·商功》：“斜解立方，得两重堵．斜解壍堵，其一为阳马，一为鳖臑．”鳖臑是我国对四个面均为直角三角形的三棱锥的古称．如图，三棱锥A BCD -是一个鳖臑，其中AB BC ⊥，AB BD ⊥，BC CD ⊥，且4AB BC DC ===，过点B 向AC 引垂线，垂足为E ，过E作CD 的平行线，交AD 于点F ，连接BF ．设三棱锥A BCD -的外接球的表面积为1S ，三棱锥A BEF -的外接球的表面积为2S ，则12S S =________．17．若体积为8的正方体的各个顶点均在一球面上，则该球的体积为______.18．在我国古代数学名著《九章算术》中，把两底面为直角三角形的直棱柱称为“堑堵”，已知三棱柱111ABC A B C -是一个“堑堵”，其中12AB BB ==，1BC =，AC =表面积为___.19．在长方体1111ABCD A B C D -中，1AB CC ==1BC =，点M 在正方形11CDD C 内，1C M ⊥平面1ACM ，则三棱锥11M ACC -的外接球表面积为______.20．在四面体S ABC -中，SA ⊥平面ABC ，120BAC ∠=︒，2SA =，BC =球的表面积为________.21．我国古代数学名著《九章算术》中将正四棱锥称为方锥.已知某方锥各棱长均为2，则其内切球的体积为______.22．已知在三棱锥P ABC -中，PA PB ==，23APB ∠=π，6ACB π∠=，则当点C 到平面PAB 的距离最大时，三棱锥P ABC -外接球的表面积为_____．23．三棱锥A BCD -中，60ABC CBD DBA ===∠∠∠，2BC BD ==，面ACD，则此三棱锥外接球的表面积为___．24．在三棱锥P ABC -中，平面PAB 垂直平面ABC，PA PB AB AC ====120BAC ∠=︒，则三棱锥P ABC -外接球的表面积为_________.25在三棱锥D ABC -中，AD ⊥平面ABC ，3AC =，BC =1cos 3BAC ∠=，若三棱锥D ABC-，则此三棱锥的外接球的表面积为______26．设A ，B ，C ，D 为球O 的球面上的四个点，满足2AB AC BC ===，DC BD ==.若四面体ABCD 的表面积为O 的表面积为______.。

高三数学专题外接球高三数学专题：外接球1.正棱柱和长方体的外接球的球心是其中心。

例1：一个正四棱柱的高为4，体积为16，其外接球的表面积是多少？解：由于正四棱柱的底面是一个正方形，所以它的体积为$V=\frac{1}{3}hS=16$，其中 $h=4$，$S$ 是正方形的面积。

解得 $S=12$。

正方形的对角线长为 $d=\sqrt{2}S=2\sqrt{6}$，所以外接球的半径为 $R=\frac{d}{2}=\sqrt{6}$，表面积为$S=4\pi R^2=24\pi$。

因此，答案为 C。

2.补形法（补成长方体）。

例2：一个三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是多少？解：将三棱锥补成长方体，如下图所示。

长方体的对角线长为 $d=\sqrt{3^2+3^2+3^2}=3\sqrt{3}$，所以外接球的半径为$R=\frac{d}{2}=\frac{3\sqrt{3}}{2}$，表面积为 $S=4\piR^2=27\pi$。

因此，答案为 B。

3.依据垂直关系找球心。

例3：一个三棱锥P-ABC 的四个顶点均在同一个球面上，底面△ABC 满足 BA=BC=6，∠ABC=π，若该三棱锥体积的最大值为3，则其外接球的体积为多少？解：根据垂直关系，三棱锥的外接球的球心位于底面△ABC 的垂心 H 上。

设球心为 O，底面中心为 M，则$OM=OH-R$，其中 $R$ 是外接球的半径。

根据勾股定理，$AH=\sqrt{AP^2-PH^2}=\sqrt{R^2-\frac{1}{4}BC^2}$，$BM=MC=\frac{1}{2}BC=3$，所以 $OM=\sqrt{OH^2-HM^2}=\sqrt{R^2-(AH+BM)^2}=\sqrt{R^2-\left(R^2-\frac{1}{4}BC^2+9\right)}=\frac{\sqrt{3}}{2}$。

由于三棱锥的体积最大值为3，所以 $AH\cdot BC=6\sqrt{3}$，解得$R=\frac{3\sqrt{3}}{2}$，体积为$V=\frac{1}{3}Ah=\frac{1}{3}\cdot 6\sqrt{3}\cdotR=9\sqrt{3}\pi$。