03函数知识要点回顾、常见题型配置(02)

3.1.2 表示函数的方法课程标准学习目标（1）在实际情境中, 会根据不同的需要选择恰当的方法（如图象法、列表法、解析法) 表示函数, 理解函数图象的作用。

（1）会求函数的解析式; （难点)（2）列表法表示函数（3）图象法表示函数。

知识点01 解析法把常量和表示自变量的字母用一系列运算符号连接起来得到的式子，叫作解析式（也叫作函数表达式或函数关系式），解析法就是用解析式来表示函数的方法。

比如正方形周长C 与边长a 间的解析式为C =4a ，圆的面积S 与半径r 的解析式S =πr 2等.求函数解析式的方法① 配凑法 ② 待定系数法③ 换元法④ 构造方程组法 ⑤ 代入法【即学即练1】已知函数f (x )=1x ，则f (x +1)=（ ）A ．f (x +1)=1x+1B ．f (x +1)=1x―1C ．f (x +1)=2x―1D ．f (x +1)=2x+1知识点02 列表法如上表，我们很容易看到y与r之间的函数关系.在初中刚学画一次函数时，想了解其图像是一直线，第一步就是列表，其实就是用表格法表示一次函数.【即学即练2】函数f(x)与g(x)的对应关系如下表．x―101x123f(x)132g(x)0―11则g(f(―1))的值为（）A．0B．3C．1D．―1知识点03 图象法如上图，很清晰的看到某天空气质量指数I与时间t两个变量之间的关系，特别是其趋势.数学中的“数形结合”也就是这回事，它是数学一大思想，在高中解题中识图和画图尤为重要.【即学即练3】购买某种饮料x听，所需钱数是y元．若每听2元，试分别用解析法、列表法、图象法将y表示成x(x∈{1,2,3,4})的函数．【题型一：解析法表示函数】例1．若函数y=f(x)对任意x∈R，均有f(x+y)=f(x)+f(y)，则下列函数可以为y=f(x)解析式的是（）A．f(x)=x+1B．f(x)=2x―1C．f(x)=2x D．f(x)=x2+x变式1-1．一个等腰三角形的周长为20，底边长y是一腰长x的函数，则（）A．y=10―x(0<x≤10)B．y=10―x(0<x<10)C．y=20―2x(5≤x≤10)D．y=20―2x(5<x<10)变式1-2．下列函数中，对任意x，不满足2f(x)=f(2x)的是（）A．f(x)=|x|B．f(x)=―2xC．f(x)=x―|x|D．f(x)=x―1变式1-3．定义在R上的函数f(x)满足f(xy)=f(x)+f(y)，且f(4)=8，则f（）A B．2C．4D．6变式1-4．若函数f(x)满足f(a+b)=f(a)+f(b)1―f(a)f(b)，且f(2)=12，f(3)=13，则f(7)=A．1B．3C．43D．83【方法技巧与总结】理解函数解析式y=f(x)，仅是用一系列运算符号连接起来得到的式子，它对定义域内任何一个值都是成立的；比如①函数f(x)=x2(x>0)，可取任何大于0的值进行赋值；②若函数f(x)满足f(xy)=f(x)+f(y)，则x ,y 取任何实数均可使得等式成立.【题型二：求函数的解析式】方法1 待定系数法例2．若二次函数f(x)满足f(x +1)―f(x)=2x ，且f(0)=1，则f(x)的表达式为（ ）A ．f(x)=―x 2―x ―1B ．f(x)=―x 2+x ―1C ．f(x)=x 2―x ―1D ．f(x)=x 2―x +1变式2-1．已知f(x)是一次函数，且2f(2)―3f(1)=5，2f(0)―f(―1)=3，则f(x)=（ ）A ．3x ―2B ．3x +2C ．92x ―12D ．4x ―1变式2-2．已知函数f(x)是一次函数，且f[f(x)―2x]=3，则f(5)=（ ）A ．11B ．9C ．7D ．5变式2-3．已知二次函数f (x )满足f(2)=―1,f(1―x)=f(x)，且f (x )的最大值是8，则此二次函数的解析式为f(x)=（ ）A ．―4x 2+4x +7B ．4x 2+4x +7C ．―4x 2―4x +7D ．―4x 2+4x ―7方法2 换元法例3．已知函数f 2)=x ―，则f(x)的解析式为（ ）A ．f(x)=x 2+1(x ≥0)B ．f(x)=x 2+1(x ≥―2)C ．f(x)=x 2(x ≥0)D ．f(x)=x 2(x ≥―2)变式3-1．已知函数f(1―x)=1―x2x2(x≠0)，则f(x)=（）A．1(x―1)2―1(x≠0)B．1(x―1)2―1(x≠1)C．4(x―1)2―1(x≠0)D．4(x―1)2―1(x≠1)变式3-2．设函数f1+=2x+1，则f(x)的表达式为（）A．1+x1―x (x≠1)B．1+xx―1(x≠1)C．1―x1+x (x≠―1)D．2xx+1(x≠―1)变式3-3．已知f1)=x+3，则f(x)=（）A．x2―2x+2(x≥0)B．x2―2x+4(x≥1)C．x2―2x+4(x≥0)D．x2―2x+2(x≥1)方法3 方程组法例4．已知定义在(0,+∞)上的函数f(x)满足f(x)=―15x，则f(2)的值为（）A．152B．154C．174D．172变式4-1．若函数f(x)，g(x)满足f(x)―=3x―4x，且f(x)+g(x)=2x+6，则f(2)+g(―1)=（）A．6B．7C．8D．9变式4-2．已知函数f(x)满足f(x)+2f(2―x)=1x―1，则f(3)的值为（）A．―73B．―109C．―415D．―16变式4-3．已知定义在R上的函数f(x)，满足f(x)+2f(―x)=2x+12.(1)求f(x)的解析式；(2)若点P(a,b)在y=f(x)图像上自由运动，求4a+2b的最小值.【方法技巧与总结】求函数解析式，可视情况而定，1 若已知函数类型，可用待定系数法；2 若求f(g(x))型函数解析式，可用换元法，此时要注意新自变量的取值范围；3 若求满足某函数方程的函数解析式，则用方程组的方法.【题型三：列表法表示函数】例5．设已知函数f(x),g(x)如下表所示：x12345f(x)54321g(x)43215则不等式f(g(x))>g(f(x))的解集为（）A．{1,3}B．{5,3}C．{2,3,4}D．{5}变式5-1．已知函数f(x),g(x)分别由下表给出：则f[g(2)]的值是（）x123f(x)131g(x)321A．1B．2C．3D．1和2变式5-2．观察下表：x―3―2―1123f(x)51―1―335g(x)1423―2―4则f[f(―1)―g(3)]=（）A．―4B．―3C．3D．5变式5-3．德国数学家狄利克在1837年时提出：“如果对于x的每一个值，y总有一个完全确定的值与之对应，则y是x的函数，”这个定义较清楚地说明了函数的内涵.只要有一个法则，使得取值范围中的每一个值，有一个确定的y和它对应就行了，不管这个对应的法则是公式、图象，表格或是其它形式.已知函数f(x)由下表给出，则f10f）x x≤11<x<2x≥2y123A．0B．1C．2D．3【方法技巧与总结】表格法表示函数，要注意看清楚变量数值之间的对应关系.【题型四：图象法表示函数】例6．如图所示的4个图象中，与所给3个事件最吻合的顺序为（）①我离开家后，心情愉快，缓慢行进，但最后发现快迟到时，加速前进；②我骑着自行车上学，但中途车坏了，我修理好又以原来的速度前进；③我快速的骑着自行车，最后发现时间充足，又减缓了速度.A．③①②B．③④②C．②①③D．②④③变式6-1．小明骑车上学，开始时匀速行驶，中途因车流量大而减速行驶，后为了赶时间加速行驶，与以上事件吻合得最好的图象是（）A．B．C．D．变式6-2．俗话说，“一分耕耘，一分收获”．那么，在实际生活中，如果把收获看成付出的函数，它们之间的关系可以怎样描述呢？情境甲：当以匀速的方式驾驶汽车时，行驶的里程与所用的时间之间的关系；情境乙：家长过分宠爱孩子，有时还有可能付出增加会导致收获减少；情境丙：在我们学习新的知识时，可能一开始效率会比较高，单位时间的付出得到的收获会比较大，但随着付出的时间越来越多，单位时间的付出得到的收获会变少．请问依次与下面三个图象所表示的收获与付出的关系相对应的情境正确的一项是（）A．甲、乙、丙B．丙、甲、乙C．甲、丙、乙D．乙、丙、甲变式6-3．已知完成某项任务的时间t与参加完成此项任务的人数x之间满足关系式t=ax+bx(a∈R,b∈R)，当x=2时，t=100；当x=4时，t=53，且参加此项任务的人数不能超过8．（1）写出t关于x的解析式；（2）用列表法表示此函数；（3）画出此函数的图象．【方法技巧与总结】图象法表示函数，达到“一目了然”的效果，对于函数图象还注意函数的定义域，函数图象的上升下降趋势，增减趋势的缓急等等！一、单选题1．已知定义在[―2,2]上的函数y=f(x)表示为:x[―2,0)0(0,2]y10―2设f(1)=m，f(x)的值域为M，则（）A．m=1,M={―2,0,1}B．m=―2,M={―2,0,1}C．m=1,M={y|―2≤y≤1}D．m=1,M={y|―2≤y≤1}2.函数y=g(x)的对应关系如下表所示，函数y=f(x)的图象是如图所示的曲线ABC，则g(f(3)―1)的值为（）x123g(x)20230―2023A．2023B．0C．―1D．―20233.设f(x)=xx2+1，则( )A．f(x)B．―f(x)C．1f(x)D．―1f(x)4.如图，公园里有一处扇形花坛，小明同学从A点出发，沿花坛外侧的小路顺时针方向匀速走了一圈(A→B→O→A)，则小明到O点的直线距离y与他从A点出发后运动的时间t之间的函数图象大致是（）A．B．C．D．5.已知函数f(x)=x3+ax2+bx+c，且0<f(―1)=f(―2)=f(―3)≤3，则（）A．c≤3B．3<c≤6C．6<c≤9D．c>96.已知f+1)=x+3，则f(x)的解析式为f(x)=（）A．x2―2x+4B．x2+3C．x2―2x+4(x≥1)D．x2+3(x≥1)7.函数f(x)满足2f(x)―f(1―x)=x，则函数f(x)=（）A．x―2B．x+13C．x―13D．―x+28.某农贸市场出售西红柿，当价格上涨时，供给量相应增加，而需求量相应减少，具体调查结果如下表：表一市场供给量单价（元/kg）2 2.4 2.8 3.2 3.64供给量（1000kg）506070758090表一市场需求量单价（元/kg）4 3.4 2.9 2.6 2.32需求量（1000kg）506065707580根据以上提供的信息，市场供需平衡点（即供给量和需求量相等时的单价）应在区间（　）A．(2.3,2.6)内B．(2.4,2.6)内C．(2.6,2.8)内D．(2.8,2.9)内二、多选题9．某工厂8年来某产品产量y与时间t的函数关系如图，则以下说法中正确的是（）A．前2年的产品产量增长速度越来越快B．前2年的产品产量增长速度越来越慢C．第2年后，这种产品停止生产D．第2年后，这种产品产量保持不变10.下列说法正确的是（）A．函数f(x+1)的定义域为[―2,2)，则函数f(x)的定义域为[―1,3)B．f(x)=x2x和g(x)=x表示同一个函数C．函数y=1x2+3的值域为0D．定义在R上的函数f(x)满足2f(x)―f(―x)=x+1，则f(x)=x3+111.已知f(0)=12，f(x+y)=f(x)f(1―y)+f(y)f(1―x)，则（）A．f(1)=12B．f(x)=12恒成立C．f(x+y)=2f(x)f(y)D．满足条件的f(x)不止一个三、填空题12．下列表示函数y=f(x)，则f(11)=．x0<x<55≤x<1010≤x<1515≤x≤20y234513.已知y=f(x)是二次函数，且f(0)=1，f(x+1)―f(x)=2x，则y=f(x)=．14.若正整数m，n只有1为公约数，则称m，n互质.对于正整数n，φ(n)是小于或等于n的正整数中与n互质的数的个数，函数φ(n)以其首位研究者欧拉命名，称为欧拉函数，例如：φ(3)=2，φ(7)=6，φ(9)=6，则下列说法正确的序号是．①φ(5)=φ(10)；②φ(2n―1)=1；③φ(32)=16；④φ(2n+2)>φ(2n)，n是正整数．四、解答题15．下图所示为某市一天24小时内的气温变化图，根据图象回答下列问题.(1)全天的最高气温、最低气温分别是多少？(2)大约在什么时刻，气温为0°C？(3)大约在什么时刻内，气温在0°C以上？(4)变量Q是关于变量t的函数吗？16.已知f(x)=1（x∈R，且x≠―1），g(x)=x2+2(x∈R)．1+x(1)求f(2)，g(2)的值；(2)求f(g(2))，g(f(2))的值；(3)求f(x)和g(x―1)的值域．17.已知二次函数f(x)满足f(x)=f(2―x)，且f(0)=―3，f(1)=―4.(1)求函数f(x)的解析式；(2)若g(x)=x+1，比较f(x)与g(x)的大小.18.已知二次函数f(x)=ax2+bx+c(a,b,c∈R)只能同时满足下列三个条件中的两个：①a=2；②不等式f(x)>0的解集为{x|―1<x<3 }；③函数f(x)的最大值为4.(1)请写出满足题意的两个条件的序号，并求出函数f(x)的解析式；(2)求关于x的不等式f(x)≥(m―1)x2+2(m∈R)的解集.19．已知函数y=f(x)与y=g(x)的定义域均为D，若对任意的x1､x2∈D(x1≠x2)都有|g(x1)―g(x2)|<|f(x1)―f(x2)|成立，则称函数y=g(x)是函数y=f(x)在D上的“L函数”.(1)若f(x)=3x+1,g(x)=x,D=R，判断函数y=g(x)是否是函数y=f(x)在D上的“L函数”，并说明理由；(2)若f(x)=x2+2,g(x)==[0,+∞)，函数y=g(x)是函数y=f(x)在D上的“L函数”，求实数a的取值范围；(3)若f(x)=x,D=[0,2]，函数y=g(x)是函数y=f(x)在D上的“L函数”，且g(0)=g(2)，求证：对任意的x1､x2∈D(x1≠x2)都有|g(x1)―g(x2)|<1.。

第03讲 一次函数的图像与性质1. 理解一次函数的定义2. 学会观察一次函数图像并分析，判断函数值随自变量的变化而变化3. 掌握求一次函数解析式方法并解决简单的几何面积问题；4.掌握一次函数与方程组及不等式的关联。

知识点1：一次函数的定义如果 y=kx+b （k ，b 是常数，k ≠0 ）的函数，叫做一次函数，k 叫比例系数。

注意：当b=0时，一次函数y=kx+b 变为y=kx ，正比例函数是一种特殊的一次函数。

知识点2：一次函数图像和性质一次函数图象与性质用表格概括下：增减性 k ＞0 k ＜0从左向右看图像呈上升趋势，y 随x 的增大而增大从左向右看图像呈下降趋势，y 随x 的增大而较少图像（草图）b ＞0 b=0b ＜0b ＜0 b=0b ＜0经过象限一、二、三一、三 一、三、四 一、二、四 二、四 二、三、四与y 轴的交点位置b ＞0，交点在y 轴正半轴上；b=0,交点在原点；b ＜0，交点在y 轴负半轴上 【提分要点】：1. 若两直线平行，则；2. 若两直线垂直，则知识点3：一次函数的平移1、一次函数图像在x 轴上的左右平移。

向左平移n 个单位，解析式y=kx+b 变化为y=k （x+n ）+b ；向右平移n 个单位解析式y=kx+b 变化为y=k （x-n ）+b 。

口诀：左加右减（对于y=kx+b 来说，对括号内x 符号的增减）（此处n 为正整数）。

2、一次函数图像在y 轴上的上下平移。

向上平移m 个单位解析式y=kx+b 变化为y=kx+b+m ；向下平移m 个单位解析式y=kx+b 变化为y=kx+b-m 。

口诀：上加下减（对于y=kx+b 来说，只改变b ）（此处m 为正整数） 知识点4：求一次函数解析式用待定系数法求一次函数解析式的步骤： 基本步骤：设、列、解、写 ⑴设：设一般式y=kx+b⑵列：根据已知条件，列出关于k 、b 的方程（组） ⑶解：解出k 、b ； ⑷写：写出一次函数式知识点5：一次函数与一元一次方程的关系直线 y=kx+b （k ≠0）与 x 轴交点的横坐标，就是一元一次方程 kx+b=0（k ≠0）的解．求 直线 y=kx+b （k ≠0）与 x 轴交点时,（1）可令 y=0，得到方程 kx+b=0（k ≠0），解方程得 __kb-=x ____________ ，（2）直线 y=kx+b 交 x 轴于点_（0，kb-）_______ , 就是直线 y=kx+b 与 x 轴交点的横坐标．知识点6：一次函数与一元一次不等式（1）由于任何一个一元一次不等式都可以转化为＞0或＜0或≥0或≤0（、为常数，≠0）的形式，所以解一元一次不等式可以看作：当一次函数的值大于0（或小于0或大于等于0或小于等于0）时求相应的自变量的取值范围.ax b +ax b +ax b +ax b +a b a y ax b =+（2）如何确定两个不等式的大小关系（≠，且）的解集的函数值大于的函数值时的自变量取值范围直线在直线的上方对应的点的横坐标范围．知识点7：一次函数与二元一次方程组1.一次函数与二元一次方程组的关系2.一次函数与二元一次方程的数形结合【题型1：一次函数的定义】【典例1-1】（2023春•安化县期末）下列关于x 的函数是一次函数的是（ ） A ．B ．C ．y ＝x 2﹣1D ．y ＝3x【典例1-2】（2023春•博兴县期末）一次函数y ＝（m ﹣2）x n ﹣1+3是关于x 的一次函数，则m ，n 的值为（ ） A ．m ≠2且n ＝2 B ．m ＝2且n ＝2C ．m ≠2且n ＝1D ．m ＝2且n ＝1【变式1-1】（2023春•兴城市期末）若函数y ＝（a ﹣2）x |a |﹣1+4是一次函数，则a 的值为（ ） A ．﹣2 B ．±2C ．2D ．0【变式1-2】（2023春•易县期末）下列函数中，y 是x 的一次函数的是（ ）ax b cx d +>+a c 0ac ≠⇔y ax b =+y cx d =+x ⇔y ax b =+y cx d =+A．y＝1B．C．y＝2x﹣3D．y＝x2【变式1-3】（2023•南关区校级开学）函数y＝（2m﹣1）x n+3+（m﹣5）是关于x的一次函数的条件为（）A．m≠5且n＝﹣2 B．n＝﹣2C．m≠且n＝﹣2D．m≠【题型2：判断一次函数图像所在象限】【典例2】（2023春•岳阳县期末）一次函数y＝x﹣1的图象一定不经过（）A．第一象限B．第二象限C．第三象限D．第四象限【变式2-1】（2023春•长沙期末）一次函数y＝3x﹣5的图象经过（）A．第一、二、三象限B．第一、二、四象限C．第二、三、四象限D．第一、三、四象限【变式2-2】（2023春•郧西县期末）在平面直角坐标系xOy中，函数y＝2x﹣1的图象经过（）A．第一、二、三象限B．第一、二、四象限C．第二、三、四象限D．第一、三、四象限【变式2-3】（2023春•黔东南州期末）一次函数y＝3x﹣2的图象经过的象限是（）A．第一、二、四象限B．第一、二、三象限C．第一、三、四象限D．第二、三、四象限【题型3：一次函数图像的性质】【典例3】（2023春•西城区校级期中）关于一次函数y＝2x﹣4的图象和性质，下列叙述正确的是（）A．与y轴交于点（0，2）B．函数图象不经过第二象限C．y随x的增大而减小D．当时，y＜0【变式3-1】（2023春•启东市期末）下列关于一次函数y＝﹣2x+2的图象的说法中，错误的是（）A．函数图象经过第一、二、四象限B．函数图象与x轴的交点坐标为（2，0）C．当x＞0时，y＜2D．y的值随着x值的增大而减小【变式3-2】（2022秋•罗湖区期末）关于函数y＝﹣2x﹣5，下列说法不正确的是（）A．图象是一条直线B．y的值随着x值的增大而减小C．图象不经过第一象限D．图象与x轴的交点坐标为（﹣5，0）【变式3-3】（2023春•邓州市期末）下列四个选项中，不符合直线y＝﹣x﹣3的性质特征的选项是（）A．经过第二、三、四象限B．y随x的增大而减小C．与x轴交于（3，0）D．与y轴交于（0，﹣3）【变式3-4】（2023春•建华区期末）关于函数y＝﹣x+3的图象，下列结论错误的是（）A．图象经过一、二、四象限B．与y轴的交点坐标为（3，0）C．y随x的增大而减小D．图象与两坐标轴相交所形成的直角三角形的面积为【题型4：根据一次函数增减性求含参取值范围】【典例4】（2023秋•射阳县校级月考）若一次函数y＝﹣3mx﹣4（m≠0），当x的值增大时，y的值也增大，则m的取值范围为（）A．m＞0B．m＜0C．0＜m＜3D．无法确定【变式4-1】（2023春•铜仁市期末）已知一次函数y＝（m+1）x﹣2，y的值随x的增大而减小，则点P（﹣m，m）所在象限为（）A．第一象限B．第二象限C．第三象限D．第四象限【变式4-2】（2023•雁塔区校级四模）若一次函数y＝（k﹣2）x+1的函数值y随x增大而增大，则（）A．k＞0B．k＜0C．k＜2D．k＞2【变式4-3】（2023•贵阳模拟）已知函数y＝（2m﹣1）x是正比例函数，且y 随x的增大而增大，那么m的取值范围是（）A．m＞B．m＜C．m＞0D．m＜0【题型5：根据k、b值判断一次函数图像的】【典例5】（2023春•港北区期末）两个一次函数y1＝ax+b与y2＝bx+a，它们在一直角坐标系中的图象可能是（）A．B．C．D．【变式5-1】（2023春•富锦市期末）同一平面直角坐标系中，函数y＝ax+b与y ＝bx+a的图象可能是（）A．B．C．D．【变式5-2】（2023春•易县期末）已知kb＞0，且b＜0，则一次函数y＝kx+b 的图象大致是（）A．B．C．D．【变式5-3】（2023春•商城县期末）一次函数y＝mx+n与y＝mnx（mn≠0），在同一平面直角坐标系的图象是（）A．B．C．D．【题型6：比较一次函数值的大小】【典例6】（2023春•丹江口市期末）一次函数y＝4x+m的图象上有三个点A（﹣2，a），B（3，b），C（﹣0.5，c），据此可以判断a，b，c的大小关系为（）A．a＜c＜b B．a＜b＜c C．c＜a＜b D．b＜c＜a【变式6-1】（2023春•甘井子区期末）已知点A（﹣2，m），B（3，n）在一次函数y＝2x+1的图象上，则m与n的大小关系是（）A．m＞n B．m＝n C．m＜n D．无法确定【变式6-2】（2023春•庐江县期末）若点M（﹣1，y1），N（2，y2）都在直线y＝﹣x+b上，则下列大小关系成立的是（）A．y1＞y2＞b B．y2＞y1＞b C．y2＞b＞y1D．y1＞b＞y2【变式6-3】（2022秋•太仓市期末）已知点，（1，y2），（﹣2，y3）都在直线上，则y1，y2，y3的大小关系是（）A．y2＜y3＜y1B．y2＜y1＜y3C．y1＜y3＜y2D．y3＜y2＜y1【题型7：一次函数的变换问题】【典例7】（2023春•东兰县期末）在平面直角坐标系中，将直线y＝2x+b沿y 轴向下平移2个单位后恰好经过原点，则b的值为（）A．﹣2B．2C．4D．﹣4【变式7-1】（2023春•通河县期末）直线y＝﹣5x向上平移2个单位长度，得到的直线的解析式为（）A．y＝5x+2B．y＝﹣5x+2C．y＝5x﹣2D．y＝﹣5x﹣2【变式7-2】（2023春•卫滨区校级期末）一次函数y＝﹣2x+b的图象向下平移3个单位长度后，恰好经过点A（2，﹣3），则b的值为（）A．4B．﹣4C．2D．﹣2【变式7-3】（2023•娄底）将直线y＝2x+1向右平移2个单位后所得图象对应的函数表达式为（）A．y＝2x+5B．y＝2x+3C．y＝2x﹣2D．y＝2x﹣3【变式7-4】（2023•临潼区一模）在平面直角坐标系中，若将一次函数y＝2x+m ﹣1的图象向右平移3个单位后，得到一个正比例函数的图象，则m的值为（）A．﹣7B．7C．﹣6D．6【题型8：求一次函数解析式】【典例8】（2023春•西华县期末）已知直线l1：y＝x+3与x轴、y轴分别交于点A、点B．（1）求A、B两点的坐标；（2）将直线l1向右平移8个单位后得到直线l2，求直线l2的解析式；（3）设直线l2与x轴的交点为P，求△P AB的面积．【变式8-1】（2023春•庐江县期末）已知某一次函数的图象与y轴的交点坐标为（0，﹣4），当x＝2时，y＝﹣3．（1）求一次函数的解析式；（2）将该函数的图象沿x轴向右平移3个单位，求平移后的图象与坐标轴围成三角形面积．【变式8-2】（2023春•商南县校级期末）如图，直线y＝﹣2x+2与x轴交于点A，与y轴交于点B．（1）求点A，B的坐标．（2）若点C在x轴上，且S△ABC ＝2S△AOB，求点C的坐标．【变式8-3】（2023春•鼓楼区校级期末）已知一次函数y＝kx+4的图象过点B （2，3）．（1）求k的值；（2）直线y＝kx+b与x轴的交点为C点，点P在该函数图象上，且点P在x 轴上方，△POC的面积为4，求P点的坐标．【题型9：一次函数与一元一次方程】【典例9】（2022春•围场县期末）一次函数y＝ax+b的图象如图所示，则方程ax+b＝0的解为（）A．x＝﹣2B．y＝﹣2C．x＝1D．y＝1【变式9-1】（2022秋•固镇县校级月考）如图，直线y＝ax+b过点（0，﹣2）和点（﹣3，0），则方程ax+b+1＝0的解是（）A．x＝﹣3B．x＝﹣2C．x＝﹣1.5D．x＝﹣1【变式9-2】（2022春•冠县期末）如图所示，一次函数y＝kx+b（k≠0）的图象经过点P（3，2），则方程kx+b＝2的解是（）A．x＝1B．x＝2C．x＝3D．无法确定【变式9-3】（2022秋•广饶县校级期末）已知关于x的一次函数y＝3x+n的图象如图，则关于x的一次方程3x+n＝0的解是（）A．x＝﹣2B．x＝﹣3C．D．【典例10】（2022秋•城关区校级期末）如图，直线y＝2x与y＝kx+b相交于点P（m，2），则关于x的方程kx+b＝2的解是（）A．x＝B．x＝1C．x＝2D．x＝4【变式10-1】（2022秋•余姚市校级期末）如图，直线y＝2x与y＝kx+b相交于点P（m，2），则关于x的方程kx+b＝2的解是．【变式10-2】（2022秋•高陵区期末）在平面直角坐标系xOy中，函数y＝kx和y＝﹣x+b的图象，如图所示，则方程kx＝﹣x+b的解为．【题型10：一次函数与一元一次不等式】【典例11】（2023春•阿克苏地区期末）如图，直线y＝﹣2x+b与x轴交于点（3，0），那么不等式﹣2x+b＜0的解集为（）A．x＜3B．x≤3C．x≥3D．x＞3【变式11-1】（2023春•两江新区期末）如图，一次函数y＝kx+b的图象与x轴和y轴的交点分别为（﹣2，0）、（0，1），求关于x的不等式kx+b＜1的解集．【变式11-2】（2023春•松江区期末）如图：点（﹣2，3）在直线y＝kx+b（k ≠0）上，则不等式kx+b≥3关于x的解集是．【变式11-3】（2021秋•建邺区期末）表1、表2分别是函数y1＝k1x+b1与y2＝k2x+b2中自变量x与函数y的对应值．则不等式y1＞y2的解集是．表1x﹣4﹣3﹣2﹣1y﹣1﹣2﹣3﹣4表2x﹣4﹣3﹣2﹣1y﹣9﹣6﹣301．（2023•乐山）下列各点在函数y＝2x﹣1图象上的是（）A．（﹣1，3）B．（0，1）C．（1，﹣1）D．（2，3）2．（2023•兰州）一次函数y＝kx﹣1的函数值y随x的增大而减小，当x＝2时，y的值可以是（）A．2B．1C．﹣1D．﹣2 3．（2023•鄂州）象棋起源于中国，中国象棋文化历史悠久．如图所示是某次对弈的残图，如果建立平面直角坐标系，使棋子“帅”位于点（﹣2，﹣1）的位置，则在同一坐标系下，经过棋子“帅”和“马”所在的点的一次函数解析式为（）A．y＝x+1B．y＝x﹣1C．y＝2x+1D．y＝2x﹣14．（2023•沈阳）已知一次函数y＝kx+b的图象如图所示，则k，b的取值范围是（）A．k＞0，b＞0B．k＞0，b＜0C．k＜0，b＞0D．k＜0，b＜0 5．（2023•益阳）关于一次函数y＝x+1，下列说法正确的是（）A．图象经过第一、三、四象限B．图象与y轴交于点（0，1）C．函数值y随自变量x的增大而减小D．当x＞﹣1时，y＜06．（2023•娄底）将直线y＝2x+1向右平移2个单位后所得图象对应的函数表达式为（）A．y＝2x+5B．y＝2x+3C．y＝2x﹣2D．y＝2x﹣3 7．（2023•台湾）坐标平面上，一次函数y＝﹣2x﹣6的图象通过下列哪一个点（）A．（﹣4，1）B．（﹣4，2）C．（﹣4，﹣1）D．（﹣4，﹣2）8．（2023•通辽）在平面直角坐标系中，一次函数y＝2x﹣3的图象是（）A．B．C．D．9．（2023•荆州）如图，直线y＝﹣x+3分别与x轴，y轴交于点A，B，将△OAB绕着点A顺时针旋转90°得到△CAD，则点B的对应点D的坐标是（）A．（2，5）B．（3，5）C．（5，2）D．（，2）10．（2022•陕西）在同一平面直角坐标系中，直线y＝﹣x+4与y＝2x+m相交于点P（3，n），则关于x，y的方程组的解为（）A．B．C．D．11．（2023•丹东）如图，直线y＝ax+b（a≠0）过点A（0，3），B（4，0），则不等式ax+b＞0的解集是（）A．x＞4B．x＜4C．x＞3D．x＜3 12．（2023•宁夏）在同一平面直角坐标系中，一次函数y1＝ax+b（a≠0）与y2＝mx+n（m≠0）的图象如图所示，则下列结论错误的是（）A．y1随x的增大而增大B．b＜nC．当x＜2时，y1＞y2D．关于x，y的方程组的解为13．（2023•盘锦）关于x的一次函数y＝（2a+1）x+a﹣2，若y随x的增大而增大，且图象与y轴的交点在原点下方，则实数a的取值范围是．14．（2023•西宁）一次函数y＝2x﹣4的图象与x轴交于点A，且经过点B（m，4）．（1）求点A和点B的坐标；（2）直接在图的平面直角坐标系中画出一次函数y＝2x﹣4的图象；（3）点P在x轴的正半轴上，若△ABP是以AB为腰的等腰三角形，请直接写出所有符合条件的P点坐标．15．（2023•温州）如图，在直角坐标系中，点A（2，m）在直线y＝2x﹣上，过点A的直线交y轴于点B（0，3）．（1）求m的值和直线AB的函数表达式；（2）若点P（t，y1）在线段AB上，点Q（t﹣1，y2）在直线y＝2x﹣上，求y1﹣y2的最大值．1．（2023秋•白银期中）下列函数中是一次函数的是（）A．y＝B．y＝x2C．y＝1D．y＝x+1 2．（2023秋•济南期中）若函数y＝（m﹣1）x+3是一次函数，则m的值为（）A．﹣1B．1C．0D．﹣1或1 3．（2023•船营区一模）一次函数y＝﹣2x+1的图象不经过的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限4．（2023•东莞市校级一模）已知点（﹣1，y1），（3，y2）在一次函数y＝2x+1的图象上，则y1，y2的大小关系是（）A．y1＜y2B．y1＝y2C．y1＞y2D．不能确定5．（2023•雁江区校级模拟）已知正比例函数y＝kx（k≠0）的函数值y随x的增大而减小，则一次函数y＝kx﹣k的图象大致是（）A．B．C．D．6．（2023秋•叶县期中）已知一次函数y＝kx+k过点（1，﹣4），则下列结论正确的是（）A．y随x增大而增大B．k＝2C．直线过点（﹣1，0）D．与坐标轴围成的三角形面积为27．（2023秋•青羊区校级期中）一次函数y＝5x﹣2的图象经过的（）A．第一、二、三象限B．第一、三、四象限C．第一、二、四象限D．第二、三、四象限8．（2023秋•福田区校级期中）下列关于函数y＝3x+2的结论中，错误的是（）A．图象经过点（﹣1，﹣1）B．点A（x1，y1），B（x2，y2）在该函数图象上，若x1＞x2，则y1＞y2C．将函数图象向下平移2个单位长度后，经过点（0，1）D．图象不经过第四象限9．（2023秋•青岛期中）若一次函数y＝2x﹣b的图象经过点（0，﹣3），则下列各点在该一次函数图象上的是（）A．（2，1）B．（2，3）C．（﹣1，1）D．（1，5）10．（2023秋•榆次区期中）小磊在画一次函数的图象时列出了如下表格，小颖看到后说有一个函数值求错了．这个错误的函数值是（）x…﹣3﹣2﹣1012…y…852﹣2﹣4﹣7…A．5B．2C．﹣2D．﹣4 11．（2023秋•碑林区校级期中）在平面直角坐标系中，将直线l1：y＝﹣3x﹣2平移后，得到直线l2：y＝﹣3x+4，则下列平移的做法正确的是（）A．将l1向下平移6个单位B．将l1向下平移2个单位C．将l1向右平移6个单位D．将l1向右平移2个单位12．（2023秋•滕州市期中）若点P（a，b）在直线y＝2x+1上，则代数式1﹣4a+2b的值为（）A．3B．﹣1C．2D．0 13．（2023秋•雁塔区校级月考）已知直线与直线l关于x轴对称，则直线l与y轴的交点坐标是（）A．（0，﹣1）B．（0，1）C．（2，0）D．（﹣2，0）14．（2023秋•市南区校级期中）已知函数y1＝﹣x﹣3，y2＝2x+9，当y1＞y2时，x的取值范围为．15．（2023•西和县一模）直线y＝kx+b经过点A（0，﹣4），且与坐标轴围成的三角形面积为4，则k＝．16．（2023秋•紫金县期中）如图，已知直线y＝kx+b的图象经过点A（0，﹣4），B（3，2），且与x轴交于点C．（1）求直线y＝kx+b的解析式；（2）求△BOC的面积．17．（2023春•鼓楼区校级期末）如图，在平面直角坐标系xOy中，已知点A（﹣2，0），点B（0，1）．（1）求直线AB的解析式；（2）若点C在直线AB上，且点C到x轴的距离为2，求点C的坐标．。

2024高考一轮复习函数知识点及最新题型归纳函数是数学领域的一个重要概念，在高考中占据着很大的比重。

下面是2024年高考一轮复习函数知识点及最新题型的详细归纳。

1.函数的定义函数是一种特殊的关系，它将一个集合的元素映射到另一个集合的元素上。

通常用f(x)表示函数，其中x是函数的自变量，f(x)是函数的因变量。

2.函数的表示方法函数可以用解析式、图像、表格等多种方式表示。

其中，解析式是最常见的表示方法，常见的函数表示如下：线性函数：f(x) = ax + b二次函数：f(x) = ax^2 + bx + c指数函数：f(x)=a^x对数函数：f(x) = loga(x)三角函数：sin(x)，cos(x)，tan(x)3.函数的性质-定义域和值域：函数的定义域是自变量能取的全部实数值的集合，值域是因变量能取的全部实数值的集合。

-奇偶性：若对于函数的定义域内的任意x，有f(-x)=f(x)，则称函数是偶函数；若对于函数的定义域内的任意x，有f(-x)=-f(x)，则称函数是奇函数。

-单调性：如果对于函数的定义域内的任意x₁和x₂，当x₁<x₂时，有f(x₁)<f(x₂)，则称函数是递增的；如果当x₁<x₂时，有f(x₁)>f(x₂)，则称函数是递减的。

-周期性：如果对于函数的定义域内的任意x，有f(x)=f(x+T)，其中T为正常数，则称函数具有周期T。

4.函数的运算函数之间可以进行加法、减法、乘法和除法等运算。

-两个函数的和：(f+g)(x)=f(x)+g(x)-两个函数的差：(f-g)(x)=f(x)-g(x)-两个函数的乘积：(f*g)(x)=f(x)*g(x)-一个函数除以另一个函数：(f/g)(x)=f(x)/g(x)随着高考的，函数的考查形式也在不断变化，以下是一些最新的函数题型归纳：-函数的图像分析：考生需要根据给定函数的解析式或表格，画出其对应的图像，然后分析图像的特点，如极值、拐点、单调性等。

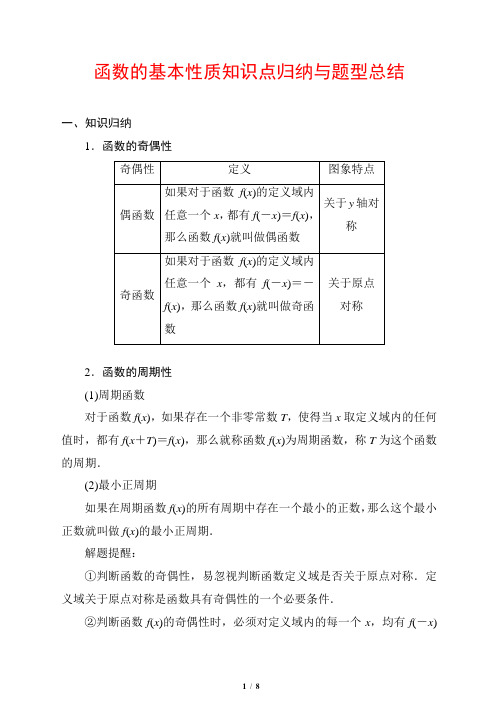
函数的基本性质知识点归纳与题型总结一、知识归纳1．函数的奇偶性2．函数的周期性(1)周期函数对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的任何值时，都有f(x＋T)＝f(x)，那么就称函数f(x)为周期函数，称T为这个函数的周期．(2)最小正周期如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期．解题提醒：①判断函数的奇偶性，易忽视判断函数定义域是否关于原点对称．定义域关于原点对称是函数具有奇偶性的一个必要条件．②判断函数f(x)的奇偶性时，必须对定义域内的每一个x，均有f(－x)＝－f (x )或f (－x )＝f (x )，而不能说存在x 0使f (－x 0)＝－f (x 0)或f (－x 0)＝f (x 0)．③分段函数奇偶性判定时，误用函数在定义域某一区间上不是奇偶函数去否定函数在整个定义域上的奇偶性．题型一 函数奇偶性的判断典型例题：判断下列函数的奇偶性： (1)f (x )＝(x ＋1)1－x1＋x； (2)f (x )＝⎩⎪⎨⎪⎧－x 2＋2x ＋1，x ＞0，x 2＋2x －1，x ＜0；(3)f (x )＝4－x 2x 2；(4)f (x )＝log a (x ＋x 2＋1)(a ＞0且a ≠1)． 解：(1)因为f (x )有意义，则满足1－x1＋x ≥0，所以－1＜x ≤1，所以f (x )的定义域不关于原点对称， 所以f (x )为非奇非偶函数． (2)法一：(定义法)当x ＞0时，f (x )＝－x 2＋2x ＋1，－x ＜0，f (－x )＝(－x )2＋2(－x )－1＝x 2－2x －1＝－f (x )； 当x ＜0时，f (x )＝x 2＋2x －1，－x ＞0，f (－x )＝－(－x )2＋2(－x )＋1＝－x 2－2x ＋1＝－f (x )．所以f (x )为奇函数． 法二：(图象法)作出函数f (x )的图象，由奇函数的图象关于原点对称的特征知函数f (x )为奇函数．(3)因为⎩⎨⎧4－x 2≥0，x 2≠0，所以－2≤x ≤2且x ≠0，所以定义域关于原点对称． 又f (－x )＝4－(－x )2(－x )2＝4－x 2x 2，所以f (－x )＝f (x )．故函数f (x )为偶函数． (4)函数的定义域为R ， 因为f (－x )＋f (x ) ＝log a [－x ＋(－x )2＋1]＋log a (x ＋x 2＋1)＝log a (x 2＋1－x )＋log a (x 2＋1＋x )＝log a [(x 2＋1－x )(x 2＋1＋x )]＝log a (x 2＋1－x 2)＝log a 1＝0， 即f (－x )＝－f (x )，所以f (x )为奇函数．通性通法：判定函数奇偶性的3种常用方法 (1)定义法(2)图象法(3)性质法①设f (x )，g (x )的定义域分别是 D 1，D 2，那么在它们的公共定义域上：奇＋奇＝奇，奇×奇＝偶，偶＋偶＝偶，偶×偶＝偶，奇×偶＝奇．②复合函数的奇偶性可概括为“同奇则奇，一偶则偶”．[提醒] (1)“性质法”中的结论是在两个函数的公共定义域内才成立的．(2)判断分段函数的奇偶性应分段分别证明f (－x )与f (x )的关系，只有对各段上的x 都满足相同的关系时，才能判断其奇偶性．题型二 函数的周期性典型例题(1)已知函数f (x )＝⎩⎪⎨⎪⎧2(1－x )，0≤x ≤1，x －1，1＜x ≤2，若对任意的n ∈N *，定义f n (x )＝f {f [f …n 个f (x )]}，则f 2 019(2)的值为( )A．0B．1C．2 D．3(2)设定义在R上的函数f(x)满足f(x＋2)＝f(x)，且当x∈[0,2)时，f(x)＝2x－x2，则f(0)＋f(1)＋f(2)＋…＋f(2 019)＝________.解析：(1)∵f1(2)＝f(2)＝1，f2(2)＝f(1)＝0，f3(2)＝f(0)＝2，∴f n(2)的值具有周期性，且周期为3，∴f2 019(2)＝f3×673(2)＝f3(2)＝2，故选C.(2)∵f(x＋2)＝f(x)，∴函数f(x)的周期T＝2，∵当x∈[0,2)时，f(x)＝2x－x2，∴f(0)＝0，f(1)＝1，∴f(0)＝f(2)＝f(4)＝…＝f(2 018)＝0，f(1)＝f(3)＝f(5)＝…＝f(2 019)＝1.故f(0)＋f(1)＋f(2)＋…＋f(2 019)＝1 010.答案：(1)C(2)1 010通性通法：1．判断函数周期性的2个方法(1)定义法．(2)图象法．2．周期性3个常用结论(1)若f(x＋a)＝－f(x)，则T＝2a.(2)若f(x＋a)＝1f(x)，则T＝2a.(3)若f(x＋a)＝－1f(x)，则T＝2a(a＞0)．题型三函数性质的综合应用函数的奇偶性、周期性以及单调性是函数的三大性质，在高考中常常将它们综合在一起命制试题，其中奇偶性多与单调性相结合，而周期性常与抽象函数相结合，并以结合奇偶性求函数值为主．多以选择题、填空题形式出现．角度一：奇偶性的应用1．函数y＝f(x)是R上的奇函数，当x＜0时，f(x)＝2x，则当x＞0时，f(x)＝()A．－2x B．2－xC．－2－x D．2x解析：选C x＞0时，－x＜0，∵x＜0时，f(x)＝2x，∴当x＞0时，f(－x)＝2－x.∵f(x)是R上的奇函数，∴当x＞0时，f(x)＝－f(－x)＝－2－x.故选C.角度二：单调性与奇偶性结合2．已知f(x)为奇函数，且当x＞0时，f(x)单调递增，f(1)＝0，若f(x－1)＞0，则x的取值范围为()A．{x|0＜x＜1或x＞2}B．{x|x＜0或x＞2}C．{x|x＜0或x＞3} D．{x|x＜－1或x＞1}解析：选A因为函数f(x)为奇函数，所以f(－1)＝－f(1)＝0，又函数f(x)在(0，＋∞)上单调递增，所以可作出函数f(x)的示意图，如图，则不等式f(x－1)＞0可转化为－1＜x－1＜0或x－1＞1，解得0＜x＜1或x＞2.角度三：周期性与奇偶性结合3.定义在R上的偶函数f(x)满足f(x＋3)＝f(x)．若f(2)＞1，f(7)＝a，则实数a的取值范围为()A．(－∞，－3) B．(3，＋∞)C．(－∞，－1) D．(1，＋∞)解析：选D∵f(x＋3)＝f(x)，∴f(x)是定义在R上的以3为周期的函数，∴f(7)＝f(7－9)＝f(－2)．又∵函数f(x)是偶函数，∴f(－2)＝f(2)，∴f(7)＝f(2)＞1，∴a＞1，即a∈(1，＋∞)．角度四：单调性、奇偶性与周期性结合4．定义在R上的奇函数f(x)满足f(x＋2)＝－f(x)，且在[0,2)上单调递减，则下列结论正确的是()A．0＜f(1)＜f(3) B．f(3)＜0＜f(1)C．f(1)＜0＜f(3) D．f(3)＜f(1)＜0解析：选C由函数f(x)是定义在R上的奇函数，得f(0)＝0.由f(x＋2)＝－f(x)，得f(x＋4)＝－f(x＋2)＝f(x)，故函数f(x)是以4为周期的周期函数，所以f(3)＝f(－1)．又f(x)在[0,2)上单调递减，所以函数f(x)在(－2,2)上单调递减，所以f(－1)＞f(0)＞f(1)，即f(1)＜0＜f(3)．故选C.通性通法：函数性质综合应用问题的常见类型及解题策略(1)函数单调性与奇偶性结合．注意函数单调性及奇偶性的定义，以及奇、偶函数图象的对称性．(2)周期性与奇偶性结合．此类问题多考查求值问题，常利用奇偶性及周期性进行交换，将所求函数值的自变量转化到已知解析式的函数定义域内求解．(3)周期性、奇偶性与单调性结合．解决此类问题通常先利用周期性转化自变量所在的区间，然后利用奇偶性和单调性求解．。

高考函数知识点和题型整理大全函数是高考数学中的一个重要知识点，几乎贯穿了整个高中数学学习的内容。

它是数学与实际问题相结合的桥梁，也是解决复杂计算和推理问题的基础工具。

本文将整理高考函数知识点和相关题型，帮助同学们系统地回顾和总结。

一、函数的定义与性质1. 函数的定义：若给定数集A和数集B，对于每一个属于A的元素x，通过一个确定的法则f，可以得出B中唯一确定的元素y与之对应，那么就称f为从A到B的一个函数。

2. 函数的性质：自变量、因变量、定义域、值域、图像与映射关系等。

二、常见函数类型及其性质1. 一次函数：一次函数是函数的一种特殊类型，其形式为y=ax+b，其中a和b 为常数，a≠0。

性质：函数图像为一条直线，斜率为a，截距为b；增减性与性质。

2. 二次函数：二次函数是函数的一种特殊类型，其形式为y=ax^2+bx+c，其中a、b和c为常数，a≠0。

性质：函数图像为一条抛物线，开口的方向由a的正负决定；顶点坐标与坐标轴交点等。

3. 幂函数：幂函数是函数的一种特殊类型，形式为y=x^a，其中a为常数。

性质：函数图像与幂指数a的奇偶性相关；增减性与性质。

4. 指数函数：指数函数是函数的一种特殊类型，形式为y=a^x，其中a为常数且a>0且a≠1。

性质：函数图像通过点(0, 1)；增减性与性质。

5. 对数函数：对数函数是函数的一种特殊类型，形式为y=loga(x)，其中a为常数且a>0且a≠1。

性质：函数图像通过点(1, 0)；增减性与性质。

6. 三角函数：三角函数是函数的一种特殊类型，包括正弦函数、余弦函数和正切函数等。

性质：函数图像的周期、对称性、单调性等。

三、函数的运算与复合1. 函数的四则运算：函数的加减乘除运算与性质。

2. 函数的复合：函数的复合运算与性质。

四、函数的图像与方程1. 方程的解与函数的零点：求解方程与函数的零点之间的关系。

2. 函数图像与方程的联系：根据函数图像求解方程，根据方程确定函数图像等。

函数必考知识点及常考题型总结（优质资料）一、函数的定义函数是指一个特定的输入与输出之间的关系。

通常情况下，函数有一个或多个输入（也可以没有输入），并且通过执行特定的算法或过程来产生一个输出。

函数的输入可以是数字、字符串、布尔值或其他值，输出也可以是数字、字符串、布尔值或其他值。

二、函数的调用与参数函数的调用是指在代码中使用函数的名称来触发函数执行的过程。

通常情况下，我们需要给函数传递参数，以便让函数使用这些参数来执行一些操作并返回结果。

参数可以是数字、字符串、布尔值或其他值。

三、函数的返回值函数的返回值是指函数执行完毕后返回的结果。

在函数定义时，我们可以指定函数的返回值类型，以便在函数执行完毕后返回一个特定的类型的值。

函数的返回值可以是数字、字符串、布尔值或其他类型的值。

四、函数的作用域与变量函数的作用域是指函数内可以访问的变量的范围。

在函数内部定义的变量只能在函数内部使用，这些变量被称为局部变量。

全局变量则可以在整个程序中使用，在函数内部也可以访问。

五、函数的递归函数的递归是指在函数内部调用自身的过程。

这样可以让函数自己不断地调用自己，直到达到某个条件为止。

递归函数通常会使用条件语句来判断是否需要继续递归，以便防止出现无限递归的情况。

六、函数的高阶函数的高阶是指函数可以作为参数传递给另一个函数，或者可以作为返回值返回给调用者。

这样可以让我们编写更为灵活的代码，使得我们可以把函数看做是数据结构的一种。

七、函数式编程函数式编程是一种编程范式，它强调的是函数的纯度和不可变性。

函数式编程通常会强调使用只读数据和不可变数据，这样可以将程序中的错误降到最低。

此外，函数式编程还可以采用递归、高阶函数等技术，来实现更为复杂的程序逻辑。

常见的函数题型：1.编写一个函数，计算两个数的和。

2.编写一个函数，计算一个数的平方。

3.编写一个函数，接受一个字符串参数，输出字符串的长度。

4.编写一个函数，接受一个整数列表参数，输出所有元素的平均值。

函数基础知识大全§1.2.1、函数的概念1、 设A 、B 是非空的数集，如果按照某种确定的对应关系f ，使对于集合A 中的任意一个数x ，在集合B中都有惟一确定的数()x f 和它对应，那么就称B A f →:为集合A 到集合B 的一个函数，记作：()A x x f y ∈=,.2、 一个函数的构成要素为：定义域、对应关系、值域.如果两个函数的定义域相同，并且对应关系完全一致，则称这两个函数相等.3.两个函数的相等：函数的定义含有三个要素，即定义域A 、值域C 和对应法则f .当函数的定义域及从定义域到值域的对应法则确定之后，函数的值域也就随之确定.因此，定义域和对应法则为函数的两个基本条件，当且仅当两个函数的定义域和对应法则都分别相同时，这两个函数才是同一个函数. §1.2.2、函数的表示法1、 函数的三种表示方法：解析法、图象法、列表法. 1.函数的三种表示法（1）解析法：就是把两个变量的函数关系，用一个等式来表示，这个等式叫做函数的解析表达式，简称解析式.（2）列表法：就是列出表格来表示两个变量的函数关系. （3）图象法：就是用函数图象表示两个变量之间的关系. 2.求函数解析式的题型有：（1）已知函数类型，求函数的解析式：待定系数法；（2）已知()f x 求[()]f g x 或已知[()]f g x 求()f x ：换元法、配凑法； （3）已知函数图像，求函数解析式；（4）()f x 满足某个等式，这个等式除()f x 外还有其他未知量，需构造另个等式解方程组法； （5）应用题求函数解析式常用方法有待定系数法等． 求函数解析式的常用方法： 1、换元法（ 注意新元的取值范围）2、待定系数法（已知函数类型如：一次、二次函数、反比例函数等）3、整体代换（配凑法） 4.赋值法：3.映射的定义：一般地，设A 、B 是两个集合，如果按照某种对应关系f ，对于集合A 中的任何一个元素，在集合B 中都有唯一的元素和它对应，那么，这样的对应（包括集合A 、B ，以及集合A 到集合B 的对应关系f ）叫做集合A 到集合B 的映射，记作f :A →B.由映射和函数的定义可知，函数是一类特殊的映射，它要求A 、B 非空且皆为数集.4.映射的概念中象、原象的理解：(1) A 中每一个元素都有象;(2)B 中每一个元素不一定都有原象，不一定只一个原象；(3)A 中每一个元素的象唯一。

函数基础知识大全§1.2.1、函数的概念1、 设A 、B 是非空的数集，如果按照某种确定的对应关系f ，使对于集合A 中的任意一个数x ，在集合B中都有惟一确定的数()x f 和它对应，那么就称B A f →:为集合A 到集合B 的一个函数，记作：()A x x f y ∈=,.2、 一个函数的构成要素为：定义域、对应关系、值域.如果两个函数的定义域相同，并且对应关系完全一致，则称这两个函数相等.3.两个函数的相等：函数的定义含有三个要素，即定义域A 、值域C 和对应法则f .当函数的定义域及从定义域到值域的对应法则确定之后，函数的值域也就随之确定.因此，定义域和对应法则为函数的两个基本条件，当且仅当两个函数的定义域和对应法则都分别相同时，这两个函数才是同一个函数. §1.2.2、函数的表示法1、 函数的三种表示方法：解析法、图象法、列表法. 1.函数的三种表示法（1）解析法：就是把两个变量的函数关系，用一个等式来表示，这个等式叫做函数的解析表达式，简称解析式.（2）列表法：就是列出表格来表示两个变量的函数关系. （3）图象法：就是用函数图象表示两个变量之间的关系. 2.求函数解析式的题型有：（1）已知函数类型，求函数的解析式：待定系数法；（2）已知()f x 求[()]f g x 或已知[()]f g x 求()f x ：换元法、配凑法； （3）已知函数图像，求函数解析式；（4）()f x 满足某个等式，这个等式除()f x 外还有其他未知量，需构造另个等式解方程组法； （5）应用题求函数解析式常用方法有待定系数法等． 求函数解析式的常用方法： 1、换元法（ 注意新元的取值范围）2、待定系数法（已知函数类型如：一次、二次函数、反比例函数等）3、整体代换（配凑法） 4.赋值法：3.映射的定义：一般地，设A 、B 是两个集合，如果按照某种对应关系f ，对于集合A 中的任何一个元素，在集合B 中都有唯一的元素和它对应，那么，这样的对应（包括集合A 、B ，以及集合A 到集合B 的对应关系f ）叫做集合A 到集合B 的映射，记作f :A →B.由映射和函数的定义可知，函数是一类特殊的映射，它要求A 、B 非空且皆为数集.4.映射的概念中象、原象的理解：(1) A 中每一个元素都有象;(2)B 中每一个元素不一定都有原象，不一定只一个原象；(3)A 中每一个元素的象唯一。

高一函数总结一、函数知识线索（1）函数定义及其性质（定义，相等函数，区间，定义域，值域，表示，映射） （2）函数性质（单调性，最值，存在性，恒成立，奇偶性） （3）基本函数（根式指数式互化，指数式运算，指数函数，指数函数性质）（指数对数互化，对数运算，对数函数，对数函数性质）（幂函数，幂函数性质）（4）函数应用（零点定义，零点存在定理，零点问题交点问题，二分法，二次函数根的分布）（5）函数应用模型（一二反指对幂） 二、题型及延展 例1与函数定义有关（1）下列四个方程中表示y 是x 的函数的是 。

①x－2y ＝6；②x 2＋y ＝1；③x＋y 2＝1y（2）如图所示，可表示函数图象的是（ ） A ．① B ．②③④ C ．①③④ D ．② 例2与函数定义域有关 (1)函数()13f x x x =-+的定义域为 。

(2)若函数()y f x =的定义域是[]0,2，则函数(2)()1f x g x x =-定义域是 。

(3)已知()211f x x +=-()21f x -的定义域为 。

例3与值域有关 (1)若函数()(0,1)x f x a a a a =->≠的定义域和值域都是0,1，则711log log 1114aa += 。

(2)函数()21g x x x =+的最小值为 。

(3)函数1)(+=x x x f 的值域 。

（4）xx x x f 21)(2++=的值域 。

（5）设()2|1|2,||11,||11x x f x x x --≤⎧⎪=⎨>⎪+⎩，则12f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦。

例4与函数表示有关 （1）设函数()f x 为一次函数，且()43f f x x =-⎡⎤⎣⎦，则()1f = 。

（2）已知函数()211f x x +=+，则()0f =。

（3）若()f x 对于定义域内的任意实数x 都有12()()21f x f x x -=+，则(2)f =（ ）（4）函数32)1(-+=+x x x f 求)(x f 例5与单调性有关（1）已知函数()()23,12,1a x x f x a x x ⎧-+≤⎪=⎨>⎪⎩在(),-∞+∞上是减函数，则a 的取值范围为 。

函数知识点总结及题型一、函数的概念函数是一种提供代码重用性和模块化的工具，它将一些指定的代码片段封装起来，形成一个独立的单元，可以在程序中多次调用。

二、函数的定义在Python中，使用关键字def来定义函数，后面跟上函数名和参数列表，然后在冒号后面编写函数体的内容。

例如：```def add(a, b):return a + b```三、函数的调用当定义了一个函数后，就可以在程序的其他地方调用这个函数，使用函数名和参数列表即可。

例如：```result = add(3, 5)```四、函数的参数函数可以接受零个或多个参数，也可以有默认参数值。

参数列表中的参数可以是位置参数或关键字参数。

例如：```def greet(name, message='Hello'):print(message, name)greet('John') # 使用默认参数值greet('Doe', message='Hi') # 传递关键字参数```五、函数的返回值函数可以有返回值，使用关键字return来返回一个值。

当函数执行到return语句时，会立即结束函数的执行，并将返回值传递给调用者。

例如：```def multiply(a, b):return a * bresult = multiply(4, 7)```六、函数的作用域函数中定义的变量具有函数作用域，即只在函数内部可见。

在函数外部是无法访问函数内部的变量的。

例如：```def my_function():name = "John"print(name)my_function() # 输出'John'print(name) # 会报错，无法访问函数内部的变量```七、递归函数递归函数是一种在函数体内调用自身的函数。

通常用于解决可以被分解成相似的子问题的问题。

例如计算阶乘、斐波那契数列等。