当前位置：文档之家 › 计算机组成原理2.2定点加减法运算

计算机组成原理2.2定点加减法运算

  • 格式：ppt
  • 大小：177.00 KB
  • 文档页数：43

下载文档原格式

  / 43

合集下载

2.2 定点加减运算

2.2 定点加减运算

3.移位功能的实现
在计算机中，通常移位操作由移位寄 存器来实现，但也有一些计算机不设置专 门的移位寄存器，而在加法器的输出端加 一个移位器。移位器是由与门和或门组成 的逻辑电路（实际是一个多路选择器）， 可以实现直传（不移位）、左斜一位送 （左移一位）和右斜一位送（右移一位） 的功能。
移位器逻辑电路
两正数相加，当最高有效位产生进位 （C1=1）而符号位不产生进位（Cs=0）时，发 生正溢；两负数相加，当最高有效位不产生进 位（C1=0）而符号位产生进位（Cs=1）时，发 生负溢。故溢出条件为
溢出= Cs C1+CsC1=Cs⊕C1
2.溢出检测方法（续）
⑶采用变形补码（双符号位补码）
叫做在真双符符，号两位个的符情号况位下都，作把为左数边的的一符部号分位参S加s1 运算。这种编码又称为变形补码。
双符号位的含义如下：
Ss1Ss2=00 结果为正数，无溢出 Ss1Ss2=01 结果正溢 Ss1Ss2=10 结果负溢 Ss1Ss2=11 结果为负数，无溢出 当两位符号位的值不一致时，表明产生溢 出，溢出条件为
溢出=Ss1⊕Ss2
2.2.4 基本的二进制加/减法器
教材 P31 图2.3
Y

附： 带符号数的移位和舍入操作
一、 带符号数的移位操作
1.原码的移位规则 不论正数还是负数，在左移或右移时，
符号位均不变，空出位一律以“0”补入。 负数的原码移位前后结果为： 左移：移位前有：1 X1 X2 … Xn-1 Xn 移位后有：1 X2 X3 … Xn 0 右移：移位前有：1 X1 X2 … Xn-1 Xn 移位后有：1 0 X1 … Xn-2 Xn-1
采用一个符号位检测溢出时，当 XXss==YYss==01，，SSss==10时时，，产生产负生溢。正 溢 ； 当

定点加、减法运算

定点加、减法运算

计算机组成原理 定点加、减法运算
符号位: 00 结果>0 11 结果<0 01 溢出 10 溢出
符号位异号溢出(用异或电路判断
计算机组成原理 定点加、减法运算
练习: X=-0.1101 Y=-0.1011 求[X+Y]补 和[X-Y]补
计算机组成原理 定点加、减法运算
[X]补=11.0011 [Y]补=11.0101 [X+Y]补=10.1000 [X-Y]补= 11.1110
计算机组成原理
计算机组成原理 定点加、减法运算
1、二进制的补码加、减法运算 1.1、公式:
[X]补+[Y]补=[X+Y]补 [X]补- [Y]补=[X-Y]补
计算机组成原理 定点加、减法运算
1.2、课堂练习
X=0.11011 Y=0.00011 X=-0.11011 Y=-0.00011
[X]补=
[X+Y]补=0.11110
[X+Y]补=1.00010
[X-Y]补= 0.11000
[X-Y]补=1.01000
计算机组成原理 定点加、减法运算
2、溢出问题 2.1、溢出概念 课堂练习:
X=0.1011 Y=0.1100 [X]补= [Y]补= [X+Y]补= [X-Y]补=
X=-0.1101 Y=-0.1011 [X]补= [Y]补= [X+Y]补= [X-Y]补=
(溢出)
计算机组成原理
计算机组成原理 定点加、减法运算
X=0.1011 Y=0.1100 [X]补=0.1011 [Y]补=0.1100 [X+Y]补=1.0111 × [X-Y]补= 1.0111
X=-0.1101 Y=-0.1011 [X]补=1.0011 [Y]补=1.0101 110

计算机组成原理 第五课

计算机组成原理 第五课
是 — —说明无错或无奇数位出错 否 — —奇数位出错
例:X0X1X2X3C =10110 (奇) X0'X1'X2'X3' C' =11110 由X0'X1'X2'X3'生成C*=
(1 ⊕ 1) ⊕ (1 ⊕ 1)
=1,则
C*⊕C' =1⊕0=1 —— 出错
(4) 优缺点
优点:简单易行,省器件. 缺点:只能发现奇数位错,无纠错能力.
2.1.4 数据校验码
1. 数据校验码:
用以发现或同时能得出错误位置特征的数据编码. 计算机中的错误类型: ; (1)固定性错误---元器件故障; ) (2)突发性错误---噪声干扰. )
2. 检错码--奇偶校验码 (1) 定义
使包括一位校验位在内的数据代码,"1"的个数总是奇 (或偶)数个为合法数据的编码.
2. 补码定点减法
(1)补码减法的规则: 推论: [X-Y]补= [X+(-Y)]补 =[X]补+[-Y]补 已知 [Y]补 ,那么 [-Y]补=? (2)求补: 由[Y]补求[-Y]补,称为对Y求补. (3)求补规则 : 不管真值Y时正数还是负数,求补的方法都是将[Y]补 可见:求补时,从[Y]补的最低位开始向高位扫描,见到第 连同符号位在内各位变反, 末位加1. 一个"1",包括这个"1"的各位不变,其余各位变反 例如:[y]补=1.1010,则环冗余校验码(CRC) CRC
n位数据位和r位校验位只有1位出错,共有n+r种情况, (1) 纠正一位错所需的校验码位数r 加上没有错的一种情况,共有n+r+1种情况,而r位二进 设待编码的信息有效位数为n,则r应满足: 制的编码数为2r,因此 2r≥n+r+1 即 r>log2n n r 1 2 2～4 3 5～11 12～26 4 5

计算机组成原理第四版第二章

计算机组成原理第四版第二章
[x]补=0.1001, [y]补=0.0101 [x]补 0. 1 0 0 1
+ [y]补 0. 0 1 0 1 [x+y]补 0. 1 1 1 0
所以x+y=+0.1110
Back
第二章 运算方法和运算器
B 补码减法
➢ 公式：
[x-y]补=[x]补-[y]补=[x]补+[-y]补
➢ 举例
已知 x=+0.1101 ， y=+0.0110，求x-y。 解： [x]补=0.1101 [y]补=0.0110 ，[-y]补=1.1010 [x]补 0. 1 1 0 1 + [-y]补 1. 1 0 1 0 [x-y]补 1 0. 0 1 1 1
最大正数，称为“上溢” 或“正溢出”
两个负数相加，结果 小于机器所能表示的最
小负数，称为“下溢” 或“负溢出”
判断方法
举例说明
Back
第二章 运算方法和运算器
溢出检测方法常用以下两种方法：
1.采用双符号位（变形补码）判断方法：
变形补码： “00”表示正数、“11”表负数，两符号位同时参加运算， 运算结果符号出现01或10表明溢出。
发生溢出；而在浮点运算时，运算结果超出尾数的表示范围 却并不一定溢出，只有当阶码也超出所能表示的范围时，才 发生溢出。
Back
3.十进制数串的表示方法
➢ 目前,大多数通用性较强的计算机都能直接 处理十进制形式表示的数据。十进制数串 在计算机内主要有两种表示形式：
➢ 1.字符串形式 ➢ 2.压缩的十进制数串形式
➢ 计算机采用定点数表示时，对于既有整数又有小数的原始数据，需要设 定一个比例因子，数据按其缩小成定点小数或扩大成定点整数再参加运 算，运算结果，根据比例因子，还原成实际数值。若比例因子选择不当， 往往会使运算结果产生溢出或降低数据的有效精度。

计算机组成原理第3讲_定点加法

计算机组成原理第3讲_定点加法
&
S0 S1 S2 S3 Xi Yi Ci-1
函数发生器
17
SN74181中一位ALU单元： 主要部分是由两个半加器组成的一位全加器。 在全加器的输入端附加了选择 类型控制输入信号M控制 输入控制S3～S0。S3～S0的16种 ALU作算术运算（M＝L）或 组合可控制16种运算。 作逻辑运算（M＝H）。
Fi
=1
Yi ≥1 & =1 ≥1 & Xi
Fi
一位全加器
12
4． 组内并行组间并行的进位链 C4 = G4+ P4C3 = G4+ P4G3+ P4 P3G2+ P4P3P2G1+ P4P3P2P1C0 仿照前面分析每一位进位的方法，每组的最高进位可分为两部分 在第一小组的最高进位C4的进位表达式中，前四项 G4+ P4G3+ P4 P3G2+ P4P3P2G1与低位来的进位C0无关，只与本小组 内的Gi和 Pi有关，称为该小组的进位生成函数GN。 GN = G4+ P4G3+ P4 P3G2+ P4P3P2G1 最后一项P4P3P2P1C0依赖于低位的进位信号，称为本小组的 传送进位，称P4P3P2P1为小组的传送函数PN。 PN = P4P3P2P1 可得各小组的组间并行进位表达式
每个小组内的进位延迟时间是2tpd 16位组内并行组间串行进位链的进位延迟时间是9tpd
11
用4位组内并行进位ALU组成16位组内并行组间串行进位的 ALU的方法： Cn+4 Cn Cn+4 Cn Cn+4 Cn Cn+4 Cn
C16 4位组内并 C12 4位组内并 C8
行进位ALU X Y 行进位ALU X Y

计算机组成原理-第2周下-2.3节定点乘法运算

计算机组成原理-第2周下-2.3节定点乘法运算

第二章 运算方法和运算器本章内容 2.1 数据与文字的表示方法 2.2 定点加法、减法运算 2.3 定点乘法运算 2.4 定点除法运算 2.5 定点运算器的组成 2.6 浮点运算方法和浮点运算器中山大学 信息科学与技术学院 陈 任 2010.92.3 定点乘法运算2.3.1 原码乘法1.人工算法与机器算法的同异性 运算规则:乘积的符号位由两数的符号位按异或运算得到, 乘积的数值部分则是两个正数相乘之积。

设n位被乘数和乘数用定点小数表示(定点整数也同样适用) 被乘数 [ｘ]原＝ｘf ｘn－1…ｘ1ｘ0 乘数 [ｙ]原＝ｙf ｙn－1…ｙ1ｙ0 则乘积[ｚ]原＝(ｘf⊕ｙf)＋(ｘn－1…ｘ1ｘ0)(ｙn－1…ｙ1ｙ0) 式中,ｘf为被乘数符号,ｙf为乘数符号。

乘积符号的运算法则是：同号相乘为正,异号相乘为负。

由于 被乘数和乘数和符号组合只有四种情况(ｘfｙf＝00,01,10,11),因 此积的符号可按“异或”(按位加)运算得到。

数值部分的运算方法与普通的十进制小数乘法类似,不过对于 用二进制表达式的数来说,其乘法规则更为简单一些。

2 设ｘ＝1101,ｙ＝1011，先用习惯方法求其乘积,其过程如下:设ｘ＝1101,ｙ＝1011，用习惯方法求其乘积,其过程如下运算的过程与十进制乘法相似:从乘数ｙ的最低位开始,若这一位 为“1”,则将被乘数ｘ写下；若这一位为“0”,则写下全0。

然 后在对乘数ｙ的高一位进行乘法运算,其规则同上,不过这一位乘 数的权与最低位乘数的权不一样,因此被乘数ｘ要左移一位。

以 此类推,直到乘数各位乘完为止,最后将它们统统加起来,变得到最 后乘积ｚ。

3问题：人们习惯的算法对机器并不完全适用。

原因之一：机器通常只有n位长,两个n位数相乘,乘积可能为2n位。

原因之二：只有两个操作数相加的加法器难以胜任将n个位积一次 相加起来的运算。

被乘数ｘ＝1101,乘数ｙ＝1011.早期计算机中为 了简化硬件结构,采 用串行的1位乘法方 案,即多次执行“加 法—移位”操作来 实现。

计算机组成原理教案(第二章)

计算机组成原理教案(第二章)

最小负数值＝－(215－1)10＝(－32767)10
1
111 111 111 111 111
例6]假设由S,E,M三个域组成的一个32位二进制字所表示的非零规格 化浮点数ｘ,真值表示为： ｘ＝(－1)s×(1.M)×2E－128 问：它所表示的规格化的最大正数、最小正数、最大负数、最小负 数是多少？ 1)最大正数 0 11 111 111 111 111 111 111 111 111 111 11
2.1.1 数据格式
计算机中常用的数据表示格式有两种
一是定点格式，数值范围有限,要求但的处理硬件比较简单。
二是浮点格式，数值范围很大，但要求硬件比较复杂。
1.定点数的表示方法
定点表示：约定机器中所有数据的小数点位置是固定不变的
(ｘ0:符号位，0代表正号，1代表负号):
纯小数和纯整数
目前计算机中多采用定点纯整数表示，因此将定点数表示的运算 简称为整数运算。
00000001 0000000011
(2).压缩的十进制数串形式
每个数位占用半个字节(即4个二进制位),其值可用二－十编码 (BCD码)或数字符的ASCII码的低4位表示。 符号位也占半个字节并放在最低数字位之后,其值选用四位编 码中的六种冗余状态中的有关值,
1 2 3 C
(＋123) 0 1 2 D
2.浮点数的表示方法
浮点表示法：把一个数的有效数字和数的范围在计算机的一个 存储单元中分别予以表示，这种把数的范围和精度分别表示的 方法，数的小数点位置随比例因子的不同而在一定范围内自 由浮动。 9 × 10－28＝0.9 × 10－27
Ｎ＝Ｒe.Ｍ Ｍ ：尾数，是一个纯小数。
e ：比例因子的指数，称为浮点数的指数，是一个整数。 R ：比例因子的基数，对于二进计数值的机器是一个常数 ，一般规定Ｒ 为2，8或16。

经典：计算机组成原理-第2章-运算方法和运算器

经典：计算机组成原理-第2章-运算方法和运算器
1加法器的流水线时钟周期至少为90ns10ns100ns如果采用同样的逻辑电路但不是流水线方式则浮点加法所需的时间为300ns因此4级流水线加法器的加速比为30010032当每个过程段的时间都是75ns时加速比为300754例30已知计算一维向量xy的求和表达式如下
第二章：运算方法和运算器
2．1 数据与文字的表示方法 2．2 定点加法、减法运算 2．3 定点乘法运算 2．4 定点除法运算 2．5 定点运算器的组成 2．6 浮点运算方法和浮点运算器
其中尾数域所表示的值是1.M。因为规格化的浮点数的尾数域最
左位（最高有效位）总是1。故这一位经常不予存储，而认为隐藏
在小数点的左边。
64位的浮点数中符号位1位，阶码域11位，尾数域52位，指数偏
移值是1023。因此规格化的64位浮点数x的真值为：
x=(－1)s ×(1.M) × 2E－1023 e=E－1023
[X]反=1.x1x2...xn 对于0，有[+0]反=[-0]反之分：
[+0]反=0.00...0
[-0]反=1.11...1
我们比较反码与补码的公式
[X]反=2-2-n+X
[X]补=2+X
可得到 [X]补=[X]反+2-n
8
若要一个负数变补码，其方法是符号位置1，其余各位0变1，1变 0，然后在最末位（2-n）上加1。
10100.10011=1.010010011*24 e=4 于是得到：S=0,E=4+127=131=10000011, M=010010011 最后得到32位浮点数的二进制存储格式为： 0100 0001 1010 0100 1100 0000 0000 0000=（41A4C000）164

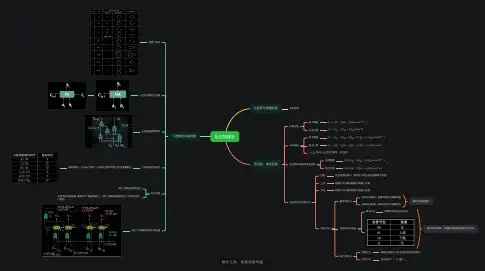
计算机组成原理之定点加减法思维导图脑图

计算机组成原理之定点加减法思维导图脑图

定点加减法
位运算与逻辑运算非常简单
定点加、减法运算补码加法定点整数[x +y ]=补[x ]+补[y ]
补(mod 2)n +1定点小数[x +y ]=补[x ]+补[y ]补(mod 2)
补码减法定点整数[x −y ]=补[x ]−补[y ]=补[x ]+补[−y ]补(mod 2)n +1定点小数[x −y ]=补[x ]−补[y ]=补[x ]+补[−y ]补(mod 2)
等于的各位取反，末位加1
[−y ]补[y ]补定点数补码的加减法运算定点整数[x ±y ]=补[x ]+补[±y ]补(mod 2)n +1定点小数
[x ±y ]=补[x ]+补[±y ]补(mod 2)溢出概念与检验方法溢出
在定点数机器中，数的大小超出定点数能表示范围上溢数据大于机器所能表示的最大正数
下溢数据小于机器所能表示的最小负数
检验方法直接判别法
同号补码相加，结果符号位与加数相反异号补码相减，结果符号位与减数相同
硬件实现较复杂
变形补码判别法模4补码采用双符号位表示补码硬件实现简单，只需要对结果的符号进行异或
进位判别法
判别方法
最高位的进位与符号位的进位是否相同判别公式溢出标志V =C C f ⨁n −1二进制加法减法器逻辑门符号
一位半加器和全加器
全加器的逻辑结构门电路的时间延迟通常采用一个与非门或者一个或非门的时间延迟作为度量单位补充内容
与非门具有函数完备性在使用多发射极晶 体管的TTL集成电路中，与非门需要的晶体管也少于其他任何门电路多位二进制数据加法/减法器。

计算机组成原理-第2周下-定点加减法运算

计算机组成原理-第2周下-定点加减法运算
丢掉
[y]补= 1 1 0 1 1 10 0110
所以
ｘ＋ｙ＝+0110
6
例: x＝-11001 ,y＝-00011，求 x+y＝？

解:[x]补=1 0 0 1 1 1， [y]补=1 1 1 1 0 1
[x]补=1 0 0 1 1 1 +
丢掉
[y]补=1 1 1 1 0 1 11 0 01 0 0 由以上三例看到,补码加法的特点: (1) 符号位要作为数的一部分一 起参加运算。 (2) 要在模2n+1的意义下相加， 即超过2n+1的进位要丢掉!
13
[例16] ｘ＝－1101, ｙ＝－1011,求ｘ＋ｙ。 [解:] [ｘ]补＝10011 [ｙ]补＝10101 [ｘ]补 ＋ [ｙ]补 [ｘ＋ｙ]补 10011 10101 01000
两个负数相加的结果成为正数,这同样是错误的。 之所以发生错误,是因为运算结果产生了溢出。两个正数相 加,结果大于机器所能表示的最大正数,称为正溢出。而两个负数 相加,结果小于机器所能表示的最小负数,称为负溢出。

21
常见的门电路

1．与门 真值表表示的两输入端与门如表2-1所示，逻辑符号如图 2-1所示。从与门的逻辑关系上可以看出，如果输入端A 作为控制端，则A的值将会决定输入端B的值是否能被输 出到端口Y。
Y AB
A
B
Y=AB
0 0 0 0 1 0 1 0 0 1 1 1 表2-1 两输入端与门的真值表
27
5．或非门

真值表表示的两输入端或非门如表2-5所示，逻辑符号如 图2-5所示。可以利用或非门的输入端A来控制输入端B。 当A=0时，（输入信号被反相输出）；当A=1时，则不管 B的值是什么，Y都为0。

计算机组成原理2.2定点加减法运算

计算机组成原理2.2定点加减法运算
• (1)当ｘ﹥0，ｙ﹥0时，有ｘ＋ｙ﹥0
• 根据数据补码的定义
• [ｘ]补＋[ｙ]补＝ｘ＋ｙ＝[ｘ＋ｙ]补 (mod 2)
证明[ｘ]补＋[ｙ]补＝[ｘ＋ｙ]补
• (2)当ｘ﹥0，ｙ﹤0，有ｘ＋ｙ>0， 或ｘ＋ｙ<0两种情况 • 根据补码定义[ｘ]补=x，[ｙ]补=2+ｙ • [ｘ]补＋[ｙ]补=x+2+y=2+(x+y) • 当ｘ＋ｙ>0时，有
• [ｘ]补＋[ｙ]补＝ｘ＋ｙ＝[ｘ＋ｙ]补(mod 2)
[ｘ]补＋[ｙ]补＝ｘ＋2＋ｙ＝2＋(ｘ＋ｙ)
证明[ｘ]补＋[ｙ]补＝[ｘ＋ｙ]补
• 当ｘ＋ｙ<0时，2 ＋ (ｘ＋ｙ) < 2， 又因(ｘ＋ｙ)<0，
• [ｘ]补＋[ｙ]补＝2＋(ｘ＋ｙ)＝[ｘ＋ｙ]补 (mod 2)
• (3)ｘ<0，ｙ>0，这种情况和第2种 情况一样
上式右边分为”2”和(2＋ｘ＋ｙ)两部分。 既然
又因(ｘ＋ｙ)<0，所以
[ｘ]补＋[ｙ]补＝2＋(ｘ＋ｙ)＝[ｘ＋ｙ]补 (mod 2)
至此我们证明了，在模2意义下，
任意两数的补码之和等于该两数之和
的补码。这是补码加法的理论基础，
其结论也适用于定点整数。
[例8] ｘ＝0.1001, ｙ＝0.0101,求ｘ＋ｙ
因此，图中最右边的全加器的起
始进位输入端被连接到功能方式线M
上，作减法时M＝1，相当于在加法器
的最低位上加1。另外，图中左边还 表示出单符号位法的溢出检测逻辑； 当Cn ＝Cn － 1 时，运算无溢出；而当 Cn≠Cn－1 时，运算有溢出，经异或门 产生溢出信号。
现在我们计算一个n位的行波进位

兰州理工大学_计算机组成原理_N02-定点加减乘法运算

兰州理工大学_计算机组成原理_N02-定点加减乘法运算

2.3.2 补码乘法
1. 补码与真值得转换公式
补码数[N]补（＝anan-1…a1a0）和真值N的 关系可以表示成：
n 1 i 0
N an 2 ai 2
n
i
（2.29）
n1 n i N (1 an )2 (1 ai )2 1 （2.30） i 0
在定点小数机器中，数的表示范围为|ｘ| <1。
溢出：|运算结果| ＞ 1
上溢：正数＋正数＞最大正数 下溢：负数＋负数＜最小负数 为了判断“溢出”是否发生，可采用两种检测的 方法： 双符号位法 单符号位法
1. 双符号位法
“变形补码”或“模4补码”，从而可使模2
补码所能表示的数的范围扩大一倍。
变形补码定义为： [ ｘ] 补＝
• 另外,图中左边还表示出单符号位法的溢 出检测逻辑；当Cn＝Cn－1时,运算无溢出； 而当Cn≠Cn－1时,运算有溢出,经异或门产 生溢出信号
三个输入端和两个输入端可 按如下逻辑方程进行联系：
Si＝Ai⊕Bi⊕Ci
Ci＋1＝AiBi＋BiCi＋CiAi
2.2.5 十进制加法器
BCD码(二—十进制码) 二进制加法器 “校正”逻辑
设有两个不带符号的二进制整数： A＝am－1…a1a0 B＝bn－1…b1b0
它们的数值分别为a和b，即
a ai 2
i 0 m 1 i
b bj 2
j 0
n 1
j
在二进制乘法中，被乘数A与乘数B相乘，产生m
＋n位乘积P： P＝pm＋n－1…p1p0
乘积P 的数值为
m 1 i n 1 j P ab ai 2 b j 2 i 0 j 0 ai b j 2

2-2 定点加减法运算

2-2 定点加减法运算

例1：已知：[A]原=1.01101，[B]原=0.01011 已知：[A]原=1.01101，[B]原 [A]原+[B]原 求：[A]原+[B]原
２、第二种算法
C’的基值补 的基值补 码的含义是 对C’的数值 的数值 部分求补
加
减 B0 → B0 是 A0=B0？ 否 C’=A*－B* 是 C0=1 ？ 否 C0=A0
其中A0、B0、C0为参与运算的 其中A0、B0、C0为参与运算的 A0 A、B的符号和补码加法后所得和 的符号。 C的符号。
判断溢出的电路图 补码加减法溢出判断方法 3、补码加减法溢出判断方法 A0 x=0.1001 、 、 y= 0.1010， 0.1010， 0.0101000， y]补 例21：：已知 x=0.1001 、 y=0.1010，，用变形补码求 补 例 ：已知 x=-0.0101001y= - Sf1 0.1010 用补码的加减法求 例3 已知 x=- - 0.0101000，求[ x + y] FA B0 是指运算结果超出机器字长所能表示的范围。 溢出是指运算结果超出机器字长所能表示的范围 溢出是指运算结果超出机器字长所能表示的范围。 ⊕ 并判断其溢出情况。 y]补并判断其溢出情况 并判断其溢出情况。 V y]补并判断其溢出情况 补并判断其溢出情况。 [ xA0 y]补 补 [x – y]补并判断其溢出情况。 。 [+ + y] x y]补 y]补并判断其溢出情况 A0’y]补 、 、[x –补并判断其溢出情况。 两个符号相同的数相加，可能产生溢出； 两个符号相同的数相加，可能产生溢出；两个符号 FA B0’ B0 Sf2 相异的数相加，不可能产生溢出。 相异的数相加，不可能产生溢出。 （1）单符号法 V=Af Bf Sf + Af Bf Sf （2）进位判断法 V= C Cf + C Cf

2.2 定点加减运算

2.2 定点加减运算

2.溢出检测方法 设：被操作数为：[X]补=Xs,X1X2…Xn 操作数为：[Y]补=Ys,Y1Y2…Yn 其和（差）为：[S]补=Ss,S1S2…Sn ⑴采用一个符号位 采用一个符号位检测溢出时，当 Xs=Ys=0，Ss=1 时 ， 产 生 正 溢 ； 当 Xs=Ys=1，Ss=0时，产生负溢。 溢出判断条件为 溢出= X s Ys Ss+Xs Ys Ss
3.补码加减运算规则 ⑴参加运算的两个操作数均用补码表 示； ⑵符号位作为数的一部分参加运算； ⑶若做加法，则两数直接相加，若做 减法，则将被减数与减数的机器负数相加； ⑷运算结果仍用补码表示。
补码加法示例 例3：A=0.1011，B=-0.1110，求A+B ∵[A]补=0.1011 [B]补=1.0010 0.1011 [A]补 + 1.0010 [B]补 1.1101 [A+B]补 ∴[A+B]补=1.1101 A+B=-0.0011
二、 带符号数的舍入操作（续）
⑷查表舍入法 查表舍入法又称ROM舍入法，因为 它用ROM来存放舍入处理表，每次经查 表来读得相应的处理结果。通常，ROM 表的容量为2 K 个单元，每个单元字长为 K-1位。舍入处理表的内容设置一般采用 的方法是：当K位数据的高K-1位为全“1” 时，让那些单元按恒舍法填入K-1位全 “1”，其余单元都按下舍上入法来填其 内容。
二、 带符号数的舍入操作（续）
⑵冯· 诺依曼舍入法 这种舍入法又称为恒置1法，即不论 多余部分q位为何代码，都把保留部分p 位的最低位置1。 ⑶下舍上入法 下舍上入就是0舍1入。用将要舍去 的q位的最高位作为判断标志，以决定保 留部分是否加1。如该位为0，则舍去整 个q位（相当于恒舍）；如该位为1，则 在保留的p位的最低位上加1。

§2.2定点加法、减法运算

§2.2定点加法、减法运算

正数太大了，向前有进位，而符号位向前 无进位；两个符号位：01，表示溢出

例: X＝-0.1100 Y＝-0.1000，求 X+Y＝？ 解: [X]补=11. 0100
+ [Y]补=11. 1000
10.1100
负数绝对值太大了对应的补码小，向前无进位，而符号 位向前有进位； 两个符号位：10，表示溢出 溢出逻辑表达式为：V=Sf1⊕ Sf2
（其中Sf1为最高符号位，Sf2为第二符号位，）
定点运算器 ——定点加减法
采用“单符号位法”
当最高有效位产生进位而符号位无进位时 , 产生上溢； 当最高有效位无进位而符号位有进位时,产生下溢。 故：溢出逻辑表达式为： V＝Cf⊕Co 其中: Cf为符号位产生的进位,Co为最高有效位产生的 进位。（显然：此逻辑关系可用异或门方便地实现）
2、不带符号位的阵列乘法器
不带符号阵列乘法器逻辑图
2、不带符号位的阵列乘法器
3、带符号位的阵列乘法器
求补电路 原理：算前求补－乘法器－算后求补，见下图

3、带符号的阵列乘法器



求补电路小结
E=0时，输入和输出相等 E=1时，则从数最右端往左边扫描，直到第一个1的时 候，该位和右边各位保持不变0⊕A=A，左边各数值位 按位取反1⊕A=乛A 可以用符号作为E 的输入 原：1.11110 补：1.00010
最高有效位向前无进位，而符号位向前有 进位；表示溢出
Cf=1 Co =0
V＝Cf⊕Co =1 溢出
采用单符号位的判断方法 例: X＝-0.100 Y＝-0.101，求 X+Y＝？ 解:
[X]补=1. 1 0 0 + [Y]补=1. 0 1 1 0. 1 1 1 两负数相加，结果应为负数，但运算结 果为正数，表明有溢出发生。数据向前 无进位，符号位向前有进位

白中英计算机组成原理第2章-运算方法与运算器

白中英计算机组成原理第2章-运算方法与运算器
按编码不同又可分为原码、反码、补码、移码……
2024年7月16日星期二
5
2.1 数据与文字的表示方法
2.1.1 数据格式 2.1.2 数的机器码表示 2.1.1 数据格式 2.1.3 字符与字符串的表示方法 2.1.4 汉字的表示方法 2.1.5 校验码
2024年7月16日星期二
6
2.1.1 数据格式——定点数
2024年7月16日星期二
3
2.0 数据的类型（1/2）
按数制分：
十进制：在微机中直接运算困难；
二进制：占存储空间少，硬件上易于实现，易于运算；
十六进制：方便观察和使用；
二-十进制：4位二进制数表示1位十进制数，转换简单。 按数据格式分：
真值：没有经过编码的直观数据表示方式，其值可带正负号， 任何数制均可；
-8 1000 0000 -7 1001 0001 -6 1010 0010 …… …… ……
可以比较直观地判断两个数据的大小； 0 0000 1000
浮点数运算时，容易进行对阶操作；
+1 0001 1001
表示浮点数阶码时，容易判断是否下溢； …… …… ……
当阶码为全0时，浮点数下溢。
+7 0111 1111
优点 与真值对应关系简单；
缺点 参与运算复杂，需要将数值位与符号位分开考虑。
2024年7月16日星期二
11
补码表示法的引入（1/3）
要将指向5点的时钟调整到3点整，应如何处理？
5-2=3
2024年7月16日星期二
5+10=3（12自动 丢失。12就是模）
12
补码表示法的引入（2/3）
继续推导： 5-2=5+10（MOD 12） 5+（-2）=5+10（MOD 12） -2=10（MOD 12）

第2章2.2定点运算和定点运算器

第2章2.2定点运算和定点运算器

∴ x+y= -0.0111
5
2.2.1 定点加、减法运算
2. 补码减法 减去一个数就是加上这个数的负数， [x-y]补=[x+(-y)]补=[x]补+[-y]补 （mod 2）
从[y]补求[-y]补的法则：将[y]补连同符号位“取反且最低位
加1，相当于求负数的补码。 (hw)
【例2-12】 x= -0.1010，y= -0.0011，求 x-y。 【解】 [x]补=1.0110 [y]补=1.1101 [-y]补=0.0011
2）采用硬件实现乘除法运算
3）并行乘除法器
•
从编码角度考虑：乘除由法结果的符ቤተ መጻሕፍቲ ባይዱ位确定比较容易，运算结果的
绝对值和参加运算的数据的符号无关，所以用原码实现也很简单。 但在现代计算机中一般还是采用补码进行乘除法运算
9
2.2.3 逻辑运算
参加逻辑运算的数据称为逻辑数，是不带符号位的二进 数通常用“1” 表示逻辑真，用“0”表示逻辑假 1 逻辑非（取反运算）
操作数的各位按位取反，使每一位0变成1，1变成0
设x=x0x1x2…xn，则逻辑非标记 【解】
x x0 x1x2 xn 【例2-14】 设x=10100010，求 x 。
x =01011101
10
2.2.3 逻辑运算
2 逻辑与 （逻辑乘） • 两个操作数相同位的数据进行按位“与”运算，两个都是1 则结果为1，两个中只要有1个为0结果就是0 一般写成“∧”或“·” • 特点 对任何数据逻辑与0都会变成0，而逻辑与1则保持原有数据 不变；可用于对一个数据的某几位清0，而其他位保持不变 【例2-15】 设x=01011101，y=10011001，求x∧y。 【解】 01011101

计算机组成原理2.2 运算方法

计算机组成原理2.2 运算方法

乘数/(低位积)
R1
最低位
原码一位乘算法
0 0 F 加 法 器 加运算
R0
0 0 0 0 1
R1
0 1 1
为各寄存器给初值
0 0被 1 乘 数 1 1 0
R2
0 0 0分0 积 0 0 部
R0
移位线路 每位1套
乘 0 1 1 数 1
R1
最低位
原码一位乘算法
0 0 1 1 0 1 F 加 法 器 加运算
1. 移位运算：左移和右移
逻辑移位 算术移位（符号位不变） 2. 移位功能的实现 a.利用寄存器移位
0 1 1 0 0 0 1 1 1 1 01 1 1 10
b.移位器(左移、右移一位、直送)
二、原码一位乘算法
定义：操作数用原码表示，从最低位开 始，
解：因为 [X]补=0.1011 [Y]补=1.0010 0.1 0 1 1 +1.0 0 1 0 1.1 1 0 1
所以 :
[X+Y]补= 1.1101
X+Y = - 0.0011
[例2]：X=0.1011, Y= -0.0010, 求 X－Y。 解：因为 [X]补=0.1011 [-Y]补=0.0010 0.1 0 1 1 所以 : [Y]补=1.1110
Y = - 0.1011
０００１００ + ００１１０１ ０１０００１ 加被乘数 ００１０００１１１１右移 移出位保存 求第四次部分积
再用一步完成２数符号异或求 积的符号, 结果为 -0.10001111
原码一位乘算法
所用逻辑线路框图
F 加 法 器 加运算 被 乘 数
R2
部分积(高位)
R0
移位线路 每位1套
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

[例11] ｘ ＝＋0.1101，ｙ＝＋0.0110， 求ｘ－ｙ。
[解:] [ｘ]补＝ 0.1101 [－ｙ]补＝1.1010 [ｙ]补＝0.0110
[ｘ ]补
＋ [－ｙ]补 [ｘ－ｙ]补 所以
0.1101
1.1010 1 0.0111
ｘ－ｙ＝＋0.0111
2.2.3 溢出概念与检测方法
在定点小数机器中，数的表示范围
2.2 定点加法、减法运算
定点加减法运算包括原码、反
码、补码三种带符号的加减运算
补码加减运算实现起来最方便
2.2.1补码加法
• 负数用补码表示后，运算器里只需要 一个加法器 补码加法的公式是：
[ｘ]补＋[ｙ]补＝[ｘ＋ｙ]补 (mod 2)
(2.17)
证明[ｘ]补＋[ｙ]补＝[ｘ＋ｙ]补
• 假设采用定点小数表示，因此证 明的先决条件是： • ︱ｘ︱﹤1，︱ｙ︱﹤1， ︱ｘ＋ｙ︱﹤1
[ｘ＋ｙ]补=0.1000
两负数的和为正数
之所以发生错误，是因为运算
结果产生了溢出。两个正数相加，
结果大于机器所能表示的最大正数，
称为上溢。而两个负数相加，结果
小于机器所能表示的最小负数，称
为下溢。
为了判断“溢出”是否发生，可采 用两种检测的方法。第一种方法是采用 双符号位法，这称为“变形补码”或 “模4补码”，从而可使模2补码所能表 示的数的范围扩大一倍。变形补码定义 为： ｘ 2 ＞ｘ≥0 [ｘ]补＝ { (2.22) ４＋ｘ 0 ＞ｘ≥ - 2
为| ｘ |<1。在运算过程中如出现大于1
的现象，称为“溢出”。在定点机中，
正常情况下溢出是不允许的。
机器定点小数表示
[例12] ｘ＝＋0.1011， ｙ＝＋0.1001，求ｘ ＋ｙ。
[ｘ＋ｙ]补=1.0100 两正数的和为负数
[例13] ｘ ＝－0.1101， ｙ ＝－0.1011，求 ｘ ＋ｙ。
(mod 2)
(2.19a)
∵[ｘ－ｙ]补＝[ｘ＋(－ｙ)]补＝[ｘ]补＋[－ｙ]补
(2.19b)
将式(2.19a)与(2.19b)相加，得
[－ｙ]补＋[ｙ]补
＝[ｘ＋ｙ]补＋[ｘ－ｙ]补－[ｘ]补－[ｘ]补
＝[ｘ＋ｙ＋ｘ－ｙ]补－[ｘ]补－[ｘ]补
＝[ｘ＋ｘ]补－[ｘ]补－[ｘ]补＝0
故 [－ｙ]补＝－[ｙ]补
常规的加法运算使用同一加法器电
路，从而简化了计算机的设计。
数用补码表示时，减法运算的公式 为：
[Ｘ－ｙ]补＝[ｘ]补－[ｙ]补＝[ｘ]补＋[－ｙ]补 (2.18)
只要证明[－ｙ]补＝－[ｙ]补，上式即得 证。 现证明如下：
∵[ｘ＋ｙ]补＝[ｘ]补＋[ｙ]补
∴[ｙ]补＝[ｘ＋ｙ]补－[ｘ]补 ∴[－ｙ]补 ＝[ｘ－ｙ]补－[ｘ]补
(mod 2)
(2.20)
从[ ｙ ] 补 求[－ ｙ ] 补 的法则是：对 [ｙ]补连同符号位一起求反，最末位加 “1”(定点小数中这个1实际上是2－n)， 即可得到[－ｙ]补。 [－ｙ]补被称为[ｙ]补的机器负数， 由[ ｙ ] 补 求[－ ｙ ] 补 的过程称为对[ ｙ ] 补
变补(求补)，表示为：
[解:]
[ｘ]补 ＝0.1001, [ｙ]补＝0.0101
[ｘ ]补
＋ [ｙ ]补 所以
0.1001
0.0101
[ｘ＋ｙ]
补
0.1110
ｘ＋ｙ＝0.1110
[ 例9] ｘ ＝＋0.1011， ｙ ＝－0.0101， 求ｘ＋ｙ。
[解:] [ｘ]补 ＝0.1011， [ｙ]补＝1.1011
[ｘ ]补 0.1011
证明[ｘ]补＋[ｙ]补＝[ｘ＋ｙ]补
• (4)ｘ<0，ｙ<0，则ｘ＋ｙ<0 ∵[ｘ]补＝2＋ｘ，[ｙ]补＝2＋ｙ ∴[ｘ]补＋[ｙ]补 ＝2＋ｘ＋2＋ｙ ＝2＋(2＋ｘ＋ｙ) • (ｘ＋ｙ)是负数，而其绝对值又小于1， 那么(2＋ｘ＋ｙ)就一定是小于2而大于1 的数，进位”2”必丢失
。 相加两数都是负数，则其 和也一定是负数。
或用同余式表示为 [ｘ]补＝4＋ｘ
• (1)当ｘ﹥0，ｙ﹥0时，有ｘ＋ｙ﹥0
• 根据数据补码的定义
• [ｘ]补＋[ｙ]补＝ｘ＋ｙ＝[ｘ＋ｙ]补 (mod 2)
证明[ｘ]补＋[ｙ]补＝[ｘ＋ｙ]补
• (2)当ｘ﹥0，ｙ﹤0，有ｘ＋ｙ>0， 或ｘ＋ｙ<0两种情况 • 根据补码定义[ｘ]补=x，[ｙ]补=2+ｙ • [ｘ]补＋[ｙ]补=x+2+y=2+(x+y) • 当ｘ＋ｙ>0时，有
上式右边分为”2”和(2＋ｘ＋ｙ)两部分。 既然
又因(ｘ＋ｙ)<0，所以
[ｘ]补＋[ｙ]补＝2＋(ｘ＋ｙ)＝[ｘ＋ｙ]补 (mod 2)
至此我们证明了，在模2意义下，
任意两数的补码之和等于该两数之和
的补码。这是补码加法的理论基础，
其结论也适用于定点整数。
[例8] ｘ＝0.1001, ｙ＝0.0101,求ｘ＋ｙ
[－Y]补＝[ [Y]补 ]变补
写成运算表达式，则为
[－ｙ]补＝﹁[ｙ]补＋2－n (2.21)
其中符号﹁表示对[ｙ] 补 作包括符号 位在内的求反操作，2 －n 表示最末位
的1。
[ 例 10] 已 知 ｘ 1 ＝ － 0.1110 ， ｘ 2 ＝ ＋ 0.1101，求：[ ｘ 1] 补 ,[－ ｘ 1] 补 ,[ ｘ 2] 补 ,[－ ｘ2]补。 [解:] [ｘ1]补＝1.0010 [－ｘ1]补＝ ﹁ [ｘ1]补＋ 2－4 ＝0.1101 ＋0.0001 ＝0.1110 [ｘ2]补＝0.1101 [－ｘ2]补＝ ﹁ [ｘ2]补＋ 2－4 ＝ 1.0010 ＋0.0001 ＝1.0011
• [ｘ]补＋[ｙ]补＝ｘ＋ｙ＝[ｘ＋ｙ]补(mod 2)
[ｘ]补＋[ｙ]补＝ｘ＋2＋ｙ＝2＋(ｘ＋ｙ)
证明[ｘ]补＋[ｙ]补＝[ｘ＋ｙ]补
• 当ｘ＋ｙ<0时，2 ＋ (ｘ＋ｙ) < 2， 又因(ｘ＋ｙ)<0，
• [ｘ]补＋[ｙ]补＝2＋(ｘ＋ｙ)＝[ｘ＋ｙ]补 (mod 2)
• (3)ｘ<0，ｙ>0，这种情况和第2种 情况一样
＋ [ｙ ]补
1.1011
[ｘ＋ｙ]补 1 0.011，补码加法的 特点，一是符号位要作为数的一部 分一起参加运算，二是要在模2的意
义下相加，即超过2的进位要丢掉。
2.2.2 补码减法
负数的减法运算也要设法化为
加法来做，其所以使用这种方法而
不使用直接减法，是因为它可以和