人教版小学四年级数学第9讲：追及问题(学生版)

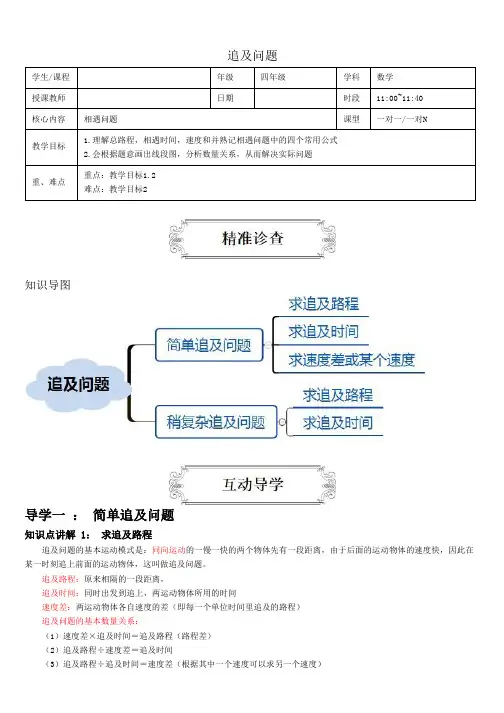
追及问题学生/课程年级四年级学科数学授课教师日期时段11:00~11:40 核心内容相遇问题课型一对一/一对N教学目标1.理解总路程，相遇时间，速度和并熟记相遇问题中的四个常用公式2.会根据题意画出线段图，分析数量关系，从而解决实际问题重、难点重点：教学目标1.2 难点：教学目标2知识导图导学一：简单追及问题知识点讲解 1：求追及路程追及问题的基本运动模式是：同向运动的一慢一快的两个物体先有一段距离，由于后面的运动物体的速度快，因此在某一时刻追上前面的运动物体，这叫做追及问题。

追及路程：原来相隔的一段距离，追及时间：同时出发到追上，两运动物体所用的时间速度差：两运动物体各自速度的差（即每一个单位时间里追及的路程）追及问题的基本数量关系：（1）速度差×追及时间＝追及路程（路程差）（2）追及路程÷速度差＝追及时间（3）追及路程÷追及时间＝速度差（根据其中一个速度可以求另一个速度）例 1. 机灵兔和大角牛在两地同时同向而行，机灵兔在前，大角牛在后，机灵兔每小时走5千米，大角牛每小时走14千米，2小时后大角牛追上了机灵兔，问2小时前，大角牛和机灵兔相距多远？我爱展示1.甲、乙两人分别从A、B两地同时出发，同向而行。

甲在前乙在后。

已知甲每分钟走50米，乙每分钟走70米，12分钟乙追上甲，A、B两地相距多远？2.甲、乙两车同时分别从A、B两地出发，同向而行，已知甲车在前，乙车在后，甲车的速度是50千米/时，乙车速度是80千米/时，3小时后乙车追上甲车，求A、B两地的距离。

知识点讲解 2：求追及时间例 1. A、B两地相距18千米，甲从A地，乙从B地同时出发同向而行，甲每小时行5千米，乙每小时行2千米，甲经过几小时追上乙？例 2. 黄艳以75米/分的速度步行去县城，出发1小时后，陆军以575米/分的速度从同一地点出发沿同一条路线去追黄艳。

追上时，黄艳还没到县城，求陆军出发后几分钟追上黄艳？我爱展示1.甲、乙两人相距150米，甲在前乙在后，甲每分钟走60米，乙每分钟走75米，两人同时向南出发，几分钟后乙追上甲？2.哥哥以80米/分的速度步行放学回家，12分钟后弟弟以200米/分的速度骑自行车从同一学校放学回家，追上时哥哥还没到家。

追及问题教学内容：追及问题（自编教材）施教学生：四年级学生执教教师：教学目标：1.知道追及问题的基本特点是：两个物体同向运动，慢的走在前，快的走在后面，它们之间的距离不断缩短，直到快者追上慢者。

并会与其他行程问题区分。

2.知道“追及时间=路程差÷速度差；速度差=路程差÷追及时间；路程差=速度差×追及时间”。

3.能利用数量关系式与画图法、假设法、比较法等思考方法解决追及问题。

4.让学生在交流合作中体验学习数学的乐趣。

教学重、难点：能利用数量关系式与画图法、假设法、比较法等思考方法解决追及问题。

教学过程：一、复习引入师：同学们，你们好！欢迎来到《思维之“数”》微课堂。

还记得上节课我们学习了什么吗？是的，相遇问题。

相遇问题中，两个物体往往是相向而行，那如果“两个物体同向运动，慢的走在前，快的走在后”又会是怎样的结果呢？根据生活经验，我们知道：它们之间的距离会不断缩短，某个时间点快者就会追上慢者。

这类问题就是我们今天要研究的“追及问题”。

（PPT）二、探究新知（一）基本数量关系青蛙在兔子前面10米，一步跳2米，兔子更快，一步跳4米，兔子追上青蛙需要跳多少步？师：先看例1，请仔细审题（5秒）。

借助数轴，每一格代表1米，（PPT）由此表示出青蛙在兔子前面10米的位置关系。

通过动画，我们发现（PPT）每跳一步，青蛙前进2米，兔子前进6米，跳一步后距离是8米（PPT），比原来缩短了2米。

再跳一步，距离是6米（PPT），又缩短了2米。

依次类推，就能得到答案。

我们发现，这其实就是一个典型的追及问题（PPT）：两者的追及距离是10米，我们把它叫做“路程差”，一步距离就缩短2米，叫做“速度差”，利用“路程差÷速度差=追及时间”的关系（PPT），列式计算（PPT）求出兔子追上青蛙需要5步。

师：同学们，现在是不是对（PPT）路程差、速度差和追及时间三个数量之间的关系有了一定的了解？三者有以下数量关系（PPT）：路程差=速度差×追及时间；速度差=路程差÷追及时间；追及时间=路程差÷速度差。

小学数学《追及问题》追及问题[含义]两个运动物体在不同地点同时出发(或者在同一地点而不是同时出发，或者在不同地点又不是同时出发)作同向运动，在后面的，行进速度要快些，在前面的，行进速度较慢些，在一定时间之内，后面的追上前面的物体。

这类叫追及问题。

[数量关系] 追及时间=追及路程÷(快速-慢速)追及路程=(快速-慢速)x追及时间速度差=追及路程÷追及时间[解题思路和方法]简单的题目直接利用公式，复杂的题目变通后利用公式。

例1：好马每天走120千米，劣马每天走75千米，劣马先走12天，好马几天能追上劣马?解：（1）劣马先走12天能走多少千米? 75x12=900(千米)（2）好马几天追上劣马? 900÷(120-75)=20(天)列成综合算式75x12÷(120-75)=900÷45=20(天)答:好马20天能追上劣马。

例2：小明和小亮在200米环形跑道上跑步，小明跑一圈用40秒，他们从同一地点同时出发，同向而跑。

小明第一次追上小亮时跑了500米，求小亮的速度是每秒多少米。

解：小明第一次追上小亮时比小亮多跑一圈，即200米，此时小亮跑了(500-200)米，要知小亮的速度，须知追及时间，即小明跑500米所用的时间。

又知小明跑200米用40秒，则跑500米用[40x(500÷200)]秒，所以小亮的速度是(500-200)÷[40x(500÷200)]=300÷100=3(米)答:小亮的速度是每秒3米。

练习题1.一辆汽车和一辆摩托车同时从甲、乙两地出发，向同一方向前进，摩托车在前，每小时行驶25千米，汽车在后，每小时行驶60千米，经过4小时汽车追上摩托车。

求甲、乙两地相距多少千米?2.一列慢车在前，速度是50千米/小时，快车在后，速度是70千米/小时，2小时后快车追上了慢车，那么原来快车和慢车相距多少千米?3.甲、乙两人分别从相距24千米的两地同时向东行驶，甲骑自行车每小时行驶13 千米，乙步行每小时走5千米，几小时后甲可以追上乙?4.一辆大客车和一辆小轿车从相距100千米的两地同时出发，同向而行，大客车在前，每小时行驶40千米，小轿车在后，每小时行驶60千米，经过几小时后两车第一次相距40千米?5.旭旭家和曼曼家在同一个胡同里相距900米，一天两人同时出发去学校。

第九讲追及问题（一）追及问题是运动的双方运动的方向正好相同，双方在运动的起始有一定的距离（双方或同时不同地，或同地不同时），而且运动的双方速度慢的在前，速度快的在后，当追及运动时，双方的运动时间是相同的，由于快的一方追及时，慢的一方也在向前运动，所以单位时间内所能追及的路程，即追及的速度是双方的速度差，这是解决追及问题的关键。

解答追及问题要理解和掌握这类问题的基本数量关系：路程差÷（速度快-速度慢）=追及时间（速度快-速度慢）×追及时间=路程差路程差÷追及时间=速度快-速度慢【例题解析】例1妹妹放学回家，以每分钟80米的速度从学校步行回家，6分钟后，哥哥骑自行车以每分钟200米的速度从学校回家，当妹妹到家时，哥哥正好追上妹妹。

问哥哥经过多少分钟追上妹妹？分析:从图中可以看出：哥哥的速度×追及时间-妹妹的速度×追及时间=妹妹6分钟行的路程即：（哥哥速度-妹妹速度）×追及时间=路程差速度差×追及时间=路程差路程差÷速度差=追及时间所以要求追及时间，需要知道路程差和速度差。

解：（1）速度差：200-80=120（米）（2）路程差：80×6=480（米）（3）追及时间：480÷120=4（分）答：问哥哥经过4分钟追上妹妹。

【边学边练】甲以每小时4千米的速度步行去学校,乙比甲晚4小时骑自行车从同一地点出发去追甲,乙每小时行12千米,乙几小时可追上甲？例2 一辆摩托车追赶比它先出发的一辆汽车。

已知这辆汽车每小时行驶28千米，摩托车每小时行驶40千米，摩托车出发后7小时追上了汽车，汽车比摩托车早出发几小时？分析 :要求汽车早出发几小时，就必须要知道汽车在摩托车出发前已行驶的千米数，即摩托车出发7小时比汽车多行的路程，为此要知道两车的速度差，而两车的速度题目已给出，故问题可以迎刃而解。

解：（1）汽车先行多少千米？（40-28）╳7=84（千米）（2）汽车早出发的时间：84÷28=3（小时）答：汽车比摩托车早出发3小时。

四年级奥数——追及问题附答案追及问题追及路程=速度差X时间1、慢车以每小时45千米的速度从甲地开往乙地，3小时后快车以每小时60千米的速度也从甲地开往乙地，问多少小时后快车追上慢车？2、两辆汽车运送货物，大卡车以每小时36千米的速度从甲地开往乙地，2小时后小卡车以每小时48千米的速度也从申地开往乙地，当小卡车追上大卡车时离甲地多远？3、两匹马在相距50米的地方同时同向出发，出发时黑马在前白马在后.如果黑马每秒跑10米，白马每秒跑12米，几秒后两马相距70米？4、一种导弹以每秒330米（音速）前进，两架飞机相距1500米同向飞行.前一架飞机的速度是每秒210米，后--架飞机的速度是每秒180 米.当后面的飞机发出导弹时，几秒可以击中前一架飞机？5、小惠从甲地骑自行车到乙地办事，每小时的速度是20千米.回来时改骑摩托车，每小时的速度是10千米，比骑自行车少用2小时，求甲、乙两地的距离.6、上午8点货车以每小时40千米的速度从甲地开往乙地，中午12点客车以每小时65千米的速度也从甲地开往乙地.为了行车安全，火车间距离不能小于10千米，那么货车最晚应在什么时间停车让客车驶过？7、汽车从甲地到乙地，以每小时20千米的速度前进，下午1点到达；以每小时30千米的速度前进，上午11点到达.如果要在中午12点到达，应该以怎.样的速度前进？8、甲、乙两人分别以每分钟60米、70米的速度同时从A地向B 地行进，丙以每分钟80米的速度从B地往A地行进.丙遇到乙3分钟后又与甲相遇，AB两地相距多少米？9、甲、乙两车相距70千米，两车同向而行，甲车每小时行55 千米，乙车每小时行45 千米。

经过几小时甲车追上乙车？10、永东小学有一条长200米的环形跑道，小明和小强同时同向从起跑线起跑。

小明每秒跑6米小强每秒跑4米，几秒后两人相遇？11、甲、乙两车相距40千米，两车同向面行。

甲车每小时行60千米，乙车每小时行50下米。

经过几小时甲车追上乙车？12、甲、乙两船同时从两个码头出发，方向相同，乙船在前，每小时行24千米，甲船在后，每小时行28千米，4小时后甲船追上乙船。

追及问题知识梳理：追及问题一般是指两个物体同方向运动，由于各自的速度不同，后者追上前者的问题。

追及问题的基本数量关系是：速度差×追及时间=追及路程解答追及问题，一定要懂得运动快的物体之所以能追上运动慢的物体，是因为两者之间存在着速度差。

抓住“追及的路程必须用速度差来追”这一道理，结合题中运动物体的地点、运动方向等特点进行具体分析，并借助线段图来理解题意，就可以正确解题。

典型例题：例1：中巴车每小时行60千米，小轿车每小时行84千米。

两车同时从相距60千米的两地同方向开出，且中巴在前。

几小时后小轿车追上中巴车？练习：1、一辆摩托车以每小时80千米的速度去追赶前面30千米处的卡车，卡车行驶的速度是每小时65千米。

摩托车多长时间能够追上？2、兄弟二人从100米跑道的起点和终点同时出发，沿同一方向跑步，弟弟在前，每分钟跑120米；哥哥在后，每分钟跑140米。

几分钟后哥哥追上弟弟？3、甲骑自行车从A地到B地，每小时行16千米。

1小时后，乙也骑自行车从A地到B地，每小时行20千米，结果两人同时到达B地。

A、B两地相距多少千米？例2：一辆汽车从甲地开往乙地，要行360千米。

开始按计划以每小时45千米的速度行驶，途中因汽车故障修车2小时。

因为要按时到达乙地，修好车后必须每小时多行30千米。

汽车是在离甲地多远处修车的？练习：1、小王家离工厂3千米，他每天骑车以每分钟200米的速度上班，正好准时到工厂。

有一天，他出发几分钟后，因遇熟人停车2分钟，为了准时到厂，后面的路必须每分钟多行100米。

小王是在离工厂多远处遇到熟人的？2、一辆汽车从甲地开往乙地，若每小时行36千米，8小时能到达。

这辆汽车以每小时36千米的速度行驶一段时间后，因排队加油用去了15分钟。

为了能在8小时内到达乙地，加油后每小时必须多行7.2千米。

加油站离乙地多少千米？3、汽车以每小时30千米的速度从甲地出发，6小时后能到达乙地。

汽车出发1小时后原路返回甲地取东西，然后立即从甲地出发。

四年级秋季第9讲追及问题（一）姓名：小知识：同向运动的物体或人相隔一定的距离，后面的速度快，前面的速度慢，经过一段时间，后者追上前者，这样的问题叫做追及问题。

追及问题中主要研究“追及路程”、“速度差”和“追及时间”三种量之间的关系。

它们有：追及路程÷速度差= 追及时间追及路程÷追及时间= 速度差速度差×追及时间= 追及路程例1：慢车以每小时行40千米的速度从甲地开往乙地，3小时后，快车以每小时60千米的速度也从甲地开往乙地，问经过多少小时间可以追上慢车？练习1．弟弟以每小时8千米的速度从家出发步行去上海野生动物园，3小时后，哥哥离家以每小时24千米的速度骑车追赶弟弟。

问：多少时间后，哥哥能追上弟弟？例2：经理与17时离开公司，以每分钟50米的速度步行回家，秘书收到紧急传真要交于经理，于是他于17时30分汽车从公司出发追赶经理，结果在离公司2000米处追上经理，并把传真给了经理，请问秘书骑车速度是多少？练习2、两地相距900千米，甲车行全程需15小时，乙车行全程需12小时，甲车先出发2小时后，乙去追甲，问乙车要走多少千米才能追上甲车？例3：甲、乙两人练习跑步，若甲让乙先跑20米，则甲跑10秒钟可以追上乙；若甲让乙先跑4秒钟，则甲跑8秒钟就能追上乙。

问：甲、乙二人的速度各是多少？练习3．一辆甲货车下午2点30分从A地出发，每小时行45千米，1.5小时后另一辆乙货车以相同速度从B地出发，下午6时两车相遇。

问A、B两地相距多少千米？例4：快车每秒行20米，慢车每秒行10米，现有两列火车同时同方向齐头行进，行15秒钟后快车超过慢车；如果两列火车车尾相齐行进，则10秒钟后快车超过慢车，求两列火车的车身长。

练习4．解放军某部小分队，以每小时6千米的速度到某地执行任务，途中休息30分后继续前进，在出发5小时后，通讯员骑摩托车以56千米的速度追赶他们。

几小可以追上他们？课堂练习：1、甲、乙两人从A地去B地，甲的速度是每小时6千米，乙的速度是每小时4千米。

教案：《追及问题》年级：四年级学科：数学教材版本：人教版教学目标：1. 让学生理解追及问题的概念，能够识别追及问题中的速度差、时间差等关键信息。

2. 培养学生运用追及问题的解决方法，解决实际问题。

3. 培养学生的逻辑思维能力和解决问题的能力。

教学重点：1. 追及问题的概念和解决方法。

2. 速度差、时间差在追及问题中的应用。

教学难点：1. 追及问题的解决方法的理解和运用。

2. 速度差、时间差的计算和应用。

教学准备：1. 教学课件或黑板。

2. 练习题。

教学过程：一、导入（5分钟）1. 引导学生回顾之前学过的行程问题的解决方法。

2. 提问：如果两个物体同时出发，一个速度快，一个速度慢，会发生什么现象？3. 学生回答，教师总结：这种现象叫做追及问题。

二、探究（15分钟）1. 出示追及问题的情景图，引导学生观察和分析。

2. 提问：如何计算追及问题的答案？3. 学生思考并回答，教师总结：追及问题的解决方法是通过计算速度差和时间差来求解。

4. 引导学生运用追及问题的解决方法，解决实际问题。

三、练习（10分钟）1. 出示练习题，让学生独立完成。

2. 教师巡回指导，解答学生的疑问。

3. 选取几道题目进行讲解，强调速度差、时间差在追及问题中的应用。

四、巩固（5分钟）1. 出示追及问题的情景图，让学生运用追及问题的解决方法进行计算。

2. 教师巡回指导，解答学生的疑问。

五、总结（5分钟）1. 让学生回顾本节课所学的内容，总结追及问题的解决方法。

2. 强调速度差、时间差在追及问题中的重要性。

六、作业（5分钟）1. 出示追及问题的练习题，让学生课后独立完成。

2. 布置学生思考：追及问题在实际生活中的应用。

教学反思：本节课通过情景图的引入，让学生直观地理解追及问题的概念。

通过探究和练习，学生能够掌握追及问题的解决方法，并能够运用速度差、时间差进行计算。

在教学过程中，教师应注重引导学生观察和分析，培养学生的逻辑思维能力和解决问题的能力。

小学四年级数学 最强大脑 第9讲 追击问题【最强大脑1：智慧库】行程问题中的另一种类型问题，解决这类问题， 要正确理解题意。

画出线段图，能更好的帮助分析和理解。

追击问题是指两个物体沿同一方向运动，慢者在前， 快者在后。

它们间的距离逐渐缩短，最后快者追上慢者，这类问题主要研究路程差、速度差、追击时间这三者间的关系。

路程差指快者与慢者两人相差的路程。

速度差指单位意境是内快者比慢者多走的路程。

追击时间指快者追上慢者所用的时间。

基本数量关系式是：Baby, Go! Go! Go!两辆汽车相距120千米，甲车在乙车前面，甲车每小时行70千米，乙车每小时行90千米，乙车追上甲车需要几个小时？过手练习1.甲车每小时行50千米，走3小时后，乙车以每小时80千米的速度去追，几小时能追上？2.良马每天行140千米，劣马每天行90千米，劣马先行15天，良马几天可以追上劣马？甲、乙两人由A地到B地，甲每分钟走60米，乙每分钟走45米，乙比甲早走4分钟，两人同时到达B地，A、B两地相距多少米？过手练习1.小明和小华从学校到电影院去看电影，小明每分钟行40米，他出发3分钟后小华才以每分钟行50米的速度出发，结果在学校与电影院的中点处小华追上了小明，学校到电影院有多少米？2.两列火车从某站相背而行，甲车每小时行58千米，先开出2小时后，乙车以每小时62千米才开出，乙车开出5小时后，两列火车相距多少千米？甲、乙两人骑自行车同地同方向出发，甲每小时行18千米，乙每小时行15千米。

乙先出发2小时后，甲才开始出发，甲追上乙需要几小时？过手练习1.甲、乙两人从A地去B地。

甲的速度是每小时6千米，乙的速度是每小时4千米。

乙先走了3小时，甲出发后多少小时可以追上乙？2.两地相距900千米。

甲走需要15天，乙走需要12天。

甲先出发2天，乙去追甲，要走多少千米才能追上？一辆汽车从甲地开往乙地，每小时行50千米，开出4小时后，一辆轿车以每小时行90千米的速度也从甲地开往乙地，在甲、乙两地的中点处轿车追上汽车，甲、乙两地相距多少千米？过手练习1.一辆汽车和一辆摩托车同时从甲乙两城同时出发，向一个方向前进，汽车在前，每小时40千米；摩托车在后，每小时75千米。