三角形中的边角关系知识点

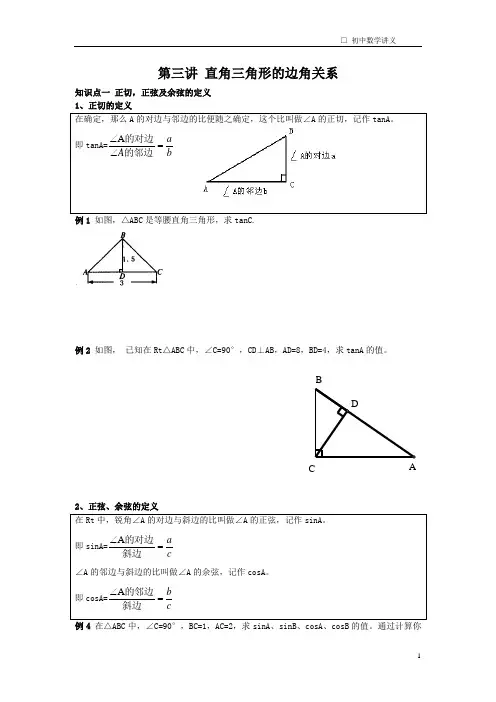
第三讲 直角三角形的边角关系知识点一 正切，正弦及余弦的定义1、正切的定义的对边与邻边的比便随之确定，这个比叫做∠A 的正切，记作例1 如图，△ABC 是等腰直角三角形，求tanC.例2 如图， 已知在Rt △ABC 中，∠C=90°，CD ⊥AB ，AD=8，BD=4，求tanA 的值。

C B A有什么发现？请加以证明。

3、三角函数的定义（重点）能判断谁的木棒更陡吗？说明理由。

同步练习：1、∠C=90°，点D 在BC 上，BD=6，AD=BC ，cos ∠ADC=53，求CD 的长。

2、P 是a 的边OA 上一点，且P 点的坐标为（3，4），求sina 、tana 的值。

3、在△ABC 中，D 是AB 的中点，DC ⊥AC ，且tan ∠BCD=31，求tanA 的值。

4、在Rt △ABC 中，∠C=90°，tanA=125，周长为30，求△ABC 的面积。

5、（2008·浙江中考）在Rt △ABC 中，CD 是斜边AB 上的中线，已知CD=2，AC=3，则sinB 的值是多少？知识点二 30°，45°，60°角的三角函数值例 求下列各式的值。

（1）︒︒-︒60tan 30sin 60sin ；（2）︒-+︒-︒45sin 22460tan 460tan 2。

同步练习：1、 求下列各式的值。

（1）︒+︒+︒45tan 30tan 330sin 2； （2）︒⋅︒+︒30cos 60tan 45cos 2。

(3) 6tan 2 30°－3sin 60°＋2tan45°(4)022)30tan 45(sin )60cos (160sin 260sin 60tan 245tan o o o o o oo-+-++----2、 已知a 为锐角，且tana=5，求aa aa sin cos 2cos 3sin +-的值。

直角三角形的边角关系知识点一、勾股定理勾股定理是指在直角三角形中，直角边的平方等于两个其他两边平方的和。

即a^2+b^2=c^2，其中c表示直角边，a和b分别表示斜边。

二、正弦定理正弦定理是指在任意三角形中，任意两边的比例等于它们所对的角的正弦值的比例。

在直角三角形中，不包含直角的两个角分别为A和B，直角所对的边为c，则正弦定理可以表示为sinA=a/c，sinB=b/c。

三、余弦定理余弦定理是指在任意三角形中，任意一边的平方等于另外两边的平方和减去它们的两倍乘以它们夹角的余弦。

在直角三角形中，不包含直角的两个角分别为A和B，直角边所对的边为c，则余弦定理可以表示为cosA=b/c，cosB=a/c。

四、正切定理正切定理是指在任意三角形中，两条边的比例等于它们所对的角的正切值的比例。

在直角三角形中，不包含直角的两个角分别为A和B，直角所对的边为c，则正切定理可以表示为tanA=a/b，tanB=b/a。

五、边角关系1.直角三角形中，一个角是90度，另外两个角的和是90度。

2.直角三角形中，直角边所对的角是90度，而另外两边所对的角是锐角。

3.直角三角形中，两个锐角的正弦、余弦、正切值彼此互为倒数。

4.直角三角形中，两个锐角的余弦值等于彼此的正弦值。

5.直角三角形中，一个锐角的正弦值等于另一个锐角的余弦值。

六、特殊三角形1.在直角三角形中，当两个直角边的长度相等时，该直角三角形为等腰直角三角形。

2.在等腰直角三角形中，两个锐角相等，且为45度。

3.在等腰直角三角形中，斜边的长度等于直角边的平方根的两倍。

以上是直角三角形的边角关系的主要知识点。

通过对直角三角形的边长和角度关系的了解，我们可以应用这些关系来解决与直角三角形相关的问题。

同时，直角三角形也是三角学中一个重要的基础概念，为后续学习提供了坚实的基础。

编号⒀九年级数学下册《直角三角形的边角关系》复习一班级姓名知识点回顾:1．直角三角形中的边角关系：（如图，在ABC中，∠C为直角）(1)三边之间的关系：(2)锐角之间的关系：(3)边角之间的关系：2．一些特殊角的三角函数值：3．锐角α的三角函数值的符号及变化规律。

(1)锐角α的三角函数值都是正值；(2)若0＜α＜90° 则sinα，tanα随α的增大而，cosα随α的增大而 . 4．常用到下面几个概念：(1)仰角、俯角：视线与水平线所成的角中，视线在水平线上方的叫做仰角，在水平线下方的叫做俯角.(2)坡度、坡角：坡面的铅直高度h与水平宽度l的比叫做坡度，常用字母i表示，h即i＝lh坡面与水平面的夹角叫做坡角，用字母α表示，则tanα＝i＝l典型例题：1、在Rt△ABC中，如果各边长度都扩大为原来的2倍，那么锐角A的正弦值（）A.扩大2倍B.缩小2倍C.扩大4倍D.没有变化2、如图：P是∠α的边OA上一点，且P点的坐标为（3，4），则sin（900 - α）＝_____________.3、计算：tan60°·sin60°－cos30°·tan45°=_____________.4、已知0°＜α＜45° 则sin α，cos α的大小关系为( )A 、sin α＞cos αB 、sin α＜cos αC 、sin α≥cos αD 、sin α≤cos α． 5、已知在Rt △ABC 中∠C＝90° 且tanA ＝31，则cosB 的值为( ) A 、1013 B 、310 C 、1010 D 10103 6、直角梯形ABCD 中，AD ∥BC ，CD ＝10，∠B＝90°，∠C＝30°则AB ＝( )A 、53B 、5C 、25D 2357、一个三角形的一边长为2，这边上的中线长为1，另两边长之和为1＋， 则这个三角形的面积为( )A. 1B.23C. D.43 8、如图，在梯形ABCD 中，AD ∥BC ，∠B=90°，AD=2，BC=5，tanC=34． （1）求点D 到BC 边的距离； （2）求点B 到CD 边的距离．9、外国船只，除特许外，不得进入我国海洋100海里以内的区域。

边角关系知识点总结1. 任意三角形的边角关系：（1）在任意三角形中，三个内角的和等于180°，即A + B + C = 180°。

（2）三角形的外角等于其不相邻的两个内角的和。

也就是说，三角形的一个内角加上其对边的外角等于180°。

（3）在任意三角形中，任意两边之和大于第三边。

即AB + BC > AC、AC + BC > AB、AB + AC > BC。

2. 直角三角形的边角关系：（1）直角三角形的三个内角中，一个为90°，一个为锐角，一个为钝角。

（2）直角三角形的斜边是其它两条边的平方和的平方根。

即c² = a² + b²。

（3）直角三角形的两个锐角互余，即一个角的余角是另一个角。

3. 等腰三角形的边角关系：（1）等腰三角形的底边相等，顶角相等。

（2）等腰三角形的底角相等，顶角相等。

（3）等腰三角形的底边上的高相等。

4. 等边三角形的边角关系：（1）等边三角形三个内角相等，每个角都是60°。

（2）等边三角形的三条边相等。

（3）等边三角形的高、中线、角平分线、垂径都是同一条线段。

5. 直角三角形、等腰三角形和等边三角形的区别：（1）直角三角形有一个角是90°，等腰三角形和等边三角形没有。

（2）等腰三角形有两条边相等，直角三角形和等边三角形没有。

（3）等边三角形的三条边都相等，直角三角形和等腰三角形没有。

6. 三角形的角平分线：（1）三角形的角平分线是指从三角形的一个角的顶点出发，把这个角平分成两个相等的角的线段。

（2）三角形的三个角都各有一条角平分线。

（3）角平分线和对边的比例关系：AB/BD = AC/CD。

7. 外接角和内切角：（1）外接角：指与三角形的外角相对应的一个角，外接角等于两个不相邻内角的和。

（2）内切角：指与三角形的内角相对应的一个角，内切角等于两个不相邻外角的和。

8. 三角形的全等条件：（1）两个三角形的三边全相等，则这两个三角形全等。

直角三角形的边角关系知识点1：锐角三角函数一、知识点讲解： 1．锐角三角函数的概念：锐角三角函数包括正弦函数，余弦函数，和正切函数，如图1－1－1，在Rt △ABC 中，∠C ＝90°，∠A 、∠B 、∠C 的对边分别为a 、b ，c ． ∠A 的正弦=A asin A=c∠的对边，即斜边；∠A 的余弦=A b cos A=c∠的邻边，即斜边,∠A 的正切=A a tan=A b∠的对边，即∠的邻边注：三角函数值是一个比值．2．特殊角是指0°，30°，45°，60°，90°的角． 3．特殊角的三角函数值．4．互为余角的三角函数关系．sin （90○－A ）=cosA ， cos （90○－A ）=sin A tan （90○－A ）= cotA cot （90○－A ）=tanA 5．同角的三角函数关系． ①平方关系：sin 2 A+cos 2A=l ②倒数关系：tanA ×cotA=1③商数关系：sin cos tan ,cot cos sin A AA A A A==④sin cos 12sin cos a a a a +=+ ⑤222tan cot (tan cot )2a a a a +=+- 二、经典例题讲解： 类型一、关于特殊的函数值 例题1、计算：()()013222sin 60-︒-+-+⋅（结果保留根号．．．．．．）中考典练1： 024cos 458(3)(1)π-+++-分值6分中考典练2：2(tan 301)____-= 中考典练3：13tan 60|2|22-+-+例题2、 2sin60°－cos30°·tan45°的结果为（ ） A 、 3 33. .22B C -D ．0 例题3、等腰直角三角形一个锐角的余弦为（ ） A 、12 32. .22B C D ．l 例4、点M(tan60°，－cos60°）关于x 轴的对称点M ′的坐标是（ ） 1111.(3,); .(3,); .(3,) .(3,)2222A B C D ----例5、在锐角△ABC 中，如果2sinC=sin90°，则∠C=__。

三角形中的边角关系知识点梳理一、 边1、根本概念〔三角形、边、 顶点的定义；三角形的符号表示〕2、按边对三角形的分类：≠⎧⎪⎨⎧⎨⎪⎩⎩不等边三角形三角形腰底等腰三角形等边三角形☆3、三边关系：〔1〕任意两边之和大于第三边 〔2〕任意两边之差小于第三边 验证：两条较短边之和与第三边的关系 二、角1、根本概念〔内角、外角〕2、按角对三角形的分类：⎧⎧⎪⎨⎩⎨⎪⎩锐角三角形斜三角形三角形钝角三角形直角三角形3、三角形的内角和〔1〕三角形三个内角和等于180°； 〔2)直角三角形的两个锐角互余； 〔3〕一个三角形最多3个锐角，最多1个钝角，最多1个直角，最少2个锐角。

三、线1、中线(1) 定义 〔2〕 重心 〔3〕中线是线段 〔4〕 表示方法 2、高线〔1〕定义 〔2〕垂心 (3〕高是线段，垂线是直线 〔4〕表示方法 〔5〕钝角三角形高的画法 3、角平分线〔1〕定义 (2)外心 〔3〕画法 〔4〕表示方法 四、方法技能归纳法在规律探索中的应用。

根底练习第1题-〔1〕 第1题-〔2〕 第1题-〔2〕1、〔1〕以AB 为边的三角形有______________；含∠ACB 的三角形有 ；在△BOC 中，OC 的对角是___________；∠OCB 的对边是___________.〔2〕图〔1〕中三角形的个数是____________;★图〔2〕中三角形的个数是____________。

2、三角形按角分类可以分为〔 〕A ．锐角三角形、直角三角形、钝角三角形；B ．等腰三角形、等边三角形、不等边三角形；C ．直角三角形、等边直角三角形；D ．以上答案都不正确3、一个等腰三角形的两边长分别是4和9，那么它的周长是___________________________4、假设三角形的三边长分别为3,4，x -1，那么x 的取值范围是_________________________5、有3cm,6cm,8cm,9cm 长的四条线段，任选其中的三条线段组成一个三角形，那么最多能组成_____个三角形6、,,a b c 是ABC 的三条边，且()()0a b c a b ++-=，那么ABC 是__________三角形7、以下说法正确的选项是_____________________〔1〕等边三角形是等腰三角形； 〔2〕三角形的两边之差大于第三边；〔3〕有两边相等的三角形一定是等腰三角形； 〔4〕一个钝角三角形一定不是等腰三角形。

直角三角形三条边的关系公式
直角三角形是指其中一个角是90度的三角形。

在直角三角形中，三条边之间有着重要的关系，可以用数学公式来表示。

1. 勾股定理：勾股定理是直角三角形中最基本的关系公式，它表示直角三角形的两条直角边的平方和等于斜边的平方。

即a²+b²=c²，其中a和b分别表示直角三角形的两条直角边，c表示斜边。

2. 正弦定理：正弦定理表示直角三角形中，任意一条边的长度与其对应的角度之间的关系。

即a/sinA=b/sinB=c/sinC，其中a、b、c分别表示直角三角形的三条边，A、B、C分别表示对应的角度。

3. 余弦定理：余弦定理表示直角三角形中，任意一条边的长度与其对应的角度之间的关系。

即a²=b²+c²-2bc*cosA，b²=a²+c²-2ac*cosB，c²=a²+b²-2ab*cosC，其中a、b、c分别表示直角三角形的三条边，A、B、C分别表示对应的角度。

这些公式的应用可以帮助我们解决直角三角形的各种问题，如求解三角形的边长、角度大小等等。

三角形的三边关系1．三角形的概念不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形．①三角形有三条边，三个内角，三个顶点.②组成三角形的线段叫做三角形的边;③相邻两边所组成的角叫做三角形的内角简称角;④相邻两边的公共端点是三角形的顶点，⑤三角形ABC 用符号表示为△ ABC ，⑥三角形ABC 的边AB 可用边AB 所对的角C的小写字母 c 表示，AC 可用b表示，BC 可用 a 表示.1:三条线段要不在同一直线上，且首尾顺次相接2:三角形是一个封闭的图形；3:△ ABC 是三角形ABC 的符号标记，单独的△没有意义例例 1 图中三角形的个数是( )A．8 B．9 C．10 D．112．三角形的三边关系三角形的任意两边之和大于第三边; 三角形的任意两边之差小于第三边.1：三边关系的依据是：两点之间线段是短2:判断三条线段能否构成三角形的方法：只要满足较小的两条线段之和大于第三条线段，便可构成三角形; 若不满足，则不能构成三角形.3:三角形第三边的取值范围是: 两边之差<第三边<两边之和例1 ：已知四组线段的长分别如下，以各组线段为边，能组成三角形的是( )A．1，2，3 B．2，5，8 C．3，4，5 D．4，5，10例2：下列各组条件中，不能组成三角形的是( )A. a+1、a+2、a+3 (a>3)B. 3cm、8cm、10 cmC. 三条线段之比为1:2:3D. 3a、5a、2a+1 (a>1)例3．△ ABC的三边长分别为4、9、x,⑴ 求x 的取值范围；⑵ 求△ ABC 周长的取值范围；⑶ 当x 为偶数时，求x ；⑷ 当△ ABC 的周长为偶数时，求x ；⑸ 若△ ABC 为等腰三角形，求x ．课堂练习1．已知长度为2cm,3cm,4cm,5cm 的四条线段，能组成多少个不等边三角形？2．已知等腰三角形的周长是14 cm ，底边与腰的比为 3 : 2 ，求各边的长.3．在ABC中，AB 9,BC 2，并且AC 为奇数，那么ABC的周长是多少？4．如图， D 是ABC内任意一点，BD 延长线与AC 交于 E 点，连结DC.求证：AB AC BD DC .3．三角形的高、中线、角平分线(1 ) 三角形的高：从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段．注意：①三角形的高是线段；②锐角三角形三条高全在三角形的内部；直角三角形有两条高是直角边，另一条在内部；钝角三角形有两条高在三角形外，另一条在内部。

2017—2018学年寒假辅导第1讲直角萨娇新的边角关系一、知识清单梳理知识点一：锐角三角函数的定义关键点拨与对应举例1.锐角三角函数正弦: sin A＝∠A的对边斜边＝ac余弦: cos A＝∠A的邻边斜边＝bc正切: tan A＝∠A的对边∠A的邻边＝ab.根据定义求三角函数值时，一定根据题目图形来理解，严格按照三角函数的定义求解，有时需要通过辅助线来构造直角三角形.2.特殊角的三角函数值度数三角函数30°45°60°sinA 122232cosA 322212tanA 331 3知识点二：解直角三角形3.解直角三角形的概念在直角三角形中，除直角外，一共有五个元素，即三条边和两个锐角，由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形．科学选择解直角三角形的方法口诀：已知斜边求直边，正弦、余弦很方便；已知直边求直边，理所当然用正切；已知两边求一边，勾股定理最方便；已知两边求一角，函数关系要记牢；已知锐角求锐角，互余关系不能少；已知直边求斜边，用除还需正余弦.例：在Rt△ABC中，已知a=5,∠A=30°，则c=,b=.4.解直角三角形的常用关系(1)三边之间的关系：a2＋b2＝c2；(2)锐角之间的关系：∠A＋∠B＝90°；(3)边角之间的关系：sinA＝=cosB=ac，cosA＝sinB=bc，tanA＝ab.(4)相等的角①商的关系:tanA= ;②平方关系:sin2A+cos2A=1.(5)互余的两角:若∠A+∠B=90°,则sinA=cosB, cosA=sinB.知识点三：解直角三角形的应用5.仰角、俯角、坡度、坡角和方向角(1)仰、俯角：视线在水平线上方的角叫做仰角.视线在水平线下方的角叫做俯角．（如图①）(2)坡度：坡面的铅直高度和水平宽度的比叫做坡度(或者叫做坡比)，用字母i表示．坡角：坡面与水平面的夹角叫做坡角，用α表示，则有i＝tanα. （如图②）(3)方向角：平面上，通过观察点Ο作一条水平线(向右为东向)和一条铅垂线(向上为北向)，则从点O出发的视线与水平线或铅垂线所夹的角，叫做观测的方向角．（如图③）解直角三角形中“双直角三角形”的基本模型：（1）叠合式（2）背靠式解题方法：这两种模型种都有一条公共的直角边，解题时，往往通过这条边为中介在两个三角形中依次求边，或通过公共边相等，列方程求解.6.解直角三角形实际应用的一般步骤(1)弄清题中名词、术语，根据题意画出图形，建立数学模型；(2)将条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形问题；(3)选择合适的边角关系式，使运算简便、准确；(4)得出数学问题的答案并检验答案是否符合实际意义，从而得到问题的解．二、 专题讲座专题一：锐角三角函数的概念注意：1.sinA 、∠cosA 、tanA 表示的是一个整体，是两条线段的比，没有 ，这些比值只与 有关，与直角三角形的 无关2.取值范围 <sinA< ； < cosA< ； tanA> 例1．如图所示，在Rt △ABC 中，∠C ＝90°．①斜边)(sin =A ＝______， 斜边)(sin =B ＝______；②斜边)(cos =A ＝______， 斜边)(cos =B ＝______；③的邻边A A ∠=)(tan ＝______，)(tan 的对边B B ∠=＝______．例2. 锐角三角函数求值：在Rt △ABC 中，∠C ＝90°，若a ＝9，b ＝12，则c ＝______，sin A ＝__ ___，cos A ＝___ ___，tan A ＝____ __， sin B ＝___ ___，cos B ＝_____ _，tan B ＝___ ___．例3．已知：如图，Rt △TNM 中，∠TMN ＝90°，MR ⊥TN 于R 点，TN ＝4，MN ＝3．求：sin ∠TMR 、cos ∠TMR 、tan ∠TMR ．类型一：直角三角形求值例4．已知Rt △ABC 中，,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B ．例5.已知A ∠是锐角，178sin =A ，求A cos ，A tan 的值类型二. 利用角度转化求值：例6．已知：如图，Rt △ABC 中，∠C ＝90°．D 是AC 边上一点，DE ⊥AB 于E 点．DE ∶AE ＝1∶2． 求：sinB 、cosB 、tanB ．例7.如图，角α的顶点为O ，它的一边在x 轴的正半轴上，另一边OA 上有一点P （3，4），则 sin α= ．A D ECBF例7图 例8图 例9图 例13图例8.如图，菱形ABCD 的边长为10cm ，DE ⊥AB ，3sin 5A =，则这个菱形的面积= cm 2． 例9.如图，沿AE 折叠矩形纸片ABCD ，使点D 落在BC 边的点F 处．已知8AB =，10BC =，AB=8,则tan EFC ∠的值为 ( ) Ａ．34 Ｂ．43 Ｃ．35 Ｄ．45类型三. 化斜三角形为直角三角形例10.如图，在△ABC 中，∠A=30°，∠B=45°，AC=23，求AB 的长．例11．已知：如图，△ABC 中，AC ＝12cm ，AB ＝16cm ，⋅=31sin A (1)求AB 边上的高CD ；(2)求△ABC 的面积S ；(3)求tan B ．例12．已知：如图，在△ABC 中，∠BAC ＝120°，AB ＝10，AC ＝5．求：sin ∠ABC 的值．类型四：利用网格构造直角三角形例13如图所示，△ABC 的顶点是正方形网格的格点，则sinA 的值为（ ） A ．12 B ．55 C ．1010D ．255对应训练：1．在Rt △ABC 中，∠ C ＝90°，若BC ＝1，AB =5，则tan A 的值为（ ）A ．55 B ．255 C ．12D ．2 2．在△ABC 中，∠C =90°，sin A=53，那么tan A 的值等于（ ） A ．35 B. 45 C. 34 D. 433. 如图，在等腰直角三角形ABC ∆中，90C ∠=︒，6AC =，D 为AC 上一点，若1tan 5DBA ∠= ，则AD 的长为( ) A ．2 B ．2 C ．1 D ．224. 如图，在Rt △ABC 中，∠C =90°，AC =8，∠A 的平分线AD =3316；求∠B 的度数及边BC 、AB 的长.DABC5．如图，在Rt △ABC 中，∠BAC=90°，点D 在BC 边上，且△ABD 是等边三角形．若AB=2，求△ABC 的周长．（结果保留根号）6．已知：如图，△ABC 中，AB ＝9，BC ＝6，△ABC 的面积等于9，求sin B ．7. 在△ABC 中，∠A=60°，AB=6 cm ，AC=4 cm ，则△ABC 的面积是 （ ）A.23 cm 2B.43 cm 2C.63 cm 2D.12 cm 28．如图，△ABC 的顶点都在方格纸的格点上，则sin A =_______.9．如图，A 、B 、C 三点在正方形网络线的交点处，若将ABC ∆绕着点A 逆时针旋转得到''B AC ∆，则'tan B 的值为（ ） A.41 B. 31 C.21D. 110．正方形网格中，AOB ∠如图放置，则tan AOB ∠的值是（ ）A ．5 5 B. 2 5 5 C.12D. 2CB A ABO专题二：特殊角的三角函数值当 时，正弦和正切值随着角度的增大而 余弦值随着角度的增大而例1．求下列各式的值．（1）︒-︒+︒60tan 45sin 230cos 2 （2）︒-︒+︒30cos 245sin 60tan 2（3）3－1+(2π－1)0－33tan30°－tan45°(4)30tan 2345sin 60cos 221⎪⎪⎭⎫ ⎝⎛︒-︒+︒+ (5) tan 45sin 301cos 60︒+︒-︒；例2．求适合下列条件的锐角α ． (1)21cos =α (2)33tan =α (3)222sin =α(4)33)16cos(6=- α （5）已知α 为锐角，且3)30tan(0=+α，求αtan 的值（6）在ABC ∆中，若0)22(sin 21cos 2=-+-B A ，B A ∠∠，都是锐角，求C ∠的度数.例3. 三角函数的增减性 1．已知∠A 为锐角，且sin A <21，那么∠A 的取值范围是（ ） A. 0°< ∠A < 30° B. 30°< ∠A ＜60° C. 60°< ∠A < 90° D. 30°< ∠A < 90° 2. 已知∠A 为锐角，且030sin cos <A ，则 （ ）A. 0°<∠ A < 60°B. 30°<∠ A < 60°C. 60°< ∠A < 90°D. 30°<∠ A < 90°例4. （三角函数在几何中的应用）已知：如图，在菱形ABCD 中，DE ⊥AB 于E ，BE ＝16cm ，⋅=1312sin A 求此菱形的周长．对应练习：1.计算：10123tan 45(2 1.41)3-⎛⎫--++- ⎪⎝⎭2.计算：1201314.330sin 21）（）（-++---π3.计算：212322cos602°. 4计算：(2014－5)0－(cos60°)-2＋38－3tan30°；5.计算：6.计算：|1﹣|﹣（）﹣1﹣4cos30°+（π﹣3.14）0．7.已知α是锐角，且sin(α+15°)=32． 计算10184cos ( 3.14)tan 3απα-⎛⎫---++ ⎪⎝⎭的值．8．已知：如图，Rt △ABC 中，∠C ＝90°，3==BC AC ，作∠DAC ＝30°，AD 交CB 于D 点，求： (1)∠BAD ； (2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD ．9. 已知：如图△ABC 中，D 为BC 中点，且∠BAD ＝90°，31tan =∠B ，求：sin ∠CAD 、cos ∠CAD 、tan ∠CAD ．10. 如图，在Rt △ABC 中，∠C=90°，53sin =B ，点D 在BC 边上，DC= AC = 6，求tan ∠BAD 的值．11.（本小题5分）如图，△ABC 中，∠A=30°，3tan 2B =，43AC =．求AB 的长.DCBAACB专题三：解直角三角形的应用例1．（2012•福州）如图，从热气球C处测得地面A、B两点的俯角分别是30°、45°，如果此时热气球C处的高度CD为100米，点A、D、B在同一直线上，则AB两点的距离是（）例1图例2图A．200米B．200米C．220米D．100（）米例2．如图，某水库堤坝横断面迎水坡AB的坡比是1：3，堤坝高BC=50m，则应水坡面AB的长度是（）A．100m B．1003m C．150m D．503m例3. “兰州中山桥”位于兰州滨河路中段白搭山下、金城关前，是黄河上第一座真正意义上的桥梁，有“天下黄河第一桥”之美誉。

（1）三角形三内角和等于180°（在球面上，三角形内角之和大于180°）；（2）三角形的一个外角等于和它不相邻的两个内角之和；（3）三角形的一个外角大于任何一个和它不相邻的内角；（4）三角形两边之和大于第三边，两边之差小于第三边；（5）在同一个三角形内，大边对大角，大角对大边.（6）三角形中的四条特殊的线段：角平分线，中线，高，中位线.（7）三角形的角平分线的交点叫做三角形的内心，它是三角形内切圆的圆心，它到各边的距离相等.（8）三角形的外接圆圆心，即外心，是三角形三边的垂直平分线的交点，它到三个顶点的距离相等.（9）三角形的三条中线的交点叫三角形的重心，它到每个顶点的距离等于它到对边中点的距离的2倍。

（10）三角形的三条高的交点叫做三角形的垂心。

（11）三角形的中位线平行于第三边且等于第三边的1/2。

（12）三角形的一边与另一边延长线的夹角叫做三角形的外角。

注意: ①三角形的内心、重心都在三角形的内部. ②钝角三角形垂心、外心在三角形外部。

③直角三角形垂心、外心在三角形的边上。

（直角三角形的垂心为直角顶点，外心为斜边中点。

）④锐角三角形垂心、外心在三角形内部。

三角形相关定理重心定理三角形的三条中线交于一点，这点到顶点的距离是它到对边中点距离的2倍．上述交点叫做三角形的重心.外心定理三角形的三边的垂直平分线交于一点．这点叫做三角形的外心.垂心定理三角形的三条高交于一点．这点叫做三角形的垂心.内心定理三角形的三内角平分线交于一点．这点叫做三角形的内心.旁心定理三角形一内角平分线和另外两顶点处的外角平分线交于一点．这点叫做三角形的旁心．三角形有三个旁心．三角形的重心、外心、垂心、内心、旁心称为三角形的五心．它们都是三角形的重要相关点．中位线定理三角形的中位线平行于第三边且等于第三边的一半．三边关系定理三角形任意两边之和大于第三边，任意两边之差小于第三边．勾股定理在Rt三角形ABC中，A≤90度，则AB·AB+AC·AC=BC·BC梅涅劳斯定理梅涅劳斯（Menelaus）定理是由古希腊数学家梅涅劳斯首先证明的。

三角形中的边角关系内容和内容解析三角形是几何学中的基本图形之一，它由三条线段组成，其中每两条线段相交于一个顶点。

在三角形中，边角关系是研究其边长和角度之间的关系。

了解三角形中的边角关系对于解决各种几何问题非常重要。

在三角形中，边角关系有很多重要的定理和性质。

首先，我们来讨论三角形的边长关系。

根据三角形的定义，任意两边之和必须大于第三边。

这就是著名的三角不等式定理。

例如，如果一个三角形的三条边的长度分别是a、b、c，那么满足条件a+b>c、a+c>b和b+c>a。

这个定理的应用非常广泛，在解决三角形问题时经常会用到。

另一个与边长相关的重要性质是三角形的周长。

三角形的周长是三个边长的和，即周长=a+b+c。

周长是三角形的一个重要度量，它描述了三角形的大小。

接下来我们来探讨三角形的角度关系。

首先，我们来讨论三角形的内角和外角关系。

在任意三角形中，三个内角的和等于180度。

这是三角形内角和定理。

例如，如果一个三角形的三个内角分别是A、B、C，那么有A+B+C=180度。

这个定理可以用于求解三角形的未知角度。

另一个与角度相关的重要性质是三角形的外角和内角关系。

在三角形的每个内角上都有一个对应的外角。

这两个角的大小之和等于180度。

例如，如果一个三角形的一个内角是A，那么它所对应的外角的大小是180度减去A的度数。

这个定理可以帮助我们求解三角形的未知角度。

除了边长和角度关系，三角形还有其他重要的边角关系。

例如，根据三角形的形状，我们可以将三角形分为等边三角形、等腰三角形和一般三角形。

等边三角形的三条边都相等，三个内角都是60度。

等腰三角形的两条边相等，两个内角也相等。

一般三角形的三条边和三个内角都没有特殊的关系。

根据三角形的角度大小，我们还可以将三角形分为锐角三角形、直角三角形和钝角三角形。

锐角三角形的三个内角都小于90度，直角三角形的一个内角是90度，钝角三角形的一个内角大于90度。

三角形中的边角关系是研究其边长和角度之间的关系。

三角形的边角关系公式
（1）三角形三内角和等于180°,这个定理的证明方法有很多种,(即辅助线的做法,)体现了几何中的一题多解的思维方法,这也是几何与众不同都地方.（2）三角形的一个外角等于和它不相邻的两个内角之和；
（3）三角形的一个外角大于任何一个和它不相邻的内角；
（4）三角形两边之和大于第三边,两边之差小于第三边；
（5）在同一个三角形内,大边对大角,大角对大边.
（6）三角形中的四条特殊的线段：角平分线,中线,高,中位线.
（注①：等腰三角形中,顶角平分线,中线,高三线互相重叠
①：三角形的中位线是两边中点的连线,它平行于第三边且等于第三边的一半)（7）三角形的角平分线的交点叫做三角形的内心,它是三角形内切圆的圆心,它到各边的距离相等.
（8）三角形的外接圆圆心,即外心,是三角形三边的垂直平分线的交点,它到三个顶点的距离相等.
（9）三角形的三条中线的交点叫三角形的重心,它到每个顶点的距离等于它到对边中点的距离的2倍.
（10）三角形的三条高的交点叫做三角形的垂心.
（11）三角形的中位线平行于第三边且等于第三边的1/2.
（12）三角形的一边与另一边延长线的夹角叫做三角形的外角.
注意:①三角形的内心、重心都在三角形的内部
.①钝角三角形垂心、垂心在三角形外部.（三条高的延长线交于一点,在三角形的外部）
①直角三角形垂心、垂心在三角形的边上.（直角三角形的垂心为直角顶点,外心为斜边中点.）
①锐角三角形垂心、垂心在三角形内部.。

1第一章 直角三角形的边角关系1.如图，在Rt △ABC 中，∠C=90°，如果锐角A 确定， =A sin , A cos = , A tan = .2.特殊角的三角函数值2.锐角三角函数的关系互余两角的三角函数关系(A 为锐角):cos sin =A ,sin cos =A . 3.锐角三角函数的性质当角度在0°～90°之间变化时：正弦值随角度的增大(或减小)而 (或 )； 余弦值随角度的增大(或减小)而 (或 )； 正切值随角度的增大(或减小)而 (或 )； 4.解直角三角形的定义在直角三角形中，除直角外，一共有5个元素，即3条边和2个锐角，由直角三角形中除直角外的已知元素求出未知元素的过程，叫做解直角三角形。

5.在Rt △ABC 中，∠C=90°，∠A ，∠B ，∠C 所对的边分别是c b a ,,。

①三边之间的关系： ；②锐角之间的关系： 。

③边角之间的关系：=A sin ,=A cos ,=A tan , =B sin ,=B cos ,=B tan , ④面积公式：ch ab S ABC 2121==△(h 为斜边上的高). 6.解直角三角形应用题中常见的概念①坡角：坡面与水平的夹角叫做坡角，用字母α表示。

坡度：坡面的铅垂高度h 和水平宽度l 的比叫 做坡度，用字母i 表示，则αtan ==lhi 。

如图②仰角、俯角：视线与水平线所成的角中，视线在水平线上方的叫做仰角，在水平线下方的叫做俯角。

如图方法1：利用锐角三角函数的概念求三角函数值例1.在Rt △ABC 中，∠C=90°，若将各边长度都扩大为原来的2倍，则∠A 的正弦值( )A.扩大2倍B.缩小2倍C.扩大4倍D.不变 方法2：利用锐角三角函数的概念进行计算的方法 例2.在△ABC 中，∠C=90°，54sin =A ，则B tan =( ) 视线视线2A.34B.43C.53D.54方法3：利用特殊角三角函数值进行计算的方法例3.01-)20082009(2-60sin30cos4--+︒︒）（= 。

三角形基础知识说明：△ABC中，角A，B，C的对边分别为a，b，c，p为三角形周长的一半，r为内切圆半径，R为外接圆半径，）h a，h b，h c分别为a，b，c边上的高S△ABC表示面积。

1．三角形的定义：三条线段首尾顺次连结所组成的图形，其中各条线段叫做三角形的边，每两条边组成的角叫做三角形的内角（简称三角形的角）．2．三角形的元素：三角形的边、角、中线、高线、角平分线、周长、面积等都叫三角形的元素．3．确定三角形的条件：在三角形的元素中，边和角叫做三角形的基本元素，其中角确定三角形的形状（定形），边确定三角形的大小（定量），三角形具有稳定性．确定三角形的条件是：已知三角形的三边（SSS）或两边及其夹角（SAS）或两角及其公共边（ASA）或两角与其中一角的对边（AAS），这也是判断两个三角形全等的主要方法，全等三角形的对应元素都相等．只知三角形的三角大小，不能确定三角形，具有相同大小的三个角的两个三角形是相似关系．4．三角形的“线”与“心”：（1）高线、垂心．（2）中线、重心及其的性质、坐标公式、向量公式及其物理意义、中线长定理．（3）中垂线、外接圆、外心．（4）内角平分线、内切圆、内心、内角平分线定理．（5）外角平分线、旁切圆、旁心、外角平分线定理．（6）中位线、中位线定理、中点三角形及其性质．5．三角形的分类：（1）按边的相等情况分：三边不等的三角形、等腰三角形、等边三角形。

（2）按最大角的情况分：锐角三角形、直角三角形、钝角三角形。

6．等腰三角形的判定与性质、四线合一7．等边三角形的判定与性质、四心合一（中心）8．三角形元素之间的关系：（1）角与角的关系：①内角和定理、②外角定理③角的性质：范围、关系．④最大角、最小角．⑤锐角三角形中任两角的和（2）边与边的关系：两边之和大于第三边，两边之差小于第三边．（“三胞胎”）（3）边与角的关系：（“三胞胎”）①对边与对角的大小关系：在三角形中，大边所对的角也较大，相等两边所对的角也相等，反之也真．②正弦定理：在一个三角形中，各边和它所对角的正弦之比都相等，都等于该三角形外接圆的直径．③余弦定理：在一个三角形中，任何一边的平方都等于其他两边的平方和减去这两边与它们夹角的余弦的乘积的二倍．④射影定理：在一个三角形中，任何两边在第三边上的射影之和都等于第三边．（4）直角三角形的性质：①勾股定理②两个锐角的关系③锐角的三角函数（边与角的联系）．④含30º角的直角三角形的性质⑤斜边上的中线长等于斜边长的一半．9．解三角形：根据三角形中已知的元素求其它未知的元素，叫解三角形．10．三角形面积公式：（1）ABC S ∆111222a b c ah bh ch === 111sin sin sin 222ab C ac B bc A === 2sin sin 2sin a B C A =CB A c BC A b sin 2sin sin sin 2sin sin 22== 22sin sin sin R A B C = (sin sin sin )Rr A B C =++4abc R =pr =． （2）若1122(),()AB x ,y AC x ,y ==，则ABC S ∆1212||x x y y =-．（3）若,AB AC ==c b ，则ABC S ∆=．1．正弦定理：(2sin sin sin R Cc B b A a ===R 为△ABC 外接圆半径）。

第七讲 直角三角形的边角关系一、知识点快速归纳理解：考点一、直角三角形的性质 1、直角三角形的两个锐角互余可表示如下：∠C=90°⇒∠A+∠B=90°2、在直角三角形中，30°角所对的直角边等于斜边的一半。

∠A=30°可表示如下： ⇒BC=21AB ∠C=90°3、直角三角形斜边上的中线等于斜边的一半 ∠ACB=90°可表示如下： ⇒CD=21AB=BD=AD D 为AB 的中点 4、勾股定理直角三角形两直角边a ，b 的平方和等于斜边c 的平方，即222c b a =+ 5、射影定理在直角三角形中，斜边上的高线是两直角边在斜边上的摄影的比例中项，每条直角边是它们在斜边上的摄影和斜边的比例中项∠ACB=90° BD AD CD •=2⇒ AB AD AC •=2CD ⊥AB AB BD BC •=2 6、常用关系式由三角形面积公式可得：AB •CD=AC •BC考点二、直角三角形的判定1、有一个角是直角的三角形是直角三角形。

2、如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

3、勾股定理的逆定理如果三角形的三边长a ，b ，c 有关系222c b a =+，那么这个三角形是直角三角形。

考点三、锐角三角函数的概念 1、如图，在△ABC 中，∠C=90°①锐角A 的对边与斜边的比叫做∠A 的正弦，记为sinA ，即casin =∠=斜边的对边A A②锐角A 的邻边与斜边的比叫做∠A 的余弦，记为cosA ， 即cbcos =∠=斜边的邻边A A③锐角A 的对边与邻边的比叫做∠A 的正切，记为tanA ，即b atan =∠∠=的邻边的对边A A A④锐角A 的邻边与对边的比叫做∠A 的余切，记为cotA ，即abcot =∠∠=的对边的邻边A A A2、锐角三角函数的概念锐角A 的正弦、余弦、正切、余切都叫做∠A 的锐角三角函数 3、一些特殊角的三角函数值 三角函数 0° 30°45°60° 90° sinα21 22 23 1cos α 123 22 21 0tan α 0 33 13不存在cot α 不存在 3133 04、各锐角三角函数之间的关系（1）互余关系： sinA=cos(90°—A)，cosA=sin(90°—A)tanA=cot(90°—A)，cotA=tan(90°—A) （2）平方关系： 1cos sin 22=+A A （3）倒数关系： tanA •tan(90°—A)=1 （4）弦切关系： tanA=AAcos sin 5、锐角三角函数的增减性 当角度在0°~90°之间变化时， （1）正弦值随着角度的增大（或减小）而增大（或减小） （2）余弦值随着角度的增大（或减小）而减小（或增大） （3）正切值随着角度的增大（或减小）而增大（或减小） （4）余切值随着角度的增大（或减小）而减小（或增大） 考点四、解直角三角形 1、解直角三角形的概念2、解直角三角形的理论依据在Rt △ABC 中，∠C=90°，∠A ，∠B ，∠C 所对的边分别为a ，b ，c（1）三边之间的关系：222c b a =+（勾股定理） （2）锐角之间的关系：∠A+∠B=90° （3）边角之间的关系：ba B ab Bc a B c b B a b A b a A c b A c a A ========cot ,tan ,cos ,sin ;cot ,tan ,cos ,sin二、知识点练习题方式方法及技巧渗透1．如图，小颖利用有一个锐角是30°的三角板测量一棵树的高度，已知她与树之间的水平距离BE 为5m ，AB 为1.5m （即小颖的眼睛距地面的距离），那么这棵树高是（ ） A ．（53332+）m B ．（3532+）m C ． 533m D ．4m 2．如图，在等腰Rt △ABC 中，∠C =90o ，AC =6，D 是AC 上一点，若tan ∠DBA =51，则AD 的长为（ ） （A ） 2 （B ）3 （C ）2 （D ）13．已知在ABC △中，90C ∠=o，设sinB n =，当B ∠是最小的内角时，n 的取值范围是（ ）A ．202n <<B ．102n << C ．303n << D ．302n << 4．如图，小正方形的边长都为1，A 、B 、C 是小正方形的顶点，则∠ABC 的度数为（ ）A ．90°B ．60°C ．45°D ．30°5．如图，已知一商场自动扶梯的长z 为10米，该自动扶梯到达的高度h 为6米，自动扶梯与地面所成的角为θ，则tan θ的值等于( )6．如图，矩形ABCD 中，AB ＞AD ，AB =a ，AN 平分∠DAB ，DM ⊥AN 于点M ，CN ⊥AN 于点N ．则DM +CN 的值为（用含a 的代数式表示）( )A ．aB ．a 54C ．a 22D ． a 23 7．在△ABC 中，∠C ＝90°，sinA ＝45，则tanB ＝ （ ） A ．43 B ．34 C ．35 D ．458．在正方形网格中，ABC △的位置如图所示，则cos B ∠的值为（ ）A ．12B ．22C ．32D ．33aNM CDAB（第6题）BA ED C30°第1题第2题CA第4题图第5题图9．计算2sin 45°的结果等于（ ）A ．2B ．1C ．22 D ．21 10．在Rt △ABC 中,∠C=90°,若AC=2BC,则sin A 的值是( )A ．12B ．2C ．5D ．5 11．在Rt △ABC 中，∠C=90°，sinA=54，则cosB 的值等于（ ） A ．53 B. 54 C. 43D. 5512．在△ABC 中，∠C ＝90°，sinA ＝45，则tanB ＝（ ） A ．43 B ．34 C ．35 D ．4513．在7,35,90,==∠=∠∆AB B C ABC Rt οο中，则BC 的长为 （ ）（A ）ο35sin 7（B ）ο35cos 7（C ）ο35cos 7 （D ）．ο35tan 714．如上右第9题图，在梯形ABCD 中，AD//BC ，AC ⊥AB ，AD=CD 54cos =∠DCA ，BC=10，则AB 的值是（ ） A ．9 B ．8 C ．6 D ．315．如图，小明为了测量其所在位置A 点到河对岸B 点之间的距离，沿着与AB 垂直的方向走了m 米，到达点C ，测得∠ACB ＝α，那么AB 等于（ ）(A) m ·sin α米 (B) m ·tan α米 (C) m ·cos α米 (D) αtan m米16．如图，△ABC 的三个顶点分别在正方形网格的格点上，则A ∠tan 的值是 （ ）A ．56 B ．65 C ．3102 D ．1010317．sin30︒的值等于 （ ） （A ）12（B ）2 （C ）3 （D ）118．已知在Rt ABC △中，390sin 5C A ∠==°，，则tan B 的值为（ ） A ．43B ．45C ．54D ．3419．如图，为测量一幢大楼的高度，在地面上距离楼底O 点20 m 的点A 处，测得楼顶B 点的仰角∠OAB A BC m α(第15题图)D BC E ＝65°，则这幢大楼的高度为 （ ） （结果保留3个有效数字）． （A ）42.8 m（B ）42.80 m （C ）42.9 m （D ）42.90 m20．如图，在正方形ABCD 中，O 是CD 边上一点，以O 为圆心，OD 为半径的半圆恰好与以B 为圆心，BC 为半径的扇形的弧外切，则∠OBC 的正弦值为 ．21．如图，已知直线1l ∥2l ∥3l ∥4l ，相邻两条平行直线间的距离都是1，如果正方形ABCD 的四个顶点分别在四条直线上，则sin α= ．22．已知：如图，梯形ABCD 中，AB//CD ，∠A=600 ，AD=5cm ，DC=6cm ，AB=10cm 。

）cosAcosB tanA ; tanB ;sin sin <>>A B 直角三角形的边角关系一、知识点回顾1、锐角A 的三角函数（1）、∠A 的正弦：在Rt △ABC 中，sinA= （2）、∠A 的余弦：在Rt △ABC 中，cosA=（3）、∠A 的正切：在Rt △ABC 中，tanA=【注】①当0°<α<90°时，0<sin α<1 ；0<cos α<1②当0°<α<45°时，0<tan α<1；当45°<α<90°时，tan α>12、锐角三角函数的性质（1）1、1A cos A sin 22=+ （2）、AAA cos sin tan = （3）、在Rt △ABC 中，sinA=cosB ，cosA=sinB（4）、对于锐角A 的每一个确定的值，其三个三角函数值也是唯一确定的。

（5）、锐角∠A 的正弦、正切值随∠A 的增大而增大；∠A 的余弦值随∠A 的增大而减小。

（如果B ∠>A ∠，那么 （6）、45°是αsin 和αcos 的值的分界点，①当0°<α<45°，αsin <αcos ；②当 45°<α<90°，αsin >αcos ；③当α=45°时，αsin =αcos ） （7）、在Rt △ABC 中，tanA>sinA （tanA=b a ，sinA=ca，而b<c ） 3、直角三角形的边角关系（1）角的关系：两锐角互余（︒=∠+∠90B A )（2）边的关系：两直角边的平方和等于斜边的平方（勾股定理，222c b a =+）（3）边与角的关系：sinA=c a ，cosA=c b ，tanA=ba， （4）直角三角形的相关性质①直角三角形斜边上的中线等于斜边的一半(如图：AB 21CD =)②30°角所对的直角边等于斜边的一半（如图，∠A=30°，AB 21BC =)4、特殊角的三角函数值三角函数0° 30° 45° 60° 90° αsinαcostan α5、解直角三角形的应用（1）、仰角、俯角从下向上看，视线与水平线的夹角叫做仰角； 从上往下看，视线与水平线的夹角叫做俯角．（2）、坡度、坡角坡面的铅垂高度（h ）和水平长度（l ）的比叫做坡面的坡度（或坡比），记作i ，即lhi =． （坡度通常写成1∶m 的形式，如i ＝1∶6．）坡面与水平面的夹角叫做坡角，记作α，有lhi =＝tan α．（显然，坡度越大，坡角α就越大，坡面就越陡．） （3）、方位角“上北下南，左西右东”.叙述方位角时，以南北为主，东西为辅.6、直角三角形可解的条件和解法（1）已知c 和∠A ，求a 和b. a= ，b=（2）已知a 和∠A ，求c 和b. b= , c= （3）已知b 和∠A ，求a 和c. a= ，c= （4）已知a 和b ，求c 和∠A. c= ，∠A=（5）在如图所示的“大套小”的图形中，Rt △ADC 和Rt △BDC 有一条公共边CD ，求CD 的长. 设CD=x ，则DABC┌ αmβαββαtan tan tan mtan -⋅在Rt △ACD 中， AC=αtan x；在Rt △BCD 中，BC=βtan x ；因为AB=AC-BC ，所以，可建立关于x 的方程:αtan x-βtan x =m （方程思想） 解得x= 即求出了CD 的长.二、专题训练。

三角形的边角关系定理三角形是我们初中数学中最基础的几何形状之一，而边角关系是研究三角形的重要内容之一。

在本文中，我们将介绍三角形的边角关系定理，深入讨论它们的定义、性质以及应用。

一、角的概念在介绍三角形的边角关系定理之前，我们首先来回顾一下角的概念。

角是由两条射线共同确定的形状，可以用一个顶点来表示。

在三角形中，我们通常用大写字母来表示角，例如∠ABC表示由线段AB和线段BC所确定的角。

二、1. 内角和定理在任意一个三角形ABC中，三个内角的和等于180度。

即∠A +∠B + ∠C = 180度。

2. 外角和定理在任意一个三角形ABC中，三个外角的和等于360度。

即∠D +∠E + ∠F = 360度，其中∠D、∠E、∠F为三角形的外角。

3. 三角形内角与外角的关系三角形的内角和外角满足以下关系：∠A + ∠D = 180度，∠B +∠E = 180度，∠C + ∠F = 180度。

4. 三角形的三边关系在任意一个三角形ABC中，三个边与对应的内角之间存在以下关系：a/sin∠A = b/sin∠B = c/sin∠C = 2R，其中a、b、c为三角形的三边长度，∠A、∠B、∠C为对应的内角度数，R为三角形外接圆半径。

三、边角关系定理的证明边角关系定理的证明涉及到数学的推导和证明方法，具体的证明过程超出了本文的范围。

在此我们只给出部分边角关系定理的证明思路，供读者参考。

1. 内角和定理的证明思路：可以利用平行线的性质，将三角形的内角分别与同一直线上的一个外角相互对应，然后利用角的性质和等式关系进行推导，最终得出∠A + ∠B + ∠C = 180度。

2. 外角和定理的证明思路：同样可以利用平行线的性质，将三角形的一条边的外角与另外两条边的内角相对应，然后利用角的性质和等式关系进行推导，最终得出∠D + ∠E + ∠F = 360度。

四、边角关系定理的应用边角关系定理在解决三角形相关问题时起着重要的作用。