当前位置：文档之家 › 高三物理有界磁场专题复习

高三物理有界磁场专题复习

  • 格式：doc
  • 大小：900.50 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

高三物理总复习磁场专题

高三物理总复习磁场专题

高三物理总复习磁场专题1. 如图所示，在匀强磁场Ｂ的区域内有一光滑倾斜金属导轨，倾角为θ，导轨间距为Ｌ，在其上垂直导轨放置一根质量为m 的导线，接以如图所示的电源，电流强度为Ｉ，通电导线恰好静止，则匀强磁场的磁感强度必须满足一定条件,下述所给条件正确的是. Ａ.Ｂ＝mgsin θ／ＩＬ，方向垂直斜面向上 Ｂ.Ｂ＝mgcos θ／ＩＬ，方向垂直斜面向下Ｃ.Ｂ＝mg/ＩＬ，方向沿斜面水平向左Ｄ.Ｂ＝mgtg θ／ＩＬ，方向竖直向上2. 如图所示，虚线区域内存在着电场强度为E 的匀强电场和磁感强度为B 的匀强磁场，已知从左方水平射入的电子穿过这一区域时未发生偏转，设重力忽略不计，则这区域内的E 和B 的方向可能是下列叙述中的①E 和B 都沿水平方向，并与电子运动方向相同 ②.E 和B 都沿水平方向，并与电子运动方向相反 ③．E 竖直向上，B 垂直纸面向外 ④．E 竖直向上，B 垂直纸面向里A 、①④B 、②④C 、①②③D 、①②④ 3. 如图所示的区域中，左边为垂直纸面向里的匀强磁场，磁感应强度为 B ，右边是一个电场强度大小未知的匀强电场，其方向平行于OC 且垂直于磁场方向．一个质量为m 、电荷量为-q 的带电粒子从P 孔以初速度V 0沿垂直于磁场方向进人匀强磁场中，初速度方向与边界线的夹角θ＝600，粒子恰好从C 孔垂直于OC 射入匀强电场，最后打在Q 点，已知OQ ＝ 2 OC ，不计粒子的重力，求：✧ ( l )粒子从P 运动到Q 所用的时间 t 。

✧ ( 2 )电场强度 E 的大小✧( 3 )粒子到达Q 点时的动能E kQ4. 在图所示的四幅图中，正确标明了通电导线所受安培力F 方向的是θ θPOQCEB θv 0B F IA BFB B FI B FI C5. 关于磁感应强度，下列说法中正确的是 A ．由F B IL=可知，B 与F 成正比，与IL 成反比B ．通电导线放在磁场中的某点，那点就有磁感应强度，如果将通电导线拿走，那点的磁感应强度就为零C ．通电导线不受安培力的地方一定不存在磁场，即B ＝0D ．磁场中某一点的磁感应强度由磁场本身决定，其大小和方向是唯一确定的，与通电导线无关6. 如图7所示是电磁流量计的示意图。

高考物理一轮总复习课后习题 第11章 磁场 第3讲 专题提升 带电粒子在有界磁场中的运动

高考物理一轮总复习课后习题 第11章 磁场 第3讲 专题提升 带电粒子在有界磁场中的运动

第3讲专题提升:带电粒子在有界磁场中的运动基础对点练题组一带电粒子在有界磁场中运动的临界、极值问题1.如图所示,纸面内有一圆心为O、半径为R的圆形磁场区域,磁感应强度的大小为B,方向垂直于纸面向里。

由距离O点0.4R处的P点沿着与PO 连线成θ=30°的方向发射速率大小不等的电子。

已知电子的质量为m,电荷量为e,不计电子的重力且不考虑电子间的相互作用。

为使电子不离开圆形磁场区域,则电子的最大速率为( )A.7eBR10m B.√29eBR10mC.21eBR40m D.(5-2√3)eBR5m2.(湖南长沙模拟)如图所示,匀强磁场的磁感应强度大小为B,方向垂直于纸面向外,其边界如图中实线所示,a、b、c、d四点共线,ab=2ac=2ae, fe 与ab平行,且ae与ab成60°角。

一粒子束在纸面内从c点垂直于ac射入磁场,粒子质量均为m、电荷量均为q(q>0),具有各种不同速率。

不计重力和粒子之间的相互作用。

在磁场中运动时间最长的粒子,其运动时间为( )A.3πm2qB B.4πm3qBC.5πm4qBD.6πm5qB3.(云南大理下关第一中学联考)如图所示,矩形ABCD区域内有垂直于纸面向里的匀强磁场,磁场的磁感应强度大小为B1,AB边长为d,BC边长为2d,O是BC边的中点,E是AD边的中点。

在O点有一粒子源,可以在纸面内向磁场各个方向射出质量均为m、电荷量均为q、相同电性的带电粒子,粒子射出的速度大小相同。

速度方向与OB边的夹角为60°的粒子恰好从E点射出磁场,不计粒子的重力及粒子间的相互作用,则( )A.粒子带正电B.粒子运动的速度大小为√2qB1dmC.粒子在磁场中运动的最长时间为πm3qB1D.磁场区域中有粒子通过的面积为4+π4d2题组二带电粒子在有界磁场中运动的多解问题4.匀强磁场中一带电粒子仅在洛伦兹力作用下做匀速圆周运动,其运动轨迹上速度方向相反的两点之间距离d与粒子速率v的关系如图所示,则该粒子经过这两点的时间间隔可能为( )A.3πd02v0B.9πd08v0C.πd0v0D.3πd016v05.如图所示,边长为a=0.4 m正方形区域ABCD内无磁场,正方形中线PQ 将区域外左右两侧分成两个磁感应强度均为B1=0.2 T的匀强磁场区域,PQ 右侧磁场方向垂直于纸面向外,PQ左侧磁场方向垂直于纸面向里。

高考物理一轮复习课件11.6带电粒子在有界磁场中的运动

高考物理一轮复习课件11.6带电粒子在有界磁场中的运动

带电粒子在有界磁场中的 运动
1、直线边界，进出两角相同
BD
2、圆形磁场，如果沿磁场半（直）径入，必沿磁场半（直）径出
证明：用对称性（不需要掌握）
C
AC
C
B
3、已知直角+两段长度，用勾股定理求半径
B
4、平行边界磁场，存在临界条件
练习7：(多选)如图所示，在坐标系的y轴右侧存在有理想边界的匀强磁场，
粒子运动轨迹与 y 轴交点的纵坐标为 y＝－2rcos 30° ＝－233d，故 D 错误.
总结 带电粒子在有界磁场中的运动 1、轨迹的圆心角=对应弦的圆心角=2弦切角 2、直线边界，进出两角相同 3、圆形磁场，如果沿磁场半（直）径入，必沿磁 场半（直）径出 4、已知直角+两段长度，用勾股定理求半径 5、平行边界磁场，存在临界条件
B.它进入磁场时的速度为 3m 2πm
C.它在磁场中运动的时间为 3qB D.它的运动轨迹与 y 轴交点的纵坐标为 3d

粒子运动轨迹如图所示，r＋rsin 30°＝d，解得粒子运 动轨迹半径为 r＝23d，故 A 正确； 由 qvB＝mvr2，r＝23d，联立解得粒子进入磁场时的速 度为 v＝qmBr＝23qmBd，故 B 正确； T＝2vπr＝2qπBm，如图由几何关系知 t＝23T，解得粒子在磁场中运动的时 间为 t＝43πqmB，故 C 错误；
磁感应强度大小为B，磁场的宽度为d，磁场方向垂直于xOy平面向里.一个
质量为m、电荷量为－q(q>0)的带电粒子，从原点O射入磁场，速度方向与
x轴正方向成30°角，粒子恰好不从右边界射出，经磁场偏转后从y轴上的某
点离开磁场.忽略粒子重力.关于该粒子在磁场中的运动情况，下列说法正确

磁场(解析版)—2025年高考物理一轮复习知识清单

磁场(解析版)—2025年高考物理一轮复习知识清单

磁场带电粒子在匀强电场中做类抛体运动的相关计算掌握磁场和磁感应强度的概念，会用磁感线描述磁场，熟悉几种常见磁场模型的磁感线分布图；会判断安培力的方向，能够计算安培力的大小，会分析计算安培力作用下导体的平衡与加速问题；掌握洛伦兹力的概念，会分析和计算带电粒子在有界磁场中运动的临界、极值问题，会分析计算带电粒子在组合场、叠加场中的问题；掌握带电粒子在磁场中的多解问题、交变磁场和立体空间中的问题；了解与磁场相关的仪器，重点掌握质谱仪、回旋加速器和霍尔效应的原理。

核心考点01 磁场中的概念一、磁场 (4)二、磁感线 (4)三、磁感应强度 (6)四、磁通量 (8)核心考点02 安培力 (10)一、安培力的方向 (10)二、安培力的大小 (11)三、安培力作用下导体的平衡与加速问题 (12)核心考点03 洛伦兹力 (14)一、洛伦兹力 (14)二、带电粒子在匀强磁场中的运动 (15)三、有界匀强磁场的运动模型 (18)四、动态圆模型 (22)五、带电粒子在组合场中的运动 (24)六、带电粒子在叠加场中的运动 (27)七、带电粒子在交变磁场的运动 (30)八、带电粒子在磁场中的多解问题 (32)九、带电粒子在立体空间的运动 (34)核心考点04 与磁场相关的仪器 (36)一、速度选择器 (36)二、质谱仪 (37)三、回旋加速器 (39)四、磁流体发电机 (41)五、电磁流量计 (42)六、霍尔效应模型 (43)01一、磁场1、磁性物质吸引铁、钴、镍等物质的性质。

2、磁体具有磁性的物体，如磁铁。

3、磁极磁体上磁性最强的区域。

任何磁体都有两个磁极，一个叫北极（N极），另一个叫南极（S极）。

并且，任何一个磁体都有两个磁极，无论怎样分割磁体，磁极总是成对出现，不存在磁单极。

【注意】同名磁极相互排斥，异名磁极相互吸引。

4、磁场的定义磁体或电流周围存在的一种特殊物质，能够传递磁体与磁体之间、磁体与电流之间、电流与电流之间的相互作用。

高中物理高考 高考物理一轮复习专题课件 专题9+磁场(全国通用)

高中物理高考 高考物理一轮复习专题课件 专题9+磁场(全国通用)

2.回旋加速器 (1)基本构造：回旋加速器的核心部分是放置在磁场中的两个D形 的金属扁盒 (如图所示)，其基本组成为：
①粒子源 ②两个D形金属盒 ③匀强磁场 ④高频电源 ⑤粒子引出装置
(2)工作原理
①电场加速 qU＝ΔEk； ②磁场约束偏转 qBv＝mvr2，v＝qmBr∝r；
③加速条件：高频电源的周期与带电粒子在 D 形盒中运动的周 2πm
知识点一 磁场及其描述 1.磁场 (1)基本特性：对放入其中的磁体、电流和运动电荷都有_磁__场__力__的 作用. (2)方向：磁场中任一点小磁针_北__极__(N__极__)的受力方向为该处的磁场 方向.
2.磁感应强度
B＝IFL
强弱
方向
北极(N极)
3.磁感应强度与电场强度的比较
磁感应强度 B 电场强度 E
要点一 通电导线在安培力作用下的运动的判断方法 [突破指南]
电流元法
把整段导线分为直线电流元，先用左手定则判 断每段电流元受力的方向，然后判断整段导线 所受合力的方向，从而确定导线运动方向.
等效法
环形电流可等效成小磁针，通电螺线管可以等 效成条形磁铁或多个环形电流，反过来等效也 成立.
特殊 通过转动通电导线到某个便于分析的特殊位置，然 位置法 后判断其所受安培力的方向，从而确定其运动方向.
A.FN1＜FN2，弹簧的伸长量减小 B.FN1＝FN2，弹簧的伸长量减小 C.FN1＞FN2，弹簧的伸长量增大 D.FN1＞FN2，弹簧的伸长量减小
解析 采用“转换研究对象法”：由于条形磁铁的磁感线是从N 极出发到S极，所以可画出磁铁在导线A处的一条磁感线，此处磁 感应强度方向斜向左下方，如图，导线A中的电流垂直纸面向外， 由左手定则可判断导线A必受 斜向右下方的安培力，由牛顿 第三定律可知磁铁所受作用力的方向是斜向左上方，所以磁铁对 斜面的压力减小，FN1＞FN2.同时，由于导线A比较靠近N极，安 培力的方向与斜面的夹角小于90°，所以电流对磁铁的作用力有 沿斜面向下的分力，使得弹簧弹力增大，可知弹簧的伸长量增大， 所以正确选项为C.

高三物理第一轮总复习课件：磁场省名师优质课赛课获奖课件市赛课一等奖课件

高三物理第一轮总复习课件：磁场省名师优质课赛课获奖课件市赛课一等奖课件

尤其提醒： （1）洛伦兹力只变化粒子速度方向不变化速度大小 （2）洛伦兹力旳方向总是与粒子速度方向垂直．所 以洛伦兹力一直不做功． （3）安培力是洛伦兹力旳宏观体现，但各自旳体现 形式不同，洛伦兹力对运动电荷永远不做功，而安培 力对通电导线可做正功，可做负功，也可不做功．
二．带电粒子在匀强磁场中旳运动规律(只受洛伦兹力）
⑶在赤道平面上，距离地球表面相等旳各点，磁感应 强度相等，且方向均水平指向北极．
二、磁感线
1.磁感线：在磁场中画出旳某些有方向旳假想曲线，使 曲线上旳任意一点旳切线方向都跟该点旳磁场方向相同， 都代表磁场中该点小磁针北极受力旳方向．
2.磁感线旳特点
⑴磁感线是闭合曲线，磁体旳外部是从N极到S极，内部 是从S极到N极； ⑵磁感线旳疏密表达磁场旳强弱，磁感线上某点旳切线 方向表达该点旳磁场方向； ⑶磁感线是人们为了形象描述磁场而假想旳．
1、速度方向与磁场方向平行
若v∥B，带电粒子不受洛伦兹力，在匀强磁场中做匀 速直线运动．
2、速度方向与磁场方向垂直
若v⊥B，带电粒子仅受洛伦兹力作用，在垂直于磁感 线旳平面内以入射速度v做匀速圆周运动．
3、带电粒子仅受洛伦兹力作用，在垂直于磁感线旳 平面内做匀速圆周运动旳基本公式：
⑴向心力公式：F向
高三物理第一轮总复习
（2023届）
第一课时 磁场及其描述
一、磁场 1.磁场：一种看不见、摸不着、存在于电流或磁体周围 旳物质，它传递着磁相互作用．(客观存在）
2.基本性质：磁场对处于其中旳磁体、电流和运动电荷 有力旳作用．
3.磁场旳方向：小磁针N极所受磁场力旳方向，或小磁 针静止时N极所指旳方向．
【例与练】 （2023全国理综）.电磁轨道炮工作原理如 图所示。待发射弹体可在两平行轨道之间自由移动， 并与轨道保持良好接触。电流I从一条轨道流入，经过 导电弹体后从另一条轨道流回。轨道电流可形成在弹 体处垂直于轨道面得磁场（可视为匀强磁场），磁感 应强度旳大小与I成正比。通电旳弹体在轨道上受到安 培力旳作用而高速射出。现欲使弹体旳出射速度增长 至原来旳2倍，理论上可采用旳措施是（ BD ） A.只将轨道长度L变为原来旳2倍 B.只将电流I增长至原来旳2倍 C.只将弹体质量减至原来旳二分之一 D.将弹体质量减至原来旳二分之一， 轨道长度L变为原来旳2倍，其他量不变

高中物理选修3-1磁场 复习 提纲+例题

高中物理选修3-1磁场 复习 提纲+例题

V2
V0
V4
2、将带电粒子在狭缝之间的运动首尾连接 起来是一个初速度为零的匀加速直线运动
3、带电粒子每经电场加速一次，回旋半径 就增大一次，每次增加的动能为⊿E ＝qU
K
所有各次半径之比为：
1 2∶ 3∶ ∶ ...
4、对于同一回旋加速器，其粒子的回旋的 最大半径是相同的。
mv 1 2 B2q 2 R2 由最大半径得： ＝ R E mv qB 2 2m
D、环形线圈有扩张的趋势
1、把一重力不计的通电直导线水平放在蹄 形磁铁磁极的正上方，导线可以自由转动， 当导线通入图示方向电流I时，导线的运动 情况是(从上往下看)（ C ） A.顺时针方向转动，同时下降 B.顺时针方向转动，同时上升 C.逆时针方向转动，同时下降 D.逆时针方向转动，同时上升
I
电流微元法
3、解题一般步骤： ①判断安培力方向 注意选择视图（视角） ②其它力受力分析 将立体受力图应转化成平面图 ③列力学方程：
平衡方程
牛二方程（动能定理） F=ILB ④列电学辅助方程: Q=It
u=IR ……. ⑤解方程及必要的讨论（“答”）
F=BIL中的L为有效长度
试指出下述各图中的安培力的大小。
安培力作用下物体的平衡问题 【例】在倾斜角为θ的光滑斜面上，置 一通有电流I，长为L，质 量为m的导 体棒，如图所示，在竖直向上的磁场中 静止，则磁感应强度B为 _________.
FN
θ
mg
F BIL mg tan mg tan B IL
F
B
FN
×
θ
F
mg
引申1：欲使它静止在斜面上, 外加磁场的磁感应
R
2
mV qB

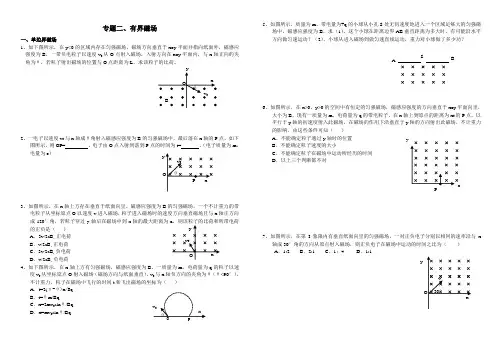
专题二、有界磁场

专题二、有界磁场

专题二、有界磁场一、单边界磁场1、如下图所示，在y<0的区域内存在匀强磁场，磁场方向垂直于xoy 平面并指向纸面外，磁感应强度为B ，一带负电粒子以速度v 0从O 点射入磁场，入射方向在xoy 平面内，与x 轴正向的夹角为θ，若粒子射出磁场的位置与O 点距离为L ，求该粒子的比荷。

2、一电子以速度v 0与x 轴成θ角射入磁感应强度为B 的匀强磁场中，最后落在x 轴的P 点，如下图所示，则OP= ，电子由O 点入射到落到P 点的时间为t= 。

（电子质量为m ，电量为e ）3、如图所示，在x 轴上方存在垂直于纸面向里、磁感应强度为B 的匀强磁场，一个不计重力的带电粒子从坐标原点O 以速度v 进入磁场，粒子进入磁场时的速度方向垂直磁场且与x 轴正方向成120°角，若粒子穿过y 轴后在磁场中到x 轴的最大距离为的正负是（ ）A ．3v/2aB ,正电荷B ．v/2aB ,正电荷C ．3v/2aB ,负电荷D ．v/2aB ,负电荷4、如下图所示，在x 轴上方有匀强磁场，磁感应强度为B ，一质量为m ，电荷量为q 的粒子以速度v 0从坐标原点O射入磁场（磁场方向与纸面垂直），v 0与x 轴负方向的夹角为θ（θ<90°），不计重力，粒子在磁场中飞行的时间t 和飞出磁场的坐标为（ ） A ．t=2(π-θ)m/Bq B ．t=θm/Bq C ．x=2mv 0sin θ/Bq D ．x=mv 0sin θ/Bq5、如图所示，质量为m 、带电量为+q 的小球从小孔S 处无初速度地进入一个区域足够大的匀强磁场中，磁感应强度为B 。

求（1）、这个小球在距离边界AB 垂直距离为多大时，有可能沿水平方向做匀速运动？（2）、小球从进入磁场到做匀速直线运动，重力对小球做了多少功？6、如图所示，在x>0，y>0的空间中有恒定的匀强磁场，磁感应强度的方向垂直于xoy 平面向里，大小为B，现有一质量为m ，电荷量为q 的带电粒子，在x 轴上到原点的距离为x 0的P 点，以平行于y 轴的初速度射入此磁场，在磁场的作用下沿垂直于y 轴的方向射出此磁场，不计重力的影响，由这些条件可知（ ） A ．不能确定粒子通过y 轴时的位置 B ．不能确定粒子速度的大小C ．不能确定粒子在磁场中运动所经历的时间D ．以上三个判断都不对7、如图所示，在第I 象限内有垂直纸面向里的匀强磁场，一对正负电子分别以相同的速率沿与x轴成30°角的方向从原点射入磁场，则正负电子在磁场中运动的时间之比为（ ） A ．1:2 B ．2:1C ．1：4D ．1:1A SB P yy二、双边界磁场1、如上图所示，一束电子（电荷量为e ）以速度v 0垂直射入磁感应强度为B 、宽度为d 的匀强磁场中，穿过磁场时速度方向与入射速度方向的夹角为30°，则电子的质量为 ，穿过磁场的时间是 。

带电粒子在有界匀强磁场中的运动-高考物理复习

带电粒子在有界匀强磁场中的运动-高考物理复习

√A.3
B.2
C.32
D.23
电子1、2在磁场中都做匀速圆周运动，根据题意 画出两电子的运动轨迹，如图所示，电子1垂直边 界射入磁场，从b点离开，则运动了半个圆周，ab 即为直径，c点为圆心； 电子2以相同速率垂直磁场方向射入磁场，经t2时间从a、b连线的中 点c离开磁场， 根据半径 r＝mBqv可知，电子 1 和 2 的半径相等， 根据几何关系可知，△aOc为等边三角形，
粒子运动轨迹与 y 轴交点的纵坐标为 y＝－2rcos 30° ＝－233d，故 D 错误.
考向4 带电粒子在多边形边界或角形区域磁场中运动
例4 (多选)(2023·河北石家庄市模拟)如图所示，△AOC为直角三角形，∠O
＝90°，∠A＝60°，AO＝L，D为AC的中点.△AOC中存在垂直于纸面向里的匀
√C.若带电粒子与挡板碰撞，则受到挡板作用力的冲量 大小为5q2BL
√D.带电粒子在磁场中运动时间可能为3πqmB
若粒子带正电，粒子与挡板MN碰撞后恰好从 Q点射出，粒子运动轨迹如图甲所示， 设轨迹半径为 r2，由几何知识得 L2＋(r2－0.5L)2 ＝r22，解得 r2＝54L，根据牛顿第二定律得 qv2B＝mvr222，解得 v2＝54qmBL， 根据动量定理得 I＝2mv2＝5q2BL，故 A 错误，C 正确； 若粒子带负电，则粒子的运动轨迹如图乙所示， 粒子做圆周运动的半径为 r1＝12L，由牛顿第二定律得 qv1B＝mvr112，解得 v1＝q2BmL，此时半径最小，速度也最小，故 B 错误；
2.平行边界(往往存在临界条件，如图所示)
3.圆形边界(进出磁场具有对称性) (1)沿径向射入必沿径向射出，如图甲所示. (2)不沿径向射入时，如图乙所示. 射入时粒子速度方向与半径的夹角为θ，射出磁场时速度方向与半径的 夹角也为θ.

高考物理磁场精讲精练有界磁场.docx

高考物理磁场精讲精练有界磁场.docx

有界磁场1. 带电粒子在匀强磁场屮运动圆心、半径及时间的确定方法.(1)圆心的确定①已知入射点、出射点、入射方向和出射方向时，可通过入射点和出射点分别作垂直于 入射方向和出射方向的直线，两条直线的交点就是圆弧轨道的圆心(如图甲所示，"为入射 点，肘为岀射点).②己知入射方向、入射点和出射点的位置时，可以通过入射点作入射方向的垂线，连接 入射点和出射点，作其中垂线，这两条垂线的交点就是圆弧轨迹的圆心(如图乙所示，P 为 入射点，〃为出射点).(2) 半径的确定可利用物理学公式或儿何知识(勾股定理、三角函数等)求出半径大小.(3) 运动时间的确定粒子在磁场中运动一周的时间为7；当粒子运动的圆弧所对应的圆心角为“时，其运 一 0OR动时间表示为：t=—T ｛或r=—).2. 重要推论(1) 当速度y —定时，弧长(或弦长)越长，圆心角越大，则带电粒子在有界磁场中运动 的吋间越长.(2) 当速率r 变化时，圆心角大的运动时间长.考向1：圆形磁场区域(1)圆形边界中，若带电粒子沿径向射入必沿径向射出，如图所示，轨迹圆与区域圆形 成相交圆，巧用几何关系解决.(2)带电粒子在圆形磁场中不沿径向，轨迹圆与区域圆相交，抓住网圆心，巧用对称性o解决.［典例1］（多选）如图肪示，以0为圆心、为艸为直径的圆的左半部分内有乖直纸面向 里的匀强磁场，三个不计重力、质量相同、带电荷量相同的带正电粒子日、力和c 以相同的 速率分别沿臼0、仅7和cO 方向垂直于磁场射入磁场区域，已知方0垂直协；&0、"与方0的 夹角都为30° ,臼、b 、c 三个粒子从射入磁场到射出磁场所用吋I'可分别为人、如 纭 则下 列给出的时间关系可能正确的是（）A. t c 解析 粒子带正电，偏转方向如图所示，粒子在磁场屮的运动周期相同，在磁场小运动的时间故粒子在磁场中运动对应的圆心角越大，运动时间越长.设粒子的运动半点射出磁场时，如图甲所示，t b = tc.当/＞斤时，粒子日对应的圆心角最小，c 对ta< tb= tc As D 正确.答案AD［典例2］ —圆筒处于磁感应强度大小为〃的匀强磁场中，磁场方向与筒的轴平行，筒 的横截面如图所示.图中直径刖的两端分别开有小孔，筒绕其中心轴以角速度•顺时针转 动.在该截而内，一带电粒子从小孔於射入筒内，射入时的运动方向与血V 成30°角.当筒 转过90°时，该粒子恰好从小孔艸飞出圆筒.不计重力.若粒子在筒内未与筒壁发生碰撞, 则带电粒子的比荷为（）3B —2B径为门圆形区域半径为乩当粒子日恰好从於点射出磁场时, 应的圆心角最大，当ta= tb= t e .同理 ,\RSWR 时,B.人> t c当粒子b 恰好从於 轨迹如图乙所示,解析 如图所示，粒子在磁场中做匀速圆周运动，圆弧』必P 所对应的圆心角由几何知答案A［典例3］（多选）如图，两个初速度大小相同的同种离子臼和・从0点沿垂直磁场方 向进入匀强磁场，最后打到屏Q 上，不计重力，下列说法正确的有（）A. 臼、方均带正电B. 白在磁场中飞行的时间比方的短C. 日在磁场中飞行的路程比力的短D. 日在尸上的落点与0点的距离比b 的近mv解析a 、b 粒子做圆周运动的半径都为画出轨迹如图所示，圆0、Q 分别为久c.co JI 2兀刃 识知为30。

2025届高三物理一轮复习磁场对运动电荷的作用(53张PPT)

2025届高三物理一轮复习磁场对运动电荷的作用(53张PPT)

答案 AB
考向4 运动的周期性形成多解带电粒子在两个相邻磁场或电场、磁场相邻的空间内形成周期性的运动而形成多解。
【典例11】 (多选)(2022·湖北卷)在如图所示的平面内,分界线SP将宽度为L的矩形区域分成两部分,一部分充满方向垂直于纸面向外的匀强磁场,另一部分充满方向垂直于纸面向里的匀强磁场,磁感应强度大小均为B,SP与磁场左右边界垂直。离子源从S处射入速度大小不同的正离子,
解析 电子在磁场中都做匀速圆周运动,根据题意画出电子的运动轨迹,如图所示,电子1垂直射进磁场,从b点离开,则运动了半个圆周,ab即为直径,c点为圆心,电子2以相同速率垂直磁场方向射入磁场,经t2时间从a、b
答案 A
考向2 带电粒子在平行边界磁场中的运动平行边界(存在临界条件,如图所示)。
【典例4】 如图所示,匀强磁场的磁感应强度为B,宽度为d,边界为CD和EF。一电子从CD边界外侧以速率v0垂直射入匀强磁场,入射方向与CD边界间夹角为θ。已知电子的质量为m,电荷量为e,为使电子能从磁场的另一侧EF射出,求:(1)电子的速率v0至少多大?(2)若θ角可取任意值,v0的最小值是多少?
答案 C
1.洛伦兹力的特点:洛伦兹力不改变带电粒子速度的_______,只改变带电粒子速度的方向。2.粒子的运动性质。(1)若v0∥B,则粒子不受洛伦兹力,在磁场中做_____________。(2)若v0⊥B,则带电粒子在匀强磁场中做_____________。
考点2 带电粒子在匀强磁场中的匀速圆周运动
平面
0
qvB
(1)带电粒子在磁场中的速度不为零,一定受到洛伦兹力作用( )(2)洛伦兹力对运动电荷不做功( )(3)同一带电粒子在A处受到的洛伦兹力大于在B处受到的洛伦兹力,则A处的磁场一定大于B处的磁场( )

高三物理一轮复习 磁场课件

高三物理一轮复习 磁场课件

磁场对通电导线的作用力
安培力
安培力是指磁场对通电导线的吸引力或排斥力，其大小与电流强度、导线长度和磁场强度有 关。
安培力的方向可以用左手定则来判断：伸开左手，让大拇指与其余四指垂直，并处于同一平 面内，将左手放入磁场中，让磁感线穿过手心，四指指向电流方向，大拇指所指的方向即为 安培力的方向。
安培力在生产生活中有广泛的应用，如电动机、发电机等。
描述磁场强弱和方向的物 理量，用符号B表示。
定义
在磁场中垂直于磁场方向 的通电导线中受到的安培 力与电流和导线长度乘积 的比值。
单位
特斯拉（T），国际单位 制中的基本单位。
磁感线的概念
STEP 01
磁感线
STEP 02
特点
描述磁场分布的闭合曲线， 曲线上每一点的切线方向 表示该点的磁场方向。
STEP 03
带电粒子在磁场中的速度选择器
速度选择器是一种特殊装置， 能够将速度为某一特定值的带 电粒子筛选出来。
在速度选择器中，电场和磁场 共同作用，使得只有满足$qE = qvB$的带数器等领域有广泛应用。
磁感应强度与磁感线
磁感应强度的定义
磁感应强度
详细描述
磁场是一种传递磁力的媒介，它对处于其中的磁体或电流产生力的作用。这种 力是相互作用的，即磁场会对处于其中的每一个磁体或电流产生力的作用，而 每一个磁体或电流也会对磁场产生反作用力。
磁场的方向
总结词
磁场的方向是指磁场中某一点处磁力线的指向，它可以用小磁针的北极指向来表示。
详细描述
磁场中某一点处的磁场方向是指该点处磁力线的指向，即在该点处放置一个小磁针时，小磁针北极所指的方向就 是该点处磁场的方向。由于磁场是一种矢量场，因此不同点处的磁场方向可能是不同的。在三维空间中，磁场方 向可以用三维向量来表示。

高考物理一轮复习 专题九 磁场课件

高考物理一轮复习 专题九 磁场课件
只知道磁感应强度大小,而未具体指出磁感应强度方向,此时必须要考虑磁感 应强度方向不确定而形成的多解 如图带正电粒子以速度v垂直进入匀强磁场,若B垂直纸面向里,其轨迹为a,若B 垂直纸面向外,其轨迹为b
临界状态不唯一
带电粒子在洛伦兹力作用下飞越有界磁场时,由于粒子运动轨迹是圆弧状,因 此,它可能穿过去了,也可能转过180°从入射界面这边反向飞出,于是形成多解
(1)若粒子以初速度v1沿y轴正向入射,恰好能经过x轴上的A(a,0)点,求v1的大小; (2)已知一粒子的初速度大小为v(v>v1),为使该粒子能经过A(a,0)点,其入射角θ(粒子初速度与x轴 正向的夹角)有几个?并求出对应的sin θ值; (3)如图乙,若在此空间再加入沿y轴正向、大小为E的匀强电场,一粒子从O点以初速度v0沿y轴 正向发射。研究表明:粒子在xOy平面内做周期性运动,且在任一时刻,粒子速度的x分量vx与其所 在位置的y坐标成正比,比例系数与场强大小E无关。求该粒子运动过程中的最大速度值vm。
解题思路 解答本题要求能够做到物理与数学相结合。图中的OA若从数学角度看其实就是一 条弦,过该弦可以作出两个相交圆,两相交圆对应的两切线即为所求的粒子速度方向所在直线。 解析 (1)带电粒子以速率v在匀强磁场B中做匀速圆周运动,半径为R,有
qvB=m v 2 ①
R
当粒子以初速度v1沿y轴正向入射,转过半个圆qB
例2 如图,真空室内存在匀强磁场,磁场方向垂直于纸面向里,磁感应强度的大小B=0.60 T。磁 场内有一块平面感光板ab,板面与磁场方向平行。在距ab为l=16 cm处,有一个点状的α粒子放射
源S,它向各个方向发射α粒子,α粒子的速率都是v=3.0×106 m/s。已知α粒子的电荷量与质量之
方法二 带电粒子在磁场中运动的多解问题的分析方法

高三物理粒子在有界磁场中运动试题答案及解析

高三物理粒子在有界磁场中运动试题答案及解析

高三物理粒子在有界磁场中运动试题答案及解析1.一个重力不计的带电粒子垂直进入匀强磁场，在与磁场垂直的平面内做匀速圆周运动．则下列能表示运动周期 T 与半径R之间的图像是（）【答案】D【解析】带电粒子在磁场中做匀速圆周运动，根据，，联立可求粒子做圆周运动的周期为，周期与轨道半径r无关，所以A、B、C错误；D正确。

【考点】本题考查带电粒子在磁场中的运动2.如图所示，在xOy平面内存在着磁感应强度大小为B的匀强磁场，第一、二、四象限内的磁场方向垂直纸面向里，第三象限内的磁场方向垂直纸面向外．P(－ L,0)、Q(0，－L)为坐标轴上的两个点．现有一电子从P点沿PQ方向射出，不计电子的重力，则.A．若电子从P点出发恰好经原点O第一次射出磁场分界线，则电子运动的路程一定为B．若电子从P点出发经原点O到达Q点，则电子运动的路程一定为πLC．若电子从P点出发经原点O到达Q点，则电子运动的路程可能为2πLD．若电子从P点出发经原点O到达Q点，则nπL（n为任意正整数）都有可能是电子运动的路程【答案】AC【解析】若电子从P点出发恰好经原点O第一次射出磁场分界线，则有运动轨迹如图所示，由几何关系知：半径R＝L，则微粒运动的路程为圆周的，即为，A正确；若电子从P点出发经原点O到达Q点，运动轨迹可能如图所示，因此则微粒运动的路程可能为πL，也可能为2πL，BD错误C正确；【考点】本题考查带电粒子在磁场中的运动。

3.如图是某离子速度选择器的原理示意图，在一半径为R 的绝缘圆柱形筒内有磁感应强度为B的匀强磁场，方向平行于轴线．在圆柱形筒上某一直径两端开有小孔M、N，现有一束速率不同、比荷均为k的正、负离子，从M孔以α角入射，一些具有特定速度的离子未与筒壁碰撞而直接从N孔射出(不考虑离子间的作用力和重力)．则从N孔射出的离子()A．是正离子，速率为kBR/cos αB．是正离子，速率为kBR/sin αC．是负离子，速率为kBR/sin αD．是负离子，速率为kBR/cos α【答案】B【解析】因为离子向下偏，根据左手定则，离子带正电，运动轨迹如图，由几何关系可知r＝，由qvB＝m可得v＝，故B正确．4.（8分）在真空中，半径的圆形区域内有匀强磁场，方向如图所示，磁感应强度B="0.2" T，一个带正电的粒子以初速度从磁场边界上直径ab的一端a射入磁场，已知该粒子的比荷，不计粒子重力．（1）求粒子在磁场中做匀速圆周运动的半径；（2）若要使粒子飞离磁场时有最大偏转角，求入射时与ab的夹角及粒子的最大偏转角．【答案】（1）（2）最大偏转角【解析】（1）粒子射入磁场后，由于不计重力，所以洛伦兹力提供圆周运动需要的向心力，根据牛顿第二定律有．（2）粒子在圆形磁场区域运动轨迹为一段半径R=5cm的圆弧，半径一定要使偏转角最大，就要求这段圆弧对应的弦最长，即为图形区域的直径，粒子运动轨迹的圆心在ab弦的中垂线上，如图所示．由几何关系可知最大偏转角【考点】带电粒子在圆形匀强磁场区域的运动5.如图所示，在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场，其边界过原点O和y轴平行于x轴正方向射入磁场，上的点a(0，L)。

高三一轮复习磁场第1讲磁场磁场对电流的作用ppt课件

高三一轮复习磁场第1讲磁场磁场对电流的作用ppt课件

8-1-3 所示.a、b 和 c 三点分别位于三角形的 3 个顶角的平分线
上，且到相应顶点的距离相等.将 a、b 和 c 处的磁感应强度大
小分别记为 B1、B2 和 B3.下列说法正确的是(
)
图 8-1-3
A.B1＝B2＜B3 B.B1＝B2＝B3 C.a 和 b 处磁场方向垂直于纸面向外，c 处磁场方向垂直于 纸面向里
Ⅰ 题型既有选择题，又有计算题.复习时要 Ⅱ 侧重对基本概念和规律的理解.
2.高考中常把磁场和其他知识综合起来 Ⅰ 考查，比如导体棒在安培力作用下的平 Ⅱ 衡和加速问题、导体棒切割磁感线产生
7. 带电粒子在匀强磁场中的 运动
8.质谱仪和回旋加速器
Ⅱ 感应电动势的问题等. 3.带电粒子在有界场、混合场中的运动
式中，I 是回路电流，L 是金属棒的长度.两弹簧各自再伸长 了Δl2＝0.3 cm，由胡克定律和力的平衡条件得
2k(Δl1＋Δl2)＝mg＋F ③ 由欧姆定律有 E＝IR ④ 式中，E 是电池的电动势，R 是电路总电阻 联立①②③④式，并代入题给数据得 m＝0.01 kg.
考点解析
考点 1 对磁感应强度 B 的理解 磁感应强度的理解
4.匀强磁场：磁感应强度大小处处______相__等____、方向处 处____相__同______的磁场称为匀强磁场.距离很近的两个异名磁 极之间的磁场、通电螺线管内部的磁场(边缘部分除外)以及平 行板电容器间的磁场，都可以认为是匀强磁场.
考点 2 电流的磁效应 磁场对电流的作用 1.电流的磁效应：奥斯特发现了电流的磁效应，即电流周 围存在磁场，可用安培定则(即右手螺旋定则)判断电流的磁场 方向.
2.(2014 年新课标Ⅰ卷)关于通电直导线在匀强磁场中所受 的安培力，下列说法正确的是( )

高三物理 复习 专题19 磁场、磁场力- 重要知识点、考点、方法总结 、讲义

高三物理 复习 专题19 磁场、磁场力- 重要知识点、考点、方法总结 、讲义
② 磁感应强度是矢量，磁场中某点的磁感应强度的方向就是该点的磁场方向。物理学中把 小磁针静止时 N 极所指的方向规定为该点的磁感应强度的方向。
③ 定义式 B F 是典型的比值定义法，与电场强度由电场本身决定一样，磁感应强度由磁 IL
场本身决定，跟该位置放不放通电导线及通电导线的电流大小等无关。
【例1】 三根相互平行的通电长直导线放在等边三角形的三个顶点上，右图为其截
体会磁场的存在，所以我们选择了例 3.4.5 这三道题，而这三道题都会用到安培力，老师不用担心学生
不会，对于高三的学生安培力是可以掌握的。而后面的安培力部分，我们将重点解决力学综合问题。
*************************************************************Байду номын сангаас**************************
直线电流的磁场
环形电流的磁场
通电螺线管的磁场
匀强磁场举例
**************************************************************************************** 这里我们只想强调电流周围有磁场这件事，但是磁场又是看不见，摸不着的东西，我们需要通过力去
面图，电流方向如图所示。若每根导线的电流均为 I ，每根直导线单独存
在时，在三角形中心 O 点产生的磁感应强度大小都是 B ，则三根导线同时
存在时 O 点的磁感应强度大小为
A．0
B． B
C． 2B
D． 3B
【答案】 C
3．磁感线 ⑴ 磁感线：在磁场中人为地画出的一些有方向的曲线，在这些曲线上，每一点的切线方向都 与该点的磁感应强度的方向一致。 ⑵ 磁感线和电场线的比较 ① 相似：磁感线和电场线都是为了形象描述场而引入的假想线，实际上不存在；磁感线和 电场线都是用来描述场的方向和强弱的曲线，都用疏密来表示场的强弱；磁感线 和电场线都不能相交，因为如果相交，在交点会出现两个切线方向，与磁场或电 场中某一点场的方向是唯一的相矛盾。 ② 区别：磁感线是闭合的，而静电场的电场线起始于正电荷终止于负电荷，是不闭合的曲

高三物理磁场知识点知识点总结

高三物理磁场知识点知识点总结

高三物理磁场知识点知识点总结高三物理磁场知识点总结在高三物理的学习中，磁场是一个重要且具有一定难度的部分。

理解和掌握磁场的相关知识，对于解决物理问题、应对高考至关重要。

下面就让我们一起来梳理一下磁场的重要知识点。

一、磁场的基本概念1、磁场的定义：磁场是存在于磁体、电流和运动电荷周围空间的一种特殊物质。

2、磁场的基本性质：磁场对放入其中的磁体、电流和运动电荷有力的作用。

3、磁感应强度：描述磁场强弱和方向的物理量，符号为 B。

定义式为 B ＝ F/IL（F 为通电导线在磁场中受到的安培力，I 为导线中的电流，L 为导线在磁场中的有效长度）。

磁感应强度是矢量，其方向为小磁针静止时 N 极所指的方向。

二、常见的磁场1、条形磁铁的磁场：外部磁场从 N 极出发，回到 S 极，内部从 S 极到 N 极，形成闭合曲线。

2、蹄形磁铁的磁场：与条形磁铁类似，两端为磁极，磁场分布也呈现出从 N 极到 S 极的规律。

3、通电直导线的磁场：右手螺旋定则（安培定则），用右手握住导线，让伸直的大拇指所指的方向与电流方向一致，弯曲的四指所指的方向就是磁感线的环绕方向。

4、通电螺线管的磁场：同样用右手螺旋定则，让右手弯曲的四指与电流的环绕方向一致，大拇指所指的那一端就是通电螺线管的N 极。

三、安培力1、定义：通电导线在磁场中受到的力称为安培力。

2、大小：F ＝BILsinθ（θ 为电流方向与磁感应强度方向的夹角）。

当电流方向与磁场方向垂直时（θ ＝ 90°），F ＝ BIL；当电流方向与磁场方向平行时（θ ＝ 0°或 180°），F ＝ 0。

3、方向：左手定则判断。

伸开左手，让磁感线垂直穿过手心，四指指向电流方向，大拇指所指的方向就是安培力的方向。

四、洛伦兹力1、定义：运动电荷在磁场中受到的力称为洛伦兹力。

2、大小：F ＝qvBsinθ（q 为电荷电量，v 为电荷运动速度，θ 为速度方向与磁感应强度方向的夹角）。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高三物理有界磁场专题复习一、带电粒子在圆形磁场中的运动例1、圆心为O 、半径为r 的圆形区域中有一个磁感强度为B 、方向为垂直于纸面向里的匀强磁场，与区域边缘的最短距离为L 的O ＇处有一竖直放置的荧屏MN ，今有一质量为m 的电子以速率v 从左侧沿ＯＯ＇方向垂直射入磁场，越出磁场后打在荧光屏上之P 点，如图１所示，求O ＇P 的长度和电子通过磁场所用的时间．解析 ：电子所受重力不计。

它在磁场中做匀速圆周运动，圆心为O ″，半径为R 。

圆弧段轨迹AB 所对的圆心角为θ，电子越出磁场后做速率仍为v 的匀速直线运动， 如图２所示，连结OB ，∵△OAO ″≌△OBO ″，又OA ⊥O ″A ，故OB ⊥O ″B ，由于原有BP ⊥O ″B ，可见O 、B 、P 在同一直线上，且∠O ＇OP =∠AO ″B =θ，在直角三角形ＯＯ＇P 中，O ＇P =(L +r )tan θ，而)2(tan 1)2tan(2tan 2θθθ-=，Rr=)2tan(θ,所以求得R 后就可以求出O ＇P 了，电子经过磁场的时间可用t =V RV AB θ=来求得。

由R V mBeV 2=得R=θtan )(.r L OP eBmV+= mVeBrR r ==)2tan(θ，2222222)2(tan 1)2tan(2tan rB e V m eBrmV -=-=θθθ 22222,)(2tan )(r B e V m eBrmVr L r L P O -+=+=θ， )2arctan(22222r B e V m eBrmV-=θ)2arctan(22222rB e V m eBrmV eB m V R t -==θ例2、如图2，半径为cm r 10=的匀强磁场区域边界跟y 轴相切于坐标原点O ，磁感强度T B 332.0=，方向垂直纸面向里．在O 处有一放射源S ，可向纸面各个方向射出速度为s m v /102.36⨯=的粒子．已知α粒子质量kg m 271064.6-⨯=，电量C q 19102.3-⨯=，试画出α粒子通过磁场空间做圆周运动的圆心轨道，求出α粒子通过磁场空间的最大偏角．MN O ,图1MNO ,图2解析：设粒子在洛仑兹力作用下的轨道半径为R ，由R v m Bqv 2= 得cm m m Bq mv R 2020.0102.3332.0102.31064.619627==⨯⨯⨯⨯⨯==--虽然α粒子进入磁场的速度方向不确定，但粒子进场点是确定的，因此α粒子作圆周运动的圆心必落在以O 为圆心，半径cm R 20=的圆周上，如图２中虚线．由几何关系可知，速度偏转角总等于其轨道圆心角．在半径R 一定的条件下，为使α粒子速度偏转角最大，即轨道圆心角最大，应使其所对弦最长．该弦是偏转轨道圆的弦，同时也是圆形磁场的弦．显然最长弦应为匀强磁场区域圆的直径．即α粒子应从磁场圆直径的A 端射出．如图２，作出磁偏转角ϕ及对应轨道圆心O '，据几何关系得212sin==R r ϕ，得060=ϕ，即α粒子穿过磁场空间的最大偏转角为060． 二、带电粒子在半无界磁场中的运动 例3、（1999年高考试题）如图3中虚线MN 是一垂直纸面的平面与纸面的交线,在平面右侧的半空间存在一磁感应强度为B 、方向垂直纸面向外的匀强磁场．Ｏ是ＭＮ上的一点，从Ｏ点可以向磁场区域发射电荷量为＋q 、质量为m 、速率为v 的粒子，粒子射入磁场时的速度可在纸面内各个方向，已知先后射入的两个粒子恰好在磁场中给定的Ｐ点相遇，Ｐ到Ｏ点的距离为Ｌ，不计重力和粒子间的相互作用．(1)求所考察的粒子在磁场中的轨道半径． (2)求这两个粒子从Ｏ点射入磁场的时间间隔．解析：(1) 粒子的初速度与匀强磁场的方向垂直,在洛仑兹力作用下,做匀速圆周运动.设圆半径为Ｒ,则据牛顿第二定律可得：R v m Bqv 2= ,解得BqmvR =(2)如图３所示，以OP 为弦的可以画出两个半径相同的圆，分别表示在Ｐ点相遇的两个粒子的轨道，圆心分别为O 1和O 2，在O 处两个圆的切线分别表示两个粒子的射入方向，它们之间的夹角为α，由几何关系知∠PO 1Q 1=∠PO 2Q 2=α从O 点射入到相遇，粒子在１的路径为半个圆周加P Q 1弧长等于αR ；粒子在２的路径为半个圆周减P Q 2弧长等于αR ．粒子１的运动时间 t 1=21T ＋v R α 粒子２的运动时间 t ２=21T －vR α两个粒子射入的时间间隔△t ＝t 1－t ２＝2vR αM N. . . . . .. . . . . .由几何关系得R cos21α=21op =21L ，解得：α=2arccos R L 2故△t ＝Bq m 4．arc cos mvLBq2例4、如图4所示，在真空中坐标xoy 平面的0>x 区域内，有磁感强度T B 2100.1-⨯=的匀强磁场，方向与xoy 平面垂直，在x 轴上的)0,10(p 点，有一放射源，在xoy 平面内向各个方向发射速率s m v /100.14⨯=的带正电的粒子，粒子的质量为kg m 25106.1-⨯=，电量为C q 18106.1-⨯=，求带电粒子能打到y 轴上的范围．解析：带电粒子在磁场中运动时有R v m Bqv 2=，则cm m Bq mv R 101.0106.1100.1100.1106.1182425==⨯⨯⨯⨯⨯⨯==---． 如图１５所示，当带电粒子打到y 轴上方的A 点与P 连线正好为其圆轨迹的直径时，A 点既为粒子能打到y 轴上方的最高点．因cm R Op 10==，cm R AP 202==，则cm OP AP OA 31022=-=．当带电粒子的圆轨迹正好与y 轴下方相切于Ｂ点时，Ｂ点既为粒子能打到y 轴下方的最低点，易得cm R OB 10==．综上，带电粒子能打到y 轴上的范围为：cm y cm 31010≤≤-．三、带电粒子在长方形磁场中的运动例5、如图5，长为L 间距为d 的水平两极板间，有垂直于纸面向里的匀强磁场，磁感强度为B ，两板不带电，现有质量为m ，电量为q 的带正电粒子（重力不计），从左侧两极板的中心处以不同速率v 水平射入，欲使粒子不打在板上，求粒子速率v 应满足什么条件． 解析：如图４，设粒子以速率1v 运动时，粒子正好打在左极板边缘（图４中轨迹１），则其圆轨迹半径为41dR =，又由 1211R v m Bqv =得m Bqdv 41=，则粒子入射速率小于1v 时可不打在板上． 设粒子以速率2v 运动时，粒子正好打在右极板边缘（图４中轨迹２），由图可得22222)2(d R L R -+=，则其圆轨迹半径为图4o cm x /cm y /p ⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯•图5⨯⨯⨯⨯⨯⨯⨯⨯→•d Lvcm /图４v 2vd d L R 44222+=，又由2222R v m Bqv =得md d L Bq v 4)4(222+=，则粒子入射速率大于2v 时可不打在板上．综上，要粒子不打在板上，其入射速率应满足：mBqd v 4<或md d L Bq v 4)4(22+>．例6、长为L 的水平极板间，有垂直纸面向内的匀强磁场，如图４所示，磁感强度为B ，板间距离也为L ，板不带电，现有质量为m ，电量为q 的带正电粒子(不计重力)，从左边极板间中点处垂直磁感线以速度V 水平射入磁场，欲使粒子不打在极板上，可采用的办法是：A ．使粒子的速度V <BqL /4m ；B ．使粒子的速度V >5BqL /4m ；C ．使粒子的速度V >BqL /m ；D ．使粒子速度BqL /4m <V <5BqL /4m 解析:由左手定则判得粒子在磁场中间向上偏，而作匀速圆周运动，很明显，圆周运动的半径大于某值r 1时粒子可以从极板右边穿出，而半径小于某值r 2时粒子可从极板的左边穿出，现在问题归结为求粒子能在右边穿出时r 的最小值r 1以及粒子在左边穿出时r 的最大值r 2，由几何知识得：粒子擦着板从右边穿出时，圆心在O 点，有： r 12＝L 2+(r 1-L /2)2得r 1=5L /4，又由于r 1=mV 1/Bq 得V 1=5BqL /4m ,∴V >5BqL /4m 时粒子能从右边穿出。

粒子擦着上板从左边穿出时，圆心在O ＇点，有r 2＝L /4，又由r 2＝mV 2/Bq =L /4得V 2＝BqL /4m∴V 2<BqL /4m 时粒子能从左边穿出。

综上可得正确答案是A 、B 。

四、带电粒子在“三角形磁场区域”中的运动例7、在边长为a 2的ABC ∆内存在垂直纸面向里的磁感强度为B 的匀强磁场，有一带正电q ，质量为m 的粒子从距Ａ点a 3的Ｄ点垂直ＡＢ方向进入磁场，如图５所示，若粒子能从ＡＣ间离开磁场，求粒子速率应满足什么条件及粒子从ＡＣ间什么范围内射出．解析：如图６所示，设粒子速率为1v 时，其圆轨迹正好与ＡＣ边相切于Ｅ点．由图知，在E AO 1∆中，11R E O =，113R a A O -=，由AO E O 11030cos =得11323R a R -=，解得a R )32(31-=，则a R a AO AE )332(23211-=-==． 又由1211R vm Bqv =得m aqB m BqR v )32(311-==，则要粒子能从ＡＣ间离开磁场，其速l lr 1OV +q V 图6图7DB•⨯⨯⨯⨯⨯⨯C图6D•⨯⨯⨯⨯⨯⨯CE 1v 1o •1R率应大于1v ．如图７所示，设粒子速率为2v 时，其圆轨迹正好与ＢＣ边相切于Ｆ点，与ＡＣ相交于Ｇ点．易知Ａ点即为粒子轨迹的圆心，则a AG AD R 32===．又由2222R v m Bqv =得m aqBv 32=，则要粒子能从ＡＣ间离开磁场，其速率应小于等于2v ．综上，要粒子能从ＡＣ间离开磁场，粒子速率应满足maqBv m aqB3)32(3≤<-． 粒子从距Ａ点a a 3~)332(-的EG 间射出．五、带电粒子在“宽度一定的无限长磁场区域”中的运动例8、如图11所示，A 、B 为水平放置的足够长的平行板，板间距离为m d 2100.1-⨯=，A 板中央有一电子源P ，在纸面内能向各个方向发射速度在s m /102.3~07⨯范围内的电子，Ｑ为P 点正上方B 板上的一点，若垂直纸面加一匀强磁场，磁感应强度T B 3101.9-⨯=，已知电子的质量kg m 31101.9-⨯=，电子电量C e 19106.1-⨯=，不计电子的重力和电子间相互作用力，且电子打到板上均被吸收，并转移到大地．求：（1）沿P Ｑ方向射出的电子击中A 、B 两板上的范围．（２）若从Ｐ点发出的粒子能恰好击中Ｑ点，则电子的发射方向（用图中θ角表示）与电子速度的大小v 之间应满足的关系及各自相应的取值范围．解析：如图１２所示，沿ＰＱ方向射出的电子最大轨迹半径由r v m Bev 2=可得Bemv r m m =，代入数据解得d m r m 21022=⨯=-． 该电子运动轨迹圆心在Ａ板上Ｈ处，恰能击中Ｂ板Ｍ处．随着电子速度的减少，电子轨迹半径也逐渐减小．击中Ｂ板的电子与Ｑ点最远处相切于Ｎ点，此时电子的轨迹半径为d ，并恰能落在Ａ板上Ｈ处．所以电子能击中Ｂ板 ＭＮ区域和Ａ板ＰＨ区域．在∆ＭＦＨ中，有d dd MF HM FH 3)2(2222-=-=，s m d PF QM /1068.2)32(3-⨯=-==， m d QN 2101-⨯==，m d PH 21022-⨯==．电子能击中Ｂ板Ｑ点右侧与Ｑ点相距m m 23101~1068.2--⨯⨯的范围．电子能击中Ａ板A图13PＰ点右侧与Ｐ点相距m 2102~0-⨯的范围．（２）如图１３所示，要使Ｐ点发出的电子能击中Ｑ点，则有Be mv r =，2sin d r =θ． 解得6108sin ⨯=θv ．v 取最大速度s m /102.37⨯时，有41sin =θ，41arcsin min =θ；v 取最小速度时有2max πθ=，s m v /1086min ⨯=．所以电子速度与θ之间应满足6108sin ⨯=θv ，且]2,41[arcsin πθ∈，]/102.3,/108[76s m s m v ⨯⨯∈六、带电粒子在相反方向的两个有界磁场中的运动例9、如图9所示，空间分布着有理想边界的匀强电场和匀强磁场．左侧匀强电场的场强大小为E 、方向水平向右，电场宽度为L ；中间区域匀强磁场的磁感应强度大小为B ，方向垂直纸面向里．一个质量为m 、电量为q 、不计重力的带正电的粒子从电场的左边缘的O 点由静止开始运动，穿过中间磁场区域进入右侧磁场区域后，又回到O 点，然后重复上述运动过程．求：（1） 中间磁场区域的宽度d ;（2） 带电粒子从O 点开始运动到第一次回到O 点所用时间t. 解析：（1）带电粒子在电场中加速，由动能定理，可得： 221mV qEL =带电粒子在磁场中偏转，由牛顿第二定律，可得：RV m BqV 2=由以上两式，可得qmELB R 21=．可见在两磁场区粒子运动半径相同，如图11所示，三段圆弧的圆心组成的三角形ΔO 1O 2O 3是等边三角形，其边长为2R ．所以中间磁场区域的宽度为qmELB R d 62160sin 0==（2）在电场中qEmLqE mV a V t 22221===， 在中间磁场中运动时间qBmT t 3232π==B B 图9图14o cm x /cmy /p ⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯•图11在右侧磁场中运动时间qBm T t 35653π==， 则粒子第一次回到O 点的所用时间为qBmqE mL t t t t 3722321π+=++=． 七、带电粒子在环形或有孔磁场中的运动例10、核聚变反应需要几百万度以上的高温，为把高温条件下高速运动的离子约束在小范围内（否则不可能发生核反应），通常采用磁约束的方法（托卡马克装置）。