整式的加减复习资料
- 格式:doc
- 大小:115.50 KB
- 文档页数:2
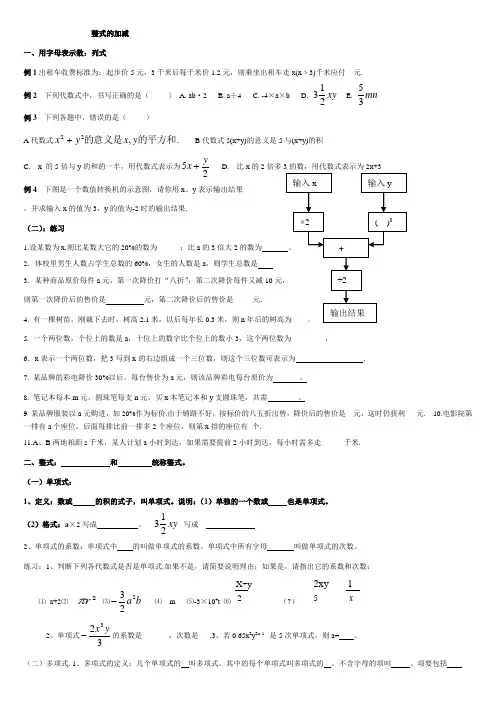
整式的加减一、用字母表示数:列式例1出租车收费标准为:起步价5元,3千米后每千米价1.2元,则乘坐出租车走x(x ﹥3)千米应付__元. 例2 下列代数式中,书写正确的是( ) A. ab ·2 B. a ÷4 C. -4×a ×b D. xy 213 E.mn 35 例3 下列各题中,错误的是( ) A 代数式.,22的平方和的意义是y x y x+ B 代数式5(x+y)的意义是5与(x+y)的积C. x 的5倍与y 的和的一半,用代数式表示为25yx+D. 比x例4 下图是一个数值转换机的示意图,请你用x 、y 表示输出结果 ,并求输入x 的值为3,y 的值为-2时的输出结果. (二):练习1.设某数为x,则比某数大它的20%的数为______;比a 的3倍大22.体校里男生人数占学生总数的60%,女生的人数是a 3.某种商品原价每件a 元,第一次降价打“八折”则第一次降价后的售价是 元,第二次降价后的售价是 4. 有一棵树苗,刚栽下去时,树高2.1米,以后每年长0.3米,则n 5. 一个两位数,个位上的数是a ,十位上的数字比个位上的数小3,这个两位数为_________,6.x 表示一个两位数,把3写到x 的右边组成一个三位数,则这个三位数可表示为 . 7. 某品牌的彩电降价30%以后,每台售价为a 元,则该品牌彩电每台原价为 。
8. 笔记本每本m 元,圆珠笔每支n 元,买x 本笔记本和y 支圆珠笔,共需 。
9 某品牌服装以a 元购进,加20%作为标价.由于销路不好,按标价的八五折出售,降价后的售价是__元,这时仍获利___元. 10.电影院第一排有a 个座位,后面每排比前一排多2个座位,则第x 排的座位有_个.11.A 、B 两地相距s 千米,某人计划a 小时到达,如果需要提前2小时到达,每小时需多走______千米. 二、整式: 和 统称整式。

第二章 《整式的加减》复习提纲一.知识梳理1. 单项式:数字与字母乘积的式子.单独的一个数或一个字母也是单项式.单项式中的数字因数叫做这个单项式的系数.一个单项式中,所有字母的指数的和叫做这个单项式的指数.2. 多项式:几个单项式的和.在多项式中,其中,每个单项式叫做多项式的项,不含字母的项叫做常数项.多项式里次数最高项的次数,叫做这个多项式的次数.注:多项式没有系数.3. 多项式的排列:通常把一个多项式的各项按照某个字母的指数从大到小(降幂)或者从小到大(升幂)的顺序排列.4. 整式:单项式与多项式统称为整式.5. 同类项:所含字母相同,并且相同字母的指数也相同的项.几个常数项也是同类项.把多项式中的同类项合并成一项,叫做合并同类项.6. 同类项法则:合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母部分不变.7.去括号法则:如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.8. 整式加减的运算法则:几个整式相加减,如果有括号就先去括号,然后再合并同类项.二.三. 不等式(组)基本练习选择题 1.下面的正确结论的是( )A .0不是单项式 B .52abc 是五次单项式 C .-4和4是同类项 D .2332330m n m n -=2.下面运算正确的是( ) A .ab b a 963=+ B .03333=-ba b a C .a a a 26834=- D .61312122=-y y 3.两个四次多项式的和的次数是( ) A.八次 B.四次 C.不低于四次 D.不高于四次 填空题4.一个多项式与221x x -+的和是32x -,则这个多项式为_______. 5.n 为整数,不能被3整除的数表示为 . 6.单项式83ab -的系数是 ,次数是 . 7.单项式25x y 、223x y 、24xy -的和为 . 8.已知单项式23m a b 与4123n a b --的和是单项式,那么m = ,n = . 9.规定一种新运算:1+--⋅=∆b a b a b a ,如1434343+--⨯=∆,请比较大小:()()34 43-∆∆- .10.轮船在逆水中前进的速度是m 千米/时,水流的速度是2千米/时,则这轮船在静水中航行的速度是 千米/时.11.某城市按以下规定收取每月的煤气费:用气不超过60立方米,按每立方米0.8元收费;如果超过60立方米,超过部分每立方米按1.2元收费.已知某户用煤气x 立方米(x >60),则该户应交煤气费 元.12.观察下列单项式:0,23x ,38x ,415x ,524x ,……,按此规律写出第13个单项式是______.解答题13. 化简: (1)2237(43)2x x x x ⎡⎤----⎣⎦; (2)22225(3)2(7)a b ab a b ab ---.14.已知041|2|2=⎪⎭⎫ ⎝⎛-++b a ,求)43()2(22ab ab ab b a +--的值.15.已知多项式238x my +-与多项式227nx y -++的差中,不含有x 、y ,求m n n m +的值.16.当m 为何值时,||2322(4)3m m x y x y --+是五次二项式.17.我国进口关税近年来有两次大幅度下调,第一次降低了40%,第二次又在第一次的基础上降低了30%.(1)若未降税前某种商品的税款为a 万元,用整式表示现在的实际税款.(2)若a =600万元,试求现在的实际税款.18.某农户2006年承包荒山若干亩,投资7800•元改造后,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售a 元,在果园就地销售每千克售b 元(b <a ).该农户将水果拉到市场出售平均每天出售1000千克,需8•人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.(1)分别用a ,b 表示两种方式出售水果的收入?(2)若a =1.3元,b =1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.(3)该农户加强果园管理,力争到明年纯收入达到15000元,那么纯收入增长率是多少(纯收入=总收入-总支出),该农户采用了(2)中较好的出售方式出售)?。

整式的加减知识点归纳及练习一、代数式概念代数式:用基本的运算符号(包括加+、减-、乘×、除÷、乘方、开方等)把数、表示数的字母连结而成的式子叫做代数式。
单独的一个数或一个字母也是代数式。
代数式书写规范:① 数及字母、字母及字母相乘时乘号省略不写,数字要写在字母前面,如12ab ;数字因数是1或-1时,“1”省略不写,如-mn ;② 除号要改写成分数线,如:a ÷b 要写成ba ; ③ 带分数及字母相乘时,带分数要化成假分数;如:ab 211要写成ab 23的形式;④ 若运算结果为加减的式子,当后面有单位时,要用括号把整个式子括起来,如(12ab +2R )平方米。
二、整式的相关概念:单项式:表示数及字母的乘积的代数式叫单项式。
单独的一个数或一个字母也是代数式。
单项式的系数:单项式中的数字因数。
说明:在单项式中,系数只及数字因数有关;单项式的次数:一个单项式中,所有字母的指数和.。
说明:在单项式中,次数只及字母有关注意:(1)单项式表示数及字母相乘时,通常把数放在字母的前面; (2)单项式的系数包括前面的符号;(3)当一个单项式的系数是1或-1时,“1”通常省略不写; (4)单项式的系数是带分数时,通常写成假分数; (5)单项式中不含有加减运算,分母中也不能有字母。
多项式:几个单项式的和叫做多项式。
说明:多项式是由几个单项式相加得到的多项式的项数:多项式中所含单项式的个数就是多项式的项数,每个单项式叫多项式的项;不含字母的项叫做常数项。
说明:多项式的项,包括符号.如多项式5-3x 2中,二次项是-3x 2.多项式的次数:多项式里,次数最高项的次数叫多项式的次数;说明:在确定多项式的次数时,应先计算出多项式的每一项的次数,然后再确定多项式的次数,即取次数最大的项的次数作为该多项式的次数.常数项的次数为0。
多项式的命名:若多项式里次数最高项的次数是n次,并且有m项,那么它就是n次m项式。
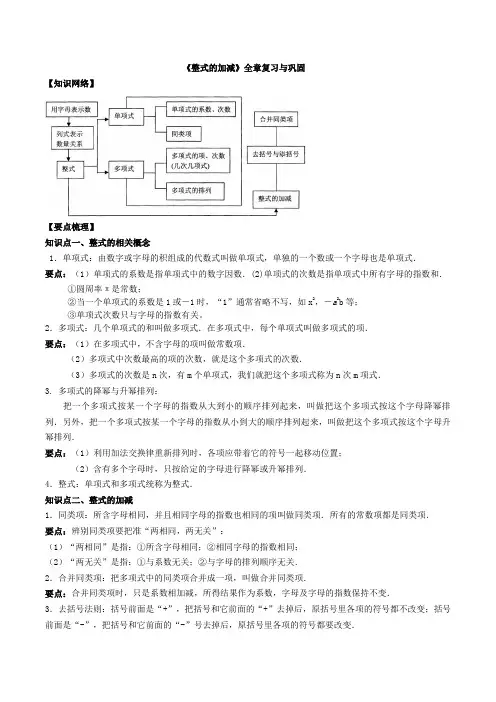
《整式的加减》全章复习与巩固【知识网络】【要点梳理】知识点一、整式的相关概念1.单项式:由数字或字母的积组成的代数式叫做单项式,单独的一个数或一个字母也是单项式.要点:(1)单项式的系数是指单项式中的数字因数.(2)单项式的次数是指单项式中所有字母的指数和.①圆周率π是常数;②当一个单项式的系数是1或-1时,“1”通常省略不写,如x2,-a2b等;③单项式次数只与字母的指数有关。
2.多项式:几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.要点:(1)在多项式中,不含字母的项叫做常数项.(2)多项式中次数最高的项的次数,就是这个多项式的次数.(3)多项式的次数是n次,有m个单项式,我们就把这个多项式称为n次m项式.3. 多项式的降幂与升幂排列:把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把这个多项式按这个字母降幂排列.另外,把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把这个多项式按这个字母升幂排列.要点:(1)利用加法交换律重新排列时,各项应带着它的符号一起移动位置;(2)含有多个字母时,只按给定的字母进行降幂或升幂排列.4.整式:单项式和多项式统称为整式.知识点二、整式的加减1.同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项.要点:辨别同类项要把准“两相同,两无关”:(1)“两相同”是指:①所含字母相同;②相同字母的指数相同;(2)“两无关”是指:①与系数无关;②与字母的排列顺序无关.2.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项.要点:合并同类项时,只是系数相加减,所得结果作为系数,字母及字母的指数保持不变.3.去括号法则:括号前面是“+”,把括号和它前面的“+”去掉后,原括号里各项的符号都不改变;括号前面是“-”,把括号和它前面的“-”号去掉后,原括号里各项的符号都要改变.4.添括号法则:添括号后,括号前面是“+”,括号内各项的符号都不改变;添括号后,括号前面是“-”,括号内各项的符号都要改变.5.整式的加减运算法则:几个整式相加减,有括号先去括号,然后再合并同类项.【典型例题】类型一、整式的相关概念1.指出下列各式中的整式、单项式和多项式,是单项式的请指出系数和次数,是多项式的请说出是几次几项式.(1)3a - (2)5 (3)2b a - (4)2x y - (5)3xy (6)x π (7)5m n + (8)1+a% (9)1()2a b h +举一反三:【变式1】(1)3xy -的次数与系数的和是________;(2)已知单项式26x y 的系数是等于单项式52m x y -的次数,则m =________;(3)若n ma b 是关于a 、b 的一个五次单项式,且系数为9,则-m+n =________.【变式2】多项式432231y y y y -+-+是______次_____项式,常数项是_______,三次项是_________.【变式3】把多项式321325x x x --+按x 的降幂排列是____________________.类型二、同类项及合并同类项2.合并同类项:(1)232338213223c c c c c c -+-+-+;(2)22220.50.40.20.8m n mn nm mn -+-.举一反三:【变式】若47a x y 与579b x y -是同类项,则a =________,b =________. 类型三、去(添)括号3. 计算 22232(12)[5(436)]x x x x x -----+举一反三:【变式1】下列式子中去括号错误的是( ).A .5x -(x -2y +5z )=5x -x +2y -5zB .2a 2+(-3a -b )-(3c -2d )=2a 2-3a -b -3c +2dC .3x 2-3(x +6)=3x 2-3x -6D .-(x -2y )-(-x 2+y 2)=-x +2y +x 2-y 2【变式2】化简:-2a+(2a-1)的结果是( ).A .-4a-1B .4a-1C .1D .-1类型四、整式的加减4. 求比多项式22523a a ab b --+少25a ab -的多项式.举一反三: 【变式】计算:11(812)3(22)32a a b c c b ---+-+类型五、化简求值5.(1)直接化简代入:已知12x =,1y =-,求225(23)2(43)x y x x x y ---的值.(2)条件求值:若523m x y +与3n x y 的和是单项式,则n m =________.(3)整体代入:已知x 2-2y =1,那么2x 2-4y+3=________.举一反三:【变式1】若实数a 满足2210a a -+=,则2245a a -+=________.【变式2】已知25m n -+=,求25(2)6360m n n m -+--的值.类型六、综合应用6. 已知多项式是否存在m ,使此多项式与x 无关?若不存在,说明理由;若存在,求出m 的值.《整式的加减》巩固练习一、选择题1.A 、B 、C 、D 均为单项式,则A+B+C+D 为().A .单项式B .多项式C .单项式或多项式D .以上都不对2.下列计算正确的个数( )① ab b a 523=+;② 32522=-y y ; ③ y x x y y x 22254=-;④ 532523x x x =+; ⑤ xy xy xy =+-33A .2B .1C .4D .03.现规定一种运算:a * b = ab + a - b ,其中a ,b 为有理数,则3 * 5的值为().A .11B .12C .13D .144.化简1(1)(1)n n a a +-+-(n 为正整数)的结果为().A .0B .-2aC .2aD .2a 或-2a5.已知a -b =-3,c+d =2,则(b+c )-(a -d )为().A .-1B .-5C .5D .16. 有理数a ,b ,c 在数轴上的位置如右图所示,则a c c b b a ++--+= ( )A .-2bB .0C .2cD .2c -2b7.当x =-3时,多项式535ax bx cx ++-的值是7,那么当x =3时,它的值是().A .-3B .-7C .7D .-178.如果32(1)n m a a --++是关于a 的二次三项式,那么m ,n 应满足的条件是().A .m =1,n =5B .m ≠1,n >3C .m ≠-1,n 为大于3的整数D .m ≠-1,n =5二、填空题9.nmx y -是关于x ,y 的一个单项式,且系数是3,次数是4,则m =________,n =________. ()()22222mx -x +3x +1-5x -4y +3x10.(1)-=+-222x y xy x (___________);(2)2a -3(b -c )=___________.(3)2561x x -+-(________)=7x+8.11.当b =________时,式子2a+ab -5的值与a 无关.12.若45a b c -+=,则30()b a c --=________. 13.某一铁路桥长100米,现有一列长度为l 米的火车从桥上通过,测得火车从开始上桥到完全过桥共用1分钟时间,则火车的速度为________.14.如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要枚棋子,摆第n 个图案需要枚棋子.三、解答题15.先化简,再求值:4x 3- [-x 2-2( x 3-12x 2+1)],其中x= -13.16.已知:a 为有理数,3210a a a +++=,求23420121...a a a a a++++++的值.17. 如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH=2cm, GK=2cm, 设BF=x cm,(1)用含x 的代数式表示CM=cm,DM=cm.(2)若x=2cm ,求长方形ABCD 的面积.…。


整式的加减复习课教案第一章:整式的概念与基本性质1.1 整式的定义1.2 整式的基本性质1.3 整式的分类第二章:整式的加减运算2.1 同类项的概念2.2 同类项的加减运算2.3 合并同类项的法则2.4 整式的加减步骤与方法第三章:多项式的加减运算3.1 多项式的定义与性质3.2 多项式的加减运算规则3.3 多项式加减的步骤与方法3.4 多项式加减的实例解析第四章:有理数的整式加减4.1 有理数与整式的关系4.2 有理数整式的加减运算规则4.3 有理数整式加减的步骤与方法4.4 有理数整式加减的实例解析第五章:分式的整式加减5.1 分式与整式的关系5.2 分式整式的加减运算规则5.3 分式整式加减的步骤与方法5.4 分式整式加减的实例解析第六章:整式的乘法运算6.1 整式乘法的概念6.2 整式乘法的基本法则6.3 整式乘法的步骤与方法6.4 整式乘法的实例解析第七章:整式的除法运算7.1 整式除法的概念7.2 整式除法的基本法则7.3 整式除法的步骤与方法7.4 整式除法的实例解析第八章:整式的混合运算8.1 混合运算的定义8.2 混合运算的顺序与规则8.3 整式混合运算的步骤与方法8.4 整式混合运算的实例解析第九章:整式的应用题9.1 应用题的特点与类型9.2 整式在应用题中的解题步骤与方法9.3 整式应用题的实例解析9.4 整式应用题的练习与拓展第十章:复习与检测10.1 复习整式的加减运算10.2 复习整式的乘除运算10.3 复习整式的混合运算10.4 复习整式的应用题10.5 检测题与答案解析重点和难点解析一、整式的概念与基本性质补充说明:整式包括单项式和多项式,它们都可以包含加、减、乘、除四种运算,但不包括指数运算。
整式的基本性质包括:同类项的定义与判断、整式的系数和次数的确定等。
二、整式的加减运算补充说明:同类项是指字母相同且相同字母的指数也相同的项。
合并同类项的法则是将同类项的系数相加减,字母部分保持不变。



整式的加减复习(一)屈家岭第一初级中学左卫东2、含有字母的式子中有乘号怎样规范书写?1、这个算式与我们小学学习的算式有何不同?它能表示量的关系吗?乘号通常写作“·”或省略不写如a ·b 或aba ×b 问题1、为了打造“中国农谷屈家岭先行区”,屈家岭工委作出决定,修建一条风情街,现风情街街道上要设计一个个长方形的花坛,已知花坛的长为a 米宽为b 米,那么这个长方形的花坛的面积是多少?ab问题2 圆的半径为R ,则这个圆的面积为七(4)班有男生m 人,女生是男生的,则女生有人某服装原价为a 元,降价10%后的价格为元。
笔记本的价格是x 元/本,圆珠笔的价格是y 元/只,买3本笔记本,4只圆珠笔共用元。
X 的5倍与y 的平方的差是正方形的边长为a ,在正方形的中间挖去一个半径为r的圆,则剩余的面积是43a 2-πr 2πR 2m 430.9a 3x+4y 5x-y 2单项式系数次数多项式项数次数整式问题3 下面各组式子有什么共同特征?0.5x 3y 2和12x 3y 2 -a 3b 和25ba 3所含字母相同,相同字母的指数相同。
象这样的式子叫做同类项把同类项合并成一项叫做合并同类项合并同类项的方法:同类项的系数相加减,字母部分不变如:0.5x 3y 2-12x 3y 2=( )x3y 2=( )0.5-12-11.5 x 3y 2-7b)-(4a-5b)又该如何合并呢?先去括号,再合并同类项那么怎样去括号呢?1.下列式子中哪些是单项式,哪些是多项式,哪些是整式?1,14.3,0,1,,,43,5,32+---m xy x a z xy axy3、(1)买单价为a 元的笔记本m 本,付出20元,应找回_______元.(20-am)(2)用字母表示图形中的绿色部分面积是________a 3m m3a-m 22、判断题:1)3a2-5ab 2的最高项系数是5()(2)xy 2的系数是0()(3)的系数是()(4)-ab 2c 的次数是2()221x 21××××4、在单项式:①a 2 ②③④-0.2y 2x ⑤中,是同类项的是221x 22xy z xy 221②④1、()14221222+--⎪⎭⎫ ⎝⎛+-x x x x 2、()⎪⎭⎫ ⎝⎛---+-+z y x y z x 543123213、先化简再求值yx xy x y y x 22222233-+-其中1,21-==y x1、已知2x m+n y2与3x4y m是同类项,则m=、n=.2、已知多项式3x2-2x-4与多项式A的和为6x-1,且式子A+(mx+1)的计算结果中不含关于x的一次项,求m的值。


1整式的加减复习资料知识点1 代数式知识点2 列代数式时应该注意的问题 (1)数与字母、字母与字母相乘时常省略“×”号或用“·”.如:-2×a=-2a ,3×a ×b=________, -2×x 2=________. (2)数字通常写在字母前面.如:mn ×(-5)=________, (a+b)×3=_______. (3)带分数与字母相乘时要化成假分数.如:221×ab=________,切勿 错误写成“221ab ”.(4)除法常写成分数的形式.如:S ÷x=xS, x ÷3=__________,x ÷312=__________ 典型例题:1、列代数式:(1)a 的3倍与b 的差的平方:___________________ (2)2a 与3的和:____________(3)x 的54与32的和:______________知识点3 代数式的值一般地,用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果,叫做代数式的值. 例如:求当x=-1时,代数式x 2-x+1的值. 解:当x=1时,x 2-x+1=12-1+1=1. ∴当x=1时,代数式x 2-x+1的值是1.对于一个代数式来说,当其中的字母取不同的值时,代数式的值一般也不相同。
请你求出: 当x=2时,代数式x 2-x+1的值。
_________________________________________________________________________________________________________________________________知识点4 单项式及相关概念由_____和_____的乘积组成的_____叫做单项式.单项式中的______叫做这个单项式的系数.一个单项式中,所有字母的______的和叫做这个单项式的次数。
整式的加减典型例题一、认识单项式、多项式1、下列各式中,书写格式正确的是 ( ) A.4·21 B.3÷2y C.xy ·3 D.ab2、下列代数式书写正确的是( )A 、48aB 、y x ÷C 、)(y x a +D 、211abc 3、在整式5abc ,-7x 2+1,-52x ,2131,24y x -中,单项式共有 ( )A.1个 B.2个 C.3个 D .4个4、代数式,21a a + 43,21,2009,,3,42mn bc a a b a xy -+中单项式的个数是()A 、3 B、4 C 、5 D 、65、写出一个关于x的二次三项式,使得它的二次项系数为-5,则这个二次三项式为 。
6、下列说法正确的是( )A、0不是单项式 B 、x 没有系数 C、37x x+是多项式 D、5xy -是单项式 二、整式列式.1、一个梯形教室内第1排有n 个座位,以后每排比前一排多2个座位,共10排.(1)写出表示教室座位总数的式子,并化简;(2)当第1排座位数是A时,即n=A,座位总数是140;当第1排座位数是B,即n =B 时,座位总数是160,求A 2+B2的值.2、若长方形长是2a+3b,宽为a +b,则其周长是( )A.6a+8b ﻩ ﻩB.12a+16bﻩﻩ C.3a+8bﻩ D.6a+4b3、a 是一个三位数,b 是一个两位数,若把b 放在a 的左边,组成一个五位数,则这个五位数为( ) A .b+a B.10b+a C. 100b +a D. 1000b+a4、(1)某商品先提价20%,后又降价20%出售,现价为a元,则原价为 元。
(2)香蕉每千克售价3元,m 千克售价____________元。
ﻫ(3)温度由5℃上升t ℃后是__________℃。
ﻫ(4)每台电脑售价x元,降价10%后每台售价为____________元。
ﻫ(5)某人完成一项工程需要a 天,此人的工作效率为__________。
整式的加减复习资料一、整式的基本概念1、单项式由数与字母的积组成的代数式叫做单项式,单独的一个数或一个字母也叫做单项式。
例如:3x、-5、abc 等都是单项式。
单项式中的数字因数叫做这个单项式的系数,一个单项式中,所有字母的指数的和叫做这个单项式的次数。
2、多项式几个单项式的和叫做多项式。
在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项。
多项式中次数最高的项的次数,叫做这个多项式的次数。
例如:2x + 3y 5 是一个多项式,它有三项,分别是 2x、3y、-5,其中-5 是常数项,这个多项式的次数是 1。
3、整式单项式和多项式统称为整式。
二、整式的加减运算1、同类项所含字母相同,并且相同字母的指数也相同的项叫做同类项。
几个常数项也是同类项。
例如:2x²y 和5x²y 是同类项,3 和-7 是同类项。
2、合并同类项把多项式中的同类项合并成一项,叫做合并同类项。
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变。
例如:3x + 2x =(3 + 2)x = 5x3、去括号法则(1)括号前是“+”号,把括号和它前面的“+”号去掉后,原括号里各项的符号都不改变。
(2)括号前是“”号,把括号和它前面的“”号去掉后,原括号里各项的符号都要改变。
例如:a +(b c) = a + b ca (b c) = a b + c4、整式的加减运算一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项。
三、整式加减运算的应用1、化简求值先将整式进行化简,然后再代入求值。
例如:已知 a = 2,b =-1,求多项式 3a²b 2ab²+ 5a²b 3ab²的值。
解:原式=(3a²b + 5a²b) (2ab²+ 3ab²)= 8a²b 5ab²当 a = 2,b =-1 时,原式= 8×2²×(-1) 5×2×(-1)²= 8×4×(-1) 5×2×1=-32 10=-422、解决实际问题利用整式的加减运算可以解决很多实际问题,例如行程问题、工程问题、销售问题等。
可编辑修改精选全文完整版七年级整式的加减1、单项式的概念:数与字母的积的代数式叫做单项式,单独的一个数或字母也是单项式。
(1)单项式中的数字因数叫做单项式的系数。
(2)一个单项式中,所有字母的指数的和叫做这个单项式的次数。
2、几个单项式的和叫做多项式(1)在多项式中,每个单项式叫做多项式的项,其中不是字母的项叫做常数项。
(2)多项式里,次数最高的项的次数,叫做这个多项式的次数。
3、整式的意义:单项式和多项式统称为整式。
4、同类项:所含字母相同,相同字母的指数也相同的项,叫做同类项。
合并同类项:把同类项合并成一项叫做合并同类项。
5、应注意的问题:(1)系数(单项式或多项式的某项)包括前面的符号,特别地,在单项式中作为系数,如a π2-的系数为π2-。
(2)单项式只允许含有乘法以及数字为除数运算;多项中必须会有加法或减法运算,但不能有以字母为除式的除法运算。
(3)多项式重新排列时,各项要连同它前面的符号一起移动。
(4)多项式不含某一字母次数的项,表示此项的系数为0,如x 2+1π不含x的一次项,说明这样的一次项x的系数为0。
基本法则1、整式加减法法则:几个整式相加减,通常用括号把每一个整式括起来,再用加减号连接,然后去括号,合并同类项.2、合并同类项法则:合并同类项时,把系数相加,字母和字母指数不变.注意:a、系数相加时,一定要带上各项前面的符号。
b、合并同类项一定要完全、彻底,不能有漏项。
c、只有是同类项才能合并。
d、合并同类项的结果可能是单项式也可能是多项式。
重点难点解析1、本节的重点是整式的有关概念;难点是正确识别多项式的项和项的系数.2、关于单项式的系数,学习中要注意:①系数要包括前面的符号;②系数是1或-1时,通常省略不写.3、关于单项式的次数:①当字母的指数是1时,“1”通常省略不写;②对于不含字母的非0数,如-2,0.5等,叫“零次单项式”.4、关于多项式的项,每项必须包括它前面的符号.5、多项式的次数的概念要正确理解,是指最高次项的次数,而不是指多项式中所有字母指数的和,要与求单项式的次数区分开.练习:1多项式222332y y x x +-是一个 次 项式,它的项是2 若y x 57 与21+--m n y x 是同类项,则 m = ,n = . 3、在 中,次数 。
整式的加减【知识要点】同类项: 所含字母相同, 相同字母的指数也相同的项一、 注: ①同类项与字母顺序无关;②几个常数也是同类项1、 合并同类项:2、 概念: 把同类项合并成一项3、 方法: ①同类项的系数相加;②字母和字母的指数不变二、 步骤: ①准确找出同类项;②利用法则, 把同类项系数相加;三、 ③利用有理数加法计算出各项系数的和, 写出结果四、 去括号:1、 意义法则: ①括号前是“+”号, 去括号后符号不变2、 ②括号前是“-”号, 去括号后符号改变方法: ①由内到外②由外到内③内外同时【典型例题】下列各题中的两项是不是同类项? 为什么?(1)y x y x 2252与;(2)b a ab 3322与;(3)ab abc 44与;(4)nm mn 与3;(5)-5与+3.【例1】 合并下列各式中的同类项。
(1)223x x +;(2)37328422++---a a a a ;(3)m n nm 222123- (4)ab a ab 342-+在式子① , ② ,③ , ④ 中, 需要先去括号, 再合并同类项的有。
先去括号, 再合并同类项。
(1))(528b a b a -++;(2))(26c a a --【例2】 下列计算结果正确的是( )。
A. B.C. D.先化简, 再求值。
, 其中 , 。
【课堂练习】一、 选择题1.下列运算正确的是( )A. B 、C. D.2、已知 是同类项, 则 的值是( )A.1B.0C.2D.33.减去 等于 的代数式是( )A. B. C. D.4.化简 的结果是( )A. B 、 C 、 D 、二、 填空题1. = 。
2.7-3x-4x2+4x-8x2-15= 。
3.2(2a2-9b)-3(-4a2+b)= 。
4.8x2-[-3x-(2x2-7x-5)+3]+4x= 。
5.单项式 的系数是______, 次数是______;6、 是 次 项式, 它的项分别是 , 其中常数项是 ;三、 7、为鼓励节约用电, 某地对居民用户用电收费标准作如下规定: 每户每月用电如果不超过100度, 那么每度电价按a 元收费;如果超过100度, 那么超过部分每度电价按b 元收费。
第二章整式的加减复习资料
一、基础知识
(一)概念1、单项式:由与的乘积式子称为单项式。
单独一个数或一个字母也是单项式,如a ,5。
·单项式的系数:单式项里的叫做单项式的系数。
·单项式的次数:单项式中叫做单项式的次数。
2、多项式:几个的和叫做多项式。
其中,每个单项式叫做多项式的,不含字母的项叫做。
·多项式的次数:多项式里的次数,叫做多项式的次数。
·多项式的命名:一个多项式含有几项,就叫几项式。
所以我们就根据多项式的项数和次数来命名一个多项式。
如:3n4-2n2+1是一个四次三项式。
3、整式:______和______统称整式。
4、同类项——必须同时具备的两个条件(缺一不可):
①所含的相同;②相同也相同。
(二)方法法则
1、合并同类项,就是把多项式中的同类项合并成一项。
方法:把各项的相加,而不变。
步骤:①找②移③合
2、去括号法则
法则1.括号外的因数是正数,去括号后原括号内各项的符号与原来的符号;法则2.括号外的因数是负数,去括号后原括号内各项的符号与原来的符号.口诀:去括号,看符号;是正号,不变号;是负号,全变号。
注意:1、要注意括号前面的符号,它是去括号后括号内各项是否变号的依据.
2、去括号时应将括号前的符号连同括号一起去掉.
3、括号前面是“-”时,去掉括号后,括号内的各项均要改变符号,不能只改变括号内第一项或前几项的符号,而忘记改变其余的符号.
4、括号前是数字因数时,要将数与括号内的各项分别相乘,不能只乘括号里的第一项.
5、遇到多层括号一般由里到外,逐层去括号。
3、整式的加减整式的加减的过程就是。
如遇到括号,则先,再,合并到为止。
(三)本章需要注意的几个问题
①整式(既单项式和多项式)中,分母一律不能含有字母。
②π不是字母,而是一个数字,③多项式相加(减)时,必须用括号把多项式括起来,才能进行计算。
④去括号时,要特别注意括号前面的因数。
二、类型题(一)概念类
1、在
3222
112
,3,1,,,,4,,
43
xy x x y m n x ab
x x
--+---
+,π
2
b
中,单项式有:
多项式有:。
2、2
aπ
-
的系数是______.3、单项式8
53
ab
-
的系数是 ,次数是;当5,2
a b
==-时,这个代数式的值是________.4、已知-7x2ym是7次单项式则m= 。
6、单项式2
5x y、22
3x y、2
4xy
-的和为.
7、写一个关于x的二次三项式,使它的二次项系数为-5,则这个二次三项式为。
8、多项式2
23
a a
--的项是。
9、一个关于b的二次三项式的二次项系数是-2,一次项系数是-0.5,常数项是3,则这个多项式是_____________。
10、7-2xy-3x2y3+5x3y2z-9x4y3z2是次项式,其中最高次项是,最高次项的系数是,常数项是,是按字母作幂排列。
11、多项式
223
7583
xy y x y x
-+-按x的降幂排列是 __.
12、如果多项式3x2+2xyn+y2是个三次多项式,那么n= .
13、代数式22
a a
-的第二项的系数是________,当1
a=-时,这个代数式的值是________.
14、已知-5xmy3与4x3yn能合并,则mn = 。
15、若
21
1
2
n n
a b
--
与
33
1
2
m
a b+
的和仍是单项式,则m=_____,n=_____.
16、两个四次多项式的和的次数是()
A.八次B.四次C.不低于四次D.不高于四次
17、多项式8
3
32
2-
+
-
-xy
y
kxy
x化简后不含xy项,则k为。
18、一个多项式加上-x2+x-2得x2-1,则此多项式应为________.
(二)化简类
1、(a3-2a2+1)-2(3a2-2a+2
1
) 2、x-2(1-2x+x2)+3(-2+3x-x2)
3、
)312(65++
-a a 4、b a b a +--)5(25、-32009)21
4(2)2(++--y x y x
6、-[]12)1(32--+--n m m
7、)(4)()(3222222y z z y y x ---+-
8、1}1]1)1([{2222-------x x x x
9、
]2)5(2[)3(22
22ab a ab b a ab ++---- 10、3(-2ab +3a )-(2a -b )+6ab ;
11、212a -[21(ab -2
a )+4a
b ]-21
ab .12、23(23)2(332)x x y z x y z --++-+;
13、2228[42(25)]m m m m m ----.(三)求值类1、已知:2||,3==b a ,求代数式
()332b a -的值.2、先化简,再求值:
(1)
{
}222
523(4)xyz x y xyz xy x y ⎡⎤----⎣⎦
,其中2-=x ,1-=y ,3=z ;
(2)
)22()(3)2(2222222b a ab b a ab b a ab -+--- 其中:1,2==b a . 3、已知0)13()2(2
2
=-++b a ,求:ab
ab b a ab ab b a 2]4)21
(62[3222-+--- 的值。
4、已知:
22
,,(1)(5)50;3m x y x m -+=满足:2
312722a b b a y 与+-)(是同类项. 求代数式:
)733()9(622
2222y xy x y xy m y x +---+-的值。
5、已知2=-n m ,1=mn ,求多项式)4()223()322(mn n m m n mn n m mn ++--+-++-的值. 6、已知ab=3,a+b=4,求3ab -[2a - (2ab-2b)+3]的值。
7、已知22222,3A a ab b B a ab b =-+=---,求:(1)A B +;(2)23A B -.
8、 一位同学做一道题:已知两个多项式A 、B ,计算2A+B ,他误将“A+B•”看成“A+2B”
求得的结果为9x2-2x+7,已知B=x2+3x -2,求正确答案.
9、有这样一道题: “计算
)3()2()232(323323223y y x x y xy x xy y x x -+-++----的值,其中1,21-==
y x ”。
甲同学把“21=x ”错抄成“21-=x ”,但他计算的结果也是正确的,
试说明理由,并求出这个结果? 10、试说明:不论x 取何值代数式
)674()132()345(323223x x x x x x x x x +--+--+---++的值是不会改变的。
11、若(x2+ax -2y +7)―(bx 2―2x +9 y -1)的值与字母x 的取值
无关,求a 、b 的值。
12、已知210x x --=,求
9442++-x x 的值. (四)规律类
1、在下面的一列数里,按规律写出第八个数
①2+5,4+5,6+5,8+5,…,__________.②1,34,59,7
16,…,____________.
2、按照规律填上所缺的单项式并回答问题:
(1)a 、2
2a -、3
3a 、4
4a -,________,__________;
(2)试写出第2009个和第2010个单项式.(3)试写出第n 个单项式. 3、一张长方形的桌子可坐6人,按下图将桌子拼起来.
按这样规律做下去第n 张桌子可以坐 人. 4、如图所示,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有n (n>1
)个点,每个图形总的点数S 是多少?当n=7,100时,S 是多少?
5、如图所示的规律摆下去,用S 表示相应的图中的点数,请表示出第n 个图中的点数S 。
并计算第2009个图中的点数。