第六章 机械的平衡习题与答案
- 格式:doc
- 大小:297.00 KB
- 文档页数:11

参考答案 第一章 绪论一,填空题1.1 能量,物料,信息1.2运动,动力 1.3制造,运动,装配 二、选择题2.1 D 2.2 B 三,简答题第二章 机械的结构分析二、综合题1.n = 7 ,p l = 9 ,p h = 121927323=-⨯-⨯=--=h l P P n F从图中可以看出该机构有2个原动件,而由于原动件数与机构的自由度数相等,故该机构具有确定的运动。
2. (a )D 、E 处分别为复合铰链(2个铰链的复合);B 处滚子的运动为局部自由度;构件F 、G 及其联接用的转动副会带来虚约束。
n = 8 ,p l = 11 ,p h = 1111128323=-⨯-⨯=--=h l P P n F3. (c )n = 6 ,p l = 7 ,p h = 313726323=-⨯-⨯=--=h l P P n F(e )n = 7 ,p l = 10 ,p h = 0101027323=-⨯-⨯=--=h l P P n F 4. (a )n = 5 ,p l = 7 ,p h = 010725323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅱ级组 因为该机构是由最高级别为Ⅱ级组的基本杆组构成的,所以为Ⅱ级机构。
(c )n = 5 ,p l = 7 ,p h = 010725323=-⨯-⨯=--=h l P P n FⅢ级组因为该机构是由最高级别为Ⅲ级组的基本杆组构成的,所以为Ⅲ级机构。
5. n = 7 ,p l =10 ,p h = 0101027323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅲ级组当以构件AB 为原动件时,该机构为Ⅲ级机构。
Ⅱ级组 Ⅱ级组 Ⅱ级组当以构件FG 为原动件时,该机构为Ⅱ级机构。
可见同一机构,若所取的原动件不同,则有可能成为不同级别的机构。
6. (a )n = 3 ,p l = 4 ,p h = 101423323=-⨯-⨯=--=h l P P n F因为机构的自由度为0,说明它根本不能运动。
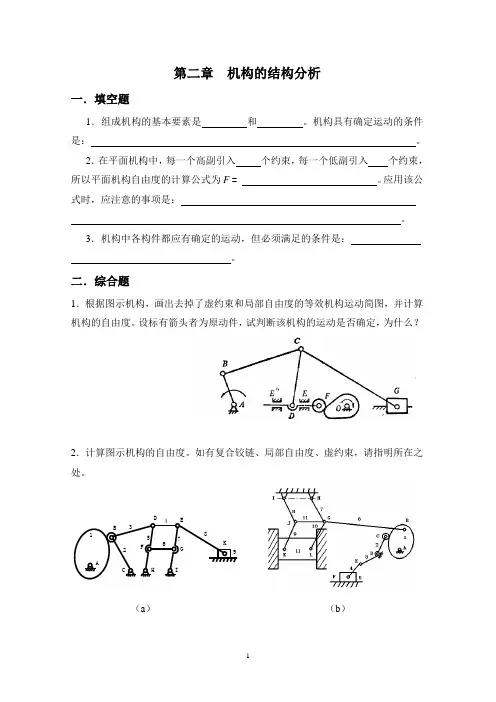
第二章 机构的结构分析一.填空题1.组成机构的基本要素是 和 。
机构具有确定运动的条件是: 。
2.在平面机构中,每一个高副引入 个约束,每一个低副引入 个约束,所以平面机构自由度的计算公式为F = 。
应用该公式时,应注意的事项是: 。
3.机构中各构件都应有确定的运动,但必须满足的条件是: 。
二.综合题1.根据图示机构,画出去掉了虚约束和局部自由度的等效机构运动简图,并计算机构的自由度。
设标有箭头者为原动件,试判断该机构的运动是否确定,为什么?2.计算图示机构的自由度。
如有复合铰链、局部自由度、虚约束,请指明所在之处。
(a ) (b )ADECHGF IBK1234567893.计算图示各机构的自由度。
(a)(b)(c)(d)(e)(f)4.计算机构的自由度,并进行机构的结构分析,将其基本杆组拆分出来,指出各个基本杆组的级别以及机构的级别。
(a)(b)(c)(d)5.计算机构的自由度,并分析组成此机构的基本杆组。
如果在该机构中改选FG 为原动件,试问组成此机构的基本杆组是否发生变化。
6.试验算图示机构的运动是否确定。
如机构运动不确定请提出其具有确定运动的修改方案。
(a)(b)第三章平面机构的运动分析一、综合题1、试求图示各机构在图示位置时全部瞬心的位置(用符号P直接在图上标出)。
ij2、已知图示机构的输入角速度ω1,试用瞬心法求机构的输出速度ω3。
要求画出相应的瞬心,写出ω3的表达式,并标明方向。
3、在图示的齿轮--连杆组合机构中,试用瞬心法求齿轮1与3的传动比ω1/ω2。
4、在图示的四杆机构中,AB l =60mm, CD l =90mm, AD l =BC l =120mm, 2ω=10rad/s ,试用瞬心法求:(1)当ϕ=165°时,点C 的速度c v ;(2)当ϕ=165°时,构件3的BC 线上速度最小的一点E 的位置及其速度的大小; (3)当0c v =u u u v时,ϕ角之值(有两个解)。
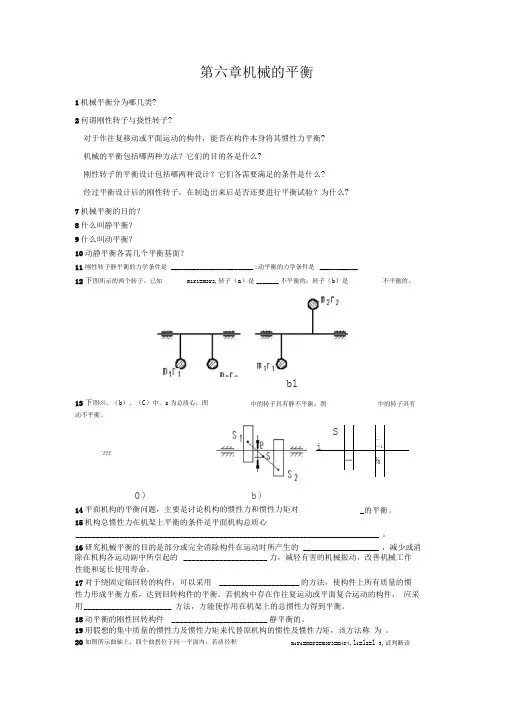
第六章机械的平衡1机械平衡分为哪几类?2何谓刚性转子与挠性转子?对于作往复移动或平面运动的构件,能否在构件本身将其惯性力平衡?机械的平衡包括哪两种方法?它们的目的各是什么?刚性转子的平衡设计包括哪两种设计?它们各需要满足的条件是什么?经过平衡设计后的刚性转子,在制造出来后是否还要进行平衡试验?为什么?7机械平衡的目的?8什么叫静平衡?9什么叫动平衡?10动静平衡各需几个平衡基面?11刚性转子静平衡的力学条件是__________________________ ;动平衡的力学条件是____________12下图所示的两个转子,已知m1r1=m2r2,转子(a)是_______ 不平衡的;转子(b)是bl13下图⑻、(b)、(C)中,s为总质心,图动不平衡。
'TTT.0)b)14平面机构的平衡问题,主要是讨论机构的惯性力和惯性力矩对15机构总惯性力在机架上平衡的条件是平面机构总质心____________________________________________________________________________ 。
16研究机械平衡的目的是部分或完全消除构件在运动时所产生的___________________ ,减少或消除在机构各运动副中所引起的_____________________ 力,减轻有害的机械振动,改善机械工作性能和延长使用寿命。
17对于绕固定轴回转的构件,可以采用 ____________________ 的方法,使构件上所有质量的惯性力形成平衡力系,达到回转构件的平衡。
若机构中存在作往复运动或平面复合运动的构件,应采用______________________ 方法,方能使作用在机架上的总惯性力得到平衡。
18动平衡的刚性回转构件 ________________________ 静平衡的。
19用假想的集中质量的惯性力及惯性力矩来代替原机构的惯性及惯性力矩,该方法称为。

第六章 机械的平衡习题6-5解:通孔I 的失去质量为()kg b V m 766.0105014.35078004922=⨯⨯⨯⨯===-ρπφρ,I 处失去质量等效于在I 的对称处添加了一个质量为0.766kg 的质量块,因此等效后的图为质径积分别为质量I :mm kg r m I I I .6.76100766.0=⨯==κ质量II :mm kg r m II II II .1002005.0=⨯==κ取质径积比例尺mmm kg .01.0=κμ,作质径积多边形如图示,得平衡质量的质径积为 mm kg mr .1.1091091.10=⨯==κμκ方位为与x 轴正向夹角107o 。
但现在要制一通孔,则制在反向方位即可。
孔直径大小为mm m br b m 42042.0102005014.37800101.10944463==⨯⨯⨯⨯⨯⨯===Φ--ρπκρπ 孔的方位与x 轴反向成107o 夹角。
习题6-7解:先将质量块2、3的质径积向两个平衡面上分解,令l l l l ===342312,有cm kg l l r m I .30032301532222=⨯⨯==κcm kg l l r m II .1503130153222=⨯⨯==κcm kg l l r m I .3.133********=⨯⨯==κcm kg l l r m II .7.26632202032333=⨯⨯==κ质量块1和4在平衡面I 和II 上的质径积分别为cm kg r m I .4004010111=⨯==κ,cm kg r m I .3003010444=⨯==κ取质径积的作图比例尺mmm kg .1.0=κμ,作质径积的矢量图如下可得第I 个平衡面上所需质径积为285kg.cm ,第二个平衡面上所需质径积为381kg.cm 。
平衡质量分别为kg r m I IbI 7.550285===κ,方位:与x 轴正向夹角60。

考试范围:xxx;满分:***分;考试时间:100分钟;命题人:xxx 学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.如图所示,用一个始终水平向右的力F,把杠杆OA从图示位置缓慢拉至水平的过程中,力F的大小将()A.变小B.不变C.变大D.先变大后变小2.如图是健身用的“跑步机”示意图。
质量为m的健身者踩在与水平面成α角的静止皮带上,用力向后蹬皮带,可使皮带以速度v匀速向后运动。
若皮带在运动的过程中受到脚的摩擦力为f,则在运动的过程中,下列说法中正确的是()A.f是皮带运动的阻力B.人相对于“跑步机”是运动的C.α角增大,人跑得更费力D.人的重力与皮带对人的支持力是一对平衡力3.如图所示,水平拉力F1(6N)将物体(G=9N)沿直线匀速拉动s1的距离,做功W1,借助滑轮组,F2使物体在同一水平面上匀速直线运动同样的距离s1,F2所拉绳端的上升距离为s2,做功为W2,则()A.W2一定小于W1B.s2一定小于s1C.F2一定大于G/3D.F2一定大于F1/34.如图所示,用甲、乙两种方式分别将同一重物提升相同的高度,若每个滑轮重相同,不计摩擦及绳重。
则下列说法正确的是A.甲绳自由端的拉力比乙的大B.甲绳自由端拉力做的总功比乙小C.两种方式,拉力做功的功率一定相等D.两种方式,机械效率相等5.如图是一种切甘蔗用的铡刀示意图,下列说法中正确的是A.刀刃很薄可以增大压力B.铡刀实质上是一种省力杠杆C.手沿F1方向用力比沿F2方向更省力D.甘蔗放在b点比a点更易被切断6.科学方法是科学思想的具体体现,初中物理中常常用到“控制变量法”、“等效替代法”、“模型法”、“类比法”等方法,下面是几个研究实例:①研究光的传播时,引入“光线”;②研究动能与速度的关系时,让物体的质量保持不变;③研究功率时把它与速度相比;④将撬棒抽象为绕某一固定点转动的硬棒;其中,采用了相同研究方法的是()A.①和②B.①和④C.②和③D.③和④7.如图中杠杆l AB=2l OA,每个钩码重力为2牛.在B点用力F1,则下列说法中正确的是A.F1大小一定为2牛B.F1大小可能为1牛C.F1大小一定为3牛D.F1 大小可能为20牛8.如下图所示的四种机械提起同一重物,不计机械自重和摩擦,最省力的是A.B.C.D.9.使用下列工具的情景中,属于费力机械的是()A.滑轮组提升重物B.自拍杆自拍C.使用扳手固定物体D.手拉行李箱10.郯城的公共自行车(如图)已遍及城区的各个地方,解决了群众出行“最后一公里”问题.下列有关公共自行车的说法,正确的是()A.车座宽大柔软是为了增大对人体的压强B.轮胎的花纹是为了减小车轮与地面的摩擦C.骑车时,自行车的脚踏板在水平位置时最省力D.自行车对地面的压力和地面对自行车的支持力是一对平衡力11.在探究“杠杆平衡条件”的实验中,杠杆在力F作用下水平平衡,如图所示,现将弹簣测力计绕B点从位置a转到位置b过程中,杠杄始终保持水平平衡,则拉力F的变化情况是()A.一直变小B.一直不变C.一直变大D.先变小后变大12.在一次提升重物的过程中,工人利用了如图所示的简单机械。
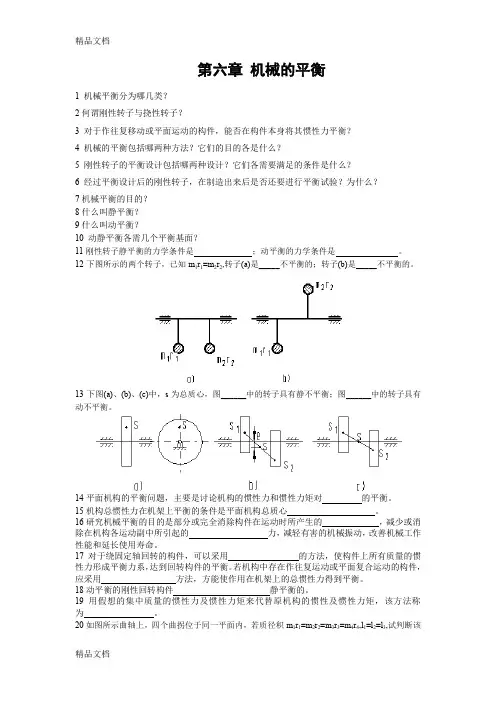
第六章机械的平衡1 机械平衡分为哪几类?2何谓刚性转子与挠性转子?3 对于作往复移动或平面运动的构件,能否在构件本身将其惯性力平衡?4 机械的平衡包括哪两种方法?它们的目的各是什么?5 刚性转子的平衡设计包括哪两种设计?它们各需要满足的条件是什么?6 经过平衡设计后的刚性转子,在制造出来后是否还要进行平衡试验?为什么?7机械平衡的目的?8什么叫静平衡?9什么叫动平衡?10 动静平衡各需几个平衡基面?11刚性转子静平衡的力学条件是;动平衡的力学条件是。
12下图所示的两个转子,已知m1r1=m2r2,转子(a)是_____不平衡的;转子(b)是_____不平衡的。
13下图(a)、(b)、(c)中,s为总质心,图______中的转子具有静不平衡;图______中的转子具有动不平衡。
14平面机构的平衡问题,主要是讨论机构的惯性力和惯性力矩对的平衡。
15机构总惯性力在机架上平衡的条件是平面机构总质心。
16研究机械平衡的目的是部分或完全消除构件在运动时所产生的,减少或消除在机构各运动副中所引起的力,减轻有害的机械振动,改善机械工作性能和延长使用寿命。
17对于绕固定轴回转的构件,可以采用的方法,使构件上所有质量的惯性力形成平衡力系,达到回转构件的平衡。
若机构中存在作往复运动或平面复合运动的构件,应采用方法,方能使作用在机架上的总惯性力得到平衡。
18动平衡的刚性回转构件静平衡的。
19用假想的集中质量的惯性力及惯性力矩来代替原机构的惯性及惯性力矩,该方法称为。
20如图所示曲轴上,四个曲拐位于同一平面内,若质径积m1r1=m2r2=m3r3=m4r4,l1=l2=l3,试判断该曲轴是否符合动平衡条件?为什么?21图示一盘形回转体,其上有四个不平衡质量,它们的大小及质心到回转轴线的距离分别为:m 110=kg ,214kg m =,316kg m =,420kg m =,1200mm r =,r 2400=mm ,3300mm r =,4140mm r =,欲使该回转体满足静平衡条件,试求需加平衡质径积m r b b 的大小和方位。

§6 机械平衡填空题:1.回转构件的直径D和轴向宽度b之比/D b符合 <=5 条件或有重要作用的回转构件,必须满足动平衡条件方能平稳地运转。
如不平衡,必须至少在 2 个校正平面上各自适当地加上或去除平衡质量,方能获得平衡。
2.只使刚性转子的惯性力得到平衡称静平衡,此时只需在 1个平衡平面中增减平衡质量;使惯性力和惯性力偶矩同时达到平衡称动平衡,此时至少要在 2个个选定的平衡平面中增减平衡质量,方能解决转子的不平衡问题。
3.刚性转子静平衡的力学条件是各偏心质量的惯性力的合力为零,而动平衡的力学条件是各偏心质量的惯性力的合力和惯性力偶矩均为零。
4.图a、b、c中,S为总质心,图 a、b 中的转子具有静不平衡,图 c 中的转子是动不平衡。
,转子a是静不平衡的,转子b是动不平衡的。
5.图示两个转子,已知mr mr1122a)b)选择题:1.设图示回转体的材料均匀,制造精确,安装正确,当它绕AA轴线回转时是处于 D 状态。
A)静不平衡B)静平衡C)完全不平衡D)动平衡2. 图示为一圆柱凸轮。
设该凸轮的材料均匀,制造精确,安装正确,则当它绕AA 轴线转动时,是处于 B 状态。
A)静不平衡B)静平衡 C)完全不平衡D)动平衡3. 图示一变直径带轮。
设该带轮的材料均匀,制造精确,安装正确,当它绕AA 轴线回转时是处于 D 状态。
A)静不平衡B)静平衡 C)完全不平衡 D)动平衡判断题:1. 若刚性转子满足动平衡条件,这时我们可以说该转子也满足静平衡条件。
(√ )2. 不论刚性回转体上有多少个平衡质量,也不论它们如何分布,只需要在任意选定两个平面内,分别适当地加平衡质量即可达到动平衡。
(√ ) 综合题1:图示为绕O 点回转的薄片圆盘,在位置1、2处钻孔,101m .r =,202m .r =,孔部分材料质量分别为110kg .m =,205kg .m =。
为进行静平衡,欲在半径05m .b r =的圆周上钻一孔。
考试范围:xxx;满分:***分;考试时间:100分钟;命题人:xxx 学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.如图所示,用一个始终水平向右的力F,把杠杆OA从图示位置缓慢拉至水平的过程中,力F的大小将()A.变小B.不变C.变大D.先变大后变小2.如图所示,重物重30N,为提升重物,现选用轻质杠杆,不考虑杠杆支点O点处的摩擦,每次利用杠杆把同一重物匀速提升相同高度,下列说法正确的是()A.当重物悬挂在A点,动力作用在C点时,该杠杆一定是省力杠杆B.当重物悬挂在A点,动力作用在C点时,拉力为20NC.当重物悬挂在A点,动力作用在B点时,拉力有可能为30ND.重物挂在A点时,利用该机械所做的有用功比挂在B点时做的有用功少3.如图所示,在探究杠杆平衡条件的实验中,杠杆正处于水平平衡状态.若在两侧钩码下分别再加挂一块完全相同的橡皮,则下列判断正确的是()A.杠杆仍能处于水平平衡状态B.杠杆不能处于水平平衡状态,左端上升C.杠杆不能处于水平平衡状态,右端上升D.上述情况均有可能发生4.如图所示,某工人在10s时间内将重为800N的物体提升2m,已知动滑轮的重为100N,不计绳重和摩擦,则下列计算结果正确的是()A.人施加的拉力大小是300N B.绳端移动的距离是6mC.滑轮组的机械效率是88.9%D.拉力的功率为160W5.如图所示,水平拉力F1(6N)将物体(G=9N)沿直线匀速拉动s1的距离,做功W1,借助滑轮组,F2使物体在同一水平面上匀速直线运动同样的距离s1,F2所拉绳端的上升距离为s2,做功为W2,则()A.W2一定小于W1B.s2一定小于s1C.F2一定大于G/3D.F2一定大于F1/36.将一个重为4.5N的物体沿斜面从底端匀速拉到顶端,已知斜面长1.2m,高为0.4m,斜面对物体的摩擦力为1N(物体的大小、空气阻力等可忽略不计).则在上述过程中A.有用功为5.4J B.额外功为1.8JC.机械效率为60%D.沿斜面向上的拉力大小为2N7.如图,O为拉杆式旅行箱的轮轴,OA为拉杆.现在拉杆端点A处施加力F,使箱体从图示位置绕O点缓慢逆时针转至竖直位置.若力F的大小保持不变,则力F的方向应()A.垂直于OA向上B.竖直向上C.沿OA向上D.水平向左8.科学方法是科学思想的具体体现,初中物理中常常用到“控制变量法”、“等效替代法”、“模型法”、“类比法”等方法,下面是几个研究实例:①研究光的传播时,引入“光线”;②研究动能与速度的关系时,让物体的质量保持不变;③研究功率时把它与速度相比;④将撬棒抽象为绕某一固定点转动的硬棒;其中,采用了相同研究方法的是()A.①和②B.①和④C.②和③D.③和④9.如图,水平桌面上的物体A重100N,物体B重40N,此时物体B恰能匀速下降;当用一水平向左的力F拉动物体A在2s内匀速向左移动1m的过程中,若不计动滑轮和绳的重力,不计绳与滑轮及滑轮轴间的摩擦,则下列说法正确的是()A.B上升了2m B.拉力F的功率为20WC.物体A与桌面间的滑动摩擦力为40N D.吊着B物体的绳子所做的功为40J 10.如图所示,甲、乙杠杆的质量和长度均相同,机械摩擦不计,分别使用甲、乙杠杆将物体A提升相同的高度,则在工作过程中,甲、乙杠杆的机械效率相比()A.甲的大B.乙的大C.一样大D.无法确定11.如图所示,斜面长3m,高0.6m,小明用绳子在6s内将重50N的物体从其底端沿斜面向上匀速拉到顶端,拉力F是15N。

第六章 机械的平衡本章知识要点归纳与总结 1.机械平衡的目的(1)设法将构件的不平衡惯性力加以平衡以消除或减少其不良影响。
(2)机械平衡的内容由于各构件的结构及运动形式的不同,其所产生的惯性力和平衡方法也不同,机械的平衡问题分为下述两类:1) 绕固定轴回转的构件的惯性力平衡可利用在构件上增加或除去一部分质量的方法予以平衡。
2) 机构的平衡使各构件惯性力的合力和合力偶得到完全或部分平衡。
2.刚性转子的平衡计算(2)刚性转子的平衡计算的步骤 1)静平衡计算①计算各偏心质量的质径积i i r m②计算平衡质径积 i i i x b b r m r m αcos )(∑-= i i i y b b r m r m αs i n )(∑-= 大小 ])()[(22y b b x b b b b r m r m r m +=相位角 ])()(a r c t a n [xb b y b b b r m r m =α2) 动平衡计算①选定两个回转平面I 及II 作为平衡基面。
②将各离心惯性力分解到平衡基面I 和II 内。
③在平衡基面I 及II 内按静平衡计算方法各加一平衡质量bI m 及bII m ,使两平衡基面内的惯性力 之和分别为零。
3.刚性转子的平衡实验(1)静平衡实验目的是使转子的质心落在其回转中心上。
静平衡实验可借助于导轨式静平衡实验装置,反复增减 平衡质量以达到静平衡;也可借助于类似单摆的平衡设备,以迅速测出转子不平衡质径积的大小和方位。
(2)动平衡实验目的是使转子获得满意的动平衡。
动平衡实验借助于专用的动平衡机。
(3)现场平衡对于尺寸很大的转子,除在制造间进行平衡,还需在现场通过直接测量机器中转子支架的振动,来确定不平衡量的大小及方位,进而进行平衡。
4.转子的许用不平衡量有两种表示方法,即质径积[mr ] 表示法和偏心距[e ]表示法,两者的关系为 mmr e ][][=5.平面机构的平衡(1)机构平衡的条件:机构的总惯性力I F 和总惯性力偶矩IM分别为零,即0,0==II MF不过,在计算中,总惯性力偶矩对基座的影响应当与外加的驱动力矩和阻抗力矩一并研究,但是 由于驱动力矩和阻抗力矩与机械的工况有关,单独平衡惯性力矩往往没有意义,故这里只讨论总惯性力的平衡问题。

第6章习题6.1机械为什么会产生速度波动?它有何危害?答:实际上,机械原动件的运动规律是由其各构件的质量、转动惯量和作用于其上的驱动力与阻抗力等因素而决定的,因而在一般情况下,原动件的速度和加速度是随时间而变化,机械在运动过程中会出现速度波动。
这种速度波动,会导致在运动副中产生附加的动压力,并一起机械的振动,从而降低机械的寿命、效率和工作质量。
6.2周期性速度波动应如何调节?它能否调节为恒稳定运转?为什么?答:在机械中安装一个具有很大转动惯量的回转构件——飞轮来调节周期性速度波动。
飞轮能够调速,是利用了它的储能作用。
由于飞轮转动惯量不可能为无穷大,而平均转速和最大盈亏功又都是有限值,所以安装飞轮后机械运转的速度仍有周期波动,只是波动的幅度减小而已。
6.3为什么在机械中安装飞轮就可以调节周期性速度波动?通常都将飞轮安装在高速轴上是什么原因?答:由于飞轮具有很大的转动惯量,因而要使其转速发生变化,就需要较大的能量,当机械出现盈功时,飞轮的角速度只作微小上升,即可将多余的能量吸收储存起来;当机械出现亏功时,机械运转速度减慢,飞轮又可将其储存的能量释放,以弥补能量的不足,而其角速度只作小幅度的下降。
当最大盈亏功与速度不均匀系数相同时,飞轮转动惯量与其轴的转速的平方值成反比,所以为减少飞轮的转动惯量,最好将飞轮安装在机械的高速轴上。
6.4非周期性速度波动应如何调节?为什么利用飞轮不能调节非周期性速度波动?答:机械运转的速度出现非周期性的波动,若长时间内驱动力矩大于阻抗力矩,机械将越转越快,甚至可能出现“飞车”现象,从而使机械遭到破坏;反之,若驱动力矩小于阻抗力矩,则机械会越转越慢,最后将停止不动。
飞轮只能延缓机械遭到破坏或停止不动,不能使驱动力矩和阻抗力矩恢复平衡关系。
对非周期性的速度波动进行调节,方法必须可以使机械重新回复稳定运转。
主要采取的方法是安装调速器。
6.5在什么条件下需要进行转动构件的静平衡?使转动构件达到静平衡的条件是什么?答:对于轴向尺寸很小的回转件(D/b>5,圆盘直径为D,其宽度为b),其质量的分布可以近似地认为在同一回转面内。
参考答案 第一章 绪论一,填空题1.1 能量,物料,信息1.2运动,动力 1.3制造,运动,装配 二、选择题2.1 D 2.2 B 三,简答题第二章 机械的结构分析二、综合题1.n = 7 ,p l = 9 ,p h = 121927323=-⨯-⨯=--=h l P P n F从图中可以看出该机构有2个原动件,而由于原动件数与机构的自由度数相等,故该机构具有确定的运动。
2. (a )D 、E 处分别为复合铰链(2个铰链的复合);B 处滚子的运动为局部自由度;构件F 、G 及其联接用的转动副会带来虚约束。
n = 8 ,p l = 11 ,p h = 1111128323=-⨯-⨯=--=h l P P n F3. (c )n = 6 ,p l = 7 ,p h = 313726323=-⨯-⨯=--=h l P P n F(e )n = 7 ,p l = 10 ,p h = 0101027323=-⨯-⨯=--=h l P P n F 4. (a )n = 5 ,p l = 7 ,p h = 010725323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅱ级组 因为该机构是由最高级别为Ⅱ级组的基本杆组构成的,所以为Ⅱ级机构。
(c )n = 5 ,p l = 7 ,p h = 010725323=-⨯-⨯=--=h l P P n FⅢ级组因为该机构是由最高级别为Ⅲ级组的基本杆组构成的,所以为Ⅲ级机构。
5. n = 7 ,p l =10 ,p h = 0101027323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅲ级组当以构件AB 为原动件时,该机构为Ⅲ级机构。
Ⅱ级组 Ⅱ级组 Ⅱ级组当以构件FG 为原动件时,该机构为Ⅱ级机构。
可见同一机构,若所取的原动件不同,则有可能成为不同级别的机构。
6. (a )n = 3 ,p l = 4 ,p h = 101423323=-⨯-⨯=--=h l P P n F因为机构的自由度为0,说明它根本不能运动。
6. 图a、b、c中,S为总质心,图 a, b 中的转子具有静不平衡,图 c 中的转子是动不平衡。
7.机构总惯性力在机架上平衡的条件是机构的总质心静止不动。
在同一轴平面内,则其中 a, b, c 轴已达静平衡, c 轴已达动平衡。
2.图示为一圆柱凸轮。
设该凸轮的材料均匀,制造精确,安装正确,则当它绕D) 动平衡
3.
D) 动平衡
D) 惯性力部分平衡,但产生附加惯性力偶矩。
四、计算题
1. 图示两个回转构件是否符合静平衡条件?是否符合动平衡条件?为什么?442对a
b 3.图示为一鼓轮,上有重块b 将不平衡质量、分解至,平面内,因为位于平面内,不用分解,所以只需要A m B m I II A m I 分解B
m 2601200260()
I B B m m ⨯=⨯-∴723kg
.I B m =7232923kg ..II I B B B m m m =+=+=在平面内,I ∑
在平面II 内由得0i i m r =∑500600II II B b m m ⨯=⨯769kg .II b m ∴=方向如图所示。
4.某转子由两个互相错开的偏心轮组成,每一偏心轮的质量均为,偏心距均为,拟在平衡平090m r 面A 、B 上半径为处添加平衡质量,使其满足动平衡条件,试求平衡质量和的大小2r ()b A m ()b B m 和方向。
第6章习题解答参考6-5图示为一钢制圆盘,盘厚b=50 mm 。
位置I 处有一直径φ=50mm 的通孔,位置Ⅱ处有一质量m 2=0.5 kg 的重块。
为了使圆盘平衡,拟在圆盘上r=200 mm 处制一通孔,试求此孔的直径与位置。
(钢的密度ρ=7.8 g /cm 3。
)m 2r 2=0.5×20=10 kg.cm 求平衡质径积 1) 图解法:取适当的比例尺作质径积矢量多边形如图所示, 所添质量为:方位如图所示,与水平方向的夹角为, 根据题目要求应在相反方向挖一通孔, 其直径为:解:根据静平衡条件有2211=++b b r m r m r m分别求位置1、2处的质径积cmkg r b r m .66.710108.75544321211=⨯⨯⨯⨯⨯==-πρϕπ)(kg rm b ⨯=μb α)(4mm b m bb ρπϕ=2)解析法:).(244.3)210cos 135cos (cos )(2211cm kg r m r m r m r m i i i x b b =+--=∑-=- α ).(416.10)210sin 135sin (cos )(2211cm kg r m r m r m r m i i i x b b =+--=∑-=- α]).(91.100166.119416.10244.3)()(2222cm kg r m r m r m y b b x b b b b ==+=+=)(5455.02091.10/kg r r m m b b b b ===孔的直径:)(22.481.178.75105455.0443cm b m b b ==⨯⨯⨯⨯==πρπϕ孔的方位:[][] 7.72244.3416.10arctan)(/)(arctan ===x b b y b b b r m r m α6—7在图示的转子中,已知各偏心质量m 1=10 kg ,m 2=15 kg ,m 3=20 kg ,m 4=10 kg ,它们的回转半径大小分别为r 1=40cm ,r 2=r 4=30cm ,r 3=20cm ,方位如图所示。
第六章机械的平衡1 机械平衡分为哪几类?2何谓刚性转子与挠性转子?3 对于作往复移动或平面运动的构件,能否在构件本身将其惯性力平衡?4 机械的平衡包括哪两种方法?它们的目的各是什么?5 刚性转子的平衡设计包括哪两种设计?它们各需要满足的条件是什么?6 经过平衡设计后的刚性转子,在制造出来后是否还要进行平衡试验?为什么?7机械平衡的目的?8什么叫静平衡?9什么叫动平衡?10 动静平衡各需几个平衡基面?11刚性转子静平衡的力学条件是;动平衡的力学条件是。
12下图所示的两个转子,已知m1r1=m2r2,转子(a)是_____不平衡的;转子(b)是_____不平衡的。
13下图(a)、(b)、(c)中,s为总质心,图______中的转子具有静不平衡;图______中的转子具有动不平衡。
14平面机构的平衡问题,主要是讨论机构的惯性力和惯性力矩对的平衡。
15机构总惯性力在机架上平衡的条件是平面机构总质心。
16研究机械平衡的目的是部分或完全消除构件在运动时所产生的,减少或消除在机构各运动副中所引起的力,减轻有害的机械振动,改善机械工作性能和延长使用寿命。
17对于绕固定轴回转的构件,可以采用的方法,使构件上所有质量的惯性力形成平衡力系,达到回转构件的平衡。
若机构中存在作往复运动或平面复合运动的构件,应采用方法,方能使作用在机架上的总惯性力得到平衡。
18动平衡的刚性回转构件静平衡的。
19用假想的集中质量的惯性力及惯性力矩来代替原机构的惯性及惯性力矩,该方法称为。
20如图所示曲轴上,四个曲拐位于同一平面内,若质径积m1r1=m2r2=m3r3=m4r4,l1=l2=l3,试判断该曲轴是否符合动平衡条件?为什么?21图示一盘形回转体,其上有四个不平衡质量,它们的大小及质心到回转轴线的距离分别为:m 110=kg ,214kg m =,316kg m =,420kg m =,1200mm r =,r 2400=mm ,3300mm r =,4140mm r =,欲使该回转体满足静平衡条件,试求需加平衡质径积m r b b 的大小和方位。
22图示一钢质圆盘。
盘厚20mm δ=,在向径1100mm r =处有一直径50mm d =的通孔,向径2200mm r =处有一重量为2N 的重块,为使圆盘满足静平衡条件,拟在向径200mm r =的圆周上再钻一通孔,试求此通孔的直径和方位(钢的重度5106.7-⨯=γ3N/mm )。
23一转子上有两个不平衡质量kg 2001=m ,kg 1002=m ,m m 501=r ,402=r mm ,选定平面Ⅰ、Ⅱ为平衡校正面,若两个平面内平衡质量的回转半径为mm 60bII bI ==r r ,求平衡质量bI m 、bII m 的大小及方位。
24图示一双缸发动机的曲轴,两曲拐在同一平面内,相隔180︒,每一曲拐的质量为50 kg ,离轴线距离为200mm ,A 、B 两支承间距离为900mm ,工作转速n =3000r/min 。
试求:(1)支承A 、B 处的动反力大小;(2)欲使此曲轴符合动平衡条件,以两端的飞轮平面作为平衡平面,在回转半径为500mm 处应加平衡质量的大小和方向。
25为了平衡曲柄滑块机构ABC 中滑块C 的往复惯性力,在原机构上附加一滑块机构ABC ',设曲柄和连杆的质量不计,滑块C 和C '质量都为m ,连杆长度l l BC BC =',试证明机构的第二级惯性力(即惯性力中具有曲柄转动频率两倍的频率分量)将获得完全平衡。
26图示盘形回转件上存在三个偏置质量,已知m110= kg ,m 215= kg ,m 310= kg ,r 150= mm ,r 2100= mm ,r 370= mm ,设所有不平衡质量分布在同一回转平面内,问应在什么方位上加多大的平衡质径积才能达到平衡?27图示盘状转子上有两个不平衡质量:m115=.k g ,m 208=.kg ,r 1140= mm ,r 2180= mm ,相位如图。
现用去重法来平衡,求所需挖去的质量的大小和相位(设挖去质量处的半径r =140mm )。
28 高速水泵的凸轮轴系由三个互相错开120︒的偏心轮组成,每一偏心轮的质量为m ,其偏心距为r ,设在平衡平面A 和B 上各装一个平衡质量m A 和m B ,其回转半径为2r ,其他尺寸如图示。
试求m A 和m B 的大小和方向(可用图解法)。
29一回转体上有三质量:1 3 kg m =,2 1 kg m =,3 4 kg m =,绕z 轴等角速度旋转,160 mm r =,2140 mm r =,390 mm r =,其余尺寸如图示,试用图解法求应在平面Ⅰ和Ⅱ处各加多大平衡质量才能得到动平衡(设平衡质量bI m 和bII m 离转动轴线的距离bI r 、bII r 为bI bII 100 mm r r ==)。
30图示为V 形发动机机构。
设每一活塞部件的质量都为m ,今在曲柄延长线上与曲柄销B 对称的点D 处加上一平衡质量m ,则该发动机的所有第一级惯性力(即惯性力上具有与曲柄转动频率相同的频率分量)将被完全平衡。
试证明之(连杆、曲柄质量不计)。
提示:曲柄滑块机构中滑块的加速度变化规律为2cos cos 2N r a r l ωϕϕ⎛⎫≈-+ ⎪⎝⎭第六章 机械的平衡11刚性转子静平衡的力学条件是不平衡惯性力的矢量和为零;动平衡的力学条件是 1)其惯性力的矢量和等于零,即∑P=0 ;(2)其惯性力矩的矢量和也等于零,即∑M=0 12子(a)是静不平衡的;转子(b)是动不平衡的。
13a),b) 中的转子具有静不平衡;图 c) 中的转子具有动不平衡。
14 机座 15 静止不动 16 惯性力;动压17 静平衡或动平衡;完全平衡或部分平衡 18一定是 19 质量代换法20该曲轴符合动平衡条件21m kg 22.01011⋅=⨯=r m (方向向上);m kg 6.54.01422⋅=⨯=r m (方向向右);m kg 8.43.01633⋅=⨯=r m (方向向下);m kg 8.214.02044⋅=⨯=r m (方向向左)。
m /m m kg 1.0⋅=mr μ0b b 44332211=++++r m r m r m r m r m由图量得m kg 96.3b b ⋅=r m 方向量得与水平夹角即与44r m夹角为45o 。
或用计算法求得:2442221133)()(r m r m r m r m r m b b -+-=96.38.28.222=+=kg m ⋅︒=135b θ,与m r 22夹角22向径r 1处挖去通孔的质量kg3.08.9/4211=⨯⨯=γδπd m质径积m m kg 301003.011⋅=⨯=r m静平衡条件:0b b 2211=++-r m r m r m 作矢量多边形,质径积m m kg 8.408.9/200222⋅=⨯=r m 得:m m kg 6.36b b ⋅=r m ︒=82.74ϕ 应在︒=18.255θ处去重,孔径为d b6.362008.9/42b b b =⨯⎪⎭⎫⎝⎛=δγπd r m6.15022b =d 76.38b =d mm23mm kg 5000502002 1 1⋅=⨯=''l lr mmm kg 5000502002"1"1⋅=⨯=l lr m mmkg 40004010022 22⋅-=⨯-=''l l r m mmkg 80004010024"2"2⋅=⨯=l l r m m m kg 640020320 b b ⋅=⨯=''r m mm kg 940020470"b "b ⋅=⨯=r mkg 67.10660/6400bI ==m kg 67.15660/9400bII ==m方向θ¡'方向θ"24 (1) 不平衡质径积引发的离心力偶矩为m N 600000100060060230001000200502⋅=⨯⎪⎭⎫ ⎝⎛⨯⨯⨯π(2) A 、B 处附加动反力R 为6670006000009.0==⨯R R N(3) 为满足动平衡条件,在飞轮处应加平衡质量m b10 2.06.0505.02.1b b =⨯⨯=⨯⨯m m kg左端飞轮,平衡质量在下方。
右端飞轮,平衡质量在上方。
25 曲柄滑块机构中滑块的加速度变化规律为⎪⎭⎫⎝⎛+-≈ϕϕω2cos cos 2l r r a Nϕω=t ω---曲柄角速度由提示得滑块的第二级惯性力ϕω2cos 2I l rmr P =正号表示沿x 轴方向。
设曲柄AB 处在α角位置,活塞C 的第二级惯性力αω2cos 2I BCBABA C l ml P =方向为A 指向C 。
活塞的第二级惯性力()αω-=1802cos22I BC BA BA C l ml P =ml l BA BA BC 222ωα'cos方向为A 指向B 。
显然,活塞C 和系统的第二级惯性力获得完全平衡。
26 111050500 kg mm m r =⨯=⋅22151001500 kg mm m r =⨯=⋅ 331070700 kg mm m r =⨯=⋅ 1r 与3r 共线,可代数相加得图3311700500200 kg mm m r m r -=-=⋅方向同3r平衡条件:b b 1122330m r m r m r m r +++= 所以依次作矢量()331122,m r m r m r +,封闭矢量b b m r 即所求,如图示。
22b b 20015001513.275 kg mm m r =+=⋅0200270arctg277.5951500θ=+=︒b b27 不平衡质径积11210 kg mm m r =⋅22144 kg mm m r =⋅静平衡条件1122b b 0m r m r m r ++= 解得b b 140 kg mm m r =⋅例6-2图 应加平衡质量b 140/140 1 kg m ==挖去的质量应在b b m r 矢量的反方向,140mm 处挖去1kg 质量。
28偏心轮的不平衡质径积C C D D E E m r m r m r mr ===分别分解到平衡平面A 和B()5/4250/200mr mr r m A C C ==()5/250/50mr mr r m B C C ==()2/250/125mr mr r m A D D ==()2/250/125mr mr r m B D D ==()5/250/50mr mr r m A E E ==()5/4250/200mr mr r m BE E ==动平衡条件()()()()0b b =+++A E E A D D A C C A r m r m r m r m ()()()()0b b =+++BE E B D D B C C B r m r m r m r m解得:()2/b b mr r m A =因为b 2r r =,所以()m m m A A 25.0b ==, ()2/b b mr r m B=因为r r b =2,所以()m m m B B 25.0b ==方向如图示。