机械工程测试技术基础第一章优秀课件 (2)
- 格式：ppt
- 大小：2.97 MB
- 文档页数：110
下载文档原格式
合集下载
机械工程测试技术基础1-2
A( )
2 1
M
M
0
0
（五）卷积特性
两个函数x1(t)与x2(t)的卷积定义为：
x1
(
)
x
2
(t
)d
记作：
x1 (t) * x2 (t)
若： x1(t) X1( f ) 则：x1(t) * x2 (t) X1( f ) X 2 ( f )
x2 (t) X 2 ( f )
δ(t)的图示可用一长度为一个单位的线段来表示，线段位于 原点，表示当时间t0=0有一冲击。若线段位于 t=t0点，则 可定义δ函数的延迟为：
(t
t0
)
0 1
t t0 t t0 ，积分值仍为1。
（2） 函数的采样性质：如果 函数与某一连续函数f(t)相 乘，显然其乘积仅在t=0处为f(0) (t)，其余各点（t 0） 之乘积均为零。如果函数与某一连续函数f(t)相乘，并在
)dt
f (t0 )
由于经过此种处理，可将f(t)在任何时刻的值提取出来，所 以称其为筛选性质，或抽样性质。当对信号进行采样时，采 样的过程及采样后信号即可利用此种性质来进行描述.
（3） 函数的与其他函数的卷积：任何函数和函数 (t)的卷
积是一种最简单的卷积积分。例如，一个矩形函数x(t)与 函数
从面积（通常也称其为 函数的强度）的角度来看：
lim (t)dt
0
S (t)dt 1
(t)
0
t0 t 0
且
+
(t)dt 1
---称之为δ函数。
机械工程测试技术基础教学PPT
测量的基础知识
#2022
*
测量的基础知识
基本量和导出量 基本量： 长度、质量、时间、温度、电流、发 光强度、物质的量 导出量：由基本量按一定函数关系来定义的
*
测量的基础知识
3、基准与标准
基准：用来保存、复现计量单位的计量器具，是最高准确度的计量器具。 国家基准、副基准和工作基准 计量标准：用于检定工作计量器具的计量器具 工作计量器具是指用于现场测量而不用检定工作的计量器具。
物质所固有，客观存在或运动状态的特征 非物质，不具有能量，传输依靠物质和能量
*
四、测试技术的内容
测试技术的内容 测量原理：实现测量所依据的物理、化 学、生物等现象及有关定律。 测量方法：分为直接或间接测量、接触 或非接触测量、破坏或非破坏测量 测量系统 数据处理
*
测试过程：首先利用酒精（敏感元件）检测出被测对象温度变化并将其转换成自身体积的变化（热胀冷缩），然后经过等截面的中空玻璃管（中间变换器）再转换成高度的变化（分析处理），最后由外面的刻度线显示出测试结果（显示、记录）并提供给观察者或输入后续的控制系统。
*
教材、参考书与课时安排 教材 机械工程测试技术基础(第3版) 熊诗波 黄长艺编著 机械工业出版社 测试技术与信号处理 郭迎福，焦锋，李曼主编 中国矿业大学出版社 课时安排 授课 ：36学时 实验 ：4学时
教材、参考书与课时安排
*
教学目的和要求 测试技术是工科院校机械类各专业本科生一门重要的技术基础课，内容包括传感器、测量电路、测试系统的特性，信号分析与数据处理 。 通过本课程的学习： 掌握传感器的原理、特点及应用，常用测试系统和测量电路以及信号分析的基本原理和分析方法。为后续课程打好基础。
领域：工业、农业、航天、军事等
#2022
*
测量的基础知识
基本量和导出量 基本量： 长度、质量、时间、温度、电流、发 光强度、物质的量 导出量：由基本量按一定函数关系来定义的
*
测量的基础知识
3、基准与标准
基准：用来保存、复现计量单位的计量器具，是最高准确度的计量器具。 国家基准、副基准和工作基准 计量标准：用于检定工作计量器具的计量器具 工作计量器具是指用于现场测量而不用检定工作的计量器具。
物质所固有，客观存在或运动状态的特征 非物质，不具有能量，传输依靠物质和能量
*
四、测试技术的内容
测试技术的内容 测量原理：实现测量所依据的物理、化 学、生物等现象及有关定律。 测量方法：分为直接或间接测量、接触 或非接触测量、破坏或非破坏测量 测量系统 数据处理
*
测试过程：首先利用酒精（敏感元件）检测出被测对象温度变化并将其转换成自身体积的变化（热胀冷缩），然后经过等截面的中空玻璃管（中间变换器）再转换成高度的变化（分析处理），最后由外面的刻度线显示出测试结果（显示、记录）并提供给观察者或输入后续的控制系统。
*
教材、参考书与课时安排 教材 机械工程测试技术基础(第3版) 熊诗波 黄长艺编著 机械工业出版社 测试技术与信号处理 郭迎福，焦锋，李曼主编 中国矿业大学出版社 课时安排 授课 ：36学时 实验 ：4学时
教材、参考书与课时安排
*
教学目的和要求 测试技术是工科院校机械类各专业本科生一门重要的技术基础课，内容包括传感器、测量电路、测试系统的特性，信号分析与数据处理 。 通过本课程的学习： 掌握传感器的原理、特点及应用，常用测试系统和测量电路以及信号分析的基本原理和分析方法。为后续课程打好基础。
领域：工业、农业、航天、军事等
机械工程测试技术ppt
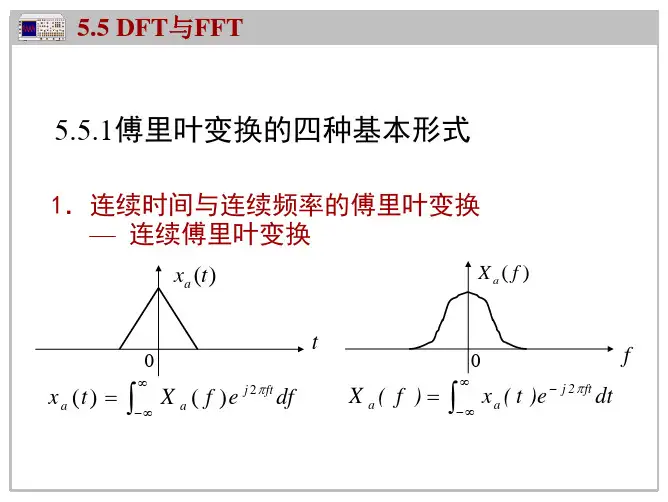
x(t )
n
C e
n
jn0t
n 0,1,2,3,
1 1 T2 Cn an jbn x(t )e jn0t dt 2 T T 2
Cn Cn e
jn
1 2 2 Cn an bn 2
bn n arctan an
n 各阶谐波分量的初相角。
1.2 周期信号与离散频谱
1.2.2 几点说明 1）满足狄里赫利条件的任何周期信号可分解成直流 分量及许多简谐分量的叠加，且这些简谐分量的角 频率必定是基波角频率的整数倍。各次谐波频率之 比必定是有理数。 信号的频率组成： {0 ,20 ,30 ,......} 例如： xt sin 2t sin 2t 准周期信号
x(t ) a0 an cos n0t bn sin n0t bn jn0t an jn0t jn0t jn0 t a0 ( e e ) j (e e ) 2 n 1 2 an jbn jn0t an jbn jn0t a0 e e 2 2 n 1
1.2 周期信号与离散频谱 4）物理意义：
A0、A1、…… An均为常数，称为谐波系数 n为从１到∞的正整数，称为谐波阶数 n ＝１时， A1为基波分量的幅值 为基波或一次谐波分量 A1 cos0t 1 n ＝2 时， A2为二次谐波分量的幅值 为二次谐波分量 A2 cos20t 2 2 0 为基波圆频率 0 2f 0 T f 0 为基波频率 T 为周期信号的周期
An
● ● ● ● ● ●
0 ω0(f0) 2ω0
(2f0)
ω(f)
1.2 周期信号与离散频谱
机械工程测试技术基础PPT(共41页)
！！！
x t a 0 n 1 1 2 a n jn b e j n 0 t 1 2 a n jn b e j n 0 t
实频谱、虚频谱 余弦函数
正弦函数
！！！
！！！
由于
0
2
T0
当 T 0 趋于无穷 时，频率间隔 成为 d，
离散谱中相邻的谱线紧靠在一起，n0 成为连续变
量，求和符号 就变为积分符号 ，则
且有
A na n 2 b n 2
tg n
an bn
*
xta0 A nco n s0tn
0
注意此二 式的区别
且有
A na n 2 b n 2
tg n
bn an
P 22-23
算例：求右图周期性三角波的傅立叶级数
解：在x(t)的一个周期中可表示为X(t)
xt
A A
2A T0 2A
t t
T0 t 0 2
xt d x t ejtdtejt
2
1 x t ejtdtejtd
2
这就是傅立叶积分
二、傅立叶变换的主要性质(P 30) 熟悉傅立叶变换的性质的重要意义 简化作用,推广于复杂复杂情况！！！
第2章 测试装置的基本特性
§2.1 概述 §2.2 测试装置的静态特性 §2.3 测试装置动态特性的数学描述 §2.4 测试装置对任意输入的响应 §2.5 实现不失真测试的条件 §2.6 测试装置动态特性的测试
0 t T0
t
T 0
2
常值分量
1 T0
a0
T0
x 2
T0
t
dt
2
2 T0
T0 2
0
A
《机械工程测试技术》绪言第一章
的测试系统，初步掌握测试信号的
分析与处理方法。 2019/11/25
6
学习内容：
（1）信号时域和频域描述方法，建立信号频
谱结构的概念，掌握频谱分析和相关分析
的基本原理和方法。
（2）掌握测量装置基本特性的评价方法和不 失真测试条件，掌握一阶、二阶线性系统 动态特性及其测定方法。
（3）了解常用传感器，常用信号调理工作原 理和性能，较合理运用。数字信号处理初 步。
2019/11/25
3
二、测试过程和测试系统的一般组成
被测 对象
传 感 器
信 号
调 理
传 输
信 号
处 理
显 示 记 录
观察 者
激励装置
反馈、控制
传 感 器—直接作用于被测量，按一定规律将被测量转换成同 样或别种量输出（通常是电信号）的器件。
信号调理—把来自传感器的信号进一步转换成更适合传输和处 理的形式。如幅值放大、阻抗转换成电压、频率等 。
dt
2
（1-8）
正弦分量
bn
2 T0
T0
2 T0
x(t) sin
n 0 t
dt
2
其中T0—x(t)的周期 ω 0=2π /T0（圆频率）n=1,2,3,…
2019/11/25
30
将式（1-7）x(t) a0 (an cos n0t bn sin n0t) 改写成 n1
信 号—把消息转换成更便于传输和处理的信息。信号是消息
的载体，是消息的一种表现形式。
2019/11/25
5
信号分类—电信号、光信号、力信号、磁信号等。
三、课程研究内容和性质
教学目的：
机械工程测试技术基础PDF版课件2
1 2)均值 E[ x(t )] = N
∑ x ( n)
n =0
N
μx
U=0 For K = 0 To N U=U+data(k) Next U=U/N
6.6 常用的数字信号处理算法
1 2 3)均方值 E[ x (t )] = N x 2 ( n) ∑
n =0 N
E2=0 For K = 0 To N E2=E2+data(k)*data(k) Next RMS=sqr(E2/N)
5.6 常用的数字信号处理算法
案例：管道压力监测与超门限报警
5.6 常用的数字信号处理算法 信号幅值报警系统设计实验：
5.6 常用的数字信号处理算法
5)周期T A T t
n=0 AT=0.8*P For K = 2 To N If data(k-1)<AT And data(k-2)<AT And data(k+1)>AT And data(k+2)>AT Then ti(n)=K n=n+1 End If Next T=(ti(2)-ti(1))*dt
5.6 常用的数字信号处理算法
样例信号：
5.6 常用的数字信号处理算法 数字滤波器系数有专用软件计算，这里我们提 供一个网络计算工具：
5.6 常用的数字信号处理算法 数字滤波应用实例:
滤除信号中的零漂和低频晃动，便于门限报警
滤除信号中的高频噪声，以便于观察轴心运动规律
5.6 常用的数字信号处理算法 思考题：
∞
⎞ ⎟δ (ω − nω1 ) ⎠
ω
5.5 DFT与FFT 3．离散时间与连续频率的傅里叶变换 — 序列傅里叶变换
X ( e jω )
∑ x ( n)
n =0
N
μx
U=0 For K = 0 To N U=U+data(k) Next U=U/N
6.6 常用的数字信号处理算法
1 2 3)均方值 E[ x (t )] = N x 2 ( n) ∑
n =0 N
E2=0 For K = 0 To N E2=E2+data(k)*data(k) Next RMS=sqr(E2/N)
5.6 常用的数字信号处理算法
案例：管道压力监测与超门限报警
5.6 常用的数字信号处理算法 信号幅值报警系统设计实验：
5.6 常用的数字信号处理算法
5)周期T A T t
n=0 AT=0.8*P For K = 2 To N If data(k-1)<AT And data(k-2)<AT And data(k+1)>AT And data(k+2)>AT Then ti(n)=K n=n+1 End If Next T=(ti(2)-ti(1))*dt
5.6 常用的数字信号处理算法
样例信号：
5.6 常用的数字信号处理算法 数字滤波器系数有专用软件计算，这里我们提 供一个网络计算工具：
5.6 常用的数字信号处理算法 数字滤波应用实例:
滤除信号中的零漂和低频晃动，便于门限报警
滤除信号中的高频噪声，以便于观察轴心运动规律
5.6 常用的数字信号处理算法 思考题：
∞
⎞ ⎟δ (ω − nω1 ) ⎠
ω
5.5 DFT与FFT 3．离散时间与连续频率的傅里叶变换 — 序列傅里叶变换
X ( e jω )
机械工程测试技术基础 _第三版_第一章
30
第四节 随机信号
二、随机信号的主要特征参数
1、 均值、方差和均方值 均值表示信号的常值分量
方差描述随机信号的波动分量。
均方值描述随机信号的强度。
31
第四节 随机信号
二、随机信号的主要特征参数
2、 概率密度函数 随机信号的概率密度函数是表示信号幅值落在指定区间的概率。如图1-22所示。
图1-22
一、概述
随机信号是不能用确定的数学关系式来描述的，不能预测其未来的任何瞬时值。 任何一次观测值只代表在其变动范围中可能产生的结果之一，但其值的变动服 从统计规律。 随机过程与样本函数如图1-21所示。
图1-21
29
第四节 随机信号
二、随机信号的主要特征参数
1） 均值、方差和均方值 2） 概率密度函数 3） 自相关函数 4） 功率谱密度函数
图1-3
4
第一节 信号的分类与描述
一、信号的分类
3.能量信号和功率信号 当电压信号满足一定条件时：则认为信号的能量是有限的，并称之为能 量有限信号。简称能量信号。 若信号在区间（- ∞ ， ∞ ）的能量是无限的，但它在有限区间的平均功
率是有限的。这种信号称为功率有限信号，或功率信号。
x 2 (t )dt
通常所说的非周期信号是指瞬变非周期信号如图1-11所示。图1-11a为矩 形脉冲信号，图1-11b为指数衰减信号，图1-11c为衰减振荡，图1-11d为 单一脉冲。
图1-11
14
第三节 瞬变非周期信号与连续频谱
一、傅里叶变换
图1-11 非周期性信号
15
第三节 瞬变非周期信号与连续频谱
一、傅里叶变换
图1-7
9
机械工程测试技术基础
PPT文档演模板
图8-19
图8-20
机械工程测试技术基础
3rew
演讲完毕，谢谢听讲!
再见，see you again
PPT文档演模板
2020/11/18
机械工程测试技术基础
图8-14
机械工程测试技术基础
•第四节 声发射测量传感器与仪器
•三、声发射测量仪器
1 、传感器 2、前置放大器 3、主放大器 4、门槛值检测器 5、振铃计数器 6、事件计数器 7、能量处理器 8、振幅分析器 9、频率分析器
PPT文档演模板
机械工程测试技术基础
•第四节 声发射测量传感器与仪器
•四、声发射技术在滚动轴承状态检测中的应用
•第一节 概述
•二、工程声学测量的有关概念
1.声音的波长、频率和声速
声源完成一周的振动，声波所传播的距离，称为声波的波长。或者是具 有相同运动状态的两相邻空气层之间的距离，称为声波的波长。 频率是每秒振动的次数。 声音传播的速度随温度的升高而增大。
PPT文档演模板
机械工程测试技术基础
•第一节 概述
5.非接触式光纤声发射传感器
目前常用的AE传感器大都采用：压电陶瓷晶体(PZT)来实现,利用PZT 的压电效应把机械量变为电量后进行检测。
PPT文档演模板
机械工程测试技术基础
•第四节 声发射测量传感器与仪器
•三、声发射测量仪器
声发射测量常用仪器如图8-14所示，包括以下几个部分。
PPT文档演模板
PPT文档演模板
单端谐振式传感器结构简单，如上所示。
机械工程测试技术基础
•第四节 声发射测量传感器与仪器
•二、声发射测量传感器
2.宽频带传感器
机械工程测试基础第一章.ppt
2 1 2 但它在有限区间（t1, t2）的平均功率是有限的，即 x (t ) dt t 2 t1 t1 这种信号称为功率有限信号或功率信号。
（1—6）
二、信号的时域描述和频域描述
用来描述信号变化规律的参考变量称为信号的描述域，信号表达成描述域 为独立变量（自变量）的函数。一个信号可以用多种描述域建立不同函数关系， 来反映不同的规律。 x(t), x(k), X(f), ε(σ),
0 t T0 / 2 T0 / 2 t 0
-T0/2
A x(t ) A
付氏级数展开
A
x (t) T0/2
0 -A
t
x(t ) a0 (a n cos n 0 t bn sin n 0 t )
n 1
1 0 1 a 0 [ x(t )dt [ Adt T0 T0 / 2 T0 T0 / 2
x(t ) a0 an bn
2
(sin
n
cosn 0 t cos n sin n 0 t )
x(t ) a0 An sin(n 0 t n ) （1—9）
n 1
式中
An an bn
2
2
bn An 、 Φ n也分别是 nω 0 的两个独立的函数， An 为幅值、 Φ n 为 相位移，几何意义清晰，可分别作出幅频谱和相频谱。
1/R 为常值系数，瞬间功率正比于电压信号平方。
信号的能量为 当x(t)满足
2 x (t ) dt
2 x (t ) dt
(1—4)
则认为信号的能量是有限的，并称之为能量有限信号，简称能量信号。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 T0
T0 /2 x(t)dt
T0 / 2
2
an
T0
TT00//22x(t)cosn0tdt
bn
2 T0
T0/2 x(t)sinn
T0/2
0tdt
0
2
T0
三角展开式中
An an2 bn2 —— n次谐波的振幅；
tan n
Байду номын сангаас
an bn
—— n次谐波的振幅；
可见，周期信号是由一个或几个，乃至无穷多个不同频率的谐波叠
（2）寻找机器振动根源用时域描述还是频域描述？
频域描
述
第二节 周期信号与离散频谱
一、傅里叶级数的三角函数展开式
在有限区间内，凡满足狄里赫利条件的周期函数都可以展开成傅里叶级数。 周期性三角函数（如图1-6所示）
图1-6
15
傅立叶级数——任何周期信号在有限区间上，当其满足狄里赫利 条件时，都可展开成一系列正交函数的线性组合的无穷级数。 傅立叶级数有多种形式 三角展开式、复指数展开式是常见的形 式 傅立叶级数三角展开式
三角级数与指数级数并不是两种不同类型的级数，而只是同一 级数的两种不同的表示方法。指数级数形式比三角级数形式更简化 更便于计算。 根据欧拉公式
图1-4
11
用坐标图描述信号时，若横坐标为时间t，纵坐标为幅值的描述方 式称为时域描述。若横坐标为频率f(或圆频率ω)，则称为频域描述。 这时实际上也是将信号中的各频率成分按序排列，故称之为信号的“频 谱”。对横坐标为频率，纵坐标为幅值的称为幅频谱；而对横坐标为频 率，纵坐标为相位的称为相频谱，图为一个简谐信号的时域及幅频谱、 相频谱的图形。
图1-3
8
3.能量信号和功率信号
能量信号：当电压信号满足一定条件时,认为信号的能 量是有限的，并称之为能量有限信号。 功率信号：若信号在区间（- ∞ ， ∞ ）的能量是无 限的，但它在有限区间的平均功率是有限的,称为功率 有限信号。
x2(t)dt 1 t2 x2(t)dt
t2 t1 t1
9
信号
加而成的。
其中第一项a0是常值项，它是周期信号中所包含的直流分量；
第二项中 Ansin(n0tn)称为谐波，An是n次谐波的振幅，φn是
其初相角。
∑ 表示周期信号可以分解为各次谐波之和。
通常把ω0称为基频，n是整数序列，各次谐波成份的频率都是ω0的 整倍数。
相邻频率的间隔 △ω＝ω0＝2π/T0 。
确定性信号
周期信号
简单周期信号
非确定性信号
复杂周期信号
非周期信号
准周期信号
瞬变非周期信号
非平稳随机过程 平稳随机过程
个态历经随机过程
非个态历经随机过程
第一节 信号的分类与描述
二、信号的时域描述和频域描述
直接测试或记录到的信号，一般是以时间为独立变量的，称其为信号的 时域描述。如图1-4所示。
信号的时域描述能够反映 信号幅值随时间的变化关 系，但是不能明显揭示信 号的频率组成关系；因此 为了研究信号的频率结构 和各频率成分的幅值、相 位关系，应对信号进行频 谱分析，把信号的时域描 述通过适当方法变成信号 的时域描述，即以频率为 独立变量来表示信号。
瞬变非周期信号——在一定时间区间内存在，或随着时间的增长而衰减至 零的信号。
如有阻尼振动系统的位移信号、用锤子敲击 物体时的敲击力信号。图2-4是后者的波形， 其数学表达式为式
FAetsin t (0<t<τ)
2.连续信号和离散信号
连续信号：若信号数学表示式中的独立变量取值是连续的 离散信号：若独立变量取离散值
机械工程测试技术基础第一章
静态与动态测量比较
被测对象 单次测量结果 N次重复测量结果
静态测量
动态测量
静态量值
连续变化的动态量值
具体数值
具体函数（记录曲线）
随机变量(一组具体数值) 随机函数(一组具体函数)
第一节 信号的分类与描述
一、信号的分类与描述
1.确定性信号与随机信号 确定性信号：信号可表为一个确定的时间函数，因而可 确定其任何时刻的量值； 随机信号：一种不能准确预测其未来瞬时值，也无法用 函数关系式来描述的信号，如汽车奔驰时产生的振动信 号、环境噪声等。 （1）周期信号 周期信号：是按一定时间间隔周而复始重复出现， 无始无终的信号。
信号时域波形
信号频域幅频谱
第一节 信号的分类与描述
二、信号的时域描述和频域描述
图1-5表示的周期方波的 时域图形、幅频谱和相频 谱三者之间的关系。
13
图1-5
信号的时域描述能够直观地反映信号瞬时值随时间的变换情况，
而频域描述则反映信号的频率组成及幅值、相位大小。
思考：
时域描 述
（1）评定机器振动烈度用时域描述还是频域描述？
的数值。
例如 集中参量的单自由度振动系统作无阻尼自由振动时，其位移x(t)
可由公式确定质点的瞬时位置
（2）非周期信号
确定信号中那些不具有周期重复性的信号称为非周期信号。
6
非周期信号——将确定性信号中那些不具有周期重复性的信号称为非周期 信号。包括准周期信号和瞬变非周期信号两种。 准周期信号：由有限个周期信号合成的，但各周期分量之间无法找到公共 周期，因而无法按某一时间间隔周而复始重复出现。 例如 x(t)sintsin 2t 是两个正弦信号的合成，其频率比 1/2 1/ ，2 不是有理数，不成谐波关系。
把x(t)展开成下式
f(t)A0 Ansin(n0tn) n1
展开过程如下：
x ( t) a 0 ( a n c o s n 0 t b n s in n 0 t)
n 1
式中 a0—常值分量 an—余弦分量的幅值 bn—正弦分量的幅值 T0—周期； ω0—圆频率， n＝1，2，3，…
a0
第二节 周期信号与离散频谱
一、傅里叶级数的三角函数展开式
19
第二节 周期信号与离散频谱
一、傅里叶级数的三角函数展开式
周期性三角波的频谱图如图1-7所示。
图1-7
20
第二节 周期信号与离散频谱
二、 傅里叶级数的复指数函数展开式
用正交函数集来表示周期信号，另一种常用的方法是傅立叶级 数的指数表示法，称为指数傅立叶级数。
如，单自由度振动系统
图1-1
3
周期信号——周期信号是定义在区间，每隔一定时间周而复始重复出 现的信号如图所示。
连续性的周期信号可表示为
x(t)=x(t+nT0)
(n=0,1，2，…)
离散性的周期信号可表示为
x(n)=x(n+mk)
(m=0, 1,2,…)
只要给出周期信号在任一周期的函数或波形，便可确知它在任一时刻