matlab自带优化工具箱遗传算法中文解释
- 格式:docx
- 大小:18.09 KB
- 文档页数:3

matlab遗传算法工具箱关于离散变量优化算例离散优化问题在实际应用中具有重要意义,其中遗传算法是一种常用的解决离散优化问题的方法。
Matlab遗传算法工具箱提供了一系列强大的函数和工具来帮助开发者实现离散变量优化算法。
本文将介绍如何使用Matlab遗传算法工具箱解决离散变量优化问题,并给出一个算例来演示其应用。
1. 算法背景离散优化问题是指在一组有限离散值中寻找最优解的问题。
这些离散值可能代表不同的决策或选择,例如在某个集合中选取最佳的元素组合。
传统的优化算法无法直接应用于离散变量优化问题,而遗传算法则具有较好的适应性。
遗传算法是一种模拟生物进化过程的优化算法,通过模拟基因的交叉、变异和选择来搜索最优解。
2. Matlab遗传算法工具箱简介Matlab遗传算法工具箱是Matlab平台上用于遗传算法优化设计和问题求解的工具包。
它提供了一系列函数和工具,可以简便地实现离散变量优化算法。
其中常用的函数包括:- ga:用于定义遗传算法的参数和问题函数,进行优化计算。
- gamultiobj:用于多目标优化的遗传算法。
- customSelectionFcn:自定义选择函数,用于指定选择操作。
- customCrossoverFcn:自定义交叉函数,用于指定交叉操作。
- customMutationFcn:自定义变异函数,用于指定变异操作。
3. 算例演示假设我们有一个离散优化问题,要在集合{1, 2, 3, 4, 5}中找到一个长度为5的序列,使得序列中所有元素的和最大。
首先,我们需要定义问题函数和适应度函数。
问题函数用于定义问题的约束条件,适应度函数则计算每个个体的适应度值。
```matlabfunction f = problemFunction(x)f = sum(x);endfunction f = fitnessFunction(x)f = -problemFunction(x); % 求和最大化,所以需要取负值end```接下来,我们可以使用Matlab遗传算法工具箱中的`ga`函数进行优化计算。

matlab遗传算法代码
1 、算法概述
遗传算法(Genetic Algorithms,GA)是一种仿生学优化算法,它借用遗传学中物
竞天择的进化规则,模拟“自然选择”与“遗传进化”得出选择最优解的过程。
其基本原
理是对现有的种群中的各个个体,将其表示成某种形式的编码,然后根据自变量与约束条件,利用杂交、变异等操作,产生新一代解的种群,不断重复这一过程,最终求出收敛到
最优解的种群。
2、遗传算法的作用
遗传算法的主要作用在于优化多元函数,能够在大量的变量影响目标函数值的情况下
寻求最优解。
和其它现有的数值优化技术比较,如梯度下降法等,遗传算法更能适应“凸”和“非凸”都能解决,不受约束条件与搜索空间的影响较大,又叫做“智能搜索法”。
在
计算机视觉等计算机技术领域,经常用遗传算法来对一系列特征参数进行搜索和调节,成
功优化提高了系统的正确处理率。
3、matlab遗传算法的实现
Matlab的遗传算法应用是基于GA Toolbox工具箱,它提供了一个功能强大的、可扩
展的包装器,可用于构建遗传算法模型。
(1)编写最优化函数:
使用和设置最优化表达式或函数、变量;
(2)设置参数编码:
设置变量的编码,比如选择0-1二进制、0-10十进制;
(3)选择遗传算法的方法
选择遗传算法的方法,可以在多个选择中选择,比如变异、杂交等;
(4)设置运算参数:
设置每代的种群数、最大进化的世代数;
(5)运行遗传算法:
根据设定的参数运行遗传算法,算出收敛到最优解的种群;
(6)获得最优解:
获得收敛到最优解的条件下的最优解,得出最优解所在位置等参数,完成整个优化搜索。

matlab遗传算法工具箱函数及实例讲解核心函数:(1)function [pop]=initializega(num,bo unds,eevalFN,eevalOps,optio ns)--初始种群的生成函数【输出参数】pop--生成的初始种群【输入参数】num--种群中的个体数目bo unds--代表变量的上下界的矩阵eevalFN--适应度函数eevalOps--传递给适应度函数的参数op tions--选择编码形式(浮点编码或是二进制编码)[p recision F_o r_B],如p recisio n--变量进行二进制编码时指定的精度F_or_B--为1时选择浮点编码,否则为二进制编码,由p recision指定精度)(2)function [x,endPop,bPop,trace Info] = ga(bounds,evalFN,evalOps,sta rtPop,op ts,...te rmFN,te rmOps,selectFN,selectOps,xOve rFNs,xOve rOps,mutFNs,mutOps)--遗传算法函数【输出参数】x--求得的最优解e ndPop--最终得到的种群bPop--最优种群的一个搜索轨迹【输入参数】bo unds--代表变量上下界的矩阵evalFN--适应度函数evalOps--传递给适应度函数的参数sta rtPop-初始种群op ts[epsilon p rob_ops display]--opts(1:2)等同于initializega的options参数,第三个参数控制是否输出,一般为0。
如[1e-6 1 0]te rmFN--终止函数的名称,如['maxGe nTerm']te rmOps--传递个终止函数的参数,如[100]selectFN--选择函数的名称,如['no rmGeo mSelect']selectOps--传递个选择函数的参数,如[0.08]xOve rFNs--交叉函数名称表,以空格分开,如['arithXover heuristicXove r simple Xove r'] xOve rOps--传递给交叉函数的参数表,如[2 0;2 3;2 0]mutFNs--变异函数表,如['boundaryMuta tio n multiNonU nifMuta tio n nonU nifMutatio n unifMuta tion']mutOps--传递给交叉函数的参数表,如[4 0 0;6 100 3;4 100 3;4 0 0]注意】matlab工具箱函数必须放在工作目录下【问题】求f(x)=x+10*sin(5x)+7*cos(4x)的最大值,其中0<=x<=9【分析】选择二进制编码,种群中的个体数目为10,二进制编码长度为20,交叉概率为0.95,变异概率为0.08【程序清单】%编写目标函数functio n[sol,eval]=fitness(sol,op tio ns)x=sol(1);eval=x+10*sin(5*x)+7*cos(4*x);%把上述函数存储为fitness.m文件并放在工作目录下initPop=initializega(10,[0 9],'fitness');%生成初始种群,大小为10[x e ndPop,bPop,trace]=ga([0 9],'fitness',[],initPop,[1e-6 1 1],'ma xGenTerm',25,'no rmGeo mSelect',...[0.08],['arithXove r'],[2],'no nU nifMuta tio n',[2 25 3]) %25次遗传迭代运算借过为:x =7.8562 24.8553(当x为7.8562时,f(x)取最大值24.8553)注:遗传算法一般用来取得近似最优解,而不是最优解。

【分享】matlab遗传算法工具箱函数及实例讲解[i=s] 本帖最后由messenger 于2009-10-14 11:09 编辑[/i]核心函数:(1)function [pop]=initializega(num,bounds,eevalFN,eevalOps,options)--初始种群的生成函数【输出参数】pop--生成的初始种群【输入参数】num--种群中的个体数目bounds--代表变量的上下界的矩阵eevalFN--适应度函数eevalOps--传递给适应度函数的参数options--选择编码形式(浮点编码或是二进制编码)[precision F_or_B],如precision--变量进行二进制编码时指定的精度F_or_B--为1时选择浮点编码,否则为二进制编码,由precision指定精度) (2)function [x,endPop,bPop,traceInfo] =ga(bounds,evalFN,evalOps,startPop,opts,...termFN,termOps,selectFN,selectOps,xOverFNs,xOverOps,mutFNs, mutOps)--遗传算法函数【输出参数】x--求得的最优解endPop--最终得到的种群bPop--最优种群的一个搜索轨迹【输入参数】bounds--代表变量上下界的矩阵evalFN--适应度函数evalOps--传递给适应度函数的参数startPop-初始种群opts[epsilon prob_ops display]--opts(1:2)等同于initializega的options 参数,第三个参数控制是否输出,一般为0。
如[1e-6 1 0]termFN--终止函数的名称,如['maxGenTerm']termOps--传递个终止函数的参数,如[100]selectFN--选择函数的名称,如['normGeomSelect']selectOps--传递个选择函数的参数,如[0.08]xOverFNs--交叉函数名称表,以空格分开,如['arithXover heuristicXover simpleXover']xOverOps--传递给交叉函数的参数表,如[2 0;2 3;2 0]mutFNs--变异函数表,如['boundaryMutation multiNonUnifMutation nonUnifMutation unifMutation']mutOps--传递给交叉函数的参数表,如[4 0 0;6 100 3;4 100 3;4 0 0]matlab遗传算法工具箱回复:【分享】matlab遗传算法工具箱函数及实例讲解[i=s] 本帖最后由messenger 于2009-5-18 16:10 编辑[/i]【注意】matlab工具箱函数必须放在工作目录下【问题】求f(x)=x+10*sin(5x)+7*cos(4x)的最大值,其中0<=x<=9【分析】选择二进制编码,种群中的个体数目为10,二进制编码长度为20,交叉概率为0.95,变异概率为0.08【程序清单】%编写目标函数function[sol,eval]=fitness(sol,options)x=sol(1);eval=x+10*sin(5*x)+7*cos(4*x);%把上述函数存储为fitness.m文件并放在工作目录下initPop=initializega(10,[0 9],'fitness');%生成初始种群,大小为10[x endPop,bPop,trace]=ga([0 9],'fitness',[],initPop,[1e-6 11],'maxGenTerm',25,'normGeomSelect',...[0.08],['arithXover'],[2],'nonUnifMutation',[2 25 3]) %25次遗传迭代运算结果为:x =7.8562 24.8553(当x为7.8562时,f(x)取最大值24.8553)注:遗传算法一般用来取得近似最优解,而不是最优解。

1. 引言遗传算法是一种模拟自然选择与遗传机制的优化算法,被广泛应用于离散变量优化问题的求解。
在Matlab软件中,有专门的工具箱可以支持遗传算法的实现与应用,极大地方便了工程技术人员进行离散变量优化问题的研究与应用。
本文将介绍Matlab遗传算法工具箱在离散变量优化算例中的应用,并通过具体案例来展示其实际求解效果。
2. Matlab遗传算法工具箱介绍Matlab遗传算法工具箱是Matlab软件的一个重要工具箱,它提供了丰富的遗传算法函数和工具,方便用户进行遗传算法的实现和应用。
在离散变量优化问题的求解中,用户可以利用工具箱提供的函数对问题进行建模、参数设置、运行算法等操作,从而快速高效地求解问题。
3. 离散变量优化算例为了更好地展示Matlab遗传算法工具箱在离散变量优化中的应用效果,我们选取了一个经典的离散变量优化问题作为算例,具体问题描述如下:设有一组零件需要进行装配,零件的形状和尺寸有多种选择。
每种零件的装配工艺和成本不同,需要选择最佳的零件组合方案来满足装配要求并使总成本最低。
假设可供选择的零件种类有n种,每种零件有m个备选方案,且装配每种零件的成本已知。
问应选择哪些零件及其具体方案才能使得总装配成本最低?4. Matlab遗传算法工具箱的应用为了利用Matlab遗传算法工具箱求解上述离散变量优化问题,我们可以按照以下步骤进行操作:1) 利用Matlab的数据处理工具,将零件的备选方案数据以矩阵的形式导入Matlab环境;2) 利用工具箱提供的函数对遗传算法的参数进行设置,例如选择交叉方式、变异方式、群体大小、迭代次数等;3) 利用工具箱提供的函数对离散变量优化问题进行编码和解码,以便算法能够对离散变量进行操作;4) 利用工具箱提供的函数编写适应度函数,用于评价每个个体的适应度;5) 利用工具箱提供的主函数运行遗传算法,获取最优解及其对应的总装配成本。
5. 案例求解结果分析通过上述步骤,我们在Matlab环境中成功应用遗传算法工具箱求解了离散变量优化问题。

遗传算法 Matlab什么是遗传算法?遗传算法是一种模拟生物进化过程的优化算法。
它模拟了自然界中的遗传、突变和选择等过程,利用这些操作来搜索和优化问题的解空间。
遗传算法具有以下几个关键步骤:1.初始化种群:通过生成一组随机解来初始化初始种群。
每个解被编码为一个染色体,染色体通常由二进制字符串表示。
2.评价适应度:使用适应度函数评估每个个体的适应度。
适应度函数通常通过衡量个体在解空间中的性能来定义。
3.选择操作:选择操作基于个体的适应度进行,通过概率选择操作来确定哪些个体应该参与繁殖下一代。
适应度较高的个体有更大的概率被选中。
4.交叉操作:选择的个体进行交叉操作,生成下一代的染色体。
交叉操作通过交换个体染色体中的信息来生成新的个体。
5.变异操作:为了保持种群的多样性,变异操作在染色体中进行随机的变异。
这个过程通过随机改变染色体中的部分基因来进行。
6.替换操作:根据新生成的染色体替换当前种群中某些个体,以此来形成新的种群。
7.重复上述步骤:重复执行上述步骤直到满足终止条件(例如达到最大迭代次数或找到满意的解)。
如何在 Matlab 中实现遗传算法?在 Matlab 中,可以使用遗传算法和优化工具箱来实现遗传算法。
以下是实现遗传算法的一般步骤:1.定义适应度函数:根据具体问题定义适应度函数,该函数衡量每个个体在解空间中的性能。
适应度函数的设计将影响到最终结果。
2.初始化种群:使用内置函数或自定义函数来生成初始种群。
每个个体都应该表示为染色体形式的解。
3.设置遗传算法参数:根据具体问题设置遗传算法的参数,如种群大小、迭代次数、选择操作和交叉操作的概率等。
4.编写遗传算法主循环:在主循环中,使用选择操作、交叉操作和变异操作来生成新的染色体,并计算每个个体的适应度。
5.选择操作:使用选择函数根据适应度值选择染色体。
具体的选择函数可以根据问题的特点进行调整。
6.交叉操作:使用交叉函数对染色体进行交叉操作,生成下一代的染色体。

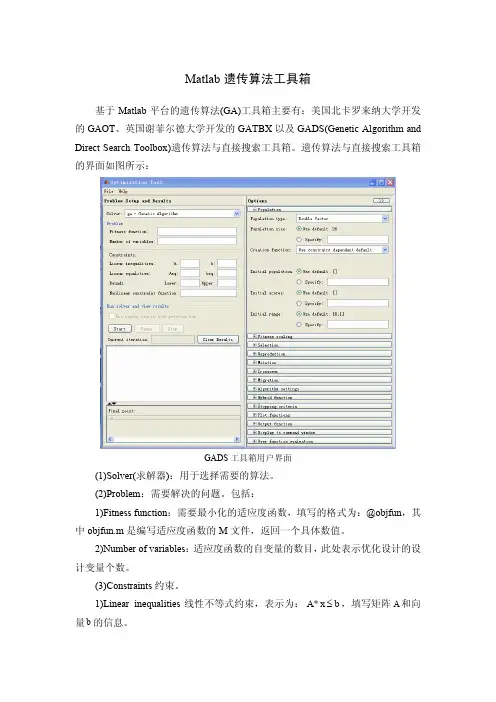
matlab自带优化工具箱遗传算法中文解释problem setup and results设置与结果problemfitness function适应度函数number of variable变量数constraints约束linear inequalities线性不等式,A*x<=b形式,其中A是矩阵,b是向量linear equalities线性等式,A*x=b形式,其中A是矩阵,b是向量bounds定义域,lower下限,upper上限,列向量形式,每一个位置对应一个变量nonlinear constraint function非线性约束,用户定义,非线性等式必须写成c=0形式,不等式必须写成c<=0形式integer variable indices整型变量标记约束,使用该项时Aeq和beq必须为空,所有非线性约束函数必须返回一个空值,种群类型必须是实数编码run solver and view results求解use random states from previous run使用前次的状态运行,完全重复前次运行的过程和结果populationpopulation type编码类型double vector实数编码,采用双精度bitstring二进制编码对于生成函数和变异函数,只能选用uniform和custom,对于杂交函数,只能使用scattered singlepoint,twopoint或custom不能使用hybrid function和nonlinear constraint functioncustom 自定义population size:种群大小creation function:生成函数,产生初始种群constraint dependent:约束相关,无约束时为uniform,有约束时为feasible population uniform:均匀分布feasible population :自适应种群,生成能够满足约束的种群initial population:初始种群,不指定则使用creation function生成,可以指定少于种群数量的种群,由creation function完成剩余的initial scores:初始值,如果不指定,则有计算机计算适应度函数作为初始值,对于整型约束不可用,使用向量表示initial range:初始范围,使用向量矩阵表示,第一行表示范围的下限,第二行表示上限fitness scaling:适应度尺度rank:等级。

matlab遗传算法种群初始化摘要:一、遗传算法简介二、MATLAB 中的遗传算法工具箱三、种群初始化方法在遗传算法中的应用四、结论正文:一、遗传算法简介遗传算法(Genetic Algorithm,GA)是一种模拟自然界生物进化过程的优化算法。
其主要思想是将进化过程中的种群、适应度函数、选择、交叉和变异等生物学概念引入到算法中,通过模拟这些生物学过程来寻找问题的最优解。
遗传算法具有较强的全局搜索能力,适用于解决复杂、非线性、非凸优化问题。
二、MATLAB 中的遗传算法工具箱MATLAB 提供了遗传算法工具箱(GA Toolbox),用户可以在MATLAB 中直接调用这个工具箱中的函数来实现遗传算法。
这个工具箱中包含了两个主要的函数:ga 和gaoptimset。
其中,ga 函数用于执行遗传算法,其语法如下:```matlab[x,fval] = ga(fitnessfcn,nvars,a,b,aeq,beq,lb,ub,nonlcon,options)```其中,fitnessfcn 表示适应度函数,nvars 表示变量个数,a 和b 分别表示交叉概率和变异概率,aeq 和beq 表示交叉和变异的约束条件,lb 和ub 表示变量范围的下界和上界,nonlcon 表示非线性约束条件,options 表示算法参数。
gaoptimset 函数用于设置遗传算法的参数,其语法如下:```matlabgaoptimset("param1",value1,"param2",value2,...)```其中,param1、value1 等表示需要设置的参数及其值。
三、种群初始化方法在遗传算法中的应用在遗传算法中,种群初始化是一个重要的步骤。
合理的种群初始化方法可以提高算法的收敛速度和搜索能力。
MATLAB 中的遗传算法工具箱提供了两种种群初始化方法:随机初始化和均匀初始化。

matlab遗传算法离散值
在MATLAB中,遗传算法(Genetic Algorithm,GA)可以用于解决离散值优化问题。
离散值优化问题是指变量的取值范围是离散的,而不是连续的。
下面我将从几个角度来解释如何在MATLAB中使用遗传算法来解决离散值优化问题。
首先,要使用MATLAB中的遗传算法来解决离散值优化问题,你需要定义适应度函数。
适应度函数的作用是根据给定的解(即染色体)计算其适应度值,这个值用来衡量解的优劣。
在离散值优化问题中,适应度函数的设计十分重要,它需要能够正确地评估离散解的质量。
其次,你需要定义变量的取值范围。
在离散值优化问题中,变量的取值范围是离散的,比如整数或者一组离散的选项。
在MATLAB 中,可以使用`gaoptimset`函数来定义变量的取值范围,以确保遗传算法搜索的解是合法的。
另外,遗传算法中的交叉和变异操作也需要针对离散值进行适当的设计。
在MATLAB中,可以使用`ga`函数来调用遗传算法求解离散值优化问题,并通过设置相应的参数来指定离散值变量的处理方
式。
最后,需要注意的是,离散值优化问题的求解可能会受到问题规模的限制。
对于大规模的离散值优化问题,遗传算法的求解效率可能会受到影响,因此需要合理设计算法参数和适应度函数,以提高求解效率。
综上所述,要在MATLAB中使用遗传算法求解离散值优化问题,需要合理设计适应度函数、定义变量取值范围、处理离散值的交叉和变异操作,并注意求解效率的问题。
希望这些信息能够帮助你更好地理解如何在MATLAB中应用遗传算法求解离散值优化问题。

智能优化算法及matlab实例1. Genetic Algorithm (遗传算法): 智能优化算法的一种,通过模拟自然选择和遗传机制来搜索问题的最优解。
在Matlab中,可以使用Global Optimization Toolbox中的gamultiobj和ga函数来实现遗传算法。
示例:matlab% 目标函数fitnessFunction = @(x) sum(x.^2);% 配置参数options = optimoptions('ga','Display','iter');% 运行遗传算法x = ga(fitnessFunction, 2, [], [], [], [], [], [], [], options);2. Particle Swarm Optimization (粒子群优化): 一种启发式优化算法,模拟鸟群或鱼群等群体行为来搜索最优解。
在Matlab中,可以使用Global Optimization T oolbox中的particleswarm函数来实现粒子群优化算法。
示例:matlab% 目标函数fitnessFunction = @(x) sum(x.^2);% 配置参数options = optimoptions('particleswarm','Display','iter');% 运行粒子群优化算法x = particleswarm(fitnessFunction, 2, [], [], options);3. Simulated Annealing (模拟退火): 一种基于概率的全局优化算法,模拟固体退火的过程来搜索最优解。
在Matlab中,可以使用Global Optimization Toolbox中的simulannealbnd函数来实现模拟退火算法。
示例:matlab% 目标函数fitnessFunction = @(x) sum(x.^2);% 配置参数options = optimoptions('simulannealbnd','Display','iter');% 运行模拟退火算法x = simulannealbnd(fitnessFunction, zeros(2,1), [], [], options);以上是三种常见的智能优化算法及其在Matlab中的实例。
遗传算法 matlab
遗传算法是一种基于生物进化原理的优化算法,通过模拟进化过程中的遗传和自然选择等机制,逐步搜索问题的最优解。
在Matlab 中,可以利用遗传算法工具箱(Genetic Algorithm Toolbox)来实现遗传算法。
首先,需要使用Matlab中的遗传算法工具箱,确保已经安装并加载该工具箱。
然后,定义问题的目标函数,即需要优化的函数。
接下来,设置遗传算法的参数,如初始种群大小、进化代数、交叉概率、变异概率等。
构建适应度函数,根据问题的具体要求,设置适应度函数的计算方式。
调用遗传算法工具箱中的函数,如ga()函数,来运行遗传算法。
其中,通过设定参数,可以设置遗传算法的运行方式,并获取最优解。
最后,对于遗传算法的结果进行处理和分析。
这是基本的遗传算法matlab 实现步骤,具体的实现可以根据不同的问题进行调整和优化。
利用Matlab进行遗传算法的优化1. 引言遗传算法是一种基于生物进化理论的优化算法,通过模拟遗传和进化的过程来寻找问题的最优解。
它在优化问题中具有广泛的应用,如工程设计、机器学习、数据挖掘等领域。
而Matlab作为一种强大的科学计算软件,提供了丰富的工具箱和函数,方便了遗传算法的实现和优化。
本文将介绍如何使用Matlab进行遗传算法的优化。
2. 遗传算法概述遗传算法模拟了生物进化的过程,通过选择、交叉和变异等操作来搜索最优解。
它具有以下几个特点:(1)群体思想:遗传算法通过维护一个候选解的群体,而不是一个解,从而增加了搜索空间的广度和深度。
(2)自适应性:遗传算法能够根据问题的不同自适应地调整参数和操作符的选择,从而更好地适应不同的优化问题。
(3)并行性:遗传算法中的操作都可以并行化执行,提高了算法的速度和效率。
3. Matlab遗传算法工具箱Matlab提供了一系列强大的遗传算法工具箱和函数,可以快速实现和优化遗传算法。
它包括了遗传算法和进化策略的相关函数,并提供了多种种群、选择、交叉和变异操作的实现方法。
同时,Matlab还提供了丰富的图形界面和可视化工具,方便用户进行参数调整和结果分析。
4. 遗传算法的实现步骤(1)问题建模:首先,需要将优化问题转化为适应度函数的最大化或最小化问题。
适应度函数的选择往往依赖于具体的优化问题,它是衡量候选解在问题中的适应程度的评价方法。
(2)初始化种群:生成一个初始的种群,种群中的个体是问题的候选解。
种群的大小和初始解的选择都会影响算法的搜索效果。
(3)选择操作:根据个体的适应度值,选择一部分个体作为新一代的父代。
常用的选择方法有轮盘赌选择、锦标赛选择等。
(4)交叉操作:通过交叉操作,将父代的基因信息混合在一起,生成新的孩子个体。
交叉操作可以增加新解的多样性。
(5)变异操作:变异操作通过随机改变个体的某些基因值来引入新的解。
变异操作可以增加解空间的探索能力。
matlab遗传算法求解曲面拟合和多参数优化Matlab遗传算法求解曲面拟合和多参数优化引言:曲面拟合和多参数优化是机器学习和数据挖掘领域中重要的问题。
曲面拟合是通过给定的数据点集,找到一个最合适的曲面模型以拟合这些数据。
而多参数优化是寻找多个参数的最佳取值,使得目标函数达到最大或最小。
遗传算法是一种启发式搜索算法,可以用来求解这类问题。
本文将介绍使用Matlab中的遗传算法工具箱来进行曲面拟合和多参数优化,并提供详细的步骤。
第一部分:曲面拟合曲面拟合的目标是通过给定的数据点集找到一个最佳曲面模型,以拟合这些数据。
在Matlab中,可以使用遗传算法工具箱来求解该问题。
下面是一步一步的操作:步骤1:导入数据和设置参数首先,需要导入拟合曲面所需的数据点集。
数据通常以矩阵的形式给出,其中每一行表示一个数据点的坐标。
除此之外,还需要设置遗传算法的一些参数,包括种群大小、迭代次数、交叉概率和变异概率等。
具体的参数设置根据具体问题而定。
步骤2:编写目标函数目标函数是遗传算法的核心,它用来评估每个个体的适应度。
在曲面拟合问题中,可以使用最小二乘法来定义适应度函数。
具体来说,可以计算每个个体拟合曲面与真实数据之间的误差,然后将这些误差累加起来作为适应度值。
步骤3:初始化种群通过随机生成一定数量的个体(即曲面模型的参数),可以初始化种群。
个体的参数可以根据实际问题设定,例如,对于二次方程的拟合,可以设置个体为三个参数:a、b、c。
步骤4:选择操作选择操作是指根据个体的适应度值选择下一代的个体。
在遗传算法中,常用的选择操作有轮盘赌选择、锦标赛选择和最佳选择等。
通过选择操作,可以保留适应度较高的个体,从而增加下一代的优势基因。
步骤5:交叉操作交叉操作是指通过交换个体的染色体片段来产生新的个体。
这个过程模拟了生物进化中的杂交行为。
在曲面拟合中,可以选择某个个体的参数与另一个个体的参数进行交换,得到一个混合的个体。
步骤6:变异操作变异操作是通过对个体的染色体进行随机改变来引入新的基因。
matlab遗传算法工具箱函数及实例讲解最近研究了一下遗传算法,因为要用遗传算法来求解多元非线性模型。
还好用遗传算法的工具箱予以实现了,期间也遇到了许多问题。
首先,我们要熟悉遗传算法的基本原理与运算流程。
基本原理:遗传算法是一种典型的启发式算法,属于非数值算法范畴。
它是模拟达尔文的自然选择学说和自然界的生物进化过程的一种计算模型。
它是采用简单的编码技术来表示各种复杂的结构,并通过对一组编码表示进行简单的遗传操作和优胜劣汰的自然选择来指导学习和确定搜索的方向。
遗传算法的操作对象是一群二进制串(称为染色体、个体),即种群,每一个染色体都对应问题的一个解。
从初始种群出发,采用基于适应度函数的选择策略在当前种群中选择个体,使用杂交和变异来产生下一代种群。
如此模仿生命的进化进行不断演化,直到满足期望的终止条件。
运算流程:Step 1:对遗传算法的运行参数进行赋值。
参数包括种群规模、变量个数、交叉概率、变异概率以及遗传运算的终止进化代数。
Step 2:建立区域描述器。
根据轨道交通与常规公交运营协调模型的求解变量的约束条件,设置变量的取值范围。
Step 3:在Step 2的变量取值范围内,随机产生初始群体,代入适应度函数计算其适应度值。
Step 4:执行比例选择算子进行选择操作。
Step 5:按交叉概率对交叉算子执行交叉操作。
Step 6:按变异概率执行离散变异操作。
Step 7:计算Step 6得到局部最优解中每个个体的适应值,并执行最优个体保存策略。
Step 8:判断是否满足遗传运算的终止进化代数,不满足则返回Step 4,满足则输出运算结果。
其次,运用遗传算法工具箱。
运用基于Matlab的遗传算法工具箱非常方便,遗传算法工具箱里包括了我们需要的各种函数库。
目前,基于Matlab的遗传算法工具箱也很多,比较流行的有英国设菲尔德大学开发的遗传算法工具箱GATBX、GAOT以及Math Works公司推出的GADS。
在MATLAB中使用遗传算法进行优化1. 引言遗传算法是一种模仿自然界进化过程的优化方法,通过模拟基因的变异、交叉和选择等操作来优化问题的解。
在很多领域,特别是在复杂优化问题中,遗传算法被广泛应用。
而MATLAB作为一种强大的数值计算工具,提供了丰富的遗传算法工具箱,使得使用遗传算法进行优化变得更加便捷。
本文将介绍如何在MATLAB中使用遗传算法进行优化,包括优化问题定义、遗传算法参数设置、编写目标函数等方面的内容。
2. 优化问题定义在使用遗传算法进行优化之前,首先需要明确优化问题的定义。
优化问题通常可以形式化为一个目标函数的最大或最小化问题。
目标函数可以是连续的、多元的,也可以是离散的。
例如,我们希望寻找一个n维向量x=[x1, x2, ..., xn],使得目标函数f(x)达到最小值。
在定义了优化问题之后,我们就可以开始在MATLAB中使用遗传算法进行求解了。
3. 遗传算法参数设置在使用遗传算法进行优化时,需要设置一些参数来指导算法的执行过程。
常用的参数包括种群大小、交叉概率、变异概率等。
种群大小决定了算法的搜索空间,通常设置为一个较大的值以增加搜索的广度和深度。
交叉概率决定了交叉操作的发生概率,较高的交叉概率可以增加种群的多样性,但也可能导致搜索过早收敛。
变异概率决定了变异操作的发生概率,适当的变异概率可以有效地避免算法陷入局部最优解。
在MATLAB中,可以通过设置遗传算法工具箱中的相应参数来进行参数设置。
例如,可以使用"gaoptimset"函数来设置种群大小、交叉概率和变异概率等参数。
同时,还可以设置其他的优化参数,例如迭代次数、停止条件等。
4. 编写目标函数在使用遗传算法进行优化时,需要编写目标函数来评估每个个体的适应度。
目标函数的定义取决于具体的优化问题。
一般来说,目标函数应当满足以下几个条件:具有确定的输入和输出;可计算;连续可微(对于连续优化问题);单调性或有界性。
matlab自带优化工具箱遗传算法中文解释
problem setup and results设置与结果
problem
fitness function适应度函数
number of variable变量数
constraints约束
linear inequalities线性不等式,A*x<=b形式,其中A是矩阵,b是向量
linear equalities线性等式,A*x=b形式,其中A是矩阵,b是向量
bounds定义域,lower下限,upper上限,列向量形式,每一个位置对应一个变量
nonlinear constraint function非线性约束,用户定义,非线性等式必须写成c=0形式,不等式必须写成c<=0形式
integer variable indices整型变量标记约束,使用该项时Aeq和beq必须为空,所有非线性约束函数必须返回一个空值,种群类型必须是实数编码
run solver and view results求解
use random states from previous run使用前次的状态运行,完全重复前次运行的过程和结果
population
population type编码类型
double vector实数编码,采用双精度
bitstring二进制编码对于生成函数和变异函数,只能选用uniform和custom,对于杂交函数,只能使用
scattered singlepoint,twopoint或custom不能使用hybrid function和nonlinear constraint function
custom 自定义
population size:种群大小
creation function:生成函数,产生初始种群
constraint dependent:约束相关,无约束时为uniform,有约束时为feasible population uniform:均匀分布
feasible population :自适应种群,生成能够满足约束的种群
initial population:初始种群,不指定则使用creation function生成,可以指定少于种群数量的种群,由creation function完成剩余的
initial scores:初始值,如果不指定,则有计算机计算适应度函数作为初始值,对于整型约束不可用,使用向量表示
initial range:初始范围,使用向量矩阵表示,第一行表示范围的下限,第二行表示上限
fitness scaling:适应度尺度
rank:等级。
将适应度排序,然后编号
proportional:按比例
top:按比例选取种群中最高适应度的个体,这些个体有等比例的机会繁衍,其余的个体被淘汰
shift linear:线性转换
custom:用户定义
selection(selection function)依据适应值选择父代
stochastic uniform:随机均匀分布
remainder:残余,取适应值的整数部分进行轮盘赌选择
uniform:不是一个好方法,但是可以用来做测试
shift linear:线性转换
roulette:轮盘赌算法
tournament:联赛选择算法
custom:自定义
reproduction复制,决定如何产生子代
elite count:精英数,直接传到下一代的个体数
crossover fraction:杂交概率
mutation(mutation function)突变
use constraint dependent 默认,与约束有关,无约束时使用gaussian有约束时使用adaptive feasible
gaussian :利用高斯分布来选取
uniform:均匀
adaptive feasible:
custom:自定义
crossover杂交
scattered:随机生成遗传二进制向量,按0-1杂交
single point:单点杂交,生成一个数字,该数字代表的位置开始两父代基因交换
two point:两点交换
intermediate:媒介,加权平均
heuristic:启发式算法
arithmetic:算术平均
custom:自定义
migration迁移
direction方向:forward n-》n+1 ;both 双向
fraction:指定迁移率,以较小数量种群为标准
interval:发生迁移的间隔
constraint parameters约束参数,对应于非线性约束求解器
initial penalty:初始罚函数大于等于1
penalty factor:处罚因子大于等于1
hybrid function混合函数,指定另外一个最小值函数,在遗传算法结束之后计算,在整数值限制的时候不可用。
none
fminsearch只用于无约束
patternsearch约束与无约束
fminunc无约束
fmincon有约束
stopping criteria停止标准
generations到达代数
time limit时间限制
fitness limit适应值限制
stall generations迟滞代数,经过多代适应值没有明显提升
stall time limit 迟滞时间限制,经过限定时间适应值没有明显提升
function tolerance 在迟滞代数内适应度函数值的改变量小于这个值,则停止
nonlinear constraint tolerance 非线性约束容忍值
plot function 绘图函数
plot interval 绘图间隔
best fitness最佳适应度值
best individual最佳个体
distance个体间平均距离
expectation期望
genealogy家系
range适应度值最小最大平均值
score diversity每一代分数的柱状图
scores每一代个体的分数
selection 描绘对每一代贡献的父代
stopping停止标准的水平
max constraint非线性约束中超出范围的最大值
custom自定义
output function输出函数自定义
display to command window
off不输出
iterative每一次迭代都输出
diagnose诊断,每一次迭代都输出,并且诊断问题信息和选项中相对于默认值的改变值final只输出最终值
evaluate fitness and constraint functions评价适应度和约束函数
in serial 分别独立评价
vectorized用同一个函数调用。