切割立体投影
- 格式:pdf
- 大小:3.66 MB
- 文档页数:93



浅谈机械制图中切割体类型“投影”原理摘要:组合体“三视图”绘制是机械制图中重要的内容,切割体类型占据组合体的比例较大,其三视图绘制显得更为重要。
本文从“投影面积叠加原理”方法,简单阐述该类图形的绘制原理。
关键词:机械制图教学投影面积叠加原理物体在光线照射下,在地面或墙壁上会产生影子。
正确理解投影原理,对绘制“三视图”有很大的帮助。
组合体“三视图”绘制是机械制图中重要的内容,切割体类型占据组合体的比例较大,其三视图绘制显得更为重要。
笔者从“投影面积叠加原理”方法,简单阐述该类图形的绘制原理。
一、切割体外观形状的效果图例图1所示一个长方形面积有几个不同形状面积相加得到相等形状、相等面积的图形。
无论8个图形在垂直位置升降到不同高度,其共同向下垂直投影面积相加后仍然等于其原来所在的长方形面积。
形状1、2、3、4等各图形尽管处于不同高度,但都与长方形图形平行,其各自投影面积分别反映对应空间图形的真实形状。
需要强调一点:长方形中分割的图形1、2、3、4等可以是不同数量与不同形状的图形,其实,切割体外观形状就是其上的长方形切割成不同形状后的效果。
但制图课不同于素描,不画阴影,不上色,只画阴影的封闭外轮廓线。
二、切割体三视图绘制的“投影”原理举一个典型的切割体三视图的绘制来阐述“投影”原理的具体运用,如图2所示。
1.主视图的“抄画”图形我们对照一下“三视图”和“轴测图”不难看出,“主视图”中①、②、③图形是“轴测图”从前边向后边投影(正投影)后各平面图形的真实形状,面积相加等于长方体正投影的长方形面积。
根据这一特点,在画“主视图”时,先画一个长方形,再在里边按照①、②、③真实形状“抄画”出各图形的真实形状,“抄画”图形符合学生的心里特点,比较实际,相对有趣味。
2.俯视图的“抄画”图形对于“俯视图”同样可以在对应长方形里边“抄画”出④、⑥、⑦各图形真实形状即可完成俯视图。
为什么不抄画⑤的形状呢?因为图形⑤是一个“正垂面”,它与水平“投影面”相交,其“投影”是相似形状,所以不能“抄画”,相似形状图形尺寸失真,不易画出。


第3章立体的投影电子教案:3.1 基本立体的投影基本立体可分为平面立体和曲面立体。
表面均为平面的基本立体称为平面立体。
常见的有棱柱、棱锥,如图3-1所示。
表面由曲面和平面或完全由曲面组成的基本立体称为曲面立体。
最常见的曲面立体是回转体,包括圆柱、圆锥、球、圆环等,如图3-2所示。
将基本体放在三投影面体系中进行投射时,为了画图、读图的方便,通常将其“放平,摆正”。
放平——就是让基本体的底面处于平行面位置。
摆正——是在放平的基础上,让其余各面尽可能处于平行面或垂直面位置。
在以后画组合体视图或零件图时也要遵循这个原则。
图3-1 平面立体图3-2曲面立体3.1.1 平面立体的投影及其表面取点在投影图上表示平面立体就是把组成立体的平面和棱线表示出来,然后判别其可见性,把看得见的棱线投影画成实线,看不见的棱线投影画成虚线。
1.棱柱(1) 棱柱的投影常见的棱柱有正四棱柱和正六棱柱,图3-3(a)所示一正六棱柱,由六个相同的矩形棱面和上下底面(正六边形)所围成。
将其放平摆正后,上、下底面为水平面,其水平投影反映实形,另外两面投影积聚为直线。
正六棱柱的六个棱面中,前后两个面是正平面,正面投影反映实形;其余四个棱面均为铅垂面。
如图3-3(b)所示,作图过程如图3-4所示。
(a)(b)图3-3正六棱柱的投影及表面取点图3-4 正六棱柱的画图方法和步骤棱柱的投影特性是:在与棱线垂直的投影面上的投影为一多边形,它反映棱柱上、下底面的实形;另两个投影都是由粗实线或虚线组成的矩形线框,它反映棱面的实形或类似形。
(2) 在棱柱表面上取点在棱柱表面上取点,其原理和方法与在平面内取点相同。
该例中正六棱柱的各个表面都处于特殊位置,因此在其表面上取点均可利用平面投影积聚性的原理作图,并判别其可见性,如图3-3(b)所示。
2.棱锥(1) 投影分析和画法常见的棱锥有正三棱锥和正四棱锥,图3-5(a)所示为一正三棱锥,锥顶为S,其底面为等边△ABC,是水平面。


立体几何中的投影与切割一、投影的概念与分类1.投影的定义:在立体几何中,将一个物体在某一平面上的影子称为投影。
a)正投影:物体垂直于投影平面的投影称为正投影。
b)斜投影:物体不垂直于投影平面的投影称为斜投影。
c)中心投影:以物体为中心,将物体在各个方向上的投影称为中心投影。
二、投影的基本性质与规律1.平行性:在同一投影面上的投影,平行线在投影后仍然是平行线。
2.相似性:在同一投影面上的投影,物体与其投影之间具有相似关系。
3.积聚性:在同一投影面上的投影,物体的面积与投影面积成比例。
4.相互性:在同一投影面上的两个物体的投影,相互之间存在一定的关系。
三、切割的概念与分类1.切割的定义:在立体几何中,将一个物体沿某一平面分割成两部分的过程称为切割。
a)水平切割:切割平面与物体的水平面平行。
b)垂直切割:切割平面与物体的垂直面平行。
c)斜切割:切割平面与物体的水平面和垂直面都不平行。
四、切割的基本性质与规律1.切割线与物体表面的关系:切割线与物体表面相交,且切割线两侧的物体表面具有相似性。
2.切割面的性质:切割面与物体表面相交,形成的交线称为切割线。
3.切割体积:切割过程中,物体体积的变化与切割平面和切割线的关系有关。
五、投影与切割在立体几何中的应用1.计算物体体积:通过投影与切割,可以将立体几何物体转化为平面几何问题,从而简化计算。
2.求解物体表面积:利用投影与切割,可以将复杂立体几何物体的表面积分解为简单图形的面积之和。
3.几何作图:在立体几何作图中,投影与切割可以帮助我们更好地理解物体形状和结构。
六、注意事项1.在学习立体几何中的投影与切割时,要注重理论知识与实际操作相结合。
2.熟练掌握投影与切割的基本性质和规律,提高解题能力。
3.培养空间想象能力,更好地理解和应用投影与切割在立体几何中的作用。
习题及方法:1.习题:一个长方体沿着其长度方向进行切割,切割平面与长方体的底面平行。
求证切割后的两部分体积之比为1:1。

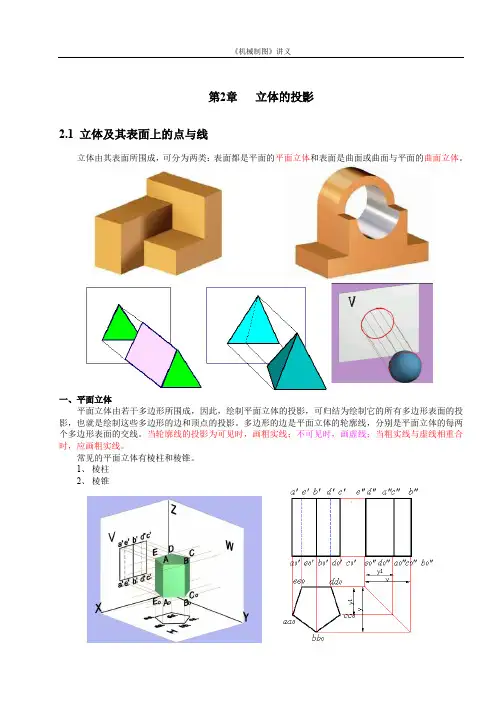
第2章立体的投影2.1 立体及其表面上的点与线立体由其表面所围成,可分为两类:表面都是平面的平面立体和表面是曲面或曲面与平面的曲面立体。
一、平面立体平面立体由若干多边形所围成,因此,绘制平面立体的投影,可归结为绘制它的所有多边形表面的投影,也就是绘制这些多边形的边和顶点的投影。
多边形的边是平面立体的轮廓线,分别是平面立体的每两个多边形表面的交线。
当轮廓线的投影为可见时,画粗实线;不可见时,画虚线;当粗实线与虚线相重合时,应画粗实线。
常见的平面立体有棱柱和棱锥。
1、棱柱2、棱锥平面立体的投影的外围轮廓总是可见的,应画粗实线;而在投影的外围轮廓内部的图线,则应根据线、面的投影分析,按前遮后、上遮下、左遮右直接判断投影的可见性,决定画粗实线或虚线,必要时还可利用交叉两直线的重影点的可见性进行判断。
二、曲面立体曲面立体由曲面或曲面与平面所围成。
有的曲面立体有轮廓线,即表面之间的交线,如圆柱;有的曲面立体有尖点,如圆锥;有的曲面立体全部由光滑的曲面所围成,如圆球。
在画曲面立体的投影时,除了画出轮廓线和尖点外,还要画出曲面投影的转向轮廓线。
曲面立体的转向轮廓线是切于曲面的诸投射线与投影面的交点的集合,也就是这些投射线所组成的平面或柱面与曲面的切线的投影,常常是曲面的可见投影和不可见投影的分界线。
曲面立体的投影就是它的所有曲面表面或曲面表面与平面表面的投影,也就是曲面立体的轮廓线、尖点的投影和曲面投影的转向轮廓线。
常见的曲面立体有圆柱、圆锥、圆球,圆环。
1、圆柱圆柱由圆柱面、顶面和底面所围成。
圆柱面由直线绕与它平行的轴线旋转而成。
因此,画圆柱的投影就是画顶面和底面及轮廓线、圆柱面投影的转向轮廓线、轴线。
当圆柱的轴线与投影面垂直时,圆柱面在轴线垂直的投影面上的投影具有积聚性。
因此,作圆柱表面2、 圆锥圆锥由圆锥面和底面所围成。
圆锥面由直线绕与它相交的轴线旋转而成。
因此,画圆锥的投影就是画尖点(即锥顶)、底面及轮廓线、圆锥面投影的转向轮廓线、轴线。

第五章 平面与立体相交顶尖球阀芯三通管南京大学环境学院盖1第五章 平面与立体相交§1 截交线 §2 平面和曲面相交2南京大学环境学院第一节 截交线截切: 用一个平面与立体相交,截去立体的一部分。
• 截平面 —— 用以截切物体的平面。
• 截交线 —— 截平面与物体表面的交线。
• 截断面 —— 因截平面的截切,在物体上形成的平面。
讨论的问题:截交线的分析和作图 。
3南京大学环境学院平面立体的截交线一、平面截切的基本形式截断面 截交线截平面截交线与截断面4南京大学环境学院截交线的性质:• 截交线是一个由直线组成的封闭的平面多边形,其 形状取决于平面立体的形状及截平面相对平面立体 的截切位置。
•平面立体的截交线是一个多边形,它的顶点是平 面立体的棱线或底边与截平面的交点。
截交线的每 条边是截平面与棱面的交线。
求截交线的实质是求两平面的交线 • 共有性:截交线既属于截平面,又属于立体表面。
5南京大学环境学院二、求截交线的方法与步骤关键是正确地画出截交线的投影。
⒈ 求截交线的两种方法:★ 求各棱线与截平面的交点→棱线法。
★ 求各棱面与截平面的交线→棱面法。
⒉ 求截交线的步骤: ★ 空间及投影分析☆ 截平面与体的相对位置确定截交 线的形状☆ 截平面与投影面的相对位置★ 画出截交线的投影分别求出截平面与棱面的交 线,并连接成多边形。
南京大学环境学院确定截交线 的投影特性6例1、求如图所示三棱锥被正垂面所截切,求作截交线的 水平投影和侧面投影。
截交线空间及投 截交线的正面投影 影分析:水平投影和侧面 投影是小于原形 的类似形截平面是正垂面, 截交线在正立面内 积聚为一线截平面截交线空间是三边形南京大学环境学院7s’ Pv 3’2’s”3” 2”具体步骤如下:(1) 求Pv与s’a’、s’b’、s’c’ 的交点1’、2’、3’为截平面与各棱线的交点Ⅰ、Ⅱ、1’1”Ⅲ的正面投影。
a’b’c’ c” a”b”(2) 根据线上取点的方法, 求出1、2、3和1”、2”、3”。
3 1s2(3) 连接各点的同面投影 即等截交线的三个投影。
(4) 补全棱线的投影。
平面与三棱锥相交8南京大学环境学院例2 求做立体被截切后的投影1’ 2’3’(4’)1”4”3”4 2139南京大学环境学院例3:求四棱锥被截切后的水平和侧面投影1′ (4′)2′ 3′1″4″ 2″ ●●●● 3″★ 空间分析4 ●31●●2●★截投交平线影面的分与形体析状的? ★ 求截几截交个交线棱线在面H相、交V ? ★ 分析面棱上线的的形投状影?★ 检查 尤其注意检查截 交线投影的类似性10南京大学环境学院我们采用的是 哪种解题方法?棱线法!11南京大学环境学院例4:求四棱锥被截切后的俯视图和左视图。
1′(2′)2●″1●″注意:2要逐三个面截共平点面:分析和 绘制Ⅰ截、交Ⅱ线两。
点当分平面别体只1有局同部时被位截于切三时个,先面假想为整上体。
被截切,求出截交线后再取局部。
12南京大学环境学院13南京大学环境学院14南京大学环境学院例5 试求正四棱锥被两平面切割后的三面投影7' 6'(8')1'(2') 4' 5' (3')空间分析:四棱锥被水平面切割, 截交线应是平面多边形 ,其水平投影反映实形 。
侧面投影是一条线。
空间分析:四棱锥被正垂面切割, 截交线也应是平面多边 形,其正面投影积聚为 一条线,水平投影侧面 投影小于实形的类似形 。
15南京大学环境学院例5 试求正四棱锥被两平面切割后的三面投影s's"作图步骤:7'7"四棱锥表面上取6'(8')8"截交线的各顶点6"1. 找出有积聚性的投影2. 确定截平面的特点1' a'(2') 4' 2"5' (3') b'd 2 c' c"3" 4" 5",数量。
1" a" (d " )3. 各棱线的交点b" 1,2,3,4,5,6,7,8。
3. 用线上取点的方法83a 1 7sc求得其余各投影。
4. 连接棱面上的交线并判断可见性。
64516b南京大学环境学院多线擦除完成作图:1.将各点连成线 2.检查漏线和多线 3.判断可见性注意不可见的线17南京大学环境学院例6 试求正四棱柱被两平面切割后的三面投影如图所示 , 四棱柱中间的切槽是由两个侧平面和 一个水平面切割而成。
平面Ⅰ为侧平面,它与四棱 柱侧面的交线为两条铅垂线 AA1,BB1。
ⅠA平面Ⅱ为一水平面,它与 四棱柱侧面和侧平面的交线共 同围成一六边形。
作图时 , 先作反映切口特 征且具有积聚性的正面投影 , 然后补画其它两面投影。
B ⅡA1B118南京大学环境学院南京大学环境学院ⅠAB ⅡA1B119例7 求四棱柱被截切截交线的投影。
侧平面6(' 7 ' )7" 6"(5 ' )4'5" 4"(3 ' )2'3"分析:1. 平面立体形体表 面性质 的分析(积聚性)2. 截平面相对投影面的位置2" 3.(平行,垂直) 截交线的空间分析及投影分析(积聚性)侧平面1'1"3 5(7)作图:正垂面4. 求棱线的交点 连线或求棱面的交线 ( 线上取点或1棱面上取线)4(6)5. 检查漏线和多 线 ..26. 判断可见性.20南京大学环境学院例8:求六棱柱被截切后的水平投影和侧面投影(1 )׳2 ׳(3) ׳4 ׳3״1 ״2״(5)׳ 6׳7׳5״ 7״4״作图方法:1 求棱线与截平面 的共有点6״2 连线3 根据可见性处理轮廓线5 763 12 421南京大学环境学院22南京大学环境学院例9 补全俯视图和左视图的投影1’ 2’(3’)4’(5’) 6’(7’)1”3”2”5”4”6”7”6 723南京大学环境学院例 10: 求正四棱台被两平面切割后的三面投影。
如图所示 , 四棱台中间的切槽是由两个侧平面和一个水平面切割而成。
Ⅰ平面Ⅰ为侧平面 , 它与前、Ⅱ后棱面的交线为等腰梯形的两腰。
平面Ⅱ为一水平面 , 它与 各棱面的交线成一矩形。
24南京大学环境学院ⅠⅡYHYW(1) 作基本体四棱台的三面投影 (2) 作切口的积聚性投影 (3) 补画切槽的侧面投影 (4) 补画切槽的水平投影 (5) 擦去被切割掉的轮廓线,判别可见性25南京大学环境学院例 11: 正四棱台被两平面切割,求三面投影。
a1`` b1``a`` b``a1b1Cc ba南京大学环境学院BA26例 12: 求八棱柱被平面P截切后的俯视图。
P′ 4′≡5′2′≡3′≡6′≡7′1′≡8′875 63 4125″ 7″8″6″ 3″4″ⅤⅣ2″ ⅦⅥ1″ ⅧⅢ ⅡⅠ截截特分投求检线交性交析影线截查 的?线棱的的交截投线形投线交影的状影?27南京大学环境学院28南京大学环境学院第二节 平面和曲面相交一、回转体截切的基本形式截交线截平面截平面截交线29南京大学环境学院截交线的性质:• 截交线是截平面与回转体表面的共有线。
• 截交线的形状取决于回转体表面的形状及截平面与回转体轴线的相对位置。
• 截交线都是封闭的平面图形。
30南京大学环境学院二、求平面与回转体的截交线的一般步骤⒈ 空间及投影分析☆ 分析回转体的形状以及截平面与回转体轴线 的相对位置,以便确定截交线的形状。
☆ 分析截平面与投影面的相对位置,明确截交 线的投影特性,如积聚性、类似性等。
找出 截交线的已知投影,预见未知投影。
⒉ 画出截交线的投影当截交线的投影为非圆曲线时,其作图步骤为: ☆ 先找特殊点,补充中间点。
☆ 将各点光滑地连接起来,并判断截交线的可见性。
31南京大学环境学院㈠ 平面与圆柱的交线矩形圆南京大学环境学院椭圆3220截平面与圆柱面的截交线的形状取决于截 平面与圆柱轴线的相对位置PVPV PVP垂直 圆PP倾斜 椭圆南京大学环境学院平行 两平行直线33平面和圆柱截交的三视图截平面位置:垂直于轴线 截交线形状:圆第一类 PPP⊥轴线截交线为圆P⊥轴线34南京大学环境学院截平面位置:倾斜于轴线截交线形状:椭圆P第二类PP斜交轴线截交线为椭圆35南京大学环境学院截平面位置:平行于轴线 截交线形状:矩形P第三类PP //轴线截交线为矩形36南京大学环境学院圆柱截交线示例37南京大学环境学院求圆柱截交线上点的方法 表面取点法:在圆柱表面取若干素线,并求出这些素线与截 平面的交点;当圆柱的轴线处于特殊位置时, 可利用圆柱的积聚性投影直接求得截交线上点 的投影38南京大学环境学院例9、如图所示,圆柱被正垂面截切,求出截交线的另 外两个投影。
5’5”具体由步于骤平如面下与:圆柱的轴线4’ 6” 4”斜交,因此截交线为一椭圆。
截((交2134)))线先再将 补的作作这全正出出些侧面截适点面投交当的投影线数投影重上量影中影的依为一3’7”(7)’3” 直的特次线一殊光转,般点滑向水点。
的轮平。
连廓投接线影起。
与来圆。
柱面的2’8” 2”投影重影为圆。
侧面投影可1’1”根据圆柱表面取点的方法求出。
786ⅥⅤ15ⅦⅣ243 平面与圆柱相交Ⅲ Ⅷ ⅠⅡ39南京大学环境学院比较不同角度的正垂面截交圆柱所得的截交线的投影。
α﹥45°α﹤45° 平面与圆柱相交南京大学环境学院α=45°40例10:求左视图虚实分界点41南京大学环境学院42南京大学环境学院在形状较为复杂的机件上,有时会见到由平面与曲面立 体相交而形成的具有缺口的曲面立体和穿孔的曲面立体,只 要逐个作出各个截平面与曲面立体的截交线,并画出截平面 之间的交线,就可以作出这些曲面立体的投影图。
43南京大学环境学院例题11 求圆柱截交线3' 4'5'3" 5"1'2'2"2 53解题步骤4"1.分析侧面投影为圆的一部分,截 交线的水平投影为椭圆的一部分;1" 2.求出截交线上的特殊点Ⅰ、Ⅱ、Ⅲ;3.求出若干个一般点Ⅳ、 Ⅴ ;4.光滑且顺次地连接各点,作出截 交线,并且判别可见性;5 整理轮廓线。
414342南京大学环境学院例题12 求圆柱截交线1'2'2"3'4'4"241" 3"解题步骤1.分析 截交线的水平投 影为直线和部分圆,侧面 投影为矩形;2.求出截交线上的特殊点 Ⅰ、Ⅱ、Ⅲ、Ⅳ;3.顺次地连接各点,作出 截交线并判别可见性;4.整理轮廓线。