高中数学 1.2.3导数的四则运算法则教学案 理 新人教B版选修2-2

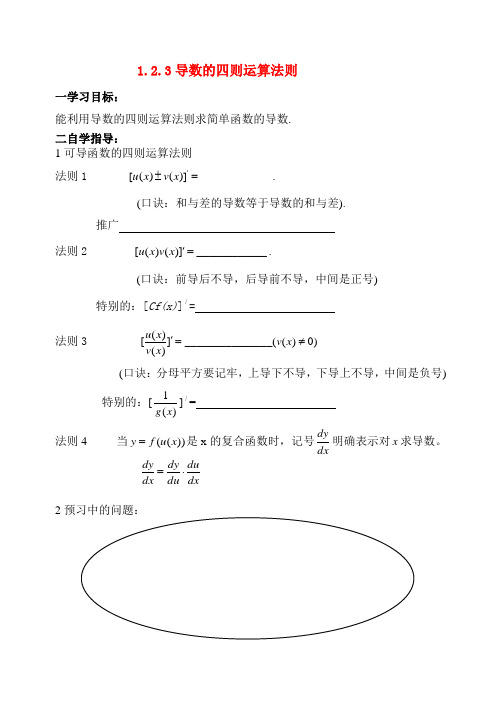
1.2.3导数的四则运算法则一学习目标：能利用导数的四则运算法则求简单函数的导数.二自学指导：1可导函数的四则运算法则法则1 '[()()]____________.u x v x ±=(口诀：和与差的导数等于导数的和与差).推广法则2 [()()]____________u x v x '=.(口诀：前导后不导，后导前不导，中间是正号)特别的：[Cf(x)]/=法则3 ()[]_______________(()0)()u x v x v x '=≠ (口诀：分母平方要记牢，上导下不导，下导上不导，中间是负号) 特别的：[)(1x g ]/= 法则4 当))((x u f y =是x 的复合函数时，记号dxdy 明确表示对x 求导数。

dx du du dy dx dy ⋅=2三 典型例题例1 求多项式函数n n n n a x a x a x a x f ++++=--1110......)(的导数。

例2 求x x y sin =的导数例3 求x y 2sin =的导数例4 求x y tan =的导数例5 求()[]'+535x 的导数求()'x 5sin 的导数四巩固练习1．下列求导运算正确的是 ( )2x 232111.()1 B.(log ) C. (x cosx)-2xsinx D.(3)3log ln 2x A x x e x x x ''''+=+===2．求下列函数的导数 (1)y=12+x x (2)32(21)(3)y x x x =-+(3)y=x xsin (4)tan y x x =-；(5)x x e y 2= (6)5)75ln(+=x y3．已知函数xe y x=在0x x =处的导数值与函数值互为相反数，求0x 的值4.已知抛物线f(x)= x 2+3x-5，求此抛物线在x=3处的切线方程5设()ln x f x a e b x =⋅+，且1(1),(1)f e f e''=-=，求实数,a b 的值。

1.2 导数的运算1.2.3 导数的四则运算法则【提出问题】我们由定义已经求出了基本初等函数的导数。

(1)(c)′＝0(c 为常数)；(2)(x n )′＝nx n －1(n 为有理数)；(3)(sin x)′＝cos x ；(4)(cos x)′＝－sin x ；(5)(a x )′＝a x ln a(a>0且a ≠1)；(6)(e x )′＝e x ；(7)(log a x)′＝1x ln a (a>0且a ≠1)；(8)(ln x)′＝1x .初等函数是由基本初等函数经过四则运算、乘方、开方和各种复合运算构成。

因此，初等函数的导数可以经过基本初等函数导数的运算而求得。

怎么求呢？我们来解决这个问题。

【获得新知】（1）函数和（或差）的求导法则设f (x )，g (x )是可导的，求f (x )±g (x )的导数。

设()()y f x g x =+，则[()()][()()][()()][()()] y f x x g x x f x g x f x x f x g x x g x f g∆=+∆++∆-+=+∆-++∆-=∆+∆所以y f g x x x∆∆∆=+∆∆∆ 所以0000limlim()lim lim x x x x y f g f g x x x x x ∆→∆→∆→∆→∆∆∆∆∆=+=+∆∆∆∆∆ 即()y f g f g ''''=+=+同理可证：()f g f g '''-=-所以(()())()()f x g x f x g x '''±=±即，两个函数的和（或差）的导数，等于这两个函数的导数和（或差）。

这个法则可推广到任意有限个函数，即1212()n n f f f f f f ''''±±±=±±±L L（2）函数积的求导法则设f (x )，g (x )是可导的，求f (x ) g (x )的导数。

1.2.3 导数的四则运算法例【教课目的】记着两个函数的和、差、积、商的导数运算法例，理解导数运算法则是把一个复杂函数求导数转变为两个或多个简单函数的求导问题；能经过运算法例求出导数后解决实质问题 .【教课要点】导数的四则运算法例【教课难点】复合函数的导数一、课前预习（阅读教材19--20 页，填写知识点 .并自学 20 页例题，※研究课上学习的例题）1.设函数 f (x), g( x) 是可导函数f (x)g( x)__________推广： ( f 1 f 2f n )'__________f ( x)g( x)__________特别地 Cf ( x)__________f ( x)_________g( x)2.复合函数的求导法例：复合函数 y f [ (x)] 对自变量x的导数y x，等于已知函数对中间变量 u(x) 的导数 y u，乘以中间变量u对自变量x的导数u x，即______________.二、课上学习：例 1. 求y x cos x 的导数.例 2. 求y sin 2x 的导数.例 3. 求 y tan x 的导数 .三、自我检测1.曲线 y x 2 2x a 与直线 y 3x 1相切时，常数a的值等于__________2.曲线y 1 x3 2 在点(1,7)处切线的倾斜角为 __________333.（1）求曲线（2）求曲线y x2 3x 1在点（1，5）处的切线方程. y x23x 1过点（2，2）处的切线方程.4.假如曲线y x3x 10 的一条切线与直线y4x 3 平行，那么曲线与切线相切的切点坐标为 _______5.函数f ( x)e xx0处的导数值与函数值互为相反数，则x0=______.在 xx6. 在曲线y x33x 26x 10 的切线中，斜率最小的切线方程为___________四、课后练习1.设函数 f ( x)cos x ，则 [ f ()]等于（）2A. 0B. 1C.1D. 以上均不正确2.设函数 f(x)sin x ，则 f(0) 等于（）A.1B.1C.0D.以上均不正确3 导数为x1的一个函数是（）A. x 2xB. 1 x2x 1C. x 1 D . 1 x2224.设函数 y f (sin x) 是可导函数，则y x等于（）A. f (sin x)B.f(sin x) cos xC. f (sin x) sin xD.f (cos x) cos x5.点 P 在曲线y x 3x 2上挪动，设点 P 处切线的倾斜角为，则角的取值范3围是（）A. [0, ]B.[0,)[ 3, ) C.[3, ) D. (2,3]22444 6.求以下函数的导数（ 1 ） y2x 33 x cosx ,x x（2） y x sin cos（ 3 ）22y sin 4xcos4x 44（ 4）y cos x（5）yx ln x（6）f ( x)1sin 2 x x 1 x。

1.2.3 导数的四则运算法则1．熟记基本初等函数的导数公式，并能运用这些公式求基本初等函数的导数．(重点) 2．掌握导数的运算法则，并能运用法则求复杂函数的导数．(难点) 3．掌握复合函数的求导法则，会求复合函数的导数．(易混点)[基础·初探]教材整理1 导数的运算法则阅读教材P 19～P 20“例1”以上部分内容，完成下列问题． 1．和差的导数[f (x )±g (x )]′＝______________. 2．积的导数(1)[f (x )g (x )]′＝____________； (2)[cf (x )]′＝______________. 3．商的导数⎣⎢⎡⎦⎥⎤f x g x ′＝____________. 【答案】 1.f ′(x )±g ′(x ) 2.(1)f ′(x )g (x )＋f (x )g ′(x ) (2)cf ′(x ) 3.g x f ′ x －f x g ′ xg x 2，g (x )≠0判断(正确的打“√”，错误的打“×”) (1)若f ′(x )＝2x ，则f (x )＝x 2.( )(2)已知函数y ＝2sin x －cos x ，则y ′＝2cos x ＋sin x ．( ) (3)已知函数f (x )＝(x ＋1)(x ＋2)，则f ′(x )＝2x ＋1.( ) 【解析】 (1)由f ′(x )＝2x ，则f (x )＝x 2＋c .(2)由y ＝2sin x －cos x ，则y ′＝(2sin x )′－(cos x )′ ＝2cos x ＋sin x .(3)由f (x )＝(x ＋1)(x ＋2)＝x 2＋3x ＋2， 所以f ′(x )＝2x ＋3.【答案】 (1)× (2)√ (3)× 教材整理2 复合函数的概念及求导法则 阅读教材P 20“例5”右边部分，完成下列问题．【答案】 x 的函数y ＝f (g (x ))d u ·d xy 对u 的导数与u对x 的导数的乘积判断(正确的打“√”，错误的打“×”)(1)函数f (x )＝x e x的导数是f ′(x )＝e x(x ＋1)．( ) (2)函数f (x )＝sin(－x )的导数为f ′(x )＝cos x ．( ) 【答案】 (1)√ (2)×[质疑·手记]预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流： 疑问1： 解惑： 疑问2： 解惑： 疑问3：[小组合作型](1)y ＝x －2＋x 2； (2)y ＝3x e x －2x＋e ； (3)y ＝ln xx 2＋1； (4)y ＝x 2－sin x 2cos x2.【自主解答】 (1)y ′＝2x －2x －3. (2)y ′＝(ln 3＋1)·(3e)x－2x ln 2.(3)y ′＝x 2＋1－2x 2·ln xx x 2＋1 2.(4)∵y ＝x 2－sin x 2cos x 2＝x 2－12sin x ，∴y ′＝2x －12cos x .1．解答此类问题时常因导数的四则运算法则不熟而失分．2．对一个函数求导时，要紧扣导数运算法则，联系基本初等函数的导数公式，当不易直接应用导数公式时，应先对函数进行化简(恒等变形)，然后求导．这样可以减少运算量，优化解题过程．[再练一题]1．(1)设函数f (x )＝sin θ3x 3＋3cos θ2x 2＋tan θ，其中θ∈⎣⎢⎡⎦⎥⎤0，512π，则导数f ′(1)的取值范围是( )A ．[－2,2]B ．[2，3]C ．[3，2]D ．[2，2](2)已知f (x )＝exx，若f ′(x 0)＋f (x 0)＝0，则x 0的值为________.【导学号：05410013】【解析】 (1)f ′(x )＝sin θ·x 2＋3cos θ·x ， ∴f ′(1)＝sin θ＋3cos θ＝2sin ⎝ ⎛⎭⎪⎫θ＋π3， ∵θ∈⎣⎢⎡⎦⎥⎤0，512π，∴sin ⎝ ⎛⎭⎪⎫θ＋π3∈⎣⎢⎡⎦⎥⎤22，1，∴2sin ⎝ ⎛⎭⎪⎫θ＋π3∈[2，2]． (2)∵f ′(x )＝ e x′x －e x·x ′x2＝e xx －1 x2(x ≠0)． ∴由f ′(x 0)＋f (x 0)＝0，得 e x 0 x 0－1 x 20＋e x 0x 0＝0， 解得x 0＝12.【答案】 (1)D (2)12(1)y ＝e2x ＋1；(2)y ＝12x －13；(3)y ＝5log 2(1－x )；(4)y ＝sin 3x ＋sin 3x .【精彩点拨】 先分析函数是怎样复合而成的，找出中间变量，分层求导． 【自主解答】 (1)函数y ＝e2x ＋1可看作函数y ＝e u和u ＝2x ＋1的复合函数，∴y ′x ＝y ′u ·u x ′＝(e u)′(2x ＋1)′＝2e u＝2e 2x ＋1.(2)函数y ＝1 2x －1 3可看作函数y ＝u －3和u ＝2x －1的复合函数， ∴y ′x ＝y ′u ·u x ′＝(u －3)′(2x －1)′＝－6u －4＝－6(2x －1)－4＝－6 2x －14.(3)函数y ＝5log 2(1－x )可看作函数y ＝5log 2u 和u ＝1－x 的复合函数， ∴y ′x ＝y ′u ·u ′x ＝(5log 2u )′·(1－x )′＝－5u ln 2＝5x －1 ln 2. (4)函数y ＝sin 3x 可看作函数y ＝u 3和u ＝sin x 的复合函数，函数y ＝sin 3x 可看作函数y ＝sin v 和v ＝3x 的复合函数．∴y ′x ＝(u 3)′·(sin x )′＋(sin v )′·(3x )′ ＝3u 2·cos x ＋3cos v ＝3sin 2x cos x ＋3cos 3x .1．解答此类问题常犯两个错误(1)不能正确区分所给函数是否为复合函数；(2)若是复合函数，不能正确判断它是由哪些基本初等函数复合而成． 2．复合函数求导的步骤[再练一题]2．求下列函数的导数． (1)y ＝x1－1－x；(2)y ＝log 2(2x 2－1)． 【解】 (1)y ＝x1－1－x＝x 1＋1－x1－1－x 1＋1－x＝x 1＋1－x1－ 1－x＝1＋1－x .设y ＝1＋u ，u ＝1－x ，则y ′＝y u ′·u x ′＝(1＋u )′·(1－x )′ ＝12u ·(－1)＝－121－x. (2)设y ＝log 2u ，u ＝2x 2－1， 则y ′＝y ′u ·u x ′＝1u ln 2·4x ＝4x2x 2－1 ln 2.[探究共研型]探究 【提示】 函数y ＝(3x ＋2)2可看出函数y ＝u 2和u ＝3x ＋2的复合函数， ∴y x ′＝y u ′·u x ′＝(u 2)′·(3x ＋2)′ ＝6u ＝6(3x ＋2)．已知函数f (x )＝ax 2＋2ln(2－x )(a ∈R )，设曲线y ＝f (x )在点(1，f (1))处的切线为l ，若直线l 与圆C ：x 2＋y 2＝14相切，求实数a 的值．【精彩点拨】 求出导数f ′(1)，写出切线方程，由直线l 与圆C 相切，建立方程求解．【自主解答】 因为f (1)＝a ，f ′(x )＝2ax ＋2x －2(x <2)， 所以f ′(1)＝2a －2，所以切线l 的方程为2(a －1)x －y ＋2－a ＝0.因为直线l 与圆相切，所以圆心到直线l 的距离等于半径，即d ＝|2－a |4 a －1 2＋1＝12，解得a ＝118.关于复合函数导数的应用及其解决方法1．应用复合函数的导数应用主要有：求在某点处的切线方程，已知切线的方程或斜率求切点，以及涉及切线问题的综合应用．2．方法先求出复合函数的导数，若已知切点则求出切线斜率、切线方程；若切点未知，则先设出切点，用切点表示切线斜率，再根据条件求切点坐标．总之，在解决此类问题时切点起着至关重要的作用．[再练一题]3．若将上例中条件改为“直线l 与圆C ：x 2＋y 2＝14相交”，求a 的取值范围．【解】 由例题知，直线l 的方程为2(a －1)x －y ＋2－a ＝0. ∵直线l 与圆C ：x 2＋y 2＝14相交，∴圆心到直线l 的距离小于半径． 即d ＝|2－a |4 a －1 2＋1<12. 解得a >118.[构建·体系]1．函数y ＝(2 017－8x )3的导数y ′＝( ) A ．3(2 017－8x )2B ．－24xC ．－24(2 017－8x )2D ．24(2 017－8x )2【解析】 y ′＝3(2 017－8x )2×(2 017－8x )′ ＝3(2 017－8x )2×(－8)＝－24(2 017－8x )2. 【答案】 C2．函数y ＝x 2cos 2x 的导数为( ) A ．y ′＝2x cos 2x －x 2sin 2x B ．y ′＝2x cos 2x －2x 2sin 2x C ．y ′＝x 2cos 2x －2x sin 2x D ．y ′＝2x cos 2x ＋2x 2sin 2x【解析】 y ′＝(x 2)′cos 2x ＋x 2(cos 2x )′ ＝2x cos 2x ＋x 2(－sin 2x )·(2x )′ ＝2x cos 2x －2x 2sin 2x . 【答案】 B3．已知f (x )＝ln(3x －1)，则f ′(1)＝________. 【解析】 f ′(x )＝13x －1·(3x －1)′＝33x －1， ∴f ′(1)＝32.【答案】 324．设曲线y ＝e ax在点(0,1)处的切线与直线x ＋2y ＋1＝0垂直，则a ＝_______.【导学号：05410014】【解析】 令y ＝f (x )，则曲线y ＝e ax在点(0,1)处的切线的斜率为f ′(0)，又切线与直线x ＋2y ＋1＝0垂直，所以f ′(0)＝2.因为f (x )＝e ax ，所以f ′(x )＝(e ax)′＝(e ax)·(ax )′＝a e ax，所以f ′(0)＝a e 0＝a ，故a ＝2.【答案】 25．求下列函数的导数．(1)y＝cos(x＋3)；(2)y＝(2x－1)3；(3)y＝e－2x＋1.【解】(1)函数y＝cos(x＋3)可以看做函数y＝cos u和u＝x＋3的复合函数，由复合函数的求导法则可得y x′＝y u′·u x′＝(cos u)′·(x＋3)′＝－sin u·1＝－sin u＝－sin(x＋3)．(2)函数y＝(2x－1)3可以看做函数y＝u3和u＝2x－1的复合函数，由复合函数的求导法则可得y x′＝y u′·u x′＝(u3)′·(2x－1)′＝3u2·2＝6u2＝6(2x－1)2.(3)y′＝e－2x＋1·(－2x＋1)′＝－2e－2x＋1.我还有这些不足：(1)(2)我的课下提升方案：(1)(2)学业分层测评(建议用时：45分钟)[学业达标]一、选择题1．函数y＝(x2－1)n的复合过程正确的是( )A．y＝u n，u＝x2－1 B．y＝(u－1)n，u＝x2C．y＝t n，t＝(x2－1)n D．y＝(t－1)n，t＝x2－1【答案】 A2．若f (x )＝1－x2sin x ，则f (x )的导数是( )A.－2x sin x － 1－x 2cos x sin 2x B.－2x sin x ＋ 1－x 2 cos x sin 2x C.－2x sin x ＋ 1－x 2 sin xD.－2x sin x － 1－x 2 sin x【解析】 f ′(x )＝1－x 2′sin x － 1－x 2· sin x ′sin 2x ＝－2x sin x － 1－x 2cos xsin 2x . 【答案】 A3．函数y ＝x ln(2x ＋5)的导数为( ) A ．ln(2x ＋5)－x 2x ＋5B ．ln(2x ＋5)＋2x2x ＋5C ．2x ln(2x ＋5)D.x 2x ＋5【解析】 y ′＝[x ln(2x ＋5)]′＝x ′ln(2x ＋5)＋x [ln(2x ＋5)]′＝ln(2x ＋5)＋x ·12x ＋5· (2x ＋5)′＝ln(2x ＋5)＋2x2x ＋5. 【答案】 B4．(2016·宁波高二检测)函数f (x )＝x ＋x ln x 在(1,1)处的切线方程为( ) A ．2x ＋y －1＝0 B ．2x －y －1＝0 C ．2x ＋y ＋1＝0D ．2x －y ＋1＝0【解析】 ∵f ′(x )＝(x ＋x ln x )′ ＝1＋x ′ln x ＋x (ln x )′ ＝1＋ln x ＋1＝2＋ln x ， ∴f ′(1)＝2＋ln 1＝2，∴函数f (x )在点(1,1)处的切线方程为y －1＝2(x －1)，即2x －y －1＝0.【答案】 B5．函数y ＝cos 2x ＋sin x 的导数为( )A ．－2sin 2x ＋cos x2xB ．2 sin 2x ＋cos x2xC ．－2sin 2x ＋sin x2xD ．2sin 2x －cos x2x【解析】 y ′＝－sin 2x ·(2x )′＋cos x ·(x )′ ＝－2sin 2x ＋12·1x cos x＝－2sin 2x ＋cos x2x .【答案】 A 二、填空题6．若曲线y ＝x ln x 上点P 处的切线平行于直线2x －y ＋1＝0，则点P 的坐标是________. 【导学号：05410015】【解析】 设P (x 0，y 0)．∵y ＝x ln x ，∴y ′＝ln x ＋x ·1x＝1＋ln x .∴k ＝1＋ln x 0.又k ＝2，∴1＋ln x 0＝2，∴x 0＝e. ∴y 0＝eln e ＝e.∴点P 的坐标是(e ，e)． 【答案】 (e ，e)7．已知函数f (x )＝f ′⎝ ⎛⎭⎪⎫π2sin x ＋cos x ，则f ′⎝ ⎛⎭⎪⎫π4＝________. 【解析】 ∵f ′(x )＝f ′⎝ ⎛⎭⎪⎫π2cos x －sin x ， ∴f ′⎝ ⎛⎭⎪⎫π2＝f ′⎝ ⎛⎭⎪⎫π2cos π2－sin π2＝－1， ∴f ′(x )＝－cos x －sin x ，∴f ′⎝ ⎛⎭⎪⎫π4＝－cos π4－sin π4＝－ 2. 【答案】 － 28．(2016·广州高二检测)若函数为y ＝sin 4x －cos 4x ，则y ′＝________________. 【解析】 ∵y ＝sin 4x －cos 4x ＝(sin 2x ＋cos 2x )·(sin 2x －cos 2x )＝－cos 2x ， ∴y ′＝(－cos 2x )′＝－(－sin 2x )·(2x )′ ＝2 sin 2x . 【答案】 2sin 2x 三、解答题9．求下列函数的导数． (1)y ＝1－2x 2；(2)y ＝esin x；(3)y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π3；(4)y ＝5log 2(2x ＋1)．【解】 (1)设y ＝u 12，u ＝1－2x 2，则y ′＝(u 12)′(1－2x 2)′＝⎝ ⎛⎭⎪⎫12u －12·(－4x )＝12(1－2x 2)－12(－4x )＝－2x1－2x 2.(2)设y ＝e u ，u ＝sin x ，则y x ′＝y u ′·u x ′＝e u ·cos x ＝e sin xcos x .(3)设y ＝sin u ，u ＝2x ＋π3，则y x ′＝y u ′·u x ′＝cos u ·2＝2cos ⎝ ⎛⎭⎪⎫2x ＋π3.(4)设y ＝5log 2u ，u ＝2x ＋1，则y ′＝y u ′·u x ′＝10u ln 2＝102x ＋1 ln 2.10．求曲线y ＝2sin 2x 在点P ⎝ ⎛⎭⎪⎫π6，12处的切线方程．【解】 因为y ′＝(2sin 2x )′＝2×2sin x ×(sin x )′＝2×2sin x ×cos x ＝2sin 2x ，所以k ＝2sin ⎝ ⎛⎭⎪⎫2×π6＝ 3.所以过点P 的切线方程为y －12＝3⎝ ⎛⎭⎪⎫x －π6，即3x －y ＋12－3π6＝0.[能力提升]1．(2016·长沙高二检测)函数y ＝sin 2x －cos 2x 的导数是() A ．2 2 cos ⎝ ⎛⎭⎪⎫2x －π4B ．cos 2x －sin 2xC ．sin 2x ＋cos 2xD ．22cos ⎝ ⎛⎭⎪⎫2x ＋π4【解析】 ∵y ′＝(sin 2x －cos 2x )′＝(sin 2x )′－(cos 2x )′＝cos 2x ·(2x )′＋sin 2x ·(2x )′＝2cos 2x ＋2sin 2x＝22⎝ ⎛⎭⎪⎫22cos 2x ＋22sin 2x ＝22cos ⎝ ⎛⎭⎪⎫2x －π4， 故选A.【答案】 A2．已知点P 在曲线y ＝4e x ＋1上，α为曲线在点P 处的切线的倾斜角，则α的取值范围是( )【导学号：05410016】A.⎣⎢⎡⎭⎪⎫0，π4 B.⎣⎢⎡⎭⎪⎫π4，π2 C.⎝ ⎛⎦⎥⎤π2，3π4 D.⎣⎢⎡⎭⎪⎫3π4，π 【解析】 因为y ＝4e x＋1， 所以y ′＝－4e x e x ＋1 2＝－4e x e 2x ＋2e x ＋1＝－4e x ＋1ex ＋2. 因为e x >0，所以e x ＋1ex ≥2，所以y ′∈[－1,0)，所以tan α∈[－1,0)． 又因为α∈[0，π)，所以α∈⎣⎢⎡⎭⎪⎫3π4，π. 【答案】 D3．曲线y ＝e －5x ＋2在点(0,3)处的切线方程为__________________________．【解析】 因为y ′＝e －5x (－5x )′＝－5e －5x ，所以k ＝－5，故切线方程为y －3＝－5(x －0)，即5x ＋y －3＝0.【答案】 5x ＋y －3＝04．已知函数f (x )＝x 3＋1(1－a )x 2－a (a ＋2)x ＋b (a ，b ∈R )．(1)若函数f (x )的图象过原点，且在原点处的切线斜率为－3，求a ，b 的值；(2)若曲线y ＝f (x )存在两条垂直于y 轴的切线，求a 的取值范围．【解】 f ′(x )＝3x 2＋2(1－a )x －a (a ＋2)．(1)由题意得⎩⎪⎨⎪⎧ f 0 ＝b ＝0，f ′ 0 ＝－a a ＋2 ＝－3，解得b ＝0，a ＝－3或a ＝1.(2)∵曲线y ＝f (x )存在两条垂直于y 轴的切线，∴关于x 的方程f ′(x )＝3x 2＋2(1－a )x －a (a ＋2)＝0有两个不相等的实数根， ∴Δ＝4(1－a )2＋12a (a ＋2)＞0，即4a 2＋4a ＋1＞0，∴a ≠－12. ∴a 的取值范围为⎝ ⎛⎭⎪⎫－∞，－12∪⎝ ⎛⎭⎪⎫－12，＋∞.。

1.2.3 导数的四则运算法则教学目标1.能利用导数的四则运算法则求解导函数.2.能运用复合函数的求导法则进行复合函数的求导． 教学知识梳理知识点一 导数的四则运算法则 已知f (x )＝x ，g (x )＝1x.思考1 f (x )，g (x )的导数分别是什么？ 答案 f ′(x )＝1，g ′(x )＝－1x2.思考2 试求G (x )＝x ＋1x ，H (x )＝x －1x 的导数．并说出G ′(x )，H ′(x )与f ′(x )，g ′(x )的关系．答案 G ′(x )＝1－1x 2.同理，H ′(x )＝1＋1x 2.∴G ′(x )＝f ′(x )＋g ′(x )，H ′(x )＝f ′(x )－g ′(x )． 思考3 [f (x )g (x )]′＝f ′(x )g ′(x )正确吗？那么⎣⎡⎦⎤f (x )g (x )′＝f ′(x )g ′(x )(g (x )≠0且g ′(x )≠0)是否正确？答案 [f (x )g (x )]′≠f ′(x )g ′(x )，⎣⎡⎦⎤f (x )g (x )′≠f ′(x )g ′(x ). 梳理 导数的四则运算法则 (1)设f (x )，g (x )是可导的，则：⎣⎡⎦⎤1g (x )′＝－g ′(x )g 2(x )(g (x )≠0)． 特别提醒：(1)[f (x )±g (x )]′＝f ′(x )±g ′(x )可推广到任意有限个函数的和(或差)的求导．(2)[af (x )±bg (x )]′＝af ′(x )±bg ′(x )．知识点二 复合函数y ＝f (u (x ))的导数．y ＝f (u (x ))是x 的复合函数，则y ′＝f ′(u (x ))＝d y d u ·d ud x ＝f ′(u )·u ′(x )．题型探究类型一 利用导数的四则运算法则求导 例1 求下列函数的导数． (1)y ＝x 3·e x ；(2)y ＝x －sin x 2cos x2；(3)y ＝x 2＋log 3x ；(4)y ＝e x ＋1e x －1.解 (1)y ′＝(x 3)′e x ＋x 3(e x )′＝3x 2e x ＋x 3e x ＝x 2(3＋x )e x . (2)∵y ＝x －12sin x ，∴y ′＝x ′－12(sin x )′＝1－12cos x .(3)y ′＝(x 2＋log 3x )′＝(x 2)′＋(log 3x )′＝2x ＋1x ln 3.(4)y ′＝(e x ＋1)′(e x －1)－(e x ＋1)(e x －1)′(e x －1)2＝e x (e x －1)－(e x ＋1)e x (e x －1)2＝－2e x (e x －1)2.反思与感悟 求函数的导数的策略(1)先区分函数的运算特点，即函数的和、差、积、商，再根据导数的运算法则求导数． (2)对于三个以上函数的积、商的导数，依次转化为“两个”函数的积、商的导数计算． 跟踪训练1 (1)已知f (x )＝(x －a )(x －b )(x －c )，则a f ′(a )＋b f ′(b )＋cf ′(c )＝________.【答案】0【解析】∵f ′(x )＝(x －a )′(x －b )(x －c )＋(x －a )(x －b )′·(x －c )＋(x －a )(x －b )(x －c )′ ＝(x －b )(x －c )＋(x －a )(x －c )＋(x －a )(x －b )， ∴f ′(a )＝(a －b )(a －c )，f ′(b )＝(b －a )(b －c )＝－(a －b )(b －c )， f ′(c )＝(c －a )(c －b )＝(a －c )(b －c )． ∴a f ′(a )＋b f ′(b )＋c f ′(c )＝a (a －b )(a －c )－b (a －b )(b －c )＋c(a －c )(b －c )＝a (b －c )－b (a －c )＋c (a －b )(a －b )(b －c )(a －c )＝0.(2)求下列函数的导数．①y ＝2x 3－3x ＋x ＋1x x ； ②y ＝x 2＋1x 2＋3；③y ＝(x ＋1)(x ＋3)(x ＋5)； ④y ＝x sin x －2cos x .解 ①313122223y x x x x --－∵＝－＋＋，1352222333.22y x x x x ---'+--∴＝②方法一 y ′＝(x 2＋1)′(x 2＋3)－(x 2＋1)(x 2＋3)′(x 2＋3)2＝2x (x 2＋3)－2x (x 2＋1)(x 2＋3)2＝4x(x 2＋3)2.方法二 ∵y ＝x 2＋1x 2＋3＝x 2＋3－2x 2＋3＝1－2x 2＋3，∴y ′＝⎝⎛⎭⎫1－2x 2＋3′＝⎝ ⎛⎭⎪⎫－2x 2＋3′ ＝(－2)′(x 2＋3)－(－2)(x 2＋3)′(x 2＋3)2＝4x(x 2＋3)2. ③方法一 y ′＝[(x ＋1)(x ＋3)]′(x ＋5)＋(x ＋1)(x ＋3)(x ＋5)′＝[(x ＋1)′(x ＋3)＋(x ＋1)(x ＋3)′](x ＋5)＋(x ＋1)(x ＋3)＝(2x ＋4)(x ＋5)＋(x ＋1)(x ＋3) ＝3x 2＋18x ＋23.方法二 ∵y ＝(x ＋1)(x ＋3)(x ＋5) ＝(x 2＋4x ＋3)(x ＋5) ＝x 3＋9x 2＋23x ＋15， ∴y ′＝(x 3＋9x 2＋23x ＋15)′ ＝3x 2＋18x ＋23.④y ′＝(x sin x )′－⎝⎛⎭⎫2cos x ′＝x ′sin x ＋x (sin x )′－2′cos x －2(cos x )′cos 2x＝sin x ＋x cos x －2sin xcos 2x.类型二 简单复合函数求导 例2 求下列函数的导数． (1)y ＝e cos x ＋1；(2)y ＝log 2(2x ＋1)； (3)y ＝2sin ⎝⎛⎭⎫3x －π6；(4)y ＝11－2x. 解 (1)设y ＝e u ，u ＝cos x ＋1，则y x ′＝y u ′·u x ′＝e u ·(－sin x )＝－e cos x ＋1sin x . (2)设y ＝log 2u ，u ＝2x ＋1，则y x ′＝y u ′·u x ′＝2u ln 2＝2(2x ＋1)ln 2.(3)设y ＝2sin u ，u ＝3x －π6，则y x ′＝y u ′·u x ′＝2cos u ×3＝6cos ⎝⎛⎭⎫3x －π6. (4)设y ＝u12-，u ＝1－2x ，则y x ′＝y u ′·u x ′＝(12u-)′·(1－2x )′＝－1232u -×(－2)＝(1－2x )32-.反思与感悟 求复合函数导数的步骤(1)确定中间变量，正确分解复合关系，即明确函数关系y ＝f (u )，u ＝g (x )．(2)分步求导(弄清每一步求导是哪个变量对哪个变量求导)，要特别注意中间变量对自变量的求导，即先求y u ′，再求u x ′.(3)计算y u ′·u x ′，并把中间变量转化为自变量．整个过程可简记为“分解—求导—回代”三个步骤，熟练以后可以省略中间过程． 跟踪训练2 (1)已知函数f (x )＝(2x ＋1)5，则f ′(0)的值为________． 【答案】10【解析】f ′(x )＝5(2x ＋1)4·(2x ＋1)′＝10(2x ＋1)4， ∴f ′(0)＝10.(2)求下列函数的导数．①y ＝3－x ；②y ＝12ln(x 2＋1)；③y ＝a 1－2x (a >0，a ≠1)．解 ①设y ＝u ，u ＝3－x ， 则y x ′＝y u ′·u x ′＝12u·(－1)＝－123－x.②设y ＝12ln u ，u ＝x 2＋1，则y x ′＝y u ′·u x ′＝12·1u ·(2x )＝12·1x 2＋1·(2x )＝xx 2＋1.③令y ＝a u ，u ＝1－2x ，则y x ′＝y u ′·u x ′＝a u ·ln a ·(－2) ＝a 1－2xln a ·(－2)＝－2a 1－2xln a .类型三 导数运算法则的综合应用 命题角度1 利用导数求函数解析式例3 (1)已知函数f (x )＝ln xx＋2xf ′(1)，试比较f (e)与f (1)的大小关系；(2)设f (x )＝(ax ＋b )sin x ＋(cx ＋d )cos x ，试确定常数a ，b ，c ，d ，使得f ′(x )＝x cos x . 解 (1)由题意得f ′(x )＝1－ln xx 2＋2f ′(1)，令x ＝1，得f ′(1)＝1－ln 11＋2f ′(1)，即f ′(1)＝－1.∴f (x )＝ln xx－2x .∴f (e)＝ln e e －2e ＝1e －2e ，f (1)＝－2，由f (e)－f (1)＝1e －2e ＋2<0，得f (e)<f (1)．(2)由已知得f ′(x )＝[(ax ＋b )s in x ＋(cx ＋d )cos x ]′ ＝[(ax ＋b )sin x ]′＋[(cx ＋d )cos x ]′＝(ax ＋b )′sin x ＋(ax ＋b )(sin x )′＋(cx ＋d )′cos x ＋(cx ＋d )(cos x )′ ＝a sin x ＋(ax ＋b )cos x ＋c cos x －(cx ＋d )sin x ＝(a －cx －d )sin x ＋(ax ＋b ＋c )cos x . 又∵f ′(x )＝x cos x ，∴⎩⎪⎨⎪⎧a －d －cx ＝0，ax ＋b ＋c ＝x ，即⎩⎪⎨⎪⎧a －d ＝0，－c ＝0，a ＝1，b ＋c ＝0，解得a ＝d ＝1，b ＝c ＝0.反思与感悟 (1)中确定函数f (x )的解析式，需要求出f ′(1)，注意f ′(1)是常数． (2)中利用待定系数法可确定a ，b ，c ，d 的值． 完成(1)(2)问的前提是熟练应用导数的运算法则．跟踪训练3 函数f (x )＝x 2x －1＋f ′(1)，则f ′(1)＝________.【答案】－1【解析】对f (x )求导，得f ′(x )＝2x －1－2x (2x －1)2＝－1(2x －1)2，则f ′(1)＝－1.命题角度2 与切线有关的问题例4 (1)若曲线y ＝x ln x 上点P 处的切线平行于直线2x －y ＋1＝0，则点P 的坐标是________． 【答案】(e ，e)【解析】设P (x 0，y 0)．∵y ＝x ln x ， ∴y ′＝ln x ＋x ·1x ＝1＋ln x ，∴k ＝1＋ln x 0.又k ＝2，∴1＋ln x 0＝2， ∴x 0＝e.∴y 0＝eln e ＝e. ∴点P 的坐标是(e ，e)．(2)已知函数f (x )＝ax 2＋bx ＋3(a ≠0)，其导函数为f ′(x )＝2x －8. ①求a ，b 的值；②设函数g (x )＝e x sin x ＋f (x )，求曲线g (x )在x ＝0处的切线方程． 解 ①因为f (x )＝ax 2＋bx ＋3(a ≠0)，所以f ′(x )＝2ax ＋b ， 又知f ′(x )＝2x －8，所以a ＝1，b ＝－8. ②由①可得g (x )＝e x sin x ＋x 2－8x ＋3， 所以g ′(x )＝e x sin x ＋e x cos x ＋2x －8， 所以g ′(0)＝e 0sin 0＋e 0cos 0＋2×0－8＝－7. 又知g (0)＝3，所以g (x )在x ＝0处的切线方程为y －3＝－7(x －0)， 即7x ＋y －3＝0.反思与感悟 (1)与切线有关的问题往往涉及切点、切点处的导数、切线方程三个主要元素．其他的条件可以进行转化，从而转化为这三个要素间的关系．(2)准确利用求导法则求出导函数是解决与切线有关的问题的第一步，也是解题的关键，务必做到准确．(3)分清已知点是否在曲线上，若不在曲线上，则要设出切点，这是解题时的易错点． 跟踪训练4 (1)设曲线y ＝2－cos x sin x在点⎝⎛⎭⎫π2，2处的切线与直线x ＋ay ＋1＝0垂直，则a ＝________. 【答案】1【解析】∵y ′＝sin 2x －(2－cos x )cos x sin 2x ＝1－2cos xsin 2x ，当x ＝π2时，y ′＝1－2cosπ2sin 2π2＝1.又直线x ＋ay ＋1＝0的斜率是－1a ，∴－1a＝－1，即a ＝1.(2)曲线y ＝e sin x 在(0,1)处的切线与直线l 平行，且与l 的距离为2，求直线l 的方程． 解 设u ＝sin x ，则y ′＝(e sin x )′＝(e u )′(sin x )′＝cos x e sin x ， 即y ′|x ＝0＝1，则切线方程为y －1＝x －0，即x －y ＋1＝0.若直线l 与切线平行，可设直线l 的方程为x －y ＋c ＝0. 两平行线间的距离d ＝|c －1|2＝2，所以c ＝3或c ＝－1.故直线l 的方程为x －y ＋3＝0或x －y －1＝0. 达标检测1．设函数y ＝－2e x sin x ，则y ′等于( ) A ．－2e x cos x B ．－2e x sin x C ．2e x sin x D ．－2e x (sin x ＋cos x )【答案】D【解析】y ′＝－2(e x sin x ＋e x cos x )＝－2e x (sin x ＋cos x )． 2．对于函数f (x )＝e x x 2＋ln x －2kx ，若f ′(1)＝1，则k 等于( )A.e 2B.e 3 C ．－e 2 D ．－e3 【答案】A【解析】∵f ′(x )＝e x (x －2)x 3＋1x ＋2k x 2，∴f ′(1)＝－e ＋1＋2k ＝1，解得k ＝e2，故选A.3．曲线y ＝xx ＋2在点(－1，－1)处的切线方程为( )A ．y ＝2x ＋1B ．y ＝2x －1C ．y ＝－2x －3D ．y ＝－2x ＋2 【答案】A【解析】∵y ′＝x ′(x ＋2)－x (x ＋2)′(x ＋2)2＝2(x ＋2)2， ∴k ＝y ′|x ＝－1＝2(－1＋2)2＝2，∴切线方程为y ＋1＝2(x ＋1)，即y ＝2x ＋1.4．函数y ＝2cos 2x 在x ＝π12处的切线斜率为________．【答案】－1【解析】由函数y ＝2cos 2x ＝1＋cos 2x ， 得y ′＝(1＋cos 2x )′＝－2sin 2x ，所以函数在x ＝π12处的切线斜率为－2sin ⎝⎛⎭⎫2×π12＝－1. 5．在曲线y ＝x 3＋3x 2＋6x －10的切线中，斜率最小的切线的方程为________________． 【答案】3x －y －11＝0【解析】∵y ′＝3x 2＋6x ＋6＝3(x 2＋2x ＋2) ＝3(x ＋1)2＋3≥3，∴当x ＝－1时，斜率最小，此时切点坐标为(－1，－14)， ∴切线方程为y ＋14＝3(x ＋1)，即3x －y －11＝0.。

1.2．1 导数的四则运算法则一、教学目标：熟记公式(C )'＝0 (C 为常数)， (x )'＝1， ( x 2 )'＝2x ，2'11x x -=⎪⎭⎫ ⎝⎛．x x 21)'(=二、教学重点：牢固、准确地记住五种常见函数的导数，为求导数打下坚实的基础.教学难点：灵活运用五种常见函数的导数.三、教学过程：（一）公式1：(C )'＝0 (C 为常数)．证明：y ＝f (x )＝C , Δy ＝f (x ＋Δx )－f (x )＝C －C ＝0,,0=∆∆x y.0lim ')('0=∆∆==∴→∆x y C x f x也就是说，常数函数的导数等于0．公式2： 函数x x f y ==)(的导数证明：（略）公式3： 函数2)(x x f y ==的导数公式4： 函数x x f y 1)(==的导数公式5： 函数x x f y ==)(的导数（二）举例分析例1. 求下列函数的导数．⑴3x ⑵21x ⑶x解：⑴=')(3x 133-x 23x = ⑵='⎪⎭⎫ ⎝⎛21x )(2'-x 32--=x 32x -= ⑶=')(x )(21'x 12121-=x 2121-=x .21x =练习求下列函数的导数：⑴ y ＝x 5； ⑵ y ＝x 6； （3）;13x y = （4）.3x y = （5）x xy 2=例2．求曲线xy 1=和2x y =在它们交点处的两条切线与x 轴所围成的三角形的面积。

例3．已知曲线2x y=上有两点A （1，1），B （2，2）。

求：（1）割线AB 的斜率； （2）在[1，1+△x ]内的平均变化率；（3）点A 处的切线的斜率； （4）点A 处的切线方程例4．求抛物线y ＝x 2上的点到直线x －y －2＝0 的最短距离．（三）课堂小结几种常见函数的导数公式(C )'＝0 (C 为常数)， (x )'＝1， ( x 2 )'＝2x ， 2'11x x -=⎪⎭⎫ ⎝⎛．x x 21)'(= （四）课后作业《习案》作业四。

高中数学人教B版选修2－2第一章《1.2.3 导数的四则运算法则》优质课公开课教案教师资格证面试试讲教案
1教学目标
1.知识与技能
掌握有限个函数的和、差、积、商的求导公式;熟练运用公式求基本初等函数的四则运算的导数,能运用导数的几何意义,求过曲线上一点的切线。

2.过程与方法
通过用定义法求函数f(x)=x+x2的导数,观察结果,发掘两个函数的和、差求导方法,给结合定义给出证明;由定义法求f(x)=x2g(x)的导数,发现函数乘积的导数,归纳出两个函数积、商的求导发则。

3.情感、态度与价值观
培养学生由特别到一般的思维方法去探索结论,培养学生实验——观察——归纳——抽象的数学思维方法。

2学情分析
探析归纳,讲练结合
3重点难点
教学重点:函数和、差、积、商导数公式的发掘与应用
教学难点:导数四则运算法则的证明
4教学过程
4.1第一学时
教学活动
1【导入】导函数的概念和导数公式表。