矩形的定义和性质

矩形定义的概念矩形是一个平面图形，由四条边组成，其特点是相对边对称、两组对边相互平行。

矩形是平行四边形的特例，也是最常见的四边形之一。

下面将详细介绍矩形的定义及其性质。

首先，根据矩形的定义，其四边是直线段，且四个内角都是直角。

这意味着矩形的对角线相等且相互平分，因此可以用对角线的长度来计算矩形的面积和周长。

矩形的定义还包括两组对边相互平行。

这意味着矩形的两条对边长度相等且平行，两条相邻边也分别相等。

因此，矩形的任意一条边可以作为宽度，另一条边作为长度。

矩形的面积可以通过宽度乘以长度来计算，公式为：面积= 宽度×长度。

由于矩形的两条对边相等，所以宽度和长度可以互换位置得到相同的面积。

例如，一个矩形的宽度为3个单位，长度为5个单位，那么它的面积就是3 ×5 = 15个单位的平方。

矩形的周长可以通过将宽度和长度相加乘以2来计算，公式为：周长= 2 ×(宽度+ 长度)。

由于矩形的两条对边相等，所以宽度和长度可以互换位置得到相同的周长。

例如，一个矩形的宽度为3个单位，长度为5个单位，那么它的周长就是2 ×(3 + 5) = 16个单位。

除了面积和周长，矩形还有其他一些重要的性质。

首先，四个内角都是直角，即为90度。

这个特点使得矩形在建筑设计中广泛应用，因为直角可以使得建筑物更加稳定和结实。

其次，矩形的两条对边相等且平行。

这意味着矩形在对称性方面具有特殊性质。

对任意一条边进行平移、旋转或反射操作，都可以得到一个完全相同的矩形。

这个性质在几何学的证明和构造中经常使用。

此外，矩形还有一些与对角线相关的性质。

矩形的对角线相等且相互平分，意味着对角线的交点是矩形的中心。

同时，通过连接矩形的对角线，可以得到一个长方形。

长方形是特殊的矩形，其对角线相等且相互平分，但它的相邻边可以不相等。

矩形还有一些特殊情况，比如正方形。

正方形是一种具有特殊性质的矩形，它的四条边长度相等、四个内角都是直角。

矩形中考要求知识点睛矩形的性质及判定1．矩形的定义：有一个角是直角的平行四边形叫做矩形．2．矩形的性质矩形是特殊的平行四边形，它具有平行四边形的所有性质，•还具有自己独特的性质：①边的性质：对边平行且相等．②角的性质：四个角都是直角．③对角线性质：对角线互相平分且相等．④对称性：矩形是中心对称图形，也是轴对称图形．直角三角形斜边上的中线等于斜边的一半．直角三角形中，30 角所对的边等于斜边的一半．点评：这两条直角三角形的性质在教材上是应用矩形的对角线推得，用三角形知识也可推得．3．矩形的判定判定①：有一个角是直角的平行四边形是矩形．判定②：对角线相等的平行四边形是矩形．判定③：有三个角是直角的四边形是矩形．例题精讲模块一矩形的概念【例1】矩形的定义：__________________的平行四边形叫做矩形．【答案】有一个角是直角；【例2】矩形的性质：矩形是一个特殊的平行四边形，它除了具有四边形和平行四边形所有的性质，还有：矩形的四个角______；矩形的对角线______；矩形是轴对称图形，它的对称轴是____________．【答案】都是直角，相等，经过对边中点的直线；【例3】矩形的判定：一个角是直角的______是矩形；对角线______的平行四边形是矩形；有______个角是直角的四边形是矩形．【答案】平行四边形；对角线相等；三个角【例4】矩形具有而平行四边形不具有的性质为（ ）A ．对角线相等B ．对角相等C ．对角线互相平分D ．对边相等【解析】省略 【答案】A【巩固】矩形ABCD 中，点H 为AD 的中点，P 为BC 上任意一点，PE HC ⊥交HC 于点E ，PF BH ⊥交BH 于点F ，当AB BC ，满足条件 时，四边形PEHF 是矩形 【解析】省略 【答案】2BC AB =模块二 矩形的性质【例5】如图，矩形ABCD 沿AE 折叠，使D 点落在BC 边上的F 点处，如果60BAF ∠=︒，则DAE ∠=FED CBA【解析】省略 【答案】15︒【例6】矩形ABCD 中，对角线AC 、BD 相交于O ，∠AOB ＝60°，AC ＝10cm ，则BC ＝______cm ，周长为 ．【答案】，【例7】如图，在矩形ABCD 中，,E F 分别是,BC AD 上的点，且BE DF =. 求证：ABE ∆≌CDF ∆.D EFCAB【解析】省略【答案】∵四边形ABCD 是矩形∴90AB AD B D =∠=∠=，. 在ABE ∆和CDF ∆中， 又∵BE DF =， ∴ABE ∆≌CDF ∆.【例8】如图，在矩形ABCD 中，点E 是BC 上一点，AE AD =，DF AE ⊥，垂足为F .线段DF 与图中的哪一条线段相等？先将你猜想出的结论填写在下面的横线上，然后再加以证明。

矩形的性质和判定【知识梳理】一、定义：有一个是直角的平行四边形是矩形。

二、性质：①矩形的四个角都是直角②矩形的对角线相互平分且相等③矩形既是中心对称图形又是轴对称图形，有两条对称轴④矩形的面积S=长×宽三、判定：①有一个角是直角的平行四边形是矩形；②有三个角是直角的四边形是矩形；③对角线相等的平行四边形是矩形；④对角线相等且互相平分的四边形是矩形。

四、矩形与平行四边形的区别与联系：①相同点1、两组对边分别平行2、两组对边分别相等3、两组对角分别相等4、对角线相互平分②区别1、有一个角是直角的平行四边形矩形2、对角线相互平分且相等【例题精讲】考点1 矩形的性质【例1】已知：如图，在矩形ABCD中，BE=CF，求证：AF=DE。

【例2】如图，在矩形ABCD 中，,E F 分别是,BC AD 上的点，且BE DF =。

求证：ABE ∆≌CDF ∆。

【例3】如图，矩形ABCD 的两条对角线相交于点O ，60AOB ∠=︒，2AB =，则矩形的对角线AC 的长是（ ） A ．2 B ．4 C ．23 D ．43【变式1】下列性质中，矩形具有而平行四边形不一定具有的是（ ） A 、对边相等 B 、对角相等 C 、对角线相等 D 、对边平行【变式2】矩形ABCD 的对角线AC 、BD 交于O ，如果ABC ∆的周长比AOB ∆的周长大10cm ，则边AD 的长是 。

【变式3】如图，矩形ABCD 沿AE 折叠，使D 点落在BC 边上的F 点处，如果60BAF ∠=︒，则DAE ∠= 。

FED CBA考点2 矩形的判定【例4】如图，在△ABC 中，AB=AC ，D 为BC 中点，四边形ABDE 是平行四边形。

求证：四边形ADCE 是矩形。

【例5】如图，在平行四边形ABCD 中，E 是CD 的中点，△ABE 是等边三角形，求证：四边形ABCD 是矩形。

ODC BAD EFCAB【变式6】如图11，已知E 是ABCD 中BC 边的中点，连接AE 并延长AE 交DC 的延长线于点F 。

矩形的性质和判定基础知识点1、矩形的性质和判定：定 义矩 形有一个内角是直角的平行四边形。

性质边对边平行，对边相等。

角 四个角相等，都是直角。

对角线互相平分，相等。

判定有一个角是直角的平行四边形是矩形。

有三个角是直角的四边形是矩形。

对角线相等的平行四边形是矩形。

2、在直角三角形中，斜边的中线等于斜边的一半。

3、矩形是轴对称图形，对称轴是对边中点的连线所在的直线。

例题剖析例1、 已知矩形ABCD 中，AB=2BC ，点E 在边DC 上，且AE=AB ，求∠EBC 的度数．【变式练习】矩形ABCD 中，AC 与BD 交于O 点，BE ⊥AC 于E ，CF ⊥BD 于F ，•求证：BE=CF ．【变式练习】在矩形ABCD 中，AC ，BD 是对角线，过顶点C 作BD•的平行线与AB 的延长线相交于点E ，求证：△ACE 是等腰三角形．例2、折叠矩形ABCD 纸片，先折出折痕BD ，再折叠使A 落在对角线BD 上A ′位置上，折痕为DG ，AB=2，BC=1。

求AG 的长。

GA`DCBA【变式练习】如图，将矩形ABCD 沿对角线BD 折叠，使点C 落在F 的位置，BF 交AD 于E ，AD=8,AB=4，求△BED 的面积。

EDC BAF例3、在△ABC中，∠ABC=90°，BD是△ABC的中线，延长BD到E，•使DE=BD，连结AE，CE，求证：四边形ABCE是矩形．【变式练习】在△ABC中，AB=AC，D为BC中点，四边形ABDE是平行四边形。

求证：四边形ADCE是矩形。

例4、已知：如图，在△ABC中，AB=AC，点D为BC中点，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E．求证：四边形ADCE为矩形．【变式练习】（2011•青岛）在▱ABCD中，E、F分别是AB、CD的中点，连接AF、CE．（1）求证：△BEC≌△DFA；（2）连接AC ，当CA=CB 时，判断四边形AECF 是什么特殊四边形？并证明你的结论【变式练习】E 为□ABCD 外一点，AE ⊥CE,BE ⊥DE ，求证：□ABCD 为矩形例5、□ABCD 中，AE 、BF 、CG 、DH 分别是各内角的平分线，E 、F 、G 、H 为它们的交点， 求证：四边形EFGH 的矩形。

矩形的定义和性质
矩形的定义：有一个角是直角的平行四边形叫做矩形。

也就是长方形。

矩形的性质：
由于矩形是特殊的平行四边形，故包含平行四边形的性质；矩形的性质大致总结如下：
1、矩形具有平行四边形的所有性质：对边平行且相等，对角相等，邻角互补，对角线互相平分、矩形的四个角都是直角。

2、矩形的对角线相等、具有不稳定性（易变形）。

矩形的常见判定方法：
1、有一个角是直角的平行四边形是矩形、对角线相等的平行四边形是矩形。

2、有三个角是直角的四边形是矩形、经过证明，在同一平面内，任意两角是直角，任意一组对边相等的四边形是矩形、对角线相等且互相平分的四边形是矩形。

初中数学矩形的内角和外角的关系是什么矩形是一种特殊的四边形，它具有许多独特的性质。

在本篇文章中，我们将详细探讨矩形的内角和外角的关系。

首先，我们先来了解一下矩形的定义和性质：矩形的定义：矩形是一种四边形，其四个内角都是直角（90度）。

矩形的对边是平行的且相等。

在矩形中，相邻的两条边也是相等的。

矩形的性质：1. 矩形的内角都是直角（90度）。

2. 矩形的对边是平行的且相等。

3. 矩形的相邻两条边也是相等的。

4. 矩形的对角线相等且互相平分。

接下来，我们来探讨矩形的内角和外角的关系。

矩形的内角和外角的关系：1. 内角和：矩形的内角和等于360度。

由于矩形有四个内角，且每个内角都是直角（90度），所以矩形的内角和为4 × 90度= 360度。

2. 外角和：矩形的外角和也等于360度。

矩形的外角是指由矩形的两个相邻内角所组成的角。

每个内角的补角就是它所对应的外角。

因此，矩形的外角和等于4 × 90度= 360度。

证明：我们可以通过几何证明来证明矩形的内角和外角和都等于360度。

首先，根据矩形的定义，我们知道矩形的四个内角都是直角（90度）。

所以，矩形的内角和为4 × 90度= 360度。

其次，我们来证明矩形的外角和也等于360度。

设矩形的四个内角为A、B、C、D，其相邻的内角对为A和B，B和C，C和D，D和A。

我们需要证明∠A + ∠B + ∠C + ∠D = 360度。

根据矩形的定义，我们知道矩形的对边是平行的且相等。

所以，∠A和∠C是同位角，∠B和∠D 是同位角。

由于同位角的性质，我们可以得出：∠A + ∠C = 180度，∠B + ∠D = 180度。

将上述两个等式相加，我们可以得到：∠A + ∠B + ∠C + ∠D = (∠A + ∠C) + (∠B + ∠D) = 180度+ 180度= 360度。

因此，我们可以得出结论：矩形的外角和等于360度。

通过了解矩形的内角和外角的关系，我们可以更好地理解和应用矩形的性质。

矩形的性质总结
- 定义：矩形是一种具有四条边和四个直角的四边形。

- 一般性质：
- 对角线相等：矩形的两条对角线相等。

- 对边平行：矩形的对边两两平行。

- 四个内角均为直角：矩形的四个内角都是直角（90度）。

- 相邻内角互补：矩形的相邻内角互补，即相邻内角的和为180度。

- 面积和周长：
- 面积：矩形的面积可以通过长度和宽度的乘积计算，即$面积=长度 \times 宽度$。

- 周长：矩形的周长可以通过长度和宽度的两倍之和计算，即$周长=2 \times (长度 + 宽度)$。

- 相似矩形：
- 引理：如果两个矩形的对应边成比例，则这两个矩形相似。

- 相似性质：相似矩形的对应边长之比相等，并且对应的内角也相等。

- 特殊性质：
- 平方矩形：长度和宽度相等的矩形被称为平方矩形，它是一种特殊的矩形。

- 黄金矩形：长边与短边之比等于黄金比（约为1.618）的矩形被称为黄金矩形，它也是一种特殊的矩形。

矩形具有以上的性质，这些性质在几何学和实际生活中有着广泛的应用。

了解和熟悉这些性质，有助于我们更好地理解和应用矩形的相关概念。

6.2矩形的性质与判定定义：有一个角是直角的平行四边形是矩形.性质：（1）矩形具有平行四边形的一切性质.（2）四个角都是直角.（3）对角线相等.（4）是轴对称图形，有4条对称轴.定理：直角三角形斜边中线等于斜边的一半.判定：（1）有一个角是直角的平行四边形是矩形；（2）对角线相等的平行四边形是矩形；（3）有三个角是直角的四边形是矩形.基础闯关矩形的定义与性质1.矩形具有而一般的平行四边形不一定具有的特征是（）。

A．对角相等 B. 对边相等 C．对角线相等 D. 对角线互相平分2.矩形具有而菱形不具有的性质是（）A.两组对边分别平行B.对角线相等C.对角线互相平分D.两组对角分别相等3.矩形的两边长分别为10cm和15cm，其中一个内角平分线分长边为两部分，这两部分分别为（）A．6cm和9cm B．5cm和10cm C．4cm和11cm D．7cm和8cm 4.在下列图形性质中，矩形不一定具有的是（）A．对角线互相平分且相等 B．四个角相等C．是轴对称图形 D．对角线互相垂直平分5.一个矩形周长是12cm, 对角线长是5cm, 那么它的面积为 .6.矩形的两条对角线的夹角是60°，一条对角线与矩形短边的和为15，那么矩形对角线的长为，短边长为 .7.已知，矩形的一条边上的中点与对边的两个端点的连线互相垂直，且该矩形的周长为24 cm，则矩形的面积为 cm2。

8.如图，矩形ABCD中，E为AD上一点，EF⊥CE交AB于F，若DE=2，矩形ABCD 的周长为16，且CE=EF，求AE的长．9.已知：如图所示，矩形ABCD 中，E 是BC 上的一点，且AE=BC ，︒=∠15EDC ．求证：AD=2AB ．10.如图，ABCD 是矩形纸片，翻折∠B 、∠D ，使BC 、AD 恰好落在AC 上。

设F 、H分别是B 、D 落在AC 上的两点，E 、G 分别是折痕CE 、AG 与AB 、CD 的交点。

矩形的性质与判定知识点矩形是我们在数学中常见的一种几何图形，它具有许多独特的性质和判定方法。

下面让我们来详细了解一下矩形的性质与判定的相关知识点。

首先，矩形的定义是：至少有三个内角都是直角的四边形是矩形。

矩形的性质有很多：1、矩形的四个角都是直角。

这是矩形最显著的特征之一。

因为直角的度数是 90 度，所以矩形的四个内角相加为 360 度。

2、矩形的对边平行且相等。

这意味着矩形的两组对边分别平行，并且长度相等。

3、矩形的对角线相等且互相平分。

两条对角线将矩形分成了四个全等的三角形。

4、矩形是中心对称图形，也是轴对称图形。

其对称中心是两条对角线的交点，对称轴有两条，分别是通过对边中点的直线。

接下来，我们来看看矩形的判定方法。

1、有一个角是直角的平行四边形是矩形。

如果一个平行四边形中有一个角是直角，那么根据平行四边形邻角互补的性质，可以得出其他三个角也都是直角，从而这个平行四边形就是矩形。

2、对角线相等的平行四边形是矩形。

因为平行四边形的对角线互相平分，当两条对角线相等时，根据三角形全等可以证明其四个角都是直角，所以这个平行四边形就是矩形。

3、有三个角是直角的四边形是矩形。

如果一个四边形中有三个角都是直角，那么根据四边形内角和为360 度，第四个角也必然是直角，从而这个四边形就是矩形。

在实际应用中，矩形的性质和判定方法有着广泛的用途。

例如，在建筑设计中，房间的形状常常接近矩形。

设计师需要利用矩形的性质来计算房间的面积、周长等，以合理规划空间和安排材料。

矩形的四个角都是直角的性质，使得建筑物的结构更加稳定，施工更加方便。

在数学解题中，如果已知一个图形是矩形，我们就可以利用矩形的性质来解决与角度、边长、对角线等相关的问题。

反之，如果要证明一个图形是矩形，就可以根据矩形的判定方法来进行推理和证明。

再比如，在制作家具时，很多桌面、柜体的表面都是矩形。

了解矩形的性质可以帮助工匠们准确地测量和切割材料，确保制作出符合要求的家具。

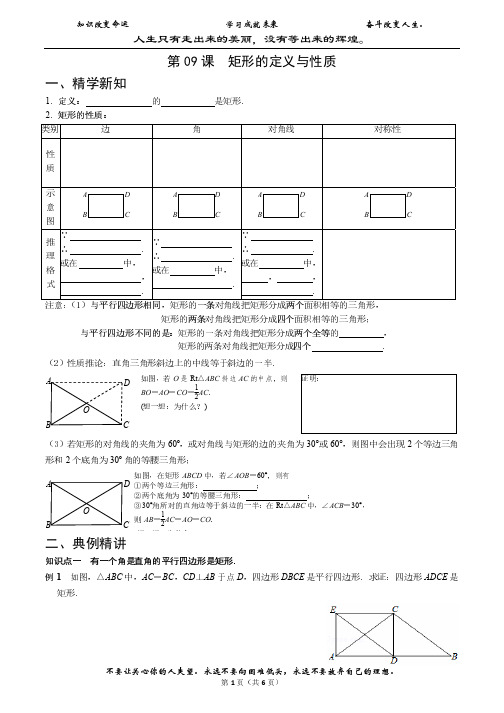
矩形的定义、性质一、知识要点引导1、矩形的定义： 定义的要素：（1） ，（2） .2、矩形的性质：（1）矩形是特殊的 ，具有 的一切性质.（2）矩形是轴对称图形，有 条对称轴，分别是经过 的直线；矩形也是中心对称图形，对称中心是 .（3）矩形的四个角都是 .（4）矩形的对角线 .3、直角三角形的性质：直角三角形斜边上的中线等于 .(注：条件①直角三角形，②斜边的中点.二者缺一不可.)二、例题分析例1．如图，矩形ABCD 的两条对角线AC 、BD 相交于点O,∠AOD=1200,AB=2cm.求矩形对角线的长.三、巩固练习1、如图, 矩形ABCD 的两条对角线AC 、BD 相交于点O,AB=6，OA=4.则BD= ，AD= .2、矩形ABCD 的周长是56cm,对角线AC 与BD 相交于点O,△OAB 与△ OBC 的周长差 是4cm,则矩形ABCD 的对角线长是.O D C BA3、如图,矩形纸片ABCD 中，已知AD=8,折叠纸片使AB 边与对角线AC 重合，点B 落在点F 处，折痕为AE ，且EF=3，则AB 的长为 .4、如图，在△ABC 中，∠ACB=90°，∠ABC=60°，BD 平分∠ABC ，点P 是BD 的中点.若AD=6，则CP 的长为 .5、如图，E 、F 分别是矩形ABCD 的对角线AC 和BD 上的点，且AE=DF.求证：BE=CF.6、如图，矩形ABCD 的对角线AC 、BD 相交于点O ，AE 平分∠BAD 交BC 于点E ， 已知∠CAE=15 °，AB=2cm ,求∠BOE 的度数和矩形的面积.7、如图，E 是矩形ABCD 的边CB 延长线上的一点，CE=CA ，F 是AE 的中点. 求证：BF ⊥FD.F E D CB A P DC BA O E D CB A F E D CB A8、如图,在矩形ABCD中,AB＝3,AD＝4, P是AD上不与A、D重合的一动点,PE⊥AC，PF⊥BD，E、F为垂足, 求PE＋PF的值.。

矩形知识点总结归纳矩形是一种常见的几何形状，在我们的日常生活和学习中起到了重要的作用。

它具有一些独特的性质和特点，本文将对矩形的定义、性质和相关公式进行总结归纳。

以下是关于矩形的各方面知识点的介绍：一、定义矩形是一种拥有四条边长度相等且相对平行的四边形。

它是特殊的平行四边形，同时也属于特殊的四边形。

二、性质1. 对角线互相平分：矩形的两条对角线互相平分，即两条对角线的交点是对角线的中点。

2. 内角度数：矩形的四个内角度数均为90度。

3. 边长关系：矩形的相邻边相等且平行。

三、周长和面积计算1. 周长：矩形的周长等于两条长边与两条短边的和，可以用公式 C = 2(a + b) 来计算，其中 a 和 b 分别表示矩形的长和宽。

2. 面积：矩形的面积是长乘以宽，可以用公式 A = a * b 来计算，其中 a 和 b 也表示矩形的长和宽。

四、对角线长度计算1. 对角线的长度：矩形的两条对角线长度相等，可以使用勾股定理来计算。

设矩形的长边长为 a，宽边长为 b，那么对角线的长度 D 可以用公式D = √(a² + b²)来计算。

五、特殊矩形除了一般的矩形外，还存在几种特殊的矩形形式：1. 正方形：正方形是一种特殊的矩形，它的四条边长度相等，且内角均为90度。

正方形的周长和面积计算公式与矩形相同，即 C = 4a 和A = a²，其中 a 表示正方形的边长。

2. 长方形：长方形也是一种矩形，特点是两条边长度不相等。

长方形的周长和面积计算公式同样适用于一般的矩形。

六、应用矩形作为一种常见的几何形状，广泛应用于日常生活和各个领域。

以下是几个典型的应用场景：1. 建筑设计：矩形是建筑设计中常见的形状之一，例如房屋的平面布局、墙壁的设计等。

2. 地理测量：在地理测量中，矩形可以用来表示土地的边界和测量区域的大小。

3. 学术研究：矩形被广泛运用于几何学的研究中，有助于推演和证明其他几何形状的性质。

矩形的性质与特点矩形作为一种常见的几何图形，具有其独特的性质和特点。

在本文中，我们将探讨矩形的定义、特征和相关性质，并讨论其在数学和实际生活中的应用。

1. 矩形的定义和基本特征矩形是一种拥有四条边、四个角均为直角的平面图形。

它的两对相邻边长度相等，对角线相等且互为半对称线。

根据这些定义，我们可以得到矩形的一些基本特征。

2. 矩形的四个角均为直角由于矩形的定义，它的四个角均为直角。

这意味着矩形的内角和为360度，且每个角的度数都为90度。

这是矩形与其他四边形的明显区别。

3. 矩形的对边相等且平行矩形的两对相邻边长度都相等，即对边相等。

同时，这两对对边也是平行的。

这意味着当我们将矩形平移或旋转时，其形状和大小保持不变。

4. 矩形的对角线相等且互为半对称线矩形的两条对角线相等且互为半对称线。

其中，半对称线是指将矩形分为两个全等的三角形。

这个性质使得矩形的对角线成为了研究和计算矩形性质的重要工具。

5. 矩形的面积和周长计算矩形的面积可通过将矩形分为两个全等的直角三角形，并利用三角形的面积公式进行计算：面积 = 长 ×宽。

而矩形的周长则是四个边长之和。

6. 矩形的性质在数学和实际生活中的应用矩形的性质和特点在数学教学和实际生活中都有广泛的应用。

在数学中，矩形作为一个简单且易于研究的几何图形，常被用于引入面积和周长的概念，以及介绍平行四边形和其他四边形的概念。

在几何证明中，我们也可以利用矩形的性质来推导其他几何定理。

在实际生活中，我们可以发现矩形的身影随处可见。

建筑物的窗户、墙壁、地板以及家具等往往采用矩形形状，因为矩形更易于设计、制造和布局。

同时，矩形在工程测量、地图绘制、电子屏幕和平面设计等领域也得到广泛应用。

总结：矩形作为一种常见的几何图形，具有四个直角、对边相等且平行、对角线相等且互为半对称线等基本特点。

它的性质在数学教学和实际生活中有着广泛的应用。

通过深入了解和研究矩形的性质，我们能够更好地理解几何学的基础知识，并将其应用于实际问题的解决中。