下载文档原格式
第5章时变电磁场和平面电磁波5.1 / 5.1-1 已知z2=1+j，求复数z的两个解。
2[解] z=1+j=jπjπ2e z1=2e=1.189ej22.5=1.099+j0.455j22.5 z2=-1.189e=-1.099-j0.4555.2 / 5.1-2 已知α是正实数，试证：(a)若α<<1,jα⎫⎛+jα≈± 1+⎪; 2⎝⎭jα⎫⎛+jα≈± 1+⎪;。
2⎭⎝(b)若α>>1,[解] ( a) α<<1: +jα=(b) α>>1:+α2ejtan-1α≈e(jααα⎫α⎫⎛⎛=± cos+jsin⎪≈± 1+j⎪ 22⎭2⎭⎝⎝+jα=+α2ejtanα-1≈⎛αe⎝jπ⎫⎪⎭ππ⎫⎛=± co+jsi⎪ 44⎭⎝=±(1+j)2=e+je，H（t）的复振幅为H =h+jh，试证5.3 / 5.1-3设E（t）的复振幅为Eii H ejωt，并求E（t）E(t)H(t)≠ReE、H（t）。
ejωt=1E ejωt+E *e-jωt [解] E(t)=ReE[][](2)1 jωt *e-jωt He+H21 * * H ej2ωt+E *H *e-j2ωt 得 E(t)H(t)=EH+EH+E41 H *+E H ej2ωt≠ReE H ejωt =ReE2H(t)=()()[][]E(t)=Re(e+jei)ejωt=Re[(e+jei)(cosωt+jsinωt)]=ecosωt-eisinωt 1 []H(t)=Re(h+jhi)ejωt=hcosωt-hisinωt E(t)H(t)=ehcos2ωt+eihisin2ωt-ehicosωtsinωt-eihcosωtsinωt []=1[eh+eihi+(eh-eihi)cos2ωt-(eh i+eih)sin2ωt] 2可见,为恒定成分与二倍频成分的叠加.5.4 / 5.1-4 将下列场矢量的瞬时值变换为复矢量，或作相反的变换：ˆE0sin(ωt-kz)+yˆ3E0cos(ωt-kz)； (a) (t)=xˆ⎢E0sinωt+3E0cos ωt+(b) (t)=x⎣ˆ+jyˆ)e(c) =(xˆjH0e(d) =-y⎡⎛⎝π⎫⎤⎪； 6⎭⎥⎦-jkz；。
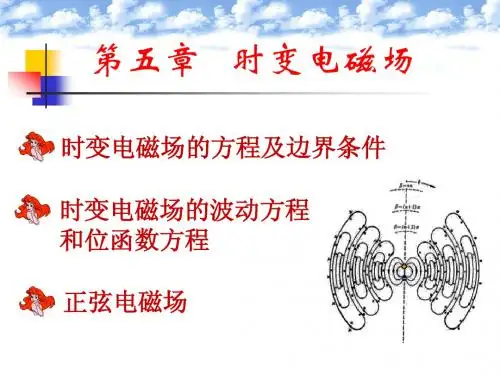
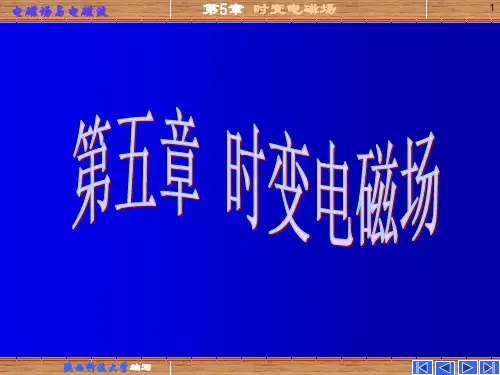
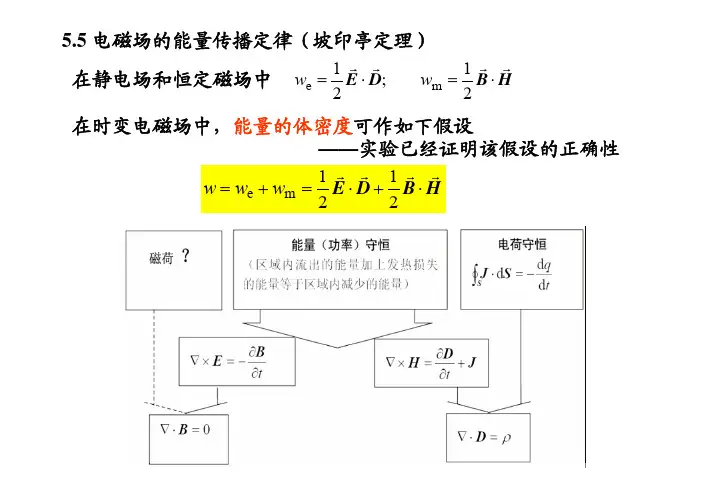
S
H H γ =∞
H
5.6 定解条件与唯一性定理
麦克斯韦方程组的微分形式、电荷守恒方程的微分形式以及分界面上的边界条件是时变电磁场必须满足的基本方程，但这组方程的解是通解，要想得到具体物理问题的定解——特解，还必须给定初始条件和边界条件，这些条件称为定解条件，与此相关的问题称为定解问题。
唯一性定理：在t>0的所有时刻，闭区域V内的电磁场是由整个V内的电和磁矢量的初始值，以及t≥0时边界上电矢量（或磁矢量）的切向分量的值所唯一确定。
第五章 时变电磁场5-1 如图5-1所示，一个宽为a 、长为b 的矩形导体框，放置在磁场中，磁感应强度为B e =B t y 0sin ω。
导体框静止时其法线方向e n 与y e 呈α角。
求导体框静止时或以角速度ω绕x 轴旋转（假定t =0时刻，α=0）时的感应电动势。
解 由于 y t B e B ωsin 0=，据 ⎰⎰⋅∂∂-=ste s Bd ， 导体框静止时，t B ab ab tBe ωωααcos cos cos 0-=⋅∂∂-= 导体框旋转时，()()tabB t ab B t ab t B tt ab B t t e ωωωωωωω2cos 2cos 221cos sin cos d 000s -=⨯⨯-=⋅∂∂-=⋅∂∂-=⋅∂∂-=⎰⎰s B5-2 设图5-2中随时间变化的磁场只有z 轴分量，并沿y 轴按B B y t B t ky z ==-(,)cos()m ω的规律分布。
现有一匝数为N 的线圈平行于xoy 平面，以速度v 沿y 轴方向移动（假定t =0时刻，线圈几何中心处y =0）。
求线圈中的感应电动势。
解 据 ()⎰⋅⨯=le l B v d 设 2,221avt y a vt y +=-=，则有 ()()[]()kvt vB Nb a vt k a vt k vB Nb y B y B v Nb e m m sin 2cos 2cos 2211⋅-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-⋅=+⋅=5-3 一半径为a 的金属圆盘，在垂直方向的均匀磁场B 中以等角速度ω旋转，其轴线与磁场平行。
在轴与圆盘边缘上分别接有一对电刷，如图5-3所示。
这一装置称为法拉第发电机。
试证明两电刷之间的电压为22Ba ω。
解 由于td d αω=，αωd d =t ，t ωα=，ωr v = 则有 ()⎰⎰=⋅=⋅⨯=a lBa r B r e 022d d ωωl B v5-4 设平板电容器极板间的距离为d ，介质的介电常数为ε0，极板间接交流电源，电压为u U t =m sin ω。
求极板间任意点的位移电流密度。
解 对于平板电容器，极间电场为均匀场，则有 t d U E m ωsin =，t dU E D m ωεεsin 0==，t d U e D J mD ωωεcos 0=∂∂= 5-5 一同轴圆柱形电容器，其内、外半径分别为cm 11=r 、cm 42=r ，长度m 5.0=l ，极板间介质的介电常数为04ε，极板间接交流电源，电压为t u π=100sin 26000 V 。
求t =10. s 时极板间任意点的位移电流密度。
解 对于同轴圆柱形电容器，由于l r <<，则极间电场强度和电压分别为r E πετ2=，12ln 2r r u πετ=，因此4ln ln 212u r r u ==πετ，r u E 14ln ⋅=，r u D 14ln 40⋅=ε，r t t D 14ln 100cos 1002600040⋅⨯⨯=∂∂=ππεJ ()250A/m 1081.64ln 100260004s 1r r rr t e e J -⨯=⋅⨯⨯==πε5-6 当一个点电荷以角速度ω作半径为R 的圆周运动时，求圆心处位移电流密度的表达式。
解 在圆心处，电位移矢量3244Rq R q r ππRe D ==，由于 αωe v r r t ==∂∂，则可得圆心处位移电流为 ()y x D t t R q R q R R q t R q t J e e e e R D ωωπωωπωππααcos sin 44442233-=⋅=⋅=∂∂⋅=∂∂= 5-7 一个球形电容器的内、外半径分别为a 和b ，内、外导体间材料的的介电常数为ε、电导率为γ，在内、外导体间加低频电压u U t =m cos ω。
求内、外导体间的全电流。
解 对于球形电容器，极间电场强度为 24r qE πε=， 电压 abab q b a q u --=⎪⎭⎫ ⎝⎛-⋅=πεπε4114，则有r a b uab E 1⋅-=，21r a b uab D ⋅-=ε 因此，传导电流密度 221cos 1r t a b ab U r a b uab E J m c ⋅⋅-=⋅-==ωγγγ 位移电流密度 21sin r t U a b ab t D J m D ⋅⋅⋅--=∂∂=ωωε 全电流密度 ()20sin cos rt t a b ab U m r J ⋅--=ωεωωγ 全电流 ()t t r ab abU J r I m ωεωωππsin cos 442--=⋅= 5-8 在一个圆形平行平板电容器的极间加上低频电压u U t =m sin ω，设极间距离为d ，极间绝缘材料的介电常数为ε，试求极板间的磁场强度。
解 圆形平行平板电容器极间的电场强度、电位移矢量及位移电流密度均为均匀场，即t d Ud u E m ωsin ==，t dU E D m ωεεsin ==，t d U t D J m D ωωεcos =∂∂= 据安培环路定律，可得 D J r r H 22ππ=，则 αωωεe H r d tU r J mD 2cos 2⋅== 5-9 在交变电磁场中，某材料的相对介电常数为εr =81、电导率为γ=42. S /m 。
分别求频率f 11=kHz 、f 21=MHz 、以及f 31=GHz 时位移电流密度和传导电流密度的比值。
解 据 f f J J c 9121007.12.421085.881--⨯=⨯⨯⨯==πγεωα，可得f 11=kHz 时，61007.1-⨯=cD J J；f 21=MHz 时，31007.1-⨯=c D J J ；f 31=GHz 时，07.1=cD J J5-10一矩形线圈在均匀磁场中转动，转轴与磁场方向垂直，转速min /r 3000=n 。
线圈的匝数100=N ，线圈的边长cm 2=a 、cm 5.2=b 。
磁感应强度B =01. T 。
计算线圈中的感应电动势。
解 转速 r/sec 50r/sec 603000r/min 3000===n ，角频率 rad/sec 100πω= 线圈截面 ab S =，磁通 t ab B ωφcos ⋅⋅=，磁链 t NBab N ωφψcos ⋅==线圈中的感应电动势t t t NBab te ωωπωψsin 57.1sin 250025.002.01.0100sin d d =⨯⨯⨯⨯⨯==-= V 11.1=有效值e5-11图5-4所示的一对平行长线中有电流i t I t ()sin =m ω。
求矩形线框中的感应电动势。
解 如图建立坐标系，则线框中任意点的磁感应强度为()()⎥⎦⎤⎢⎣⎡+--=-+-=a b r r a b i r i a b r i B πμπμπμ222 元磁通 r Bh d d =φ，则线圈所链绕的磁通zzc b b c b b a a c t b c b a b b a b c b i e e ⎪⎭⎫ ⎝⎛+⋅+=⎪⎭⎫ ⎝⎛+-+-+-+==⎰+ln 2ln ln 2d πμπμφφ线圈的感应电动势()()t c b a a c b h I t d e m ωπμωφcos ln 2d ++⋅-=-= 5-11 一根导线密绕成一个圆环，共100匝，圆环的半径为5cm ，如图5-5所示。
当圆环绕其垂直于地面的直径以500 r /min 的转速旋转时，测得导线的端电压为mV 5.1（有效值），求地磁场磁感应强度的水平分量。
解 转速 r/s 60500r/min 500==n ，角频率 rad/s 605002⨯=πω， 线圈截面 222m 00785.005.0=⨯==ππr S通过线圈的磁通量 t BS ωφcos =，相应的磁链 t NBS N ωφψcos ==，则线圈的电动势为 t NBS te ωωψsin d d =-=， 电动势的有效值 V 105.1260500205.0100232-⨯=⨯⨯⨯⨯==B NBS e ππω有效值因此，所求地磁 T 1016.5500205.010*******.1523--⨯=⨯⨯⨯⨯⨯=ππB 5-13 真空中磁场强度的表达式为()x t H H z z z β-ω==sin 0e e H ，求空间的位移电流密度和电场强度。
解 据磁场强度表达式，可得电场强度 ()x e E y βω-=sin 0e E ，又00ωεβεμ==HE，则 y x t H e E )sin(00βωωεβ-=，()y x t H e D βωωβ-=sin 0 位意电流密度 ()()y y D x t H x t H t e e D J βωββωωωβ-=-=∂∂=cos cos 005-14 已知在某一理想介质中的位移电流密度为J e D x t z =-25sin()ωμ A /m 2，介质的介电常数为ε0，磁导率为μ0。
求介质中的电场强度E 和磁场强度H 。
解 据位移电流表达式，可得 ()2A/m 5sin 2μz t tx e D-=∂∂ω 则可得电位移矢量 ()x z e e D 5cos 2--=ωω，电场强度 ()x z e e DE 5cos 2--==ωωεε磁场强度 ()()A/m 5cos 525cos 0μωωβωεy x z t z e E e e H --=--=5-15 由两个大平行平板组成电极，极间介质为空气，两极之间电压恒定。
当两极板以恒定速度v 沿极板所在平面的法线方向相互靠近时，求极板间的位移电流密度。
解 设两极板间的初始距离为0x ，在时刻t ，极板间的距离为x ，则vt x x -=0， 极间电场强度 x UE =，电位移矢量 vtx U x U D -==000εε 因此，位移电流密度 xvt x vU t e D J ⎥⎦⎤⎢⎣⎡-=∂∂=200)(ε 第六章 电磁场能量6-1 一个空气介质的电容器，若保持极板间电压不变，向电容器的极板间注满介电常数为εε=40的油，问注油前后电容器中的能量密度将如何改变？若保持电荷不变，注油前后电容器中的能量密度又将如何改变？解 平行极板间电场强度和电位移矢量分别为 d UE =，d U D ε= 当极板间电压不变时，空气介质中电场能量密度 02202121ε⋅⋅==dU ED w注油后电场能量密度 00224421w dU w =⋅⋅=ε当极板上电荷不变时，极板上的电荷面密度SQ =σ ，则电场强度 εσ=E ，电位移矢量 σ=D ，空气介质中电场能量密度0202121εσ⋅=⋅=ED w 注油后电场能量密度 00225.042w w =⨯⨯=εσ6-2 内、外两个半径分别为a 、b 的同心球面极板组成的电容器，极板间介质的介电常数为ε0，当内、外电极上的电荷分别为q ±时，求电容器内储存的静电场能量。
