运筹学

运筹学的定义
运筹学是一门研究决策的学科，它综合了数学、统计学、信息学、经济学、管理学等多个领域的知识和技术，旨在通过科学的方法来解决实际问题。

运筹学在现代社会中拥有广泛的应用，涉及到许多领域，如物流、交通、金融、医疗、能源等。

运筹学的主要目标在于找到最优解决方案。

例如，在物流领域，如何在有限的时间内将货物运输到目的地，同时降低运输成本；在金融领域，如何通过科学的投资策略来最大化收益，同时降低风险。

这些问题都可以通过运筹学的方法来解决。

为了实现这些目标，运筹学应用了许多技术和方法。

其中最常用的是线性规划，即在一组约束条件下最小化或最大化一个线性函数。

除此之外，运筹学还包括非线性规划、整数规划、动态规划、图论、排队论、模拟等等方法。

这些方法都有不同的应用场景，可以根据具体问题的特点选择最合适的方法。

运筹学的应用不仅限于商业领域，也可以用于解决社会问题。

例如，在医疗领域，如何最大化患者的生存率，同时降低医疗成本；在能源领域，如何通过科学的能源规划来提高能源利用效率，降低污染和排放。

这些问题都需要运筹学的方法来提供解决方案。

运筹学是一门非常实用的学科，它可以为我们提供科学的决策方法，解决实际问题。

随着科技的发展和社会的进步，运筹学的应用范围
也将更加广泛。

我们应该深入学习和应用运筹学的知识和方法，为实现更高效、更节约、更可持续的社会发展做出贡献。

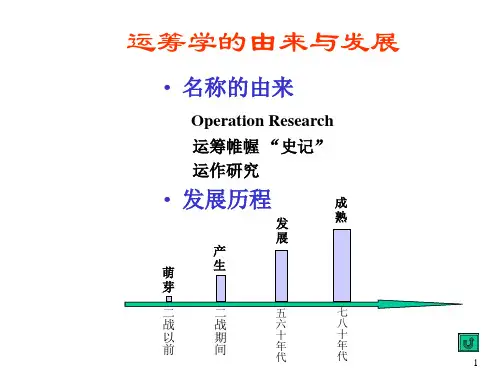
运筹学综述运筹学的简介一：什么是运筹学？运筹学是Operations Research的英文单词缩写。

运筹学界的元老说运筹学是执行部门对所控制的业务做出决策提供数量上的依据的科学或利用所有应用科学执行部门对其所属业务作出决策提供数量上依据的一门科学；世界上最早的运筹学协会说运筹学是运用科学方法来解决工业、商业、政府、国防等部门里有关人力、机器、物资、金钱等大型系统的指挥或管理中所出现的复杂问题的一门学科,其目的是“帮助管理者以科学方法确定其方针和行动”。

二:运筹学的三个来源1、军事二战期间例一：在第二次世界大战期间，鲍德西雷达站的研究——“布莱克特马戏团”的出色工作，Bawdsey雷达站—Blackett杂技班专门就改进空防系统进行研究。

成员组成：心理学家3，数学家2，数学物理学家2，天文物理学家1，普通物理学家1，陆军军官1，测量员1。

研究的问题是设计将雷达信息传送给指挥系统及武器系统的最佳方式；雷达与防空武器的最佳配置；对探测、信息传递、作战指挥、战斗机与防空火力协调等获得成功，大大提高了英国本土的防空能力,不久以后在对抗德国对英伦三岛的狂轰滥炸中发挥了极大的作用，堪称运筹学的发祥与典范，展示了运筹学的本色与特色。

二战期间例二：大西洋反潜战——Morse小组的重要工作。

1942年麻省Morse教授应美国大西洋舰队反潜战官员Baker舰长的请求担任反潜战运筹组的计划与监督工作，其最出色的工作之一是协助英国打破了德国对英吉利海峡的海上封锁，研究所提出的两条重要建议是：将反潜攻击由反潜舰艇投掷水雷改为飞机投掷深水炸弹，起爆深度由100米改为25米左右，即当德方潜艇刚下潜时攻击效果最佳；运送物资的船队及护航舰艇的编队由小规模、多批次改为大规模、少批次，从而减少了损失率丘吉尔采纳Morse的建议，从而打破德国封锁；重创德国潜艇部队；Morse同时获得英国及美国战时最高勋章二战期间例三：英国战斗机中队援法决策。

运筹学涉及的数学知识
摘要：
一、引言
二、运筹学简介
三、线性规划
四、整数规划
五、动态规划
六、网络优化
七、总结
正文：
运筹学是一门运用数学和统计学方法对实际问题进行建模、优化和求解的学科。

它广泛应用于生产调度、交通运输、资源分配等领域。

本文将简要介绍运筹学涉及的数学知识。

首先，线性规划是运筹学的基础知识。

线性规划研究在一定约束条件下线性目标函数的最优化问题。

它可以用矩阵表示，并使用单纯形法等数学方法求解。

其次，整数规划是线性规划的特殊情况，要求部分或全部变量取整数值。

整数规划在运输、调度和选址等问题中具有重要意义。

常用的求解方法有分枝定界法、割平面法等。

动态规划是另一种重要的优化方法。

它将问题分解成相互联系的子问题，通过求解子问题并将结果存储起来，以避免重复计算，从而提高效率。

动态规
划广泛应用于最短路径、背包问题等领域。

网络优化是运筹学的另一个重要分支，研究在网络结构中的最优化问题。

这类问题可以描述为带权的有向图，通过求解最短路径、最大流等问题，可以有效地改善网络的性能。

总之，运筹学涉及的数学知识包括线性规划、整数规划、动态规划和网络优化等。

运筹学的概念运筹学是一种综合性学科，它在现代管理中起着至关重要的作用。

运筹学是一种运用数学、统计学、计算机科学以及其他相关领域的方法和理论来帮助制定最优决策的学科。

它的主要目标是通过通过信息分析和决策模型来使决策者在制定决策时更加合理、科学和精准。

下面是对运筹学概念的详细介绍。

一、运筹学的基本定义运筹学（Operations Research，简称OR）是一门科学，通过使用计算机和数学模型，研究如何最好地利用有限资源来达到预期目标，主要研究方法包括优化、数理统计、决策分析、模拟等。

二、运筹学的发展历程运筹学是在二战期间发展出来的，主要应用于军事后勤问题的解决。

之后，运筹学学科马不停蹄地在各个领域快速发展，至今已经成为了一门广泛的学科。

三、运筹学的应用范围运筹学在各个领域都有广泛的应用，例如生产制造、物流管理、金融风险管理、医疗管理、资源分配等。

它在实践中的应用能够使企业和组织在有限的资源下获得最大收益。

例如，电商企业可以利用运筹学和网络优化技术来解决配送问题。

医院可以利用运筹学与供应链的整合优化来提高采购成本的效率。

银行等金融机构则可以利用运筹学来建立风险管理模型，减轻市场波动造成的经济损失。

四、运筹学的关键技术该学科主要基于优化、数学建模、统计推断和计算机仿真等关键技术。

对于不同的问题，会采用不同的技术手段。

例如，对于线性规划问题，使用线性规划算法进行求解；对于决策树问题，可以使用决策树算法进行求解；对于复杂的大规模问题，可以使用数学建模与计算机仿真技术进行求解。

总之，运筹学是为了解决实际问题而产生的一种学科，它在生产、经济、政策等许多领域有广泛应用，发展迅速，使得成本降低、管理规范化、业务流程优化等问题得到了解决。

运筹学的起源与发展运筹学是一门研究优化资源配置、提高系统效率的学科。

从古代的军事思想和管理哲学中起源，运筹学经过多个阶段的发展，已成为解决现实问题不可或缺的工具。

1、运筹学的起源运筹学的思想可以追溯到古代。

例如，古代的军事家在策划战役时，会考虑兵力、战略和战术等因素，力求以最小的代价取得最大的胜利。

这种对资源优化配置的追求，正是运筹学的核心思想。

在管理哲学中，运筹学也得到了应用，如古代的皇帝在治理国家时，会考虑各种资源、政策和社会稳定等因素，以制定出最优的政策。

2、运筹学的发展运筹学真正的发展是在20世纪初。

当时，由于工业革命的出现，人们开始面对更加复杂的大规模问题，如生产计划、物资管理和交通运输等。

这些问题的出现促进了运筹学的诞生。

2.1产生阶段20世纪初，一些科学家开始运用数学和统计学方法来解决实际问题。

例如，亨利·福特在生产线上采用流水线生产方式，大大提高了汽车的生产效率。

这个阶段的主要成果是确定了运筹学的基本研究方法和应用领域。

2.2发展阶段在20世纪中叶，运筹学得到了进一步发展。

随着计算机技术的进步，运筹学开始采用更加高效的算法和优化技术，以解决更加复杂的问题。

例如，兰德公司在这个时期为美国军方提供了一系列重要的优化方案，为美国在冷战中的胜利做出了贡献。

2.3成熟阶段进入21世纪，运筹学已经发展成为一门成熟的学科。

随着大数据和人工智能等新技术的出现，运筹学开始与这些领域深度融合，形成了诸多新的研究方向和应用领域。

例如，机器学习和人工智能技术在运筹学中的应用，为解决实际问题提供了更加强大的支持。

3、运筹学的应用运筹学在各个领域都有广泛的应用。

在商业领域，运筹学被用来制定供应链管理、生产计划和库存管理等策略，以提高企业的效率和竞争力。

例如，亚马逊通过运用运筹学算法来优化其物流和仓储系统，从而实现了高效的商品配送和服务。

在工业领域，运筹学被应用于生产过程优化、设备维护和能源管理等方面。

运筹学的名词解释运筹学（Operations Research），又被称为运筹学、管理科学或决策科学，是一门综合运用数学、经济学和工程学等多学科的方法和技术，解决复杂问题的学科。

运筹学的主要目标是通过最优化方法和决策分析，提高系统的效率、效果和可行性。

运筹学的应用范围非常广泛，几乎涉及到各个领域，包括工业制造、物流管理、交通运输、金融投资、医疗卫生、军事战略、环境保护等等。

无论是企业的生产调度、供应链管理，还是城市交通的拥堵优化、航空航线的规划，运筹学都能发挥重要作用。

在运筹学的分析中，最为常见的方法之一是最优化。

最优化在数学中是一个非常重要的概念，它可以帮助我们找到一个系统或者问题的最佳解决方案。

最优化方法可以通过建立数学模型和运用优化算法来实现。

在实际应用中，最优化方法可以用来解决资源利用、成本控制、风险管理等问题，从而提高整个系统的效率和竞争力。

除了最优化方法，运筹学还涉及到决策分析。

决策分析是通过建立决策模型，分析不同决策方案的优劣，并选择最佳的决策方案。

决策分析可以帮助管理者在不确定性和风险下作出明智的决策。

在现实生活中，决策分析可以应用于项目管理、投资决策、市场营销、风险评估等方面，对于优化资源配置和风险控制起到关键作用。

运筹学的研究方法可以分为定量研究和定性研究两大类。

定量研究是基于数学、统计和计算机等工具，通过数据分析和模型建立，进行量化分析的研究方法。

定量研究可以提供精确的数据和结果，有助于准确判断问题的本质和解决方案的有效性。

而定性研究则更注重于描述性和解释性的研究方法，通过文字叙述、案例分析等方式，挖掘问题背后的隐含规律和原因。

定性研究可以帮助我们深入理解问题的本质，从而更好地制定解决方案。

运筹学的发展离不开计算机的支持。

随着计算机技术的进步，运筹学得以快速发展并取得了重大的突破。

计算机可以进行大规模的数据分析和模型求解，提高运筹学的效率和精确度。

同时，计算机还可以完成复杂的运算和优化算法，为决策提供多种方案，并通过模拟实验进行验证。