实验四介观动力学模拟

化学反应动力学模型的建立与分析一、化学反应动力学模型建立的步骤1.收集实验数据：首先需要进行实验，收集反应物浓度随时间变化的数据。

实验条件可以根据需要进行调节，如温度、浓度、催化剂等。

可以通过实验方法，如光谱、色谱、电位法、质谱等对反应物浓度进行测定。

2. 确定反应级数：根据实验数据分析反应级数。

一级反应速率与反应物浓度成正比，二级反应速率与反应物浓度的平方成正比。

可以通过对反应物浓度进行对数处理，绘制ln[A] vs t或者1/[A] vs t得到指数趋势图，从图形上判断反应级数。

3.构建速率方程：根据反应级数确定速率方程。

一级反应速率方程为r=k[A]，二级反应速率方程为r=k[A]²。

可以将速率方程与实验数据进行拟合，确定反应速率常数k。

4.推导反应机理：通过实验数据和速率方程，推导反应机理。

可以根据速率方程，确定反应的中间产物和反应活化能。

二、化学反应动力学模型分析的方法1.速率常数的求解：速率常数k是化学反应速率与反应物浓度的关系参数，可以通过实验数据拟合得到。

常见的拟合方法有线性拟合和非线性拟合。

可以通过最小二乘法拟合实验数据点，得到速率常数的估计值。

2.动力学模型的验证：建立化学反应动力学模型后，需要进行模型验证。

可以使用其他实验数据进行验证，或者通过计算机模拟进行验证。

验证的目的是确认模型的准确性和可靠性，以便用于预测和解释其他化学反应。

3.动力学参数的确定：根据实验数据和模型分析结果，确定动力学参数，如反应速率常数k、反应级数、反应活化能等。

这些参数可以提供反应机制、反应速率常数以及温度、压力等条件的依赖关系。

4.动力学模型的应用：通过分析动力学模型，可用于预测反应速率、优化反应条件、设计反应工艺和控制反应过程。

通过改变温度、浓度、催化剂等条件，可以实现改变反应速率和反应选择性的目的。

总结：建立和分析化学反应动力学模型是研究反应速率和机理的重要方法。

通过收集实验数据，确定反应级数和速率方程，推导反应机理，可以建立动力学模型。

分子动力学模拟实验步骤
嘿，朋友们！今天咱来聊聊分子动力学模拟实验步骤这档子事儿。

咱先得有个明确的目标吧，就好比你要去个地方，得知道去哪儿呀！这分子动力学模拟实验也一样，你得清楚自己要研究啥。

然后呢，就是选个合适的模型啦。

这就像你出门得挑双合脚的鞋子，模型不对，那后面的路可就不好走咯。

得仔细琢磨琢磨，找个能准确反映实际情况的模型。

接下来，设置好各种参数。

这可不能马虎，就跟你调电视音量似的，得恰到好处。

温度啊、压力啊、粒子间的相互作用啥的，都得考虑周全。

再之后，让计算机开始运算吧！这计算机就像个勤劳的小蜜蜂，嗡嗡嗡地帮咱干活。

咱就等着看它给出的结果。

在这过程中，你得时刻盯着点，看看有没有啥不对劲的地方。

这就好比你煮汤的时候得时不时看看火，别煮糊了呀。

等计算机算完了，就该分析结果啦。

这可需要点真本事，得从那些密密麻麻的数据里找出有用的信息。

这就像在一堆沙子里找金子，得有耐心，还得有好眼神。

分析完结果，要是不满意咋办？那就重新来呗！别灰心，科学家们不都是这样一点点摸索过来的嘛。

你说这分子动力学模拟实验像不像搭积木？一块一块地往上搭，搭错了就重新来，直到搭出你想要的那个城堡。

这中间的乐趣和挑战，只有试过才知道呀！
总之，分子动力学模拟实验可没那么简单，但也绝对不是高不可攀的。

只要咱一步一个脚印，认真去做，肯定能发现其中的奥秘。

大家加油干吧，说不定下一个重大发现就是你做出来的呢！
原创不易，请尊重原创，谢谢!。

化学反应动力学模型建立与模拟方法教程为了深入了解化学反应过程并预测其动力学行为，建立适当的模型是至关重要的。

化学反应动力学模型的建立能够提供相关参数和反应速率方程，从而使研究者能够更好地理解反应机理和优化反应条件。

本文将介绍化学反应动力学模型建立与模拟的基本步骤和方法。

第一步是数据收集。

在建立反应动力学模型之前，需要收集实验数据。

实验数据应包含反应物浓度、反应温度和反应速率等信息。

这些数据可通过实验室实验或文献调研获得。

数据收集是建立可靠模型的基础，因此务必确保数据的准确性和全面性。

第二步是选择适当的模型。

根据反应的特性和目的，可以选择不同类型的动力学模型。

常见的模型包括一级反应、二级反应、阻滞动力学和微分动力学等。

选取合适的模型需要考虑反应机理和反应条件等因素。

第三步是参数估计。

参数估计是建立反应动力学模型过程中的关键步骤。

参数包括反应速率常数、活化能和反应级数等。

参数估计可以通过不同的统计方法、优化算法和曲线拟合等进行。

最常用的方法是最小二乘法，通过最小化实验数据和模型预测值之间的平方误差来估计参数。

第四步是模型验证。

模型验证是确认所建立模型的可靠性和准确性的重要环节。

通过将模型的预测结果与实验数据进行比较，可以评估模型的精确度和适用性。

如果模型表现良好，即能够准确预测实验数据，则可以认为该模型是可靠的。

除了建立动力学模型，还可以利用模型进行反应模拟。

反应模拟可以预测不同反应条件下的反应动力学行为。

通过改变反应物浓度、温度和反应时间等参数，可以预测反应速率和产物生成量的变化趋势。

反应模拟能够帮助研究者优化反应条件，提高反应效率和选择合适的反应条件。

在进行反应模拟之前，需要对模型进行合理的参数选择。

参数选择可以基于实验数据或文献中已有的参数值。

同时，也可以通过灵敏度分析来评估参数对模型预测结果的影响程度。

灵敏度分析可以帮助确定关键参数，进一步优化模型。

反应模拟的过程中，可以使用不同的数值方法求解动力学方程。

分子动力学模拟实验报告篇一：分子动力学实验报告 md2分子动力学实验报告（ XX 至 XX 学年第_2_学期）班级：姓名：学号：实验名称：晶体点缺陷成绩：一、实验目的计算空位形成能和间隙原子形成能。

探究形成的空位和间隙原子所在的位置不同其形成能的变化。

以及空位和间隙原子的浓度不同时其空位能和间隙原子形成能的变化。

二、实验原理点缺陷普遍存在于晶体材料中，它是晶体中最基本的结构缺陷，对材料的物理和化学性质影响很大。

根据点缺陷相对于理想晶格位置可能出现的几种主要偏差状态，可将其命名如下：（1）空位：正常节点位置上出现的原子空缺。

（2）间隙原子（离子）：指原子（离子）进入正常格点位置之间的间隙位(本文来自：小草范文网:分子动力学模拟实验报告)置。

（3）杂质原子（离子）：晶体组分意外的原子进入晶格中即为杂质，杂质原子若取代晶体中正常格点位置上的原子（离子）即为置换原子（离子），也可进入正常格点位置之间的间隙位置而成为填隙的杂质原子（离子）。

一般情况下，空位、间隙原子都是构成晶体的原子或离子偏离原有格点所形成的热缺陷。

在一定温度下，晶体中各原子的热振动状态和能量并不同，遵循麦克斯韦分布规律。

热振动的原子某一瞬间可能获得较大的能量，这些较高能量的原子可以挣脱周围质点的作用而离开平衡位置，进入到晶格内的其他位置，于是在原来的平衡格点位置上留下空位。

根据原子进入晶格内的不同位置，可以将缺陷分为弗伦克尔（Frenkel）缺陷和肖特基（Schottky）缺陷。

点缺陷都只有一个原子大小的尺度，因此不容易通过实验对其进行直接的观察。

而且实验方法研究缺陷时利用较多的还是缺陷对晶体性质的影响。

例如，通过测量晶体的膨胀率和电阻率的变化规律，即可对点缺陷的存在、运动和相互作用等方面展开间接的研究。

分子动力学方法对金属材料原子尺度物理和化学过程的研究具有实验法无法比拟的优势，可直观的模拟和分析晶体中的点缺陷。

若我们搭建完整晶体的原子个数为N，能量为E1，通过删除和增加一个原子得到空位和间隙原子，充分弛豫后体系能量为E2，则空位形成能Ev 和间隙原子形成能Ei分别为：三、实验过程（1）进入2_point文件夹$cd口2_point（2）运行in.inter文件，得到Cu的八面体间隙原子的图像，以及体系的总能量的变化，计算出八面体间隙原子的形成能。

化学反应的动力学模拟化学反应中的动力学过程是指反应速率的变化规律，即反应物转化为生成物的速率。

为了更好地理解和研究化学反应的动力学规律，科学家们发展了许多动力学模拟方法。

本文将介绍一些常用的化学反应动力学模拟技术及其应用。

一、量子力学方法量子力学是一种精确描述原子和分子行为的数学理论。

在化学反应动力学模拟中，研究人员通常使用量子力学方法，如密度泛函理论（DFT）和分子力场（MM）等。

DFT可以模拟物质的电子结构和分子振动，通过计算反应物和过渡态的能量，可以得到反应的活化能、反应速率常数等动力学参数。

分子力场方法则是通过精确描述原子间相互作用势能曲线，进而计算反应的转化率和反应速率。

二、分子动力学模拟方法分子动力学模拟是一种基于牛顿力学原理的计算方法，通过模拟原子和分子的运动轨迹，研究它们在不同温度和压力下的行为。

分子动力学模拟可以计算反应物和过渡态的构象、能量、速度等信息，从而预测反应的速率常数和反应机理。

三、反应坐标方法反应坐标方法是一种通过构建反应的势能面来模拟化学反应动力学的方法。

在反应坐标方法中，将反应转化为一系列过渡态，通过计算过渡态的活化能、反应路径等参数，可以探究反应的速率和反应机理。

常用的反应坐标方法有能均面动力学和内禀反应坐标。

四、蒙特卡洛模拟方法蒙特卡洛模拟是一种随机模拟方法，通过大量的概率采样，模拟系统的演化过程。

在化学反应的动力学模拟中，蒙特卡洛模拟能够模拟反应物和过渡态的构象空间，通过大量的随机采样，可以得到反应的速率和转化率等动力学参数。

五、应用案例动力学模拟在化学反应中有广泛的应用。

例如，科学家通过动力学模拟探究了一系列重要反应的速率常数和反应机理。

同时，动力学模拟还可以帮助研究人员优化反应条件，提高反应的速率和选择性。

总结：化学反应的动力学模拟方法包括量子力学方法、分子动力学模拟、反应坐标方法和蒙特卡洛模拟等。

这些方法能够帮助我们理解反应的速率和机理，优化反应条件，推动化学反应领域的研究和应用。

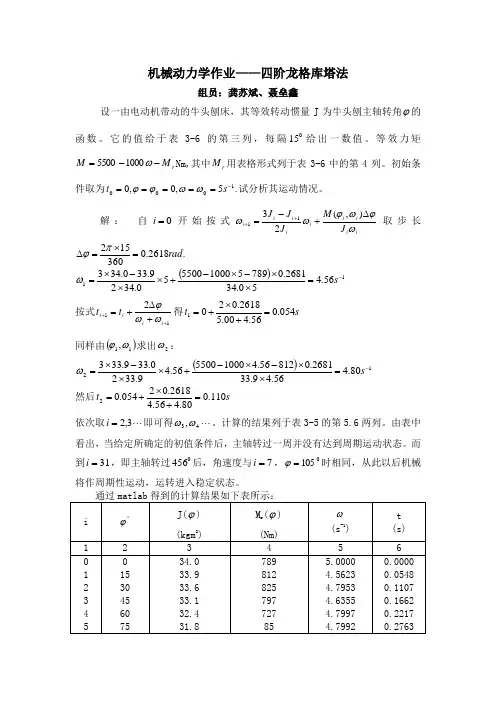
机械动力学作业——四阶龙格库塔法组员：龚苏斌、聂垒鑫设一由电动机带动的牛头刨床，其等效转动惯量J 为牛头刨主轴转角ϕ的函数。

它的值给于表3-6的第三列，每隔015给出一数值。

等效力矩r M M --=ω10005500Nm,其中r M 用表格形式列于表3-6中的第4列。

初始条件取为.5,0,01000-=====s t ωωϕϕ试分析其运动情况。

解： 自0=i 开始按式ii i i i i i i i J M J J J ωϕωϕωω∆+-=++),(2311取步长.2618.0360152rad =⨯=∆πϕ ()1156.450.342681.078951000550050.3429.330.343-=⨯⨯-⨯-+⨯⨯-⨯=s ω 按式112+++∆+=i i i i t t ωωϕ得s t 054.056.400.52618.0201=+⨯+=同样由()11,ωϕ求出2ω：()1280.456.49.332681.081256.41000550056.49.3320.339.333-=⨯⨯-⨯-+⨯⨯-⨯=s ω 然后s t 110.080.456.42618.02054.02=+⨯+=依次取 3,2=i 即可得 43,ωω。

计算的结果列于表3-5的第5.6两列。

由表中看出，当给定所确定的初值条件后，主轴转过一周并没有达到周期运动状态。

而到31=i ，即主轴转过0456后，角速度与7=i ，0105=ϕ时相同，从此以后机械将作周期性运动，运转进入稳定状态。

运用四阶龙格—库塔公式)22(6143211k k k k i i ++++=+ωω其中，),(1i i hf k ωϕ=、)2,2(12k h hf k i i ++=ωϕ、)2,2(23k hhf k i i ++=ωϕ、),(33k h hf k i i ++=ωϕ。

主要函数ωϕωωϕωϕJ d dJM f 2),(),(2-=,其中ϕϕ∆-=+i i i J J d dJ 1)(利用上述的公式在matlab 中编写程序，主要就是编写循环函数。

动力学模拟的主要步骤那动力学模拟呢，一开始得确定模拟的系统。

这就像是你要搭建一个小世界，你得先想好这个世界里都有啥呀。

比如说，是一堆原子呢，还是一些分子，得把这些参与的“小成员”都确定好。

这一步可不能马虎哦，要是少了哪个关键的“小成员”，那后面模拟出来的结果可能就会差之千里啦。

接着呢，要给这个系统设定初始条件。

这就好比给这个小世界一个初始的状态。

比如这些原子或者分子的初始位置、初始速度啥的。

你想啊，如果一开始就乱套了，那这个小世界的发展肯定也不正常呀。

就像玩游戏，开局的布局和状态要是不对，后面可就难搞喽。

然后呢，就是选择合适的力场啦。

力场就像是这个小世界里的规则制定者。

它决定了这些原子或者分子之间是怎么相互作用的。

不同的力场适用于不同的系统哦。

选错了力场，就像是在足球比赛里用了篮球的规则，那整个游戏就乱套啦。

再之后就是进行模拟计算啦。

这个时候计算机就开始忙乎起来啦，根据前面设定的那些条件和规则，开始计算这个系统随着时间的推移会发生什么样的变化。

这就像是看着这个小世界慢慢发展，看原子们怎么跑来跑去，分子们怎么相互碰撞、结合或者分开。

这个过程可能会有点漫长呢，就像等一朵花开一样，要有耐心。

最后呀，得对模拟的结果进行分析。

这就像是看完一场电影后，要总结一下电影讲了啥一样。

看看模拟出来的数据是不是符合我们的预期，有没有发现什么新的有趣的现象。

要是结果不太对，那可能就得回头看看前面的步骤是不是哪里出了岔子。

动力学模拟虽然有点复杂，但就像一场有趣的探索之旅呢。

每一步都很重要，就像拼图一样，少了一块都拼不出完整的画面。

宝子，这么一讲是不是感觉也没那么神秘啦？。

《计算材料学》实验讲义粗粒度模拟实验名称：介观动力学模拟一、前言1、介观模拟简介长期以来，化学家致力于从分子水平研究物质及其变化，而化学工程工作者主要研究物质在宏观体系的行为，介观层次的化学正是联系微观及宏观的桥梁，是从分子到材料的必由之路，同生命过程也有密切的关联。

由于介观模拟能够模拟的空间尺度（纳米到微米）、时间尺度（纳秒到微妙）更大，应用介观模拟方法可以模拟更加复杂的体系，例如：高分子熔体，高分子稀溶液自组装，表面活性剂溶液自组装，磷脂膜等胶体化学，高分子，生物大分子相关的内容。

目前介观模拟的方法很多，例如耗散颗粒动力学模拟方法(dissipative particle dynamics，DPD)，它是根据Hoogerbrugge和Koelman提出的一种针对柔性(soft)球模型流体动力学的模拟，并通过引入粒子间的谐振动势，来模拟聚合物的性质；元胞动力学方法（CDS），基于重整化群理论，对时间相关的Ginzburg-Landau方程直接用数值计算的方法在离散空间上进行描述。

其中单个元胞的演化通常用双曲正切函数表示；动态密度泛函方法（DDFT或MesoDyn），应用于高分子体系，建立在粗粒化高斯链模型的基础上，实际上是一个动态的自洽场方法，使用了朗之万方程（Langevin’s equation）来描述体系演化的动力学。

（1）MS-Mesocite简介MS Mesocite是一个基于粗粒度模拟方法的、可以对广泛体系进行模拟研究的分子力学工具集，模拟的对象大小尺寸在纳米到微米尺度范围，相应地，模拟变化的时间范围落在纳秒至微秒区间。

MS Mesocite的模拟对象遍及多种工业领域，比如复合材料、涂料、化妆品以及药物控缓释等，它可以提供流体在平衡态下、在有剪切力存在下以及其它受限制条件下的结构与动力学性质。

MS Mesocite 的突出特点是使用完全区别于传统介观模拟技术，转而采用力场(Forcefield)方法—比如MS Martini力场—来描述粗粒度之间的相互作用，从而得到体系的结构、和动力学特性，分析函数主要有角度分布，密度分布，径向分布函数，二面角分布，均方根位移等。

化学反应中的动力学分析与模拟第一章：引言化学反应是化学学科的核心之一，它涉及到许多重要的现象和过程。

了解化学反应机理和动力学是化学领域的重要研究方向之一。

通过动力学分析和模拟，可以更好地理解化学反应的动态过程和反应规律，为化学反应的设计和优化提供指导。

本文旨在介绍化学反应动力学分析和模拟的基本概念，探讨重要的化学反应动力学模型，并评估现代计算机模拟方法在化学反应动力学研究中的应用。

第二章：化学动力学基础化学反应动力学研究的基础是化学反应动力学方程。

这些方程描述了反应物质在不同温度、压力、浓度或电场等条件下发生反应的速率。

反应速率的确定需要考虑以下因素：反应物浓度、反应物种类、反应条件（如温度和压力）和催化剂。

在化学领域，最常见的化学反应动力学方程形式为速率常数表达式。

速率常数k是描述反应速率的重要物理量，它与反应物的浓度、反应物种类和温度等因素有关。

在理论研究中，k通常由反应物分子之间碰撞的频率和能量来确定。

第三章：反应动力学模型化学预测模型是化学反应动力学模拟研究的核心。

反应动力学模型可以帮助研究人员更好地理解反应机理和预测反应成果。

下面介绍几种化学反应动力学模型：1. 一阶反应模型一阶反应模型是最常用的动力学模型之一。

在一阶反应中，反应物分子以自身浓度及速率常数k为基础反应。

一阶反应模型对于不同化学反应涉及了种类相似的动态过程，如放射性射线的衰变和许多金属腐蚀。

2. 二阶反应模型二阶反应模型是描述许多化学反应的动力学模型。

在这种模型中，两个反应物分子交换电子，生成新的化合物。

二阶反应模型通常涉及带电离，酸碱反应和许多重要的生化反应。

3. 多级反应模型多级反应模型常用于描述极其复杂的反应动态。

在多级反应中，一种化学物质的生成需要通过多个中间步骤完成。

多级反应模型能够更好地描述反应动态和机理。

第四章：化学反应动力学的模拟计算化学方法已经成为现代化学科学中的重要组成部分。

通过计算机模拟，可以对复杂的化学反应机理和动态等进行定量研究。