匀速曲线运动的定义

根据匀速曲线运动规律的公式总结与应用
一、匀速曲线运动规律的公式总结
匀速曲线运动是指物体在运动过程中速度大小不变，但方向不断改变的运动。

根据匀速曲线运动规律，可以总结出以下公式：
1. 弧长公式
匀速曲线运动中，物体在曲线上所走过的弧长与它所经过的角度成正比。

根据弧长公式可得：
弧长 = 半径 ×弧度
2. 圆周角公式
圆周角是指物体在匀速曲线运动过程中所经过的角度，它与物体所走过的弧长成正比。

圆周角公式可以表示为：
圆周角 = 弧长 / 半径
3. 线速度公式
线速度是指物体在匀速曲线运动过程中的瞬时速度，它与物体所走过的弧长、角速度以及半径之间的关系可以表示为：线速度 = 弧长 ×角速度 = 半径 ×角速度
二、匀速曲线运动规律的应用
匀速曲线运动规律的公式可以应用于实际问题的求解和分析。

以下是一些应用场景：
1. 机械工程中的齿轮传动
在机械工程中，齿轮传动是常见的运动形式。

使用匀速曲线运
动规律的公式，可以计算齿轮的线速度，进而进行传动效率的分析
和设计优化。

2. 汽车转弯的力学分析
汽车在转弯时会产生离心力和向心力，通过应用匀速曲线运动
规律的公式，可以计算出车辆在转弯过程中所受的力，进而进行车
辆稳定性的分析和驾驶控制的优化。

3. 弹射器的建模与设计
弹射器是一种常见的工程装置，通过匀速曲线运动规律的公式，可以进行弹射器的建模和设计，计算出弹射速度、弹射轨迹等参数，进而进行弹射器性能的优化。

总之，匀速曲线运动规律的公式总结与应用有助于解决各种实际问题，为相关领域的研究和实践提供了基础和指导。

高中物理必修二曲线运动公式一、曲线运动的基本概念曲线运动是指物体在空间中沿着曲线轨迹运动的过程。

在高中物理必修二中，我们主要学习的是匀速圆周运动和抛体运动这两种曲线运动。

1. 匀速圆周运动匀速圆周运动是指物体在圆周轨道上以恒定的速度做曲线运动。

在这种运动中，物体的速度大小保持不变，但速度方向不断改变，因此物体始终受到向心力的作用。

2. 抛体运动抛体运动是指物体在水平方向上受到初速度，而在竖直方向上受到重力作用，从而形成的曲线运动。

抛体运动可以分为竖直上抛、竖直下抛、水平抛和斜上抛四种情况。

二、曲线运动的基本公式1. 匀速圆周运动公式（1）线速度公式：v = rω其中，v表示线速度，r表示圆周半径，ω表示角速度。

（2）向心力公式：F = mv^2/r其中，F表示向心力，m表示物体质量，v表示线速度，r表示圆周半径。

2. 抛体运动公式（1）竖直上抛公式：h = v0t 1/2gt^2其中，h表示物体上升的高度，v0表示初速度，g表示重力加速度，t表示时间。

（2）竖直下抛公式：h = 1/2gt^2其中，h表示物体下落的高度，g表示重力加速度，t表示时间。

（3）水平抛公式：x = v0t，y = 1/2gt^2其中，x表示物体水平位移，y表示物体竖直位移，v0表示初速度，g表示重力加速度，t表示时间。

（4）斜上抛公式：x = v0cosθt，y = v0sinθt 1/2gt^2其中，x表示物体水平位移，y表示物体竖直位移，v0表示初速度，θ表示抛射角，g表示重力加速度，t表示时间。

三、曲线运动的应用曲线运动在生活中有着广泛的应用，如：1. 匀速圆周运动：汽车转弯、地球绕太阳公转等。

2. 抛体运动：投篮、投掷标枪等。

通过对曲线运动公式的学习，我们可以更好地理解生活中的各种曲线运动现象，为解决实际问题提供理论依据。

高中物理必修二曲线运动公式一、曲线运动的分类及特点在高中物理必修二中，我们学习到的曲线运动主要分为两大类：匀速圆周运动和抛体运动。

【高中物理】高中物理必修二第五章知识点：曲线运动
高中物理是高中学习的重要学科，整理了高中物理知识点，供广大高中生学习参考，希望有所帮助！
>>>
高中物理
必修二各章知识点汇总<&lt
高中英语
;<
第五章曲线运动
一、知识点
(一)曲线运动的条件：再分外力与运动方向无此一条直线上
(二)曲线运动的研究方法：运动的合成与分解(平行四边形定则、三角形法则)
(三)曲线运动的分类：合力的性质(坯变速箱：元显恭甩运动、非匀变速箱曲线：匀速圆周运动)
(四)匀速圆周运动
1受力分析，所受到合力的特点：向心力大小、方向
2向心加速度、线速度、角速度的定义(文字、定义式)
3向心力的公式(多角度的：线速度、角速度、周期、频率、转回)
(五)平抛运动
1受力分析，只受到重力
2速度，水平、竖直方向分速度的表达式;位移，水平、竖直方向位移的表达式
3速度与水平方向的夹角、加速度与水平方向的夹角
(五)离心运动的定义、条件
二、实地考察内容、建议及方式
1曲线运动性质的判断：明确曲线运动的条件、牛二定律(选择题)
2匀速圆周运动中的动态变化：熟练掌握匀速圆周运动各物理量之间的关系式(挑选、填空题)
3匀速圆周运动中物理量的计算：受力分析、向心加速度的几种表示方式、合力提供向心力(计算题)
3运动的制备与水解：分后运动与和运动的等时性、耦合性(挑选、填空题)
4平抛运动相关：平抛运动中速度、位移、夹角的计算，分运动与和运动的等时性、等效性(选择、填空、计算)
5Vergt运动：临界条件、最小静摩擦力、匀速圆周运动有关排序(挑选、排序)。

【知识梳理】一、匀速圆周运动：质点沿圆周运动，如果在相等的时间里通过的圆弧长度相等，这种运动就叫做匀速圆周运动。

（举例：电风扇转动时，其上各点所做的运动；地球和各个行星绕太阳的运动，都认为是匀速圆周运动。

）注意：匀速圆周运动是变速曲线运动，匀速圆周运动的轨迹是圆，是曲线运动，运动的速度方向时刻在变化，因而匀速圆周运动不是匀速运动，而是变速曲线。

“匀速”二字仅指在相等的时间里通过相等的弧长。

二、线速度：物体做匀速圆周运动时，通过的弧长S 与时间t 的比值就是线速度的大小。

用符号v 表示： tS v =1、线速度是物体做匀速圆周运动的瞬时速度。

2、线速度是矢量，它既有大小，也有方向．线速度的方向-----在圆周各点的切线方向上．3、匀速圆周运动的线速度不是恒定的，方向是时刻变化的三、角速度：圆周半径转过的角度ϕ与所用时间t 的比值。

用ω表示：公式：tϕω=单位：s rad /匀速圆周运动的快慢也可以用角速度来描述。

物体在圆周上运动得越快，连接运动物体和圆心的半径在同样的时间内转过的角度就越大。

对某一确定的匀速圆周运动而言，角速度ω是恒定。

四、周期和频率匀速圆周运动是一种周期性的运动．周期（T ）：做匀速圆周运动的物体运动一周所用的时间，单位是s 。

周期也是描述匀速圆周运动快慢的物理量，周期长运动慢，周期短运动快。

频率（f ）：物体ls 由完成匀速圆周运动的圈数，单位是赫兹，记作“Hz ”．周期和频率互为倒数．频率也是描述匀速圆周运动快慢的物理量，频率低运动慢，频率高运动快。

Tf 1=转速n ：做匀速圆周运动的物体单位时间内转过的圈数叫转速。

单位是r/s 、r/min 。

五、线速度、角速度、周期间的关系 1、定性关系三个物理量都是描述匀速圆周运动的快慢，匀速圆周运动得越快，线速度越大、角速度越大、周期越小． 2、定量关系设想物体沿半径为r 的圆周做匀速圆周运动，则在一个周期内转过的弧长为π2r ，转过的角度为π2，因此有 T r v π2=，Tπω2= 比较可知：v ＝ωr ＝2πnr ＝2πfr 结论：由v ＝r ω知，当v 一定时，ω与r 成反比；当ω一定时，v 与r 成正比；当r 一定时，v 与ω成正比。

匀速圆周运动知识点解析1．匀速圆周运动的定义(1)轨迹是圆周的运动叫圆周运动。

(2)质点沿圆周运动，如果在相同时间里通过的弧长相等，这种运动叫匀速圆周运动。

(3)匀速圆周运动是最简单的圆周运动形式，也是最基本的曲线运动之一。

(4)匀速圆周运动是一种理想化的运动形式。

许多物体的运动接近这种运动，具有一定的实际意义。

一般圆周运动，也可以取一段较短的时间(或弧长)看成是匀速圆周运动。

2．周期(1)物体做匀速圆周运动时，运动一周所用的时间。

(2)周期用符号T表示，单位是秒。

(3)周期是反映重复性运动的运动快慢的物理量。

它从另一个角度描述了物体的运动。

3．线速度(1)物体做匀速圆周运动时，通过的弧长s跟通过这段弧长所用时间t的比值，叫运动物体线速度大小。

线速度的方向为圆周上某点的切线方向。

(2)线速度的计算公式：(3)线速度的意义：线速度实质上还是物体某一时刻的瞬时速度，虽然是用弧长和时间的比定义了速度大小，但当时间t趋于零时，弧长和为区别角速度而取名为线速度。

4．角速度转过这些角度所用时间t的比值，叫物体做匀速圆周运动的角速度。

(2)角速度计算公式：(3)角速度单位为：弧度/秒(rad/s)。

(4)角速度是矢量，方向为右手螺旋法则的大拇指的指向。

(5)角速度是描述转动快慢的物理量。

在描述转动效果时，它比用线速度描述更具有代表性。

5．向心加速度(1)匀速圆周运动的加速度方向匀速圆周运动的速度大小不变，速度的方向时刻在变，由于速度方向的变化，质点一定具有加速度，该加速度反映速度方向变化的快慢，该加速度的方向沿着半径指向圆心。

设质点沿半径是r的圆周做匀速圆周运动，在某时刻它处于A点，速度是vA，经过很短时间Δt后，运动到B点，速度为vB。

根据矢量合成的三角形法则可知，矢量vA与Δv之和等于vB，所以Δv是质点在A点时的加速度。

如图4-20。

时Δv便垂直于vA。

而vA是圆的切线，故Δv是指向圆心的。

即A点加速度指向圆心，所以匀速圆周运动的加速度又叫向心加速度。

四、曲线运动一、知识网络二、画龙点睛概念1、曲线运动：⑴曲线运动定义：曲线运动是一种轨迹是曲线的运动，其速度方向随时间不断变化⑵曲线运动中质点的瞬时速度方向：就是曲线的切线方向⑶曲线运动是一种变速运动，因为物体速度方向不断变化，所以曲线运动的物体总有加速度【注意】曲线运动一定是变速运动，一定具有加速度；但变速运动或具有加速度的运动不一定是曲线运动⑷两种常见的曲线运动：平抛运动和匀速圆周运动2、物体做曲线运动的条件：⑴曲线运动的物体所受的合外力不为零，合外力产生加速度，使速度方向（大小）发生变化⑵曲线运动的条件：物体所受的合外力F与物体速度方向不在同一条直线上⑶力决定了给定物体的加速度，力与速度的方向关系决定了物体运动的轨迹F（或a）跟v在一直线上→直线运动：a恒定→匀变速直线运动；a变化→变加速直线运动。

F（或a）跟v不在一直线上→直线运动：a恒定→匀变速曲线运动；a变化→变加速曲线运动⑷根据质点运动轨迹大致判断受力方向：做曲线运动的物体所受的合外力必指向运动轨迹的内侧，也就是运动轨迹必夹在速度方向与合外力方向之间。

⑸常见运动的类型有：①a=0：匀速直线运动或静止。

②a恒定：性质为匀变速运动，分为：①‘v、a同向，匀加速直线运动；②、v、a反向，匀减速直线运动；③’v、a成角度，匀变速曲线运动（轨迹在v、a之间，和速度v的方向相切，方向逐渐向a的方向接近，但不可能达到。

）③a变化：性质为变加速运动。

如简谐运动，加速度大小、方向都随时间变化。

例题：如图所示，物体在恒力F作用下沿曲线从A运动到B，这时，突然使它所受力反向，大小不变，即由F变为－F。

在此力作用下，物体以后运动情况，下列说法正确的是A．物体不可能沿曲线Ba运动；B．物体不可能沿直线Bb运动；C．物体不可能沿曲线Bc运动；D．物体不可能沿原曲线由B返回A。

解析：因为在曲线运动中，某点的速度方向是轨迹上该点的切线方向，如图所示，在恒力作用下AB为抛物线，由其形状可以画出v A方向和F方向。

曲线运动一、曲线运动1、所有物体的运动从轨迹的不同可以分为两大类：直线运动和曲线运动。

2、曲线运动的产生条件：合外力方向与速度方向不共线（≠0°，≠180°）性质：变速运动3、曲线运动的速度方向：某点的瞬时速度方向就是轨迹上该点的切线方向。

4、曲线运动一定收到合外力，“拐弯必受力，”合外力方向：指向轨迹的凹侧。

若合外力方向与速度方向夹角为θ，特点：当0°＜θ＜90°，速度增大； 当0°＜θ＜180°，速度增大； 当θ=90°，速度大小不变。

5、曲线运动加速度：与合外力同向，切向加速度改变速度大小；径向加速度改变速度方向。

6、关于运动的合成与分解 （1）合运动与分运动定义：如果物体同时参与了几个运动，那么物体实际发生的运动就叫做那几个运动的合运动。

那几个运动叫做这个实际运动的分运动．特征：① 等时性；② 独立性；③ 等效性；④ 同一性。

（2）运动的合成与分解的几种情况：①两个任意角度的匀速直线运动的合运动为匀速直线运动。

②一个匀速直线运动和一个匀变速直线运动的合运动为匀变速运动，当二者共线时轨迹为直线，不共线时轨迹为曲线。

③两个匀变速直线运动合成时，当合速度与合加速度共线时，合运动为匀变速直线运动；当合速度与合加速度不共线时，合运动为曲线运动。

二、小船过河问题1、渡河时间最少：无论船速与水速谁大谁小，均是船头与河岸垂直，渡河时间min dt v =船，合速度方向沿v 合的方向。

2、位移最小：①若v v >船水，船头偏向上游，使得合速度垂直于河岸，船头偏上上游的角度为cos v v θ=水船，最小位移为min l d=。

②若v v <船水，则无论船的航向如何，总是被水冲向下游，则当船速与合速度垂直时渡河位移最小，船头偏向上游的角度为cos v v θ=船水，过河最小位移为min cos v dl d v θ==水船。

什么是曲线运动曲线运动是指物体在运动过程中所经过的轨迹呈曲线形状的运动。

与直线运动不同，曲线运动要考虑各种因素对运动轨迹的影响。

曲线运动是物理学中一个重要的概念，广泛应用于自然科学、工程技术等领域。

本文将介绍曲线运动的基本概念、种类、影响因素、应用及未来发展。

一、曲线运动的基本概念曲线运动是指物体在运动过程中所经过的轨迹呈曲线形状的运动。

曲线运动的轨迹可分为平面曲线和空间曲线两种。

平面曲线运动是指物体在平面内沿着曲线路径运动；而空间曲线运动则是指物体在三维空间中沿着曲线路径运动。

曲线运动还可分为匀速曲线运动和变速曲线运动两种。

匀速曲线运动是指物体在曲线路径上匀速运动，即物体在单位时间内运动的路程相等；而变速曲线运动则是指物体在曲线路径上速度不断变化的运动。

曲线运动的速度由切线方向的瞬时速度和法线方向的瞬时速度组成。

切线方向的瞬时速度是指物体在曲线路径上切线方向上的瞬时速度；而法线方向的瞬时速度则是指物体在曲线路径上法线方向上的瞬时速度。

二、曲线运动的种类曲线运动可分为两大类：一是平面曲线运动，包括圆周运动、椭圆运动、抛物线运动、双曲线运动等；二是空间曲线运动，包括螺旋线运动、球面运动、圆锥曲线运动等。

其中，圆周运动是指物体在一个定圆上绕圆心运动的运动。

例如，地球绕着太阳做圆周运动。

椭圆运动是指物体在一个椭圆曲线上运动。

例如，地球的公转轨道大致呈椭圆形。

抛物线运动是指物体沿着抛物线路径上的运动。

例如，投掷物体的轨迹大致呈抛物线形状。

双曲线运动是指物体沿着双曲线路径上的运动。

例如，两个质点间的引力运动的轨迹大致呈双曲线形状。

螺旋线运动是指物体同时在轴向和径向上做运动，呈螺旋状。

例如，飞机在升降时的轨迹呈螺旋线形状。

球面运动是指物体在一个球面上绕球心做运动。

例如，地球自转时的轨迹呈球面运动。

圆锥曲线运动是指物体在一个圆锥曲线上做运动。

例如，火箭升空时的轨迹大致呈圆锥曲线形状。

三、曲线运动的影响因素曲线运动的轨迹不仅与物体本身的质量、体积、形状等因素有关，还与运动速度、运动场景、外部力等因素密切相关。

物体运动的三种基本方式
物体的运动方式有三种：直线运动、曲线运动和旋转运动。

1、直线运动：所谓直线运动是指物体以固定方向和速度沿着一定的
直线运动，可以是匀速直线运动或是变速直线运动。

物体直线运动时，物
体位置随时间的变化可用绝对位移或变化量表示，运动轨迹是一条直线，
可能会有位置的偏移，但运动的方向是固定的。

2、曲线运动：曲线运动是指物体在一定的运动轨迹上移动，运动轨
迹一般是椭圆、圆或抛物线等曲线，可以是匀速曲线运动或是变速曲线运动。

物体曲线运动时，物体位置随时间的变化可以用极坐标来表示，物体
的运动轨迹是椭圆、圆或抛物线等曲线，运动轨迹上的位置和速度会随时
间变化，但运动的方向是固定的。

3、旋转运动：所谓旋转运动，是指物体围绕某一固定的点沿抛物线
运动的运动方式，也称为自转运动，物体的运动情况可用角度或转速大小
来表示，例如日头的自转，地球的公转等。

物体旋转运动可以是匀速旋转，也可以是变速旋转，但运动的方向是固定的。

初二初三物理知识点总结归纳物理是一门研究物质、能量以及它们之间相互关系的科学。

在初二初三阶段，学生们学习了许多基础的物理知识点，本文将对这些知识进行总结归纳。

一、力学1. 运动和力- 运动的基本概念：匀速直线运动、变速直线运动、匀速曲线运动、变速曲线运动- 力的基本概念：力的定义、力的性质、力的单位- 牛顿第一定律：惯性、惯性系、惯性原理- 牛顿第二定律：F=ma，力的等效作用、力的合成、合力的分解 - 牛顿第三定律：作用力和反作用力2. 动能和功- 动能：动能的概念、动能定律、动能守恒- 功：功的概念、功的计算、功率3. 万有引力和运动定律- 引力的概念：万有引力定律、重力与物体质量的关系、地球重力的影响- 运动的规律：行星运动、人造卫星、天体运动的周期和速度二、热学1. 温度和热量- 温度的度量：摄氏度、华氏度、绝对温度- 热量的传递：传导、对流、辐射- 内能和物态变化：相变、焓变、热容2. 物质的热性质- 比热容：热容、比热容的概念与计算- 热膨胀：线膨胀、体膨胀、热膨胀的应用三、声学1. 声音的产生和传播- 声音的产生：声源、振动、声音的传播媒质- 声音的传播：机械波、纵波、横波、声速2. 声音的特性和应用- 声音的特性：频率、响度、音调、共振- 声音的应用：声纳、超声波、音叉、共鸣四、光学1. 光的传播和折射- 光的传播：光的直线传播、光的照明和照射- 光的折射：光的折射定律、折射率2. 光的反射和成像- 光的反射：光的反射定律、反射镜- 成像：平面镜成像、球面镜成像、透镜成像3. 光和颜色- 光的色散：光的折射、白光的分光、光谱- 颜色：滤波和叠色、颜色的原理、光的三基色五、电学1. 电荷和电场- 电荷：正电荷、负电荷、电荷守恒- 电场：场强、电场线、电场力2. 电流和电路- 电流：电流的概念、电流的计算、电路元件- 电路：串联电路、并联电路、电阻以及欧姆定律3. 磁学- 磁性和电磁感应：磁性物质、磁铁的基本性质、电磁感应的现象和规律- 电磁感应和电磁感应定律：法拉第电磁感应定律、电动势和感应电流以上是初二初三物理的主要知识点总结和归纳。

一、 曲线运动 ⒈速度的方向：质点在某一点的瞬时速度，沿曲线在这一点的 方向。

⒉运动的性质：作曲线运动的物体，速度的方向时刻在改变，所以曲线运动一定是 运动，也就是具有 。

⒊质点做曲线运动的条件：⑴从动力学角度看：物体所受 跟物体 方向不在一条直线上，物体就做曲线运动；⑵从运动学角度看：物体的 方向与 方向不在同一条直线上。

⒋曲线运动的轨迹：做曲线运动的物体，其轨迹向 所指一方弯曲，若已知物体的运动轨迹，可判断出物体所受合外力的大致方向 。

二、 运动的合成与分解⒈分运动和合运动：一个物体同时参与几个运动，参与的这几个运动都是分运动，物体的 运动就是合运动。

⒉运动的合成：即由几个 求合运动。

⑴同一直线上的两分运动的合成：同向相 ，反相相 。

⑵不在同一直线上的两分运动的合成，按照 法则进行合成⒊两直线运动的合运动性质和运动轨迹：由两分运动的性质及合初速度和合加速度方向关系共同决定。

⑴两个分运动是匀速直线运动，则合运动是 直线运动或 .⑵已知两个分运动都是匀加速直线运动（互成一定角度，不共线）则合运动是：Ⅰ.合合与v a 共线是 直线运动；Ⅱ.合合与v a 不共线是 曲线运动.⑶一个分运动是匀速，另一个是匀加速（初速度为零），则合运动：Ⅰ.合合与v a 共线⎪⎩⎪⎨⎧-=+=atv v at v v 00合合反向，同向， Ⅱ.合合与v a 不共线： 曲线运动⒊运动的分解：是运动合成的 运算。

⑴分解原则：根据运动的 效果分解或 分解。

处理曲线运动问题的常用方法是把曲线运动按实际效果分解成两个方向上的 运动。

⑵合运动和分运动的关系：Ⅰ.等时性：各分运动经历的时间与合运动经历的时间Ⅱ.独立性：一个物体同时参与几个分运动，各分运动 进行，不受其它分运动的影响。

Ⅲ.等效性：各分运动的叠加与合运动有 的效果。

三、 小船渡河问题⒈处理方法：小船在有一定水速的水中过河时，实际上参与了两个方向的分运动，即随水流的运动（ 的运动）和相对水的运动（即在 中的船的运动），船的 运动是合运动；也可将船的实际速度沿 河岸和 河岸方向分解。

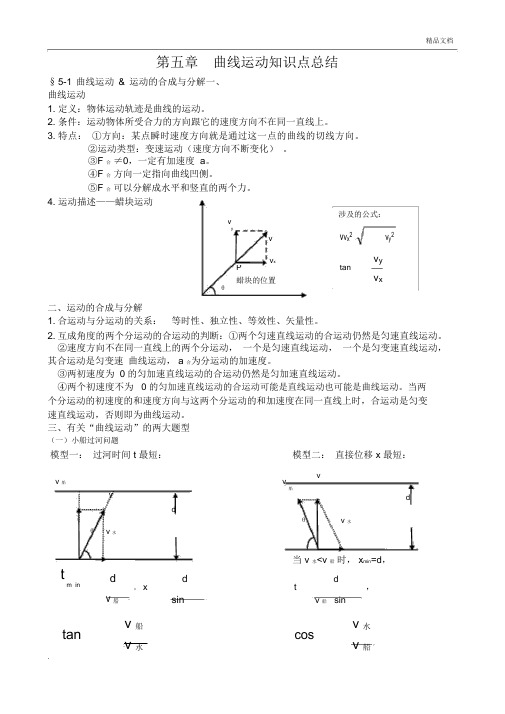
精品文档第五章曲线运动知识点总结§ 5-1 曲线运动 & 运动的合成与分解一、曲线运动1. 定义：物体运动轨迹是曲线的运动。

2. 条件：运动物体所受合力的方向跟它的速度方向不在同一直线上。

3. 特点： ①方向：某点瞬时速度方向就是通过这一点的曲线的切线方向。

②运动类型：变速运动（速度方向不断变化） 。

③F 合 ≠0，一定有加速度 a 。

④F 合 方向一定指向曲线凹侧。

⑤F 合 可以分解成水平和竖直的两个力。

4. 运动描述——蜡块运动涉及的公式：vvyv v x 2v y 2v xv yPtan蜡块的位置v xθ二、运动的合成与分解1. 合运动与分运动的关系： 等时性、独立性、等效性、矢量性。

2. 互成角度的两个分运动的合运动的判断：①两个匀速直线运动的合运动仍然是匀速直线运动。

②速度方向不在同一直线上的两个分运动， 一个是匀速直线运动， 一个是匀变速直线运动，其合运动是匀变速 曲线运动， a 合为分运动的加速度。

③两初速度为 0 的匀加速直线运动的合运动仍然是匀加速直线运动。

④两个初速度不为 0 的匀加速直线运动的合运动可能是直线运动也可能是曲线运动。

当两个分运动的初速度的和速度方向与这两个分运动的和加速度在同一直线上时，合运动是匀变速直线运动，否则即为曲线运动。

三、有关“曲线运动”的两大题型（一）小船过河问题模型一： 过河时间 t 最短：模型二： 直接位移 x 最短：v 船vvv船ddθv 水θ v 水当 v 水<v 船 时， x min =d ，tm ind d td，v 船， xv 船 sinsintanv 船cosv 水v 水v 船.精品文档模型三：间接位移x 最短：v 船v船dθAθv 水当 v 水>v 船时，x min dcostd，cos v 船 sinsmin(v水 - v船cos )Lv船sin v水L，v船v 船v 水（二）绳杆问题 ( 连带运动问题 )1、实质：合运动的识别与合运动的分解。

曲线运动相关公式及定理匀速圆周运动定义：质点沿圆周运动，如果在任意相等的时间里通过的圆弧长度都相等，这种运动就叫做“匀速圆周运动”，亦称“匀速率圆周运动”因为物体作圆周运动时速率不变，但速度方向随时发生变化。

公式：1、v(线速度)=S/t=2πr/T=ωr=2πrf (S代表弧长，t代表时间，r代表半径)2、ω(角速度)=θ/t=2π/T=2πn （θ表示角度或者弧度）3、T（周期）=2πr/v=2π/ω4、n（转速）=1/T=v/2πr=ω/2π5、Fn（向心力）=mrω^2=mv^2/r=mr4π^2/T^2=mr4π^2f^26、an（向心加速度）=rω^2=v^2/r=r4π^2/T^2=r4π^2n^27、v过顶点时最大速度v=（gr）^（1/2）匀速圆周运动向心力公式的推导设一质点在A处的运动速度为Va,在运动很短时间⊿t后,到达B点,设此是的速度为Vb由于受向心力的作用而获得了一个指向圆心速度⊿v，在⊿v与Va的共同作用下而运动到B点，达到Vb的速度则矢量Va+矢量⊿v=矢量Vb，矢量⊿v=矢量Vb-矢量Va用几何的方法可以得到Va与Vb的夹角等于OA与OB的夹角，当⊿t非常小时⊿v/v=s/r（说明：由于质点做匀速圆周运动，所以Va=Vb=v，s表示弧长，r表示半径）所以⊿v=sv/r⊿v/⊿t=s/⊿t * v/r，其中⊿v/⊿t表示向心加速度a，s/⊿t 表示线速度所以a=v^2/r=rω^2=r4π^2/T^2=r4π^2n^2F（向心力）=ma=mv^2/r=mrω^2=4π^2/T^2相关介绍描述匀速圆周运动快慢的物理量(1)线速度v①意义：描述质点沿圆弧运动的快慢，线速度越大，质点沿圆弧运动越快。

②定义：线速度的大小等于质点通过的弧长s与所用时间t的比值。

③单位：m/s。

④矢量：方向在圆周各点的切线方向上。

⑤就是物体做匀速圆周运动的瞬时速度。

⑥质点做匀速圆周运动时，线速度大小不变，但方向时刻在改变，故其线速度不是恒矢量。

曲线运动知识点总结曲线运动是物理学研究中的一个重要概念，它也是大学物理课程必修的一部分。

曲线运动包括了受力作用时的运动类型，比如，摆、滚子或抛体。

本文将以总结形式介绍曲线运动的相关知识，包括曲线运动的定义、曲线运动的性质和曲线运动中的基本概念。

曲线运动是指一个物体沿着曲线运动的场景，最常见的可以是抛物线，圆曲线，双曲线等。

在分析曲线运动的基础上，物理学家研究了曲线运动的物理性质。

曲线运动在位置和速度中都具有非常明显的变化，从而构成了曲线运动的定义。

曲线运动的性质：（1）它具有明显的位置变化，抛物线或圆曲线的运动就是典型例子。

在抛物线运动中，物体首先以一定的加速度在水平方向运动，然后以负加速度在垂直方向上下运动。

（2）它具有明显的速度变化，当物体在某处位置稳定时，它的速度便为零；当物体在某个方向的加速运动时，它的速度逐渐增加；当物体在某个方向的减速运动时，它的速度逐渐减小。

（3）它具有受力作用的特点，受力作用的物体一定不是匀速运动的，也不能假定速度为常量，它的速度将会随着受力作用的大小而不断变化。

曲线运动中的基本知识点：（1）加速度：加速度是指物体运动过程中，其速度变化的速率。

加速度可以是正值，表示物体正在变快；也可以是负值，表示物体正在变慢。

（2）运动轨迹：运动轨迹是一种连续的空间曲线，它表示物体沿着它走过的路径的形状。

（3）动量：动量是物体运动过程中，其运动量的变化。

动量的大小取决于物体的速度和质量。

（4）重力：重力是一种引力，它使得物体在受力作用时减速甚至停止运动。

（5）能量：运动中物体存在多种能量，包括动能和重力能等。

以上就是曲线运动的基本性质和相关知识点的总结。

曲线运动受力作用，其运动轨迹、速度、动量和能量的变化，对于科学家来说有着重要的意义，也是一些大学物理学课程的重要知识点。

本文就是曲线运动的总结，希望能够为读者提供一些帮助。