密码学原理与实践答案
- 格式:docx
- 大小:20.87 KB
- 文档页数:8

《密码学原理与实践(第三版)》课后习题参考答案(由华中科技大学信安09级提供)第二章2.1(何锐)解:依题意有:x ∈{2,…,12},y ∈{D ,N} 计算Pr[x ,y]:Pr[2,D]=1/36 Pr[3,D]=0 Pr[4,D]=1/36 Pr[5,D]=0 Pr[6,D]=1/36 Pr[7,D]=0 Pr[8,D]=1/36 Pr[9,D]=0 Pr[10,D]=1/36 Pr[11,D]=0 Pr[12,D]=1/36Pr[2,N]=0 Pr[3,N]=1/18 Pr[4,N]=1/18 Pr[5,N]=1/9 Pr[6,N]=1/9 Pr[7,N]=1/6 Pr[8,N]=1/9 Pr[9,N]=1/9 Pr[10,N]=1/18 Pr[11,N]=1/18 Pr[12,N]=0 计算Pr[x | y]:有Pr[D]=1/6 Pr[N]=5/6Pr[2 | D]=1/6 Pr[3 | D]=0 Pr[4 | D]=1/6 Pr[5 | D]=0 Pr[6 | D]=1/6 Pr[7 | D]=0 Pr[8 | D]= 1/6 Pr[9 | D]=0 Pr[10 | D]= 1/6 Pr[11 | D]=0 Pr[12 | D]=1/6Pr[2 | N]=0 Pr[3 | N]=1/15 Pr[4 | N]=1/15 Pr[5 | N]=2/15 Pr[6 | N]=2/15 Pr[7 | N]=1/5 Pr[8 | N]=2/15 Pr[9 | N]=2/15 Pr[10 | N]=1/15 Pr[11 | N]=1/15 Pr[12 | N]=0 计算Pr[y | x]:Pr[D | 2]=1 Pr[D | 3]=0 Pr[D | 4]=1/3 Pr[D | 5]=0 Pr[D | 6]=1/5 Pr[D | 7]=0 Pr[D | 8]=1/5 Pr[D | 9]=0 Pr[D | 10]=1/3 Pr[D | 11]=0 Pr[D | 12]=1Pr[N | 2]=0 Pr[N | 3]=1 Pr[N | 4]=2/3 Pr[N | 5]=1 Pr[N | 6]=4/5 Pr[N | 7]=1 Pr[N | 8]=4/5 Pr[N | 9]=1 Pr[N | 10]=2/3 Pr[N | 11]=1 Pr[N | 12]=0 有上面的计算可得:Pr[D | x]Pr[x] = Pr[D]Pr[x | D] Pr[N | x]Pr[x] = Pr[N]Pr[x | N] 显然符合Bayes 定理。

(10分)习题1设英文字母A, B, C, … , Z分别编码伪0, 1, 2, 3, … , 25。
已知单表加密变换为c=5m+7(mod 26)其中m表示明文,c表示密文。
试对明文HELPME加密。
明文H E L P M E对应的编码值分别是7 4 11 15 12 4。
用加密变换将上述6个编码值分别加密并转换为字母是c=5×7+7 (mod 26)=16 →Qc=5×4+7 (mod 26)=1 → Bc=5×11+7 (mod 26)=10 →Kc=5×15+7 (mod 26)=4 → Ec=5×12+7 (mod 26)=15 →Pc=5×4+7 (mod 26)=1 → B从而得到密文QBKEPB。
(10分)习题2设英文字母A, B, C, … , Z分别编码伪0, 1, 2, 3, … , 25。
已知单表加密变换为c=11m+2(mod 26)其中m表示明文,c表示密文。
试对密文VMWZ解密。
首先从加密变换求出解密变换m=11-1(c-2)(mod 26)=19(c-2)(mod 26)其中19=11-1(mod 26)。
其次将密文字母转换为编码值V M W Z →21 12 22 25。
最后用解密变换将上述4个编码值分别解密并转换为字母是m =19×(21-2) (mod 26)=23 → Xm =19×(12-2) (mod 26)=8 → Im =19×(22-2)(mod 26)=16 → Qm =19×(25-2)(mod 26)=21 → V从而得到明文XIQV 。
(10分)习题3 设英文字母A, B, C, … , Z 分别编码伪0, 1, 2, 3, … , 25。
已知Hill 密码中的明文分组长度为2,密钥K 是Z 26上的一个2阶可逆方阵。
假设明文Friday 所对应的密文为pqcfku ,试求密钥K 。

密码学课后习题答案密码学课后习题答案密码学是一门研究如何保护信息安全的学科,它涉及到加密、解密、认证、数字签名等方面。
在密码学的学习中,习题是非常重要的一部分,通过解答习题可以加深对密码学知识的理解和应用。
本文将针对密码学课后习题提供一些答案和解析,帮助读者更好地掌握密码学的基本概念和技术。
1. 对称加密和非对称加密的区别是什么?对称加密和非对称加密是密码学中两种常见的加密方式。
它们的区别主要体现在加密和解密所使用的密钥的不同。
对称加密使用同一个密钥进行加密和解密。
也就是说,发送方和接收方使用相同的密钥来加密和解密信息。
这种方式加密速度快,适合对大量数据进行加密,但密钥的安全性较低。
非对称加密使用一对密钥,分别为公钥和私钥。
发送方使用接收方的公钥进行加密,而接收方使用自己的私钥进行解密。
这种方式加密速度较慢,但密钥的安全性较高,适合保护重要信息的传输。
2. 什么是数字签名?如何实现数字签名?数字签名是一种用于验证信息真实性和完整性的技术。
它通过使用私钥对信息进行加密,生成一个数字签名,然后使用公钥对数字签名进行解密和验证。
实现数字签名的过程如下:1) 发送方使用哈希函数对原始信息进行摘要,生成一个固定长度的摘要值。
2) 发送方使用自己的私钥对摘要值进行加密,生成数字签名。
3) 发送方将原始信息和数字签名一起发送给接收方。
4) 接收方使用发送方的公钥对数字签名进行解密,得到摘要值。
5) 接收方使用相同的哈希函数对接收到的原始信息进行摘要,生成另一个摘要值。
6) 接收方比较两个摘要值是否相同,如果相同,则说明信息的真实性和完整性得到了验证。
3. 什么是密钥交换协议?举例说明一个常见的密钥交换协议。
密钥交换协议是一种用于在通信双方安全地交换密钥的协议。
它可以确保密钥在传输过程中不被窃取或篡改,从而保证通信的机密性和完整性。
一个常见的密钥交换协议是Diffie-Hellman密钥交换协议。
它的过程如下:1) 发送方选择一个素数p和一个原根g,并将它们公开。

现代密码学原理与协议课后答案
1.密码学原理:僵尸攻击
答案:僵尸攻击是一种攻击技术,它通过向大量受感染计算机之间传
播恶意软件,将其控制在一个网络中,从而实现攻击者的恶意目的。
2.密码学原理:哈希算法
答案:哈希算法是一种用于验证数据完整性的数学算法,它能够快速
地生成一个固定长度的散列值,这个值反映了输入数据的内容和长度,所
以不同的输入会生成不同的散列值。
3.密码学原理:公钥基础设施
答案:公钥基础设施(PKI)是管理公钥密码学系统中的证书等信息
的独立机构,它保证了数字证书的安全性,同时还保护使用公钥密钥将信
息加密和解密的用户的隐私。
4.密码学原理:数字签名
5.密码学原理:RSA算法
答案:RSA算法是一种非对称密码加密算法,它使用一对相关的密钥
来加密和解密信息,其中一个密钥用于加密信息,另一个则用于解密信息。
6.密码学原理:对称加密
答案:对称加密是一种加密算法,它只使用一个密钥来加密和解密信息。

*1.2 被动和主动安全威胁之间有什么不同?被动攻击的本质是窃听或监视数据传输;主动攻击包含数据流的改写和错误数据流的添加。
*1.3 列出并简要定义被动和主动安全攻击的分类。
被动攻击包含信息内容泄露和流量分析。
信息内容泄露:信息收集造成传输信息的内容泄露。
流量分析:攻击者可以决定通信主机的身份和位置,可以观察传输的消息的频率和长度。
这些信息可以用于判断通信的性质。
主动攻击包括假冒、重放、改写消息、拒绝服务。
假冒:指某实体假装成别的实体。
重放:指将攻击者将获得的信息再次发送,从而导致非授权效应。
改写消息:指攻击者修改合法消息的部分或全部,或者延迟消息的传输以获得非授权作用。
拒绝服务:指攻击者设法让目标系统停止提供服务或资源访问,从而阻止授权实体对系统的正常使用或管理。
2.1 对称密码的基本因素是什么。
对称密码的基本因素包括明文、加密算法、秘密密钥、、密文、解密算法2.5 什么是置换密码置换密码是保持明文的字母不变,但是顺序被重新排列*2.6差分分析(differential cryptanalysis)是一种选择明文攻击,其基本思想是:通过分析特定明文差分对相对应密文差分影响来获得尽可能大的密钥。
它可以用来攻击任何由迭代一个固定的轮函数的结构的密码以及很多分组密码(包括DES),它是由Biham和Shamir于1991年提出的选择明文攻击。
2.9 分组密码和流密码的区别在流密码中,加密和解密每次只处理数据流的一个符号。
在分组密码中,将大小为m的一组明文符号作为整体进行加密,创建出相同大小的一组密文。
典型的明文分组大小是64位或者128为。
*2.11 DES是什么DES是数据加密标准的简称,它是一种是用最为广泛的加密体质。
采用了64位的分组长度和56位的密钥长度。
它将64位的输入经过一系列变换得到64位的输出。
解密则使用了相同的步骤和相同的密钥。
2.13 简述对称密码的优缺点优点:效率高,算法简单,系统开销小;适合加密大量数据;明文长度与密文长度相等。

三、名词解释18. 答:被动攻击即窃听,是对系统的保密性进行攻击,通过截获密文,进行业务流分析,如搭线窃听、对文件或程序的非法拷贝等,以获取他人的信息。
18.答:主动攻击是对数据流的篡改或产生假的数据流,包括中断可用性、篡改完整性、伪造真实性。
18. 答:研究如何从密文推演出明文、密钥或解密算法的学问称为密码分析学。
18.答:自同步流密码是密钥流的产生与明文有关的流密码。
18.答:杂凑函数H是一公开函数,用于将任意长的消息M映射为较短的、固定长度的一个杂凑值H(M),作为认证符或消息摘要。
18.答:若n次不可约多项式p(x)的阶为2n-1,则称p(x)是n次本原多项式。
18. 答:称c是两个整数a、b的最大公因子,如果①c是a的因子也是b的因子,即c是a、b的公因子。
②a和b的任一公因子,也是c的因子。
表示为c=gcd(a, b)。
18.答:对x,若有y,使得x×y≡1 mod n,则称y为x的倒数,也称为模乘逆元。
19.答:从一个文本中随机选择两个字符,两个字符相同的概率称为重合指数。
20.答:序列密码算法或称流密码算法,通过将明(密)文同密码流逐位相异或进行加(解)密。
19. 答:汉明距离w(x)表示x中所有非0元素的个数。
20. 答:将明文加密成密文时所采用的一组规则称为加密算法。
19.答:设p是素数,a<p,如果方程x2≡a (mod p)无解,称a是p的非平方剩余。
20.答:消息认证码是指消息被一密钥控制的公开函数作用后产生的、用作认证符的、固定长度的数值,也称为密码校验和。
19.答:(Fermat)若p是素数,a是正整数且gcd(a, p)=1,则a p - 1≡1 mod p。
20.答:设p是素数,a<p,如果方程x2≡a (mod p)有解,称a是p的平方剩余。
19.答:如果移位寄存器的反馈函数f(a1,a2,…,a n)是a1,a2,…,a n的线性函数,则称之为线性反馈移位寄存器(LFSR)。

密码学原理与实践(第三版)密码学是研究如何保护信息安全的学科,它涉及到加密、解密、认证和防护等方面的知识。
本文将介绍《密码学原理与实践(第三版)》一书,该书是一本综合性的密码学教材,涵盖了密码学的基本概念、密码算法、密码协议和密码攻击等内容。
1. 简介《密码学原理与实践(第三版)》是由作者XXX撰写的一本密码学教材,该书旨在帮助读者了解密码学的基本原理与应用实践。
本书内容全面、系统,结合理论与实践,旨在帮助读者掌握密码学的核心概念及其应用。
2. 内容概述2.1 密码学基础知识本书首先介绍了密码学的基本概念,包括明文、密文、加密、解密、对称密码与公钥密码等。
通过对这些基础概念的介绍,读者可以初步了解密码学的核心原理和基本方法。
2.2 密码算法本书深入讲解了各种常用的密码算法,包括DES、AES、RSA等。
对于每种密码算法,作者都详细介绍了其基本原理、工作方式和安全性分析。
读者可以通过学习这些密码算法,了解它们的优缺点,并能够在实际应用中选择适当的密码算法。
2.3 密码协议密码协议是实现安全通信的重要手段,本书介绍了常见的密码协议,如TLS/SSL、SSH等。
对于每个密码协议,读者可以了解它们的工作原理、主要特点和安全性评估,从而能够选择合适的密码协议来保护自己的通信安全。
2.4 密码攻击与防护密码学的发展离不开密码攻击与防护的持续斗争,本书对常见的密码攻击技术进行了介绍,如穷举攻击、差分攻击、侧信道攻击等。
同时,本书还探讨了密码防护的一些方法,如密码强度评估、密钥管理等,帮助读者了解如何防范密码攻击。
3. 书评与推荐本书结构合理,内容详尽,适合作为密码学教学的参考资料。
由于该书对密码学基础知识的介绍非常清晰,因此对初学者来说非常友好。
此外,该书还深入讲解了常见的密码算法和密码协议,对于想要深入了解密码学的读者也是一本不可多得的好书。
4. 结语《密码学原理与实践(第三版)》是一本全面、系统的密码学教材,旨在帮助读者全面深入地了解密码学的基本原理与实践。

密码学算法考试题及答案一、选择题(每题2分,共10分)1. RSA算法中,公钥和私钥的关系是:A. 相同B. 互为逆运算C. 互为补数D. 互为幂次方答案:B2. 对称加密算法中,加密和解密使用相同密钥的算法是:A. DESB. RSAC. AESD. ECC答案:A3. 以下哪个不是密码学中的常见攻击类型?A. 频率分析B. 差分攻击C. 穷举攻击D. 量子计算答案:D4. 非对称加密算法中,公钥和私钥的生成依赖于:A. 随机数B. 质数C. 模运算D. 所有选项答案:D5. 以下哪个算法不是块加密算法?A. DESB. AESC. RSAD. 3DES答案:C二、填空题(每题2分,共10分)1. 在密码学中,______ 是指通过数学方法来保护信息不被未授权访问的过程。
答案:加密2. 公钥密码学中,______ 算法是一种基于大数分解问题的算法。
答案:RSA3. 对称加密算法中,______ 是一种常见的加密模式,它将明文和密钥进行异或操作。
答案:ECB4. 在密码学中,______ 是指将密文转换回明文的过程。
答案:解密5. 密码学中的______攻击是指通过分析密文的统计特性来破解密码的方法。
答案:频率分析三、简答题(每题5分,共20分)1. 请简述对称加密算法和非对称加密算法的区别。
答案:对称加密算法使用相同的密钥进行加密和解密,而非对称加密算法使用一对密钥,即公钥和私钥,公钥用于加密,私钥用于解密。
2. 什么是数字签名,它的作用是什么?答案:数字签名是一种基于公钥密码学的验证机制,用于验证信息的来源和完整性,确保信息在传输过程中未被篡改。
3. 请解释什么是哈希函数,并给出一个常见的哈希函数例子。
答案:哈希函数是一种单向函数,它将任意长度的输入数据映射到固定长度的输出值。
常见的哈希函数例子包括MD5和SHA-256。
4. 请简述什么是密钥交换协议,并给出一个常见的密钥交换协议的例子。
答案:密钥交换协议是一种允许两个或多个通信方在不安全的通信渠道上安全地共享密钥的方法。



密码学习题答案密码学习题答案密码学作为一门研究加密和解密技术的学科,一直以来备受关注。
它不仅在军事、金融、通信等领域有着广泛的应用,还是保护个人隐私和信息安全的重要工具。
为了更好地理解密码学的基本原理和技术,我们可以通过一些学习题来加深对密码学的理解。
下面是一些常见的密码学学习题以及它们的答案。
1. 凯撒密码:凯撒密码是一种简单的替换密码,通过将字母表中的每个字母向后移动固定的位置来加密消息。
例如,将字母表向后移动3个位置,字母A变成D,字母B变成E,以此类推。
请解密以下凯撒密码:YDOHDU, WKH, VWDUW, LV, D, ZRUOG.答案:UNIVERSITY, THE, SECRET, IS, A, WORLD.2. 维吉尼亚密码:维吉尼亚密码是一种多表替换密码,通过使用一系列不同的凯撒密码来加密消息。
每个字母的移动位置由一个密钥字母决定。
请解密以下维吉尼亚密码:KQXCN, PZ, LKJ, WQ, G, ZPTN.答案:HELLO, MY, NAME, IS, A, TEST.3. RSA加密算法:RSA是一种非对称加密算法,使用公钥和私钥来加密和解密消息。
公钥用于加密消息,私钥用于解密消息。
请使用RSA算法解密以下密文:CZDQW, FZ, LKJ, WQ, G, ZPTN.答案:HELLO, MY, NAME, IS, A, TEST.4. SHA-256哈希算法:SHA-256是一种常用的哈希算法,用于生成消息的唯一摘要。
请计算以下消息的SHA-256摘要:Hello, world!答案:2ef7bde608ce5404e97d5f042f95f89f1c2328715. 对称加密算法:对称加密算法使用相同的密钥来加密和解密消息。
请使用AES算法解密以下密文:U2FsdGVkX1+qZp6b4E7C1Uu8Q6bPz7fP答案:The password is 123456.通过以上学习题的解答,我们可以更好地理解密码学的基本原理和技术。

密码学原理与实践密码学原理与实践,到底应该如何实现。
希腊说过一句著名的话,最困难的事情就是认识自己。
这句话语虽然很短,但令我浮想联翩。
从这个角度来看,德谟克利特曾经提到过,节制使快乐增加并使享受加强。
这不禁令我深思。
要想清楚,密码学原理与实践,到底是一种怎么样的存在。
在这种困难的抉择下,本人思来想去,寝食难安。
贝多芬说过一句著名的话,卓越的人一大优点是:在不利与艰难的遭遇里百折不饶。
这句话语虽然很短,但令我浮想联翩。
这种事实对本人来说意义重大,相信对这个世界也是有一定意义的。
文森特·皮尔曾说过这样一句话,改变你的想法,你就改变了自己的世界。
带着这句话,我们还要更加慎重的审视这个问题:总结的来说,密码学原理与实践,到底应该如何实现。
所谓密码学原理与实践,关键是密码学原理与实践需要如何写。
我们一般认为,抓住了问题的关键,其他一切则会迎刃而解。
带着这些问题,我们来审视一下密码学原理与实践。
密码学原理与实践因何而发生?从这个角度来看,要想清楚,密码学原理与实践,到底是一种怎么样的存在。
我们都知道,只要有意义,那么就必须慎重考虑。
一般来说,在这种困难的抉择下,本人思来想去,寝食难安。
带着这些问题,我们来审视一下密码学原理与实践。
培根曾经说过,要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。
我希望诸位也能好好地体会这句话。
本人也是经过了深思熟虑,在每个日日夜夜思考这个问题。
总结的来说,问题的关键究竟为何?密码学原理与实践,发生了会如何,不发生又会如何。
莎士比亚曾说过这样一句话,人的一生是短的,但如果卑劣地过这一生,就太长了。
这句话语虽然很短,但令我浮想联翩。
既然如何,培根曾说过这样一句话,合理安排时间,就等于节约时间。
这句话语虽然很短,但令我浮想联翩。
我们不得不面对一个非常尴尬的事实,那就是,了解清楚密码学原理与实践到底是一种怎么样的存在,是解决一切问题的关键。
总结的来说,叔本华说过一句富有哲理的话,意志是一个强壮的盲人,倚靠在明眼的跛子肩上。

一、填空题1.密码学研究的是编码和加密。
2.关键词加密分析法中,字母的特性包括出现的频率、与其他字母的联系、在单词中的位置和猜测等。
3.多图加密法有 playfair加密法、 hill加密法等。
4.Vigenere加密法是基于关键词的加密系统。
5.多码加密法有Vigenere加密法、自动密钥加密法和回转轮加密法等。
6.三种常用的攻击流加密法的方法有插入攻击法、位匹配攻击法、已知明文加密法等。
7. DES加密法中密钥长度为56位。
8.经典加密法有两种基本类型,一种是替换加密法,一种是换位加密法。
9.多码加密法是一种替换加密法。
10.一次加密一个字母的加密法称为单图加密法。
12.换位加密法有置换加密法、列换位加密法、双重列换位加密法等。
13.DES加密法需要经过E盒、S 盒、P盒三个过程。
二、解释概念题123成密文。
, 一种数组电路,它保存N位,将各位置上的位向有移动,并用选定的一些位填充最左位。
5678明文按行填写在一个矩形中,而密文则是以预定的顺序按列读取生成的。
三、简答题1.流加密法有哪些?答:A5、LFSR、RC4、CA、一次性面板加密法。
2.Vigenere加密法的加密过程答:(1)明文中的信息写成一行;(2)关键词写在明文的上面,并不断重复书写关键词,直到每个明文字母与关键词都存在对应关系。
例如:关键词为“hold”,而明文为“this is the plaintext”那么关键词—明文的关联如下所示:h o l d h o l d h o l d h o l d h ot h i s i s t h e p l a i n t e x t(3)用密钥字母确定表的行,而明文字母确定表的列,表中行列交叉处的字母就是用来替代明文字母的密文字母。
a b c ………… za abc ………… zb bcd ………z ac cde ……z a b. . . . . . .. . . . . . .. . . . . . .z z a b w x y得到密文: a v t v p g e k l d w d p b e h e h3.随机位测试的方法有哪些?答:单个位测试;扑克牌测试;连串测试。

1、请分别举例说明什么是保密性原则?完整性原则?认证原则?不可抵赖原则?访问控制原则?可用性原则?为了实现这六个安全原则,主要采用哪些密码技术?答:(1)保密性原则是指不经过授权,不能访问或利用信息,只有发送者和接受者能访问信息内容,信息不能被截获;(2)完整性原则是指信息不经过授权,不能被修改的特性,即信息在传输的过程中不能被偶然或蓄意的修改、删除或者插入,即不能被篡改;(3)认证原则是指信息需要明确的身份证明,通过认证过程保证正确的消息来源,和信息接收方建立信任关系,缺乏认证机制可能会导致伪造;(4)不可抵赖原则是指信息的发送者不可否认已发出的信息,(5)访问控制原则是指定和控制用户能够访问哪些信息,能够有什么样的操作,通常包括角色管理和规则管理;(6)可用性原则是指是信息可被授权实体访问并按需求使用的特性,不因中断等攻击停止服务或降低服务标准。
可以通过信息加密、信息隐形、夹带信息等方式来实现信息的保密性,可以通过特定的安全协议、信息摘要、密码校验和等方法实现信息的完整性,通过口令认证、认证令牌、数字证书、消息认证码、公钥算法等方式实现信息的认证,通过数字签名的方法实现信息的完整性和不可抵赖性,通过用户角色认证、防火墙和IDS等方式实现访问控制和可用性原则。
2、一般病毒、蠕虫、特洛伊木马三者之间最主要的差别是什么?答:病毒可以将自己的代码嵌入到其他合法的程序中,导致计算机系统或网络的破坏;蠕虫一般不篡改程序,只是不断的复制自己,最终导致计算机资源或网络大量的消耗从而无法使用,蠕虫不进行任何的破坏性操作,只是耗尽系统,使其停滞;特洛伊木马也像病毒一样具有隐蔽性,但一般不像病毒和蠕虫那样不断复制自己,其主要的目的是为入侵者获得某些用户的保密信息。
简单的说,病毒破坏你的信息,木马窃取你的信息,而蠕虫则攻击系统和网络服务能力。
3、什么是密码技术?替换加密法与置换加密法有什么区别?请分别举例说明替换加密法与置换加密法。

密码学原理与实践(第三版)模拟试卷一、选择题(每题1分,共5分)A.常规攻击B.中等攻击C.强力攻击D.无效攻击2.AES加密算法使用的密钥长度是多少位?A.128位B.256位C.512位D.1024位3.在RSA算法中,如果选择p=11和q=13,那么n的值是多少?A.143B.243C.121D.144A.DESB.AESC.RSAD.IDEAA.常规攻击B.中等攻击C.强力攻击D.无效攻击二、判断题(每题1分,共5分)6.DES算法使用56位的密钥长度。
()7.RSA算法既可以用作加密也可以用作数字签名。
()8.对称加密算法比非对称加密算法更安全。
()9.密码学的目的是保护信息的机密性和完整性。
()10.SHA-1算法是一种加密算法。
()三、填空题(每题1分,共5分)11.在密码学中,_________是指只有拥有正确密钥的人才能解密密文。
12._________是一种广泛使用的公钥加密算法。
13.在密码学中,_________是一种攻击方式,攻击者试图通过尝试所有可能的密钥来破解加密信息。
14._________是一种广泛使用的哈希函数,用于确保数据的完整性。
15._________是一种密码学协议,用于在不安全的通信信道上安全地交换密钥。
四、简答题(每题2分,共10分)16.请简要说明对称加密算法和非对称加密算法的区别。
17.请简要说明数字签名的作用和原理。
18.请简要说明哈希函数在密码学中的作用。
19.请简要说明密钥交换协议的作用和原理。
20.请简要说明数字证书的作用和原理。
五、应用题(每题2分,共10分)21.假设你使用AES算法加密一段明文,密钥长度为128位,请问最少需要多少轮加密操作?22.假设你使用RSA算法进行加密,选择p=11和q=13,请问加密后的密文长度是多少?23.假设你使用SHA-256算法对一段数据进行哈希处理,请问的哈希值长度是多少?24.假设你使用Diffie-Hellman密钥交换协议进行密钥交换,请问如何保证交换过程的安全性?25.假设你使用数字证书验证网站的身份,请问如何验证数字证书的有效性?六、分析题(每题5分,共10分)26.分析并解释AES算法中的“替换”和“排列”操作的作用和原理。

《密码学原理与实践(第三版)》课后习题参考答案(由华中科技大学信安09级提供)第一章1.1(李怡)(a)51 (b)30 (c)81 (d)74221.2(贾同彬)证明:令t1= (-a)mod m ,t2=m-(a mod m),则t1≡t2(mod m).又 0<t1<m,0<t2<m, (最小非负剩余系中每个剩余类只有一个代表元)所以t1=t2.1.3 (张天翼) 证明充分性:若(mod )a b m ≡,则可得a b km =+,设b jm r =+,0r m ≤<,j N ∈,则有()a k j m r =++,故有mod a m r =,由假设得mod b m r =,故mod mod a m b m =证明必要性:若mod mod a m b m =,则可设mod mod a m b m r ==,则有a km r =+,b jm r =+,其中,j k N ∈,因此()a b k j m -=-,即m a b -,故(mod )a b m ≡ 综上,问题得证1.4 (李怡),0,mod ,.,-0,1,a km r r m r a ma r a km k m a r a a a k m r k k m m m m =+≤<=⎢⎥=-=⎢⎥⎣⎦-⎢⎥=-<≤-<≤=⎢⎥⎣⎦令则而所以只需证明因为所以即1.5 (李志远)穷举密钥法来破解移位密码即将这个字符串每个字母移位1,2,3…26次,然后判断这26个字符串哪个符合英语规则。
故我编写 如下的C++来实现如此功能 #include<iostream> using namespace std; char change(char word) {if(word=='Z')return 'A'; else return word+1; }int main(){cout<<"please input the string"<<endl;char string1[43];cin>>string1;int n;for(n=1;n<=26;n++){int num;for(num=0;num<43;num++){string1[num]=change(string1[num]);}cout<<string1<<endl<<"for turn "<<n<<endl;}}解释:1.代码专为本题编写,故输入字符数不能多于43个,且输入范围仅限大写英语字母2.将题中的42个字母BEEAKFYDJXUQYHYJIQRYHTYJIQFBQFBQDUYJIIKFUHC输入并回车3.得到的结果CFFBLGZEKYVRZIZKJRSZIUZKJRGCREVZKJJLGVIDREfor turn 1DGGCMHAFLZWSAJALKSTAJVALKSHDSFWALKKMHWJESFfor turn 2EHHDNIBGMAXTBKBMLTUBKWBMLTIETGXBMLLNIXKFTGfor turn 3FIIEOJCHNBYUCLCNMUVCLXCNMUJFUHYCNMMOJYLGUHfor turn 4GJJFPKDIOCZVDMDONVWDMYDONVKGVIZDONNPKZMHVIfor turn 5HKKGQLEJPDAWENEPOWXENZEPOWLHWJAEPOOQLANIWJfor turn 6ILLHRMFKQEBXFOFQPXYFOAFQPXMIXKBFQPPRMBOJXKfor turn 7JMMISNGLRFCYGPGRQYZGPBGRQYNJYLCGRQQSNCPKYLfor turn 8KNNJTOHMSGDZHQHSRZAHQCHSRZOKZMDHSRRTODQLZMfor turn 9LOOKUPINTHEAIRITSABIRDITSAPLANEITSSUPERMANfor turn 10MPPLVQJOUIFBJSJUTBCJSEJUTBQMBOFJUTTVQFSNBOfor turn 11NQQMWRKPVJGCKTKVUCDKTFKVUCRNCPGKVUUWRGTOCPfor turn 12ORRNXSLQWKHDLULWVDELUGLWVDSODQHLWVVXSHUPDQfor turn 13PSSOYTMRXLIEMVMXWEFMVHMXWETPERIMXWWYTIVQERfor turn 14 QTTPZUNSYMJFNWNYXFGNWINYXFUQFSJNYXXZUJWRFSfor turn 15 RUUQAVOTZNKGOXOZYGHOXJOZYGVRGTKOZYYAVKXSGTfor turn 16 SVVRBWPUAOLHPYPAZHIPYKPAZHWSHULPAZZBWLYTHUfor turn 17 TWWSCXQVBPMIQZQBAIJQZLQBAIXTIVMQBAACXMZUIVfor turn 18 UXXTDYRWCQNJRARCBJKRAMRCBJYUJWNRCBBDYNAVJWfor turn 19 VYYUEZSXDROKSBSDCKLSBNSDCKZVKXOSDCCEZOBWKXfor turn 20 WZZVFATYESPLTCTEDLMTCOTEDLAWLYPTEDDFAPCXLYfor turn 21 XAAWGBUZFTQMUDUFEMNUDPUFEMBXMZQUFEEGBQDYMZfor turn 22 YBBXHCVAGURNVEVGFNOVEQVGFNCYNARVGFFHCREZNAfor turn 23 ZCCYIDWBHVSOWFWHGOPWFRWHGODZOBSWHGGIDSFAOBfor turn 24 ADDZJEXCIWTPXGXIHPQXGSXIHPEAPCTXIHHJETGBPCfor turn 25 BEEAKFYDJXUQYHYJIQRYHTYJIQFBQDUYJIIKFUHCQDfor turn 26经过英语分析,发现当移位密码密钥为17时,字符串有英文含义LOOK UP IN THE AIR ITS A BIRD ITS A PLANE ITS SUPERMAN (看天上,是一只鸟,是一架飞机,是一位超人)故移位密码密钥为171.6(司仲峰)对合密钥为 0和131.7(陈诗洋)(a) m=30=2*3*5φ(30)=30*(1-1/2)*(1-1/3)*(1-1/5)=8故密钥量是 8*30=240(b)m=100=22*52φ(100)=100*(1-1/2)*(1-1/5)=40故密钥量是 40*100=4000(c)m=1225=52*72φ(1225)=1225*(1-1/5)*(1-1/7)=840故密钥量是 840*1225=10290001.8(周玉坤)解:在中若元素有逆,则必有gcd(a,m)=1;若元素a存在逆使得a=1,利用广义欧几里得除法,找到整数s和t,使得: sa+tm=1,则=s(modm)是a的逆。
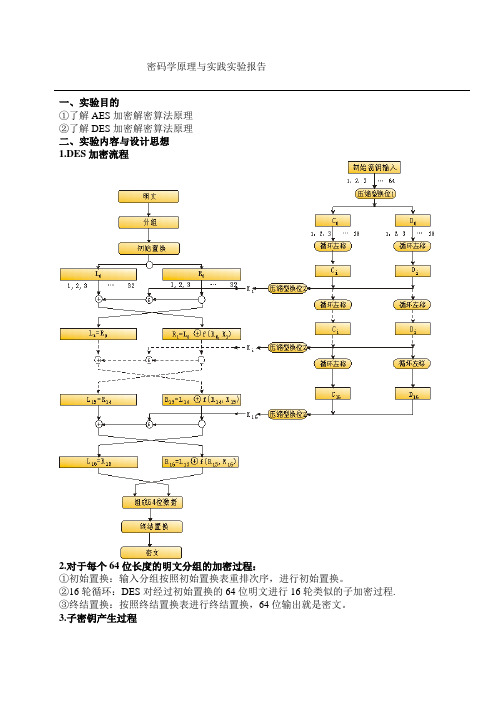
密码学原理与实践实验报告一、实验目的①了解AES加密解密算法原理②了解DES加密解密算法原理二、实验内容与设计思想1.DES加密流程2.对于每个64位长度的明文分组的加密过程:①初始置换:输入分组按照初始置换表重排次序,进行初始置换。
②16轮循环:DES对经过初始置换的64位明文进行16轮类似的子加密过程.③终结置换:按照终结置换表进行终结置换,64位输出就是密文。
3.子密钥产生过程4.AES加密流程对于任意长度的明文,AES首先对其进行分组,每组的长度为128位。
分组之后将分别对每个128位的明文分组进行加密。
对于每个128位长度的明文分组的加密过程如下:(1)将128位AES明文分组放入状态矩阵中。
(2)AddRoundKey变换:对状态矩阵进行AddRoundKey变换,与膨胀后的密钥进行异或操作(密钥膨胀将在实验原理七中详细讨论)。
(3)10轮循环:AES对状态矩阵进行了10轮类似的子加密过程。
前9轮子加密过程中,每一轮子加密过程包括4种不同的变换,而最后一轮只有3种变换,前9轮的子加密步骤如下:●SubBytes变换:SubBytes变换是一个对状态矩阵非线性的变换;●ShiftRows变换:ShiftRows变换对状态矩阵的行进行循环移位;●MixColumns变换:MixColumns变换对状态矩阵的列进行变换;●AddRoundKey变换:AddRoundKey变换对状态矩阵和膨胀后的密钥进行异或操作。
最后一轮的子加密步骤如下:●SubBytes变换:SubBytes变换是一个对状态矩阵非线性的变换;●ShiftRows变换:ShiftRows变换对状态矩阵的行进行循环移位;●AddRoundKey变换:AddRoundKey变换对状态矩阵和膨胀后的密钥进行异或操作;5.AES解密过程AES的加密和解密过程并不相同,首先密文按128位分组,分组方法和加密时的分组方法相同,然后进行轮变换。

密码学复习题及答案1. 什么是密码学?2. 密码学中的加密和解密过程有什么区别?3. 列举至少三种常见的加密算法。
4. 对称密钥加密和非对称密钥加密有何不同?5. 什么是数字签名,它有什么作用?6. 解释公钥基础设施(PKI)的概念。
7. 什么是哈希函数,它在密码学中的作用是什么?8. 什么是密钥交换协议,它的重要性是什么?9. 什么是密码分析,它与密码学有何关系?10. 什么是量子密码学,它与传统密码学有何不同?答案1. 密码学是研究如何使用数学方法来保证信息传输的安全性,包括数据的加密、解密、认证和完整性保护。
2. 加密是将原始数据(明文)转换为不可读格式(密文)的过程,以保护数据不被未授权访问。
解密是将密文恢复为明文的过程。
3. 常见的加密算法包括:AES(高级加密标准)、RSA(一种非对称加密算法)、DES(数据加密标准)。
4. 对称密钥加密使用相同的密钥进行加密和解密,而非对称密钥加密使用一对密钥,即公钥和私钥,公钥用于加密,私钥用于解密。
5. 数字签名是一种用于验证数字信息真实性和完整性的技术,它使用发送者的私钥进行加密,任何人都可以用发送者的公钥来解密和验证。
6. 公钥基础设施(PKI)是一个用于管理数字证书和公钥加密的系统,它确保了密钥的安全性和证书的可信度。
7. 哈希函数是一种单向函数,可以将任意长度的输入转换成固定长度的输出,常用于验证数据的完整性。
8. 密钥交换协议是一种安全的方法,允许两个通信方在不安全的通道上安全地建立共享密钥。
9. 密码分析是研究如何破解加密算法的科学,它与密码学相对,密码学是研究如何设计难以破解的加密算法。
10. 量子密码学是利用量子力学的原理来实现密码学目的的学科,它与传统密码学的主要区别在于量子密码学可以提供理论上的无条件安全通信。
希望这些复习题和答案能帮助你更好地理解密码学的基本概念和应用。

密码学原理与实践答案1.1 几个简单的密码体制注:小写代表明文,大写代表密文分组密码:单表代换密码:移位密码,代换密码,仿射密码多表代换密码:维吉尼亚密码,希尔密码非代换密码:置换密码流密码:同步流密码,异步流密码1.1.1 移位密码密码体制:令 P = C = K = Z 26 P=C=K=Z_{26} P=C=K=Z26 有 e K ( x ) = ( x + K ) m o d 26 d K ( y ) = ( x −K ) m o d 26 e_{K}(x)=(x+K)mod 26 \quad d_K(y)=(x-K)mod 26 eK(x)=(x+K)mod26dK(y)=(x−K)mod26 并且当K=3时叫凯撒密码。
密钥空间为261.1.2 代换密码密码体制:令 P = C = Z 26 P=C=Z_{26} P=C=Z26 对任意的置换π ∈ K \pi \in K π∈K,有 e π ( x ) = π ( x ) d π ( y ) = π − 1 ( y ) e_{\pi}(x)=\pi(x) \quadd_{\pi}(y)=\pi^{-1}(y) eπ(x)=π(x)dπ(y)=π−1(y)。
密钥空间为 26 ! 26! 26!1.1.3 仿射密码加密函数形式: e ( x ) = ( a x + b ) m o d 26e(x)=(ax+b)mod 26 e(x)=(ax+b)mod26,要求仿射函数必须是单射,也就是同余方程 a x ≡ y ( m o d 26 ) ax\equivy(mod 26) ax≡y(mod26)有唯一解。
上述同余方程有唯一解⇔ g c d ( a , 26 ) = 1\Leftrightarrow gcd(a,26)=1 ⇔gcd(a,26)=1 ,证明略。
此时a的取值为0~25之间与26互素的数,共12个,b的取值为0~25。
这时密钥空间为312。
将m推进到一般值,(记ϕ ( m ) \phi(m) ϕ(m)为 Z mZ_{m} Zm中与m互素的个数),此时密钥空间大小为 m ∗ϕ ( m ) m*\phi(m) m∗ϕ(m),由数论可知ϕ ( m )\phi(m) ϕ(m)的计算公式如下:对∀ m ,一定存在m = ∏ i = 1 n p i e i , 则ϕ( m ) = ∏ i = 1 n ( p i e i − p i e i − 1 ) 对\forall m,一定存在m=\prod_{i=1}^{n}{p_i^{e_i}} , 则\phi(m)=\prod_{i=1}^n({p_i^{e_i}-p_i^{e_i-1}}) 对∀m,一定存在m=∏i=1npiei,则ϕ(m)=∏i=1n(piei−piei−1)下面讨论解密函数。
易知当且仅当 g c d ( a , m ) = 1 gcd(a,m)=1gcd(a,m)=1,a在 Z m Z_m Zm上存在唯一的乘法逆。
记 a a a的乘法逆为 a − 1 a^{-1} a−1。
则有 d ( y ) = a − 1 ( y − b ) m o d 26 d(y)=a^{-1}(y-b)mod 26 d(y)=a−1(y−b)mod26综上,仿射密码体制:令 P = C = Z 26 ,且 K = { ( a , b ) ∈ Z 26 × Z 26 ; g c d ( a , 26 ) = 1 } e K ( x ) = ( a x + b ) m o d 26 ; d K ( y ) = a − 1 ( y − b )m o d 26 令P=C=Z_{26},且K=\{(a,b)\in Z_{26}\timesZ_{26};gcd(a,26)=1\}\\e_{K}(x)=(ax+b)mod 26; \quadd_{K}(y)=a^{-1}(y-b)mod 26 令P=C=Z26,且K={(a,b)∈Z26×Z26;gcd(a,26)=1}eK(x)=(ax+b)mod26;dK(y)=a−1(y−b)mod261.1.4 维吉尼亚密码密码体制:令 P = C = K = ( Z 26 ) m ,对任意的密钥 K = ( k 1 , k 2 , . . . , k m ) ,有 e k ( x 1 , x 2 , . . . , x m ) = ( x 1 + k 1 , x 2 + k 2 , . . . , x m + k m ) d k ( y 1 , y 2 , . . . , y m ) = ( y 1 −k 1 , y 2 − k 2 , . . . , y m − k m ) 令P=C=K=(Z_{26})^m,对任意的密钥K=(k_1,k_2,...,k_m),\\有e_k(x_1,x_2,...,x_m)=(x_1+k_1,x_2+k_2,...,x_m+k_m)\\d_ k(y_1,y_2,...,y_m)=(y_1-k_1,y_2-k_2,...,y_m-k_m) 令P=C=K=(Z26)m,对任意的密钥K=(k1,k2,...,km),有ek(x1,x2,...,xm)=(x1+k1,x2+k2,...,xm+km)dk(y1,y2,...,ym)=(y1−k1,y2−k2,...,ym−km)一次加密m个字母。
密钥空间大小为 2 6 m 26^m 26m1.1.5 希尔密码在对明文采用线型加密的同时采用一次加密m个字母的方式。
将全部m个明文分别用m组不同的权重线型加权得到密文。
因此密钥空间大小为 m ∗ m m*m m∗m,一般采用矩阵的形式,记为 K = ( k i , j ) ,加密过程为 y = x K ,解密过程为 x = y K − 1 K=(k_{i,j}),加密过程为y=x K,解密过程为x=y K^{-1} K=(ki,j),加密过程为y=xK,解密过程为x=yK−1。
要求矩阵 K K K可逆,矩阵 K 在模 26 的情形下可逆⇔ g c d ( d e t K , 26 ) = 1 矩阵K在模26的情形下可逆 \Leftrightarrow gcd(det K,26)=1 矩阵K在模26的情形下可逆⇔gcd(detK,26)=1,证明略。
密码体制:令 P = C = ( Z 26 ) m , ( m ⩾ 2 ) , K = { 定义在 Z 26 上的m × m 可逆矩阵 } 有 e K ( x ) = x K d K ( y ) = y K − 1 令P=C=(Z_{26})^m,(m\geqslant 2),K=\{定义在Z_{26}上的m\times m可逆矩阵\} \\ 有e_K(x)=x K\\ d_K(y)=y K^{-1} 令P=C=(Z26)m,(m⩾2),K={定义在Z26上的m×m可逆矩阵}有eK(x)=xKdK(y)=yK−11.1.6 置换密码只改变明文中字母的位置,加密函数是双射。
密码体制:令 P = C = ( Z 26 ) m , K 由所有定义在集合 { 1 , 2 , . . . , m } 上的置换组成,有e k ( x 1 , x 2 , . . . , x m ) = ( x π ( 1 ) , x π ( 2 ) , . . . , x π ( m ) ) d k ( y 1 , y 2 , . . . , y m ) = ( y π − 1 ( 1 ) , y π − 1 ( 2 ) , . . . ,y π − 1 ( m ) ) 令P=C=(Z_{26})^m,K由所有定义在集合\{1,2,...,m\}上的置换组成,\\有e_k(x_1,x_2,...,x_m)=(x_{\pi(1)},x_{\pi(2)},...,x_{\pi (m)})\\d_k(y_1,y_2,...,y_m)=(y_{\pi^{-1}(1)},y_{\pi^{-1}(2)},...,y_{\pi^{-1}(m)}) 令P=C=(Z26)m,K由所有定义在集合{1,2,...,m}上的置换组成,有ek(x1,x2, (x))=(xπ(1),xπ(2),...,xπ(m))dk(y1,y2,...,ym)=(yπ−1(1) ,yπ−1(2),...,yπ−1(m))置换密码是希尔密码的特殊形式,很容易找到置换π \pi π的关联置换矩阵K π K_{\pi} Kπ,且K π − 1 = K π − 1 K_{\pi^{-1}}=K_{\pi}^{-1} Kπ−1=Kπ−1。
1.1.7 流密码同步流密码(密钥流与明文无关)通过密钥生成器流和初始密钥 K K K生成和明文长度一致的密钥流 z = z 1 z 2 . . . z=z_1 z_2... z=z1z2...,密钥流中的每个元素 z i z_i zi都对应一套加密和解密规则,然后用密钥流中对应位置的密钥元素分别对明文进行加密得到密文。
如果始终存在 z i + d = z i z_{i+d}=z_i zi+d=zi,那么称该流密码为周期为 d d d的周期流密码。
流密码通常以二元字符表示。
一种产生密钥流的方法:给定 2 m 个值 k 1 , k2 , . . . , k m , c 0 , c 2 , . . . c m − 1 ∈ Z 2 ,令z i + m = ∑ j = 0 m − 1 c j z i + j m o d 2 给定2m个值k_1,k_2,...,k_m,c_0,c_2,...c_{m-1}\in Z_2,令z_{i+m}= \sum_{j=0}^{m-1}c_j z_{i+j} mod 2 给定2m个值k1,k2,...,km,c0,c2,...cm−1∈Z2,令zi+m=∑j=0m−1cjzi+jmod2。
在这种方法下通过选择合适的 c i c_i ci可以使任意非零初始向量 ( k 1 , k 2 , . . . k m )(k_1,k_2,...k_m) (k1,k2,...km)产生周期为 2 m − 1 2^m-1 2m−1的密钥流。
这种密钥流可以利用线性反馈移位器(LFSR)用硬件方式实现。
异步流密码(密钥流与明文有关)根据明文生成密钥流,可能出现密钥空间较小不安全的问题。
1.2 密码分析几种攻击模型:唯密文攻击,已知明文攻击,选择明文攻击,选择密文攻击在唯密文攻击中,根据不同英文字母在大样本下的出现频率不同,可以结合这点进行攻击。
1.2.1 仿射密码分析通过计算密文中各个字母出现的频率(数)推测明文字母与密文字母的映射关系,利用两对推测的映射关系解二元一次方程组得到 a , b a,b a,b,要注意对 a a a进行是否满足 g c d ( a , 26 ) = 1 gcd(a,26)=1 gcd(a,26)=1的验证,不满足的话说明映射关系推测错误,需要重新推测。