大学物理(下)(29)

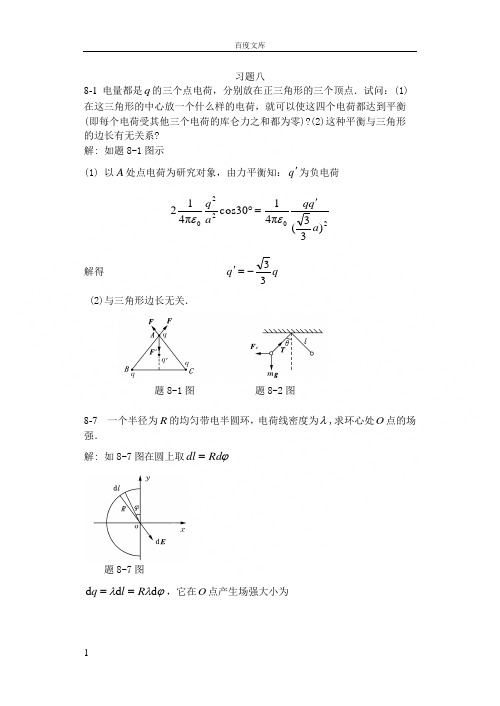
习题八8-1 电量都是q的三个点电荷，分别放在正三角形的三个顶点．试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解: 如题8-1图示(1) 以A处点电荷为研究对象，由力平衡知：q'为负电荷2220)33(π4130cosπ412aq qaq'=︒εε解得qq33-='(2)与三角形边长无关．题8-1图题8-2图8-7 一个半径为R的均匀带电半圆环，电荷线密度为λ,求环心处O点的场强．解: 如8-7图在圆上取ϕRddl=题8-7图ϕλλddd Rlq==，它在O点产生场强大小为20π4d d RR E εϕλ=方向沿半径向外 则 ϕϕελϕd sin π4sin d d 0RE E x ==ϕϕελϕπd cos π4)cos(d d 0RE E y -=-=积分RR E x 000π2d sin π4ελϕϕελπ==⎰0d cos π400=-=⎰ϕϕελπRE y∴ RE E x 0π2ελ==，方向沿x 轴正向．8-11 半径为1R 和2R (2R ＞1R )的两无限长同轴圆柱面，单位长度上分别带有电量λ和-λ,试求:(1)r ＜1R ；(2) 1R ＜r ＜2R ；(3) r ＞2R 处各点的场强．解: 高斯定理0d ε∑⎰=⋅q S E s取同轴圆柱形高斯面，侧面积rl S π2= 则 rl E S E Sπ2d =⋅⎰对(1) 1R r <0,0==∑E q(2) 21R r R << λl q =∑∴ rE 0π2ελ=沿径向向外(3) 2R r >=∑q∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电，电荷的面密度分别为1σ和2σ，试求空间各处场强．解: 如题8-12图示，两带电平面均匀带电，电荷面密度分别为1σ与2σ，两面间， n E)(21210σσε-= 1σ面外， n E )(21210σσε+-= 2σ面外， n E)(21210σσε+= n：垂直于两平面由1σ面指为2σ面．题8-16图8-16 如题8-16图所示，在A ，B 两点处放有电量分别为+q ,-q 的点电荷，AB 间距离为2R ，现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点，求移动过程中电场力作的功． 解: 如题8-16图示0π41ε=O U 0)(=-RqR q 0π41ε=O U )3(R qR q -Rq 0π6ε-= ∴ Rqq U U q A o C O 00π6)(ε=-=8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R ．试求环中心O 点处的场强和电势． 解: (1)由于电荷均匀分布与对称性，AB 和CD 段电荷在O 点产生的场强互相抵消，取θd d R l =则θλd d R q =产生O 点Ed 如图，由于对称性，O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E yR 0π4ελ=［)2sin(π-2sin π-］R0π2ελ-=(2) AB 电荷在O 点产生电势，以0=∞U⎰⎰===AB200012ln π4π4d π4d R R x x x x U ελελελ同理CD 产生 2ln π402ελ=U 半圆环产生 0034π4πελελ==R R U∴ 0032142ln π2ελελ+=++=U U U U O 8-22 三个平行金属板A ，B 和C 的面积都是200cm 2，A 和B 相距4.0mm ，A与C 相距2.0 mm ．B ，C 都接地，如题8-22图所示．如果使A 板带正电3.0×10-7C ，略去边缘效应，问B 板和C 板上的感应电荷各是多少?以地的电势为零，则A 板的电势是多少?解: 如题8-22图示，令A 板左侧面电荷面密度为1σ，右侧面电荷面密度为2σ题8-22图(1)∵ AB AC U U =，即 ∴ AB AB AC AC E E d d = ∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A=得 ,32S q A =σ Sq A 321=σ而 7110232-⨯-=-=-=A C q S q σC C10172-⨯-=-=S q B σ(2) 301103.2d d ⨯===AC AC AC A E U εσV 8-23 两个半径分别为1R 和2R （1R ＜2R )的同心薄金属球壳，现给内球壳带电+q ，试计算：(1)外球壳上的电荷分布及电势大小；(2)先把外球壳接地，然后断开接地线重新绝缘，此时外球壳的电荷分布及电势；*(3)再使内球壳接地，此时内球壳上的电荷以及外球壳上的电势的改变量．解: (1)内球带电q +；球壳内表面带电则为q -,外表面带电为q +，且均匀分布，其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R R qrr q r E U εε (2)外壳接地时，外表面电荷q +入地，外表面不带电，内表面电荷仍为q -．所以球壳电势由内球q +与内表面q -产生：0π4π42020=-=R q R q U εε8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳，介质相对介电常数为r ε，金属球带电Q ．试求： (1)电介质内、外的场强； (2)电介质层内、外的电势；(3)金属球的电势．解: 利用有介质时的高斯定理∑⎰=⋅q S D Sd(1)介质内)(21R r R <<场强303π4,π4rrQ E r r Q D r εε ==内; 介质外)(2R r <场强303π4,π4r r Q E r Qr D ε ==外(2)介质外)(2R r >电势rQE U 0rπ4r d ε=⋅=⎰∞外 介质内)(21R r R <<电势2020π4)11(π4R Q R r qr εεε+-=)11(π420R r Qr r -+=εεε(3)金属球的电势r d r d 221⋅+⋅=⎰⎰∞R R R E E U 外内⎰⎰∞+=22220π44πdr R R Rr r Qdrr Q εεε)11(π4210R R Qr r-+=εεε 8-28 如题8-28图所示，在平行板电容器的一半容积内充入相对介电常数为rd r d ⋅+⋅=⎰⎰∞∞rrE E U 外内r ε的电介质．试求：在有电介质部分和无电介质部分极板上自由电荷面密度的比值．解: 如题8-28图所示，充满电介质部分场强为2E ，真空部分场强为1E，自由电荷面密度分别为2σ与1σ 由∑⎰=⋅0d q S D得11σ=D ，22σ=D而 101E D ε=,202E D r εε=d21U E E == ∴r D D εσσ==1212题8-28图 题8-29图8-29 两个同轴的圆柱面，长度均为l ，半径分别为1R 和2R (2R ＞1R )，且l >>2R -1R ，两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时，求：(1)在半径r 处(1R ＜r ＜2R ＝，厚度为dr ，长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量；(2)电介质中的总电场能量； (3)圆柱形电容器的电容．解: 取半径为r 的同轴圆柱面)(S则 rlD S D S π2d )(=⋅⎰当)(21R r R <<时，Q q =∑∴ rlQD π2=(1)电场能量密度 22222π82l r Q D w εε== 薄壳中 rlrQ rl r l r Q w W εευπ4d d π2π8d d 22222=== (2)电介质中总电场能量⎰⎰===211222ln π4π4d d R R VR R l Q rl r Q W W εε (3)电容：∵ CQ W 22=∴ )/ln(π22122R R lW Q C ε== 习题九9-8 在真空中，有两根互相平行的无限长直导线1L 和2L ，相距0.1m ，通有方向相反的电流，1I =20A,2I =10A ，如题9-8图所示．A ，B 两点与导线在同一平面内．这两点与导线2L 的距离均为5.0cm ．试求A ，B 两点处的磁感应强度，以及磁感应强度为零的点的位置．题9-8图解：如题9-8图所示,A B方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B在2L 外侧距离2L 为r 处则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r mT9-11 氢原子处在基态时，它的电子可看作是在半径a =0.52×10-8cm 的轨道上作匀速圆周运动，速率v =2.2×108cm ·s -1．求电子在轨道中心所产生的磁感应强度和电子磁矩的值．解：电子在轨道中心产生的磁感应强度3004aav e B πμ ⨯= 如题9-11图，方向垂直向里，大小为134200==a evB πμ T 电子磁矩m P在图中也是垂直向里，大小为242102.92-⨯===eva a T e P m π 2m A ⋅ 题9-11图 题9-12图9-12 两平行长直导线相距d =40cm ，每根导线载有电流1I =2I =20A ，如题9-12图所示．求：(1)两导线所在平面内与该两导线等距的一点A 处的磁感应强度；(2)通过图中斜线所示面积的磁通量．(1r=3r =10cm,l=25cm)．解：(1) 5210104)2(2)2(2-⨯=+=dIdIBAπμπμT方向⊥纸面向外(2)取面元rlS dd=6121110102.23ln31ln23ln2])(22[1211-+⨯=πμ=πμ-πμ=-πμ+πμ=⎰l Il Il IldrrdIrIrrrΦWb9-13 一根很长的铜导线载有电流10A，设电流均匀分布.在导线内部作一平面S，如题9-13图所示．试计算通过S平面的磁通量(沿导线长度方向取长为1m的一段作计算)．铜的磁导率μμ=.解：由安培环路定律求距圆导线轴为r处的磁感应强度⎰∑μ=⋅lIlBd222RIrrBμπ=∴22RIrBπμ=题 9-13 图磁通量602)(1042-===⋅=Φ⎰⎰πμπμIdrRIrS dB RsmWb题9-15图9-15 题9-15图中所示是一根很长的长直圆管形导体的横截面，内、外半径分别为a ,b ，导体内载有沿轴线方向的电流I ，且I 均匀地分布在管的横截面上．设导体的磁导率0μμ≈，试证明导体内部各点)(b r a << 的磁感应强度的大小由下式给出：r a r a b IB 22220)(2--=πμ解：取闭合回路r l π2= )(b r a <<则 ⎰π=⋅lr B l B 2d2222)(a b Ia r I ππππ--=∑∴ )(2)(22220a b r a r I B --=πμ 9-16 一根很长的同轴电缆，由一导体圆柱(半径为a )和一同轴的导体圆管(内、外半径分别为b ,c )构成，如题9-16图所示．使用时，电流I 从一导体流去，从另一导体流回．设电流都是均匀地分布在导体的横截面上，求：(1)导体圆柱内(r ＜a ),(2)两导体之间(a ＜r ＜b )，（3）导体圆筒内(b ＜r ＜c )以及(4)电缆外(r ＞c )各点处磁感应强度的大小解： ⎰∑μ=⋅LI l B 0d(1)a r < 2202RIr r B μπ=202R IrB πμ=(2) b r a << I r B 02μπ=rIB πμ20=(3)c r b << I bc b r I r B 0222202μμπ+---= )(2)(22220b c r r c I B --=πμ (4)c r > 02=r B π0=B题9-16图题9-17图题9-21图9-21 边长为l =0.1m 的正三角形线圈放在磁感应强度B =1T 的均匀磁场中，线圈平面与磁场方向平行.如题9-21图所示，使线圈通以电流I =10A ，求： (1)线圈每边所受的安培力； (2)对O O '轴的磁力矩大小；(3)从所在位置转到线圈平面与磁场垂直时磁力所作的功．解： (1) 0=⨯=B l I F bcB l I F ab⨯= 方向⊥纸面向外，大小为866.0120sin ==︒IlB F ab NB l I F ca⨯=方向⊥纸面向里，大小866.0120sin ==︒IlB F ca N(2)IS P m =B P M m⨯= 沿O O '方向，大小为221033.443-⨯===B l I ISB M m N ⋅(3)磁力功 )(12ΦΦ-=I A∵ 01=Φ B l 2243=Φ ∴221033.443-⨯==B l IA J9习题十10-1 一半径r =10cm 的圆形回路放在B =0.8T 的均匀磁场中．回路平面与B垂直．当回路半径以恒定速率tr d d =80cm ·s -1收缩时，求回路中感应电动势的大小．解: 回路磁通 2πr B BS m ==Φ感应电动势大小40.0d d π2)π(d d d d 2====trr B r B t t m Φε V 10-2 一对互相垂直的相等的半圆形导线构成回路，半径R =5cm ，如题10-2图所示．均匀磁场B =80×10-3T ，B 的方向与两半圆的公共直径(在Oz 轴上)垂直，且与两个半圆构成相等的角α 当磁场在5ms 内均匀降为零时，求回路中的感应电动势的大小及方向．解: 取半圆形cba 法向为i， 题10-2图则 αΦcos 2π21B R m =同理，半圆形adc 法向为j，则αΦcos 2π22B R m=∵ B 与i 夹角和B 与j夹角相等，∴ ︒=45α则 αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tBR t m αεV方向与cbadc 相反，即顺时针方向．题10-4图10-4 如题10-4图所示，载有电流I 的长直导线附近，放一导体半圆环MeN 与长直导线共面，且端点MN 的连线与长直导线垂直．半圆环的半径为b ，环心O 与导线相距a ．设半圆环以速度v 平行导线平移．求半圆环内感应电动势的大小和方向及MN 两端的电压 N M U U -．解: 作辅助线MN ，则在MeNM 回路中，沿v方向运动时0d =m Φ ∴ 0=MeNM ε 即 MN MeN εε= 又∵ 0cos d ln 02a bMN a bIv a bvB l a bμεππ+--==<+⎰所以MeN ε沿NeM 方向，大小为ba ba Iv -+ln20πμ M 点电势高于N 点电势，即ba ba Iv U U N M -+=-ln20πμ 题10-5图10-5如题10-5所示，在两平行载流的无限长直导线的平面内有一矩形线圈．两导线中的电流方向相反、大小相等，且电流以tId d 的变化率增大，求： (1)任一时刻线圈内所通过的磁通量；(2)线圈中的感应电动势． 解: 以向外磁通为正则 (1)]ln [lnπ2d π2d π2000dad b a b Ilr l r Ir l r Iab b ad d m +-+=-=⎰⎰++μμμΦ(2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε10-6 如题10-6图所示，用一根硬导线弯成半径为r 的一个半圆．令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转．整个电路的电阻为R ．求：感应电流的最大值．题10-6图解: )cos(2π02ϕωΦ+=⋅=t r B S B m∴ Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε ∴ RBfr R I m22π==ε 10-7 如题10-7图所示，长直导线通以电流I =5A ，在其右方放一长方形线圈，两者共面．线圈长b =0.06m ，宽a =0.04m ，线圈以速度v =0.03m ·s -1垂直于直线平移远离．求：d =0.05m 时线圈中感应电动势的大小和方向．题10-7图解: AB 、CD 运动速度v方向与磁力线平行，不产生感应电动势． DA 产生电动势⎰==⋅⨯=AD I vb vBb l B v d2d )(01πμεBC 产生电动势)(π2d )(02d a Ivbl B v CB+-=⋅⨯=⎰με∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad d Ibv μεεε V 方向沿顺时针．10-8 长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动．已知导轨处于均匀磁场B 中，B 的方向与回路的法线成60°角(如题10-8图所示)，B的大小为B =kt (k 为正常)．设t =0时杆位于cd 处，求：任一时刻t 导线回路中感应电动势的大小和方向．解: ⎰==︒=⋅=22212160cos d klvt lvkt Blvt S B mΦ∴ klvt tm-=-=d d Φε 即沿abcd 方向顺时针方向．题10-8图10-9 一矩形导线框以恒定的加速度向右穿过一均匀磁场区，B的方向如题10-9图所示．取逆时针方向为电流正方向，画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0)．解: 如图逆时针为矩形导线框正向，则进入时0d d <Φt,0>ε； 题10-9图(a)题10-9图(b) 在磁场中时0d d =tΦ,0=ε； 出场时0d d >tΦ，0<ε，故t I -曲线如题10-9图(b)所示. 题10-10图10-10 导线ab 长为l ，绕过O 点的垂直轴以匀角速ω转动，aO =3l磁感应强度B 平行于转轴，如图10-10所示．试求： （1）ab 两端的电势差； （2）b a ,两端哪一点电势高?解: (1)在Ob 上取dr r r +→一小段 则 ⎰==320292d l Ob l B r rB ωωε 同理 ⎰==302181d l Oa l B r rB ωωε ∴ 2261)92181(l B l B Ob aO ab ωωεεε=+-=+= (2)∵ 0>ab ε 即0<-b a U U ∴b 点电势高．题10-11图10-11 如题10-11图所示，长度为b 2的金属杆位于两无限长直导线所在平面的正中间，并以速度v平行于两直导线运动．两直导线通以大小相等、方向相反的电流I ，两导线相距2a ．试求：金属杆两端的电势差及其方向． 解：在金属杆上取r d 距左边直导线为r ，则ba b a Iv r r a r Iv l B v ba ba BAAB -+-=-+-=⋅⨯=⎰⎰+-ln d )211(2d )(00πμπμε∵ 0<AB ε ∴实际上感应电动势方向从A B →，即从图中从右向左， ∴ ba ba Iv U AB -+=ln0πμ 题10-12图10-12 磁感应强度为B的均匀磁场充满一半径为R 的圆柱形空间，一金属杆放在题10-12图中位置，杆长为2R ，其中一半位于磁场内、另一半在磁场外．当tBd d ＞0时，求：杆两端的感应电动势的大小和方向．解： ∵ bc ab ac εεε+=tBR B R t t ab d d 43]43[d d d d 21=--=-=Φε=-=tabd d 2Φεt BR B R t d d 12π]12π[d d 22=-- ∴ tB R R acd d ]12π43[22+=ε∵0d d >tB∴ 0>ac ε即ε从c a →10-13 半径为R 的直螺线管中，有dtdB＞0的磁场，一任意闭合导线abca ，一部分在螺线管内绷直成ab 弦，a ,b 两点与螺线管绝缘，如题10-13图所示．设ab =R ，试求：闭合导线中的感应电动势． 解：如图，闭合导线abca 内磁通量)436π(22R R B S B m -=⋅= Φ∴ tB R R i d d )436π(22--=ε ∵0d d >tB∴0<i ε，即感应电动势沿acba ，逆时针方向．题10-13图题10-14图∴ 题10-15图 10-15 一无限长的直导线和一正方形的线圈如题10-15图所示放置(导线与线圈接触处绝缘)．求：线圈与导线间的互感系数．解： 设长直电流为I ，其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2aaIa r r Ia μμΦ∴ 2ln π2012aI M μΦ==10-16 一矩形线圈长为a =20cm ，宽为b =10cm ，由100匝表面绝缘的导线绕成，放在一无限长导线的旁边且与线圈共面．求：题10-16图中(a)和(b)两种情况下，线圈与长直导线间的互感．解：(a)见题10-16图(a)，设长直电流为I ，它产生的磁场通过矩形线圈的磁通为2ln π2d 2πd 020)(12Ia r r Ia S B bb S μμΦ⎰⎰==⋅= ∴ 6012108.22ln π2-⨯===a N I N M μΦ H (b)∵长直电流磁场通过矩形线圈的磁通012=Φ，见题10-16图(b) ∴ 0=M题10-16图题10-17图10-20 一无限长圆柱形直导线，其截面各处的电流密度相等，总电流为I ．求：导线内部单位长度上所储存的磁能．解：在R r <时 20π2R I B r μ=∴ 4222002π82Rr I B w m μμ== 取 r r V d π2d =(∵导线长1=l )则 ⎰⎰===R R m I R r r I r r w W 00204320π16π4d d 2μμπ。

第11章光的量子效应及光子理论一、 选择题1. 金属的光电效应的红限依赖于: 【 C 】(A)入射光的频率； (B)入射光的强度；(C)金属的逸出功； (D)入射光的频率和金属的逸出功。

2. 已知某单色光照射到一金属表面产生了光电效应，若此金属的逸出电势是U 0（使电子从金属逸出需做功eU 0），则此单色光的波长λ必须满足： 【 A 】hceU )D (;hceU )C (;eU hc )B (;eU hc)A (0≥≤≥≤λλλλ 3. 关于光电效应有下列说法：(1) 任何波长的可见光照射到任何金属表面都能产生光电效应；(2) 对同一金属如有光电子产生，则入射光的频率不同，光电子的初动能不同； (3) 对同一金属由于入射光的波长不同，单位时间内产生的光电子的数目不同； (4) 对同一金属，若入射光频率不变而强度增加一倍，则饱和光电流也增加一倍。

其中正确的是： 【 D 】(A) (1)，(2)，(3)； (B) (2)，(3)，(4)； (C) (2)，(3)； (D)(2)，(4)二、填空题1. 当波长为300 nm 光照射在某金属表面时，光电子的能量范围从0到.J 100.419-⨯在作上述光电效应实验时遏止电压为V 5.2U a =；此金属的红限频率Hz 104140⨯=ν。

2. 频率为100MHz 的一个光子的能量是J 1063.626-⨯，动量的大小是s N 1021.234⋅⨯-。

3. 如果入射光的波长从400nm 变到300nm ，则从表面发射的光电子的遏止电势增大（增大、减小）V 03.1U =∆。

4. 某一波长的X 光经物质散射后，其散射光中包含波长大于X 光和波长等于X 光的两种成分，其中大于X 光波长的散射成分称为康普顿散射。

三、计算题1. 已知钾的红限波长为558 nm ，求它的逸出功。

如果用波长为400 nm 的入射光照射，试求光电子的最大动能和遏止电压。

由光电方程2m mv 21A h +=ν，逸出功0h A ν=，0chA λ=，eV 23.2A =用波长为400nm 的入射光照射，光电子的最大动能：A h mv 212m -=ν A chE km -=λ，将nm 400=λ和eV 23.2A =代入得到：eV 88.0E km =遏止电压：a 2m eU mv 21=，2m a mv e21U =，V 88.0U a = 2. 从铝中移出一个电子需要4.2 eV 的能量，今有波长为200 nm 的光投射至铝表面。

一、 选择题1. 对一个作简谐振动的物体，下面哪种说法是正确的？ [ C ](A) 物体处在运动正方向的端点时，速度和加速度都达到最大值； (B) 物体位于平衡位置且向负方向运动时，速度和加速度都为零； (C) 物体位于平衡位置且向正方向运动时，速度最大，加速度为零；(D) 物体处在负方向的端点时，速度最大，加速度为零。

2. 一沿X 轴作简谐振动的弹簧振子，振幅为A ，周期为T ，振动方程用余弦函数表示，如果该振子的初相为43π，则t=0时，质点的位置在： [ D ](A) 过1x A 2=处，向负方向运动； (B) 过1x A 2=处，向正方向运动；(C) 过1x A 2=-处，向负方向运动；(D) 过1x A 2=-处，向正方向运动。

3. 一质点作简谐振动，振幅为A ，在起始时刻质点的位移为/2A ，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为 [ B ]4. 图(a)、(b)、(c)为三个不同的谐振动系统，组成各系统的各弹簧的倔强系数及重物质量如图所示，(a)、(b)、(c)三个振动系统的ω (ω为固有圆频率)值之比为： [ B ](A) 2：1：1； (B) 1：2：4； (C) 4：2：1； (D) 1：1：25. 一弹簧振子，当把它水平放置时，它可以作简谐振动，若把它竖直放置或放在固定的光滑斜面上如图，试判断下面哪种情况是正确的： [ C ](A) 竖直放置可作简谐振动，放在光滑斜面上不能作简谐振动； (B) 竖直放置不能作简谐振动，放在光滑斜面上可作简谐振动； (C) 两种情况都可作简谐振动； (D) 两种情况都不能作简谐振动。

6. 一谐振子作振幅为A 的谐振动，它的动能与势能相等时，它的相位和坐标分别为： [ C ](4)题(5)题2153(A),or ;A;(B),;A;332663223(C),or ;A;(D),;A4433ππ±±π±±±π±ππ±±π±±±π±7. 一质点沿x 轴作简谐振动，振动方程为 10.04cos(2)3x t ππ=+（SI ），从t = 0时刻起，到质点位置在x = -0.02 m 处，且向x 轴正方向运动的最短时间间隔为 [ D ](A)s 81； (B) s 61； (C) s 41； (D) s 218. 图中所画的是两个简谐振动的振动曲线，这两个简谐振动叠加后合成的余弦振动的初相为[ C ](A) π23； (B) π； (C) π21 ； (D) 0二、 填空题9. 一简谐振动用余弦函数表示，振动曲线如图所示，则此简谐振动的三个特征量为： A=10cm , /6rad /s =ωπ，/3=φπ10. 用40N 的力拉一轻弹簧，可使其伸长20 cm 。

习题八8-1 电量都是q的三个点电荷，分别放在正三角形的三个顶点．试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解: 如题8-1图示(1) 以A处点电荷为研究对象，由力平衡知：q'为负电荷2220)33(π4130cosπ412aq qaq'=︒εε解得qq33-='(2)与三角形边长无关．题8-1图题8-2图8-7 一个半径为R的均匀带电半圆环，电荷线密度为λ,求环心处O点的场强．解: 如8-7图在圆上取ϕRddl=题8-7图ϕλλddd Rlq==，它在O点产生场强大小为20π4d d RR E εϕλ=方向沿半径向外 则 ϕϕελϕd sin π4sin d d 0RE E x ==ϕϕελϕπd cos π4)cos(d d 0RE E y -=-=积分RR E x 000π2d sin π4ελϕϕελπ==⎰0d cos π400=-=⎰ϕϕελπRE y∴ RE E x 0π2ελ==，方向沿x 轴正向．8-11 半径为1R 和2R (2R ＞1R )的两无限长同轴圆柱面，单位长度上分别带有电量λ和-λ,试求:(1)r ＜1R ；(2) 1R ＜r ＜2R ；(3) r ＞2R 处各点的场强． 解: 高斯定理0d ε∑⎰=⋅q S E sϖϖ取同轴圆柱形高斯面，侧面积rl S π2=则 rl E S E Sπ2d =⋅⎰ϖϖ对(1) 1R r <0,0==∑E q(2) 21R r R << λl q =∑∴ rE 0π2ελ=沿径向向外(3) 2R r >=∑q∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电，电荷的面密度分别为1σ和2σ，试求空间各处场强．解: 如题8-12图示，两带电平面均匀带电，电荷面密度分别为1σ与2σ， 两面间， n E ϖϖ)(21210σσε-=1σ面外， n E ϖϖ)(21210σσε+-= 2σ面外， n E ϖϖ)(21210σσε+=n ϖ：垂直于两平面由1σ面指为2σ面．题8-16图8-16 如题8-16图所示，在A ，B 两点处放有电量分别为+q ,-q 的点电荷，AB 间距离为2R ，现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点，求移动过程中电场力作的功． 解: 如题8-16图示0π41ε=O U 0)(=-RqR q0π41ε=O U )3(R qR q -Rq 0π6ε-= ∴ Rqq U U q A o C O 00π6)(ε=-=8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R ．试求环中心O 点处的场强和电势． 解: (1)由于电荷均匀分布与对称性，AB 和CD 段电荷在O 点产生的场强互相抵消，取θd d R l =则θλd d R q =产生O 点E ϖd 如图，由于对称性，O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E yR 0π4ελ=［)2sin(π-2sin π-］R0π2ελ-=(2) AB 电荷在O 点产生电势，以0=∞U⎰⎰===AB200012ln π4π4d π4d R R x x x x U ελελελ 同理CD 产生 2ln π402ελ=U半圆环产生 0034π4πελελ==R R U∴ 0032142ln π2ελελ+=++=U U U U O 8-22 三个平行金属板A ，B 和C 的面积都是200cm 2，A 和B 相距4.0mm ，A 与C 相距2.0 mm ．B ，C 都接地，如题8-22图所示．如果使A 板带正电3.0×10-7C ，略去边缘效应，问B 板和C 板上的感应电荷各是多少?以地的电势为零，则A 板的电势是多少?解: 如题8-22图示，令A 板左侧面电荷面密度为1σ，右侧面电荷面密度为2σ题8-22图(1)∵ AB AC U U =，即 ∴ AB AB AC AC E E d d = ∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A=得 ,32S q A =σ Sq A 321=σ 而 7110232-⨯-=-=-=A C q S q σC C10172-⨯-=-=S q B σ(2) 301103.2d d ⨯===AC AC AC A E U εσV 8-23 两个半径分别为1R 和2R （1R ＜2R )的同心薄金属球壳，现给内球壳带电+q ，试计算：(1)外球壳上的电荷分布及电势大小；(2)先把外球壳接地，然后断开接地线重新绝缘，此时外球壳的电荷分布及电势；*(3)再使内球壳接地，此时内球壳上的电荷以及外球壳上的电势的改变量． 解: (1)内球带电q +；球壳内表面带电则为q -,外表面带电为q +，且均匀分布，其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R Rqr r q r E U εεϖϖ(2)外壳接地时，外表面电荷q +入地，外表面不带电，内表面电荷仍为q -．所以球壳电势由内球q +与内表面q -产生：0π4π42020=-=R q R q U εε8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳，介质相对介电常数为r ε，金属球带电Q ．试求： (1)电介质内、外的场强； (2)电介质层内、外的电势； (3)金属球的电势．解: 利用有介质时的高斯定理∑⎰=⋅q S D S ϖϖd(1)介质内)(21R r R <<场强303π4,π4rrQ E r r Q D r εεϖϖϖϖ==内; 介质外)(2R r <场强303π4,π4r r Q E r Qr D εϖϖϖ==外(2)介质外)(2R r >电势rQE U 0rπ4r d ε=⋅=⎰∞ϖϖ外 介质内)(21R r R <<电势2020π4)11(π4R Q R r qr εεε+-=)11(π420R r Qr r -+=εεε(3)金属球的电势r d r d 221ϖϖϖϖ⋅+⋅=⎰⎰∞R R R E E U 外内⎰⎰∞+=22220π44πdr R R Rr r Qdrr Q εεε)11(π4210R R Q r r-+=εεε rd r d ϖϖϖϖ⋅+⋅=⎰⎰∞∞rrE E U 外内8-28 如题8-28图所示，在平行板电容器的一半容积内充入相对介电常数为r ε的电介质．试求：在有电介质部分和无电介质部分极板上自由电荷面密度的比值．解: 如题8-28图所示，充满电介质部分场强为2E ϖ，真空部分场强为1E ϖ，自由电荷面密度分别为2σ与1σ 由∑⎰=⋅0d q S D ϖϖ得11σ=D ，22σ=D而 101E D ε=,202E D r εε=d21U E E == ∴r D D εσσ==1212题8-28图 题8-29图8-29 两个同轴的圆柱面，长度均为l ，半径分别为1R 和2R (2R ＞1R )，且l >>2R -1R ，两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时，求：(1)在半径r 处(1R ＜r ＜2R ＝，厚度为dr ，长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量；(2)电介质中的总电场能量； (3)圆柱形电容器的电容．解: 取半径为r 的同轴圆柱面)(S则 rlD S D S π2d )(=⋅⎰ϖϖ当)(21R r R <<时，Q q =∑∴ rlQD π2=(1)电场能量密度 22222π82l r Q D w εε== 薄壳中 rlrQ rl r l r Q w W εευπ4d d π2π8d d 22222=== (2)电介质中总电场能量⎰⎰===211222ln π4π4d d R R VR R l Q rl r Q W W εε (3)电容：∵ CQ W 22=∴ )/ln(π22122R R lW Q C ε== 习题九9-8 在真空中，有两根互相平行的无限长直导线1L 和2L ，相距0.1m ，通有方向相反的电流，1I =20A,2I =10A ，如题9-8图所示．A ，B 两点与导线在同一平面内．这两点与导线2L 的距离均为5.0cm ．试求A ，B 两点处的磁感应强度，以及磁感应强度为零的点的位置．题9-8图解：如题9-8图所示,A B ϖ方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B ϖ在2L 外侧距离2L 为r 处则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r mT9-11 氢原子处在基态时，它的电子可看作是在半径a =0.52×10-8cm 的轨道上作匀速圆周运动，速率v =2.2×108cm ·s -1．求电子在轨道中心所产生的磁感应强度和电子磁矩的值．解：电子在轨道中心产生的磁感应强度3004aav e B πμϖϖϖ⨯= 如题9-11图，方向垂直向里，大小为134200==a evB πμ T 电子磁矩m P ϖ在图中也是垂直向里，大小为242102.92-⨯===eva a T e P m π 2m A ⋅ 题9-11图 题9-12图9-12 两平行长直导线相距d =40cm ，每根导线载有电流1I =2I =20A ，如题9-12图所示．求：(1)两导线所在平面内与该两导线等距的一点A 处的磁感应强度；(2)通过图中斜线所示面积的磁通量．(1r =3r =10cm,l =25cm)．解：(1) 52010104)2(2)2(2-⨯=+=d I d I B A πμπμ T 方向⊥纸面向外(2)取面元r l S d d =612010110102.23ln 31ln 23ln 2])(22[1211-+⨯=πμ=πμ-πμ=-πμ+πμ=⎰l I l I l I ldr r d I r I r r r ΦWb9-13 一根很长的铜导线载有电流10A ，设电流均匀分布.在导线内部作一平面S ，如题9-13图所示．试计算通过S 平面的磁通量(沿导线长度方向取长为1m 的一段作计算)．铜的磁导率0μμ=.解：由安培环路定律求距圆导线轴为r 处的磁感应强度⎰∑μ=⋅lI l B 0d ϖ2202RIr r B μπ=∴ 202R IrB πμ=题 9-13 图 磁通量 60020)(1042-===⋅=Φ⎰⎰πμπμI dr RIr S d B Rs m ϖϖ Wb 题9-15图9-15 题9-15图中所示是一根很长的长直圆管形导体的横截面，内、外半径分别为a ,b ，导体内载有沿轴线方向的电流I ，且I 均匀地分布在管的横截面上．设导体的磁导率0μμ≈，试证明导体内部各点)(b r a << 的磁感应强度的大小由下式给出：r a r a b IB 22220)(2--=πμ解：取闭合回路r l π2= )(b r a <<则 ⎰π=⋅lr B l B 2d ϖϖ2222)(a b Ia r I ππππ--=∑∴ )(2)(22220a b r a r I B --=πμ 9-16 一根很长的同轴电缆，由一导体圆柱(半径为a )和一同轴的导体圆管(内、外半径分别为b ,c )构成，如题9-16图所示．使用时，电流I 从一导体流去，从另一导体流回．设电流都是均匀地分布在导体的横截面上，求：(1)导体圆柱内(r ＜a ),(2)两导体之间(a ＜r ＜b )，（3）导体圆筒内(b ＜r ＜c )以及(4)电缆外(r ＞c )各点处磁感应强度的大小 解：⎰∑μ=⋅LI l B 0d ϖϖ(1)a r < 2202RIr r B μπ=202R IrB πμ=(2) b r a << I r B 02μπ=rIB πμ20=(3)c r b << I bc b r I r B 0222202μμπ+---= )(2)(22220b c r r c I B --=πμ (4)c r > 02=r B π0=B题9-16图题9-17图题9-21图9-21 边长为l =0.1m 的正三角形线圈放在磁感应强度B =1T 的均匀磁场中，线圈平面与磁场方向平行.如题9-21图所示，使线圈通以电流I =10A ，求： (1)线圈每边所受的安培力； (2)对O O '轴的磁力矩大小；(3)从所在位置转到线圈平面与磁场垂直时磁力所作的功．解： (1) 0=⨯=B l I F bc ϖϖϖB l I F ab ϖϖϖ⨯= 方向⊥纸面向外，大小为866.0120sin ==︒IlB F ab NB l I F ca ϖϖϖ⨯=方向⊥纸面向里，大小866.0120sin ==︒IlB F ca N(2)IS P m =B P M m ϖϖϖ⨯= 沿O O '方向，大小为221033.443-⨯===B l I ISB M m N ⋅(3)磁力功 )(12ΦΦ-=I A∵ 01=Φ B l 2243=Φ ∴221033.443-⨯==B l IA J9习题十10-1 一半径r =10cm 的圆形回路放在B =0.8T 的均匀磁场中．回路平面与B ϖ垂直．当回路半径以恒定速率trd d =80cm ·s -1 收缩时，求回路中感应电动势的大小．解: 回路磁通 2πr B BS m ==Φ感应电动势大小40.0d d π2)π(d d d d 2====trr B r B t t m Φε V 10-2 一对互相垂直的相等的半圆形导线构成回路，半径R =5cm ，如题10-2图所示．均匀磁场B =80×10-3T ，B 的方向与两半圆的公共直径(在Oz 轴上)垂直，且与两个半圆构成相等的角α 当磁场在5ms 内均匀降为零时，求回路中的感应电动势的大小及方向．解: 取半圆形cba 法向为i ϖ， 题10-2图则 αΦcos 2π21B R m =同理，半圆形adc 法向为j ϖ，则αΦcos 2π22B R m=∵ B ϖ与i ϖ夹角和B ϖ与j ϖ夹角相等，∴ ︒=45α则 αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tBR t m αεV方向与cbadc 相反，即顺时针方向．题10-4图10-4 如题10-4图所示，载有电流I 的长直导线附近，放一导体半圆环MeN 与长直导线共面，且端点MN 的连线与长直导线垂直．半圆环的半径为b ，环心O 与导线相距a ．设半圆环以速度v 平行导线平移．求半圆环内感应电动势的大小和方向及MN 两端的电压 N M U U -．解: 作辅助线MN ，则在MeNM 回路中，沿v ϖ方向运动时0d =m Φ ∴ 0=MeNM ε 即 MN MeN εε= 又∵0cos d ln 02a bMN a bIv a bvB l a bμεππ+--==<+⎰所以MeN ε沿NeM 方向，大小为ba ba Iv -+ln20πμ M 点电势高于N 点电势，即ba ba Iv U U N M -+=-ln20πμ 题10-5图10-5如题10-5所示，在两平行载流的无限长直导线的平面内有一矩形线圈．两导线中的电流方向相反、大小相等，且电流以tId d 的变化率增大，求： (1)任一时刻线圈内所通过的磁通量；(2)线圈中的感应电动势． 解: 以向外磁通为正则(1) ]ln [lnπ2d π2d π2000dad b a b Ilr l r Ir l r Iab b ad d m +-+=-=⎰⎰++μμμΦ (2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε10-6 如题10-6图所示，用一根硬导线弯成半径为r 的一个半圆．令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转．整个电路的电阻为R ．求：感应电流的最大值．题10-6图解: )cos(2π02ϕωΦ+=⋅=t r B S B m ϖϖ∴ Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε ∴ RBfr R I m22π==ε 10-7 如题10-7图所示，长直导线通以电流I =5A ，在其右方放一长方形线圈，两者共面．线圈长b =0.06m ，宽a =0.04m ，线圈以速度v =0.03m ·s -1垂直于直线平移远离．求：d =0.05m 时线圈中感应电动势的大小和方向．题10-7图解: AB 、CD 运动速度v ϖ方向与磁力线平行，不产生感应电动势． DA 产生电动势⎰==⋅⨯=AD I vb vBb l B v d2d )(01πμεϖϖϖBC 产生电动势)(π2d )(02d a Ivbl B v CB+-=⋅⨯=⎰μεϖϖϖ∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad d Ibv μεεε V 方向沿顺时针．10-8 长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动．已知导轨处于均匀磁场B ϖ中，B ϖ的方向与回路的法线成60°角(如题10-8图所示)，B ϖ的大小为B =kt (k 为正常)．设t =0时杆位于cd 处，求：任一时刻t 导线回路中感应电动势的大小和方向． 解:⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m ϖϖΦ∴ klvt tm-=-=d d Φε 即沿abcd 方向顺时针方向．题10-8图10-9 一矩形导线框以恒定的加速度向右穿过一均匀磁场区，B ϖ的方向如题10-9图所示．取逆时针方向为电流正方向，画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0)．解: 如图逆时针为矩形导线框正向，则进入时0d d <Φt,0>ε； 题10-9图(a)题10-9图(b) 在磁场中时0d d =tΦ,0=ε； 出场时0d d >tΦ，0<ε，故t I -曲线如题10-9图(b)所示. 题10-10图10-10 导线ab 长为l ，绕过O 点的垂直轴以匀角速ω转动，aO =3l磁感应强度B 平行于转轴，如图10-10所示．试求： （1）ab 两端的电势差； （2）b a ,两端哪一点电势高? 解: (1)在Ob 上取dr r r +→一小段则 ⎰==320292d l Ob l B r rB ωωε 同理 ⎰==302181d l Oa l B r rB ωωε ∴2261)92181(l B l B Ob aO ab ωωεεε=+-=+= (2)∵ 0>ab ε 即0<-b a U U ∴b 点电势高．题10-11图10-11 如题10-11图所示，长度为b 2的金属杆位于两无限长直导线所在平面的正中间，并以速度v ϖ平行于两直导线运动．两直导线通以大小相等、方向相反的电流I ，两导线相距2a ．试求：金属杆两端的电势差及其方向． 解：在金属杆上取r d 距左边直导线为r ，则ba b a Iv r r a r Iv l B v b a b a BA AB-+-=-+-=⋅⨯=⎰⎰+-ln d )211(2d )(00πμπμεϖϖϖ ∵ 0<AB ε ∴实际上感应电动势方向从A B →，即从图中从右向左， ∴ ba ba Iv U AB -+=ln0πμ 题10-12图10-12 磁感应强度为B ϖ的均匀磁场充满一半径为R 的圆柱形空间，一金属杆放在题10-12图中位置，杆长为2R ，其中一半位于磁场内、另一半在磁场外．当tBd d＞0时，求：杆两端的感应电动势的大小和方向．解： ∵ bc ab ac εεε+=tBR B R t t ab d d 43]43[d d d d 21=--=-=Φε=-=tabd d 2Φεt BR B R t d d 12π]12π[d d 22=-- ∴ tB R R acd d ]12π43[22+=ε∵0d d >tB∴ 0>ac ε即ε从c a →10-13 半径为R 的直螺线管中，有dtdB＞0的磁场，一任意闭合导线abca ，一部分在螺线管内绷直成ab 弦，a ,b 两点与螺线管绝缘，如题10-13图所示．设ab =R ，试求：闭合导线中的感应电动势． 解：如图，闭合导线abca 内磁通量)436π(22R R B S B m -=⋅=ϖϖΦ∴ tB R R i d d )436π(22--=ε ∵0d d >tB∴0<i ε，即感应电动势沿acba ，逆时针方向．题10-13图题10-14图。

北京理工大学大学物理教材电子版1、29．生产和生活中，人们选择材料时会考虑材料的物理性质，下面属于主要从密度的角度考虑选材料的是（）[单选题] *A．用塑料作为插座外壳的材料B．用铝合金作为制作飞机的材料(正确答案)C．用橡胶作为汽车轮胎的材料D．用钨作为白炽灯泡灯丝的材料2、20．如图所示，体积相等的A、B两种实心球由不同物质制成，此时天平平衡。

则制成A、B两种实心球的物质密度之比ρA：ρB为（）[单选题] *A．1：1B．2：3C．5：1D．3：2(正确答案)3、7．舞龙舞狮是我国民间的传统习俗，舞龙舞狮过程中，往往用敲锣和击鼓来助兴，下列说法正确的是（）[单选题] *A．锣鼓声响起时远近不同的观众都能听到，说明声音传播不需要时间B．越用力敲击锣面，锣面振动幅度会越大，发出声音的音调越高C．人们能区分锣声和鼓声，主要是它们的音色不同(正确答案)D．围观的一些小孩捂住耳朵，是为了在传播过程中减弱噪声4、4．只要物体做直线运动，物体就处于平衡状态．[判断题] *对错(正确答案)5、D.环形电流的电流强度跟m成反比(正确答案)下列说法不符合分子动理论观点的是（）*A.用气筒打气需外力做功，是因为分子间的后斥力作用(正确答案)B.温度升高，布朗运动显著，说明悬浮颗粒的分子运动剧烈C.相距较远的两个分子相互靠近的过程中，分子势能先减小后增大D.相距较远的两个分子相互靠近的过程中，分子间引力先增大后减小(正确答案)6、下列事例中，属于用热传递的方式改变物体内能的是（）[单选题]A．用锯条锯木头，锯条温度升高B．用炉灶烧水，水温升高(正确答案)C．气缸内气体被压缩，温度升高D．用力搓手，手会发热7、【判断题】1N=1Kg.m/s [判断题] *对(正确答案)错用显微镜观察悬浮在液体中的花粉的运动，下面的哪些说法与观察到的结果相符（）* A.制成的悬浮液体静置的时间越长，花粉微粒的运动械匙微弱8、29．下列说法正确的是（）[单选题] *A．洗澡时，洗澡水的适宜温度约为40℃(正确答案)B．0℃的冰比0℃的水冷C．正常情况下，人的体温约为4℃D．人体感到舒适的气温约为30℃9、30．如图，我国首款国际水准的大型客机C919在上海浦东机场首飞成功，标志着我国航空事业有了重大突破。

一、填空题1、一竖直悬挂的轻质弹簧的下端挂上质量m 的小球后，其平衡状态下弹簧伸长0l ，则该弹簧的劲度系数=k 0l m g，该弹性振子的振动周期=T gl 02π。

2、一质点作简谐运动，其振动曲线如题2图所示。

根据此图，它的振幅=A cm 4，用余弦函数描述时初 相位=ϕ32π-，P 点的速度方向 向下 。

3、已知某简谐运动的振动曲线如题3图所示，则此简谐运动的运动方程为：)365cos(4ππ-=t x 。

4、一简谐运动的振动曲线如题4图所示，则相应的以余弦函数表示的该振动方程为=x )2cos(04.0ππ-t 。

5、如题5图所示0=t 时一沿x 轴正方向传播的平面简谐波的波形曲线，则：（1）此平面简谐波的振幅=A cm 2，=λm 40，（2）0=t 时O 、P 两处质点的速度方向： O 向下，P 向上 。

6、一质点作简谐振动，其振动曲线如题6图所示，根据此图，它的周期T= 3.43s ，用余弦函数描述时初相位=ϕπ32-。

7、一质点沿x 轴以0=x 为平衡位置坐简谐振动，频率为0.25Hz ，0=t 时cm x 37.0-=，而速度等于零，则振幅A=0.37cm ，振动的数值表达式为)21cos(37.0ππ±=t x 。

8、已知弹性媒质中平面波波动方程为()Cx Bt A y -=cos ，式中A 、B 、C 均为恒量，则波的振幅为 A ，波速为CB ，频率为π2B ，波长为C π2 。

9、已知一简谐运动的运动方程为)5310cos(41π+=t x ，另有一同方向的简谐运动)10cos(62φ+=t x ，则合振幅的最大值为cm 10，此时φ值最小为53π。

（1x 、2x 单位为cm ）10、题10图所画的是两个简谐运动的振动曲线， 若这两个简谐运动可叠加，则合成的余弦振动的 合振幅为2A，初相位为0。

11、某一简谐运动的振动方程为m t x )22cos(5.01ππ+=，另一个同频率、同振幅的简谐运动2的相位落后2π。

选择题1. （陈勋）如图所示，折射率为n2，厚度为e的透明介质薄膜的上方和下方的透明介质折射率分别为n1和n3，且n1<n2,n2>n3,若用波长为λ的单色平行光垂直入射到该薄膜上，则薄膜上下表面反射光束的光程差是（）（A）2n2e （B）2 n2e -λ/2 （C）2 n2e -λ（D）2 n2e -λ/(2 n2)2、（黄奕乔）在下列几种说法中，正确的是：A 相等光程的几何距离必然相等B 光行进相同的光程，经历的时间必然相等C 几何距离大的，其光程必然较大D 相同的光程必然有相同的对应的真空距离3. （姜亚永）如图1.1所示，折射率为n2 、厚度为e的透明介质薄膜的上方和下方的透明介质的折射率分别为n1和n3，已知n1＜n2＞n3，若用波长为λ的单色平行光垂直入射到该薄膜上，则从薄膜上、下两表面反射的光束（用①②示意）的光程差是(A) 2n2e. (B) 2n2e－λ/(2 n2).(C) 2n2e －. (D)2n2e －/2.4、（李凯钥）机械波的表达式为y=0.05cos (6πt+0.06πx) (m),则（）A．波长为100m B.波速为10 m/s图1.1C. 周期为1/3 sD.波沿x 轴正方向传播5、（陈跃彪）设声波在媒介中的传播速度为u ，声源的频率为 γS ，若声源S 不动，而接收器R 相对于媒介以速度V R 沿S 、R 连线向着声源S 运动，则接收器R 接受到的信号频率为 ( )﹙A ﹚γS ； ﹙B ﹚u V u R +γS ； ﹙C ﹚u V u R -γS ；﹙D ﹚R V u u-γS6．（刘海峰）两个相干波源发出的简谐波叠加时，下列各种情况中，能发生干涉的是[ ]。

(A)若两个相干波源的振幅相同，振动方向相同，初相位也相同，但频率不同；(B) 若两个相干波源的振幅相同，频率相同，初相位也相同，但振动方向不同；(C) 若两个相干波源的振幅相同，频率相同，振动方向也相同，但相位差不恒定；(D) 若两个相干波源的频率相同，振动方向相同，相位差恒定，但初相位不同，振幅不同7．一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1／4时，其动能为振动总能量的(A) 9／16． (B) 11／16．(C) 13／16． (D) 15／16．8、（白利娟）在杨氏双缝干涉实验中，形成的干涉条纹中，位于对称中心两侧的暗纹中心的距离为（ ）A 、D λ/dB 、2 D λ/dC 、3D λ/d D 、4D λ/d9、（孙玉琼）两个质点各自作简谐振动，它们的振幅相同、周期相同。

《大学物理》（下）复习提纲第6章 恒定电流的磁场(1) 掌握磁场，磁感应强度，磁力线，磁通量等概念，磁场中的高斯定理，毕奥一沙伐一拉普拉斯定律。

(2) 掌握安培环路定律，应用安培环路定律计算磁场.(3)掌握安培定律，会用安培定律计算磁场力。

会判断磁力矩的方向。

会判断霍尔效应电势的方向。

1． 边长为2a 的等边三角形线圈，通有电流I ，则线圈中 心处的磁感强度的大小为________________．2． 边长为l 的正方形线圈，分别用图示两种方式通以电流I (其中ab 、cd 与正方形共面)，在这两种情况下，线圈在其中心产生的磁感强度的大小分别为3．一无限长载流直导线，通有电流I ，弯成如图形状．设各线段皆在纸面内，一无限长载流直导线，通有电流I ，弯成如图形状．设各线段皆在纸面内，则P 点磁感强度B的大小为________________．则P 点磁感强度B的大小为4． 一无限长载有电流I 的直导线在一处折成直角，P 点位于导线所在平面内，距一条折线的延长线和另一条导线的距离都为a ，如图．求P点的磁感强度B．5．无限长直导线在P 处弯成半径为R 的圆，当通以电流I 时，则在圆心O 点的磁感强度大小等于（A ）R I πμ20 （B ）240RIμ6．如图所示，用均匀细金属丝构成一半径为R 的圆环C ，电流I 由导线1流入圆环A 点，并由圆环B 点流入导线2．设导线1和导线2与圆环共面，则环心O 处的磁感强度大小 为________________________，方向___________________．7． 真空中电流分布如图，两个半圆共面，且具有公共圆心，试求O 点处的磁感强度．8．均匀磁场的磁感强度B 与半径为 r 的圆形平面的法线n的夹角为α ，今以圆周为边界，作一个半球面S ，S 与圆形平面组成 封闭面如图．则通过S 面的磁通量Φ =________________．9．如图，两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上，稳恒电流I从a 端流入而从d 端流出，则磁感强度B沿图中闭合路径L 的积分⎰⋅Ll d B 等于10．如图，流出纸面的电流为2I，流进纸面的电流为I，则下述各式中哪一个是正确的？11．如图，在一圆形电流I所在的平面内，选取一个同心圆形闭合回路L，则由安培环路定理可知(A) 0d=⎰⋅LlB，且环路上任意一点B = 0．(B) 0d=⎰⋅LlB，且环路上任意一点B≠0．(C) 0d≠⎰⋅LlB，且环路上任意一点B≠0．(D) 0d≠⎰⋅LlB，且环路上任意一点B =常量．［］12. 有一同轴电缆，其尺寸如图所示，它的内外两导体中的电流均为I，且在横截面上均匀分布，但二者电流的流向正相反，则(1) 在r < R1处磁感强度大小为________________．(2) R1< r< R2处磁感强度大小为________________．(2) 在r > R3处磁感强度大小为________________．13. 两根长直导线通有电流I，图示有三种环路；在每种情况下，⎰⋅L l dB等于：_______________________(对环路a)．_______________________(对环路b)．_______________________(对环路c)．14． 在图(a)和(b)中各有一半径相同的圆形回路L 1、L 2，圆周内有电流I 1、I 2，其分布相同，且均在真空中，但在(b)图中L 2回路外有电流I 3，P 1、P 2为两圆形回路上的对应点，则：(A) =⎰⋅1d L l B⎰⋅2d L l B, 21P P B B =(B) ≠⎰⋅1d L l B⎰⋅2d L l B, 21P P B B =．(C) =⎰⋅1d Ll B⎰⋅2d L l B, 21P P B B ≠．(D)≠⎰⋅1d L l B ⎰⋅2d L l B , 21P P B B ≠． ［ ］15．把轻的导线圈用线挂在磁铁N 极附近，磁铁的轴线穿过线圈中心，且与线圈在同一平面内，如图所示．当线圈内通以如图所示方向的电流时，线圈将(A) 不动． (B) 发生转动，同时靠近磁铁． (C) 发生转动，同时离开磁铁． (D) 不发生转动，只靠近磁铁．(E) 不发生转动，只离开磁铁． ［ ］16. 如图，一根载流导线被弯成半径为R 的1/4圆弧，放在磁感强度为B 的均匀磁场中，则载流导线ab （电流I 顺时针方向流动）所受磁场的作用力的大小为____________，方向_________________．17．如图，均匀磁场中放一均匀带正电荷的圆环，其线电荷密度为λ，圆环可绕通过环心O 与环面垂直的转轴旋转．当圆环以角速度ω转动时，圆环受到的磁力矩为 ___ _________， 其方向__________________________．L 1 2I 3(a)(b)⊙18．有两个半径相同的环形载流导线A 、B ，它们可以自由转动和移动，把它们放在相互垂直的位置上，如图所示，将发生以下哪一种运动?(A) A 、B 均发生转动和平动，最后两线圈电流同方向并紧靠在一起． (B) A 不动，B 在磁力作用下发生转动和平动． (C) A 、B 都在运动，但运动的趋势不能确定．(D) A 和B 都在转动，但不平动，最后两线圈磁矩同方向平行．19．如图，在一固定的无限长载流直导线的旁边放置一个可以自由移动和转动的圆形的刚性线圈，线圈中通有电流，若线圈与直导线在同一平面，见图(a)，则圆线圈的运动将是 ______________________ _________； 若线圈平面与直导线垂直，见图(b)，则圆线圈将 __________________________________________________。