最新整理(小升初图形必学)求阴影部分的面积doc资料

【史上最全小学求阴影部份面积专题—含谜底】之马矢奏春创作时间：二O二一年七月二十九日小学及小升初复习专题-圆与求阴影部份面积----完整谜底在最后面目标：通过专题复习,加强学生对图形面积计算的灵活运用.并加深对面积和周长概念的理解和区分.面积求解年夜致分为以下几类：1、从整体图形中减去局部；2、割补法,将不规则图形通过割补,转化陈规则图形.重难点：观察图形的特点,根据图形特点选择合适的方法求解图形的面积.能灵活运用所学过的基本的平面图形的面积求阴影部份的面积.例1.求阴影部份的面积. (单元:厘米)例2.正方形面积是7平方厘米,求阴影部份的面积.(单元:厘米)积.(单元:厘米)例5.求阴影部份的面积.(单元:厘米)例6.如图：已知小圆半径为2厘米,年夜圆半径是小圆的3倍,问：空白部份甲比乙的面积多几多厘米？例7.求阴影部份的面积.(单元:厘米)例8.求阴影部份的面积.(单元:厘米)例9.求阴影部份的面积.(单元:厘米)例10.求阴影部份的面积.(单元:厘米)例11.求阴影部份的面积.(单元:厘米)例12.求阴影部份的面积.(单元:厘米)元:厘米)米,求阴影部份的面积.例16.求阴影部份的面积.(单元:厘米)例17.图中圆的半径为5厘米,求阴影部份的面积.(单元:厘米) 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部份的周长.例19.正方形边长为2厘米,求阴影部份的面积.例20.如图,正方形ABCD的面积是36平方厘米,求阴影部份的面积.例21.图中四个圆的半径都是1厘米,求阴影部份的面积. 例22. 如图,正方形边长为8厘米,求阴影部份的面积.例23.图中的4个圆的圆心是正方形的4个极点,,它们的公共点是该正方形的中心,如果每例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部份连成一个花瓣图形,图中的个圆的半径都是1厘米,那么阴影部份的面积是几多？黑点是这些圆的圆心.如果圆周π率取3.1416,那么花瓣图形的的面积是几多平方厘米？例25.如图,四个扇形的半径相等,求阴影部份的面积.(单元:厘米) 例26.如图,等腰直角三角形ABC和四分之一圆DEB,AB=5厘米,BE=2厘米,求图中阴影部份的面积.例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部份,求阴影部份的面积.例28.求阴影部份的面积.(单元:厘米)例29.图中直角三角形ABC的直角三角形的直角边AB=4厘米,BC=6厘米,扇形BCD所在圆是以B为圆心,半径为BC的圆,∠CBD=,问：阴影部份甲比乙面积小几多？例30.如图,三角形ABC是直角三角形,阴影部份甲比阴影部份乙面积年夜28平方厘米,AB=40厘米.求BC的长度.例31.如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部份的面积.例32.如图,年夜正方形的边长为6厘米,小正方形的边长为4厘米.求阴影部份的面积.例33.求阴影部份的面积.(单元:厘米) 例34.求阴影部份的面积.(单元:厘米)例35.如图,三角形OAB是等腰三角形,OBC是扇形,OB=5厘米,求阴影部份的面积.完整谜底例1解：这是最基本的方法：圆面积减去等腰直角三角形的面积,×-2×1=1.14（平方厘米）例2解：这也是一种最基本的方法用正方形的面积减去圆的面积.设圆的半径为 r,因为正方形的面积为7平方厘米,所以=7,所以阴影部份的面积为：7-=7-例3解：最基本的方法之一.用四个圆组成一个圆,用正方形的面积减去圆的面积, 所以阴影部份的面积：2×2-π＝0.86平方厘米.例4解：同上,正方形面积减去圆面积, 16-π()=16-4π=3.44平方厘米例5解：这是一个用最经常使用的方法解最罕见的题,为方便起见,我们把阴影部份的每一个小部份称为“叶形”,是用两个圆减去一个正方形, 例6解：两个空白部份面积之差就是两圆面积之差（全加上阴影部份）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部份的8倍.如何无关）例7解：正方形面积可用(对角线长×对角线长÷2,求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8解：右面正方形上部阴影部份的面积,即是左面正方形下部空白部份面积,割补以后为圆,所以阴影部份面积为：π(例9解：把右面的正方形平移至左边的正方形部份,则阴影部份合成一个长方形, 所以阴影部份面积为：2×3=6平方厘米例10解：同上,平移左右两部份至中间部份,则合成一个长方形,所以阴影部份面积为2×1=2平方厘米(注: 8、9、10三题是简单割、补或平移)例11解：这种图形称为环形,可以用两个同心圆的面积差或差的一部份来求.（π -π）×=例12. 解：三个部份拼成一个半圆面积．π()÷２＝14.13平方厘米例13解: 连对角线后将"叶形"剪开移到右上面的空白部份,凑成正方形的一半.所以阴影部份面积为：8×8÷2=32平方厘米例14解：梯形面积减去圆面积,(4+10)×4-π=28-4π=15.44平方厘米 .例15. 分析: 此题比上面的题有一定难度,这是"叶形"的一个半.解: 设三角形的直角边长为r,则=12,=6圆面积为：π÷2=3π.圆内三角形的面积为12÷2=6,阴影部份面积为：(3π-6)×例16解：［π＋π－π］ =π(116-36)=40π=125.6平方厘米例19解：右半部份上面部份逆时针,下面部份顺时针旋转到左半部份,组成一个矩形.所以面积为：1×2=2平方厘米例20解：设小圆半径为r,4=36, r=3,年夜圆半径为R,=2=18,将阴影部份通过转动移在一起构成半个圆环,所以面积为:π(-例21.解：把中间部份分成四等分,分别放在上面圆的四个角上,补成一个正方形,边长为2厘米,所以面积为：2×2=4平方厘米例22解法一: 将左边上面一块移至右边上面,补上空白,则左边为一三角形,右边一个半圆.阴影部份为一个三角形和一个半圆面积之和.π()÷2+4×4=8π+16=41.12平方厘米解法二: 补上两个空白为一个完整的圆.所以阴影部份面积为一个圆减去一个叶形,叶形面积为:π()÷2-4×4=8π-16 所以阴影部份的面积为:π(例23解：面积为４个圆减去８个叶形,叶形面积为：π-1×1=π-1所以阴影部份的面积为:4π-8(π-1)=8平方厘米例24分析：连接角上四个小圆的圆心构成一个正方形,各个小圆被切去例25分析：四个空白部份可以拼成一个以２为半径的圆．所以阴影部份的面积为梯形面积减去圆的面积,4×(4+7)÷2-π例26解: 将三角形CEB以B为圆心,逆时针转动90度,到三角形ABD位置,阴影部份成为三角形ACB面积减去个小圆面积,为: 5×5÷2-π例27解: 因为2==4,所以=2 以AC为直径的圆面积减去三角形ABC面积加上弓形AC面积,π-2×2÷4+[π÷4-2]=π-1+(π-1)=π-2=1.14平方厘米例28解法一：设AC中点为B,阴影面积为三角形ABD面积加弓形BD的面积,三角形ABD的面积为:5×5÷2=12.5弓形面积为:[π÷2-5×5]÷2=7.125所以阴影面积为:12.5+7.125=19.625平方厘米解法二：右上面空白部份为小正方形面积减去小圆面积,其值为：5×5-π=25-π阴影面积为三角形ADC减去空白部份面积,为：10×5÷2-（25-π）=π=19.625平方厘米例29. 解: 甲、乙两个部份同补上空白部份的三角形后合成一个扇形BCD,一个成为三角例30. 解：两部份同补上空白部份后为直角三角形ABC,一个为半圆,设BC长为X,则40X÷2-π形ABC,此两部份差即为：π×－例31.解：连PD、PC转换为两个三角形和两个弓形,两三角形面积为：△APD面积+△QPC面积=（5×10+5×5）=37.5两弓形PC、PD面积为：π-5×5所以阴影部份的面积为：37.5+π-25=51.75平方厘米例32解：三角形DCE的面积为:×4×10=20平方厘米梯形ABCD的面积为:(4+6)×4=20平方厘米从而知道它们面积相等,则三角形ADF面积即是三角形EBF面积,阴影部份可补成圆ABE的面积,其面积为：π÷4=9π=28.26平方厘米例33.解:用年夜圆的面积减去长方形面积再加上一个以2为半径的圆ABE面积,为(π+π)-6 =例34解：两个弓形面积为：π-3×4÷2=π-6阴影部份为两个半圆面积减去两个弓形面积,结果为π+π-（π-6）=π（4+-）+6=6平方厘米例35解：将两个同样的图形拼在一起成为圆减等腰直角三角形[π÷4-×5×5]÷2=（π-时间：二O二一年七月二十九日。

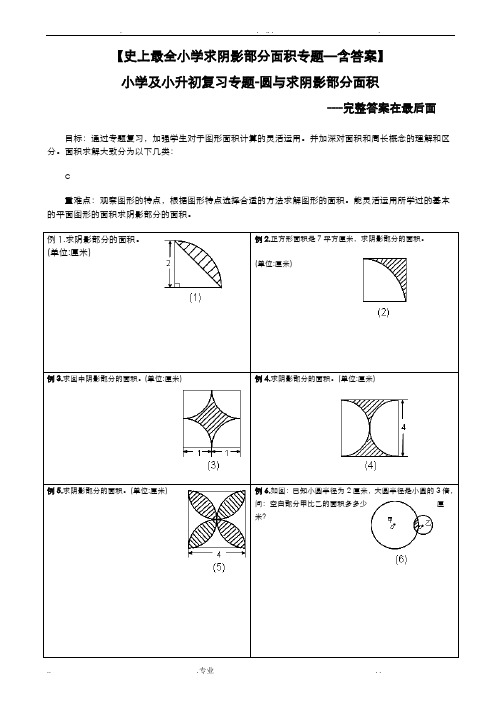
【史上最全小学求阴影部分面积专题—含答案】 小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标：通过专题复习，加强学生对于图形面积计算的灵活运用。

并加深对面积和周长概念的理解和区分。

面积求解大致分为以下几类：c重难点：观察图形的特点，根据图形特点选择合适的方法求解图形的面积。

能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。

例1.求阴影部分的面积。

(单位:厘米)例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)例3.求图中阴影部分的面积。

(单位:厘米)例4.求阴影部分的面积。

(单位:厘米)例5.求阴影部分的面积。

(单位:厘米)例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？例7.求阴影部分的面积。

(单位:厘米)例8.求阴影部分的面积。

(单位:厘米)例9.求阴影部分的面积。

(单位:厘米)例10.求阴影部分的面积。

(单位:厘米)例11.求阴影部分的面积。

(单位:厘米)例12.求阴影部分的面积。

(单位:厘米)例13.求阴影部分的面积。

(单位:厘米)例14.求阴影部分的面积。

(单位:厘米)例15.已知直角三角形面积是12平方厘米，求阴影部分的面积。

例16.求阴影部分的面积。

(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。

(单位:厘米) 例18.如图，在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。

例19.正方形边长为2厘米，求阴影部分的面积。

例20.如图，正方形ABCD的面积是36平方厘米，求阴影部分的面积。

例21.图中四个圆的半径都是1厘米，求阴影部分的面积。

例22.如图，正方形边长为8厘米，求阴影部分的面积。

例23.图中的4个圆的圆心是正方形的4个顶点，，它们的公共点是该正方形的中心，如果每个圆的半径都是1厘米，那么阴影部分的面积是多少？例24.如图，有8个半径为1厘米的小圆，用他们的圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心。

【史上最全小学求阴影部分面积专题—含答案】之蔡仲巾千创作小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标：通过专题复习，加强学生对于图形面积计算的灵活运用。

并加深对面积和周长概念的理解和区分。

面积求解大致分为以下几类：1、从整体图形中减去局部；2、割补法，将不规则图形通过割补，转化成规则图形。

重难点：观察图形的特点，根据图形特点选择合适的方法求解图形的面积。

能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。

例1.求阴影部分的面积。

(单位:厘米)例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)例3.求图中阴影部分的面积。

(单位:厘米)例4.求阴影部分的面积。

(单位:厘米)例5.求阴影部分的面积。

(单位:厘米)例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？例7.求阴影部分的面积。

(单位:厘米)例8.求阴影部分的面积。

(单位:厘米)例9.求阴影部分的面积。

(单位:厘米)例10.求阴影部分的面积。

(单位:厘米)例11.求阴影部分的面积。

(单位:厘米)例12.求阴影部分的面积。

(单位:厘米)例13.求阴影部分的面积。

(单位:厘米)例14.求阴影部分的面积。

(单位:厘米)例15.已知直角三角形面积是12平方厘米，求阴影部分的面积。

例16.求阴影部分的面积。

(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。

(单位:厘米) 例18.如图，在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。

例19.正方形边长为2厘米，求阴影部分的面积。

例20.如图，正方形ABCD的面积是36平方厘米，求阴影部分的面积。

例21.图中四个圆的半径都是1厘米，求阴影部分的面积。

例22. 如图，正方形边长为8厘米，求阴影部分的面积。

例23.图中的4个圆的圆心是正方形的4个顶点，，它们的公共点是该正方形的中心，如果每个圆的半径都是1厘米，那么阴影部分的面积是多少？例24.如图，有8个半径为1厘米的小圆，用他们的圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心。

2017年小升初复习专题-求阴影部分面积（含答案）目标：巩固小学几何图形计算公式，并通过专题复习，加强学生对于图形面积计算的灵活运用。

1、几何图形计算公式：1)正方形：周长＝边长×4 C=4a 面积=边长×边长S=a×a2)正方体：表面积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长V=a×a×a3)长方形：周长=(长+宽)×2 C=2(a+b) 面积=长×宽S=ab4)长方体：表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh) 体积=长×宽×高V=abh5)三角形：面积=底×高÷2 s=ah÷26)平行四边形：面积=底×高s=ah7)梯形：面积=(上底+下底)×高÷2 s=(a+b)×h÷28)圆形：周长=直径×Π=2×Π×半径C=Πd=2Πr 面积=半径×半径×Π9)圆柱体：侧面积=底面周长×高表面积=侧面积+底面积×2 体积=底面积×高10)圆锥体：体积=底面积×高÷32、面积求解大致分为以下几类：➢从整体图形中减去局部；➢割补法，将不规则图形通过割补，转化成规则图形。

重难点：观察图形的特点，根据图形特点选择合适的方法求解图形的面积。

能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。

例1.求阴影部分的面积。

(单位:厘米) 例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)例3.求图中阴影部分的面积。

(单位:厘米)例4.求阴影部分的面积。

(单位:厘米)例5.求阴影部分的面积。

(单位:厘米) 例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？例7.求阴影部分的面积。

小升初数学阴影面积专题
一、 考点、热点回顾
1、 面积单位：平方厘米（2cm )/平方分米(2dm )/平方米(2m )
2、 基本面积公式：长方形ab S = 正方形2a S =
3、 梯形 2)(÷⨯+=h b a S S=(a+b)h ÷2 菱形 2÷⨯b a
圆2r S π= 扇形 ︒
÷=3602r n S π 二、典型例题
例1：图中阴影部分面积为
例2：如图长方形ABCD 的面积是16平方厘米，三角形ABE 和三角形ADF 的面积分别是
3平方厘米和4平方厘米，则阴影部分的面积为
变式训练：如例2图，长方形ABCD 的面积是35平方厘米，三角形ABE 和三角形ADF 的
面积分别是5平方厘米和7平方厘米，则阴影部分的面积为
例3：计算下列图形的阴影面积
⑴ 已知半圆半径为2cm
⑵
⑶
⑷
⑸图中阴影①比阴影②面积小48平方，AB=40cm，求BC的长。

⑹梯形面积是48平方厘米，阴影部分比空白部分
少12平方厘米，求阴影部分面积。

三、习题练习
1、求第一图和第三图阴影部分面积
4、已知AB=8cm，AD=12cm，三角形ABE和
三角形ADF的面积，各占长方形ABCD的
1/3，求三角形AEF的面积。

（完整版）⼩升初图形阴影部分⾯积教案（包含答案）⼩升初图形阴影部分⾯积（专题）课堂引导：问题:⼤家的⼩学⽣活马上就要结束了，在⼩学中我们学习过哪些⼏何图形呢？知识点回顾：正⽅形的⾯积＝长⽅形的⾯积＝梯形的⾯积＝三⾓形的⾯积＝圆的⾯积＝⼤家想⼀想，我们还有哪些⾯积公式没有想到？扇形的⾯积＝？平⾏四边形的⾯积=？互动环节：我画⼤家猜，怎样计算下列阴影部分的⾯积⽬的：引导学⽣初步掌握阴影部分⾯积的计算⽅法。

三⾓形⾯积涂⾊⾯积=长⽅形⾯积+涂⾊部分⾯积=长⽅形⾯积+半圆⾯积×2圆形⾯积涂⾊部分⾯积=长⽅形⾯积+涂⾊⾯积=外圆⾯积—内圆⾯积涂⾊⾯积=正⽅形⾯积—三⾓形⾯积问题：⼀、序号为1、2、3、6的图形，它们的阴影部分⾯积是怎样计算？⼤家有没有发现什么规律！引导学⽣回答出来：涂⾊部分⾯积是⼏个简单图形⾯积的差2、那么序号为4、5、7的图形，它们的阴影部分的⾯积⼜是怎样计算？根据题意引导学⽣回答：涂⾊部分⾯积是⼏个简单图形⾯积的和经典题型【例题1】：图中两个正⽅形的边长分别是6厘⽶和4厘⽶，求阴影部分的⾯积。

【试⼀试】：1、边长分别为3厘⽶与5厘⽶的两个正⽅形拼在⼀起（如图）。

求阴影部分的⾯积。

、求图形阴影部分⾯积（单位：厘⽶）2【例题s 【分析与解答】：上图中，要求整个图形的⾯积，只要先求出上⾯半圆的⾯积，再求出下⾯正⽅形的⾯积，然后把它们相加就可以了.4÷2=2（⽶）4×4+2×2×3.14÷2=22.28（平⽅厘⽶）【试⼀试】：长⽅形长6厘⽶，宽4厘⽶，求阴影部分的⾯积。

【分析与解答】：上图中，若求阴影部分的⾯积，只需先求出长⽅形⾯积再减去⾥⾯圆的⾯积即可.4÷2=2（⽶）6×4-2×2×3.14＝11.44（平⽅厘⽶）【例题】3、计算如图阴影部分的⾯积．（单位：厘⽶）考点组合图形的⾯积．1526356a ti m e an dA l l t h i n e g o o d f o r s 分析分析图后可知，10厘⽶不仅是半圆的直径，还是长⽅形的长，根据半径等于直径的⼀半，可以算出半圆的半径，也是长⽅形的宽，最后算出长⽅形和半圆的⾯积，⽤长⽅形的⾯积减去半圆的⾯积也就是阴影部分的⾯积．解答解：10÷2=5（厘⽶），长⽅形的⾯积=长×宽=10×5=50（平⽅厘⽶），半圆的⾯积=πr 2÷2=3.14×52÷2=39.25（平⽅厘⽶），阴影部分的⾯积=长⽅形的⾯积﹣半圆的⾯积，=50﹣39.25，=10.75（平⽅厘⽶）；答：阴影部分的⾯积是10.75．4、求如图阴影部分的⾯积．（单位：厘⽶）考点组合图形的⾯积；梯形的⾯积；圆、圆环的⾯积．1526356分析阴影部分的⾯积等于梯形的⾯积减去直径为4厘⽶的半圆的⾯积，利⽤梯形和半圆的⾯积公式代⼊数据即可解答．解答解：（4+6）×4÷2÷2﹣3.14×÷2，=10﹣3.14×4÷2，a ti m b e i n g a r e g o o d f o =10﹣6.28，=3.72（平⽅厘⽶）；答：阴影部分的⾯积是3.72平⽅厘⽶．【试⼀试】：求阴影部分图形的⾯积．（单位：厘⽶）考点组合图形的⾯积．1526356分析求阴影部分的⾯积可⽤梯形⾯积减去圆⾯积的，列式计算即可．解答解：（4+10）×4÷2﹣3.14×42÷4，=28﹣12.56，=15.44（平⽅厘⽶）；答：阴影部分的⾯积是15.44平⽅厘⽶．点评解答此题的⽅法是⽤阴影部分所在的图形（梯形）⾯积减去空⽩图形（扇形）的⾯积，即可列式解答．　【例题】A l l th i n gs in t h e i r b e i n g a r e g o o d f o r 5．求阴影部分的⾯积．单位：厘⽶．考点组合图形的⾯积；三⾓形的周长和⾯积；圆、圆环的⾯积．1526356分析（1）圆环的⾯积等于⼤圆的⾯积减⼩圆的⾯积，⼤圆与⼩圆的直径已知，代⼊圆的⾯积公式，从⽽可以求出阴影部分的⾯积；（2）阴影部分的⾯积=圆的⾯积﹣三⾓形的⾯积，由图可知，此三⾓形是等腰直⾓三⾓形，则斜边上的⾼就等于圆的半径，依据圆的⾯积及三⾓形的⾯积公式即可求得三⾓形和圆的⾯积，从⽽求得阴影部分的⾯积．解答解：（1）阴影部分⾯积：3.14×﹣3.14×，=28.26﹣3.14，=25.12（平⽅厘⽶）；（2）阴影部分的⾯积：3.14×32﹣×（3+3）×3，=28.26﹣9，=19.26（平⽅厘⽶）；答：圆环的⾯积是25.12平⽅厘⽶，阴影部分⾯积是19.26平⽅厘⽶．点评此题主要考查圆和三⾓形的⾯积公式，解答此题的关键是找准圆的半径．h i n g s i n t h e i r b e i n 【试⼀试】：求下图阴影部分的⾯积．（单位：厘⽶）考点组合图形的⾯积．1526356分析先求出半圆的⾯积3.14×（10÷2）2÷2=39.25平⽅厘⽶，再求出空⽩三⾓形的⾯积10×（10÷2）÷2=25平⽅厘⽶，相减即可求解．解答解：3.14×（10÷2）2÷2﹣10×（10÷2）÷2 =39.25﹣25=14.25（平⽅厘⽶）．答：阴影部分的⾯积为14.25平⽅厘⽶．点评考查了组合图形的⾯积，本题阴影部分的⾯积=半圆的⾯积﹣空⽩三⾓形的⾯积．【例题】6、求出如图阴影部分的⾯积：单位：厘⽶．an dAl l th i n g s i n t h e f o r s 考点组合图形的⾯积．1526356专题平⾯图形的认识与计算．分析由题意可知：阴影部分的⾯积=长⽅形的⾯积﹣以4厘⽶为半径的半圆的⾯积，代⼊数据即可求解．解答解：8×4﹣3.14×42÷2，=32﹣25.12，=6.88（平⽅厘⽶）；答：阴影部分的⾯积是6.88平⽅厘⽶．点评解答此题的关键是：弄清楚阴影部分的⾯积可以由哪些图形的⾯积和或差求出．【试⼀试】：如图，求阴影部分的⾯积．（单位：厘⽶）考点组合图形的⾯积．1526356分析根据图形可以看出：阴影部分的⾯积等于正⽅形的⾯积减去4个扇形的⾯积．正⽅形的⾯积等于（10×10）100平⽅厘⽶，4个扇形的⾯积等于半径为（10÷2）5厘⽶atim e an dAl l th i 的圆的⾯积，即：3.14×5×5=78.5（平⽅厘⽶）．解答解：扇形的半径是：10÷2，=5（厘⽶）；10×10﹣3.14×5×5，100﹣78.5，=21.5（平⽅厘⽶）；答：阴影部分的⾯积为21.5平⽅厘⽶．点评解答此题的关键是求4个扇形的⾯积，即半径为5厘⽶的圆的⾯积．【例题】7、求阴影部分⾯积（单位：厘⽶）8、求阴影部分⾯积（单位：厘⽶）【试⼀试】：求阴影部分的⾯积。

小学复习专题-圆与求阴影部分面积目标：通过专题复习，加强学生对于图形面积计算的灵活运用。

并加深对面积和周长概念的理解和区分。

面积求解大致分为以下几类：1、从整体图形中减去局部；2、割补法，将不规则图形通过割补，转化成规则图形。

重难点：观察图形的特点，根据图形特点选择合适的方法求解图形的面积。

能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。

求阴影部分的面积。

(单位:厘米影部分甲比阴影，问：阴影部分甲比乙面积小多少？求举一反三★巩固练习【专1】下图中，大小正方形的边长分别是9厘米和5厘米，求阴影部分的面积。

【专1-1】.右图中，大小正方形的边长分别是12厘米和10厘米。

求阴影部分面积。

【专1-2】. 求右图中阴影部分图形的面积及周长。

【专2】已知右图阴影部分三角形的面积是5平方米，求圆的面积。

【专2-1】已知右图中，圆的直径是2厘米，求阴影部分的面积。

【专2-2】求右图中阴影部分图形的面积及周长。

【专2-3】求下图中阴影部分的面积。

（单位：厘米）【专3】求下图中阴影部分的面积。

【专3-1】求右图中阴影部分的面积。

【专3-2】求右图中阴影部分的面积。

【专3-3】求下图中阴影部分的面积。

这是最基本的方法：×7-=7-π()=16--)=100.48)×圆，÷π()=3.14π×=解：梯形面积减去4-π，÷2=3π-6)×解：πππ］π(1164=36, r=3=2=18,-阴影部分为一个三角形和一个半圆平方π-1×1=:4π-8(=22-面积减去ππ-π-1+(÷小圆面积，其值为：5-π=25-×－（面积为：π-5×: :37.5+π÷4=9π=28.26大圆的面积减去长方形面积再加圆(π)-6×13ππ2=+π4+-圆÷4-举一反三★巩固练习-answer【专1】（5+9）×5÷2+9×9÷2－（5+9）×5÷2=40.5（平方厘米）【专1-1】（10+12）×10÷2+3.14×12×12÷4－（10+12）×10÷2=113.04（平方厘米）【专1-2】面积：6×（6÷2）－3.14×（6÷2）×（6÷2）÷2=3.87（平方厘米）周长：3.14×6÷2+6＋（6÷2）×2=21.42（厘米）【专2】2r×r÷2=5 即r×r=5圆的面积=3.14×5=15.7（平方厘米）【专2-1】3.14×（2÷2）×（2÷2）－2×2÷2=1.14（平方厘米）【专2-2】面积：3.14×6×6÷4－3.14×（6÷2）×（6÷2）÷2=14.13 （平方厘米）周长：2×3.14×6÷4+3.14×6÷2+6=24.84 （厘米）【专2-3】（6+4）×4÷2－（4×4－3.14×4×4÷4）=16.56（平方厘米）【专3】6×3－3×3÷2=13.5（平方厘米）【专3-1】8×（8÷2）÷2=16（平方厘米）【专3-2】3.14×4×4÷4－4×4÷2=4.56（平方厘米）【专3-3】5×5÷2=12.5（平方厘米）。

小学复习专题-圆与求阴影部分面积目标：通过专题复习，加强学生对于图形面积计算的灵活运用。

并加深对面积和周长概念的理解和区分。

面积求解大致分为以下几类：1、从整体图形中减去局部；2、割补法，将不规则图形通过割补，转化成规则图形。

重难点：观察图形的特点，根据图形特点选择合适的方法求解图形的面积。

能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。

求阴影部分的面积。

(单位:厘米影部分甲比阴影，问：阴影部分甲比乙面积小多少？求举一反三★巩固练习【专1】下图中，大小正方形的边长分别是9厘米和5厘米，求阴影部分的面积。

【专1-1】.右图中，大小正方形的边长分别是12厘米和10厘米。

求阴影部分面积。

【专1-2】. 求右图中阴影部分图形的面积及周长。

【专2】已知右图阴影部分三角形的面积是5平方米，求圆的面积。

【专2-1】已知右图中，圆的直径是2厘米，求阴影部分的面积。

【专2-2】求右图中阴影部分图形的面积及周长。

【专2-3】求下图中阴影部分的面积。

（单位：厘米）【专3】求下图中阴影部分的面积。

【专3-1】求右图中阴影部分的面积。

【专3-2】求右图中阴影部分的面积。

【专3-3】求下图中阴影部分的面积。

这是最基本的方法：×7-=7-π()=16--)=100.48)×圆，÷π()=3.14π×=解：梯形面积减去4-π，÷2=3π-6)×解：πππ］π(1164=36, r=3=2=18,-阴影部分为一个三角形和一个半圆平方π-1×1=:4π-8(=22-面积减去ππ-π-1+(÷小圆面积，其值为：5-π=25-×－（面积为：π-5×::阴影部分可补成37.5+π÷4=9π=28.26大圆的面积减去长方形面积再加圆(π)-6×13ππ2=+π4+-圆÷4-举一反三★巩固练习-answer【专1】（5+9）×5÷2+9×9÷2－（5+9）×5÷2=40.5（平方厘米）【专1-1】（10+12）×10÷2+3.14×12×12÷4－（10+12）×10÷2=113.04（平方厘米）【专1-2】面积：6×（6÷2）－3.14×（6÷2）×（6÷2）÷2=3.87（平方厘米）周长：3.14×6÷2+6＋（6÷2）×2=21.42（厘米）【专2】2r×r÷2=5 即r×r=5圆的面积=3.14×5=15.7（平方厘米）【专2-1】3.14×（2÷2）×（2÷2）－2×2÷2=1.14（平方厘米）【专2-2】面积：3.14×6×6÷4－3.14×（6÷2）×（6÷2）÷2=14.13 （平方厘米）周长：2×3.14×6÷4+3.14×6÷2+6=24.84 （厘米）【专2-3】（6+4）×4÷2－（4×4－3.14×4×4÷4）=16.56（平方厘米）【专3】6×3－3×3÷2=13.5（平方厘米）【专3-1】8×（8÷2）÷2=16（平方厘米）【专3-2】3.14×4×4÷4－4×4÷2=4.56（平方厘米）【专3-3】5×5÷2=12.5（平方厘米）。

【史上最全小学求阴影部分面积专题—含答案】小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标：通过专题复习，加强学生对于图形面积计算的灵活运用。

并加深对面积和周长概念的理解和区分。

面积求解大致分为以下几类：1、从整体图形中减去局部；2、割补法，将不规则图形通过割补，转化成规则图形。

重难点：观察图形的特点，根据图形特点选择合适的方法求解图形的面积。

能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。

例1.求阴影部分的面积。

例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)(单位:厘米)例4.求阴影部分的面积。

(单位:厘米)例3.求图中阴影部分的面积。

(单位:厘米)例5.求阴影部分的面积。

(单位:厘米)例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米例7.求阴影部分的面积。

(单位:厘米)例8.求阴影部分的面积。

(单位:厘米)例9.求阴影部分的面积。

(单位:厘米)例10.求阴影部分的面积。

(单位:厘米)例11.求阴影部分的面积。

(单位:厘米)例12.求阴影部分的面积。

(单位:厘米)例13.求阴影部分的面积。

(单位:厘米)例14.求阴影部分的面积。

(单位:厘米)例15.已知直角三角形面积是12平方厘米，求阴影部分的面积。

例16.求阴影部分的面积。

(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。

(单位:厘米) 例18.如图，在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。

例19.正方形边长为2厘米，求阴影部分的面积。

例20.如图，正方形ABCD的面积是36平方厘米，求阴影部分的面积。

例21.图中四个圆的半径都是1厘米，求阴影部分的面积。

例22.如图，正方形边长为8厘米，求阴影部分的面积。

例23.图中的4个圆的圆心是正方形的4个顶点，，它们的公共点是该正方形的中心，如果每个圆的半径都是1厘米，那么阴影部分的面积是多少例24.如图，有8个半径为1厘米的小圆，用他们的圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心。

史上最全小学求阴影部分面积专题—含答案小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标：通过专题复习,加强学生对于图形面积计算的灵活运用;并加深对面积和周长概念的理解和区分;面积求解大致分为以下几类：1、从整体图形中减去局部；2、割补法,将不规则图形通过割补,转化成规则图形;重难点：观察图形的特点,根据图形特点选择合适的方法求解图形的面积;能灵活运用所学过的基本的平面图形的面积求阴影部分的面积;例1.求阴影部分的面积;例2.正方形面积是7平方厘米,求阴影部分的面积;单位:厘米单位:厘米例3.求图中阴影部分的面积;单位:厘米例4.求阴影部分的面积;单位:厘米例5.求阴影部分的面积;单位:厘米例6.如图：已知小圆半径为2厘米,大圆半径是小圆的3倍,问：空白部分甲比乙的面积多多少厘米例7.求阴影部分的面积;单位:厘米例8.求阴影部分的面积;单位:厘米例9.求阴影部分的面积;单位:厘米例10.求阴影部分的面积;单位:厘米例11.求阴影部分的面积;单位:厘米例12.求阴影部分的面积;单位:厘米例13.求阴影部分的面积;单位:厘米例14.求阴影部分的面积;单位:厘米例16.求阴影部分的面积;单位:厘米例15.已知直角三角形面积是12平方厘米,求阴影部分的面积;例17.图中圆的半径为5厘米,求阴影部分的面积;单位:厘米例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长;例19.正方形边长为2厘米,求阴影部分的面积;例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积;例21.图中四个圆的半径都是1厘米,求阴影部分的面积; 例22.如图,正方形边长为8厘米,求阴影部分的面积;例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心;如果圆周π率取,那么花瓣图形的的面积是多少平方厘米例25.如图,四个扇形的半径相等,求阴影部分的面积;单位:厘米例26.如图,等腰直角三角形ABC和四分之一圆DEB,AB=5厘米,BE=2厘米,求图中阴影部分的面积;例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求阴影部分的面积;例28.求阴影部分的面积;单位:厘米例29.图中直角三角形ABC的直角三角形的直角边AB=4厘米,BC=6厘米,扇形BCD所在圆是以B为圆心,半径为BC的圆,∠CBD=,问：阴影部分甲比乙面积小多少例30.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米;求BC的长度;例31.如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部分的面积;例32.如图,大正方形的边长为6厘米,小正方形的边长为4厘米;求阴影部分的面积;例33.求阴影部分的面积;单位:厘米例34.求阴影部分的面积;单位:厘米例35.如图,三角形OAB是等腰三角形,OBC是扇形,OB=5厘米,求阴影部分的面积;完整答案例1解：这是最基本的方法：圆面积减去等腰直角三角形的面积,×-2×1=平方厘米例2解：这也是一种最基本的方法用正方形的面积减去圆的面积;设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为：7-=7-×7=平方厘米例3解：最基本的方法之一;用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积：2×2-π＝平方厘米;例4解：同上,正方形面积减去圆面积, 16-π=16-4π=平方厘米例5解：这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π×2-16=8π-16=平方厘米另外：此题还可以看成是1题中阴影部分的8倍;例6解：两个空白部分面积之差就是两圆面积之差全加上阴影部分π-π=平方厘米注：这和两个圆是否相交、交的情况如何无关例7解：正方形面积可用对角线长×对角线长÷2,求正方形面积为：5×5÷2=所以阴影面积为：π÷=平方厘米注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形例8解：右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为：π=平方厘米例9解：把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为：2×3=6平方厘米例10解：同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米注: 8、9、10三题是简单割、补或平移例11解：这种图形称为环形,可以用两个同心圆的面积差或差的一部分来求;π-π×=×=平方厘米例12.解：三个部分拼成一个半圆面积．π÷２＝平方厘米例13解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半.所以阴影部分面积为：8×8÷2=32平方厘米例14解：梯形面积减去圆面积,4+10×4-π=28-4π=平方厘米 . 例15.分析: 此题比上面的题有一定难度,这是"叶形"的一个半.解: 设三角形的直角边长为r,则=12,=6圆面积为：π÷2=3π;圆内三角形的面积为12÷2=6, 阴影部分面积为：3π-6×=平方厘米例16解：π＋π－π=π116-36=40π=平方厘米例17解：上面的阴影部分以AB为轴翻转后,整个阴影部分成为梯形减去直角三角形,或两个小直角三角形AED、BCD面积和;所以阴影部分面积为：5×5÷2+5×10÷2=平方厘米例18解：阴影部分的周长为三个扇形弧,拼在一起为一个半圆弧,所以圆弧周长为：2××3÷2=厘米例19解：右半部分上面部分逆时针,下面部分顺时针旋转到左半部分,组成一个矩形;所以面积为：1×2=2平方厘米例20解：设小圆半径为r,4=36, r=3,大圆半径为R,=2 =18,将阴影部分通过转动移在一起构成半个圆环,所以面积为:π-÷2=π=平方厘米例21.解：把中间部分分成四等分,分别放在上面圆的四个角上,补成一个正方形,边长为2厘米,所以面积为：2×2=4平方厘米例22解法一: 将左边上面一块移至右边上面,补上空白,则左边为一三角形,右边一个半圆.阴影部分为一个三角形和一个半圆面积之和. π÷2+4×4=8π+16=平方厘米解法二: 补上两个空白为一个完整的圆.所以阴影部分面积为一个圆减去一个叶形,叶形面积为:π÷2-4×4=8π-16所以阴影部分的面积为:π-8π+16=平方厘米例23解：面积为４个圆减去８个叶形,叶形面积为：π-1×1=π-1所以阴影部分的面积为:4π-8π-1=8平方厘米例24分析：连接角上四个小圆的圆心构成一个正方形,各个小圆被切去个圆,这四个部分正好合成３个整圆,而正方形中的空白部分合成两个小圆．解：阴影部分为大正方形面积与一个小圆面积之和．为：4×4+π=平方厘米例25分析：四个空白部分可以拼成一个以２为半径的圆．所以阴影部分的面积为梯形面积减去圆的面积,4×4+7÷2-π=22-4π=平方厘米例26解: 将三角形CEB以B为圆心,逆时针转动90度,到三角形ABD位置,阴影部分成为三角形ACB面积减去个小圆面积,为: 5×5÷2-π÷4=平方厘米例27解: 因为2==4,所以=2 以AC为直径的圆面积减去三角形ABC面积加上弓形AC面积,π-2×2÷4+π÷4-2=π-1+π-1=π-2=平方厘米例28解法一：设AC中点为B,阴影面积为三角形ABD面积加弓形BD的面积,三角形ABD的面积为:5×5÷2=弓形面积为:π÷2-5×5÷2=所以阴影面积为:+=平方厘米解法二：右上面空白部分为小正方形面积减去小圆面积,其值为：5×5-π=25-π阴影面积为三角形ADC减去空白部分面积,为：10×5÷2-25-π=π=平方厘米例29.解: 甲、乙两个部分同补上空白部分的三角形后合成一个扇形BCD,一个成为三角形ABC,此两部分差即为：π×－×4×6＝5π-12=平方厘米例30.解：两部分同补上空白部分后为直角三角形ABC,一个为半圆,设BC长为X,则40X÷2-π÷2=28所以40X-400π=56 则X=厘米例31.解：连PD、PC转换为两个三角形和两个弓形,两三角形面积为：△APD面积+△QPC面积= 5×10+5×5= 例32解：三角形DCE的面积为:×4×10=20平方厘米梯形ABCD的面积为:4+6×4=20平方厘米从而知道它们面积相等,则三角形ADF面积等于三角形EBF面积,阴影部两弓形PC、PD面积为：π-5×5所以阴影部分的面积为：+π-25=平方厘米分可补成圆ABE的面积,其面积为：π÷4=9π=平方厘米例33.解:用大圆的面积减去长方形面积再加上一个以2为半径的圆ABE面积,为π+π-6=×13π-6=平方厘米例34解：两个弓形面积为：π-3×4÷2=π-6 阴影部分为两个半圆面积减去两个弓形面积,结果为π+π-π-6=π4+-+6=6平方厘米例35解：将两个同样的图形拼在一起成为圆减等腰直角三角形π÷4-×5×5÷2=π-÷2=平方厘米。