实验二 根据二叉树的抽象数据类型的定义,使用二叉链表实现一个二叉树
- 格式:doc
- 大小:120.00 KB
- 文档页数:10

数据结构实验报告二叉树数据结构实验报告:二叉树引言:数据结构是计算机科学中的重要基础,它为我们提供了存储和组织数据的方式。
二叉树作为一种常见的数据结构,广泛应用于各个领域。
本次实验旨在通过实践,深入理解二叉树的概念、性质和操作。
一、二叉树的定义与性质1.1 定义二叉树是一种特殊的树结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
二叉树可以为空树,也可以是由根节点和左右子树组成的非空树。
1.2 基本性质(1)每个节点最多有两个子节点;(2)左子树和右子树是有顺序的,不能颠倒;(3)二叉树的子树仍然是二叉树。
二、二叉树的遍历2.1 前序遍历前序遍历是指首先访问根节点,然后按照先左后右的顺序遍历左右子树。
在实际应用中,前序遍历常用于复制一颗二叉树或创建二叉树的副本。
2.2 中序遍历中序遍历是指按照先左后根再右的顺序遍历二叉树。
中序遍历的结果是一个有序序列,因此在二叉搜索树中特别有用。
2.3 后序遍历后序遍历是指按照先左后右再根的顺序遍历二叉树。
后序遍历常用于计算二叉树的表达式或释放二叉树的内存。
三、二叉树的实现与应用3.1 二叉树的存储结构二叉树的存储可以使用链式存储或顺序存储。
链式存储使用节点指针连接各个节点,而顺序存储则使用数组来表示二叉树。
3.2 二叉树的应用(1)二叉搜索树:二叉搜索树是一种特殊的二叉树,它的左子树上的节点都小于根节点,右子树上的节点都大于根节点。
二叉搜索树常用于实现查找、插入和删除等操作。
(2)堆:堆是一种特殊的二叉树,它满足堆序性质。
堆常用于实现优先队列,如操作系统中的进程调度。
(3)哈夫曼树:哈夫曼树是一种带权路径最短的二叉树,常用于数据压缩和编码。
四、实验结果与总结通过本次实验,我成功实现了二叉树的基本操作,包括创建二叉树、遍历二叉树和查找节点等。
在实践中,我进一步理解了二叉树的定义、性质和应用。
二叉树作为一种重要的数据结构,在计算机科学中有着广泛的应用,对于提高算法效率和解决实际问题具有重要意义。

实验报告4班级:数学091 姓名:陈浩学号:200912010220编成实现:二叉树采用二叉链表存储,要求建立一颗二叉树,并输出要求的树状形式与节点编号程序代码如下:#include<stdio.h>#include<stdlib.h>#include<malloc.h>#if 1typedef struct Node{int num;char data;struct Node* LChild;struct Node* RChild;}BiTNode,*BiTree;void CreateBiTree(BiTree *bt){char ch;ch=getchar();if(ch=='.') *bt=NULL;else{*bt=(BiTree)malloc(sizeof(BiTNode));(*bt)->data=ch;CreateBiTree(&((*bt)->LChild));CreateBiTree(&((*bt)->RChild));}}void PostOrder(BiTree root){if(root!=NULL){PostOrder(root->LChild);PostOrder(root->RChild);scanf("%d",&(root->num));}}int PrintTree(BiTree bt,int nLayer,int flag) {int i;if(bt == NULL) return 1;PrintTree( bt->RChild, nLayer+1,flag);for(i=0;i<nLayer;i++)printf(" ");if(flag==1)printf("%c\n",bt->data);elseprintf("%d\n",bt->num);PrintTree( bt->LChild, nLayer+1,flag);return 0;}void main(){void CreateBiTree(BiTree *bt);int PrintTree(BiTree bt,int nLayer,int flag);void PostOrder(BiTree root);BiTree bt=NULL;printf("input the data of the Node:\n");CreateBiTree(&bt);PrintTree( bt,1,1);printf("input the num of the Node:from 1 to n(n is the number of the node):\n");PostOrder(bt);PrintTree( bt,1,0);}#endif运行结果:。

第6章树和二叉树习题解答一、下面是有关二叉树的叙述,请判断正误(每小题1分,共10分)(√)1. 若二叉树用二叉链表作存贮结构,则在n个结点的二叉树链表中只有n—1个非空指针域。
(×)2.二叉树中每个结点的两棵子树的高度差等于1。
(√)3.二叉树中每个结点的两棵子树是有序的。
(×)4.二叉树中每个结点有两棵非空子树或有两棵空子树。
(×)5.二叉树中每个结点的关键字值大于其左非空子树(若存在的话)所有结点的关键字值,且小于其右非空子树(若存在的话)所有结点的关键字值。
(应当是二叉排序树的特点)(×)6.二叉树中所有结点个数是2k-1-1,其中k是树的深度。
(应2i-1)(×)7.二叉树中所有结点,如果不存在非空左子树,则不存在非空右子树。
(×)8.对于一棵非空二叉树,它的根结点作为第一层,则它的第i层上最多能有2i—1个结点。
(应2i-1)(√)9.用二叉链表法(link-rlink)存储包含n个结点的二叉树,结点的2n个指针区域中有n+1个为空指针。
(正确。
用二叉链表存储包含n个结点的二叉树,结点共有2n个链域。
由于二叉树中,除根结点外,每一个结点有且仅有一个双亲,所以只有n-1个结点的链域存放指向非空子女结点的指针,还有n+1个空指针。
)即有后继链接的指针仅n-1个。
(√)10. 〖01年考研题〗具有12个结点的完全二叉树有5个度为2的结点。
最快方法:用叶子数=[n/2]=6,再求n2=n0-1=5二、填空(每空1分,共15分)1.由3个结点所构成的二叉树有5种形态。
2. 【计算机研2000】一棵深度为6的满二叉树有n1+n2=0+ n2= n0-1=31 个分支结点和26-1 =32个叶子。
注:满二叉树没有度为1的结点,所以分支结点数就是二度结点数。
3.一棵具有257个结点的完全二叉树,它的深度为9。
(注:用⎣ log2(n) ⎦+1= ⎣ 8.xx ⎦+1=94.【全国专升本统考题】设一棵完全二叉树有700个结点,则共有350个叶子结点。

#include<iostream>using namespace std;template<class T> struct Binode{T data;Binode<T> *lch;Binode<T> *rch;};template<class T>class Bitree{private:void create(Binode<T>*&R,T data[],int i);void Destroy(Binode<T> *R);public:Binode<T>*root;Bitree(T data[]);Bitree(){};void preorder(Binode<T>*R);void Inorder(Binode<T>*R);void Postorder(Binode<T>*R);void Levelorder(Binode<T>*R);/*void find(T data[]);*/int Depth(Binode<T> *R,int d);void path(Binode<T>* root,char);~Bitree();};template<class T>void Bitree<T>::create(Binode<T>*&R,T data[],int i) {if(data[i-1]!=0){R=new Binode<T>;R->data=data[i-1];R->lch=R->rch=NULL;create(R->lch,data,2*i);create(R->rch,data,2*i+1);}}/*template<class T>void Bitree<T>::find(T data[]) {*/template <class T>Bitree<T>::Bitree(T data[]){create(root,data,1);}template <class T>void Bitree<T>::preorder(Binode<T>*R){if(R!=NULL){cout<<R->data;preorder(R->lch);preorder(R->rch);}}template <class T>void Bitree<T>::Inorder(Binode<T>*R){if(R!=NULL){Inorder(R->lch);cout<<R->data;Inorder(R->rch);}}template <class T>void Bitree<T>::Postorder(Binode<T>*R) {if(R!=NULL){Postorder(R->lch);Postorder(R->rch);cout<<R->data;}}template<class T>void Bitree<T>::Levelorder(Binode<T>*R) {Binode<T>* queue[10000];int f=0,r=0;if(R!=NULL)queue[++r]=R;while(f!=r){Binode<T>*p=queue[++f];cout<<p->data;if(p->lch!=NULL)queue[++r]=p->lch;if(p->rch!=NULL)queue[++r]=p->rch;}}//销毁二叉树template <class T>void Bitree<T>::Destroy(Binode<T> *R){if (R!=NULL) {Destroy(R->lch);Destroy(R->rch);delete R;}}template <class T>Bitree<T>::~Bitree(){Destroy(root);}template <class T>int Bitree<T>::Depth(Binode<T> *R,int d){if (R==NULL) return d;if ((R->lch==NULL) && (R->rch==NULL))return d+1;else{int m = Depth(R->lch,d+1);int n = Depth(R->rch,d+1);return n>m? n:m;}}template<class T>void Bitree<T>::path(Binode<T>* root,char m)//求路径{Binode<T>* stack[10000];Binode<T>*s;int tag[10000];int top=0;s=root;do{while(s!=NULL){top++;stack[top]=s;tag[top]=0;s=s->lch;}if(top> 0){if(tag[top]==1){if(stack[top]->data==m){cout<< "路径: ";for(int i=1;i <=top;i++)cout<<stack[i]->data;break;}top--;}else{s=stack[top];if(top> 0){s=s->rch;tag[top]=1;}}}}while(s!=NULL||top!=0);}void main(){char buf[400]={0};for(int i = 0;i<5;i++)buf[i] = i+65;Bitree<char> ChBiTree(buf);cout<<"前序遍历是"<<endl;ChBiTree.preorder(ChBiTree.root);cout<<endl;cout<<"中序遍历是"<<endl;ChBiTree.Inorder(ChBiTree.root);cout<<endl;cout<<"后序遍历是"<<endl;ChBiTree.Postorder(ChBiTree.root);cout<<endl;cout<<"层序遍历是"<<endl;ChBiTree.Levelorder(ChBiTree.root);cout<<endl;cout<<"此二叉树的深度是"<<ChBiTree.Depth(ChBiTree.root,0)<<endl;ChBiTree.path(ChBiTree.root,buf[4]);}。

二叉树操作设计和实现实验报告一、目的:掌握二叉树的定义、性质及存储方式,各种遍历算法。
二、要求:采用二叉树链表作为存储结构,完成二叉树的建立,先序、中序和后序以及按层次遍历的操作,求所有叶子及结点总数的操作。
三、实验内容:1、分析、理解程序程序的功能是采用二叉树链表存储结构,完成二叉树的建立,先序、中序和后序以及按层次遍历的操作。
如输入二叉树ABD###CE##F##,链表示意图如下:2、添加中序和后序遍历算法//========LNR 中序遍历===============void Inorder(BinTree T){if(T){Inorder(T->lchild);printf("%c",T->data);Inorder(T->rchild);}}//==========LRN 后序遍历============void Postorder(BinTree T){if(T){Postorder(T->lchild);Postorder(T->rchild);printf("%c",T->data);}}3、调试程序,设计一棵二叉树,输入完全二叉树的先序序列,用#代表虚结点(空指针),如ABD###CE##F##,建立二叉树,求出先序、中序和后序以及按层次遍历序列,求所有叶子及结点总数。
(1)输入完全二叉树的先序序列ABD###CE##F##,程序运行结果如下:(2)先序序列:(3)中序序列:(4)后序序列:(5)所有叶子及结点总数:(6)按层次遍历序列:四、源程序代码#include"stdio.h"#include"string.h"#include"stdlib.h"#define Max 20 //结点的最大个数typedef struct node{char data;struct node *lchild,*rchild;}BinTNode; //自定义二叉树的结点类型typedef BinTNode *BinTree; //定义二叉树的指针int NodeNum,leaf; //NodeNum为结点数,leaf为叶子数//==========基于先序遍历算法创建二叉树==============//=====要求输入先序序列,其中加入虚结点"#"以示空指针的位置========== BinTree CreatBinTree(void){BinTree T;char ch;if((ch=getchar())=='#')return(NULL); //读入#,返回空指针else{T=(BinTNode *)malloc(sizeof(BinTNode)); //生成结点T->data=ch;T->lchild=CreatBinTree(); //构造左子树T->rchild=CreatBinTree(); //构造右子树return(T);}}//========NLR 先序遍历=============void Preorder(BinTree T){if(T) {printf("%c",T->data); //访问结点Preorder(T->lchild); //先序遍历左子树Preorder(T->rchild); //先序遍历右子树}}//========LNR 中序遍历===============void Inorder(BinTree T){if(T){Inorder(T->lchild);printf("%c",T->data);Inorder(T->rchild);}}//==========LRN 后序遍历============void Postorder(BinTree T){if(T){Postorder(T->lchild);Postorder(T->rchild);printf("%c",T->data);}}//=====采用后序遍历求二叉树的深度、结点数及叶子数的递归算法======== int TreeDepth(BinTree T){int hl,hr,max;if(T){hl=TreeDepth(T->lchild); //求左深度hr=TreeDepth(T->rchild); //求右深度max=hl>hr? hl:hr; //取左右深度的最大值NodeNum=NodeNum+1; //求结点数if(hl==0&&hr==0) leaf=leaf+1; //若左右深度为0,即为叶子。
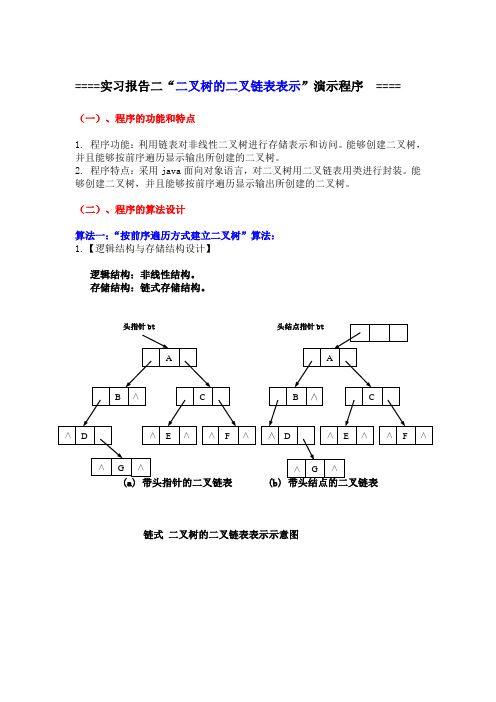
====实习报告二“二叉树的二叉链表表示”演示程序==== (一)、程序的功能和特点1. 程序功能:利用链表对非线性二叉树进行存储表示和访问。
能够创建二叉树,并且能够按前序遍历显示输出所创建的二叉树。
2. 程序特点:采用java面向对象语言,对二叉树用二叉链表用类进行封装。
能够创建二叉树,并且能够按前序遍历显示输出所创建的二叉树。
(二)、程序的算法设计算法一:“按前序遍历方式建立二叉树”算法:1.【逻辑结构与存储结构设计】逻辑结构:非线性结构。
存储结构:链式存储结构。
头指针bt链式二叉树的二叉链表表示示意图2.3.【算法设计】创建二叉链表文字说明:(1).首先按前序输入二叉树。
(2).判断是否是封闭结点的标识,如果不是则创建二叉链表,递归生成其左右子树。
(3).如果是封闭结点标识则结束;(4).插入成功返回二叉链表的头指针。
4.【高级语言代码】//按前序遍历方式建立二叉树public BinTreeNode preOrderCreate ( BinTreeNode p ) {double item=0.0;System.out.println("按照前序遍历次序每次输入一个结点值。
");try { /* 键盘接受一个double数 */BufferedReader br=new BufferedReader(new InputStreamReader(System.in));item=Double.parseDouble(br.readLine());} catch(IOException e){}if ( item != RefValue ) { //读入的不是参照值p=new BinTreeNode(item);p.leftChild=preOrderCreate(p.leftChild); //递归生成左子树p.rightChild=preOrderCreate(p.rightChild); //递归生成右子树//实参是空二叉树,得到返回的子二叉树}else//读入的是参照数p=null; //封闭叶子结点return p; //返回二叉树p}}算法二:“按前序遍历方式输出二叉树”算法:1.【逻辑结构与存储结构设计】逻辑结构:非线性结构。
数据结构实验报告实验名称:实验二——根据二叉树的抽象数据类型的定义,使用二叉链表实现一个二叉树学生姓名:郭江枫班级:2017211125班内序号:10学号:2017210722日期:2018年5月24日1.实验要求根据二叉树的抽象数据类型的定义,使用二叉链表实现一个二叉树基本要求:根据二叉树的抽象数据类型的定义,使用二叉链表实现一个二叉树。
二叉树的基本功能:1、二叉树的建立2、前序遍历二叉树3、中序遍历二叉树4、后序遍历二叉树5、按层序遍历二叉树6、求二叉树的深度7、求指定结点到根的路径8、二叉树的销毁9、其他:自定义操作编写测试main()函数测试线性表的正确性2. 程序分析2.1 存储结构编码表存储结构:二叉树二叉树结点结构:template<class T>struct node//定义结点{T data;//数据node<T>*lch;//左孩子node<T>*rch;//右孩子};2.2 关键算法分析实现该项目需要有如下步骤:步骤一:创建二叉树步骤二:前序遍历步骤三:中序遍历步骤四:后序遍历步骤五:层序遍历步骤六:计算树的深度步骤七:求指定结点到根的路径步骤八:二叉树的销毁步骤一:根据顺序存储结构和性质5,可知如果当前节点的位置为i ,则左孩子位置为2i ,右孩子为2i+1.所以,创建二叉树以顺序存储结构为输入,采用先建立根结点,再建立左右孩子的方法递归建立二叉链表的二叉树。
template<class T>void creat(node<T>*&R, T data[], int i, int n)//创建二叉树{if (i <= n&&data[i - 1])//如果n 个数据没有存储完并且数据不为空{R = new node<T>;//定义一个新结点R->data = data[i - 1];//将第i 个数据赋给R 的datacreat(R->lch, data, 2 * i, n);//递归,建立左子树creat(R->rch, data, 2 * i + 1, n);//递归,建立右子树}else R = NULL;//如果不满足,则为空}步骤二:由二叉树的前序遍历定义,结合递归,写出前序遍历的递归算法。
问题描述利用二叉查找树(BST)实现一个动态查找表基本要求(1)使用二叉树(BST)来实现。
(2)二叉树使用链式结构(二叉链表)实现。
(3)实现BST的构建,查找两个功能。
一需求分析1.输入的形式:输入要存储元素的个数n (正整数),n个元素的值(设为整数)和要查找元素的值;2.输出的形式:输出是否找到(查找成功\不成功)和查找时比较的次数(正整数):3.程序所能达到的功能:要求输入用户设定个元素,再输入要查找的元素,输出是否找到和查找时比较的次数;4.测试数据输入:5//BST的节点数请输入数据:43 54 32 12 57 //五个数据请输入查找数:54 //查找54输岀:查找成功2 //返回成功和查找时比较的次数请输入查找数:12 //查找12输出:查找成功3 //返回成功和查找吋比较的次数请输入查找的数:50 //查找50输出:杏找不成功3 //返回成功和查找时比较的次数二概要设计抽象数据类型的定义BST,二叉查找树,先定义一个二叉树节点,然后实现二叉查找树的功能。
数据对象:整数数据关系:数裾元素属于同一集合,是二叉树,如果对其做屮序遍历呈递增序列基本操作:遍历,二叉树的构建,查找,插入算法的基本思想将输入的BST的元素川插入的方法存进BST巾(由于BST中任何结点的左孩子小于该节点,右孩子大于该节点,所以用递归方法比较插入)。
判断输入要查找的元素是否在BST中(递归比较要查找的元素与当前元素的值的大小,若小于当前值,则查找其左子树;若大于,则查找其右子树),若在,则输出位罝;若不在,则插入到BST中,并输出其位罝程序的流程:程序由三个模块组成:(1)输人模块:输入二叉查找树的元素个数、元素的值,以及要查找的数(2)查找模块:判断该元素是否在二叉查找树中,若未找到,则插入到二叉查找树中。
(3)输出模块:输出是否找到。
若找到,则输出位置;若未找到,则输出插入的位置。
三详细设计(1)物理数据类型因为要实现一个动态杏找表,对一个数进行查找,用线性表实现所用的时间代价比较高,而用二叉查找表来实现的话时间代价显剧较低,故可以构建一个二叉查找树,来实现动态查找。
数据结构实验报告—二叉树数据结构实验报告—二叉树引言二叉树是一种常用的数据结构,它由节点和边构成,每个节点最多有两个子节点。
在本次实验中,我们将对二叉树的基本结构和基本操作进行实现和测试,并深入了解它的特性和应用。
实验目的1. 掌握二叉树的基本概念和特性2. 熟练掌握二叉树的基本操作,包括创建、遍历和查找等3. 了解二叉树在实际应用中的使用场景实验内容1. 二叉树的定义和存储结构:我们将首先学习二叉树的定义,并实现二叉树的存储结构,包括节点的定义和节点指针的表示方法。
2. 二叉树的创建和初始化:我们将实现二叉树的创建和初始化操作,以便后续操作和测试使用。
3. 二叉树的遍历:我们将实现二叉树的前序、中序和后序遍历算法,并测试其正确性和效率。
4. 二叉树的查找:我们将实现二叉树的查找操作,包括查找节点和查找最大值、最小值等。
5. 二叉树的应用:我们将探讨二叉树在实际应用中的使用场景,如哈夫曼编码、二叉搜索树等。
二叉树的定义和存储结构二叉树是一种特殊的树形结构,它的每个节点最多有两个子节点。
节点被表示为一个由数据和指向其左右子节点的指针组成的结构。
二叉树可以分为三类:满二叉树、完全二叉树和非完全二叉树。
二叉树可以用链式存储结构或顺序存储结构表示。
- 链式存储结构:采用节点定义和指针表示法,通过将节点起来形成一个树状结构来表示二叉树。
- 顺序存储结构:采用数组存储节点信息,通过计算节点在数组中的位置来进行访问和操作。
二叉树的创建和初始化二叉树的创建和初始化是二叉树操作中的基础部分。
我们可以通过手动输入或读取外部文件中的数据来创建二叉树。
对于链式存储结构,我们需要自定义节点和指针,并通过节点的方式来构建二叉树。
对于顺序存储结构,我们需要定义数组和索引,通过索引计算来定位节点的位置。
一般来说,初始化一个二叉树可以使用以下步骤:1. 创建树根节点,并赋初值。
2. 创建子节点,并到父节点。
3. 重复步骤2,直到创建完整个二叉树。
⼆叉树的⼆叉链表表⽰与实现前⾯⼏节讲到的结构都是⼀种线性的数据结构,今天要说到另外⼀种数据结构——树,其中⼆叉树最为常⽤。
⼆叉树的特点是每个结点⾄多只有两棵⼦树,且⼆叉树有左右字⼦树之分,次序不能任意颠倒。
⼆叉树的存储结构可以⽤顺序存储和链式存储来存储。
⼆叉树的顺序存储结构由⼀组连续的存储单元依次从上到下,从左到右存储完全⼆叉树的结点元素。
对于⼀般⼆叉树,应将其与完全⼆叉树对应,然后给每个结点从1到i编上号,依次存储在⼤⼩为i-1的数组中。
这种⽅法只适⽤于完全⼆叉树,对⾮完全⼆叉树会浪费较多空间,最坏情况⼀个深度为k的⼆叉树只有k个结点,却需要长度为2的k次⽅减⼀长度的⼀位数组。
事实上,⼆叉树⼀般使⽤链式存储结构,由⼆叉树的定义可知,⼆叉树的结点由⼀个数据元素和分别指向其左右孩⼦的指针构成,即⼆叉树的链表结点中包含3个域,这种结点结构的⼆叉树存储结构称之为⼆叉链表。
⼆叉链表的存储结构typedef struct tnode {elemtype data;struct tnode *lchild;struct tnode *rchild;}*bitree, bitnode;创建⼀棵⼆叉树(按先序序列建⽴)1int create_bitree(bitree *bt)2 {3 elemtype data;45 scanf("%d", &data);6if (0 == data) {7 *bt = NULL;8 } else {9 *bt = (bitree)malloc(sizeof(bitnode));10if (!(*bt))11 exit(OVERFLOW);12 (*bt)->data = data;13 create_bitree(&(*bt)->lchild);14 create_bitree(&(*bt)->rchild);15 }16return OK;17 }View Code按先序次序输⼊⼆叉树的结点值,0表⽰空树。