山西省大同市天镇四中2012年八年级数学上册 第十四章《一次函数》测试题(无答案) 新人教版

一、选择题1、下列函数(1) y=Ji x (2) y=2x-l (3)y=-(A) 4 个 (B) 3 个 (C) 2 个 (D) 1 个2、下面哪个点不在函数y = -2x + 3的图像上（ ）k=-,b = l24、卜列•次磁估随稈（伪fl 诚Wtfl 握（二、填空一次函数练习题(A) y = 3x (C)(D) y = -3x-25、已知一次窗数y=kx+b 的图彖如图所示, 则k, b 的符号是（(A)k>0, b>0(B) k>0, b<0(D) k<0, b<0(A) k = --y b = -\(B) k =2（4）y=2',-3x 中，是一次函数的有（(A) (-5, 13)(B) (0.5, 2)(C) (3, 0)(D) (1, 1)3、直线y 二kx+b 在坐标系屮的位置如图，贝叽 ）（第13题图）(C) (C)kvO, b>0 k=-,b = -\2O(D)10、点P （a, b ）在第二彖限，则直线y=ax+b 不经过第 _________11. 己知一次函数y 二kx-k+4的图彖与y 轴的交点坐标是（0, -2）,那么这个一次函数的表达式6、 7、 则这个止比例函数的表达式是象限。

已知一个正比例函数的图彖经过点（-2, 4）, 若函数y= -2x ni+2是止比例窗数，则m 的值是已知一次函数y=kx+5的图象经过点（-1, 2）,则k= _________已知y 与x 成正比例，且当x = l 时，y = 2,则当x=3时，y=的函数关系的图象是（(A) (B) (C) (D)12、已知点A（-一，a）, B（3, b）在函数y二-3x+4的象上则a与b的人小关系是。

213、地面气温是20°C,如果每升高100m,气温下降6°C,则气温t CO与高度h （m）的函数关系式是__________oV14. 一次函数尸kx+b与y=2x+l平行，且经过点（-3, 4）,则表达式为：_______________ 。

八年级数学《一次函数》测试卷（满分：100分 时间：60分钟）姓名 得分一、选择题（每题3分，共30分）1.过点(2,3)的正比例函数解析式是（ ） A.23y x = ； B.6y x = ； C.21y x =- ； D.32y x = ； 2．直线y ＝－x ＋2和直线y ＝x －2的交点P 的坐标是（ ）A. (2，0)B. (－2，0)C. (0，2)D. (0，－2)3．下列函数中，当x>0时，y 随x 的增大而减小的是（ ）A.x y =B.2+=x yC.2+-=x yD.2x y =4．一次函数y=ax+b 的图像如图所示，则下面结论中正确的是（ ）A ．a ＜0,b ＜0B ．a ＜0,b ＞0C ．a ＞0,b ＞0D ．a ＞0,b ＜05．如图，直线b kx y +=与x 轴交于点(－4 , 0)，则y > 0时，x 的取值范围是( )A ．x >－4B ．x >0C ．x <－4D ．x <0（第4题） （第5题）6．直线 y=43x ＋4与 x 轴交于 A ，与y 轴交于B, O 为原点，则△AOB 的面积为（ ） A ．12 B ．24 C ．6 D ．107．关于正比例函数y=-2x,下列结论正确的是（ ）A ．图像必经过点（-1，-2）B ．图像经过第一、三象限C ．y 随x 的增大而减小 D.不论x 取何值，总有y<08．一次函数y=kx+6，y 随x 的增大而减小，则一次函数的图象不经过（ ）A.第一象限B.第二象限C.第三象限D.第四象限9. 无论m 取任何非零实数,一次函数y=mx-(3m+2)的图象过定点（ ）A 、(3,2)B 、(3,-2)C 、(-3,2)D 、(-3,-2)10．一次函数a x y +=2，b x y +-=的图象都经过A （-2，0），且与y 轴分别交于B 、C 两点，则△ABC 的面积为（ ）A.4B.5C.6D.7二、填空题（每题5分，共20分）x y0 -411．已知一次函数y=kx+5过点P(-1,2),则k= 。

一次函数测试题一、填空1、已知一个正比例函数的图象经过点（-2，4），则这个正比例函数的表达式是。

2、若函数y= -2x m+2 是正比例函数，则m 的值是。

3、已知一次函数y=kx+5 的图象经过点（-1，2），则k= 。

4、已知y 与x 成正比例，且当x＝1 时，y＝2，则当x=3 时，y= 。

5、点P（a，b）在第二象限，则直线y=ax+b 不经过第象限。

6、已知一次函数y=kx-k+4 的图象与y 轴的交点坐标是(0，-2)，那么这个一次函数的表达式是。

17、已知点A(- ，a), B(3，b)在函数y=-3x+4 的象上,则a 与b 的大小关系是2。

8、地面气温是20℃,如果每升高100m,气温下降6℃,则气温t（℃）与高度h（m）的函数关系式是。

9、一次函数y=kx+b 与y=2x+1 平行,且经过点(-3,4),则表达式为：。

10、写出同时具备下列两个条件的一次函数表达式（写出一个即可）。

（1）y 随着x 的增大而减小，（2）图象经过点（1，-3）。

二、选择题111、下列函数（1）y=πx (2)y=2x-1 (3)y=x 函数的有（）(4)y=2-1-3x（A）4 个（B）3 个（C）2 个（D）1 个12、下面哪个点不在函数y =-2x +3 的图像上（）（A）（-5，13）（B）（0.5，2）（C）（3，0）（D）（1，1）13、直线y=kx+b 在坐标系中的位置如图，则( ) （第13 题图）（A）k =-1, b=-12（B）k =-1, b=12（C）k =1, b =-12（D）k =1, b = 1 214、下列一次函数中，随着增大而减小而的是（）（A）y = 3x （B）y = 3x - 2 （C）y = 3 + 2x （D）y =-3x - 215、已知一次函数y=kx+b 的图象如图所示，则k，b 的符号是( )(A) k>0，b>0 (B) k>0，b<0(C) k<0，b>0 (D) k<0，b<0（第 15 题图）16、函数y=(m+1)x-(4m-3)的图象在第一、二、四象限，那么m 的取值范围是( )（A）m <34（B）-1 <m <34（C）m <-1 （D）m >-117、一支蜡烛长20 厘米,点燃后每小时燃烧5 厘米,燃烧时剩下的高度h (厘米) 与燃烧时间t (时)的函数关系的图象是( )(A)(B) （C）（D）18、下图中表示一次函数 y＝mx+n 与正比例函数 y＝m nx(m ，n 是常数，且mn<0)图像的是( )．三、计算题19、已知一个正比例函数和一个一次函数的图象相交于点 A(1，4)，且一次函数的图象与 x 轴交于点 B(3，0)(1)求这两个函数的解析式；(2)画出它们的图象；20、已知y -2 与x 成正比，且当x=1 时，y= -6(1)求y 与x 之间的函数关系式(2)若点(a，2)在这个函数图象上，求a 的值21、已知一次函数y=kx+b 的图象经过点(-1， -5)，且与正比例函数y= 图象相交于点(2，a)，求(1)a 的值(2)k，b 的值(3)这两个函数图象与x 轴所围成的三角形的面积。

八年级数学《一次函数》测试卷班级姓名得分一、填空题（每格 3 分，共 54 分）1、圆的面积公式S= πr 2 中，此中变量是，常量是.2、已知函数关系式为 y=2x － 2，当 x= － 1 时， y 的值为.3、已知函数 y=1.中，自变量 x 的取值范围为x 2414、在函数① y= － 5x+1 ，② y=，③ y=3x 2 ，④ y= x ，⑤ 5+2x 中，是一次函数的有x 2，是正比率函数的有（只要填写序号） .5、若一次函数 y= （ m － 2） x+2 的图象经过点（ -1 ， -4 ），则 m= .6、正比率函数 y=3x 的图象是经过点 A （，3），B （3， ）的一条直线；一次函数 y= － 2x+5 的图象是经过点 C （， 1），D （ 1，）的一条直线 .7、一次函数 y= － x+1 的图象与 x 轴的交点坐标是（，），与 y 轴的交点坐标是（，） .8、一次函数 y=（ 2m － 1 ）x+3 ，y 跟着 x 的增大而增大，则m 的取值范围是9、直线 y=x+1 与直线 y= － x+1 的交点坐标是（ ， ） .10 、一个一次函数的图象经过点（ 1， 2），且 y 跟着 x 的增大而减小，则这个函数的分析式 能够是 （只要写出一个切合条件的函数分析式）.（skm ） 11 、如图：某物体运动的行程 s （ km ）与运动时间 t （ h ）成正比率关系，当 t=2 时，物体运动所经过的行程为 · km ，当 t=7 时，物体5· km. 4运动所经过的行程为 · 3· 2· 1· · · 1 2 3.t （h ）二、选择题（每题 3 分，共 15 分）12 、一次函数 y=x － 2 的图象不经过 --------------------------------------------------------- （）A 、第一象限B 、第二象限C 、第三象限D 、第四象限13 、函数 y 1=－ 5x 、y 2=－2x 、y 3= x的共同点是-----------------------------------------（）2A 、图象位于同样象限B 、y 随 x 的增大而减小C 、y 随 x 的增大而增大D 、图象都经过原点 14 、已知（ x 1， y 1）、（ x 2， y 2 ）、（x 3， y 3）是直线 y=3x － 1 上的三点，若x 1 ＞ x 2 ＞ x 3，则 y 1、 y 2、 y 3 的大小关系是 --------------------------------------------------------------（）A 、 y 3＞y 2＞ y 1B 、 y 1＞ y 2 ＞ y 3C 、 y 1＞y 3＞ y 2D 、 y 3 ＞y 1 ＞ y 215 、若 y=（ k+1 ）x+k 2－ 1 是 x 的正比率函数，则 k 的取值为 -----------------------（）A 、 k=1B 、 k= － 1C 、 k=1 或 k= － 1D 、 k ≠116 、小明饭后出去漫步，从家中走 20 分钟到一个离家900 米的报亭看 10 分钟的报纸后，用 15 分钟返回家里，以下几个图中，能表示小明离家的时间与距离之间的关系的是 -----------------------------------------------------------------------------------------------（ ）y （米）y （米）y （米）y （米）900 900 900 90020 30 45 x （分）20 30 x （分）2045x （分） 0203040x （分）三、解答题17 、（ 6 分）某安装工程队现已安装机器40 台，计划此后每日安装12 台，求：⑴安装机器的总台数y 与天数 x 的函数关系式；⑵一个月后安装机器的台数（以30 天计）18 、（ 6 分）已知 y 是 x 的一次函数，且当x=8 时， y=15 ：当 x= － 10 时， y= － 3，求：⑴这个一次函数的分析式；⑵当 y= － 2 时，求 x 的值；⑶若 x 的取值范围是－ 2 ＜ x＜ 3，求 y 的取值范围 .19 、（ 6 分）一个长方形的周长为18，一边长为xcm ，⑴求它的另一边长y 对于 x 的函数分析式，以及x 的取值范围；⑵若 x 为整数，当x 为什么值时， y 的值最小，最小值是多少？x y320 、（ 6 分）利用函数图象求方程组的解x y1y······· · · · · ·0· · · · · ·x····21 、（ 7 分）右图是某汽车行驶的行程S（ km ）与时间 t（分）的函数关系图，察看图中所提S(km)40供的信息，解答以下问题：⑴汽车在前9 分钟内的均匀速度是km/ 分；⑵汽车在半途停了多长时间？；⑶当 16≤t≤30 时， S 与 t 的函数关系式.129 1630t( 分)拓展题（每题 5 分）1、若直线y=2x+b 与两坐标轴围成的三角形的面积是9 ，则 b=.2、假如一次函数y=mx+1 与 y=nx － 2 的图象订交于x 轴上一点，那么m∶n=.3、已知直线m 与直线 y= － 0.5x+2 平行，且与 y 轴交点的纵坐标为8 ，求直线 m 的分析式 .4、已知一次函数y=kx+b的图象过点（1，2），且与y 轴交于点P，若直线y= － 0.5x+2与y 轴的交点为Q，点Q 与点p 对于x 轴对称，求这个函数分析式.。

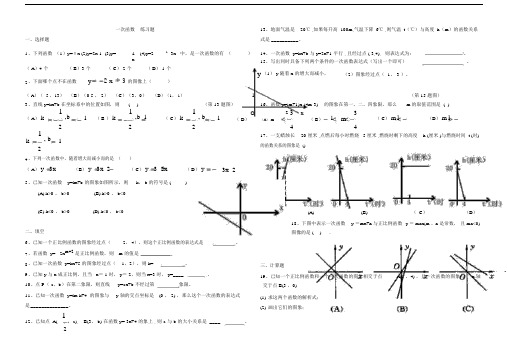
一次函数 练习题13、地面气温是 20℃ ,如果每升高 100m,气温下降 6℃ ,则气温 t （℃）与高度 h （m ）的函数关系 一、选择题式是 __________。

1 、下列函数 （1）y=πx (2)y=2x-1 (3)y=1 (4)y=2 -1-3x 中，是一次函数的有 （）14、一次函数 y=kx+b 与 y=2x+1 平行 , 且经过点 (-3,4), 则表达式为： 。

x15、写出同时具备下列两个条件的一次函数表达式（写出一个即可）。

（ A ）4 个（ B ）3 个 （ C ） 2 个 （ D ） 1 个y （1） y 随着 x 的增大而减小，（2）图象经过点（ 1，-3 ）。

y 2 x 3 的图像上（2 、下面哪个点不在函数）（ A ）（ -5 ，13） （B ）（0.5 ， 2） （C ）（3，0） （D ）（1， 1）1（第 15 题图）3 、直线 y=kx+b 在坐标系中的位置如图，则 ( )（第 13 题图）16、函数 y=(m+1)x-(4m-3) 的图象在第一、二、四象限，那么 m 的取值范围是 ( )（ A ） k1,b1（ B ） k1,b 1（ C ） k1, b1O2 3x1 3 （ C ） m1（D ） m1（ D ）（A ） m（ B ）m22244k1, b1 17、一支蜡烛长20 厘米 ,点燃后每小时燃烧 5 厘米 ,燃烧时剩下的高度 h (厘米 )与燃烧时间 t (时)的函数关系的图象是 ()24 、下列一次函数中，随着增大而减小而的是 （ ）（ A ） y 3x（B ） y 3x 2（ C ） y 3 2x（ D ） y 3x 25 、已知一次函数 y=kx+b 的图象如图所示，则k ， b 的符号是 ()(A) k>0 ， b>0(B) k>0 ， b<0(C) k<0 ， b>0 (D) k<0 ， b<0二、填空6 、已知一个正比例函数的图象经过点（ - 2， 4），则这个正比例函数的表达式是。

一次函数测试题一、填空1、已知一个正比例函数的图象经过点（-2，4），则这个正比例函数的表达式是。

2、若函数y= -2x m+2 是正比例函数，则m 的值是。

3、已知一次函数y=kx+5 的图象经过点（-1，2），则k= 。

4、已知y 与x 成正比例，且当x＝1 时，y＝2，则当x=3 时，y= 。

5、点P（a，b）在第二象限，则直线y=ax+b 不经过第象限。

6、已知一次函数y=kx-k+4 的图象与y 轴的交点坐标是(0，-2)，那么这个一次函数的表达式是。

7、已知点A(- ，a), B(3，b)在函数y=-3x+4 的象上,则a 与b 的大小关系是2。

8、地面气温是20℃,如果每升高100m,气温下降6℃,则气温t（℃）与高度h（m）的函数关系式是。

9、一次函数y=kx+b 与y=2x+1 平行,且经过点(-3,4),则表达式为：。

10、写出同时具备下列两个条件的一次函数表达式（写出一个即可）。

（1）y 随着x 的增大而减小，（2）图象经过点（1，-3）。

二、选择题111、下列函数（1）y=πx (2)y=2x-1 (3)y=x(4)y=2-1-3x（A）4 个（B）3 个（C）2 个（D）1 个12、下面哪个点不在函数y =-2x +3 的图像上（）（A）（-5，13）（B）（0.5，2）（C）（3，0）（D）（1，1）13、直线y=kx+b 在坐标系中的位置如图，则( ) （第13 题图）（A）k =-1, b=-12（B）k =-1, b=12（C）k =1, b =-12（D）k =1, b = 1214、下列一次函数中，随着增大而减小而的是（）（A）y = 3x （B）y = 3x - 2 （C）y = 3 +2x （D）y =-3x - 215、已知一次函数y=kx+b 的图象如图所示，则k，b 的符号是( )(A) k>0，b>0 (B) k>0，b<0(C) k<0，b>0 (D) k<0，b<0（第 15 题图）16、函数y=(m+1)x-(4m-3)的图象在第一、二、四象限，那么m 的取值范围是( ) （A）m <34（B）-1 <m <34（C）m <-1 （D）m>-117、一支蜡烛长20 厘米,点燃后每小时燃烧5 厘米,燃烧时剩下的高度h (厘米)与燃烧时间t (时)的函数关系的图象是( )(A)(B) （C）（D）18、下图中表示一次函数 y＝mx+n 与正比例函数 y＝m nx(m ，n 是常数，且mn<0)图像的是( )．三、计算题19、已知一个正比例函数和一个一次函数的图象相交于点 A(1，4)，且一次函数的图象与 x 轴交于点 B(3，0)(1)求这两个函数的解析式；(2)画出它们的图象；20、已知y -2 与x 成正比，且当x=1 时，y= -6(1)求y 与x 之间的函数关系式(2)若点(a，2)在这个函数图象上，求a 的值21、已知一次函数y=kx+b 的图象经过点(-1， -5)，且与正比例函数y= 图象相交于点(2，a)，求(1)a 的值(2)k，b 的值(3)这两个函数图象与x 轴所围成的三角形的面积。

八年级上册数学一次函数测试题及答案填空题.
（1）点A在y轴右侧,距y轴6个单位长度,距x轴8个单位长度,则A点的坐标是,A点离开原点的距离是.
（2）点（-3,2）,（a,a+1）在函数y=kx-1的图像上,则k=a= （3）正比例函数的图像经过点（-3,5）,则函数的关系式是.
（4）函数y=-5x+2与x轴的交点是,与y轴的交点是,与两坐标轴围成的三角形面积是.
(5）已知y与4x-1成正比例,且当x=3时,y=6,写出y与x的函数关系式.
（6）写出下列函数关系式
①速度60千米的匀速运动中,路程S与时间t的关系
②等腰三角形顶角y与底角x之间的关系
③汽车油箱中原有油100升,汽车每行驶50千米耗油9升,油箱剩余油量y（升）与汽车行驶路程x（千米）之间的关系
④矩形周长30,则面积y与一条边长x之间的关系
在上述各式中,是一次函数,是正比例函数（只填序号）
（7）正比例函数的图像一定经过点.
（8）若点（3,a）在一次函数y=3x+1的图像上,则.
（9）一次函数y=kx-1的图像经过点（-3,0）,则k=.
（10）已知y与2x+1成正比例,且当x=3时,y=6,写出y与x的函数关系式.
（11）函数y=-x+m^2与y=4x-1的图像交于轴,则m=.
答案：
（1）、（6,+8）和（6,-8）、10（2）、-1、-1（3）、y=-x
（4）、(0.4,0)、(0,2)、0.4（5）、y=（4x-1）
（6）、s=60t、y=180-2x、y=100-0.18x、y=x(x-15)、①②③､①
（7）、（0,0）（8）、10（9）、-（10）、y=（2x+1）
（11）、正负。

一次函数 测试题一、填空1、已知一个正比例函数的图象经过点（－2,4),则这个正比例函数的表达式是 。

2、若函数y= -2ｘｍ+２是正比例函数,则m 的值是 。

３、已知一次函数ｙ＝kx+５的图象经过点(-1，２)，则k= 。

4、已知ｙ与x 成正比例，且当x=1时,y ＝2,则当x ＝3时,y=__＿_ 。

5、点P(a ，ｂ）在第二象限,则直线y=ax+ｂ不经过第 象限。

６、已知一次函数ｙ=kx-k+4的图象与y 轴的交点坐标是(０,-２），那么这个一次函数的表达式是____＿__＿＿_＿___。

7、已知点A （-21,a), B(3,ｂ)在函数y=－3ｘ＋4的象上，则a 与b 的大小关系是____ 。

8、地面气温是20℃，如果每升高100m,气温下降6℃,则气温t(℃）与高度h （m ）的函数关系式是＿__＿____＿＿。

9、一次函数y=kx+ｂ与ｙ=2ｘ+1平行,且经过点(-3,４),则表达式为: 。

１０、写出同时具备下列两个条件的一次函数表达式(写出一个即可） 。

(1)y 随着ｘ的增大而减小, （２)图象经过点(1，-３)。

二、选择题1１、下列函数(１）y=πx (２）y=2x-１ (3)ｙ＝错误! (4）y ＝2-1-３x 中,是一次函数的有( ）(A ）4个 （B)3个 （C)2个 （D ）1个12、下面哪个点不在函数32+-=x y 的图像上（ )（A ）（-5,13） (B)(0.5,２） （Ｃ)(3，0) （D ）(1,1） 13、直线y ＝kx+b 在坐标系中的位置如图,则（ ) (第13题图)（A ）1,12k b =-=- （B)1,12k b =-= （Ｃ)1,12k b ==- （D)1,12k b == 14、下列一次函数中,随着增大而减小而的是 （ ）（A ）x y 3= （Ｂ）23-=x y (Ｃ）x y 23+= （D ）23--=x y15、已知一次函数y=kx ＋b 的图象如图所示,则ｋ,b 的符号是( )(Ａ)k＞0，b>0 (Ｂ）k>0，b＜0（C）k<0,b>0 (Ｄ) k<0，b＜0（第１5题图) 16、函数ｙ=(ｍ+1)x-(４m－3)的图象在第一、二、四象限，那么m的取值范围是( )（A）34m< (B)314m-<<（C)1m<- (D)1m>-17、一支蜡烛长2０厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h (厘米)与燃烧时间t (时)的函数关系的图象是( )（A)(Ｂ）（Ｃ)（Ｄ) 1８、下图中表示一次函数y＝mx+n与正比例函数ｙ=m nｘ（ｍ ,n是常数,且mn<０)图像的是( ).三、计算题１9、已知一个正比例函数和一个一次函数的图象相交于点A（1,4)，且一次函数的图象与x 轴交于点Ｂ(3，0)（1)求这两个函数的解析式;(2)画出它们的图象；20、已知ｙ－2与x成正比,且当x＝1时，y= －6。

一次函数 测试题一、填空1、已知一个正比例函数的图象经过点（-2，4），则这个正比例函数的表达式是 。

2、若函数y= -2x m+2是正比例函数，则m 的值是 。

3、已知一次函数y=kx+5的图象经过点（-1，2），则k= 。

4、已知y 与x 成正比例，且当x ＝1时，y ＝2，则当x=3时，y=____ 。

5、点P （a ，b ）在第二象限，则直线y=ax+b 不经过第 象限。

6、已知一次函数y=kx-k+4的图象与y 轴的交点坐标是(0，-2)，那么这个一次函数的表达式是______________。

7、已知点A(-21，a), B(3，b)在函数y=-3x+4的象上,则a 与b 的大小关系是____ 。

8、地面气温是20℃,如果每升高100m,气温下降6℃,则气温t （℃）与高度h （m ）的函数关系式是__________。

9、一次函数y=kx+b 与y=2x+1平行,且经过点(-3,4),则表达式为： 。

10、写出同时具备下列两个条件的一次函数表达式（写出一个即可） 。

（1）y 随着x 的增大而减小， （2）图象经过点（1，-3）。

二、选择题11、下列函数（1）y=πx (2)y=2x-1 (3)y=1x(4)y=2-1-3x 中，是一次函数的有（ ）（A ）4个 （B ）3个 （C ）2个 （D ）1个12、下面哪个点不在函数32+-=x y 的图像上（ ）（A ）（-5，13） （B ）（0.5，2） （C ）（3，0） （D ）（1，1）13、直线y=kx+b 在坐标系中的位置如图，则( ) （第13题图）（A）1,1 2k b=-=-（B）1,1 2k b=-=（C）1,1 2k b==-（D）1,1 2k b== 14、下列一次函数中，随着增大而减小而的是（）（A）xy3=（B）23-=xy（C）xy23+=（D）23--=xy15、已知一次函数y=kx+b的图象如图所示，则k，b的符号是( )(A) k>0，b>0 (B) k>0，b<0(C) k<0，b>0 (D) k<0，b<0（第15题图）16、函数y=(m+1)x-(4m-3)的图象在第一、二、四象限，那么m的取值范围是( )（A）34m<（B）314m-<<（C）1m<-（D）1m>-17、一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h (厘米)与燃烧时间t (时)的函数关系的图象是( )(A) (B) （C）（D）18、下图中表示一次函数y＝mx+n与正比例函数y＝m nx(m ，n是常数，且mn<0)图像的是( )．三、计算题19、已知一个正比例函数和一个一次函数的图象相交于点A(1，4)，且一次函数的图象与x轴交于点B(3，0)(1)求这两个函数的解析式；(2)画出它们的图象；20、已知y -2与x成正比，且当x=1时，y= -6(1)求y与x之间的函数关系式(2)若点(a，2)在这个函数图象上，求a 的值21、已知一次函数y=kx+b的图象经过点(-1， -5)，且与正比例函数y= 12x的图象相交于点(2，a)，求(1)a的值(2)k，b的值(3)这两个函数图象与x轴所围成的三角形的面积。