材料力学-切应力计算(完整资料).doc

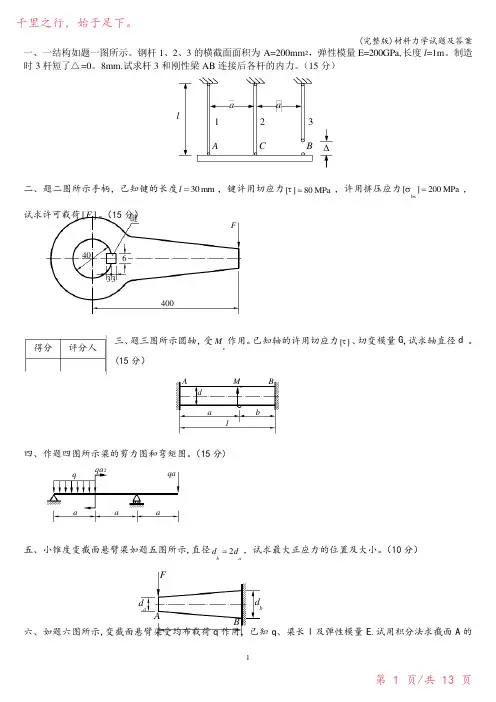
一、一结构如题一图所示。

钢杆1、2、3的横截面面积为A=200mm 2，弹性模量E=200GPa,长度l =1m 。

制造时3杆短了△=0。

8mm.试求杆3和刚性梁AB 连接后各杆的内力。

（15分）aalABC123∆二、题二图所示手柄，已知键的长度30 mm l =，键许用切应力[]80 MPa τ=，许用挤压应力bs[]200 MPa σ=，试求许可载荷][F 。

（15分）三、题三图所示圆轴，受eM 作用。

已知轴的许用切应力[]τ、切变模量G ,试求轴直径d 。

(15分）四、作题四图所示梁的剪力图和弯矩图。

（15分)五、小锥度变截面悬臂梁如题五图所示,直径2bad d =，试求最大正应力的位置及大小。

（10分）六、如题六图所示,变截面悬臂梁受均布载荷q 作用，已知q 、梁长l 及弹性模量E .试用积分法求截面A 的得分评分人F键40633400Aal bM eBd a a aqqaqa 2dbBda AF挠度w A 和截面C 的转角θC .（15分)七、如图所示工字形截面梁AB ,截面的惯性矩672.5610zI -=⨯m 4，求固定端截面翼缘和腹板交界处点a 的主应力和主方向。

（15分）一、（15分)（1）静力分析（如图（a）)1N F2N F3N F图(a)∑=+=231,0N N N yF F F F（a)∑==31,0N N CF F M(b)（2）几何分析（如图（b)）1l∆2l∆3l∆∆图（b）wql /3x lhb 0b (x )b (x )BAC 50kN AB0.75m303030140150zya∆=∆+∆+∆3212l l l(3）物理条件EA l F l N 11=∆，EA l F l N 22=∆，EAl F l N 33=∆ （4）补充方程∆=++EAlF EA l F EA l F N N N 3212 （c） （5）联立（a）、（b）、(c)式解得:kN FkN FF N N N 67.10,33.5231===二、(15分）以手柄和半个键为隔离体，S0, 204000OM F F ∑=⨯-⨯=取半个键为隔离体，bsS20F F F ==由剪切：S []s FA ττ=≤，720 N F = 由挤压:bs bs bs bs[][], 900N FF Aσσ=≤≤取[]720N F =.三、（15分）eABM M M +=0ABϕ=， A B M a M b ⋅=⋅得 e B a M M a b =+, e A b MM a b=+当a b >时 e316π ()[]M ad a b τ≥+；当b a >时 e316π ()[]M bd a b τ≥+。

word格式-可编辑-感谢下载支持材料力学常用公式1.外力偶矩计算公式（P功率，n转速）2.弯矩、剪力和荷载集度之间的关系式3.轴向拉压杆横截面上正应力的计算公式（杆件横截面轴力F N，横截面面积A，拉应力为正）4.轴向拉压杆斜截面上的正应力与切应力计算公式（夹角a 从x轴正方向逆时针转至外法线的方位角为正）5.纵向变形和横向变形（拉伸前试样标距l，拉伸后试样标距l1；拉伸前试样直径d，拉伸后试样直径d1）6.纵向线应变和横向线应变7.泊松比8.胡克定律9.受多个力作用的杆件纵向变形计算公式?10.承受轴向分布力或变截面的杆件，纵向变形计算公式11.轴向拉压杆的强度计算公式12.许用应力，脆性材料，塑性材料13.延伸率14.截面收缩率15.剪切胡克定律（切变模量G，切应变g ）16.拉压弹性模量E、泊松比和切变模量G之间关系式17.圆截面对圆心的极惯性矩（a）实心圆（b）空心圆18.圆轴扭转时横截面上任一点切应力计算公式（扭矩T，所求点到圆心距离r）19.圆截面周边各点处最大切应力计算公式20.扭转截面系数，（a）实心圆（b）空心圆21.薄壁圆管（壁厚δ≤ R0 /10 ，R0为圆管的平均半径）扭转切应力计算公式22.圆轴扭转角与扭矩T、杆长l、扭转刚度GH p的关系式23.同一材料制成的圆轴各段内的扭矩不同或各段的直径不同（如阶梯轴）时或24.等直圆轴强度条件25.塑性材料；脆性材料26.扭转圆轴的刚度条件?或27.受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式,28.平面应力状态下斜截面应力的一般公式,29.平面应力状态的三个主应力,,30.主平面方位的计算公式31.面内最大切应力32.受扭圆轴表面某点的三个主应力，，33.三向应力状态最大与最小正应力,34.三向应力状态最大切应力35.广义胡克定律36.四种强度理论的相当应力37.一种常见的应力状态的强度条件，38.组合图形的形心坐标计算公式，39.任意截面图形对一点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之和的关系式40.截面图形对轴z和轴y的惯性半径? ,41.平行移轴公式（形心轴z c与平行轴z1的距离为a，图形面积为A ）42.纯弯曲梁的正应力计算公式43.横力弯曲最大正应力计算公式44.矩形、圆形、空心圆形的弯曲截面系数? ，，45.几种常见截面的最大弯曲切应力计算公式（为中性轴一侧的横截面对中性轴z的静矩，b为横截面在中性轴处的宽度）46.矩形截面梁最大弯曲切应力发生在中性轴处47.工字形截面梁腹板上的弯曲切应力近似公式48.轧制工字钢梁最大弯曲切应力计算公式49.圆形截面梁最大弯曲切应力发生在中性轴处50.圆环形薄壁截面梁最大弯曲切应力发生在中性轴处51.弯曲正应力强度条件52.几种常见截面梁的弯曲切应力强度条件53.弯曲梁危险点上既有正应力σ又有切应力τ作用时的强度条件或，54.梁的挠曲线近似微分方程55.梁的转角方程56.梁的挠曲线方程?57.轴向荷载与横向均布荷载联合作用时杆件截面底部边缘和顶部边缘处的正应力计算公式58.偏心拉伸（压缩）59.弯扭组合变形时圆截面杆按第三和第四强度理论建立的强度条件表达式，60.圆截面杆横截面上有两个弯矩和同时作用时，合成弯矩为61.圆截面杆横截面上有两个弯矩和同时作用时强度计算公式62.63.弯拉扭或弯压扭组合作用时强度计算公式64.剪切实用计算的强度条件65.挤压实用计算的强度条件66.等截面细长压杆在四种杆端约束情况下的临界力计算公式67.压杆的约束条件：（a）两端铰支μ=l（b）一端固定、一端自由μ=2（c）一端固定、一端铰支μ=0.7（d）两端固定μ=0.568.压杆的长细比或柔度计算公式，69.细长压杆临界应力的欧拉公式70.欧拉公式的适用范围71.压杆稳定性计算的安全系数法72.压杆稳定性计算的折减系数法73.关系需查表求得。

外力偶矩传动轴所受的外力偶矩通常不是直接给出，而是根据轴的转速n 与传递的功率P 来计算。

当功率P 单位为千瓦（kW ），转速为n （r/min ）时，外力偶矩为m).(N 9549e nPM =当功率P 单位为马力（PS ），转速为n （r/min ）时，外力偶矩为m).(N 7024e nPM =2.5.2切应力计算公式横截面上某一点切应力大小为 p pT I ρτ=(3-12) 式中p I 为该截面对圆心的极惯性矩，ρ为欲求的点至圆心的距离。

圆截面周边上的切应力为 max tTW τ=(3-13) 式中p t I W R=称为扭转截面系数，R 为圆截面半径。

2.5.3 切应力公式讨论（1） 切应力公式（3-12）和式（3-13）适用于材料在线弹性范围内、小变形时的等圆截面直杆；对小锥度圆截面直杆以及阶梯形圆轴亦可近似应用，其误差在工程允许范围内。

（2） 极惯性矩p I 和扭转截面系数t W 是截面几何特征量，计算公式见表3-3。

在面积不变情况下，材料离散程度高，其值愈大；反映出轴抵抗扭转破坏和变形的能力愈强。

因此，设计空心轴比实心轴更为合理。

表3-3实心圆 （外径为d ）432p d I π=316t d W π=空心圆 （外径为D ， 内径为d ）44(1)32p D I a π=-d a D=44(1)16t D W a π=-2.5.4强度条件圆轴扭转时，全轴中最大切应力不得超过材料允许极限值，否则将发生破坏。

因此，强度条件为[]max maxt T W ττ⎛⎫=≤⎪⎝⎭ (3-14) 对等圆截面直杆 []maxmaxt T W ττ=≤ （3-15）式中[]τ为材料的许用切应力。

3.1.1中性层的曲率与弯矩的关系1zMEI ρ=(3-16)式中，ρ是变形后梁轴线的曲率半径；E 是材料的弹性模量；E I 是横截面对中性轴Z 轴的惯性矩。

3.1.2横截面上各点弯曲正应力计算公式 ZMy I σ=(3-17) 式中，M 是横截面上的弯矩；Z I 的意义同上；y 是欲求正应力的点到中性轴的距离最大正应力出现在距中性轴最远点处 max max max max z zM My I W σ=∙= （3-18） 式中，max z z I W y =称为抗弯截面系数。

材料力学剪切力计算公式材料力学剪切力计算是在剪切变形时计算所施加的剪切力的过程。

剪切力是指垂直于应力平面施加的力，它会导致物体内部的剪切变形。

在材料力学中，剪切力可以通过剪切应力和剪切区域的面积来计算。

下面将详细介绍材料力学中剪切力的计算公式。

在剪切力计算中，剪切应力是最基本的参数。

剪切应力（τ）是指均匀剪切力对剪切区域的作用，从而产生剪切变形。

剪切应力可以通过所施加的剪切力和剪切区域的面积来计算。

其公式可以写为：τ=F/A公式中，τ表示剪切应力，F表示施加的剪切力，A表示剪切区域的面积。

剪切力的计算依赖于施加的力的类型和材料的性质。

下面将根据不同的情况介绍剪切力的计算公式。

1.剪切力的计算公式-单向剪切当剪切力在单一方向上施加时，剪切力的计算相对简单。

其公式可以写为：F=τ*A公式中，F表示剪切力，τ表示剪切应力，A表示剪切区域的面积。

在实际应用中，可以通过实验测量剪切应力和剪切区域的面积，然后将它们代入计算公式，从而得到剪切力的值。

2.剪切力的计算公式-多向剪切当剪切力在多个方向上施加时，剪切力的计算较为复杂。

在这种情况下，需要考虑不同方向上的剪切应力，然后将其分解为各个方向的剪切力。

剪切力的计算公式可以根据剪切应力的分解来推导。

假设剪切力沿x、y和z方向施加，剪切面分别为xy、yz和zx平面。

利用数学向量的分解规则，可以得到剪切力的三个分量：F_x = τ_xy * A_xy * cos(θ_xy)F_y = τ_yz * A_yz * cos(θ_yz)F_z = τ_zx * A_zx * cos(θ_zx)公式中，Fx、Fy和Fz分别表示沿x、y和z方向的剪切力，τxy、τyz和τzx分别表示剪切面上的剪切应力，Axy、Ayz和Azx分别表示对应剪切面的面积，θxy、θyz和θzx分别表示剪切面与相应方向的夹角。

通过计算这三个分量的和，即可得到总剪切力。

F=√(F_x^2+F_y^2+F_z^2)通过上述计算公式，可以计算在多向剪切应力施加下的剪切力。

材料力学扭转切应力计算公式材料的力学性质是表征其对外力作用的响应能力的重要指标。

扭转切应力是材料在受到扭转力矩作用时所产生的应力。

在许多工程和科学研究中，通过计算和测量扭转切应力可以获得材料的力学性能参数，如剪切模量和剪切强度等。

在材料力学中，扭转切应力计算公式主要有两种形式：切应力公式和剪切应力公式。

1.切应力公式：切应力（Shear Stress）指材料内部产生的由于外力而对于材料内部其中一剖面的剪切应力。

一般情况下，切应力可以采用切应力图形表示。

τ=T/S其中，τ是切应力，T是扭转力矩，S是截面积。

切应力的单位一般是帕斯卡（Pa）或兆帕（MPa）。

在实际应用中，我们常常会遇到不同形状的材料，如圆形、方形、矩形等。

对于这些不同形状的截面，切应力的计算公式也有所不同。

对于圆截面，切应力的计算公式为：τ=T/(π*r^2)对于矩形截面，切应力的计算公式为：τ=T/(b*h)其中，b是矩形截面的宽度，h是矩形截面的高度。

2.剪切应力公式：剪切应力（Shear Strain）是材料在受到剪切力作用时所产生的应变。

在扭转切应力的计算中，剪切应力是切应力的一个重要参数。

剪切应力的计算公式如下：γ=θ*h/l其中，γ是剪切应力，θ是材料的扭转角度，h是扭转试样的高度，l是扭转试样的长度。

剪切应力可以用来计算材料的剪切模量（Shear Modulus），剪切模量可以通过下式计算得到：G=τ/γ其中，G是剪切模量。

综上所述，材料力学扭转切应力计算公式主要有切应力公式和剪切应力公式，通过这些公式可以计算得到材料的扭转切应力、剪切模量等力学性能参数。

这些参数可以用于工程设计和科学研究中，帮助人们了解材料的力学性能和应用范围。

第四章 弹性杆横截面上的切应力分析§4-3梁横力弯曲时横截面上的切应力梁受横弯曲时,虽然横截面上既有正应力 σ,又有切应力 τ。

但一般情况下,切应力对梁的强度与变形的影响属于次要因素,因此对由剪力引起的切应力,不再用变形、物理与静力关系进行推导,而就是在承认正应力公式(6-2)仍然适用的基础上,假定剪应力在横截面上的分布规律,然后根据平衡条件导出剪应力的计算公式。

1.矩形截面梁对于图4-15所示的矩形截面梁,横截面上作用剪力F Q 。

现分析距中性轴z 为y 的横线1aa 上的剪应力分布情况。

根据剪应力成对定理,横线1aa 两端的剪应力必与截面两侧边相切,即与剪力F Q 的方向一致。

由于对称的关系,横线1aa 中点处的剪应力也必与F Q 的方向相同。

根据这三点剪应力的方向,可以设想1aa 线上各点切应力的方向皆平行于剪力F Q 。

又因截面高度h 大于宽度b,切应力的数值沿横线1aa 不可能有太大变化,可以认为就是均匀分布的。

基于上述分析,可作如下假设:1)横截面上任一点处的切应力方向均平行于剪hj 力F Q 。

2)切应力沿截面宽度均匀分布。

基于上述假定得到的解,与精确解相比有足够的精确度。

从图4-16a 的横弯梁中截出dx 微段,其左右截面上的内力如图4-16b 所示。

梁的横截面尺寸如图4-16c 所示,现欲求距中性轴z 为y 的横线1aa 处的切应力 τ。

过1aa 用平行于中性层的纵截面11cc aa 自dx 微段中截出一微块(图4-16d)。

根据切应力成对定理,微块的纵截面上存在均匀分布的剪应力 τ'。

微块左右侧面上正应力的合力分别为1N 与2N ,其中图4-16图4-15*1I 1**z z A z A S I M dA I My dA N ===⎰⎰σ (4-29) *1II 2)()(**z z Az A S I dM M dA I y dM M dA N +=+==⎰⎰σ (4-30) 式中,*A 为微块的侧面面积,)(II I σσ为面积*A 中距中性轴为 1y 处的正应力,⎰=*1*A z dA y S 。

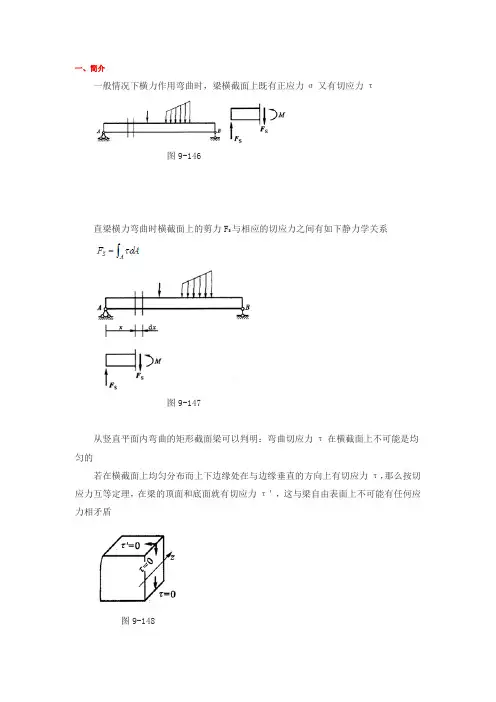
一、简介一般情况下横力作用弯曲时，梁横截面上既有正应力σ又有切应力τ图9-146直梁横力弯曲时横截面上的剪力F S与相应的切应力之间有如下静力学关系图9-147从竖直平面内弯曲的矩形截面梁可以判明：弯曲切应力τ在横截面上不可能是均匀的若在横截面上均匀分布而上下边缘处在与边缘垂直的方向上有切应力τ，那么按切应力互等定理，在梁的顶面和底面就有切应力τ＇，这与梁自由表面上不可能有任何应力相矛盾图9-148至于不在横截面上下边缘处的切应力τ，因为与之互等的切应力τ＇在梁的纵截面上，它作为纵截面上切向分布内力的集度，当然可以存在图9-149事实上，木梁横力弯曲时的剪切破坏就发生在纵截面上(木材的顺纹抗剪强度远低于横纹抗剪抗度)直梁弯曲切应力的分析也是从分析与中性层平行的纵截面上的切应力τ＇入手的 一般情况下，梁的强度由正应力控制，但有些情况下必须考虑切应力的影响，并按切应力进行强度校核例如在截面上有较大剪力F s作用而弯矩较小，梁的跨度短而截面较高，组合截面梁的腹板较薄等情况下都必须考虑切应力二、几个具体截面的切应力计算设梁的横截面为矩形，b为宽度，h为高度，且h＞b，F s为横截面剪力图9-150对切应力分布做如下假设1)横截面上任一点切应力方向均与剪力F s平行2)距中性轴相等远处切应力大小相等求：横截面上任一点的切应力剪应力公式F s为横截面上的剪力I z为横截面对中性轴y的惯性矩b为横截面的宽度为切应力所在y处横线以外部分横截面面积对中性轴的静矩 横截面面积对中性轴的静矩为图9-151将静矩代入切应力计算公式得矩形横截面上切应力τ矩形截面高度(y轴)按2次抛物线规律变化图9-152在横截面上下边缘处τ=0；在中性轴上y＝0处τ有最大值在y＝0处将代入矩形截面切应力计算公式中，得故矩形截面梁横截面上最大切应力为平均切应力的1.5倍其他几种形状截面梁的截面切应力均在中性轴上达到最大值，其分别为工字形图9-153圆形薄壁圆环图9-154三、切应力强度条件弯曲切应力强度条件是。